Abstract
Background: Dynamic multiobjective optimization problems (DMOPs) involve multiple conflicting and time-varying objectives, and dynamic multiobjective algorithms (DMOAs) aim to find Pareto optima that are closer to the real one in the new environment as soon as possible. In particular, the introduction of transfer learning in DMOAs has led to good results in solving DMOPs. However, the selection of valuable historical knowledge and the mitigation of negative transfer remain important problems in existing transfer learning-based DMOAs. Method: A DMOA based on multi-environment knowledge selection and transfer (MST-DMOA) is proposed in this article. First, by clustering historical Pareto optima, some representative solutions that can reflect the main evolutionary information are selected as knowledge of the environment. Second, the similarity between the historical and current environments is evaluated, and then the knowledge of multiple similar environments is selected as valuable historical knowledge to construct the source domain. Third, solutions with high quality in the new environment are obtained to form the target domain, which can better help historical knowledge to adapt to the current environment, thus effectively alleviating negative transfer. Conclusions: We compare the proposed MST-DMOA with five state-of-the-art DMOAs on fourteen benchmark test problems, and the experimental results verify the excellent performance of MST-DMOA in solving DMOPs.
1. Introduction
Dynamic multiobjective optimization problems (DMOPs) aim to optimize multiple conflicting objectives simultaneously when the objective functions or constraints dynamically change over time [1]. A typical real-life scenario is a hybrid renewable energy system, which ensures a continuous energy supply during weather and seasonal variations [2]. In a dynamic environment, this system framework needs to integrate various process and energy units in order to maximize the system’s reliability, while minimizing the system’s cost and emissions.
In recent decades, dynamic multiobjective optimization algorithms (DMOAs) have become the mainstream methods when handling DMOPs. In particular, the embedding of transfer learning techniques into evolutionary algorithms has attracted widespread attention and has been proven to have the potential to solve different types of DMOPs [3]. Although the objective function dynamically changes in various environments, the characteristics of the problem still have a certain degree of correlation. Thus, transfer learning-based DMOAs combine the advantages of both memory and prediction mechanisms, using some optimal solutions or search experience obtained from historical environments as the source domain to accelerate the convergence of the initial solutions in a new environment.
It is worth noting that the source domain is a key factor in transfer learning, as it contains useful knowledge to assist the target domain in learning [4]. The quality of the knowledge in the source domain largely determines the effectiveness of transfer learning-based DMOAs. Jiang et al. [3] proposed a transfer learning framework for DMOAs that uses transfer component analysis to exploit useful knowledge from previous environments, effectively tracking changing Pareto fronts and accelerating convergence. In addition, the combination of sample geodesic flow-based transfer learning and a memory mechanism [5] aims to utilize historical information to obtain a new initial population. However, using the estimator to filter out high-quality solutions from all nondominated solutions obtained in the historical environment requires a long time. The knowledge-guided transfer strategy-based DMOA [6] re-evaluates the central and extreme solutions of historical environments to find the most similar environment for transfer learning. The multi-strategy adaptive selection-based DMOA [7] adaptively constructs the source domain according to the fitness values and diversity fluctuations of Pareto-optimal solutions (POSs), and the knee point-based transfer learning method [8] selects knee points from the last environment to be integrated with the imbalanced transfer learning technique. However, when selecting only one environment as the source of knowledge in the source domain, we ignore the roles of other environments, which also contain important historical information. Therefore, the question of how to obtain sufficient information from historical environments and represent it concisely and adequately as the knowledge of the source domain is the first problem for transfer learning-based DMOAs. Furthermore, positive knowledge transfer is beneficial for problem solving [9], but reducing negative transfer and finding more effective transfer solutions still pose certain difficulties [10]. When the training and testing samples are extremely different, knowledge transfer may lead to incorrect search directions, resulting in poor performance [4]. Thus, the question of how to select high-quality solutions to form the target domain and guide the positive transfer of knowledge is the second problem faced by transfer learning-based DMOA.
In order to overcome the problems in the above methods, a multi-environment knowledge selection and transfer-based DMOA (MST-DMOA) is proposed in this article. The focus of MST-DMOA is to acquire historical knowledge and transfer it to the current environment, in order to generate initial populations with high quality under dynamic environments. Specifically, we perform the adaptive clustering of the POSs in each environment by the density-based spatial clustering of applications with noise (DBSCAN), and we then use the centroid of each cluster to select the nearest POS. The POSs filtered through clustering can effectively represent the main evolutionary information in each environment while saving storage space; this is considered as the knowledge of the environment. When the environment changes, these POSs are used to evaluate the similarity between the historical environments and the current environment, and we then construct the source domain with knowledge from similar environments. In addition, some high-quality solutions are obtained from the new environment to construct the target domain, which can help the historical knowledge to adapt to the current environment and effectively alleviate negative transfer.
The remainder of this article is organized as follows. Section 2 describes some related work. The details of the proposed MST-DMOA are provided in Section 3. Section 4 compares MST-DMOA with five state-of-the-art algorithms. Finally, Section 5 presents a summary of this article and outlines future work.
2. Related Work
2.1. Dynamic Multiobjective Optimization Problems
The basic characteristic of DMOPs is the presence of multiple conflicting optimization objectives that change over time. Without loss of generality, the general form of DMOPs is defined as
where represents a D-dimensional decision vector in decision space . t is the time variable, is the ith objective function and m is the number of objectives. Based on the above formulation, some definitions are provided as follows.
Definition 1
(Dynamic Pareto Domination). At time t, suppose that decision vector is regarded to dominate , represented by , only in conditions of
Definition 2
(Dynamic Pareto-Optimal Set). Denote PS(t) as a dynamic Pareto-optimal set at time t, which consists of all solutions that are not dominated by any other decision vectors at time t, i.e.,
Definition 3
(Dynamic Pareto-Optimal Front). At time t, a dynamic Pareto-optimal front, represented by POF(t), is the objective vector of PS(t).
2.2. Dynamic Multiobjective Optimization Algorithms
Most existing DMOAs can be classified into the following categories: diversity-based, memory-based and prediction-based algorithms.
Diversity-based DMOAs introduce diversified solutions into the new population once the environment changes, with the aim of avoiding the algorithm becoming trapped in local optima. Deb et al. [11] proposed the dynamic NSGA-II, which replaces the individuals in a population with random or mutated individuals during environmental changes to increase the diversity. The change response strategy [12] reuses a portion of the old solutions in combination with randomly generated solutions to reinitialize the population. Ma et al. [13] introduced a multiregional co-evolutionary algorithm to improve the population diversity by designing a multiregional diversity maintenance mechanism. Hu et al. [1] utilized gap-filling technology to maintain diversity in the population search process. It is worth noting that introducing diversity can lead to the loss of some useful historical information, and there is an imbalance between diversity and convergence.
Memory-based DMOAs store useful information from previous environments and reuse it when an environmental change appears. Chen et al. [14] implemented a dynamic two-archive evolutionary algorithm that maintains two co-evolving populations simultaneously. These two populations complement each other, with one focusing on convergence and the other on diversity. The explicit memory [15] stores all nondominated solutions during the evolution process and provides reusable solutions for similar emerging environments. Xu et al. proposed a memory-enhanced DMOA based on decomposition [16], which stores the POSs from various historical environments in an archive. When an environmental change occurs, the most suitable POSs are retrieved from the archive to construct the initial population. Memory-based DMOAs perform well when dealing with periodic changes in DMOPs. However, when faced with random changes or nonlinear variation problems, the stored historical information may not adapt to the new environment and can even mislead the population search.
Prediction-based DMOAs excavate useful historical information and anticipate a high-quality population in a new environment using a prediction model. MOEA/D-SVR [17] maps the solutions into a high-dimensional space to find nonlinear relationships among different environments and constructs the predictor with support vector regression (SVR). The inverse Gaussian process model [18] explores the patterns of environmental change in an objective space and then evaluates the position of the POS through reverse mapping. When a change is detected, the population prediction strategy [19] uses the center points obtained from the previous environments to predict the next center point and uses the previous manifolds to estimate the next manifold. Muruganantham et al.[20] utilized a Kalman filter to guide the search for the locations of new POSs to generate an initial population after an environmental change. However, the solutions in different environments are non-independently identically distributed (non-IID) [21], and the above methods may not produce satisfactory results in these types of DMOPs.
2.3. Transfer Learning
Transfer learning aims to use knowledge gained from previous tasks to help to solve different but related problems [7]. Based on [4], a domain consists of two parts: a feature space and a marginal probability distribution , which can be denoted by , . A task can be described as , where is the label space, and the predictive function can be learned from data to predict the corresponding label for a new instance.
According to the different situations between the source and target domains and tasks, transfer learning is divided into three categories: inductive transfer learning, transformational transfer learning and unsupervised transfer learning. In inductive transfer learning, regardless of whether the source domain and the target domain are the same, the target task is different from the source task. Some labeled data in the target domain are required to induce the objective prediction model used in the target domain. In transductive transfer learning, the source and target tasks are the same, while the source and target domains are different. In this case, there are no available labeled data in the target domain, while a large number of labeled data can be used in the source domain. Finally, in unsupervised transfer learning, the target task is different from but related to the source task. In this scenario, all samples in both the source and target domains are not labeled.
3. Proposed MST-DMOA
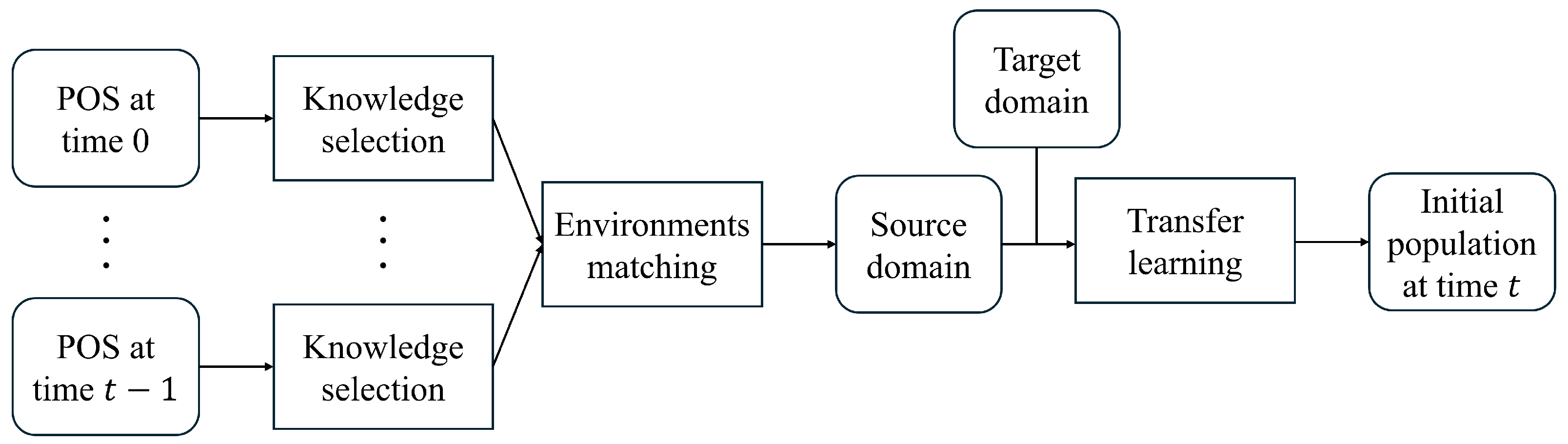
The details of the proposed MST-DMOA are elaborated in this section and the framework of MST-DMOA is shown in Algorithm 1; the associated symbols used in the pseudocode are provided in Table 1. Briefly, some POSs are selected as knowledge via a clustering method, which can represent the valuable information of the environment. Then, we evaluate the similarity between the historical and current environments and construct a source domain with rich historical knowledge. In addition, some solutions in the new environment are generated as the target domain, which can guide the positive transfer of knowledge. Transfer learning aligns the distribution of the source and target domains so that historical knowledge can be adapted to the current environment. Finally, the initial population can be obtained by the solutions in the source domain, which can help any population-based multiobjective optimization algorithm to rapidly find the POS of the optimization problem. Figure 1 depicts the workflow of MST-DMOA.
| Algorithm 1 Framework of MST-DMOA |
|

Table 1.
Descriptions of symbols.
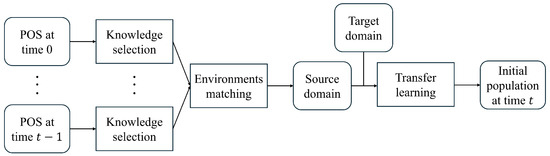
Figure 1.
Workflow of MST-DMOA.
3.1. Knowledge Selection
To detect changes in the environment, the POSs obtained from the last environment are re-evaluated under the current environment. We determine whether the environment has changed by calculating the average Euclidean distance between the POSs’ last and current objective values. When the difference is less than , the POSs obtained from the last environment significantly approximate the true POSs under the current environment and can be directly transferred into an initial population in the current environment. Otherwise, it is considered that the environment has changed.
In a DMOP, historical POSs may provide valuable guidance for the exploration of a future environment [14,16], making them suitable to be represented as the knowledge of environments. However, storing all POSs will consume a large amount of storage space and computational resources, while insufficient POSs may result in the loss of critical information.
As a density-based clustering algorithm, DBSCN does not require assumptions about the number and shape of clusters, but classifies high-density continuous regions into a cluster [22]. The introduction of clustering with DBSCAN can reserve the historical information of most POSs, which is an important evolutionary characteristic, and this can be represented as knowledge of the environment. There are two parameters that need to be fixed in DBSCAN: the neighborhood radius r and the minimal number of solutions for a dense region. They can be automatically determined according to [23]. Let a region with a radius of r centered at a solution be a dense region, and it contains at least solutions. For each solution, an r-neighborhood can be defined:
where equals the set of solutions in a circle with radius r centered on x. If , then x is seen as the core solution, and the core solution x is directly density-reachable from solutions in . The process of clustering starts with a core solution and recursively adds all directly density-reachable solutions to the same cluster.
Finally, the environmental POSs will be adaptively clustered into n clusters by DBSCAN. Based on the centroid of each cluster used to find the nearest POS, all selected POSs () are represented as knowledge of this environment.
3.2. Environment Matching
Transfer learning explores the potential correlations between changing environments [24,25] and reuses past experiences to solve new tasks. Therefore, knowledge obtained from similar environments is more conducive to providing valuable guidance for evolution in the current environment. The question of how to match historical environments that are similar to the current environment and select the appropriate knowledge to construct the source domain is key to achieving efficient knowledge transfer in transfer learning-based DMOAs.
When two environments in DMOPs are similar, the corresponding POSs and POFs are also similar to each other [16]. Through this assumption, it is possible to find historical environments that are similar to the current environment and construct source domains with valuable historical information. Compared to selecting only the most similar historical environment, as in [6], MST-DMOA selects knowledge from multiple historical environments, expanding the sources of knowledge in the source domain. Multiple environments contain richer potential valuable information compared to a single environment, and this information may be complementary, serving to enhance the generalization performance of population prediction [26,27].
Once a new environment occurs, we re-evaluate the knowledge () of each historical environment in the current environment. By calculating the average Euclidean distance between the historical and current objective values of , the similarity between the historical and current environments can be obtained.
where n is the number of POSs selected as knowledge. Let be the ith representative POS in the kth historical environment, and is its objective value. After re-evaluating under the current environment, its new objective values can be obtained. denotes the Euclidean distance between the historical and current objective values. Re-evaluating instead of all POSs in the new environment can reduce the computational costs while retaining sufficient historical information. Obviously, a smaller average Euclidean distance means greater similarity between the two environments. Therefore, using in similar environments to construct the source domain is conducive to providing candidate solutions that are close to the real POSs in the current environment, and the details are displayed in Algorithm 2.
3.3. Target Domain Construction
To reduce the occurrence of negative transfer, selecting high-quality solutions in the new environment to construct the target domain can effectively guide the knowledge transfer process. Although DMOPs are dynamically changing, there are some dynamic characteristics of two consecutive environments that may exhibit potential correlations [28]. Therefore, the Pareto optima of the previous environment are evolved via a static multiobjective optimization algorithm (SMOA) to obtain the new population in the current environment. In addition, we randomly generate a population of size N and combine it with to obtain P with 2N solutions, which is the source of the solutions in the target domain. Then, we utilize nondominated sorting to rank all solutions in P into l layers and select N solutions from the layers with the best Pareto-based ranks to construct the target domain. This process is presented in Algorithm 3.
| Algorithm 2 Environment Matching |
|
| Algorithm 3 Target Domain Construction |
|
3.4. Transfer Learning
Referring to the different forms of transfer learning, most transfer learning-based DMOAs can be considered transductive learning with a consistent task, i.e., minimizing the objective functions. Some POSs that have already converged in historical environments are represented as knowledge in the source domain, and their labels (nondominated relationships) are available. However, when the environment changes, the nondominated relationships between the solutions in the source domain may change due to differences in the distribution of the POSs between different environments, resulting in the unavailability of label information in the target domain. Transfer learning can mine the associations between the search spaces in the historical and current environments and align the distributions of the POSs in the different environments, thus adapting the historical knowledge to the current environment.
As a domain adaptation method in transfer learning, subspace distribution alignment between infinite subspaces (SDA-IS) [29] constructs a geodesic flow path from the source domain subspace to the target domain subspace, and it aligns the distribution between such infinite subspaces on the geodesic flow path. After obtaining the source domain and the target domain, principal component analysis (PCA) [30] is used to extract their feature vectors as corresponding subspaces, denoted as and , respectively. Nondominated solutions can be seen as ()-dimensional segmented manifolds [31], where m is the number of objectives; thus, the subspace dimension d is set to . Therefore, the mapping matrix can be expressed as
where is the orthogonal complement of , and and are orthogonal matrices of and by singular value decomposition. are diagonal matrices based on the principal angle of and , and the diagonal elements of are , and , and . In addition, , where and are the mapping solutions of the source and target domains.
The purpose of transfer learning is to align the distribution of the source and target domains so that historical knowledge can better adapt to the current environment. After calculation through the mapping matrix, the solutions in the source domain can form an initial population in the new environment to accelerate the convergence, as shown in Algorithm 4.
| Algorithm 4 Transfer Learning |
|
3.5. Computational Complexity
The computational cost of MST-DMOA consists of four main operations, namely environmental change detection, source domain construction, target domain construction and transfer learning. Environmental change detection re-evaluates all solutions in the population, which costs . To construct the source domain, we utilize DBSCAN to select knowledge and match the similarity of the environments using and , respectively, where n denotes the number of selected solutions for knowledge representation and T denotes the number of historical environments. In addition, we consider the target domain construction costs and transfer learning costs ). Due to , the overall computational complexity of MST-DMOA is .
4. Experiments
4.1. Benchmark Functions and Performance Metrics
To comprehensively evaluate the proposed MST-DMOA, we adopt benchmark functions DF1-DF14 from the CEC 2018 dynamic multiobjective optimization benchmark test suite [32] in the experiments. Unlike other problem suites representing only one or several aspects of simple scenes, DF’s 14 benchmark functions cover diverse properties and represent a variety of real-world scenarios well. These include time-dependent POF/PS geometries, irregular POF shapes, disconnectivity, knee regions/points, long tails and so on. Therefore, the DF test suite can be used to effectively verify the performance of algorithms to solve various problems.
As a performance metric that reflects both diversity and convergence, the inverted generational distance (IGD) measures the average distance between the obtained POF and the corresponding real POF as follows:
where and are the real POF and the POF obtained by a DMOA at time t, respectively. is the minimum Euclidean distance between x and the individuals in , and is the cardinality of .
The mean inverted generational distance (MIGD) is a variant of the IGD and is defined as the average of the IGD values over the number of environmental changes:
where T is a set of discrete time points and is the number of environmental changes in a run. A smaller MIGD value indicates that the DMOA has better performance in terms of diversity and convergence.
4.2. Compared Algorithms and Experimental Settings
In order to verify the performance of the proposed MST-DMOA, five popular DMOAs are selected to be compared, namely KT-DMOA [8], KTS-DMOA [6], Tr-DMOA [3], SVR-DMOA [17] and KF-DMOA [20]. Among them, KT-DMOA, KTS-DMOA and Tr-DMOA are currently popular transfer learning-based DMOAs, while SVR-DMOA and KF-DMOA are classical prediction-based DMOAs. These algorithms are of a similar type to our method and have good effects in handling DMOPs. By comparing it with them, the performance of MST-DMOA can be objectively demonstrated. For a fair comparison, the specific parameters of these algorithms are set according to the original references, and all testing methods include MOEA/D [33] as the static MOEA optimizer.
The time variable t of DF1-DF14 is depicted as , where and are the severity and frequency of environmental changes, respectively, and denotes the maximum iteration counter. A low implies a severely changing environment and a low denotes a rapidly changing environment. For all benchmarks, there are three groups of environmental parameters adopted, [3], and the total number of generations is fixed to to ensure that there are 50 environmental changes in each run. In addition, the dimension of the search space is set to 10, and the population size N is fixed at 100 for bi-objective problems or 105 for three-objective problems [34]. Therefore, the stopping condition in Algorithm 1 is that all evaluations are exhausted, and the total the number of evaluations is .
4.3. Comparisons with Other DMOAs
In this section, the proposed MST-DMOA is compared with five other advanced DMOAs. The MIGD values of the six algorithms on 14 benchmarks are reported in Table 2, where the best MIGD value for each instance of the test problems is highlighted in bold. The Wilcoxon rank-sum test [35] is performed with a 0.05 significance level to ensure the statistical significance of the differences between MST-DMOA and the other algorithms. In addition, (+), (−) and (=) in Table 2 indicate that the performance of MST-DMOA is better than, worse than or similar to that of the corresponding competitor, respectively.

Table 2.
MIGD Values of six algorithms on fourteen DF problems under various test settings.
As can be observed from Table 2, MST-DMOA achieves the best performance on 32 out of 42 test instances in terms of the MIGD. More precisely, MST-DMOA performs better than all competitors on all three test instances of DF1, DF2, DF3, DF4, DF5, DF7, DF10 and DF14. Moreover, we can see that MST-DMOA is slightly inefficient on one instance of DF9, DF11 and DF12, but this still indicates the competitive performance of our method in solving dynamic problems.
MST-DMOA is slightly inferior to the compared algorithms on DF6; this problem has been recognized as a challenge due to its knee regions/points and long tails [32]. Some edge solutions may be considered noise and ignored by DBSCAN, but they represent valuable information about the environment, thus affecting the correct transfer learning of historical knowledge. As a result, the performance of MST-DMOA will be slightly reduced. It is worth noting that KT-DMOA focuses on selecting knee points as knowledge for transfer learning, which makes it particularly effective in knee regions, leading to better performance than MST-DMOA in DF6.
As for DF8, although the POSs change with time, they have a stationary centroid. The invariance of the POSs’ centroids can lead to consistent knowledge representation in environments with significant differences; therefore, this is not conducive to the matching of similar environments and the reuse of appropriate historical knowledge.
MST-DMOA performs more poorly than its competitors on the three instances of DF13. DF13 has continuous and disconnected POS geometries, which causes some solutions in a disconnected state to have few neighborhoods; hence, they cannot be presented as knowledge by clustering. Such circumstances may lead to incorrect search directions due to insufficient knowledge, which will decrease the performance of MST-DMOA due to negative transfer.
In general, MST-DMOA is suitable for the solution of most DMOPs, because MST-DMOA obtains rich and valuable knowledge from multiple similar historical environments, and the high-quality target domain helps the knowledge to adapt well to the current environment. However, the knowledge from different environments is difficult to distinguish due to the clustering of POSs with fixed centroids, which may mislead the environment matching process. In addition, for scenarios in which the POSs have sparse distributions, some key solutions may be treated as noise, resulting in insufficient knowledge acquired. The above issues may cause MST-DMOA to fall slightly behind the compared algorithms.
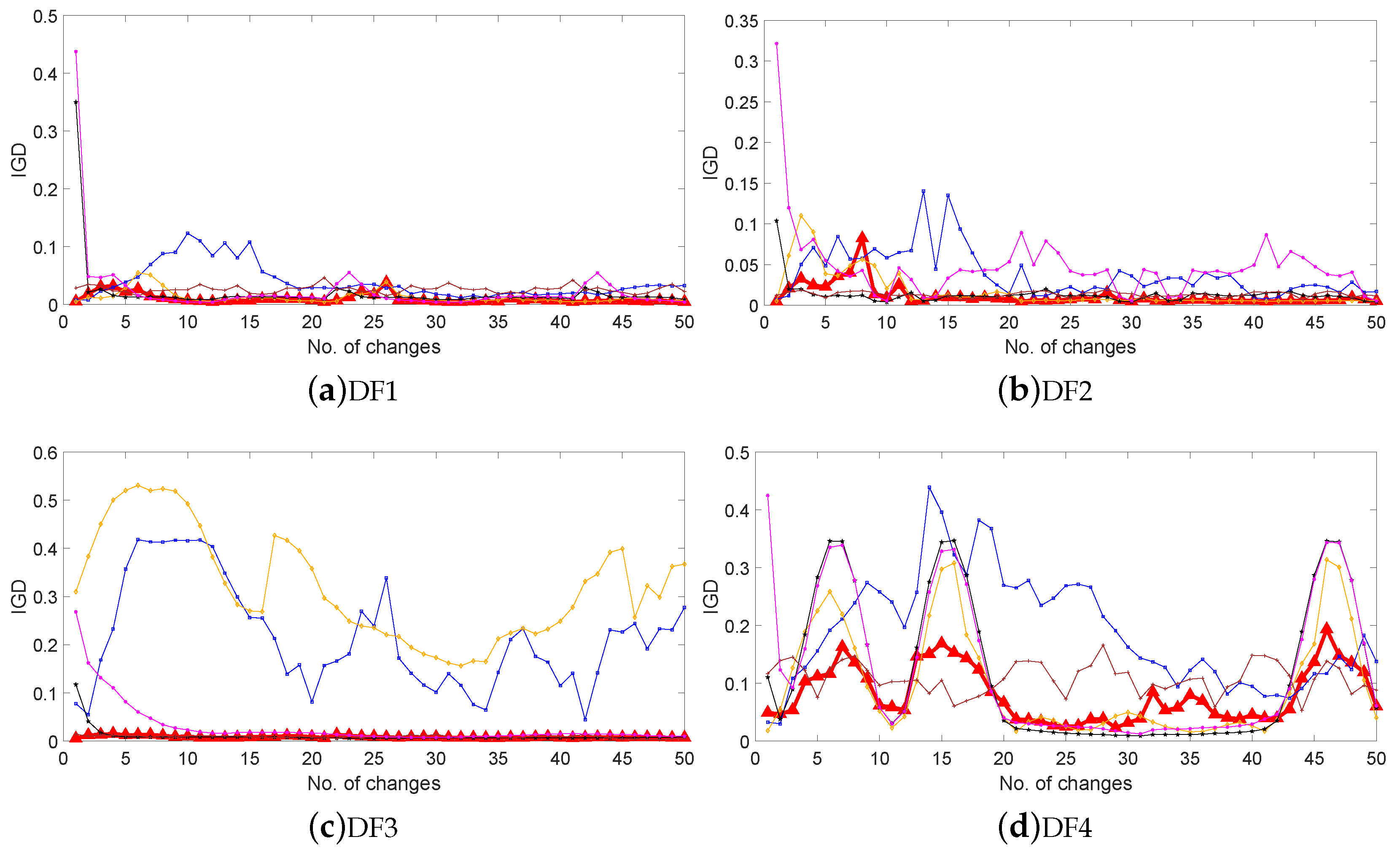
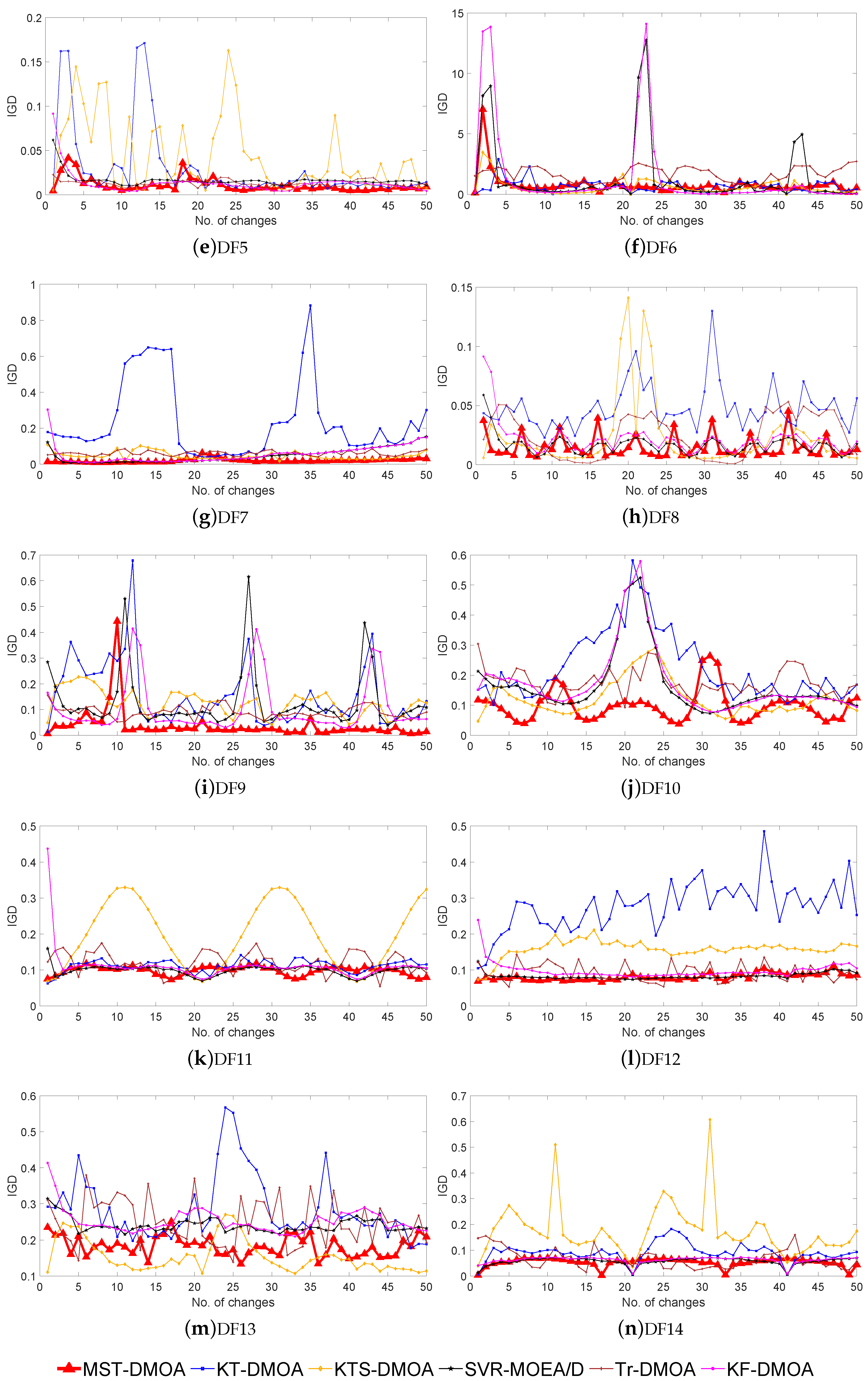
Moreover, Figure 2 plots the IGD values obtained by the six algorithms after each environmental change for the 14 DF problems in the configuration ( = 10 and = 10). The horizontal coordinate represents the changing environment, while the vertical coordinate represents the IGD value of the algorithm in the environment, i.e., the average distance between the obtained POF and the corresponding real POF. We can observe from Figure 2 that most of the curves obtained by MST-DMOA are located at the bottom and are smoother than the other curves, indicating that, compared with the other algorithms, our method can produce stable and accurate predictions in frequently changing environments. This verifies the effectiveness and stability of MST-DMOA in tracking varying POFs.
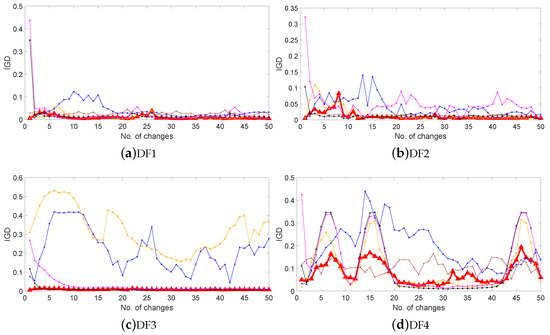
Figure 2.
IGD values of six algorithms on fourteen DF problems with (,) = (10,10).
Figure 2.
IGD values of six algorithms on fourteen DF problems with (,) = (10,10).
4.4. Effectiveness of Transfer Learning
In order to verify the effectiveness of transfer learning in MST-DMOA, the compared version is constructed as MST-DMOA w/o TL, where “w/o” stands for “without” and "TL" denotes transfer learning. More specifically, MST-DMOA w/o TL directly reuses the selected historical knowledge, i.e., using the solutions in the source domain as the initial population of the new environment, without executing the transfer learning process.
Table 3 shows the MIGD values of MST-DMOA and MST-DMOA w/o TL on the 14 test problems in the configuration ( = 10 and = 10). MST-DMOA achieves the best performance for all test instances, indicating that transfer learning is effective for our method. This is because transfer learning can align the distributional differences between different environments, adapting the historical knowledge to the current environment.

Table 3.
Effectiveness testing of transfer learning.
4.5. Adaptation Study
MST-DMOA is designed to generate an initial population with high quality for an SMOA when an environmental change occurs. To explore whether different SMOAs have an effect on the performance of MST-DMOA, we select three popular SMOAs, namely MOEA/D [33], SPEA2 [36] and PAES [37], as baseline optimizers for MST-DMOA, generating MST-MOEA/D, MST-SPEA2 and MST-PAES, respectively. In addition, to enable the three SMOAs to independently run in dynamic environments, they are modified as DMOAs via randomly initializing a partial population when the environment changes, thus obtaining DA-MOEA/D, DA-SPEA2 and DA-PAES. The average MIGD values of the above six algorithms on fourteen DF problems are shown in Table 4.

Table 4.
Average MIGD values of six algorithms on fourteen DF problems.
We can observe from Table 4 that MST-MOEA/D, MST-NSGA-II and MST-RM-MEDA are significantly better than DA-MOEA/D, DA-NSGA-II and DA-RM-MEDA, respectively. Table 4 effectively demonstrates the outstanding performance of MST-DMOA, as it can generate an initial population with high quality and accelerate the convergence to the true POFs in the new environment. As a result, the effectiveness of MST-DMOA is reflected in the prediction of the initial population rather than SMOAs. Therefore, the proposed MST-DMOA possesses high adaptability and outstanding performance, proving that it can collaborate with various SMOAs.
5. Conclusions
This article proposes a multi-environment knowledge selection and transfer method based on DMOAs, termed MST-DMOA, which aims to use knowledge gained from historical environments to help to generate a high-quality initial population in the new environment. Specifically, some representative solutions that can reflect the main evolutionary information are selected as knowledge for each environment by DBSCAN. When the environment changes, we calculate the similarity between the historical environments and the current environment and then construct the source domain with knowledge from similar environments as they can provide valuable historical information. At the same time, some high-quality solutions are obtained in the new environment to form the target domain. A geodesic flow path is constructed between the source and target domains, and the mapping matrix can be calculated by aligning the distribution of the subspaces with the geodesic flow. Finally, the solutions in the source domain can help to generate the initial population in the new environment according to this mapping matrix.
The proposed MST-DMOA is compared with five state-of-the-art DMOAs on the DF benchmark test suite, and the results demonstrate the excellent performance of MST-DMOA in handling DMOPs. In the future, the adaptation of the proposed algorithm to extreme changing environments may be a meaningful research topic. Moreover, MST-DMOA will be further expanded in future research and applied to more real-world optimization scenarios.
Author Contributions
Conceptualization, J.Y.; methodology, J.Y.; software, J.Y.; validation, J.Y.; formal analysis, J.Y.; investigation, J.Y.; resources, W.S.; data curation, J.Y.; writing—original draft preparation, J.Y.; writing—review and editing, W.S.; visualization, J.Y.; supervision, W.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are available upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hu, Y.; Zheng, J.; Jiang, S.; Yang, S.; Zou, J. Handling dynamic multiobjective optimization environments via layered prediction and subspace-based diversity maintenance. IEEE Trans. Cybern. 2021, 53, 2572–2585. [Google Scholar] [CrossRef] [PubMed]
- Sharma, R.; Kodamana, H.; Ramteke, M. Multi-objective dynamic optimization of hybrid renewable energy systems. Chem. Eng. Process.-Process Intensif. 2022, 170, 108663. [Google Scholar] [CrossRef]
- Jiang, M.; Huang, Z.; Qiu, L.; Huang, W.; Yen, G.G. Transfer learning-based dynamic multiobjective optimization algorithms. IEEE Trans. Evol. Comput. 2017, 22, 501–514. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]
- Jiang, M.; Wang, Z.; Qiu, L.; Guo, S.; Gao, X.; Tan, K.C. A fast dynamic evolutionary multiobjective algorithm via manifold transfer learning. IEEE Trans. Cybern. 2020, 51, 3417–3428. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, G.; Jiang, M.; Gong, D.; Liang, J. A knowledge guided transfer strategy for evolutionary dynamic multiobjective optimization. IEEE Trans. Evol. Comput. 2022, 27, 1750–1764. [Google Scholar] [CrossRef]
- Li, H.; Wang, Z.; Lan, C.; Wu, P.; Zeng, N. A novel dynamic multiobjective optimization algorithm with non-inductive transfer learning based on multi-strategy adaptive selection. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 16533–16547. [Google Scholar] [CrossRef]
- Jiang, M.; Wang, Z.; Hong, H.; Yen, G.G. Knee point-based imbalanced transfer learning for dynamic multiobjective optimization. IEEE Trans. Evol. Comput. 2020, 25, 117–129. [Google Scholar] [CrossRef]
- Lin, J.; Liu, H.L.; Tan, K.C.; Gu, F. An effective knowledge transfer approach for multiobjective multitasking optimization. IEEE Trans. Cybern. 2020, 51, 3238–3248. [Google Scholar] [CrossRef]
- Lin, J.; Liu, H.L.; Xue, B.; Zhang, M.; Gu, F. Multiobjective multitasking optimization based on incremental learning. IEEE Trans. Evol. Comput. 2019, 24, 824–838. [Google Scholar] [CrossRef]
- Deb, K.; Rao N, U.B.; Karthik, S. Dynamic multi-objective optimization and decision-making using modified NSGA-II: A case study on hydro-thermal power scheduling. In Proceedings of the International Conference on Evolutionary Multi-Criterion Optimization, Matsushima, Japan, 5–8 March 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 803–817. [Google Scholar]
- Chen, Q.; Ding, J.; Yang, S.; Chai, T. A novel evolutionary algorithm for dynamic constrained multiobjective optimization problems. IEEE Trans. Evol. Comput. 2019, 24, 792–806. [Google Scholar] [CrossRef]
- Ma, X.; Yang, J.; Sun, H.; Hu, Z.; Wei, L. Multiregional co-evolutionary algorithm for dynamic multiobjective optimization. Inf. Sci. 2021, 545, 1–24. [Google Scholar] [CrossRef]
- Chen, R.; Li, K.; Yao, X. Dynamic multiobjectives optimization with a changing number of objectives. IEEE Trans. Evol. Comput. 2017, 22, 157–171. [Google Scholar] [CrossRef]
- Sahmoud, S.; Topcuoglu, H.R. A memory-based NSGA-II algorithm for dynamic multi-objective optimization problems. In Proceedings of the Applications of Evolutionary Computation: 19th European Conference, EvoApplications 2016, Porto, Portugal, 30 March–1 April 2016; Proceedings, Part II 19. Springer: Berlin/Heidelberg, Germany, 2016; pp. 296–310. [Google Scholar]
- Xu, X.; Tan, Y.; Zheng, W.; Li, S. Memory-enhanced dynamic multi-objective evolutionary algorithm based on Lp decomposition. Appl. Sci. 2018, 8, 1673. [Google Scholar] [CrossRef]
- Cao, L.; Xu, L.; Goodman, E.D.; Bao, C.; Zhu, S. Evolutionary dynamic multiobjective optimization assisted by a support vector regression predictor. IEEE Trans. Evol. Comput. 2019, 24, 305–319. [Google Scholar] [CrossRef]
- Zhang, H.; Ding, J.; Jiang, M.; Tan, K.C.; Chai, T. Inverse gaussian process modeling for evolutionary dynamic multiobjective optimization. IEEE Trans. Cybern. 2021, 52, 11240–11253. [Google Scholar] [CrossRef]
- Zhou, A.; Jin, Y.; Zhang, Q. A population prediction strategy for evolutionary dynamic multiobjective optimization. IEEE Trans. Cybern. 2013, 44, 40–53. [Google Scholar] [CrossRef]
- Muruganantham, A.; Tan, K.C.; Vadakkepat, P. Evolutionary dynamic multiobjective optimization via kalman filter prediction. IEEE Trans. Cybern. 2015, 46, 2862–2873. [Google Scholar] [CrossRef]
- Jiang, M.; Wang, Z.; Guo, S.; Gao, X.; Tan, K.C. Individual-based transfer learning for dynamic multiobjective optimization. IEEE Trans. Cybern. 2020, 51, 4968–4981. [Google Scholar] [CrossRef]
- Dockhorn, A.; Braune, C.; Kruse, R. An alternating optimization approach based on hierarchical adaptations of dbscan. In Proceedings of the 2015 IEEE Symposium Series on Computational Intelligence, Cape Town, South Africa, 7–10 December 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 749–755. [Google Scholar]
- Gebril, I.H.; El-Mouadib, F.A.; Mansori, H.A. Automatic Generation of Epsilon (Eps) Value for DBSCAN Using Genetic Algorithms. In Proceedings of the 2024 IEEE 4th International Maghreb Meeting of the Conference on Sciences and Techniques of Automatic Control and Computer Engineering (MI-STA), Tripoli, Libya, 19–21 May 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 26–30. [Google Scholar]
- Rossi, C.; Abderrahim, M.; Díaz, J.C. Tracking moving optima using Kalman-based predictions. Evol. Comput. 2008, 16, 1–30. [Google Scholar] [CrossRef]
- Zhou, L.; Feng, L.; Gupta, A.; Ong, Y.S.; Liu, K.; Chen, C.; Sha, E.; Yang, B.; Yan, B. Solving dynamic vehicle routing problem via evolutionary search with learning capability. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 890–896. [Google Scholar]
- Xia, Y.; Shen, C.; Chen, Z.; Kong, L.; Huang, W.; Zhu, Z. Multisource domain transfer learning for bearing fault diagnosis. In Proceedings of the 2021 International Conference on Sensing, Measurement & Data Analytics in the era of Artificial Intelligence (ICSMD), Nanjing, China, 21–23 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Liu, Z.G.; Ning, L.B.; Zhang, Z.W. A new progressive multisource domain adaptation network with weighted decision fusion. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 1062–1072. [Google Scholar] [CrossRef] [PubMed]
- Tan, K.C.; Feng, L.; Jiang, M. Evolutionary transfer optimization-a new frontier in evolutionary computation research. IEEE Comput. Intell. Mag. 2021, 16, 22–33. [Google Scholar] [CrossRef]
- Sun, B.; Saenko, K. Subspace distribution alignment for unsupervised domain adaptation. In Proceedings of the BMVC, Swansea, UK, 7–10 September 2015; Volume 4, pp. 24.1–24.10. [Google Scholar]
- Greenacre, M.; Groenen, P.J.; Hastie, T.; d’Enza, A.I.; Markos, A.; Tuzhilina, E. Principal component analysis. Nat. Rev. Methods Prim. 2022, 2, 100. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, A.; Jin, Y. RM-MEDA: A regularity model-based multiobjective estimation of distribution algorithm. IEEE Trans. Evol. Comput. 2008, 12, 41–63. [Google Scholar] [CrossRef]
- Jiang, S.; Yang, S.; Yao, X.; Tan, K.C.; Kaiser, M.; Krasnogor, N. Benchmark Functions for the cec’2018 Competition on Dynamic Multiobjective Optimization; Technical Report; Newcastle University: Newcastle, UK, 2018. [Google Scholar]
- Zhang, Q.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Liang, Z.; Wu, T.; Ma, X.; Zhu, Z.; Yang, S. A dynamic multiobjective evolutionary algorithm based on decision variable classification. IEEE Trans. Cybern. 2020, 52, 1602–1615. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, D. An improved SPEA2 algorithm with local search for multi-objective investment decision-making. Appl. Sci. 2019, 9, 1675. [Google Scholar] [CrossRef]
- Knowles, J.; Corne, D. The pareto archived evolution strategy: A new baseline algorithm for pareto multiobjective optimisation. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; IEEE: Piscataway, NJ, USA, 1999; Volume 1, pp. 98–105. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).