Intelligent Manufacturing in Wine Barrel Production: Deep Learning-Based Wood Stave Classification
Abstract
1. Introduction
- We create an image database of staves for wine barrel production. The database contains 1805 images of complete staves and 4238 manually labeled cropped images (1.3 cm2) of the staves. The database is available upon reasonable request.
- We develop a preprocessing pipeline using classical techniques to remove background noise and enhance the most important features, followed by classification with a deep learning model cropped images of wine barrel staves with noticeable heterogeneity, achieving high precision and low execution time.
- We design a system that can be implemented in an automated machine that processes staves continuously. The entire process, from image acquisition to stave grading, takes fewer than 2 s.
2. Data Acquisition and Preprocessing
2.1. Optical Setup and Development Environment
2.2. Image Filtering with Classic Techniques
3. Crop Classification Using Deep Learning
3.1. First Classification Approach
3.2. Crops/Data Augmentation and Labeling
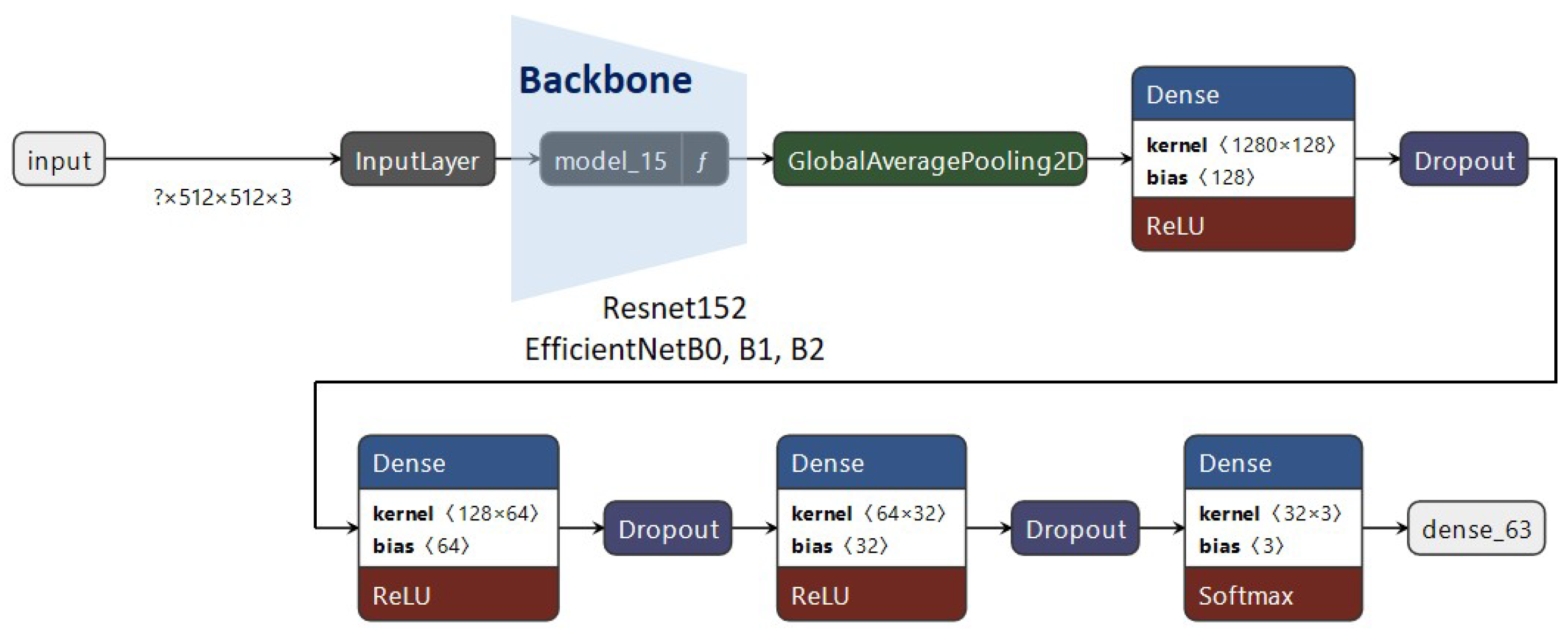
3.3. Used Architectures
3.4. Training Strategies and Results
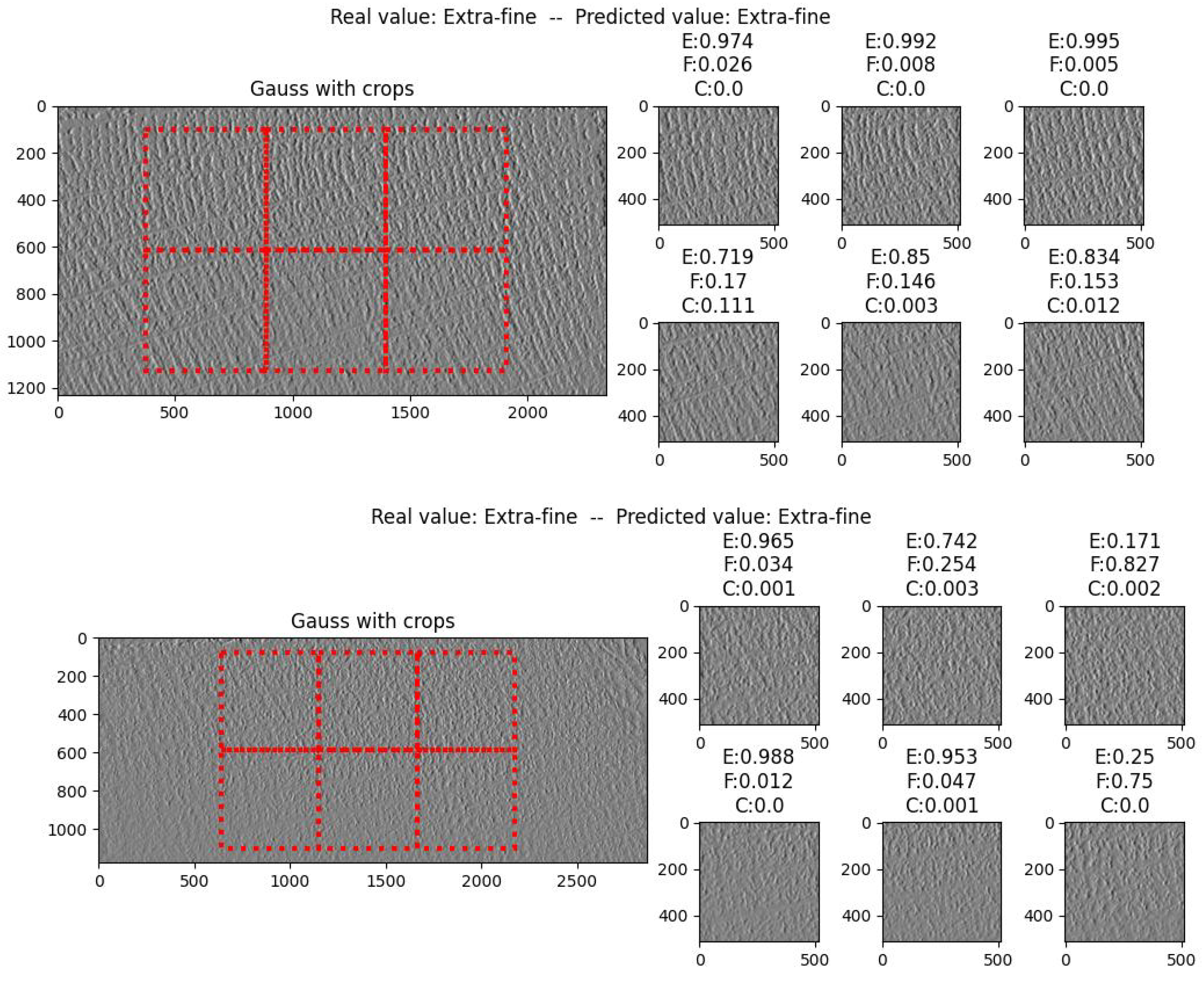
3.5. Saliency Maps and Grad-CAM Analysis
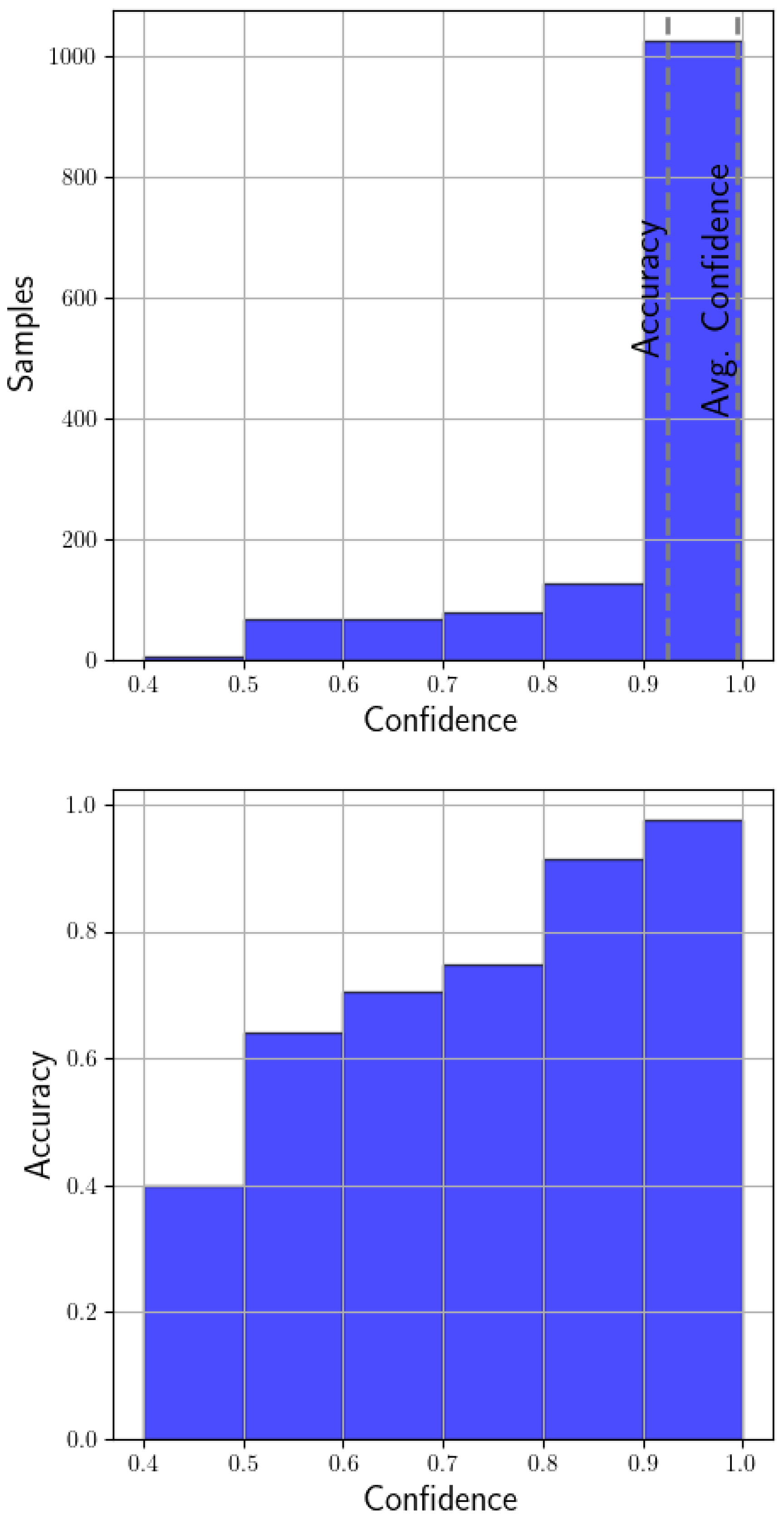
3.6. Model Calibration Analysis
4. Stave Classification Based on Crops
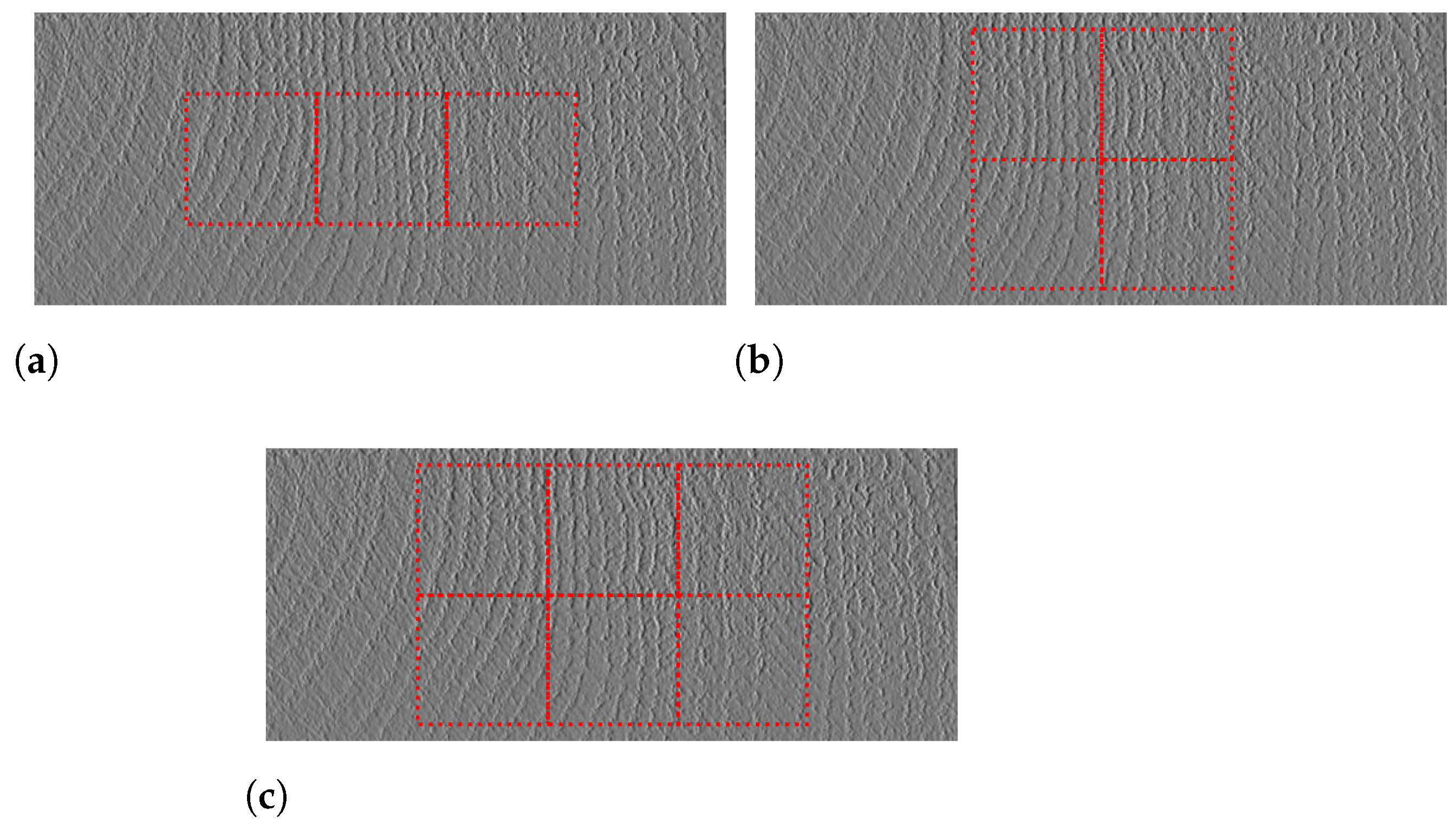
4.1. Strategies for Crop Selection
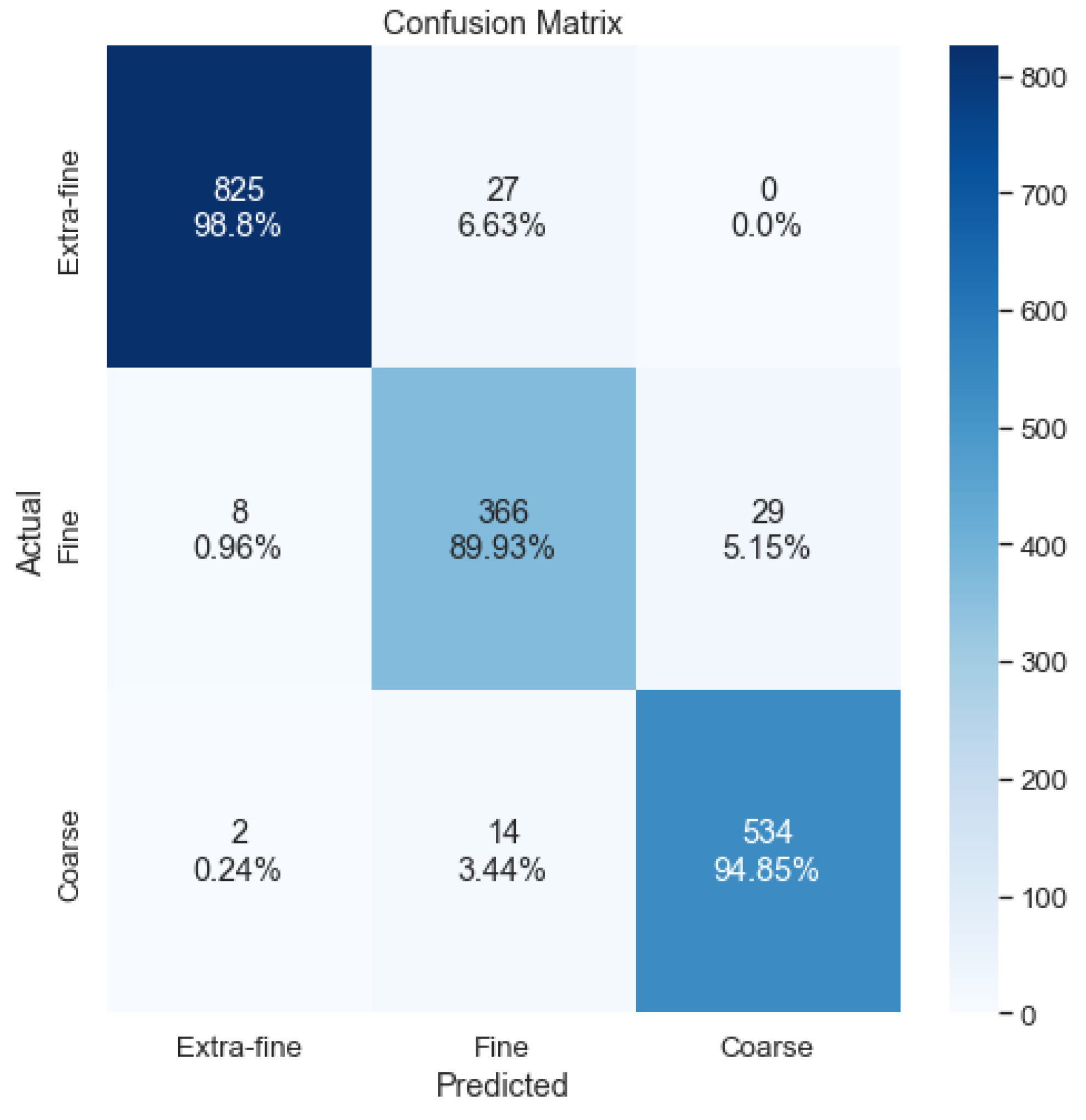
4.2. Voting System Design and Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sánchez-Gómez, R.; del Alamo-Sanza, M.; Nevares, I. Volatile composition of oak wood from different customised oxygenation wine barrels: Effect on red wine. Food Chem. 2020, 329, 127181. [Google Scholar] [CrossRef] [PubMed]
- Botezatu, A.; Essary, A. A Guide to Traditional Oak Barrels; Technical Report; The Texas A & M University System: College Station, TX, USA, 2020. [Google Scholar]
- Sun, P. Wood quality defect detection based on deep learning and multicriteria framework. Math. Probl. Eng. 2022, 4878090. [Google Scholar] [CrossRef]
- Kolus, A.; Wells, R.; Neumann, P. Production quality and human factors engineering: A systematic review and theoretical framework. Appl. Ergon. 2018, 73, 55–89. [Google Scholar] [CrossRef] [PubMed]
- Nurthohari, Z.; Murti, M.; Setianingsih, C. Wood quality classification based on texture and fiber pattern recognition using hog feature and svm classifier. In Proceedings of the IEEE International Conference on Internet of Things and Intelligence System, Bali, Indonesia, 5–7 November 2019; pp. 123–128. [Google Scholar] [CrossRef]
- Kwon, O.; Lee, H.; Lee, M.; Jang, S.; Yang, S.; Park, S.; Choi, I.; Yeo, H. Automatic wood species identification of Korean softwood based on convolutional neural networks. J. Korean Wood Sci. Technol. 2017, 45, 797–808. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, J.; Wang, A.; Ren, H.; Emam, M. Multi-fusion approach for wood microscopic images identification based on deep transfer learning. Appl. Sci. 2021, 11, 7639. [Google Scholar] [CrossRef]
- de Geus, A.; Backes, A.; Gontijo, A.; Albuquerque, G.; Souza, J. Amazon wood species classification: A comparison between deep learning and pre-designed features. Wood Sci. Technol. 2021, 55, 857–872. [Google Scholar] [CrossRef]
- Niskanen, M.; Silvén, O.; Kauppinen, H. Wood inspection with non-supervised clustering. Mach. Vis. Appl. 2003, 13, 275–285. [Google Scholar] [CrossRef]
- Urbonas, A.; Raudonis, V.; Maskeliūnas, R.; Damaševičius, R. Automated identification of wood veneer surface defects using faster region-based convolutional neural network with data augmentation and transfer learning. Appl. Sci. 2019, 9, 4898. [Google Scholar] [CrossRef]
- He, T.; Liu, Y.; Yu, Y.; Zhao, Q.; Hu, Z. Application of deep convolutional neural network on feature extraction and detection of wood defects. Measurement 2020, 152, 107357. [Google Scholar] [CrossRef]
- Fabijańska, A.; Danek, M. DeepDendro—A tree rings detector based on a deep convolutional neural network. Comput. Electron. Agric. 2018, 150, 353–363. [Google Scholar] [CrossRef]
- Shi, J.; Xiang, W.; Liu, Q.; Shah, S. MtreeRing: An R package with graphical user interface for automatic measurement of tree ring widths using image processing techniques. Dendrochronologia 2019, 58, 125644. [Google Scholar] [CrossRef]
- Martin, D. A practical guide to machine vision lighting. Adv. Illum. 2007, 2007, 1–3. [Google Scholar]
- Olivari, L.; Olivari, L. Influence of Programming Language on the Execution Time of Ant Colony Optimization Algorithm. Teh. Glas. 2022, 16, 231–239. [Google Scholar] [CrossRef]
- Gordillo, A.; Calero, C.; Moraga, M.Á.; García, F.; Fernandes, J.P.; Abreu, R.; Saraiva, J. Programming languages ranking based on energy measurements. Softw. Qual. J. 2024. [Google Scholar] [CrossRef]
- ONNX. ONNX: Open Neural Network Exchange, Version 1.16.1; Linux Foundation: San Francisco, CA, USA, 2024.
- Moru, D.; Borro, D. Analysis of different parameters of influence in industrial cameras calibration processes. Measurement 2021, 171, 108750. [Google Scholar] [CrossRef]
- Gonzalez, R.; Woods, R. Digital Image Processing; Pearson: London, UK, 2018. [Google Scholar]
- Forsyth, D.; Ponce, J. Computer Vision: A Modern Approach; Pearson: London, UK, 2012. [Google Scholar]
- GmbH, M.S. HALCON—The Powerful Software for Your Machine Vision Application. Version 22. 2024. Available online: https://www.mvtec.com/products/halcon (accessed on 22 October 2024).
- Wong, S.; Gatt, A.; Stamatescu, V.; McDonnell, M. Understanding Data Augmentation for Classification: When to Warp? In Proceedings of the International Conference on Digital Image Computing: Techniques and Applications, Gold Coast, Australia, 30 November–2 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In International Conference on Machine Learning; PMLR: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Ying, X. An Overview of Overfitting and its Solutions. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. arXiv 2017. [Google Scholar] [CrossRef]
- Ali, S.; Abuhmed, T.; El-Sappagh, S.; Muhammad, K.; Alonso-Moral, J.; Confalonieri, R.; Guidotti, R.; Ser, J.; Díaz-Rodríguez, N.; Herrera, F. Explainable artificial intelligence (xAI): What we know and what is left to attain trustworthy artificial intelligence. Inf. Fusion 2023, 99, 101805. [Google Scholar] [CrossRef]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep inside convolutional networks: Visualising image classification models and saliency maps. In Proceedings of the Workshop at International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar] [CrossRef]
- Selvaraju, R.; Das, A.; Vedantam, R.; Cogswell, M.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar] [CrossRef]
- Guo, C.; Pleiss, G.; Sun, Y.; Weinberger, K.Q. On calibration of modern neural networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1321–1330. [Google Scholar] [CrossRef]
- Niculescu-Mizil, A.; Caruana, R. Predicting good probabilities with supervised learning. In Proceedings of the 22nd International Conference on Machine Learning, Bonn, Germany, 7–11 August 2005; pp. 625–632. [Google Scholar] [CrossRef]
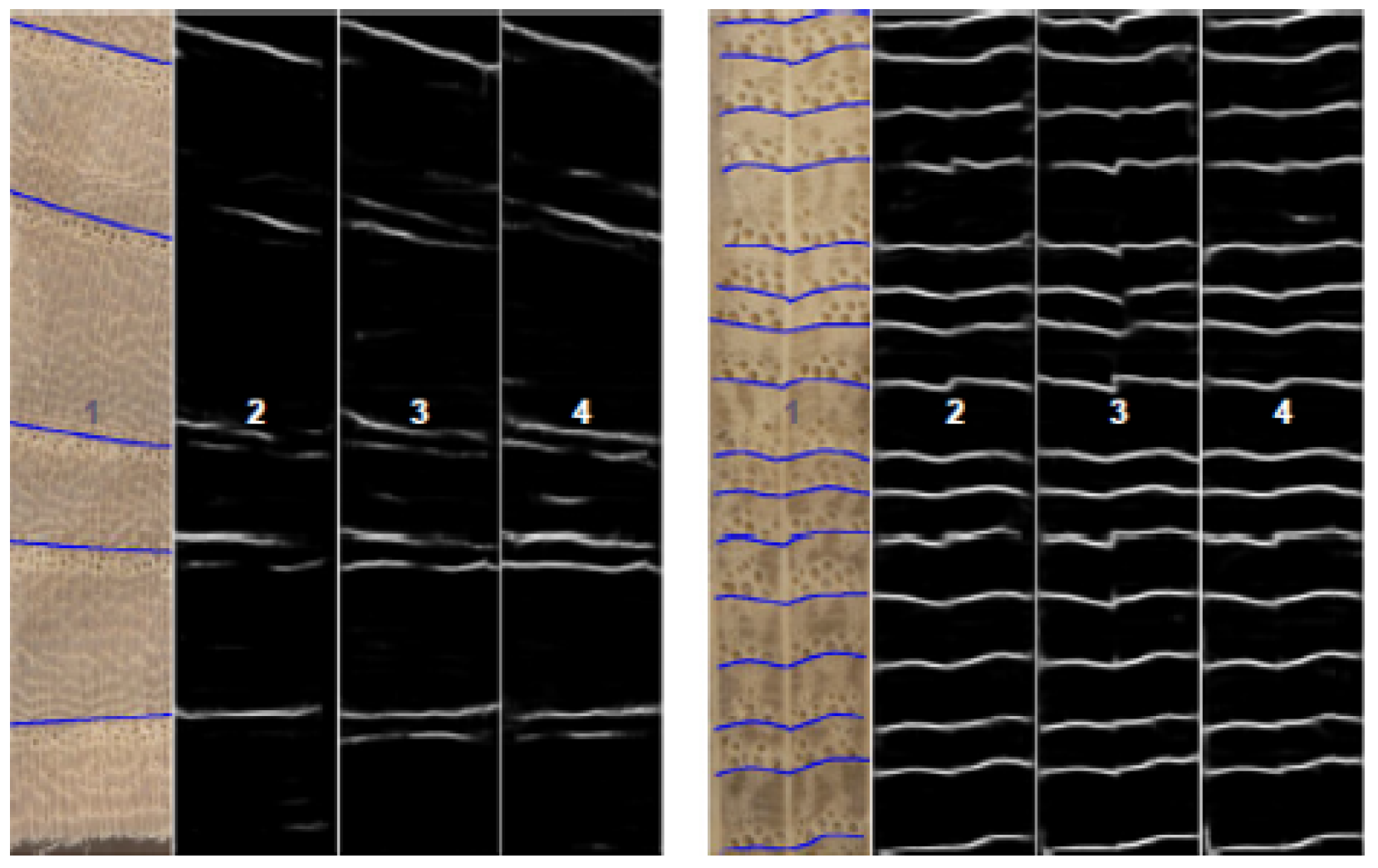
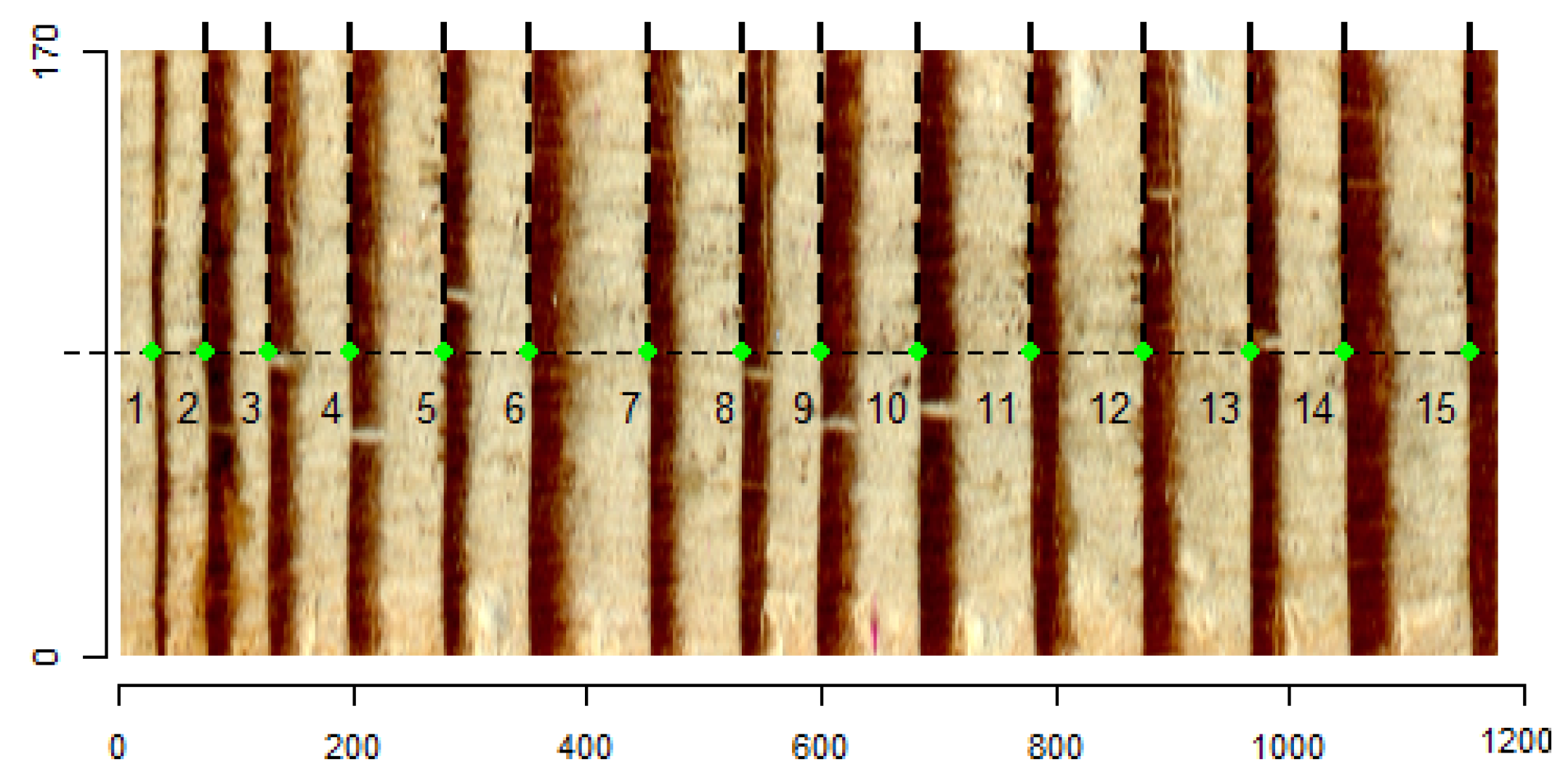




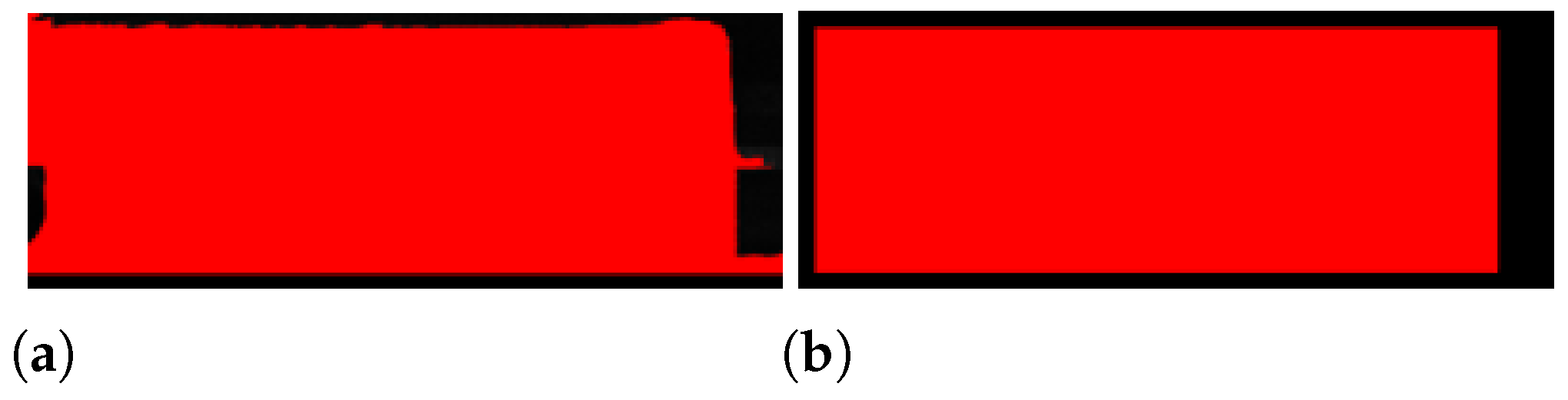


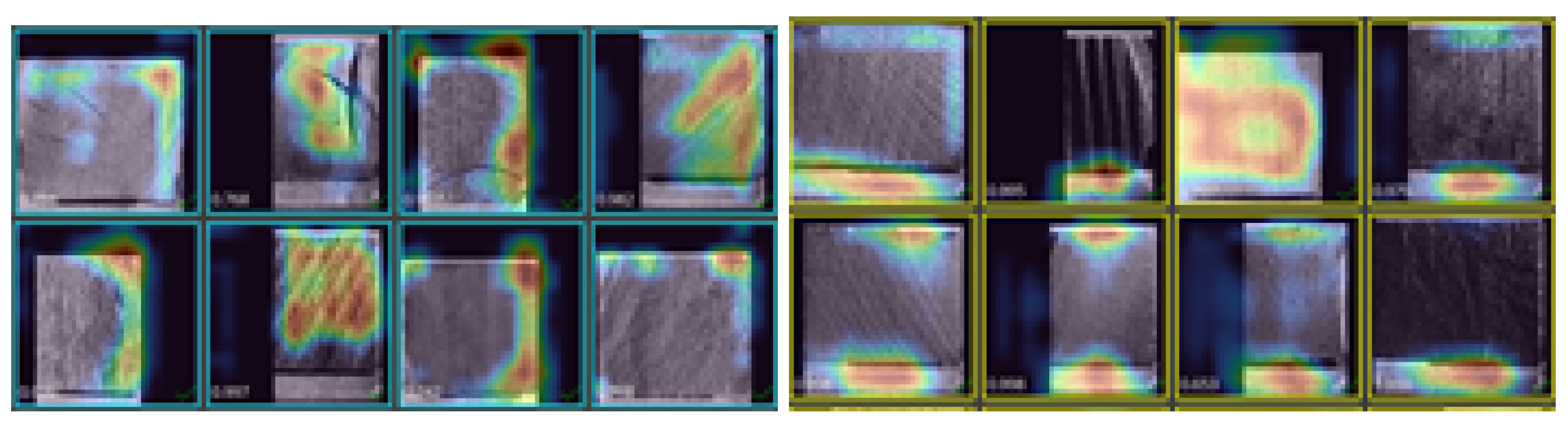





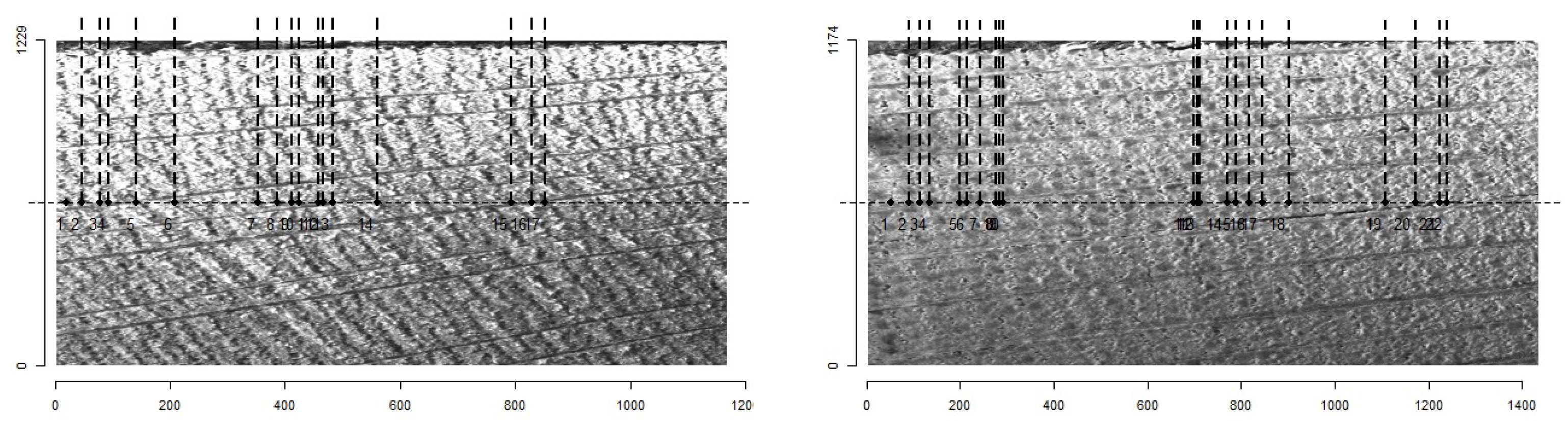
| Class | Rings/Crop (1.3 cm2) | Created |
|---|---|---|
| Coarse | x ≤ 5 | 1605 |
| Fine | 6 ≤ x ≤ 9 | 1636 |
| Extra fine | x ≥ 10 | 997 |
| Class | Created Crops | Augmented Crops | Total |
|---|---|---|---|
| Coarse | 1605 | 0 | 1605 |
| Fine | 1636 | 0 | 1636 |
| Extra fine | 997 | 582 | 1579 |
| Class | Train | Validation | Test | Total Crops |
|---|---|---|---|---|
| Coarse | 1077 | 87 | 441 | 1605 |
| Fine | 1059 | 87 | 490 | 1636 |
| Extra fine | 1051 | 87 | 441 | 1579 |
| Parameter | Stage 1 | Stage 2 | Stage 3 | Stage 4 |
|---|---|---|---|---|
| Epochs | 50 | 100 | ||
| Loss function | Categorical crossentropy | |||
| Metric | Categorical accuracy | |||
| Optimizer | Adam (LR = ) | Adam (LR = ) | ||
| Class weights | ||||
| Base model | Not trainable | ResNet 152V2: 350 last layers EfficientNet: 150 last layers | ||
| D. Aug | Rescale: 1/255 Rotation: 10° | Rescale: 1/255 Rotation: 15° W/H shift: 0.2 Zoom range: 0.2 Channel shift: 0.2 Shear range: 0.1 Vertical flip Horizontal flip | ||
| Model | Stage 1 | Stage 2 | Stage 3 | Stage 4 |
|---|---|---|---|---|
| ResNet 152V2 | 0.78 | 0.86 | 0.87 | 0.87 |
| EfficientNet B2 | 0.75 | 0.82 | 0.84 | 0.84 |
| EfficientNet B1 | 0.77 | 0.84 | 0.85 | 0.87 |
| EfficientNet B0 | 0.77 | 0.80 | 0.78 | 0.80 |
| Parameter | Stage 5 | Stage 6 |
|---|---|---|
| Epochs | 100 | 30 |
| Optimizer | Adam (LR = ) | AdamW (LR = , WD = 5) |
| Base model | 300 last layers | Whole model |
| D. Aug | Rotation: 25° W/H shift: 0.3 Channel shift: 0.4 Shear range: 0.3 Vertical and horizontal flip | Rotation: 15° W/H shift: 0.2 Channel shift: 0.2 Shear range: 0.3 Vertical and horizontal flip |
| Model | Acc. 5 | Acc. 6 |
|---|---|---|
| EfficientNet B1 | 0.88 | 0.92 |
| Class | Staves |
|---|---|
| Coarse | 852 |
| Fine | 432 |
| Extra fine | 550 |
| Crop∖Threshold | 0.5 | 0.6 | 0.7 | 0.8 |
|---|---|---|---|---|
| 3 central crops | 0.899 | 0.911 | 0.915 | 0.912 |
| 4 central crops | 0.899 | 0.905 | 0.902 | 0.905 |
| 6 central crops | 0.927 | 0.930 | 0.936 | 0.956 |
| Crop Function | Acc. |
|---|---|
| 3 central crops | 0.912 |
| 4 central crops | 0.910 |
| 6 central crops | 0.935 |
| Crop∖Threshold | 0.5 | 0.6 | 0.7 | 0.8 |
|---|---|---|---|---|
| 3 central crops | 0.900 | 0.910 | 0.912 | 0.915 |
| 4 central crops | 0.909 | 0.909 | 0.908 | 0.909 |
| 6 central crops | 0.932 | 0.930 | 0.932 | 0.941 |
| Strategy | Best accuracy | Cross-Classification Errors |
|---|---|---|
| Sum of crops | 0.956 (6 crops/0.8 threshold) | 2 (coarse classified as extra fine) |
| Sum of probs | 0.935 (6 crops) | 0 |
| Hybrid [selected] | 0.941 (6 crops/0.8 threshold) | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ricardo, F.A.; Eizaguirre, M.; Moru, D.K.; Borro, D. Intelligent Manufacturing in Wine Barrel Production: Deep Learning-Based Wood Stave Classification. AI 2024, 5, 2018-2036. https://doi.org/10.3390/ai5040099
Ricardo FA, Eizaguirre M, Moru DK, Borro D. Intelligent Manufacturing in Wine Barrel Production: Deep Learning-Based Wood Stave Classification. AI. 2024; 5(4):2018-2036. https://doi.org/10.3390/ai5040099
Chicago/Turabian StyleRicardo, Frank A., Martxel Eizaguirre, Desmond K. Moru, and Diego Borro. 2024. "Intelligent Manufacturing in Wine Barrel Production: Deep Learning-Based Wood Stave Classification" AI 5, no. 4: 2018-2036. https://doi.org/10.3390/ai5040099
APA StyleRicardo, F. A., Eizaguirre, M., Moru, D. K., & Borro, D. (2024). Intelligent Manufacturing in Wine Barrel Production: Deep Learning-Based Wood Stave Classification. AI, 5(4), 2018-2036. https://doi.org/10.3390/ai5040099







