Electrically Tunable and Reconfigurable Topological Edge State Laser
Abstract
:1. Introduction
2. Model and Simulation
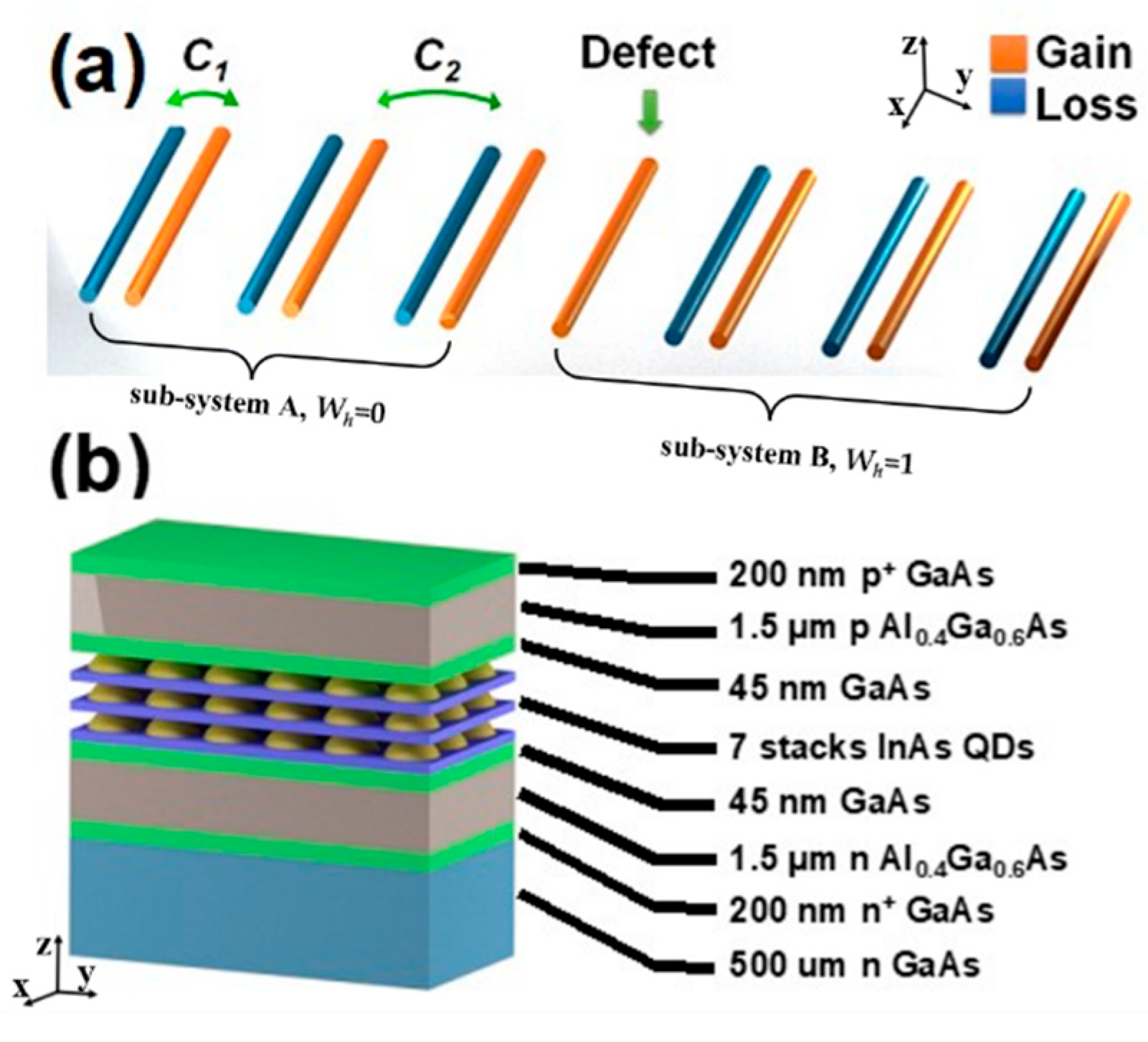
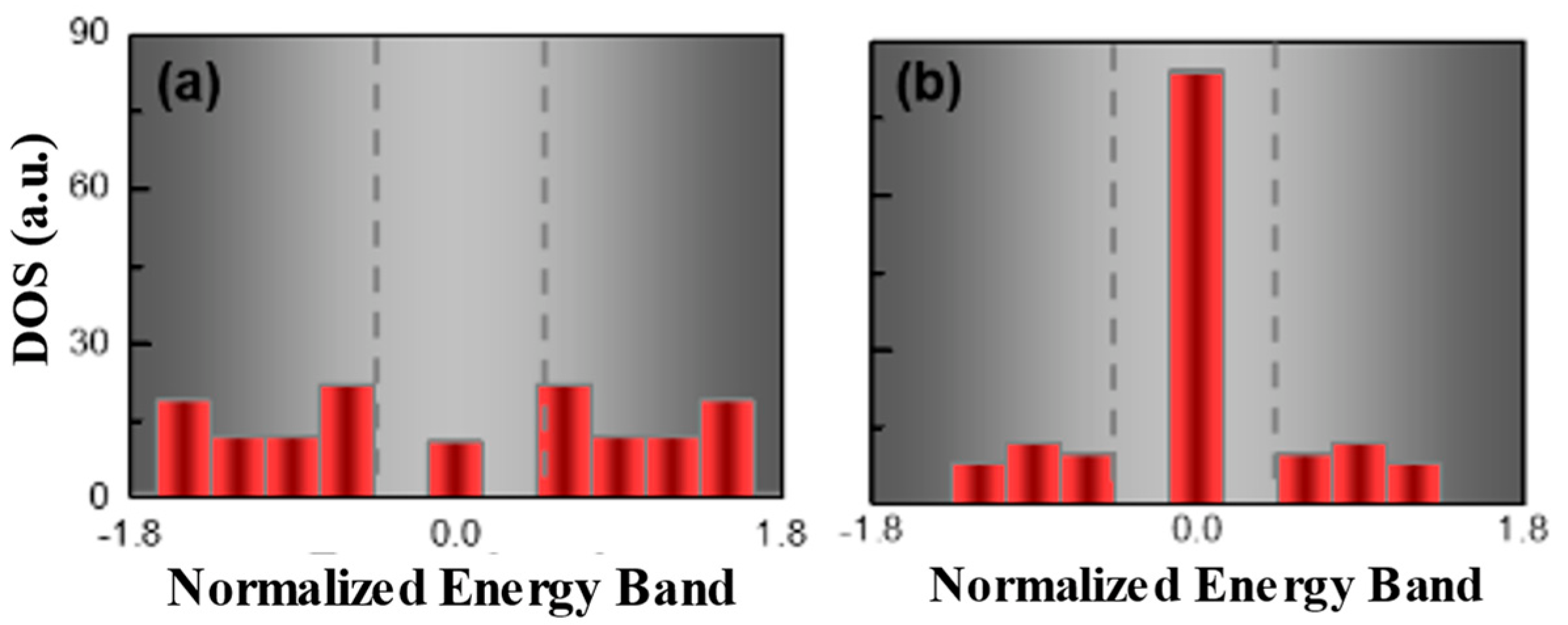
2.1. Non-Hermitian Topological Laser Chain
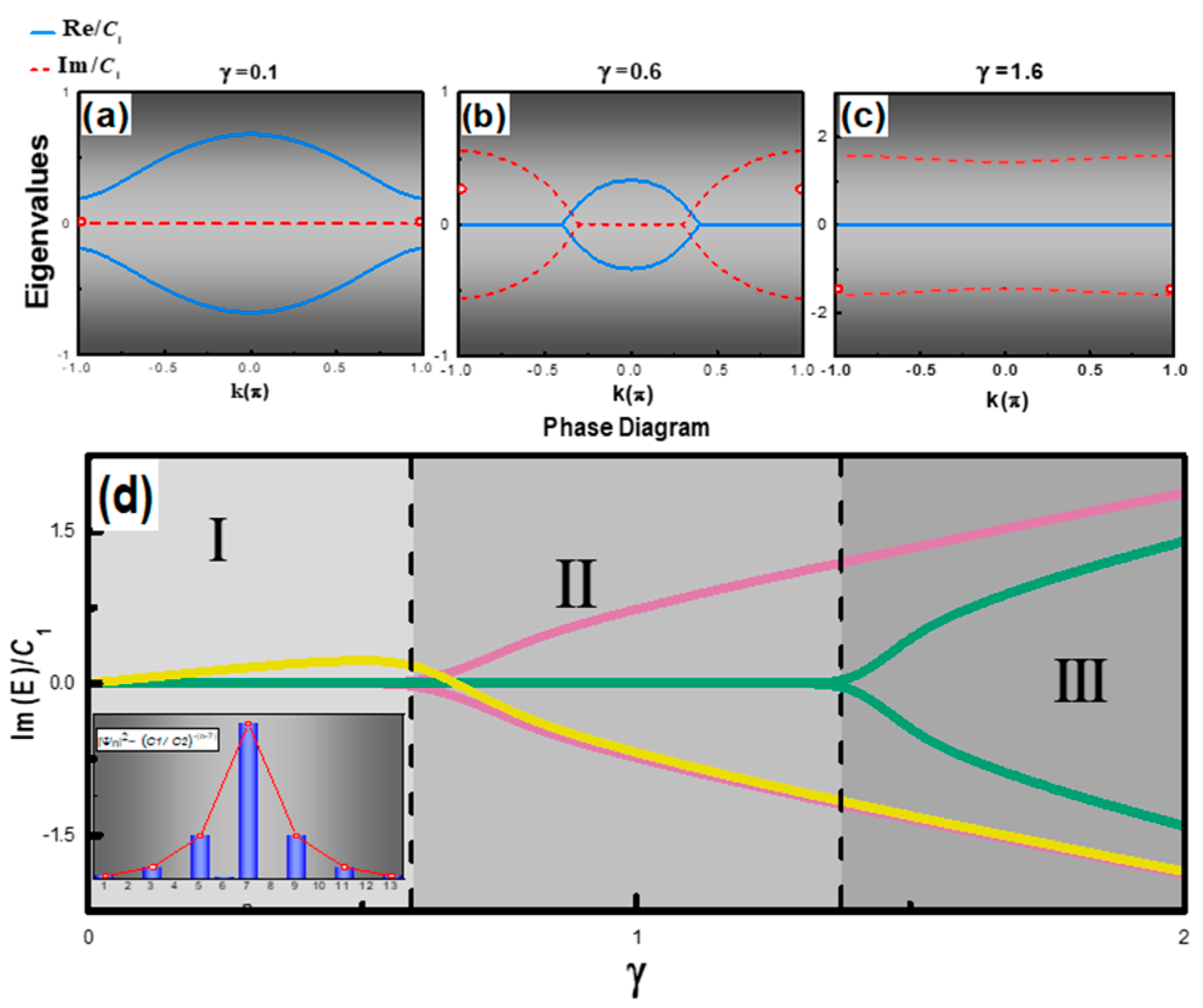
2.2. Phase Transition of Non-Hermitian Topological Laser Chain
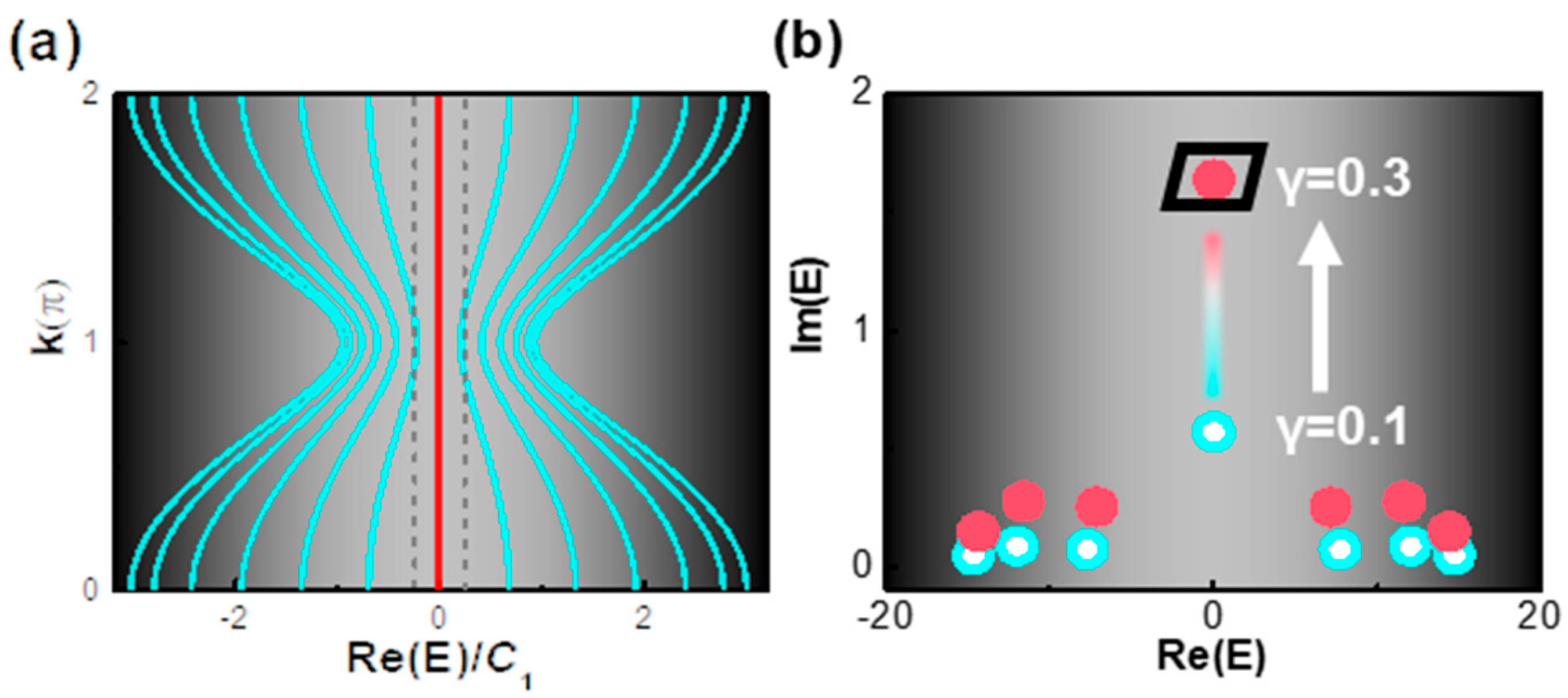
2.3. Complex Eigenvalue Diagrams of Non-Hermitian Topological Laser Chain
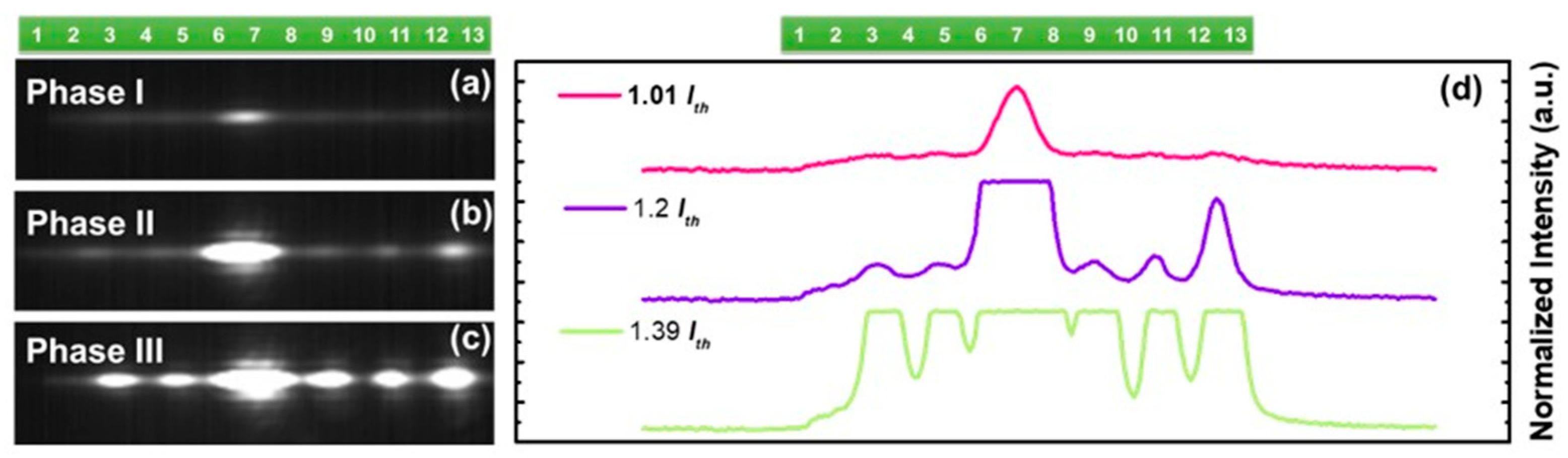
3. Experimental Results
3.1. Experimental Demonstration of Non-Hermitian Topological Laser Chain
3.2. Reconfiguration of Non-Hermitian Topological Laser Chain
3.3. Topological Laser Chain Fabrication
3.4. Near-Field Measurement
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Qi, X.-L.; Hughes, T.; Zhang, S.-C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 2008, 78, 195424. [Google Scholar] [CrossRef] [Green Version]
- Fu, L.; Kane, C.L. Topological insulators with inversion symmetry. Phys. Rev. B 2007, 76, 045302. [Google Scholar] [CrossRef] [Green Version]
- Köenig, M.; Wiedmann, S.; Brüene, C.; Roth, A.; Buhmann, H.; Molenkamp, L.W.; Qi, X.-L.; Zhang, S.-C. Quantum Spin Hall Insulator State in HgTe Quantum Wells. Science 2007, 318, 766–770. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hsieh, D.; Qian, D.; Wray, L.; Xia, Y.; Hor, Y.S.; Cava, R.J.; Hasan, M.Z. A topological Dirac insulator in a quantum spin Hall phase. Nature 2008, 452, 970–974. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef] [Green Version]
- Hsieh, D.; Xia, Y.; Qian, D.; Wray, L.; Meier, F.; Dil, J.H.; Osterwalder, J.; Patthey, L.; Fedorov, A.V.; Lin, H.; et al. Observation of Time-Reversal-Protected Single-Dirac-Cone Topological-Insulator States in Bi2Te3 and Se2Te3. Phys. Rev. Lett. 2009, 103, 146401. [Google Scholar] [CrossRef] [Green Version]
- Qi, X.-L.; Zhang, S.-C. The quantum spin Hall effect and topological insulators. Phys. Today 2009, 63, 33–38. [Google Scholar] [CrossRef] [Green Version]
- Qi, X.-L.; Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057–1110. [Google Scholar] [CrossRef] [Green Version]
- Fu, L.; Kane, C.L. Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator. Phys. Rev. Lett. 2008, 100, 096407. [Google Scholar] [CrossRef] [Green Version]
- Poli, C.; Bellec, M.; Kuhl, U.; Mortessagne, F.; Schomerus, H. Selective enhancement of topologically induced interface states in a dielectric resonator chain. Nat. Commun. 2015, 6, 6710. [Google Scholar] [CrossRef] [Green Version]
- Rechtsman, M.C.; Zeuner, J.M.; Plotnik, Y.; Lumer, Y.; Podolsky, D.; Dreisow, F.; Nolte, S.; Segev, M.; Szameit, A. Photonic Floquet topological insulators. Nature 2013, 496, 196–200. [Google Scholar] [CrossRef] [PubMed]
- Umucalılar, R.O.; Carusotto, I. Artificial gauge field for photons in coupled cavity arrays. Phys. Rev. A 2011, 84, 043804. [Google Scholar] [CrossRef] [Green Version]
- Hafezi, M.; Demler, E.A.; Lukin, M.D.; Taylor, J.M. Robust optical delay lines with topological protection. Nat. Phys. 2011, 7, 907–912. [Google Scholar] [CrossRef]
- Fang, K.; Yu, Z.; Fan, S. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation. Nat. Photon. 2012, 6, 782–787. [Google Scholar] [CrossRef]
- Hafezi, M.; Mittal, S.; Fan, J.; Migdall, A.; Taylor, J.M. Imaging topological edge states in silicon photonics. Nat. Photon. 2013, 7, 1001–1005. [Google Scholar] [CrossRef] [Green Version]
- Cheng, X.; Jouvaud, C.; Ni, X.; Mousavi, S.H.; Genack, A.Z.; Khanikaev, A.B. Robust reconfigurable electromagnetic pathways within a photonic topological insulator. Nat. Mater. 2016, 15, 542–548. [Google Scholar] [CrossRef]
- Lu, L.; Joannopoulos, J.D.; Soljačić, M. Topological photonics. Nat. Photonics 2014, 8, 821. [Google Scholar] [CrossRef] [Green Version]
- Bandres, M.A.; Wittek, S.; Harari, G.; Parto, M.; Ren, J.; Segev, M.; Christodoulides, D.N.; Khajavikhan, M. Topological insulator laser: Experiments. Science 2018, 359, eaar4005. [Google Scholar] [CrossRef] [Green Version]
- Parto, M.; Wittek, S.; Hodaei, H.; Harari, G.; Bandres, M.A.; Ren, J.; Rechtsman, M.C.; Segev, M.; Christodoulides, D.N.; Khajavikhan, M. Complex edge—State phase transitions in 1D topological laser arrays. arXiv preprint 2017, arXiv:1709.00523. [Google Scholar]
- Zhao, H.; Miao, P.; Teimourpour, M.H.; Malzard, S.; El-Ganainy, R.; Schomerus, H.; Feng, L. Topological hybrid silicon microlasers. Nat. Commun. 2018, 9, 981. [Google Scholar] [CrossRef]
- St-Jean, P.; Goblot, V.; Galopin, E.; Lemaître, A.; Ozawa, T.; Le Gratiet, L.; Sagnes, I.; Bloch, J.; Amo, A. Lasing in topological edge states of a one-dimensional lattice. Nat. Photonics 2017, 11, 651–656. [Google Scholar] [CrossRef] [Green Version]
- Parto, M.; Wittek, S.; Hodaei, H.; Harari, G.; Bandres, M.A.; Ren, J.; Rechtsman, M.C.; Segev, M.; Christodoulides, D.N.; Khajavikhan, M. Edge-Mode Lasing in 1D Topological Active Arrays. Phys. Rev. Lett. 2018, 120, 113901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bahari, B.; Ndao, A.; Vallini, F.; El Amili, A.; Fainman, Y.; Kanté, B. Nonreciprocal lasing in topological cavities of arbitrary geometries. Science 2017, 358, 636–640. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pilozzi, L.; Conti, C. Topological cascade laser for frequency comb generation in PT-symmetric structures. Opt. Lett. 2017, 42, 5174–5177. [Google Scholar] [CrossRef] [Green Version]
- Longhi, S. Non-Hermitian Gauged Topological Laser Arrays. Ann. Phys. 2018, 530, 1800023. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Li, C.; Hu, X.; Ao, Y.; Zhao, Y.; Gong, Q. Applications of Topological Photonics in Integrated Photonic Devices. Adv. Opt. Mater. 2017, 5, 1700357. [Google Scholar] [CrossRef]
- Rüter, C.E.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Segev, M.; Kip, D. Observation of parity-time symmetry in optics. Nat. Phys. 2010, 6, 192. [Google Scholar] [CrossRef] [Green Version]
- Guo, A.; Salamo, G.; Duchesne, D.; Morandotti, R.; Volatier-Ravat, M.; Aimez, V.; Siviloglou, G.; Christodoulides, D. Observation of P T-symmetry breaking in complex optical potentials. Phys. Rev. Lett. 2009, 103, 093902. [Google Scholar] [CrossRef] [Green Version]
- El-Ganainy, R.; Makris, K.G.; Christodoulides, D.N.; Musslimani, Z.H. Theory of coupled optical PT-symmetric structures. Opt. Lett. 2007, 32, 2632–2634. [Google Scholar] [CrossRef]
- Feng, L.; Ayache, M.; Huang, J.; Xu, Y.-L.; Lu, M.-H.; Chen, Y.-F.; Fainman, Y.; Scherer, A. Nonreciprocal Light Propagation in a Silicon Photonic Circuit. Science 2011, 333, 729–733. [Google Scholar] [CrossRef] [Green Version]
- Peng, B.; Özdemir, Ş.K.; Lei, F.; Monifi, F.; Gianfreda, M.; Long, G.L.; Fan, S.; Nori, F.; Bender, C.M.; Yang, L. Parity-time-symmetric whispering-gallery microcavities. Nat. Phys. 2014, 10, 394–398. [Google Scholar] [CrossRef] [Green Version]
- Feng, L.; Wong, Z.J.; Ma, R.-M.; Wang, Y.; Zhang, X. Single-mode laser by parity-time symmetry breaking. Science 2014, 346, 972–975. [Google Scholar] [CrossRef] [PubMed]
- Chong, Y.; Ge, L.; Stone, A.D. P T-Symmetry Breaking and Laser-Absorber Modes in Optical Scattering Systems. Phys. Rev. Lett. 2011, 106, 093902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hodaei, H.; Miri, M.-A.; Heinrich, M.; Christodoulides, D.N.; Khajavikhan, M. Parity-time-symmetric microring lasers. Science 2014, 346, 975–978. [Google Scholar] [CrossRef]
- Su, W.P.; Schrieffer, J.; Heeger, A.J. Solitons in polyacetylene. Phys. Rev. Lett. 1979, 42, 1698. [Google Scholar] [CrossRef]
- Malkova, N.; Hromada, I.; Wang, X.; Bryant, G.; Chen, Z. Observation of optical Shockley-like surface states in photonic superlattices. Opt. Lett. 2009, 34, 1633–1635. [Google Scholar] [CrossRef]
- Delplace, P.; Ullmo, D.; Montambaux, G. Zak phase and the existence of edge states in graphene. Phys. Rev. B 2011, 84, 195452. [Google Scholar] [CrossRef] [Green Version]
- Zak, J. Berry’s phase for energy bands in solids. Phys. Rev. Lett. 1989, 62, 2747. [Google Scholar] [CrossRef]
- Bender, C.M.; DeKieviet, M.; Klevansky, S.P. PT quantum mechanics. Philos. Trans. A Math. Phys. Eng. Sci. 2013, 371, 20120523. [Google Scholar] [CrossRef] [Green Version]
- Weimann, S.; Kremer, M.; Plotnik, Y.; Lumer, Y.; Nolte, S.; Makris, K.G.; Segev, Y.P.Y.L.M.; Rechtsman, M.C.; Szameit, A. Topologically protected bound states in photonic parity-time-symmetric crystals. Nat. Mater. 2016, 16, 433–438. [Google Scholar] [CrossRef]
- Yuce, C. Topological phase in a non-Hermitian PT symmetric system. Phys. Lett. A 2015, 379, 1213–1218. [Google Scholar] [CrossRef] [Green Version]
- Coldren, L.A.; Corzine, S.W.; Mašanović, M.L. Diode Lasers and Photonic Integrated Circuits; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Yao, R.; Zheng, B.; An, S.; Haerinia, M.; Ding, J.; Lee, C.-S.; Zhang, H.; Guo, W. Electrically Tunable and Reconfigurable Topological Edge State Laser. Optics 2022, 3, 107-116. https://doi.org/10.3390/opt3020013
Li H, Yao R, Zheng B, An S, Haerinia M, Ding J, Lee C-S, Zhang H, Guo W. Electrically Tunable and Reconfigurable Topological Edge State Laser. Optics. 2022; 3(2):107-116. https://doi.org/10.3390/opt3020013
Chicago/Turabian StyleLi, Hang, Ruizhe Yao, Bowen Zheng, Sensong An, Mohammad Haerinia, Jun Ding, Chi-Sen Lee, Hualiang Zhang, and Wei Guo. 2022. "Electrically Tunable and Reconfigurable Topological Edge State Laser" Optics 3, no. 2: 107-116. https://doi.org/10.3390/opt3020013
APA StyleLi, H., Yao, R., Zheng, B., An, S., Haerinia, M., Ding, J., Lee, C.-S., Zhang, H., & Guo, W. (2022). Electrically Tunable and Reconfigurable Topological Edge State Laser. Optics, 3(2), 107-116. https://doi.org/10.3390/opt3020013





