1. Introduction
Current asymmetric key cryptography systems are based on algorithms whose mathematical operations are trivial in a direction, but their corresponding reverse operations are practically unsolvable in low computational times [
1]. Several algorithms in public-key (asymmetric-key) cryptography base their security on the assumption that the discrete logarithm problem has no efficient solution [
2,
3]. P. Shor proposed a quantum algorithm that allows solving the problem of factoring large integers and computing the discrete logarithm [
4,
5]. The emergence of quantum computing drives the need for a paradigm shift. Quantum communication could protect sensitive data and digital infrastructure in the future. For this, it is necessary to design and deploy quantum networks protected from hacking attacks and other security lacks.
There are numerous successful experiments on quantum communication at distances over 100 km on fiber optic channels [
6,
7]. However, trying to put a realistic approach orienting to a commercial implementation into real conditions, distances below 50 km have been considered based on the experiences [
8]. It is demonstrated that at those distances with current commercial equipment such as those manufactured by the ID Quantique SA company achieve remarkable results. This device makes it possible to exchange around 100,000 quantum keys in one hour [
9]. We can find methodologies to design commercial quantum networks through the distribution of quantum repeaters, such as the one proposed by I. García-Cobo and H. D. Menéndez (2021) [
10].
2. Challenges, Scope, and Contributions
The implementation of commercial fiber optic quantum networks requires management. In a commercial exploitation scenario, the needs for network availability, service quality assurance, and ability to recover from unforeseen incidents arise. This article aims to respond to the needs derived from the use of commercial fiber optic networks for use in the creation of a quantum network. It is based on previous work carried out for the design of the network, focusing on methods that are resilient to attacks or degradation due to its use or accidents. We propose a method to achieve a robust and reliable quantum network model. A network management method is presented, which allows its continuous work with the lesser possible impact. This method could face possible sabotage to any node or channel.
3. Distribution of Nodes in the Quantum Network
To build a network that connects all the inhabitants to each other, a distributed network of repeaters must be designed. To carry out this distribution, a methodology based on grouping of municipalities is used, through a k-medoid algorithm [
10]. This algorithm will help to select those that are physically closer to each other. Afterward, the algorithm will facilitate the selection of the central or main municipality within the group. This municipality will be considered as a candidate to host a repeater. The methodology, finally, will try to connect the possible repeaters between them to generate a distribution network by using the described method again.
Repeaters Network
To guarantee that any municipality within the network can communicate with any other, it is necessary to establish a repeater network based on the representative municipalities selected in the previous step and organized by clusters and environments. A cluster is a group of municipalities with at least one repeater and an environment is a group of repeaters. This network is defined as follows:
Each representative municipality will connect with all the municipalities in its cluster. In this way, all the municipalities of the same cluster will be able to exchange quantum keys using the repeater. It is guaranteed that the repeater is at a lower distance than D (where D is the maximum acceptable distance—we considered 50 km) with respect to each municipality in its cluster.
Each repeater will connect to all repeaters in its environment that are within a distance lower than D. Thus, if various repeaters are close to one another, different routing can be used to reduce key distribution cluster.
These criteria when creating networks not only facilitate the achievement of better routing, but also identify possible isolated regions. To be able to find these regions, it will be enough to calculate the number of connected components of the network. Formally, the network is an undirected polygonal graph (
G), divided into vertices (
V), which represent the municipalities and edges (
E) that represent those municipalities that either are within a cluster and are connected to its repeater, or are repeaters to a distance lower than D, between them. In this way, the number of connected components of the graph can be calculated in several ways, where the most representative are the multiplicity of their eigenvalues, or the estimation using random paths [
11]. If the number of connected components of the graph is at least one, the network is totally connected.
4. Security in Quantum Communications
The security of the channels on which quantum communication protocols are implemented reside in the properties of quantum mechanics—as long as it behaves as postulated by Fox (2006) [
12]. Considering these principles, when an attacker named Eve interacts with the key that is distributed, it causes a disturbance in the communication that could be detected by Alice and/or Bob. In this concept, Eve must not have access to the devices that Alice and Bob use for exchanging quantum keys, which will obtain a secure communication. In addition, up until now, the classic channel was authenticated by recognizing what Alice and Bob claimed to really be. Here are some of the attacks on the quantum channel that need to be considered.
4.1. Beam Splitting Attack
This attack is probably the most damaging that can be carried out on fiber optic quantum key distribution systems. As described by Calsamiglia et al. (2002) [
13], there are losses associated with the channel itself. In this attack, this circumstance is used to extract part of the key by means of an optical coupler on the quantum channel without Bob being aware of Eve’s presence.
4.2. Photon Number Splitting Attack
As described by Sabottke et al. (2012) [
14] in a Photon Number Splitting Attack (PNS), Eve will perform a non-destructive measurement of the number of photons in each pulse. If she detects more than one photon in each pulse, she will store one of them to measure. The rest will be sent to Bob [
15].
4.3. Intercept and Resend Attack
Finally, we find the easiest attack we can carry out [
16]. Eve intercepts the photons, measures them using a random basis, and returns the photons to Alice.
5. Approach to a Network Management System
The repeaters (network nodes) must recognize the complete topology of the network, as well as some instructions to know where to redirect their messages in case they are not themselves the destination of these.
A related network has been designed on the territory under study (Spain) as an application case. All repeaters are interconnected in such a way that this objective is achieved. The next step is to implement the logic to establish the optimal path for a message to arrive between any pair of points on the network. Every municipality must be able to communicate with the rest.
5.1. Network Topology
The first of the features is based on a network topology map. This map identifies the complete network, its different nodes, and the networks that relate these nodes. The information of the designed network must be housed in the management element for each node and in each final element of the network. An abstraction of the physical implementation of the network can be established, in such a way that this topology, based on the fiber network itself and the repeaters, constitutes a true logical topology. It serves each part of the network. These topology files provide the necessary instructions so that an end user can route the request to first point. In the same way, based on these defined paths, the quantum repeaters will know the next nodes to be (subsidiary network) and where to transmit the information.
5.2. Cost Matrix
The population distribution in the territory is not homogeneous. There is an atomizing effect on demographic distributions. In the application of the node distribution, exclusive distance criteria have been considered (although the premise of municipalities with more than 1000 inhabitants has been taken into account in previous work [
10]). This constitutes an in-homogeneous configuration of the network load. Initially, a cost matrix is defined according to the target population served by each node. Each node is signaled by an identifier and a number that link with the population served. We add complexity to the matrix by indicating the distance between each of the connected nodes. In this way, we have created the first matrix.
5.3. Node and Channel Health Check
Each node can continuously verify its saturation status, the requests that it is attending, and other variables that can be defined linked to its specific status. That information is transmitted to the rest of the elements of the network, thus obtaining global status information of the system, which is known by every element of the system.
5.4. Searching the Optimal Path
One of the objectives of this research consists of introducing a novel element in the management of the quantum network. Considering for each repeater: its dimension (the target population of each node), the distance between them and their instantaneous health, the packet routing process can be given intelligence. The method consists of building a dynamic matrix that can be used for obtaining a cost algorithm to determine the optimal way to deliver the messages. At the beginning of the simulation, the nodes start from the defined network topology and the initial cost matrix. In the moment when a user sends a message through the quantum network, the system can route that message. The automatic sending of quality data (health information) between nodes for the network and its nodes will modify the routing of the message between Alice and Bob. This method is proposed based on the algorithm introduced by Dijkstra (1959) [
17]. If problems are detected in a channel, its weight will increase, then the path will be modified consistently.
5.5. Justification Based on Previous Research
There are previous works in which the usefulness of the application of the Dijkstra algorithm for the intelligent management of fiber optic networks is discussed and tested [
18]. We found comparisons of the use of the chosen algorithm—Dijkstra—versus others—Heuristics, Yen KSP, and some others—on large networks with random node generation tests [
19], showing the prevalence of Dijkstra use. Its usefulness to guarantee the quality of the service provided QoS in network management is also analyzed [
20].
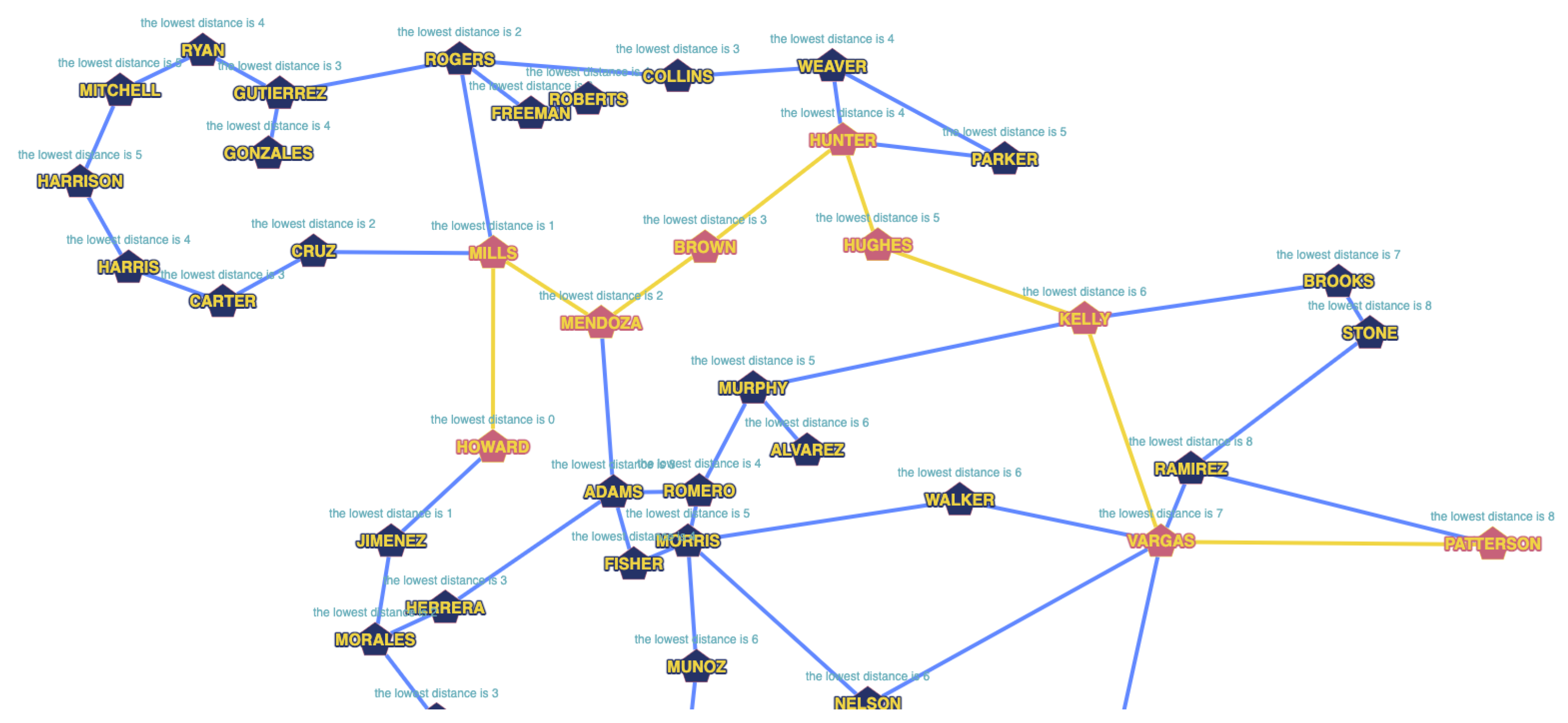
6. Simulation
To test the method, the sudden inoperability of one of the nodes or the disconnection of a part of the network due to a problem in one of the segments is simulated. The simulation starts from an ideal network in which the different nodes and their connections are shown in the
Figure 1. An initialization state with no network element saturation is supposed.
In this representation of the network (
Figure 2), the nodes—vertices—(marked with pentagons) are quantum repeaters. They are assigned a
name identifier to mark each node. The network that links the nodes—edges—has an assigned dimension (weight), which is ideal and equal to 0.
In our simulation (
Figure 3), we start from the node identified as
and go to the one identified as
. We apply Dijkstra’s algorithm to calculate the initial optimal path. The initial optimal path whose length is 8 is:
⟹
⟹
⟹
⟹
⟹
⟹
⟹
⟹
.
6.1. Deleting a Node
When eliminating a node from the network, it cannot send its status to the rest of the nodes, so they will stop managing the distribution of packets. Consequently, there will be unavailability in that node and in those channels that link the node with its neighbors, but alternative paths can be traced, solving the interruption. As an example, in
Figure 4, the node identified with
is eliminated and the algorithm is calculated again.
After deleting , the optimal path is: ⟹⟹⟹⟹⟹⟹⟹⟹.
6.2. Canceling a Segment
If a segment that links a pair of nodes becomes unused, the nodes will stop using that channel. By using Dijkstra algorithm’s calculation, a new path will be traced to be able to route the messages accordingly. In that simulation, from initial state, the segment that linked node
and node
was eliminated (
Figure 5):
When segment connecting and is invalidated new optimal path is: ⟹⟹⟹⟹⟹⟹⟹⟹⟹.
7. Conclusions
The main contribution of this article consists of the dynamic calculation of the optimal routes in two concurrent scenarios:
In situations of a saturation of a node and an element of the network, the algorithm will dynamically create a new route, guaranteeing the delivery of the message.
At the time of sabotage or incident that renders an element of the quantum network useless, the algorithm will isolate the possible attacked node—or segment of the network, depending on the case—and will redirect the traffic using alternative routes to guarantee the best possible performance of the network.
We managed to provide robustness and reliability to our quantum network. We introduced a network management method that allows its continuity with the least possible impact, in the face of an imponderable event, whether voluntary or derived from the use of the nodes and the channel.