Angle-Resolved Optical Characterization of a Plasmonic Triangular Array of Elliptical Holes in a Gold Layer
Abstract
:1. Introduction
2. Materials and Methods
2.1. Nanofabrication
2.2. Optical Characterization
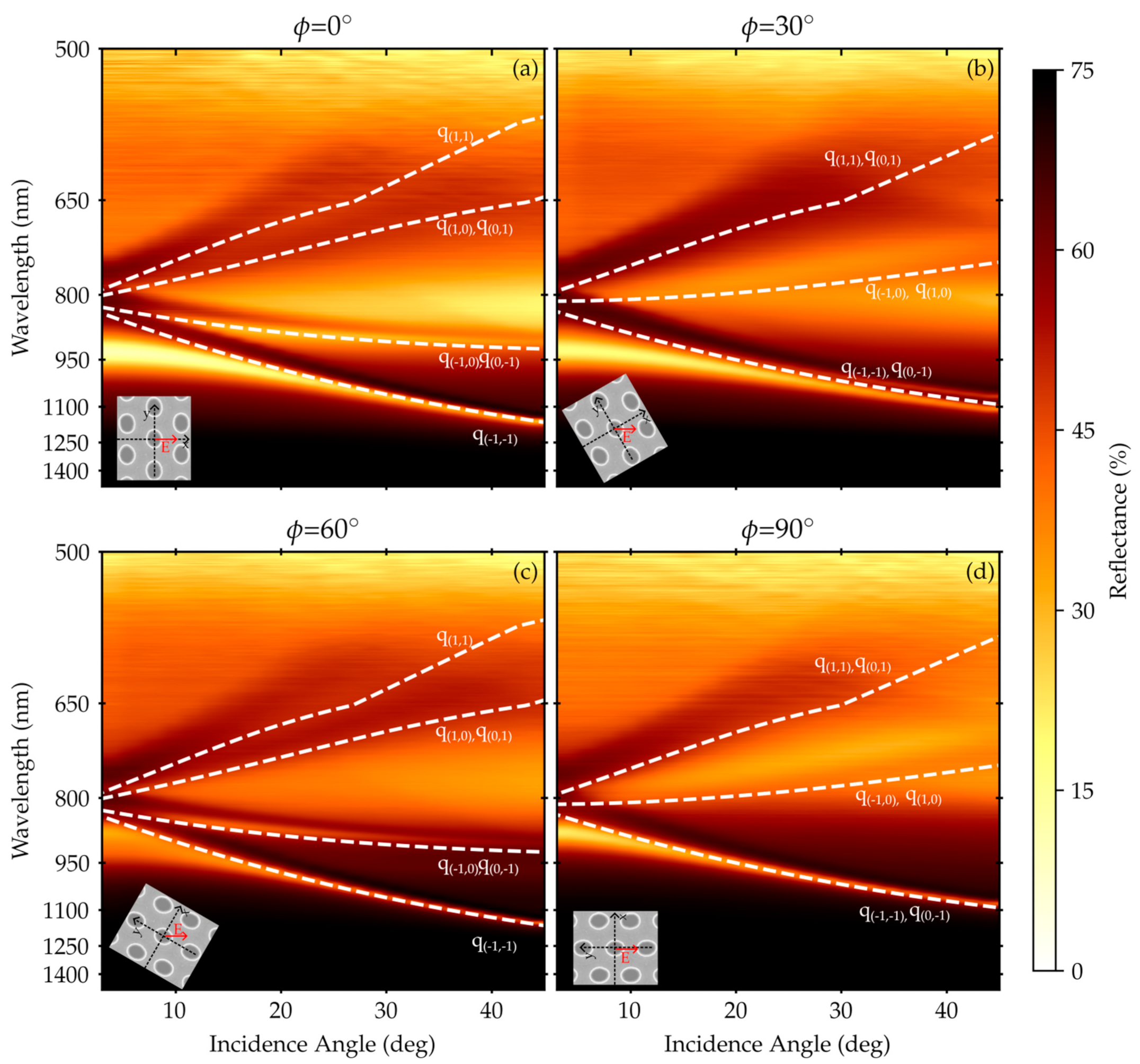
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Finite-Difference Time-Domain Simulations
References
- Yang, K.; Yao, X.; Liu, B.; Ren, B. Metallic Plasmonic Array Structures: Principles, Fabrications, Properties, and Applications. Adv. Mater. 2021, 33, 2007988. [Google Scholar] [CrossRef] [PubMed]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007; ISBN 978-0-387-33150-8. [Google Scholar]
- García De Abajo, F.J. Colloquium: Light Scattering by Particle and Hole Arrays. Rev. Mod. Phys. 2007, 79, 1267–1290. [Google Scholar] [CrossRef]
- Sun, L.L.; Leo, Y.S.; Zhou, X.; Ng, W.; Wong, T.I.; Deng, J. Localized Surface Plasmon Resonance Based Point-of-Care System for Sepsis Diagnosis. Mater. Sci. Energy Technol. 2020, 3, 274–281. [Google Scholar] [CrossRef]
- Escobedo, C. On-Chip Nanohole Array Based Sensing: A Review. Lab. Chip 2013, 13, 2445. [Google Scholar] [CrossRef] [PubMed]
- Bottazzi, B.; Fornasari, L.; Frangolho, A.; Giudicatti, S.; Mantovani, A.; Marabelli, F.; Marchesini, G.; Pellacani, P.; Therisod, R.; Valsesia, A. Multiplexed Label-Free Optical Biosensor for Medical Diagnostics. J. Biomed. Opt. 2014, 19, 017006. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; Lin, H.; Lin, S.; Wu, J.; Li, W.; Meng, F.; Yang, Y.; Huang, X.; Jia, B.; Kivshar, Y. Hybrid Anisotropic Plasmonic Metasurfaces with Multiple Resonances of Focused Light Beams. Nano Lett. 2021, 21, 8917–8923. [Google Scholar] [CrossRef] [PubMed]
- Angelini, M.; Manobianco, E.; Pellacani, P.; Floris, F.; Marabelli, F. Plasmonic Modes and Fluorescence Enhancement Coupling Mechanism: A Case with a Nanostructured Grating. Nanomaterials 2022, 12, 4339. [Google Scholar] [CrossRef] [PubMed]
- Bauch, M.; Toma, K.; Toma, M.; Zhang, Q.; Dostalek, J. Plasmon-Enhanced Fluorescence Biosensors: A Review. Plasmonics 2014, 9, 781–799. [Google Scholar] [CrossRef]
- Brolo, A.G.; Kwok, S.C.; Moffitt, M.G.; Gordon, R.; Riordon, J.; Kavanagh, K.L. Enhanced Fluorescence from Arrays of Nanoholes in a Gold Film. J. Am. Chem. Soc. 2005, 127, 14936–14941. [Google Scholar] [CrossRef]
- Guo, P.-F.; Wu, S.; Ren, Q.-J.; Lu, J.; Chen, Z.; Xiao, S.-J.; Zhu, Y.-Y. Fluorescence Enhancement by Surface Plasmon Polaritons on Metallic Nanohole Arrays. J. Phys. Chem. Lett. 2010, 1, 315–318. [Google Scholar] [CrossRef]
- Cui, X.; Tawa, K.; Hori, H.; Nishii, J. Tailored Plasmonic Gratings for Enhanced Fluorescence Detection and Microscopic Imaging. Adv. Funct. Mater. 2010, 20, 546–553. [Google Scholar] [CrossRef]
- Liu, Y.; Blair, S. Fluorescence Enhancement from an Array of Subwavelength Metal Apertures. Opt. Lett. 2003, 28, 507. [Google Scholar] [CrossRef] [PubMed]
- Cialla, D.; März, A.; Böhme, R.; Theil, F.; Weber, K.; Schmitt, M.; Popp, J. Surface-Enhanced Raman Spectroscopy (SERS): Progress and Trends. Anal. Bioanal. Chem. 2012, 403, 27–54. [Google Scholar] [CrossRef] [PubMed]
- Hering, K.; Cialla, D.; Ackermann, K.; Dörfer, T.; Möller, R.; Schneidewind, H.; Mattheis, R.; Fritzsche, W.; Rösch, P.; Popp, J. SERS: A Versatile Tool in Chemical and Biochemical Diagnostics. Anal. Bioanal. Chem. 2008, 390, 113–124. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Tian, H.; Huang, L.; Chen, Q.; Yang, Y.; Zeng, R.; Xu, J.; Chen, S.; Zhou, X.; Liu, G.; et al. Well-Ordered Au Nanoarray for Sensitive and Reproducible Detection of Hepatocellular Carcinoma-Associated miRNA via CHA-Assisted SERS/Fluorescence Dual-Mode Sensing. Anal. Chem. 2023, 95, 5955–5966. [Google Scholar] [CrossRef] [PubMed]
- Gu, Y.; Zhang, L.; Yang, J.K.W.; Yeo, S.P.; Qiu, C.-W. Color Generation via Subwavelength Plasmonic Nanostructures. Nanoscale 2015, 7, 6409–6419. [Google Scholar] [CrossRef]
- Raj Shrestha, V.; Lee, S.-S.; Kim, E.-S.; Choi, D.-Y. Polarization-Tuned Dynamic Color Filters Incorporating a Dielectric-Loaded Aluminum Nanowire Array. Sci. Rep. 2015, 5, 12450. [Google Scholar] [CrossRef]
- Ellenbogen, T.; Seo, K.; Crozier, K.B. Chromatic Plasmonic Polarizers for Active Visible Color Filtering and Polarimetry. Nano Lett. 2012, 12, 1026–1031. [Google Scholar] [CrossRef] [PubMed]
- Ebbesen, T.W.; Lezec, H.J.; Ghaemi, H.F.; Thio, T.; Wolff, P.A. Extraordinary Optical Transmission through Sub-Wavelength Hole Arrays. Nature 1998, 391, 667–669. [Google Scholar] [CrossRef]
- Degiron, A.; Ebbesen, T.W. The Role of Localized Surface Plasmon Modes in the Enhanced Transmission of Periodic Subwavelength Apertures. J. Opt. A Pure Appl. Opt. 2005, 7, S90–S96. [Google Scholar] [CrossRef]
- Liu, H.; Lalanne, P. Microscopic Theory of the Extraordinary Optical Transmission. Nature 2008, 452, 728–731. [Google Scholar] [CrossRef]
- Martín-Moreno, L.; García-Vidal, F.J.; Lezec, H.J.; Pellerin, K.M.; Thio, T.; Pendry, J.B.; Ebbesen, T.W. Theory of Extraordinary Optical Transmission through Subwavelength Hole Arrays. Phys. Rev. Lett. 2001, 86, 1114–1117. [Google Scholar] [CrossRef] [PubMed]
- Barnes, W.L.; Murray, W.A.; Dintinger, J.; Devaux, E.; Ebbesen, T.W. Surface Plasmon Polaritons and Their Role in the Enhanced Transmission of Light through Periodic Arrays of Subwavelength Holes in a Metal Film. Phys. Rev. Lett. 2004, 92, 107401. [Google Scholar] [CrossRef]
- Martin-Moreno, L.; Garcia-Vidal, F.J. Optical Transmission through Circular Hole Arrays in Optically Thick Metal Films. Opt. Express 2004, 12, 3619–3628. [Google Scholar] [CrossRef]
- Sepúlveda, B.; Alaverdyan, Y.; Alegret, J.; Käll, M.; Johansson, P. Shape Effects in the Localized Surface Plasmon Resonance of Single Nanoholes in Thin Metal Films. Opt. Express 2008, 16, 5609. [Google Scholar] [CrossRef] [PubMed]
- Degiron, A.; Lezec, H.J.; Barnes, W.L.; Ebbesen, T.W. Effects of Hole Depth on Enhanced Light Transmission through Subwavelength Hole Arrays. Appl. Phys. Lett. 2002, 81, 4327–4329. [Google Scholar] [CrossRef]
- Mary, A.; Rodrigo, S.G.; Martín-Moreno, L.; García-Vidal, F.J. Theory of Light Transmission through an Array of Rectangular Holes. Phys. Rev. B 2007, 76, 195414. [Google Scholar] [CrossRef]
- Genet, C.; Ebbesen, T.W. Light in Tiny Holes. Nature 2007, 445, 39–46. [Google Scholar] [CrossRef]
- Garcia-Vidal, F.J.; Martin-Moreno, L.; Ebbesen, T.W.; Kuipers, L. Light Passing through Subwavelength Apertures. Rev. Mod. Phys. 2010, 82, 729–787. [Google Scholar] [CrossRef]
- Shafiq, R.; Khan, A.D.; Al-Harbi, F.F.; Ali, F.; Armghan, A.; Asif, M.; Rehman, A.U.; Ali, E.M.; Arpanaei, F.; Alibakhshikenari, M.; et al. Optical Transmission Plasmonic Color Filter with Wider Color Gamut Based on X-Shaped Nanostructure. Photonics 2022, 9, 209. [Google Scholar] [CrossRef]
- Wang, Y.; Qin, Y.; Zhang, Z. Extraordinary Optical Transmission Property of X-Shaped Plasmonic Nanohole Arrays. Plasmonics 2014, 9, 203–207. [Google Scholar] [CrossRef]
- Balaur, E.; Sadatnajafi, C.; Kou, S.S.; Lin, J.; Abbey, B. Continuously Tunable, Polarization Controlled, Colour Palette Produced from Nanoscale Plasmonic Pixels. Sci. Rep. 2016, 6, 28062. [Google Scholar] [CrossRef] [PubMed]
- Langley, D.; Balaur, E.; Sadatnajafi, C.; Abbey, B. Dual Pitch Plasmonic Devices for Polarization Enhanced Colour Based Sensing. In SPIE BioPhotonics Australasia, Proceedings of the SPIE Biophotonics Australasia 2016, Adelaide, Australia, 16–19 October 2016; Hutchinson, M.R., Goldys, E.M., Eds.; SPIE Digital Library: Bellingham, WA, USA, 2016; p. 1001338. [Google Scholar]
- Sadatnajafi, C.; Balaur, E.; Abbey, B. Bimodal Plasmonic Color Filters Enable Direct Optical Imaging of Ion Implantation in Thin Films. Adv. Funct. Mater. 2022, 32, 2009419. [Google Scholar] [CrossRef]
- Gordon, R.; Brolo, A.G.; McKinnon, A.; Rajora, A.; Leathem, B.; Kavanagh, K.L. Strong Polarization in the Optical Transmission through Elliptical Nanohole Arrays. Phys. Rev. Lett. 2004, 92, 037401. [Google Scholar] [CrossRef]
- Gordon, R.; Hughes, M.; Leathem, B.; Kavanagh, K.L.; Brolo, A.G. Basis and Lattice Polarization Mechanisms for Light Transmission through Nanohole Arrays in a Metal Film. Nano Lett. 2005, 5, 1243–1246. [Google Scholar] [CrossRef]
- Li, J.; Iu, H.; Wan, J.T.K.; Ong, H.C. The Plasmonic Properties of Elliptical Metallic Hole Arrays. Appl. Phys. Lett. 2009, 94, 033101. [Google Scholar] [CrossRef]
- Strelniker, Y.M. Theory of Optical Transmission through Elliptical Nanohole Arrays. Phys. Rev. B 2007, 76, 085409. [Google Scholar] [CrossRef]
- Wu, S.; Zhou, L.; Wang, Y.; Wang, G.; Wang, Q.; Huang, C.; Zhu, Y. Optical Properties of a Metal Film Perforated with Coaxial Elliptical Hole Arrays. Phys. Rev. E 2010, 81, 057601. [Google Scholar] [CrossRef]
- Ai, B.; Basnet, P.; Larson, S.; Ingram, W.; Zhao, Y. Plasmonic Sensor with High Figure of Merit Based on Differential Polarization Spectra of Elliptical Nanohole Array. Nanoscale 2017, 9, 14710–14721. [Google Scholar] [CrossRef]
- Lovera, P.; Jones, D.; O’Riordan, A. Elliptical Nanohole Array in Thin Gold Film as Micrometer Sized Optical Filter Set for Fluorescent-Labelled Assays. J. Phys. Conf. Ser. 2011, 307, 012006. [Google Scholar] [CrossRef]
- Petronijevic, E.; Belardini, A.; Leahu, G.; Cesca, T.; Scian, C.; Mattei, G.; Sibilia, C. Circular Dichroism in Low-Cost Plasmonics: 2D Arrays of Nanoholes in Silver. Appl. Sci. 2020, 10, 1316. [Google Scholar] [CrossRef]
- Ali, H.; Petronijevic, E.; Pellegrini, G.; Sibilia, C.; Andreani, L.C. Circular Dichroism in a Plasmonic Array of Elliptical Nanoholes with Square Lattice. Opt. Express 2023, 31, 14196. [Google Scholar] [CrossRef]
- Petronijevic, E.; Ghahri, R.; Sibilia, C. Plasmonic Elliptical Nanohole Arrays for Chiral Absorption and Emission in the Near-Infrared and Visible Range. Appl. Sci. 2021, 11, 6012. [Google Scholar] [CrossRef]
- Aigner, A.; Tittl, A.; Wang, J.; Weber, T.; Kivshar, Y.; Maier, S.A.; Ren, H. Plasmonic Bound States in the Continuum to Tailor Light-Matter Coupling. Sci. Adv. 2022, 8, eadd4816. [Google Scholar] [CrossRef]
- Zagaglia, L.; Zanotti, S.; Minkov, M.; Liscidini, M.; Gerace, D.; Claudio Andreani, L. Polarization States and Far-Field Optical Properties in Dielectric Photonic Crystal Slabs. Opt. Lett. 2023, 48, 5017. [Google Scholar] [CrossRef]
- Tang, Y.; Liang, Y.; Yao, J.; Chen, M.K.; Lin, S.; Wang, Z.; Zhang, J.; Huang, X.G.; Yu, C.; Tsai, D.P. Chiral Bound States in the Continuum in Plasmonic Metasurfaces. Laser Photonics Rev. 2023, 17, 2200597. [Google Scholar] [CrossRef]
- Solak, H.H.; Dais, C.; Clube, F. Displacement Talbot Lithography: A New Method for High-Resolution Patterning of Large Areas. Opt. Express 2011, 19, 10686. [Google Scholar] [CrossRef] [PubMed]
- Balaur, E.; Sadatnajafi, C.; Abbey, B. Large-Scale Fabrication of Optically Active Plasmonic Arrays via Displacement Talbot Lithography. J. Phys. Conf. Ser. 2020, 1455, 012005. [Google Scholar] [CrossRef]
- Giudicatti, S.; Marabelli, F.; Valsesia, A.; Pellacani, P.; Colpo, P.; Rossi, F. Interaction among Plasmonic Resonances in a Gold Film Embedding a Two-Dimensional Array of Polymeric Nanopillars. J. Opt. Soc. Am. B 2012, 29, 1641. [Google Scholar] [CrossRef]
- Giudicatti, S.; Valsesia, A.; Marabelli, F.; Colpo, P.; Rossi, F. Plasmonic Resonances in Nanostructured Gold/Polymer Surfaces by Colloidal Lithography: Plasmonic Resonances in Nanostructured Gold/Polymer Surfaces. Phys. Status Solidi A 2010, 207, 935–942. [Google Scholar] [CrossRef]
- Lumerical Inc. Available online: https://www.Lumerical.Com/Products/Fdtd/ (accessed on 20 December 2023).





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Angelini, M.; Jefimovs, K.; Pellacani, P.; Kazazis, D.; Marabelli, F.; Floris, F. Angle-Resolved Optical Characterization of a Plasmonic Triangular Array of Elliptical Holes in a Gold Layer. Optics 2024, 5, 195-206. https://doi.org/10.3390/opt5010014
Angelini M, Jefimovs K, Pellacani P, Kazazis D, Marabelli F, Floris F. Angle-Resolved Optical Characterization of a Plasmonic Triangular Array of Elliptical Holes in a Gold Layer. Optics. 2024; 5(1):195-206. https://doi.org/10.3390/opt5010014
Chicago/Turabian StyleAngelini, Margherita, Konstantins Jefimovs, Paola Pellacani, Dimitrios Kazazis, Franco Marabelli, and Francesco Floris. 2024. "Angle-Resolved Optical Characterization of a Plasmonic Triangular Array of Elliptical Holes in a Gold Layer" Optics 5, no. 1: 195-206. https://doi.org/10.3390/opt5010014
APA StyleAngelini, M., Jefimovs, K., Pellacani, P., Kazazis, D., Marabelli, F., & Floris, F. (2024). Angle-Resolved Optical Characterization of a Plasmonic Triangular Array of Elliptical Holes in a Gold Layer. Optics, 5(1), 195-206. https://doi.org/10.3390/opt5010014





