Admission Control in Home Energy Management Systems Using Theatre and Hybrid Actors
Abstract
:1. Introduction
2. Related Work
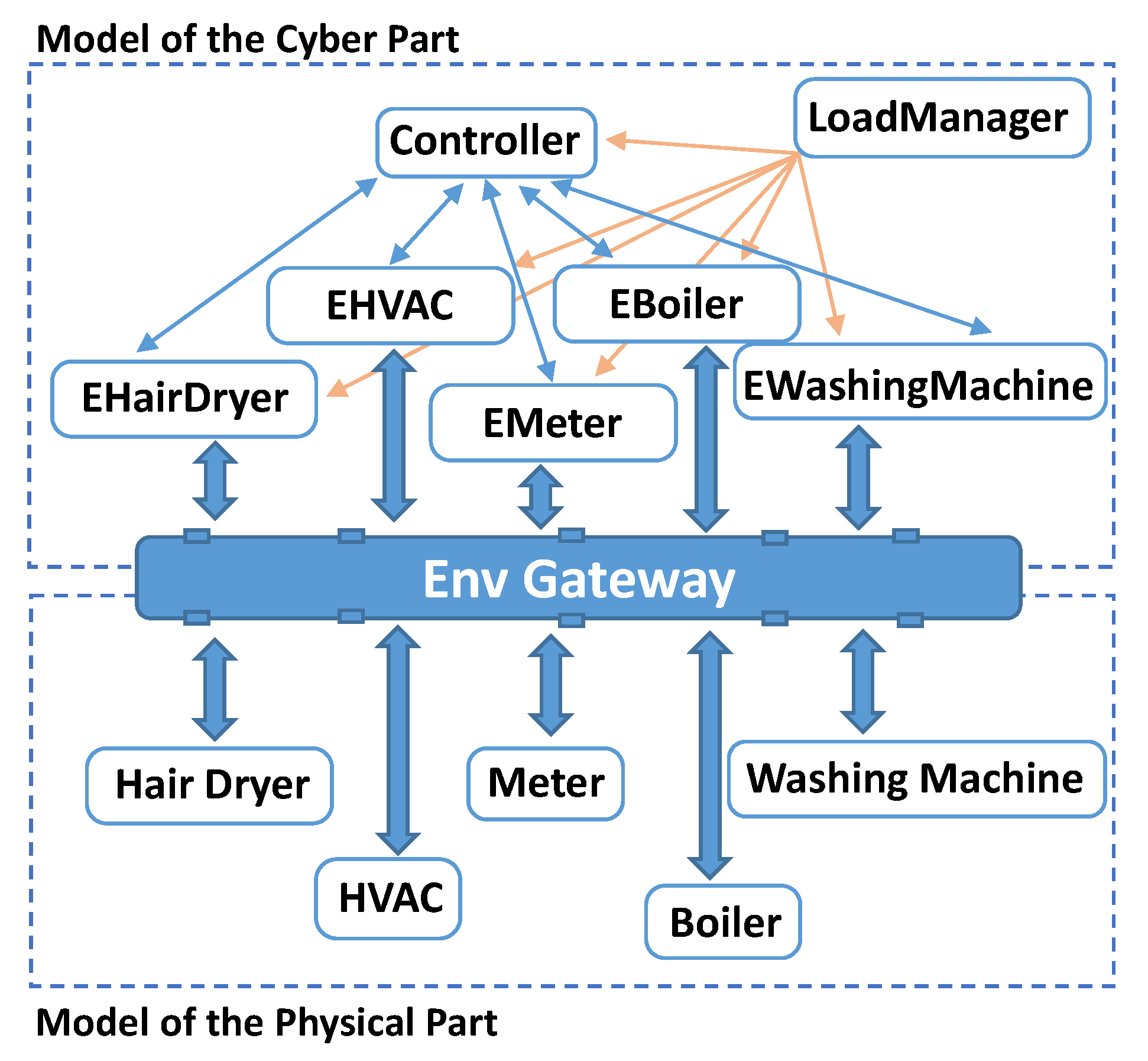
3. A Home Energy Management System
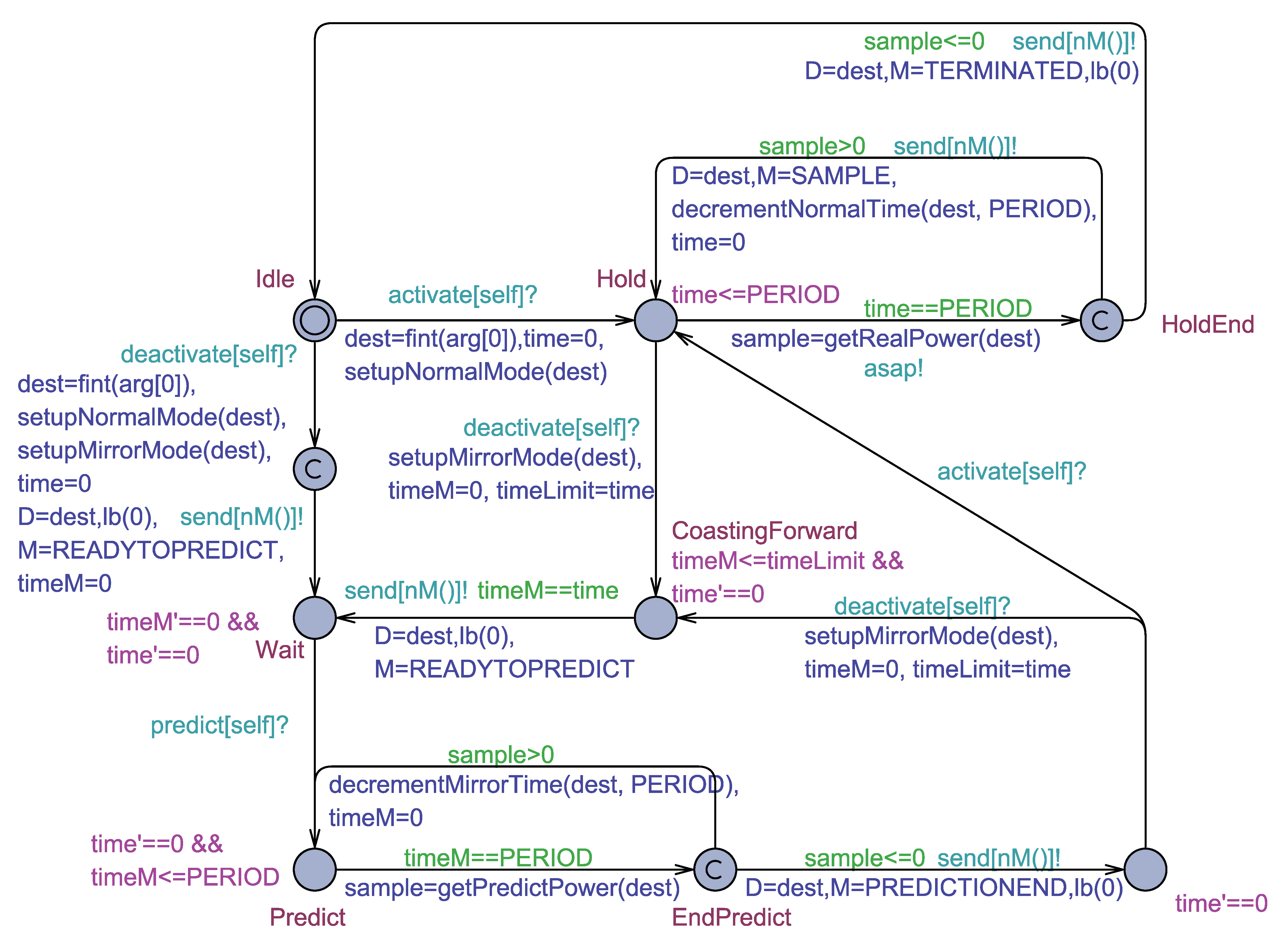
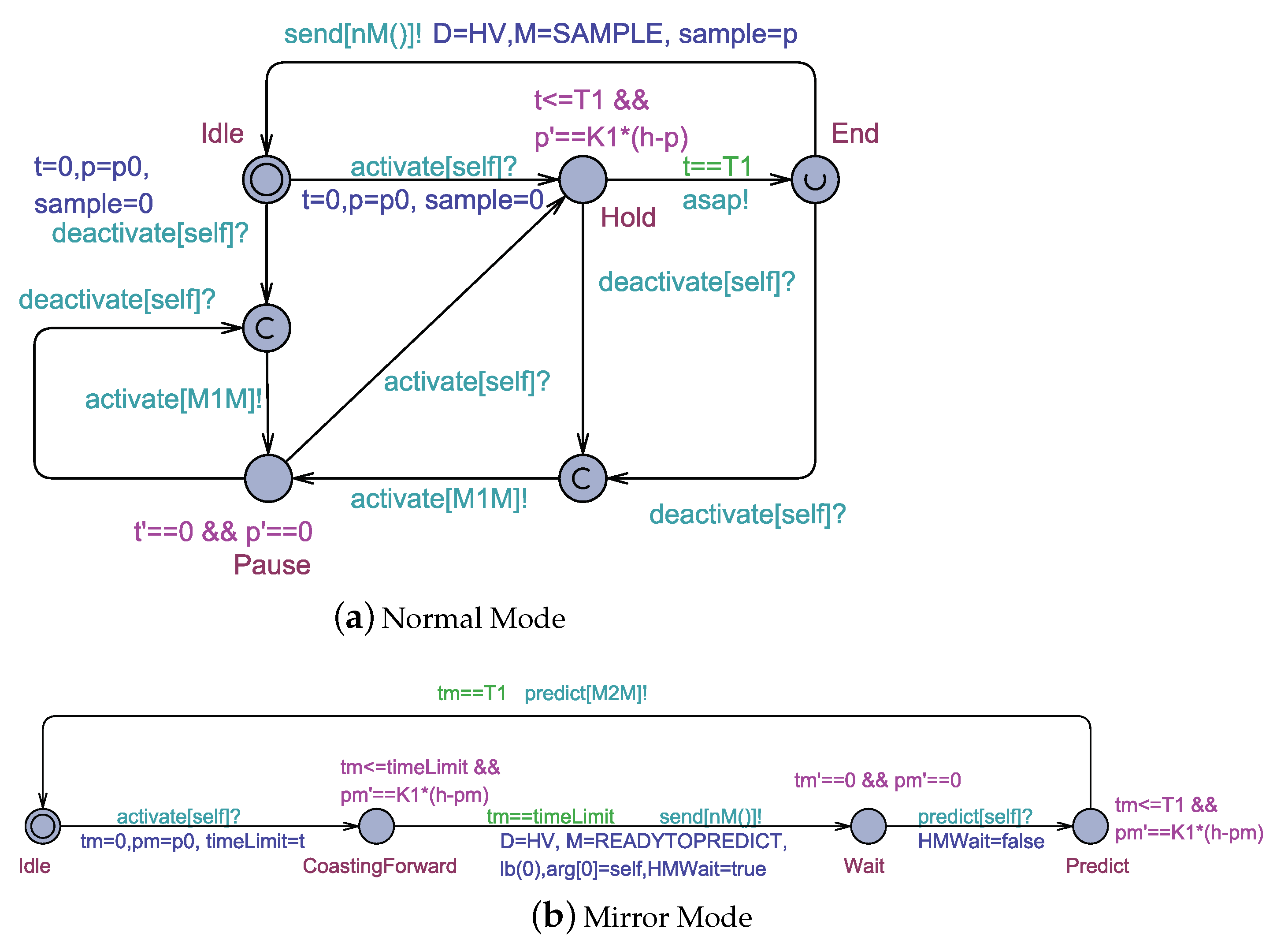
- Active: The load is operating and consumes real power. In this state, the time of the load evolves as the load performs its operation.
- Coasting Forward: The load is not operating and the time of the load gets frozen, i.e., it does not evolve. This phase is preparatory to the prediction state. Since the evolution of the consumption curves during prediction must start from the exact instant in which the load stopped to be active, a coasting forward phase is required to ensure that the prediction curve, starting from the beginning, reaches this instant. In the case a load was not yet activated, during the coasting forward, no operations are carried out.
- Prediction: The load is not operating but the time of the load evolves according to a virtual time notion exploited only for prediction purposes. Once started, the prediction phase runs to completion.
4. Modelling Using Actors and Uppaal
4.1. Basic Issues of Theatre
4.2. Introducing Hybrid Actors
4.3. Cross-Model Aspects When Modelling with Hybrid Theatre
5. The Uppaal Model for the Home Energy Management System
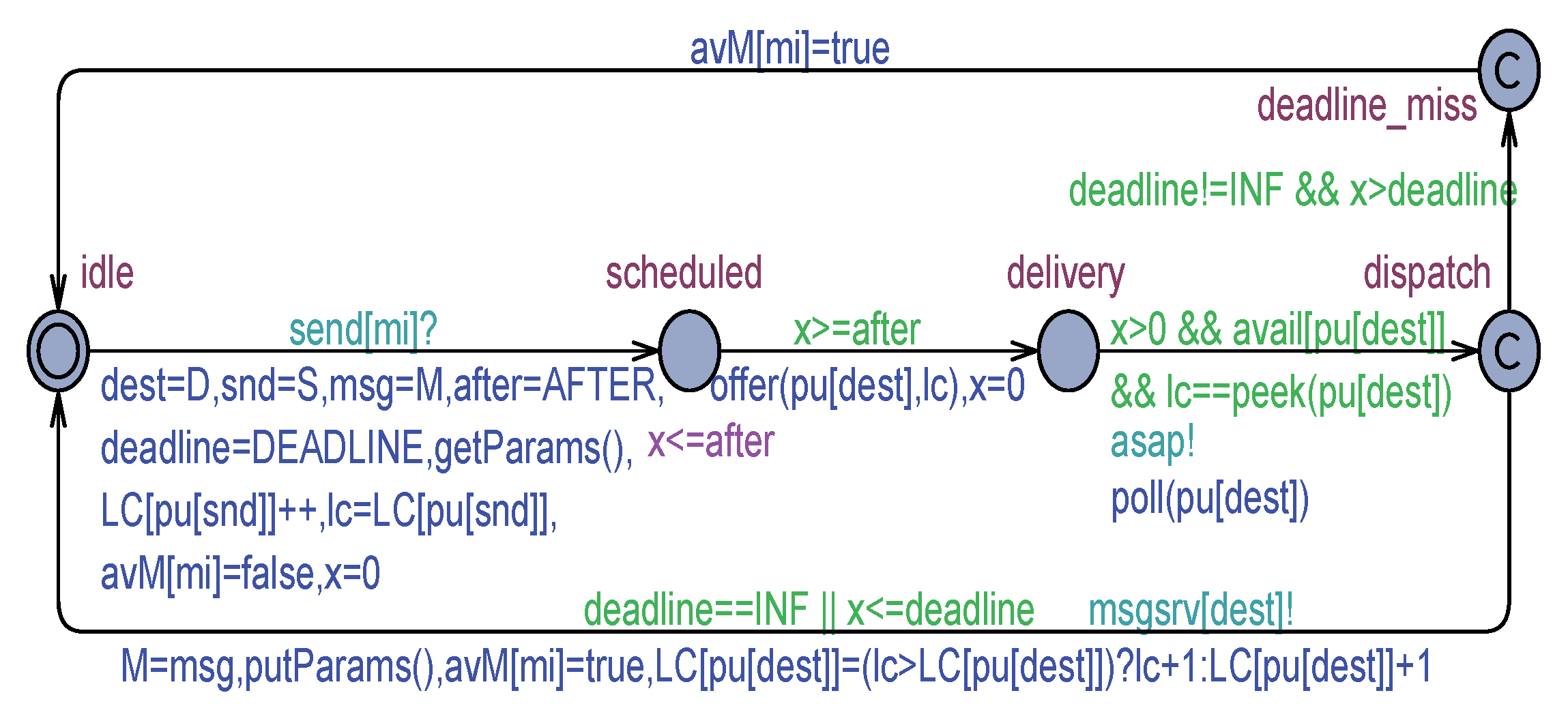
5.1. The Uppaal Model for the Tabular Load Actors
5.2. The Uppaal Model for the HVAC actor
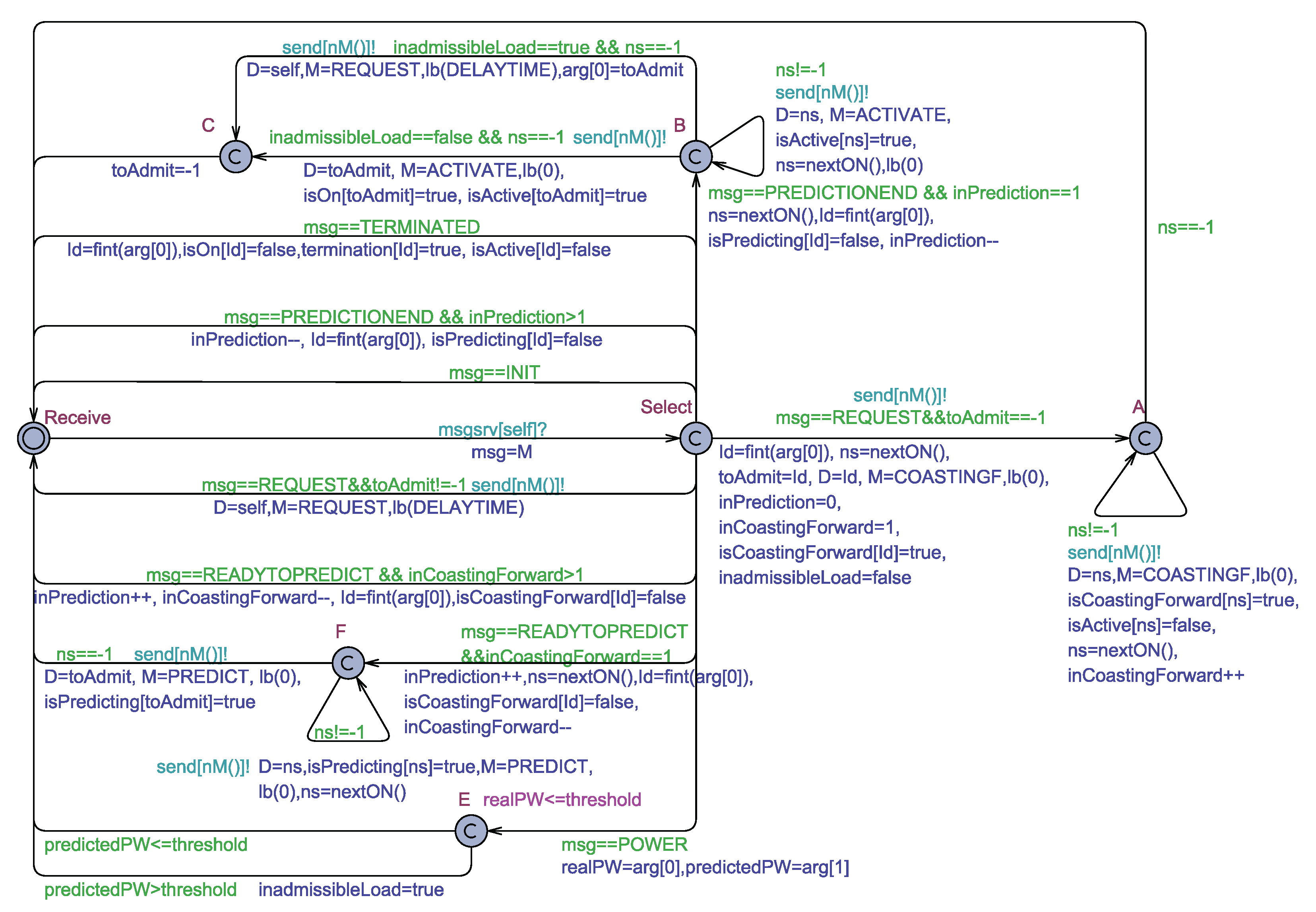
5.3. The Uppaal Model for the Controller Actor
- the controller sends to each active load (if any) the COASTINGF message;
- as soon as all the loads replied with a READYTOPREDICT, the controller sends them a PREDICT message;
- when all the loads replied with a PREDICTIONEND, the controller checks the value of the inadmissibleLoad variable, thus deciding to admit or defer the new load. In the former case, an ACTIVATE message is sent to the new load;
- an ACTIVATE message is sent to each previously active loads.
5.4. The Uppaal Model for the Meter Actor
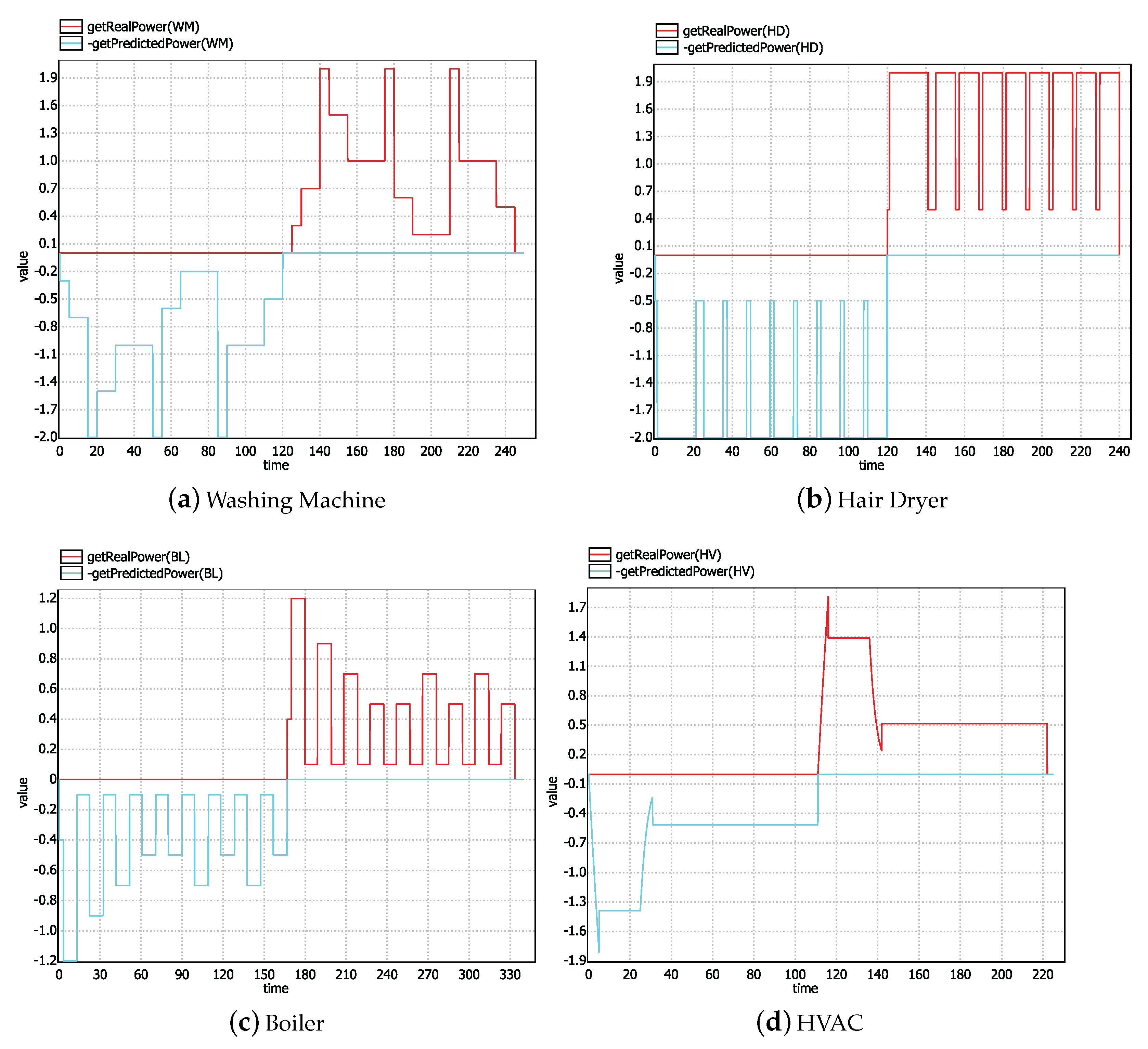
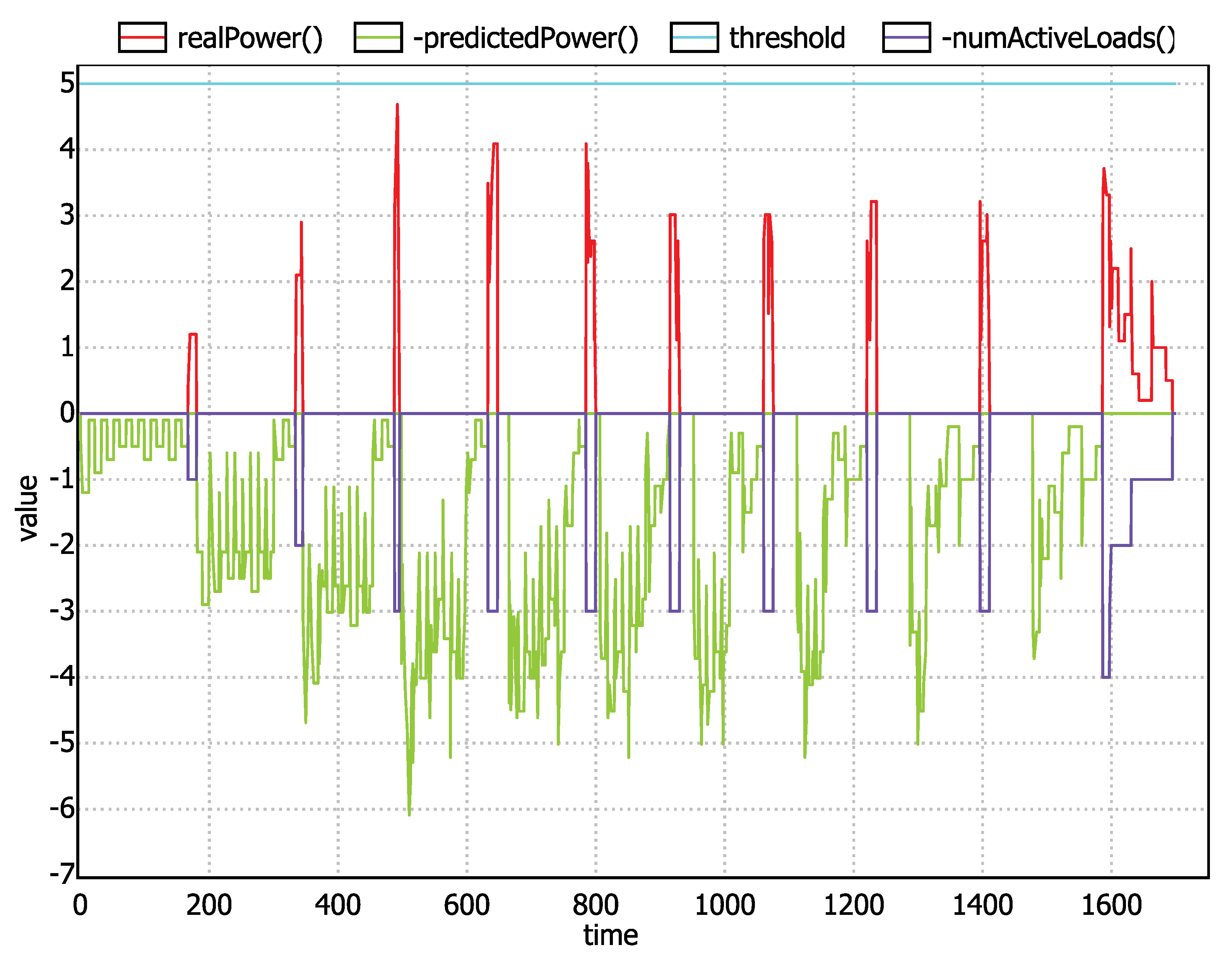
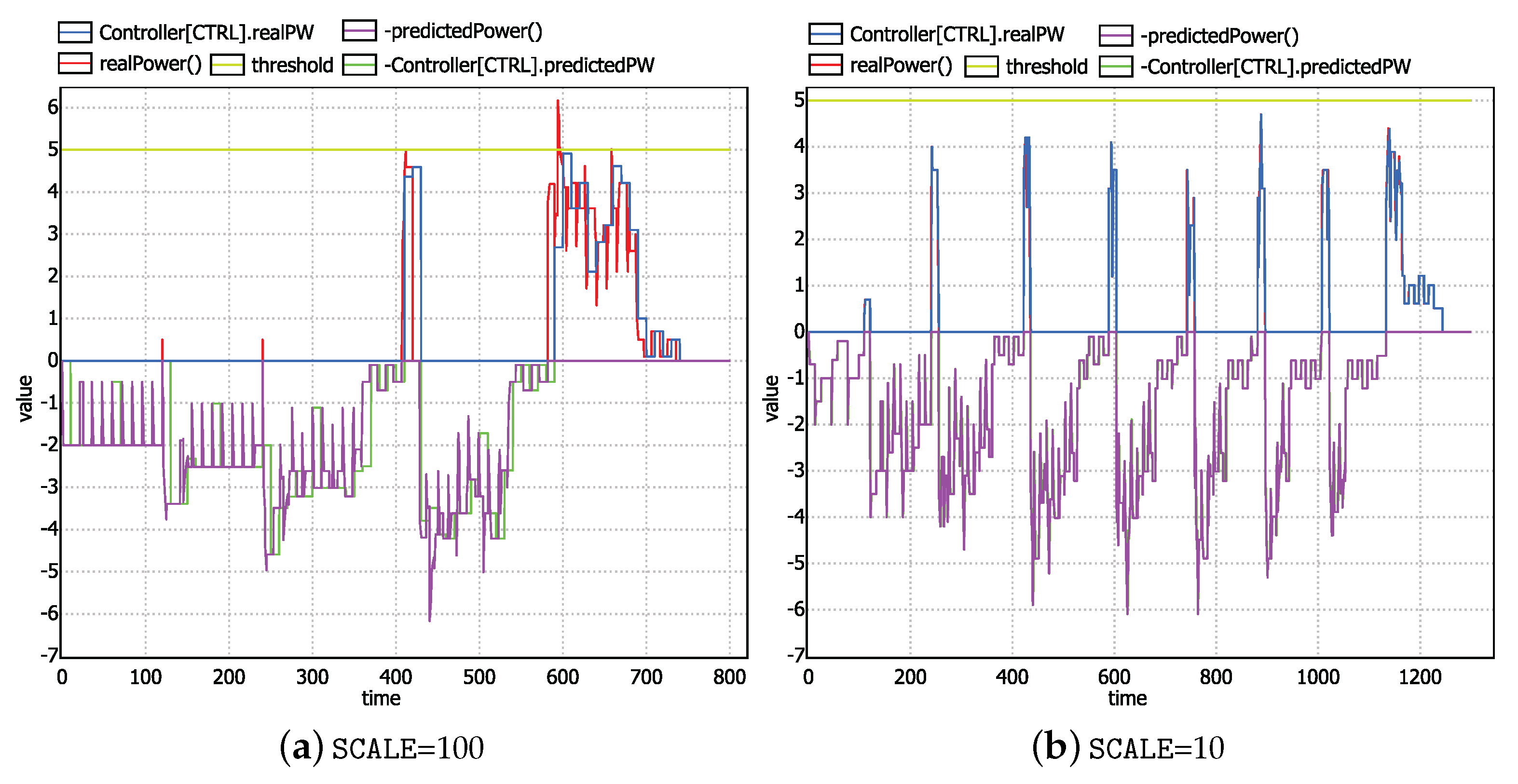
6. Property Checking and Experimental Results
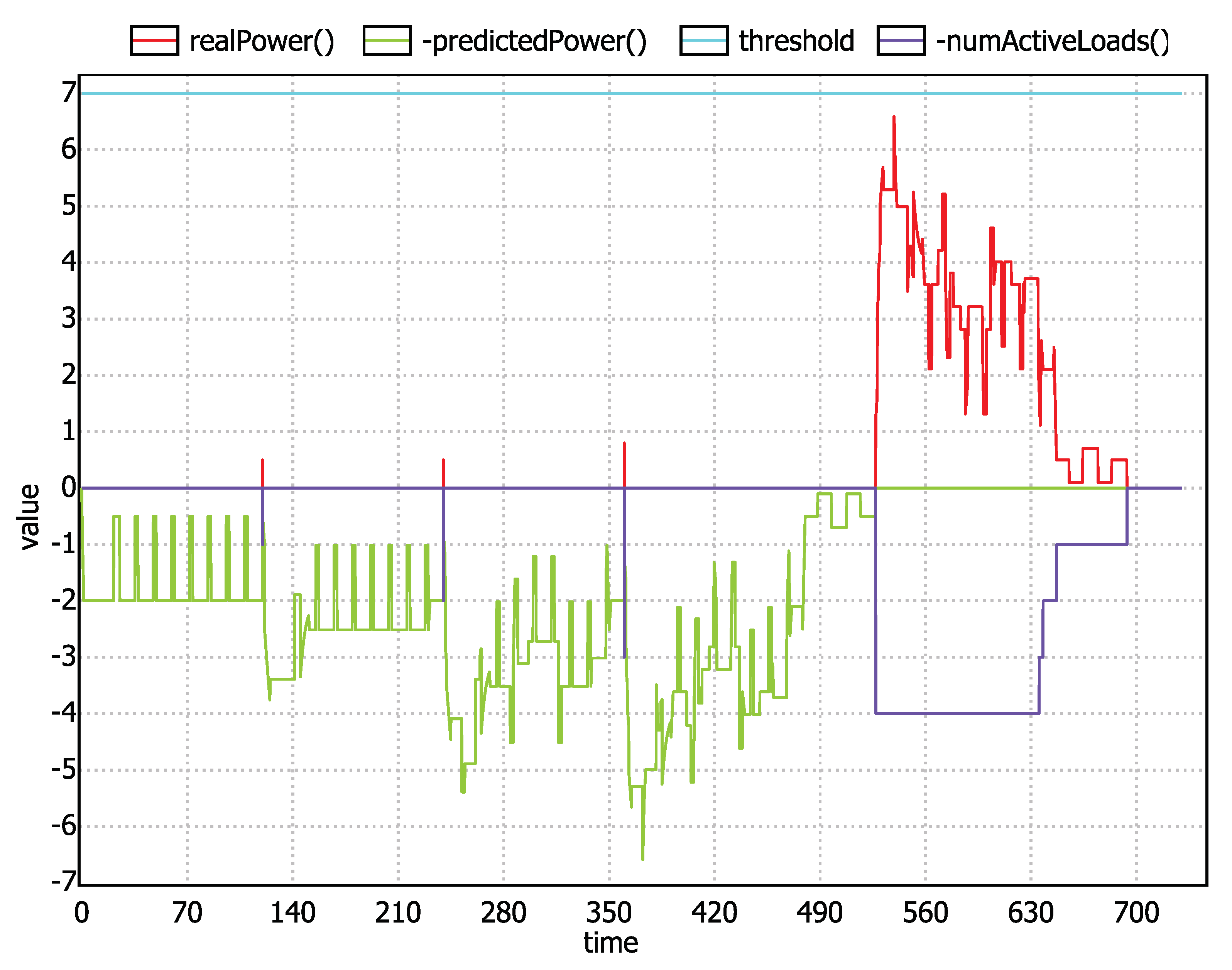
7. Conclusions
- Extending the case study by considering more complex scheduling policies and by using a more general deterministic version of Theatre actors;
- Completing the development of the proposed HEMS with preliminary and final system implementation;
- Enhancing the capabilities of the envGateway by offering basic design constructs and mechanisms for simplifying modelling and analysis of more complex physical environments;
- Experimenting with the proposed approach in more-general IoT-based applications, e.g., in augmented environments like smart homes and smart offices;
- Investigating the possibility of exhaustive model checking a Hybrid Theatre model, by following an approach similar to that adopted in Hybrid Rebeca [12].
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Saleem, Y.; Crespi, N.; Rehmani, M.H.; Copeland, R. Internet of Things-aided Smart Grid: Technologies, Architectures, Applications, Prototypes, and Future Research Directions. IEEE Access 2019. [Google Scholar] [CrossRef]
- Pawlaszczyk, D.; Strassburger, S. Scalability in Distributed Simulations of Agent-Based Models. In Proceedings of the Winter Simulation Conference (WSC), Austin, TX, USA, 13–16 December 2009; pp. 1189–1200. [Google Scholar]
- Siebert, L.C.; Ferreira, L.R.; Yamakawa, E.K.; Custódio, E.S.; Aoki, A.R.; Fernandes, T.S.P.; Cardoso, K.H. Centralized and decentralized approaches to demand response using smart plugs. In Proceedings of the 2014 IEEE PES T D Conference and Exposition, Chicago, IL, USA, 14–17 April 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Errapotu, S.M.; Wang, J.; Gong, Y.; Cho, J.; Pan, M.; Han, Z. SAFE: Secure Appliance Scheduling for Flexible and Efficient Energy Consumption for Smart Home IoT. IEEE Internet Things J. 2018, 5, 4380–4391. [Google Scholar] [CrossRef]
- Moulema, P.; Mallapuram, S.; Yu, W.; Griffith, D.; Golmie, N.; Su, D. Admission Control-Based Load Protection in the Smart Grid. In Security and Privacy in Cyber Physical Systems; John Wiley & Sons, Ltd.: Hoboken, NY, USA, 2017; Chapter 19; pp. 399–421. [Google Scholar] [CrossRef]
- Jaradat, M.; Jarrah, M.; Jararweh, Y.; Al-Ayyoub, M.; Bousselham, A. Integration of renewable energy in demand-side management for home appliances. In Proceedings of the 2014 International Renewable and Sustainable Energy Conference (IRSEC), Ouarzazate, Morocco, 17–19 October 2014; pp. 571–576. [Google Scholar] [CrossRef]
- Chaouch, H.; Ben Hadj Slama, J. Modeling and simulation of appliances scheduling in the smart home for managing energy. In Proceedings of the 2014 International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Tunis, Tunisia, 3–6 November 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Mocanu, E.; Mocanu, D.C.; Nguyen, P.H.; Liotta, A.; Webber, M.E.; Gibescu, M.; Slootweg, J.G. On-line Building Energy Optimization using Deep Reinforcement Learning. IEEE Trans. Smart Grid 2018, 10, 3698–3708. [Google Scholar] [CrossRef] [Green Version]
- Tundis, A.; Faizan, A.; Mühlhäuser, M. A Feature-Based Model for the Identification of Electrical Devices in Smart Environments. Sensors 2019, 19, 2611. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, K.D.; Kumar, P. An Overview and Some Challenges in Cyber-Physical Systems. J. Indian Inst. Sci. 2013, 93, 341–352. [Google Scholar]
- Nigro, L.; Sciammarella, P.F. Qualitative and Quantitative Model Checking of Distributed Probabilistic Timed Actors. Simul. Model. Pract. Theory 2018, 87, 343–368. [Google Scholar] [CrossRef]
- Jahandideh, I.; Ghassemi, F.; Sirjani, M. Hybrid Rebeca: Modeling and Analyzing of Cyber-Physical Systems. In Cyber Physical Systems. Model-Based Design; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Lee, E.A. The Problem with Threads. Computer 2006, 39, 33–42. [Google Scholar] [CrossRef]
- Nigro, C.; Nigro, L.; Sciammarella, P.F. Modelling and analysis of multi-agent systems using UPPAAL SMC. Int. J. Simul. Process. Model. 2018, 13, 73. [Google Scholar] [CrossRef]
- Cicirelli, F.; Nigro, L. Control Centric Framework for Model Continuity in Time-dependent Multi-agent Systems. Concurr. Comput. Pract. Exper. 2016, 28, 3333–3356. [Google Scholar] [CrossRef]
- Cicirelli, F.; Nigro, L.; Sciammarella, P.F. Model continuity in cyber-physical systems: A control-centered methodology based on agents. Simul. Model. Pract. Theory 2018, 83, 93–107. [Google Scholar] [CrossRef]
- Agha, G.; Palmskog, K. A Survey of Statistical Model Checking. ACM Trans. Model. Comput. Simul. 2018, 28, 6:1–6:39. [Google Scholar] [CrossRef]
- David, A.; Larsen, K.G.; Legay, A.; Mikuăionis, M.; Poulsen, D.B. Uppaal SMC Tutorial. Int. J. Softw. Tools Technol. Transf. 2015, 17, 397–415. [Google Scholar] [CrossRef] [Green Version]
- Cicirelli, F.; Nigro, L. Home Energy Management Using Theatre with Hybrid Actors. In Proceedings of the 23rd IEEE/ACM International Symposium on Distributed Simulation and Real Time Applications, Cosenza, Italy, 7–9 October 2019; pp. 162–169. [Google Scholar]
- Cicirelli, F.; Nigro, L. Using Deterministic Theatre for Energy Management in Smart Environments. In Sustainable Intelligent Systems; Joshi, A., Nagar, A.K., Marín-Raventós, G., Eds.; Springer: Singapore, 2021; pp. 189–214. [Google Scholar] [CrossRef]
- Agha, G. Actors: A Model of Concurrent Computation in Distributed Systems; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Lohstroh, M.; Lee, E.A. Deterministic Actors. In Proceedings of the 2019 Forum for Specification and Design Languages (FDL), Southampton, UK, 2–4 September 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Sirjani, M.; Lee, E.A.; Khamespanah, E. Verification of Cyberphysical Systems. Mathematics 2020, 8, 1068. [Google Scholar] [CrossRef]
- Jafari, A.; Khamespanah, E.; Sirjani, M.; Hermanns, H.; Cimini, M. PTRebeca: Modeling and analysis of distributed and asynchronous systems. Sci. Comput. Program. 2016, 128, 22–50. [Google Scholar] [CrossRef]
- Cicirelli, F.; Nigro, L.; Sciammarella, P.F. Seamless Development in Java of Distributed Real-Time Systems using Actors. Int. J. Simul. Process. Model. 2020, 15, 13. [Google Scholar] [CrossRef]
- Remani, T.; Jasmin, E.A.; Ahamed, T.P.I. Residential Load Scheduling With Renewable Generation in the Smart Grid: A Reinforcement Learning Approach. IEEE Syst. J. 2019, 13, 3283–3294. [Google Scholar] [CrossRef]
- O’Neill, D.; Levorato, M.; Goldsmith, A.; Mitra, U. Residential Demand Response Using Reinforcement Learning. In Proceedings of the 2010 First IEEE International Conference on Smart Grid Communications, Gaithersburg, MD, USA, 4–6 October 2010; pp. 409–414. [Google Scholar] [CrossRef]
- Palensky, P.; Dietrich, D. Demand Side Management: Demand Response, Intelligent Energy Systems, and Smart Loads. IEEE Trans. Ind. Inform. 2011, 7, 381–388. [Google Scholar] [CrossRef] [Green Version]
- Cicirelli, F.; Grimaldi, D.; Furfaro, A.; Nigro, L.; Pupo, F. MADAMS: A Software Architecture for the Management of Networked Measurement Services. Comput. Stand. Interfaces 2006, 28, 396–411. [Google Scholar] [CrossRef]
- Nigro, L.; Sciammarella, P.F. Time Synchronization in Wireless Sensor Networks: A Modeling and Analysis Experience Using Theatre. In Proceedings of the 2018 IEEE/ACM 22nd International Symposium on Distributed Simulation and Real Time Applications (DS-RT), Madrid, Spain, 15–17 October 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Karmani, R.K.; Agha, G. Actors. In Encyclopedia of Parallel Computing; Padua, D., Ed.; Springer: Boston, MA, USA, 2011; pp. 1–11. [Google Scholar] [CrossRef]
- Sirjani, M. Power is Overrated, Go for Friendliness! Expressiveness, Faithfulness, and Usability in Modeling: The Actor Experience. In Principles of Modeling: Essays Dedicated to Edward A. Lee on the Occasion of His 60th Birthday; Lohstroh, M., Derler, P., Sirjani, M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 423–448. [Google Scholar] [CrossRef]
- Henzinger, T.A. The Theory of Hybrid Automata. In Verification of Digital and Hybrid Systems; Inan, M.K., Kurshan, R.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 265–292. [Google Scholar] [CrossRef]
- Lohstroh, M.; Lee, E. An Interface Theory for the Internet of Things. Softw. Eng. Form. Methods 2015, 9276, 20–34. [Google Scholar] [CrossRef] [Green Version]
- Lamport, L. Time, clocks and the ordering of events in a distributed system. Commun. ACM 1978, 21, 558–565. [Google Scholar] [CrossRef]
- Jerad, C.; Lee, E.A. Deterministic Timing for the Industrial Internet of Things. In Proceedings of the 2018 IEEE International Conference on Industrial Internet (ICII), Seattle, WA, USA, 21–23 October 2018; pp. 13–22. [Google Scholar] [CrossRef]



| Message Type | Sender | Receiver | Description |
|---|---|---|---|
| INIT | Load Manager | ELoad | Setting-up load parameters |
| ON | Load Manager | ELoad | Switch-on a load. After switched-on, the load sends a REQUEST message to the controller |
| REQUEST | ELoad | Controller | Used by a load to ask the controller to become active |
| ACTIVATE | Controller | ELoad | Activates and makes operating a load. A previously active load resumes its operation from the point it was suspended last. An active load consumes real power |
| COASTINGF | Controller | ELoad | Suspends load activity (if any) and prepares the load to predict its remaining power consumption |
| READYTOPREDICT | ELoad | Controller | Communicates to the controller that the coasting forward phase is completed and that the load is ready to simulate its remaining power consumption |
| Load Mode | ELoad | Used to communicate that the current mode completed the coasting forward | |
| PREDICT | Controller | ELoad | Communicates that a load can start the prediction phase |
| PREDICTIONEND | Load Mode | ELoad | Used to communicate that the current mode completed its simulation phase |
| ELoad | Controller | Used to communicate that a load completed its simulation phase | |
| TERMINATED | ELoad | Controlled | Used to communicate that a load completed its task |
| SAMPLE | Load Mode | ELoad | Used to communicate that the current mode completed its behaviour |
| POWER | Meter | Controller | Communicates the instantaneous cumulative power consumption, both predicted and real, of the loads |
| Identifier | Type | Description |
|---|---|---|
| isOn | boolean array | an element is true if the corresponding load was admitted by the controller |
| nextON | function | iterates on the array of admitted loads |
| inPrediction | integer var | number of loads which are in prediction |
| inCoastingForward | integer var | number of loads which are in coasting forward |
| isCoastingForward | boolean array | an element is true if the corresponding load is in coasting forward |
| toAdmit | integer var | the load that asked for admission |
| isActive | boolean array | an element is true if the corresponding load is active |
| termination | boolean array | indicates whether a load has completed its execution |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cicirelli, F.; Nigro, L. Admission Control in Home Energy Management Systems Using Theatre and Hybrid Actors. Modelling 2021, 2, 288-307. https://doi.org/10.3390/modelling2020015
Cicirelli F, Nigro L. Admission Control in Home Energy Management Systems Using Theatre and Hybrid Actors. Modelling. 2021; 2(2):288-307. https://doi.org/10.3390/modelling2020015
Chicago/Turabian StyleCicirelli, Franco, and Libero Nigro. 2021. "Admission Control in Home Energy Management Systems Using Theatre and Hybrid Actors" Modelling 2, no. 2: 288-307. https://doi.org/10.3390/modelling2020015
APA StyleCicirelli, F., & Nigro, L. (2021). Admission Control in Home Energy Management Systems Using Theatre and Hybrid Actors. Modelling, 2(2), 288-307. https://doi.org/10.3390/modelling2020015







