Cost Optimization of Reinforced Concrete Section According to Flexural Cracking
Abstract
:1. Introduction
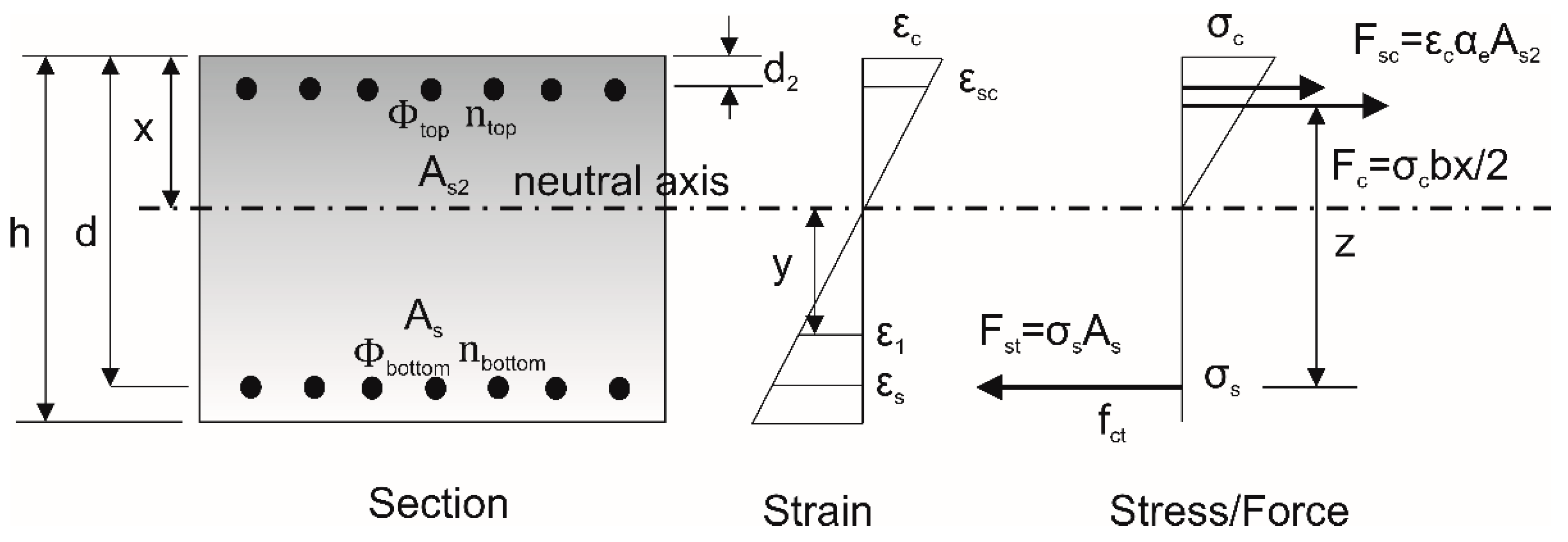
2. Mechanics of Flexural Cracking
2.1. Direct Calculation of Crack Width
2.2. Control of Cracking without Direct Calculation
3. Discrete Optimization Model OPTCON
3.1. MINLP Problem Formulation
3.2. MINLP Optimization Model
3.2.1. Input Data
3.2.2. Variables
3.2.3. Cost Objective Function
3.2.4. Mechanical Inequality Constraints
- Condition 1: The maximum crack width must be limited to an acceptable value.
- Condition 2: The compressive stress in the concrete must be limited to the design compressive concrete.
- Condition 3: The design tensile stress in the steel must be limited to the design tensile strength of the steel.
3.2.5. Design (in)Equality Constraints
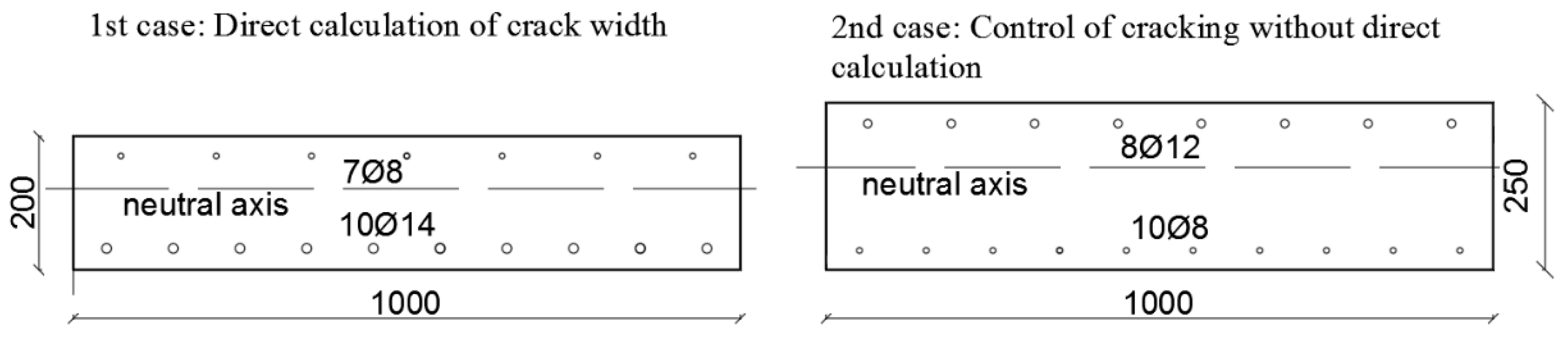
4. Numerical Example
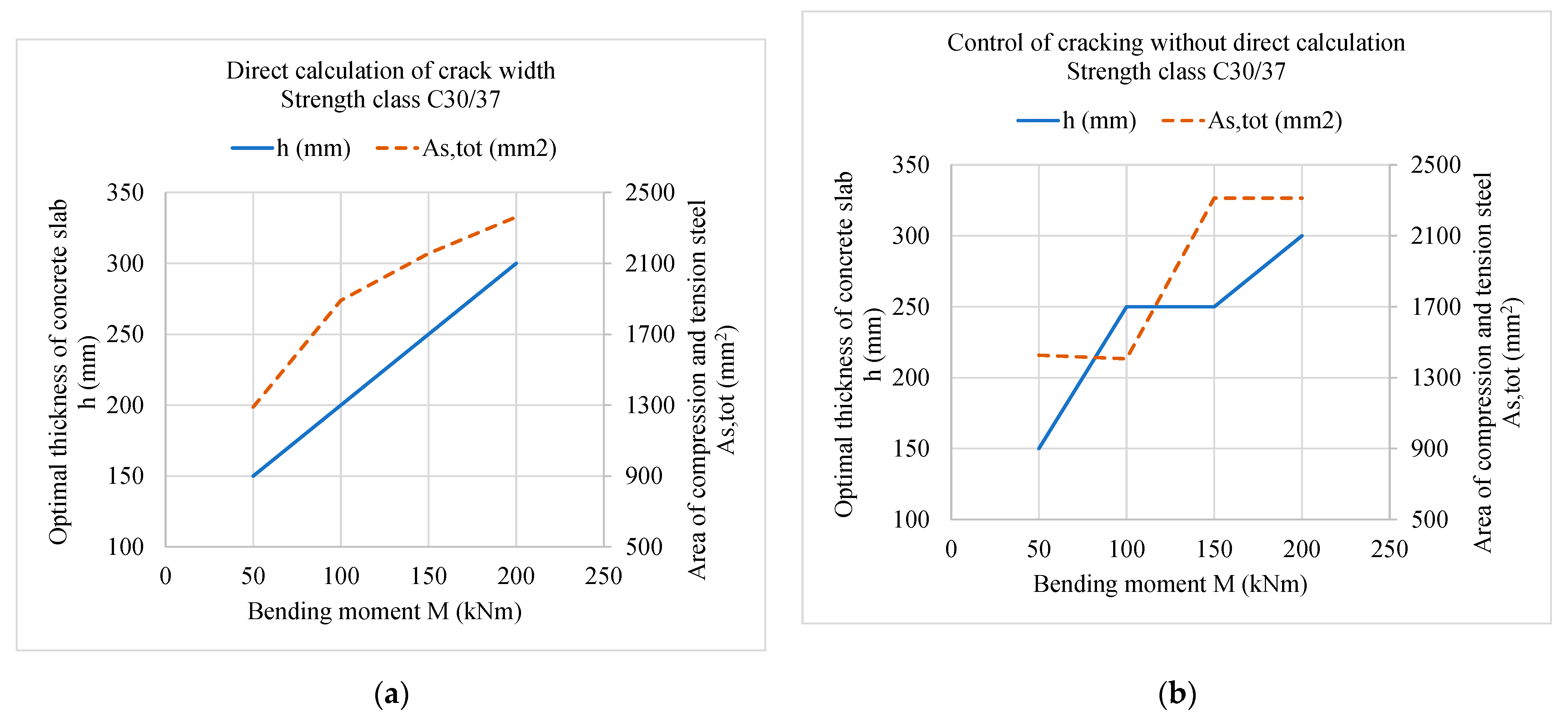
5. Parametric Analysis of an Optimally Designed Reinforced Concrete Slab
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Chi, M.; Kirstein, A.F. Flexural cracks in reinforced concrete beams. ACI J. Proc. 1958, 54, 865–878. [Google Scholar]
- Gergely, P.; Lutz, L.A. Maximum crack width in reinforced concrete flexural members. Am. Concr. Inst. 1968, 20, 87–117. [Google Scholar]
- Oh, B.H.; Kang, Y.-J. New formulas for maximum crack width and crack spacing in reinforced concrete flexural members. ACI Struct. J. 1987, 84, 103–112. [Google Scholar]
- Frosch, R.J. Another Look at Cracking and Crack Control in Reinforced Concrete. ACI Struct. J. 1999, 96, 437–442. [Google Scholar]
- Theiner, Y.; Hofstetter, G. Numerical prediction of crack propagation and crack widths in concrete structures. Eng. Struct. 2009, 31, 1832–1840. [Google Scholar] [CrossRef]
- EN1992-1-1 2004; CEN Eurocode 2 Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. BSI: London, UK, 2004.
- ACI 318R-95 1995; ACI (American Concrete Institute) Building Code Requirement for Reinforced Concrete. ACI: Farmington Hills, MI, USA, 1995.
- Basri, M.; Bakar, C.; Saifulnaz, R.; Rashid, M.; Amran, M.; Jaafar, M.S.; Vatin, N.I.; Fediuk, R. Flexural Strength of Concrete Beam Reinforced with CFRP Bars: A Review. Materials 2022, 15, 1144. [Google Scholar]
- Brown, R.H. Minimum cost selection of one-way slab thickness. J. Struct. Div. ASCE 1975, 101, 2585–2590. [Google Scholar] [CrossRef]
- Jones, H.L. Minimum Cost Prestressed Concrete Beam Design. J. Struct. Eng. 1985, 111, 2464–2478. [Google Scholar] [CrossRef]
- MacRae, A.J.; Cohn, M.Z. Optimization of Prestressed Concrete Flat Plates. J. Struct. Eng. 1987, 113, 943–957. [Google Scholar] [CrossRef]
- Kanagasundaram, S.; Karihaloo, B.L. Minimum-cost design of reinforced concrete structures. Comput. Struct. 1991, 41, 1357–1364. [Google Scholar] [CrossRef]
- Al-Salloum, Y.A.; Siddiqi, G.H. Cost-Optimum Design of Reinforced Concrete (RC) Beams. ACI Struct. J. 1994, 91, 647–655. [Google Scholar] [CrossRef]
- Jelusic, P.; Kravanja, S. Optimal design of timber-concrete composite floors based on the multi-parametric MINLP optimization. Compos. Struct. 2017, 179, 285–293. [Google Scholar] [CrossRef]
- Jelušič, P.; Žlender, B. Optimal design of piled embankments with basal reinforcement. Geosynth. Int. 2018, 25, 150–163. [Google Scholar] [CrossRef]
- Waheed, J.; Azam, R.; Riaz, M.R.; Shakeel, M.; Mohamed, A.; Ali, E. Metaheuristic-Based Practical Tool for Optimal Design of Reinforced Concrete Isolated Footings: Development and Application for Parametric Investigation. Buildings 2022, 12, 471. [Google Scholar] [CrossRef]
- Kravanja, S.; Klanšek, U.; Žula, T. Mass, Direct Cost and Energy Life-Cycle Cost Optimization of Steel-Concrete Composite Floor Structures. Appl. Sci. 2021, 11, 10316. [Google Scholar] [CrossRef]
- Rady, M.; Mahfouz, S.Y.; Taher, S.E.-D.F. Optimal Design of Reinforced Concrete Materials in Construction. Materials 2022, 15, 2625. [Google Scholar] [CrossRef] [PubMed]
- Solorzano, G.; Plevris, V. Optimum design of RC footings with genetic algorithms according to ACI 318-19. Buildings 2020, 10, 110. [Google Scholar] [CrossRef]
- Kashani, A.R.; Gandomi, M.; Camp, C.V.; Gandomi, A.H. Optimum design of shallow foundation using evolutionary algorithms. Soft Comput. 2020, 24, 6809–6833. [Google Scholar] [CrossRef]
- Chaudhuri, P.; Maity, D. Cost optimization of rectangular RC footing using GA and UPSO. Soft Comput. 2020, 24, 709–721. [Google Scholar] [CrossRef]
- Jelušič, P.; Žlender, B. Optimal Design of Reinforced Pad Foundation and Strip Foundation. Int. J. Geomech. 2018, 18, 04018105. [Google Scholar] [CrossRef]
- Jelušič, P.; Žlender, B. Optimal design of pad footing based on MINLP optimization. Soils Found. 2018, 58, 277–289. [Google Scholar] [CrossRef]
- Rahmanian, I.; Lucet, Y.; Tesfamariam, S. Optimal design of reinforced concrete beams: A review. Comput. Concr. 2014, 13, 457–482. [Google Scholar] [CrossRef]
- Pierott, R.; Hammad, A.W.A.; Haddad, A.; Garcia, S.; Falcón, G. A mathematical optimisation model for the design and detailing of reinforced concrete beams. Eng. Struct. 2021, 245, 112861. [Google Scholar] [CrossRef]
- Stochino, F.; Lopez Gayarre, F. Reinforced Concrete Slab Optimization with Simulated Annealing. Appl. Sci. 2019, 9, 3161. [Google Scholar] [CrossRef] [Green Version]
- Ghandi, E.; Shokrollahi, N.; Nasrolahi, M. Optimum cost design of reinforced concrete slabs using cuckoo search optimization algorithm. Iran Univ. Sci. Technol. 2017, 7, 539–564. [Google Scholar]
- Sánchez-Olivares, G.; Tomás, A. Optimization of Reinforced Concrete Sections under Compression and Biaxial Bending by Using a Parallel Firefly Algorithm. Appl. Sci. 2021, 11, 2076. [Google Scholar] [CrossRef]
- De Medeiros, G.F.; Kripka, M. Optimization of reinforced concrete columns according to different environmental impact assessment parameters. Eng. Struct. 2014, 59, 185–194. [Google Scholar] [CrossRef]
- Aslay, S.E.; Dede, T. 3D cost optimization of 3 story RC constructional building using Jaya algorithm. Structures 2022, 40, 803–811. [Google Scholar] [CrossRef]
- Mei, L.; Wang, Q. Structural optimization in civil engineering: A literature review. Buildings 2021, 11, 66. [Google Scholar] [CrossRef]
- Ben Seghier, M.E.A.; Ouaer, H.; Ghriga, M.A.; Menad, N.A.; Thai, D.K. Hybrid soft computational approaches for modeling the maximum ultimate bond strength between the corroded steel reinforcement and surrounding concrete. Neural Comput. Appl. 2021, 33, 6905–6920. [Google Scholar] [CrossRef]
- Jelušič, P.; Žlender, B. Soil-nail wall stability analysis using anfis. Acta Geotech. Slov. 2013, 10, 61–73. [Google Scholar]
- Jelušič, P.; Žlender, B.; Dolinar, B. NLP Optimization Model as a Failure Mechanism for Geosynthetic Reinforced Slopes Subjected to Pore-Water Pressure. Int. J. Geomech. 2016, 16, C4015003. [Google Scholar] [CrossRef]
- Brook, A.; Kendrick, D.; Meeraus, A. GAMS, a user’s guide. ACM Signum Newsl. 1988, 23, 10–11. [Google Scholar] [CrossRef]


| Steel Stress σs (N/mm2) | Maximum Bar Spacing slim (mm) wk = 0.3 |
|---|---|
| 160 | 300 |
| 200 | 250 |
| 240 | 200 |
| 280 | 150 |
| 320 | 100 |
| 360 | 50 |
| Variable | Allowable Discrete Values |
|---|---|
| h (mm) | 100, 150, 200, 250, 300, 350, 400 |
| ϕbottom (mm) | 8, 10, 12, 14, 16, 18, 20 |
| ϕtop (mm) | 8, 10, 12, 14, 16, 18, 20 |
| nbottom (-) | 4, 5, 6, 7, 8, 9, 10 |
| ntop (-) | 4, 5, 6, 7, 8, 9, 10 |
| h (mm) | 100, 150, 200, 250, 300, 350, 400 |
| Input Name | Symbol | Value |
|---|---|---|
| Compressive strength | fck | 30 MPa |
| Mean concrete strength at cracking | fcm,t | 38 MPa |
| Mean concrete tensile strength | fct,eff | 2.9 MPa |
| Modulus of elasticity of concrete | Ecm | 32.8 GPa |
| Yield stress of steel | fyk | 500 GPa |
| Modulus of elasticity of steel | Es | 200 GPa |
| Density of steel | ρs | 7850 kg/m3 |
| Width of concrete section | b | 1000 mm |
| Applied moment | M | 100 kNm |
| Cover of concrete | c | 25 mm |
| Modular ratio | αe | 18.27 |
| Final creep coefficient | φ | 2.0 |
| Minimum bar spacing | smin | 60 mm |
| Maximum bar spacing | smax | 200 mm |
| Moment redistribution | δ | 1 |
| Cost of concrete | Ccon | 95 €/m3 |
| Cost of steel | Csteel | 1.0 €/kg |
| 1st case: Direct calculation of crack width | wlim | 0.3 mm |
| 2nd case: Control of cracking without direct calculation | slim | 500–1.25·σs |
| Optimal Design Variables | Symbol | 1st Case: Direct Calculation of Crack Width | 2nd Case: Control of Cracking without Direct Calculation |
|---|---|---|---|
| Thickness of concrete slab | h (mm) | 200 | 250 |
| Bottom bar diameter | φbottom (mm) | 14 | 8 |
| Top bar diameter | φtop (mm) | 8 | 12 |
| Number of bottom bars | nbottom (-) | 10 | 10 |
| Number of top bars | ntop (-) | 7 | 8 |
| Calculated values | |||
| Fully cracked neutral axis depth | xc (mm) | 78.483 | 82.516 |
| Concrete stress | σc (MPa) | 17.897 | 12.608 |
| Stress in tension steel | σs (MPa) | 372.951 | 386.589 |
| Effective tension area | Ac,eff (mm2) | 38,966.237 | 55,325.476 |
| Area of tension steel | As (mm2) | 1539.380 | 502.655 |
| Area of compression steel | As2 (mm2) | 351.858 | 904.779 |
| Steel-to-concrete ratio (As/Ac,eff) | ρp,eff (-) | 0.040 | 0.009 |
| Max. final crack spacing | sr,max (mm) | 145.245 | 217.730 |
| Average strain for crack width | εsm − εcm (μstrain) | 1611.973 | 1188.591 |
| Calculated crack width | wk (mm) | 0.234 | 0.259 |
| Material costs | COSTS (€/m2) | 33.846 | 34.798 |
| Input Name | Design Data 1 | Design Data 2 | Design Data 3 | Design Data 4 |
|---|---|---|---|---|
| M (kNm) | 100 | 100 | 100 | 100 |
| Strength classes | C20/25 | C30/37 | C40/50 | C50/60 |
| fck (MPa) | 20 | 30 | 40 | 50 |
| fcm (MPa) | 28 | 38 | 48 | 58 |
| fct (MPa) | 2.2 | 2.9 | 3.5 | 4.1 |
| Ecm (GPa) | 30.0 | 32.8 | 35.2 | 37.3 |
| Ccon (€/m3) | 80 | 95 | 110 | 125 |
| 1st case: Direct calculation of crack width | ||||
| h (mm) | 250 | 200 | 200 | 200 |
| φbottom (mm) | 12 | 8 | 10 | 10 |
| φtop (mm) | 10 | 14 | 14 | 14 |
| nbottom (-) | 5 | 10 | 7 | 7 |
| ntop (-) | 10 | 7 | 9 | 9 |
| COSTS (€/m2) | 31.961 | 33.846 | 36.008 | 39.008 |
| 2nd case: Control of cracking without direct calculation | ||||
| h (mm) | 250 | 250 | 200 | 200 |
| φbottom (mm) | 12 | 12 | 12 | 12 |
| φtop (mm) | 8 | 8 | 10 | 10 |
| nbottom (-) | 10 | 10 | 10 | 10 |
| ntop (-) | 9 | 8 | 9 | 9 |
| COSTS (€/m2) | 31.936 | 34.798 | 36.156 | 39.156 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jelušič, P. Cost Optimization of Reinforced Concrete Section According to Flexural Cracking. Modelling 2022, 3, 243-254. https://doi.org/10.3390/modelling3020016
Jelušič P. Cost Optimization of Reinforced Concrete Section According to Flexural Cracking. Modelling. 2022; 3(2):243-254. https://doi.org/10.3390/modelling3020016
Chicago/Turabian StyleJelušič, Primož. 2022. "Cost Optimization of Reinforced Concrete Section According to Flexural Cracking" Modelling 3, no. 2: 243-254. https://doi.org/10.3390/modelling3020016
APA StyleJelušič, P. (2022). Cost Optimization of Reinforced Concrete Section According to Flexural Cracking. Modelling, 3(2), 243-254. https://doi.org/10.3390/modelling3020016






