Predictive Analysis of Mechanical Properties in Cu-Ti Alloys: A Comprehensive Machine Learning Approach
Abstract
:1. Introduction
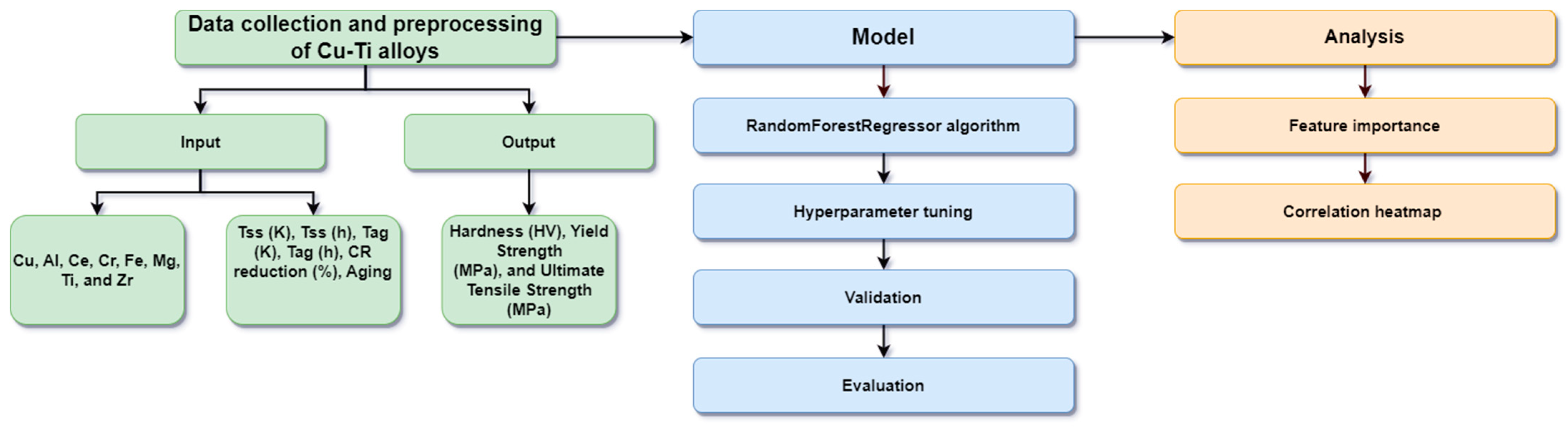
2. Data and Methodology
2.1. Data Collection and Preprocessing
2.2. Model Training, Testing, Validation, and Analysis
3. Results and Discussions
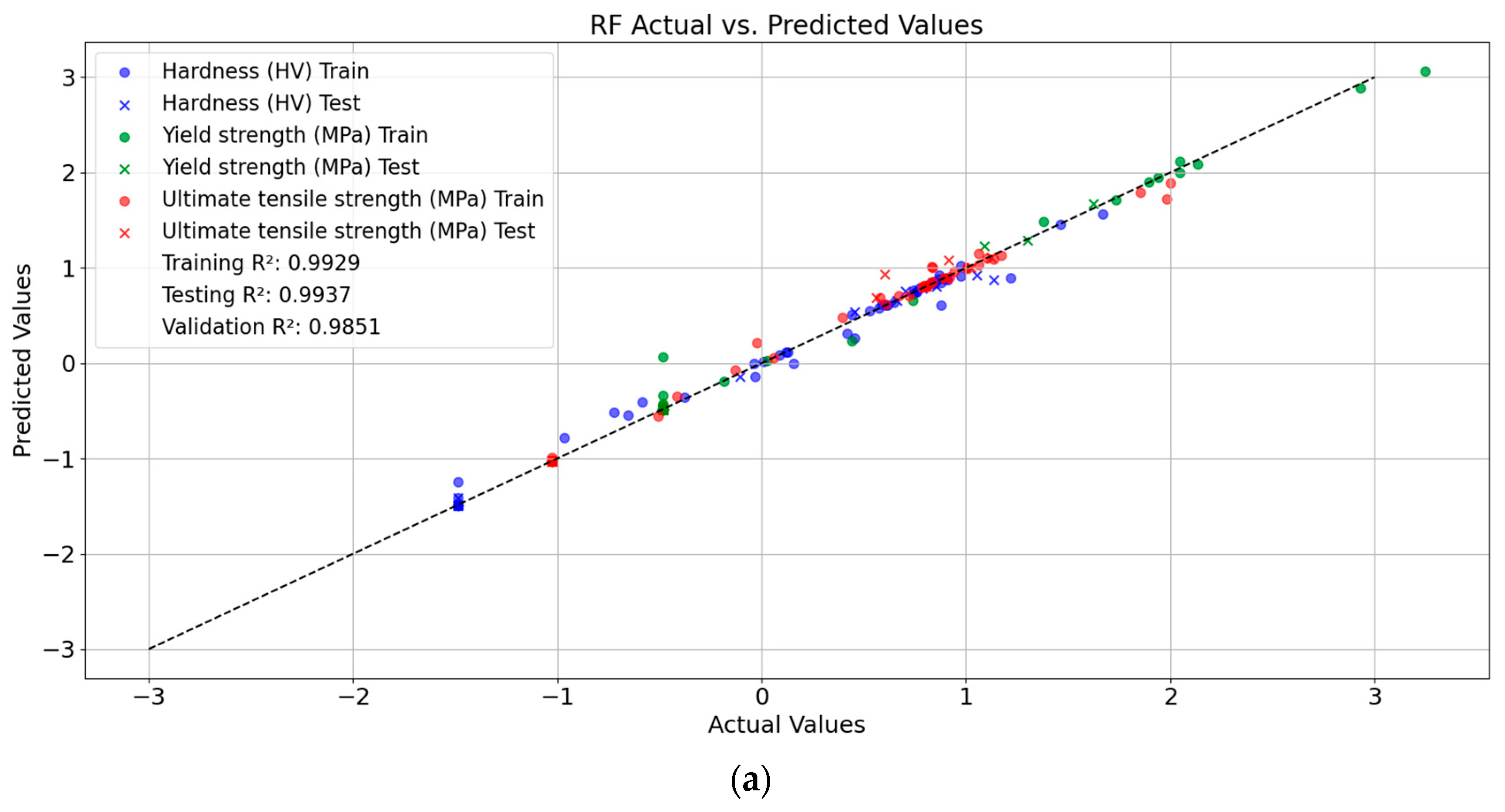
3.1. Model Performance and Validation
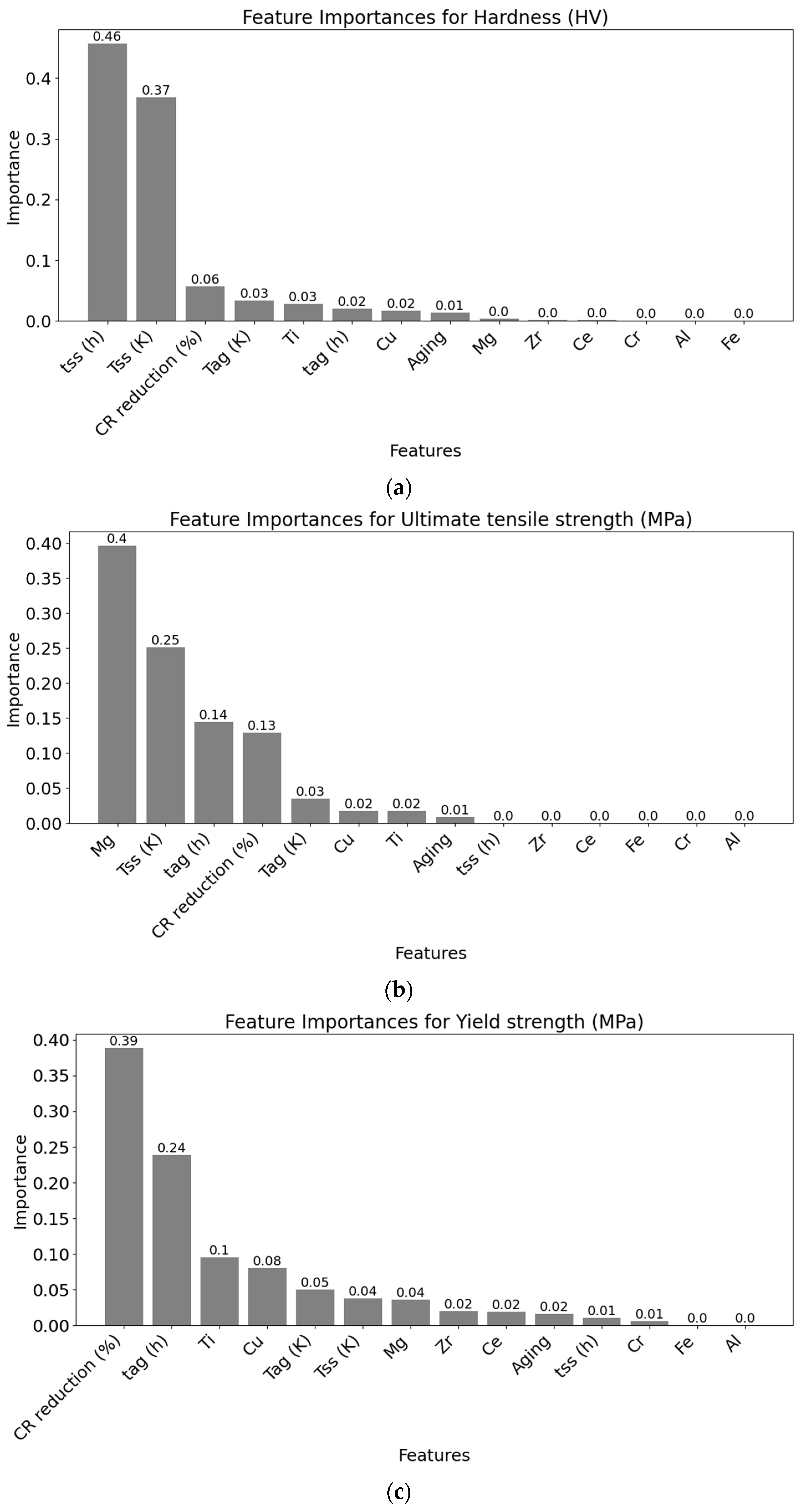
3.2. Feature Importance and Inter-Feature Relationships
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, L.; Cui, Z.; Meng, X.; Zhang, X.; Zhang, X.; Song, X.; Tang, N.; Xiao, Z.; Lei, Q.; Li, Z. Effects of Microelements on the Microstructure Evolution and Properties of Ultrahigh Strength Cu–Ti Alloys. Mater. Sci. Eng. A 2021, 823, 141581. [Google Scholar] [CrossRef]
- Semboshi, S.; Kaneno, Y.; Takasugi, T.; Masahashi, N. Suppression of Discontinuous Precipitation in Cu-Ti Alloys by Aging in a Hydrogen Atmosphere. Metall. Mater. Trans. A 2020, 51, 3704–3712. [Google Scholar] [CrossRef]
- Vorotilo, S.; Loginov, P.A.; Churyumov, A.Y.; Prosviryakov, A.S.; Bychkova, M.Y.; Rupasov, S.I.; Orekhov, A.S.; Kiryukhantsev-Korneev, P.V.; Levashov, E.A. Manufacturing of Conductive, Wear-Resistant Nanoreinforced Cu-Ti Alloys Using Partially Oxidized Electrolytic Copper Powder. Nanomaterials 2020, 10, 1261. [Google Scholar] [CrossRef] [PubMed]
- Liao, Y.; Guo, C.; Zhou, C.; Xie, W.; Yang, B.; Wang, H. Strengthening of Cu-Ti Alloys by Stabilization of Metastable Β′ Phase with Addition of Gd Element. Mater. Today Commun. 2024, 39, 108671. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, D.; Liu, H.; Zhang, Y.; Song, H.; Xu, Y.; Zhang, S. Research on Hot Deformation Behavior of Cu-Ti Alloy Based on Machine Learning Algorithms and Microalloying. Mater. Today Commun. 2024, 39, 108783. [Google Scholar] [CrossRef]
- Huang, Z.; Shi, R.; Xiao, X.; Fu, H.; Chen, Q.; Xie, J. Mechanism Investigation on High-Performance Cu-Cr-Ti Alloy via Integrated Computational Materials Engineering. Mater. Today Commun. 2021, 27, 102378. [Google Scholar] [CrossRef]
- Zhao, Q.; Yang, H.; Liu, J.; Zhou, H.; Wang, H.; Yang, W. Machine Learning-Assisted Discovery of Strong and Conductive Cu Alloys: Data Mining from Discarded Experiments and Physical Features. Mater. Des. 2021, 197, 109248. [Google Scholar] [CrossRef]
- Zhao, B.; Yu, T.; Ding, W.; Li, X.; Su, H. BP Neural Network Based Flexural Strength Prediction of Open-Porous Cu-Sn-Ti Composites. Prog. Nat. Sci. Mater. Int. 2018, 28, 315–324. [Google Scholar] [CrossRef]
- Pan, S.; Wang, Y.; Yu, J.; Yang, M.; Zhang, Y.; Wei, H.; Chen, Y.; Wu, J.; Han, J.; Wang, C.; et al. Accelerated Discovery of High-Performance Cu-Ni-Co-Si Alloys through Machine Learning. Mater. Des. 2021, 209, 109929. [Google Scholar] [CrossRef]
- Xie, B.; Fang, Q.; Li, J.; Liaw, P.K. Predicting the Optimum Compositions of High-Performance Cu–Zn Alloysviamachine Learning. J. Mater. Res. 2020, 35, 2709–2717. [Google Scholar] [CrossRef]
- Gorsse, S.; Gouné, M.; Lin, W.-C.; Girard, L. Dataset of Mechanical Properties and Electrical Conductivity of Copper-Based Alloys. Figshare. Collection. 2023. Available online: https://springernature.figshare.com/collections/Dataset_of_mechanical_properties_and_electrical_conductivity_of_copper-based_alloys/6475600/1 (accessed on 21 July 2024). [CrossRef]
- Gorsse, S.; Gouné, M.; Lin, W.-C.; Girard, L. Dataset of Mechanical Properties and Electrical Conductivity of Copper-Based Alloys. Sci. Data 2023, 10, 504. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wu, D.; Jennings, C.; Terpenny, J.; Gao, R.X.; Kumara, S. A Comparative Study on Machine Learning Algorithms for Smart Manufacturing: Tool Wear Prediction Using Random Forests. J. Manuf. Sci. Eng. 2017, 139, 071018. [Google Scholar] [CrossRef]
- Kolev, M. COF-RF-Tool: A Python Software for Predicting the Coefficient of Friction of Open-Cell AlSi10Mg-SiC Composites Using Random Forest Model. Softw. Impacts 2023, 17, 100520. [Google Scholar] [CrossRef]
- Gerstorfer, Y.; Krieg, L.; Hahn-Klimroth, M. A Notion of Feature Importance by Decorrelation and Detection of Trends by Random Forest Regression. arXiv 2023, arXiv:2303.01156. [Google Scholar] [CrossRef]
- Kolev, M. A Novel Approach to Predict the Effect of Chemical Composition and Thermo-Mechanical Processing Parameters on Cu–Ni–Si Alloys Using a Hybrid Deep Learning and Ensemble Learning Model. Compos. Commun. 2024, 48, 101903. [Google Scholar] [CrossRef]


| Mean | Std | Min | 25% | 50% | 75% | Max | |
|---|---|---|---|---|---|---|---|
| Cu | 96.29 | 1.26 | 92.91 | 95.70 | 96.80 | 96.95 | 98.50 |
| Al | 0.13 | 0.00 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 |
| Ce | 0.10 | 0.00 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 |
| Cr | 0.34 | 0.01 | 0.33 | 0.33 | 0.34 | 0.34 | 0.34 |
| Fe | 0.27 | 0.00 | 0.27 | 0.27 | 0.27 | 0.27 | 0.27 |
| Mg | 0.48 | 0.72 | 0.15 | 0.15 | 0.15 | 0.16 | 2.00 |
| Ti | 3.34 | 1.09 | 1.50 | 2.70 | 3.00 | 3.20 | 6.18 |
| Zr | 0.12 | 0.08 | 0.10 | 0.10 | 0.10 | 0.10 | 0.44 |
| Tss (K) | 1151.49 | 60.07 | 1023.00 | 1123.00 | 1123.00 | 1223.00 | 1223.00 |
| tss (h) | 3.56 | 6.40 | 0.25 | 0.25 | 2.00 | 2.00 | 24.00 |
| CR reduction (%) | 60.80 | 24.58 | 15.00 | 50.00 | 60.00 | 90.00 | 90.00 |
| Tag (K) | 678.13 | 31.66 | 623.00 | 653.00 | 673.00 | 723.00 | 723.00 |
| tag (h) | 22.04 | 36.52 | 1.00 | 4.00 | 8.00 | 16.00 | 168.00 |
| Hardness (HV) | 295.28 | 72.53 | 75.00 | 245.00 | 320.00 | 340.00 | 455.00 |
| Yield strength (MPa) | 747.72 | 345.59 | 112.00 | 492.50 | 811.50 | 950.00 | 1400.00 |
| Ultimate tensile strength (MPa) | 853.92 | 256.17 | 217.00 | 780.00 | 892.00 | 982.00 | 1450.00 |
| Model | Training R2 | Testing R2 | Validation R2 |
|---|---|---|---|
| RF | 0.9929 | 0.9937 | 0.9851 |
| DT | 0.9871 | 0.9703 | 0.8822 |
| SVR | 0.9519 | 0.9651 | 0.9593 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolev, M. Predictive Analysis of Mechanical Properties in Cu-Ti Alloys: A Comprehensive Machine Learning Approach. Modelling 2024, 5, 901-910. https://doi.org/10.3390/modelling5030047
Kolev M. Predictive Analysis of Mechanical Properties in Cu-Ti Alloys: A Comprehensive Machine Learning Approach. Modelling. 2024; 5(3):901-910. https://doi.org/10.3390/modelling5030047
Chicago/Turabian StyleKolev, Mihail. 2024. "Predictive Analysis of Mechanical Properties in Cu-Ti Alloys: A Comprehensive Machine Learning Approach" Modelling 5, no. 3: 901-910. https://doi.org/10.3390/modelling5030047
APA StyleKolev, M. (2024). Predictive Analysis of Mechanical Properties in Cu-Ti Alloys: A Comprehensive Machine Learning Approach. Modelling, 5(3), 901-910. https://doi.org/10.3390/modelling5030047






