Acausal Fuel Cell Simulation Model for System Integration Analysis in Early Design Phases
Abstract
:1. Introduction
2. Methods
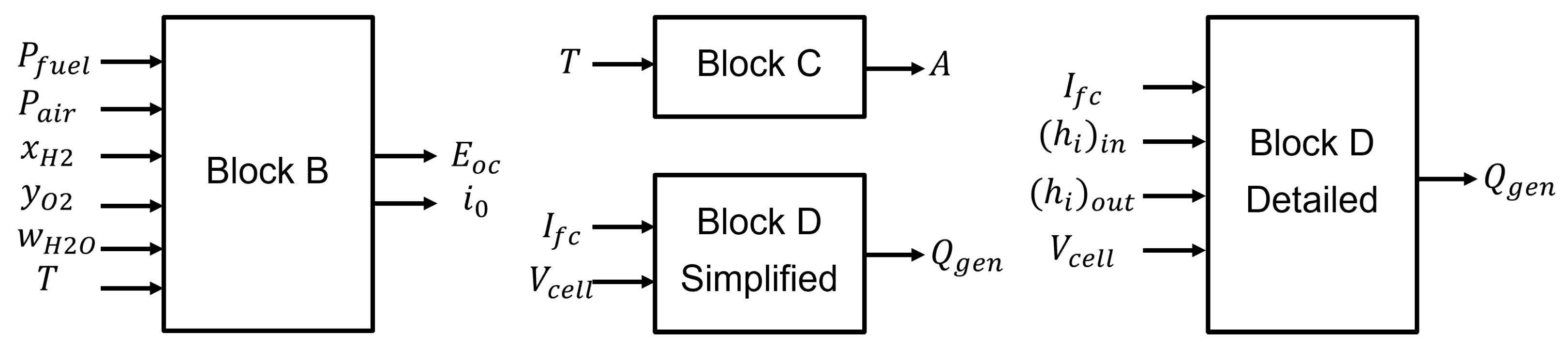
2.1. Block A: Rates of Utilization
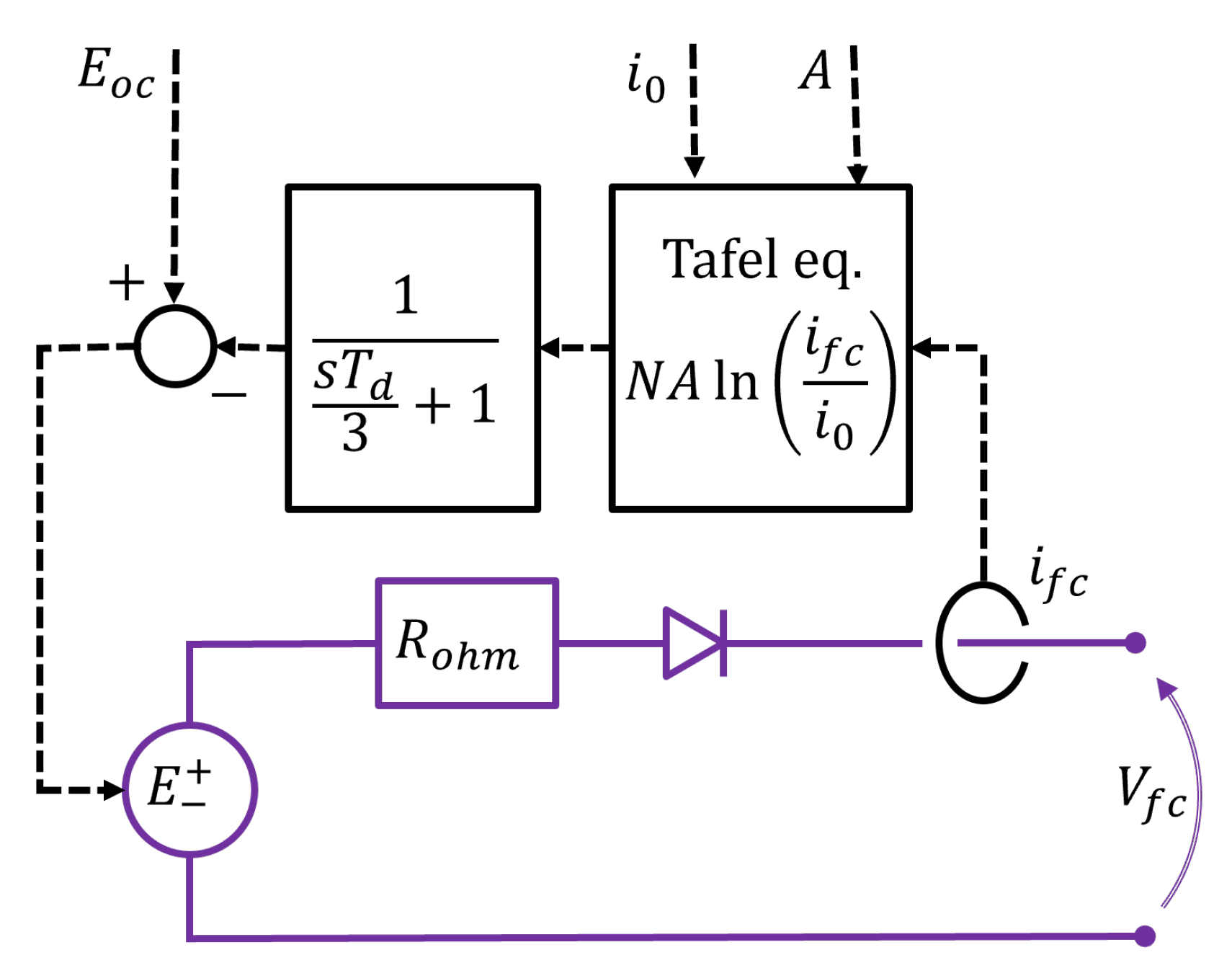
2.2. Block B: Open Circuit Voltage and Exchange Current
2.3. Block C: Tafel Slope
2.4. Block D: Thermal Model
2.5. Model Parameters
2.6. Model in OpenModelica
2.7. PEMFC Stack Block
2.8. Model of the Balance of Plant
2.9. Validation
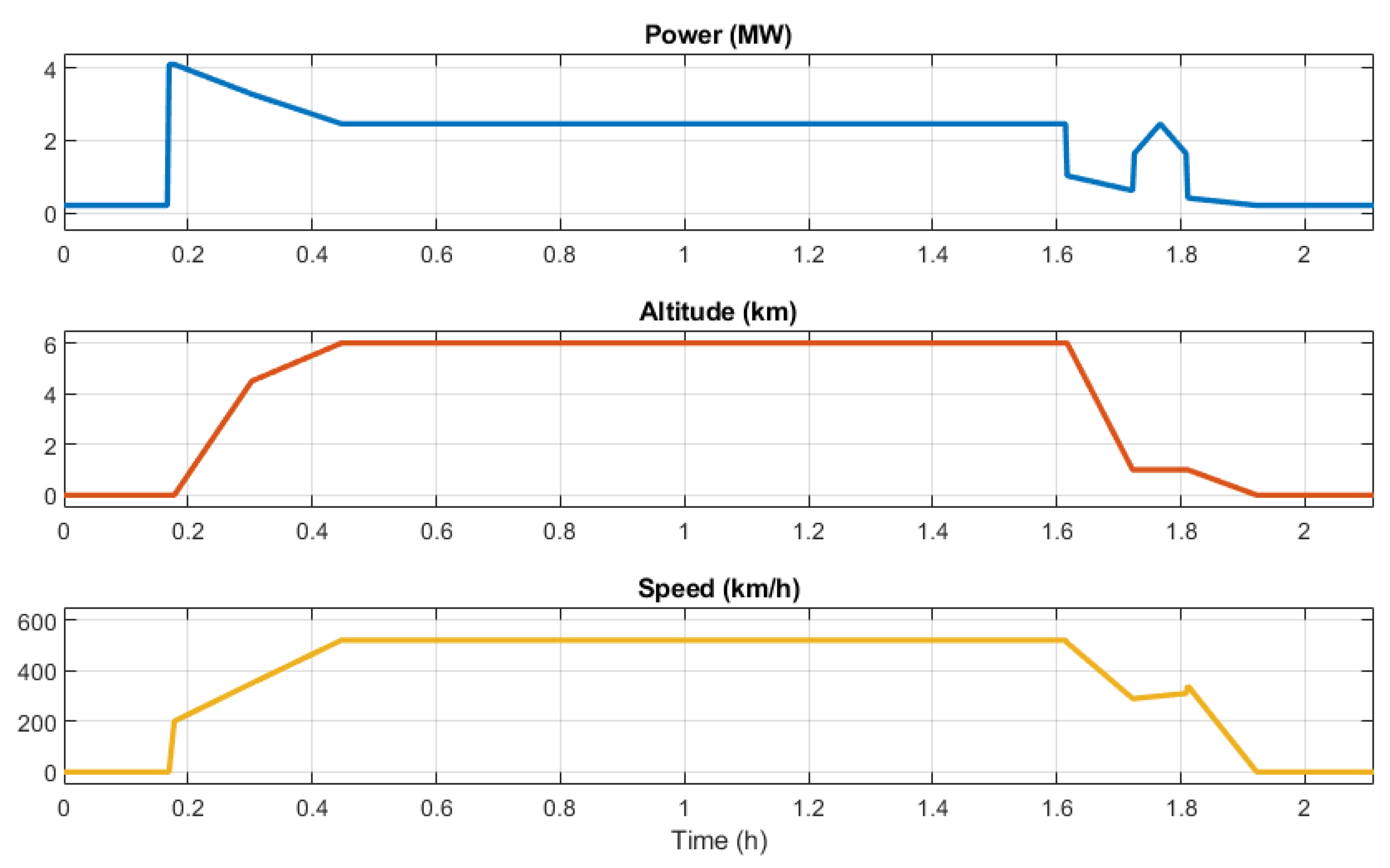
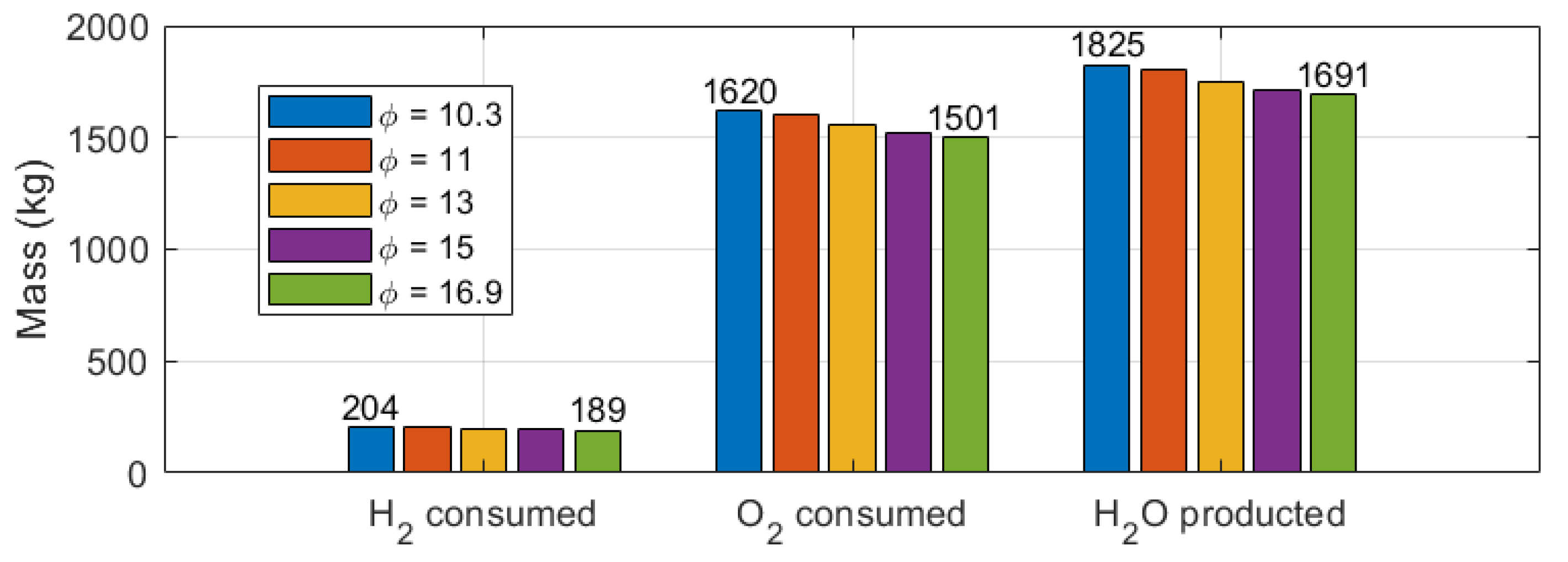
3. Results: Case Study for Regional Aircraft Fuel Cell Scaling
- The maximum fuel cell stack power is equal to the maximum power required by the mission profile, and the rated power is equal to the cruising power.
- The rated fuel cell stack power equals the maximum power required by the mission profile.
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PEMFC | Proton Exchange Membrane Fuel Cell |
| ATR | Avions de Transport Régional |
| SOFC | Solid Oxide Fuel Cell |
| BoP | Balance of Plant |
| ICAO | International Civil Aviation Organization |
| IATA | International Air Transport Association |
| OCV | Open Circuit Voltage |
| CFDs | Computational Fluid Dynamics |
| MDB | Model-Based Design |
| APU | Auxiliary Power Unit |
| ICE | Internal Combustion Engine |
| ISA | International Standard Atmosphere |
Appendix A
| Authors’ Names, Year [Reference] | Fuel Cell | Model Dim. | Validation with Exp. Data | Research Focus | |
|---|---|---|---|---|---|
| P | S | ||||
| Bernardi, 1990 [13] | X | 1D | Ballard Technologies Corporation (1988) | Membrane humidification requirements | |
| Bernardi and Verbrugge, 1991 [12] | X | 1D | [55] | Internal resistances of the cathode and membrane | |
| Springer et al., 1991 [15] | X | 1D | Prototech electrodes | Water transport influence on performance | |
| Bernardi and Verbrugge, 1992 [14] | X | 1D | [55] | Current density limitation | |
| van Bussel et al., 1998 [16] | X | 2D | Nafion 117 cell | Effect of water on current density | |
| Dutta et al., 2000 [17] | X | 3D | [56,57] | Three-dimensional effects in membrane mass transport | |
| Rowe and Li, 2001 [20] | X | 1D | [55] | Temperature and water distributions | |
| Berning et al., 2002 [19] | X | 3D | [55] | Transport phenomena in membrane | |
| Thanapalan et al., 2008 [21] | X | 0D | PEMFC Test station | Simulation study and control analysis | |
| Souleman et al., 2009 [58] | X | X | 0D | NedStack PS6 Hpower EPAC-500 | Use of data from the FC datasheet |
| Gebregergis et al., 2009 [28] | X | 0D | Tubular SOFC by NanoDynamics | Real-time simulation with equivalent circuit | |
| Rubio Gonzalez et al., 2010 [23] | X | 1D | - | Multiple FC effect using Modelica | |
| Andersson et al., 2011 [32] | X | 1D | Forschungszentrum Jülich, Germany | Flexible tool for integration studies | |
| Lakshmi et al., 2013 [33] | X | 0D | [28] | Model with a single transfer function | |
| Costamagna et al., 2015 [29] | X | 2D | Rolls Royce Fuel Cell System Ltd. Data | Reactants’ composition and temperature relationship | |
| Ho, 2016 [30] | X | 3D | Previous studies | Dynamic response of different parameters | |
| Kravos et al., 2020 [22] | X | 0D–1D | - | PEMFC controllability | |
| Bianchi et al., 2020 [31] | X | 2D | EIS analysis on real fuel cell | Study on the composition of the membrane | |
| Authors’ Names, Year [Reference] | Fuel Cell Type | Power (kW) | Validation with Exp. Data | Fuel | Case Study | ||
|---|---|---|---|---|---|---|---|
| P | S | H2 | Other | ||||
| Gummalla et al., 2006 [41] | X | 300 | - | Reformed fuel | APU replacement in short-range aircraft | ||
| Himansu et al., 2006 [44] | X | 50 | - | X | SOFC/Gas turbine system for high-altitude aircraft | ||
| Santarelli et al., 2009 [43] | X | 20 | - | Natural gas | SOFC as source of electric and thermal power | ||
| Pratt et al., 2013 [35] | X | 12 | HyPM 12 PEMFC | X | Impact of fuel-cell-based electric power system | ||
| Correa et al., 2015 [40] | X | 20 | Flight tests | X | Fuel cell as primary energy supply | ||
| Kadyk et al., 2018 [37] | X | 27,600 | [59] | X | Fuel cell as primary energy supply | ||
| Collins and McLarty, 2020 [45] | X | - | NASA data | X | SOFC/GT/Battery architecture | ||
| Schröder et al., 2021 [36] | X | 845 | [60] | X | APU replacement | ||
| Vidovi´c et al., 2022 [34] | X | 1.2 | Nexa 1200 | X | BoP modeling | ||
| Hartmann et al., 2022 [39] | X | 4100 | [36,61] | X | Cryogenic hydrogen feeds fuel cell primary power source system in regional aircraft | ||
| Hawa et al., 2022 [62] | X | 120 | - | Hydrocarbon | SOFC/PEMFC comparison | ||
| Li et al., 2023 [63] | X | 6 | [64] | Ammonia fuel | SOFC/ICE hybrid power systems | ||
Appendix B

Appendix C
| Parameter | FC | FC | FC | FC | FC |
|---|---|---|---|---|---|
| N | 11,330 | 12,100 | 14,300 | 16,500 | 18,590 |
| (sec) | 20 | 20 | 20 | 20 | 20 |
| (V) | 11,330 | 12,100 | 14,300 | 16,500 | 18,590 |
| (V) | 11,268 | 12,034 | 14,222 | 16,410 | 18,489 |
| (V) | 8734 | 9328 | 11,024 | 12,720 | 14,331 |
| (V) | 7622 | 8140 | 9620 | 11,100 | 12,506 |
| (A) | 540 | 540 | 540 | 540 | 540 |
| (A) | 287 | 287 | 287 | 287 | 287 |
| (K) | 360 | 360 | 360 | 360 | 360 |
| 0.55 | 0.55 | 0.55 | 0.55 | 0.55 | |
| (atm) | 1 | 1 | 1 | 1 | 1 |
| (L/min) | 1.2800 × | 1.3670 × | 1.6155 × | 1.8641 × | 2.1002 × |
| (atm) | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | |
| 0.21 | 0.21 | 0.21 | 0.21 | 0.21 | |
| (J/kg·K) | 1300 | 1300 | 1300 | 1300 | 1300 |
| M (kg) | 1957 | 2090 | 2470 | 2850 | 3211 |
| (K) | 300 | 300 | 300 | 300 | 300 |
| (kg/s) | 3.9357 × | 4.2032 × | 4.9674 × | 5.7316 × | 6.4576 × |
| (kg/s) | 5.8052 × | 6.1997 × | 7.3269 × | 8.4542 × | 9.5250 × |
References
- ICAO. Aviation Benefits Report 2019. 2019. Available online: https://www.icao.int/sustainability/Documents/AVIATION-BENEFITS-2019-web.pdf (accessed on 10 April 2024).
- Mission-Possible-Partnership. Making Net-Zero Aviation Possible. 2022. Available online: https://www.missionpossiblepartnership.org/action-sectors/aviation/ (accessed on 10 April 2024).
- IATA. Executive Summary—Net Zero Roadmaps. 2023. Available online: https://www.iata.org/contentassets/8d19e716636a47c184e7221c77563c93/executive-summary—net-zero-roadmaps.pdf (accessed on 10 April 2024).
- Yusaf, T.; Faisal Mahamude, A.S.; Kadirgama, K.; Ramasamy, D.; Farhana, K.; Dhahad, H.A.; Abu Talib, A.R. Sustainable hydrogen energy in aviation—A narrative review. Int. J. Hydrogen Energy 2024, 52, 1026–1045. [Google Scholar] [CrossRef]
- Adler, E.J.; Martins, J.R.R.A. Hydrogen-powered aircraft: Fundamental concepts, key technologies, and environmental impacts. Prog. Aerosp. Sci. 2023, 141, 100922. [Google Scholar] [CrossRef]
- Reiman, A. AMC’s Hydrogen Future: Sustainable Air Mobility. Ph.D. Thesis, Air University, Islamabad, Pakistan, 2009. [Google Scholar]
- Barabanova, K. ZeroAvia and PowerCell Sign Deal for Serial Delivery of LTPEM Hydrogen Fuel Cell Stacks. 2022. Available online: https://zeroavia.com/powercell-mou/ (accessed on 1 January 2024).
- Fuel Cell Handbook, 7th ed.; U.S. Department of Energy, Office of Fossil Energy, National Energy Technology Laboratory: Morgantown, WV, USA, 2016; OCLC: 957455519.
- Pukrushpan, J.T.; Stefanopoulou, A.G.; Peng, H. Control of Fuel Cell Power Systems: Principles, Modeling, Analysis, and Feedback Design; Advances in Industrial Control; Springer: London, UK; New York, NY, USA, 2004. [Google Scholar]
- Larminie, J.; Dicks, A. Fuel Cell Systems Explained, 2nd ed.; Wiley: New York, NY, USA, 2003. [Google Scholar] [CrossRef]
- Fritzson, P. Principles of Object-Oriented Modeling and Simulation with Modelica 3.3: A Cyber-Physica Approach; John Wiley & Sons: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Bernardi, D.M.; Verbrugge, M.W. Mathematical model of a gas diffusion electrode bonded to a polymer electrolyte. AIChE J. 1991, 37, 1151–1163. [Google Scholar] [CrossRef]
- Bernardi, D.M. Water-Balance Calculations for Solid-Polymer-Electrolyte Fuel Cells. J. Electrochem. Soc. 1990, 137, 3344–3350. [Google Scholar] [CrossRef]
- Bernardi, D.M.; Verbrugge, M.W. A Mathematical Model of the Solid-Polymer-Electrolyte Fuel Cell. J. Electrochem. Soc. 1992, 139, 2477. [Google Scholar] [CrossRef]
- Springer, T.E.; Zawodzinski, T.A.; Gottesfeld, S. Polymer Electrolyte Fuel Cell Model. J. Electrochem. Soc. 1991, 138, 2334–2342. [Google Scholar] [CrossRef]
- van Bussel, H.P.L.H.; Koene, F.G.H.; Mallant, R.K.A.M. Dynamic model of solid polymer fuel cell water management. J. Power Sources 1998, 71, 218–222. [Google Scholar] [CrossRef]
- Dutta, S.; Shimpalee, S.; Van Zee, J. Three-dimensional numerical simulation of straight channel PEM fuel cells. J. Appl. Electrochem. 2000, 30, 135–146. [Google Scholar] [CrossRef]
- Dutta, S.; Shimpalee, S.; Van Zee, J. Numerical prediction of mass-exchange between cathode and anode channels in a PEM fuel cell. Int. J. Heat Mass Transf. 2001, 44, 2029–2042. [Google Scholar] [CrossRef]
- Berning, T.; Lu, D.M.; Djilali, N. Three-dimensional computational analysis of transport phenomena in a PEM fuel cell. J. Power Sources 2002, 106, 284–294. [Google Scholar] [CrossRef]
- Rowe, A.; Li, X. Mathematical modeling of proton exchange membrane fuel cells. J. Power Sources 2001, 102, 82–96. [Google Scholar] [CrossRef]
- Thanapalan, K.; Williams, J.; Liu, G.; Rees, D. Modelling of a PEM fuel cell system. IFAC Proc. Vol. 2008, 41, 4636–4641. [Google Scholar] [CrossRef]
- Kravos, A.; Ritzberger, D.; Tavcar, G.; Hametner, C.; Jakubek, S.; Katrasnik, T. Thermodynamically consistent reduced dimensionality electrochemical model for proton exchange membrane fuel cell performance modelling and control. J. Power Sources 2020, 454, 227930. [Google Scholar] [CrossRef]
- Rubio Gonzalez, M.A.; Urquia, A.; Dormido, S. Dynamic modelling of PEM fuel cells using the FuelCellLib Modelica library. Math. Comput. Model. Dyn. Syst. 2010, 16, 165–194. [Google Scholar] [CrossRef]
- Sumeshan, S.; Kumar, D.R.; Krishna, B. Simulink Model of Proton Exchange Membrane Fuel Cell. In Proceedings of the 2022 7th International Conference on Environment Friendly Energies and Applications (EFEA), Bagatelle Moka MU, Mauritius, 14–16 December 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Njoya Motapon, S. A Generic Fuel Cell Model and Experimental Validation. Ph.D. Thesis, Ecole De Technologie Superieure, Montreal, QC, Canada, 2008. [Google Scholar]
- The-MathWorks. Designing Fuel Cell Systems Using System-Level Design; White Paper. 2022. Available online: https://www.mathworks.com/campaigns/offers/fuel-cell-systems-for-electrical-mobility.html (accessed on 22 October 2023).
- Spiegel, C. PEM Fuel Cell Modeling and Simulation Using Matlab; OCLC: 1033832673; Academic Press/Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Gebregergis, A.; Pillay, P.; Bhattacharyya, D.; Rengaswemy, R. Solid Oxide Fuel Cell Modeling. IEEE Trans. Ind. Electron. 2009, 56, 139–148. [Google Scholar] [CrossRef]
- Costamagna, P.; Grosso, S.; Travis, R.; Magistri, L. Integrated Planar Solid Oxide Fuel Cell: Steady-State Model of a Bundle and Validation through Single Tube Experimental Data. Energies 2015, 8, 13231–13254. [Google Scholar] [CrossRef]
- Ho, T.X. Dynamic characteristics of a solid oxide fuel cell with direct internal reforming of methane. Energy Convers. Manag. 2016, 113, 44–51. [Google Scholar] [CrossRef]
- Bianchi, F.R.; Spotorno, R.; Piccardo, P.; Bosio, B. Solid Oxide Fuel Cell Performance Analysis through Local Modelling. Catalysts 2020, 10, 519. [Google Scholar] [CrossRef]
- Andersson, D.; Åberg, E.; Eborn, J.; Yuan, J.; Sunden, B. Dynamic Modeling of a Solid Oxide Fuel Cell System in Modelica. Int. Conf. Fuel Cell Sci. Eng. Technol. 2011, 44052, 593–602. [Google Scholar] [CrossRef]
- Lakshmi, T.V.V.S.; Geethanjali, P.; Krishna, P.S. Mathematical modelling of solid oxide fuel cell using Matlab/Simulink. In Proceedings of the 2013 Annual International Conference on Emerging Research Areas and 2013 International Conference on Microelectronics, Communications and Renewable Energy, Kanjirapally, India, 4–6 June 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Vidović, T.; Tolj, I.; Radica, G.; Bodrožić Ćoko, N. Proton-Exchange Membrane Fuel Cell Balance of Plant and Performance Simulation for Vehicle Applications. Energies 2022, 15, 8110. [Google Scholar] [CrossRef]
- Pratt, J.W.; Klebanoff, L.E.; Munoz-Ramos, K.; Akhil, A.A.; Curgus, D.B.; Schenkman, B.L. Proton exchange membrane fuel cells for electrical power generation on-board commercial airplanes. Appl. Energy 2013, 101, 776–796. [Google Scholar] [CrossRef]
- Schröder, M.; Becker, F.; Kallo, J.; Gentner, C. Optimal operating conditions of PEM fuel cells in commercial aircraft. Int. J. Hydrogen Energy 2021, 46, 33218–33240. [Google Scholar] [CrossRef]
- Kadyk, T.; Winnefeld, C.; Hanke-Rauschenbach, R.; Krewer, U. Analysis and Design of Fuel Cell Systems for Aviation. Energies 2018, 11, 375. [Google Scholar] [CrossRef]
- Kadyk, T.; Schenkendorf, R.; Hawner, S.; Yildiz, B.; Römer, U. Design of Fuel Cell Systems for Aviation: Representative Mission Profiles and Sensitivity Analyses. Front. Energy Res. 2019, 7, 440189. [Google Scholar] [CrossRef]
- Hartmann, C.; Nøland, J.K.; Nilssen, R.; Mellerud, R. Dual Use of Liquid Hydrogen in a Next-Generation PEMFC-Powered Regional Aircraft with Superconducting Propulsion. IEEE Trans. Transp. Electrif. 2022, 8, 4760–4778. [Google Scholar] [CrossRef]
- Correa, G.; Santarelli, M.; Borello, F.; Cestino, E.; Romeo, G. Flight test validation of the dynamic model of a fuel cell system for ultra-light aircraft. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 229, 917–932. [Google Scholar] [CrossRef]
- Gummalla, M.; Pandy, A.; Braun, R.; Carriere, T.; Yamanis, J.; Vanderspurt, T.; Hardin, L.; Welch, R. Fuel Cell Airframe Integration Study for Short-Range Aircraft; NASA/CR—2006-214457/VOL1; NASA: Hanover, MD, USA, 2006.
- Fernandes, M.; De, P.; Andrade, S.; Bistritzki, V.; Fonseca, R.; Zacarias, L.; Gonçalves, .H.; De Castro, A.; Domingues, R.; Matencio, T. SOFC-APU systems for aircraft: A review. Int. J. Hydrogen Energy 2018, 43, 16311–16333. [Google Scholar] [CrossRef]
- Santarelli, M.; Cabrera, M.; Calì, M. Analysis of Solid Oxide Fuel Cell Systems for More-Electric Aircraft. J. Aircr. 2009, 46, 269–283. [Google Scholar] [CrossRef]
- Himansu, A.; Freeh, J.; Steffen, C.; Tornabene, R.; Wang, X.Y. Hybrid solid oxide fuel cell/Gas turbine system design for high altitude long endurance aerospace missions. In Proceedings of the Fourth International ASME Conference on Fuel Cell Science, Engineering and Technology, Irvine, CA, USA, 19–21 June 2006. [Google Scholar] [CrossRef]
- Collins, J.M.; McLarty, D. All-electric commercial aviation with solid oxide fuel cell-gas turbine-battery hybrids. Appl. Energy 2020, 265, 114787. [Google Scholar] [CrossRef]
- Cavini, L. Fuel Cell Simulation Model for Aircraft Integration Analysis in Early Design Phases. Diploma Thesis, Politecnico di Torino, Turin, Italy, 2024. [Google Scholar]
- O’Hayre, R.P.; Cha, S.W.; Colella, W.G.; Prinz, F.B. Fuel Cell Fundamentals, 3rd ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2016. [Google Scholar]
- Nehrir, M.H.; Wang, C. Modeling and Control of Fuel Cells: Distributed Generation Applications; OCLC: ocn298597847; IEEE Press Series on Power Engineering; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Zhang, G.; Kandlikar, S.G. A critical review of cooling techniques in proton exchange membrane fuel cell stacks. Int. J. Hydrogen Energy 2012, 37, 2412–2429. [Google Scholar] [CrossRef]
- Bargal, M.H.; Abdelkareem, M.A.; Tao, Q.; Li, J.; Shi, J.; Wang, Y. Liquid cooling techniques in proton exchange membrane fuel cell stacks: A detailed survey. Alex. Eng. J. 2020, 59, 635–655. [Google Scholar] [CrossRef]
- San Martín, I.; Ursúa, A.; Sanchis, P. Modelling of PEM Fuel Cell Performance: Steady-State and Dynamic Experimental Validation. Energies 2014, 7, 670–700. [Google Scholar] [CrossRef]
- Horizon-Fuel-Cell-Technologies. Open-Cathode PEM Fuel Cells. Available online: https://www.horizonfuelcell.com/fuel-cell (accessed on 13 August 2024).
- ZEROAVIA. SuperStack Datasheet. Available online: https://zeroavia.com/wp-content/uploads/2024/05/SuperStack-Datasheet-6-digital.pdf (accessed on 4 June 2024).
- Petzold, L.R. Description of DASSL: A Differential/Algebraic System Solver; Technical Report SAND-82-8637; CONF-820810-21; Sandia National Labs.: Livermore, CA, USA, 1982. [Google Scholar]
- Ticianelli, E.A.; Derouin, C.R.; Redondo, A.; Srinivasan, S. Methods to Advance Technology of Proton Exchange Membrane Fuel Cells. J. Electrochem. Soc. 1988, 135, 2209. [Google Scholar] [CrossRef]
- Yi, J.S.; Nguyen, T.V. Multicomponent Transport in Porous Electrodes of Proton Exchange Membrane Fuel Cells Using the Interdigitated Gas Distributors. J. Electrochem. Soc. 1999, 146, 38. [Google Scholar] [CrossRef]
- Fuller, T.F.; Newman, J. Water and Thermal Management in Solid-Polymer-Electrolyte Fuel Cells. J. Electrochem. Soc. 1993, 140, 1218–1225. [Google Scholar] [CrossRef]
- Souleman, N.M.; Tremblay, O.; Dessaint, L.A. A generic fuel cell model for the simulation of fuel cell vehicles. In Proceedings of the 2009 IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–10 September 2009; pp. 1722–1729. [Google Scholar] [CrossRef]
- Kulikovsky, A.A. A Physically–Based Analytical Polarization Curve of a PEM Fuel Cell. J. Electrochem. Soc. 2013, 161, F263. [Google Scholar] [CrossRef]
- Becker, F.; Pillath, F.; Kallo, J. Cathode Exhaust Gas Recirculation for Polymer Electrolyte Fuel Cell Stack. Fuel Cells 2018, 18, 568–575. [Google Scholar] [CrossRef]
- Jiao, K.; Xuan, J.; Du, Q.; Bao, Z.; Xie, B.; Wang, B.; Zhao, Y.; Fan, L.; Wang, H.; Hou, Z.; et al. Designing the next generation of proton-exchange membrane fuel cells. Nature 2021, 595, 361–369. [Google Scholar] [CrossRef]
- Hawa, H.A.; Roychoudhury, S.; Junaedi, C. Hybridized, High Pressure, Liquid Fueled Solid Oxide Fuel Cell (SOFC) for Aircraft Primary Power. In Proceedings of the 2022 IEEE Transportation Electrification Conference & Expo (ITEC), Anaheim, CA, USA, 15–17 June 2022; pp. 1051–1056. [Google Scholar] [CrossRef]
- Li, C.; Wang, Z.; Liu, H.; Qin, J.; Wei, L. Comparative study on the performance of the application of clean alternative fuels in SOFC/ICE hybrid power systems on electric aircraft. Front. Energy Res. 2023, 11, 1146587. [Google Scholar] [CrossRef]
- Zhao, F.; Virkar, A.V. Dependence of polarization in anode-supported solid oxide fuel cells on various cell parameters. J. Power Sources 2005, 141, 79–95. [Google Scholar] [CrossRef]



| Parameter | Gaseous Water Product | Liquid Water Product |
|---|---|---|
| Reaction | ||
| Reaction Enthalpy () | −241.83 kJ/mol | −285.83 kJ/mol |
| Standard-State Entropy () | −44.34 J/(mol K) | −163.23 J/(mol K) |
| Gibbs Free Energy () | −228.61 kJ/mol | −237.16 kJ/mol |
| Standard Potential () | 1.184 V | 1.229 V |
| Parameter | Equation |
|---|---|
| Exchange Current | |
| Ohmic Resistance | |
| Factor | |
| Tafel Slope | |
| Partial Pressure | |
| Partial Pressure | |
| Parameter | |
| Activation Energy | |
| Nernst Voltage | |
| Dimensionless Parameter |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cavini, L.; Liscouët-Hanke, S.; Viola, N. Acausal Fuel Cell Simulation Model for System Integration Analysis in Early Design Phases. Modelling 2024, 5, 1435-1453. https://doi.org/10.3390/modelling5040074
Cavini L, Liscouët-Hanke S, Viola N. Acausal Fuel Cell Simulation Model for System Integration Analysis in Early Design Phases. Modelling. 2024; 5(4):1435-1453. https://doi.org/10.3390/modelling5040074
Chicago/Turabian StyleCavini, Leonardo, Susan Liscouët-Hanke, and Nicole Viola. 2024. "Acausal Fuel Cell Simulation Model for System Integration Analysis in Early Design Phases" Modelling 5, no. 4: 1435-1453. https://doi.org/10.3390/modelling5040074
APA StyleCavini, L., Liscouët-Hanke, S., & Viola, N. (2024). Acausal Fuel Cell Simulation Model for System Integration Analysis in Early Design Phases. Modelling, 5(4), 1435-1453. https://doi.org/10.3390/modelling5040074









