Simulation Analysis of the Annular Liquid Disturbance Induced by Gas Leakage from String Seals During Annular Pressure Relief
Abstract
:1. Introduction
2. Numerical Simulation Method
2.1. Governing Equations of Fluid Motion
2.1.1. Continuity Equation
2.1.2. Energy Equation
2.1.3. Momentum Equation
2.1.4. Turbulence Model
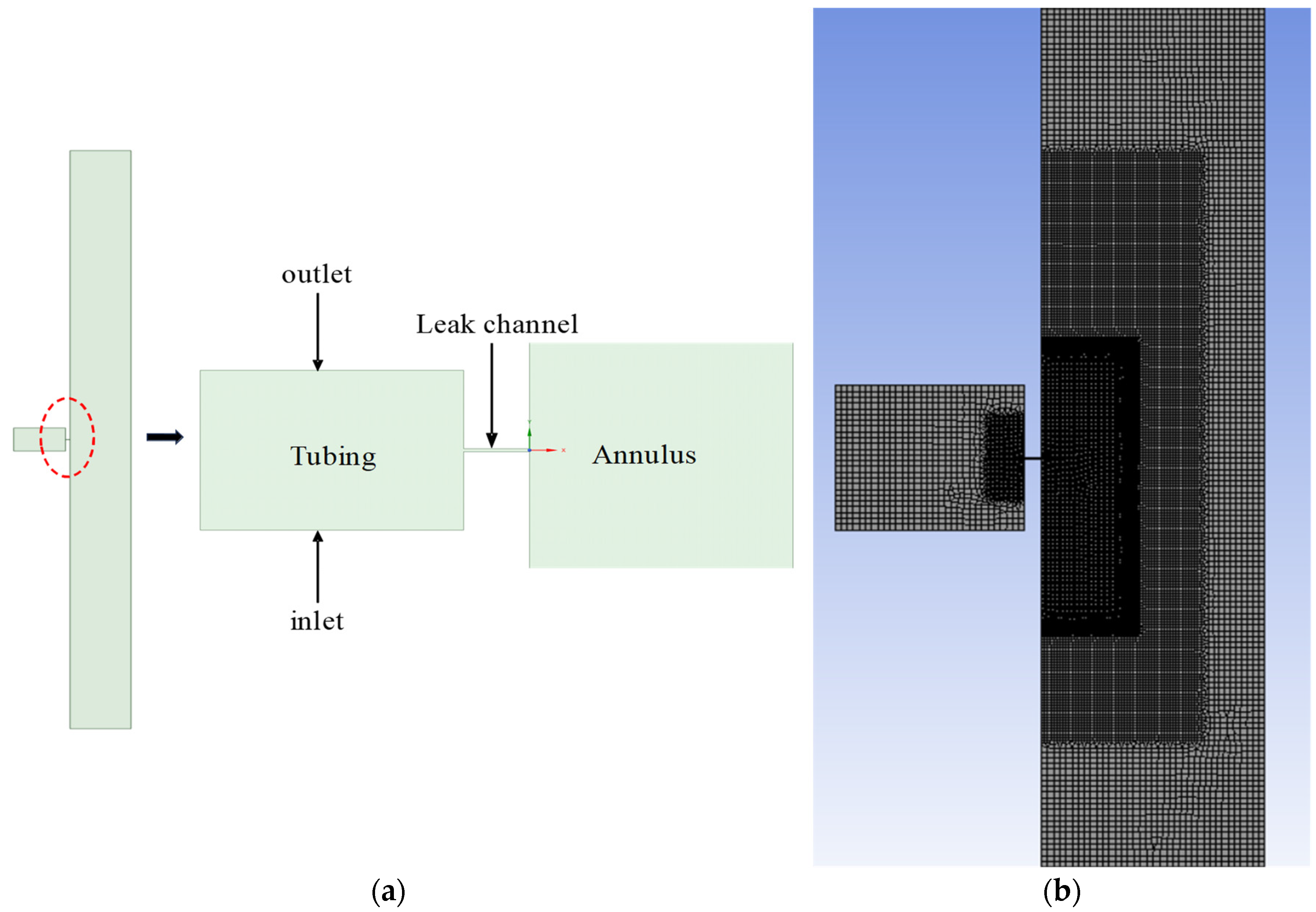
2.2. Geometric Models and Meshing
2.3. Mesh Independence Verification
3. Results and Discussion
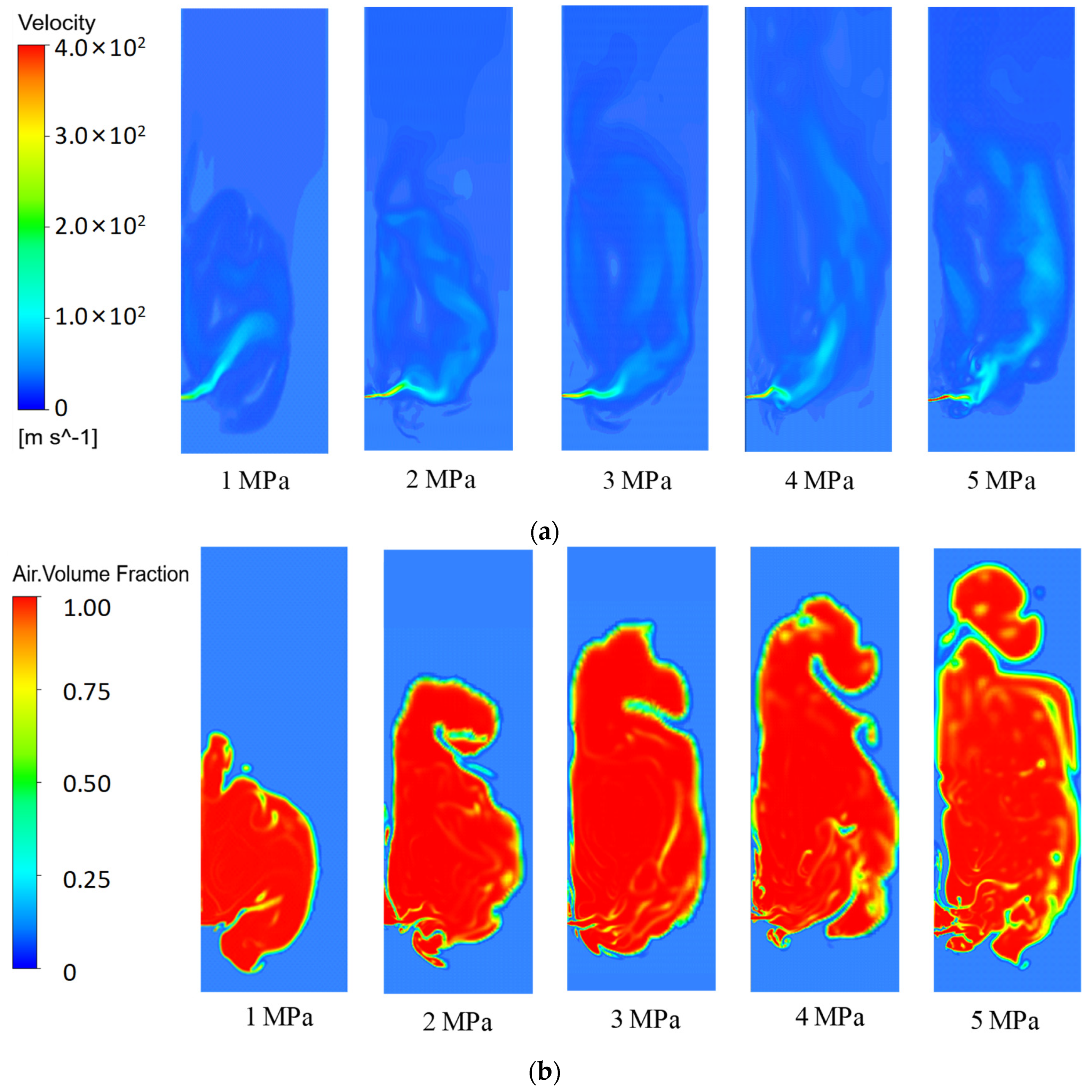
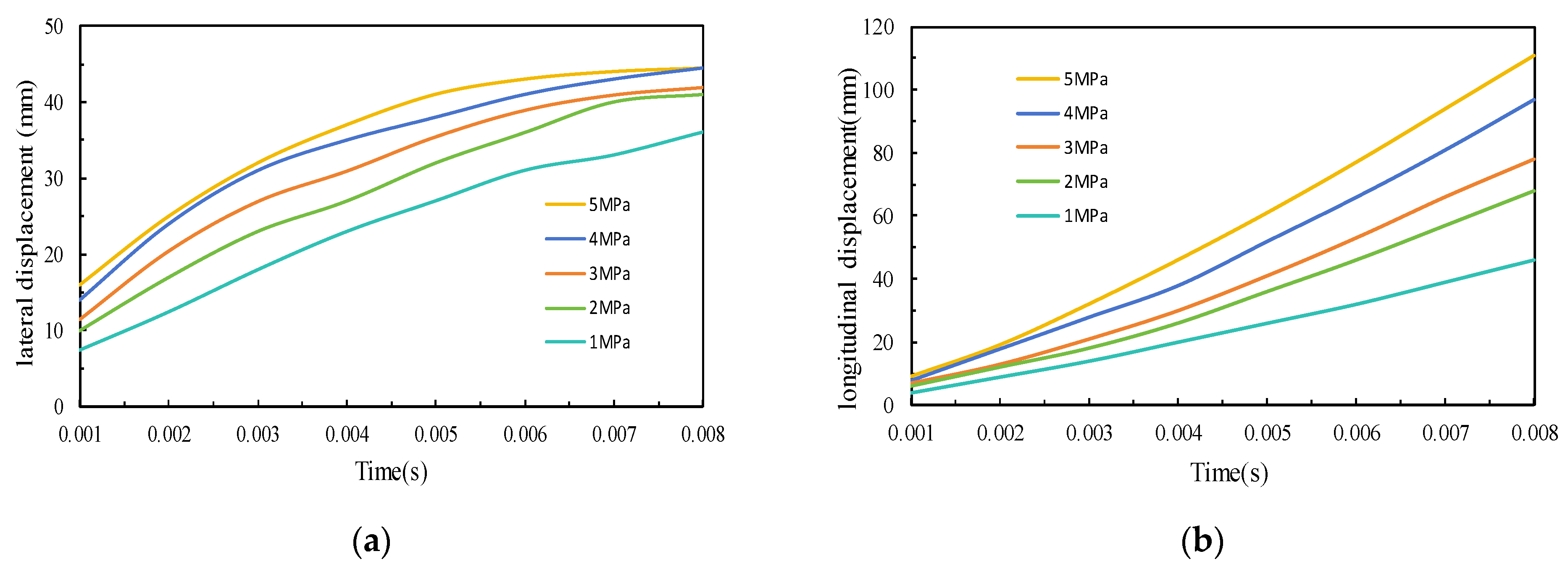
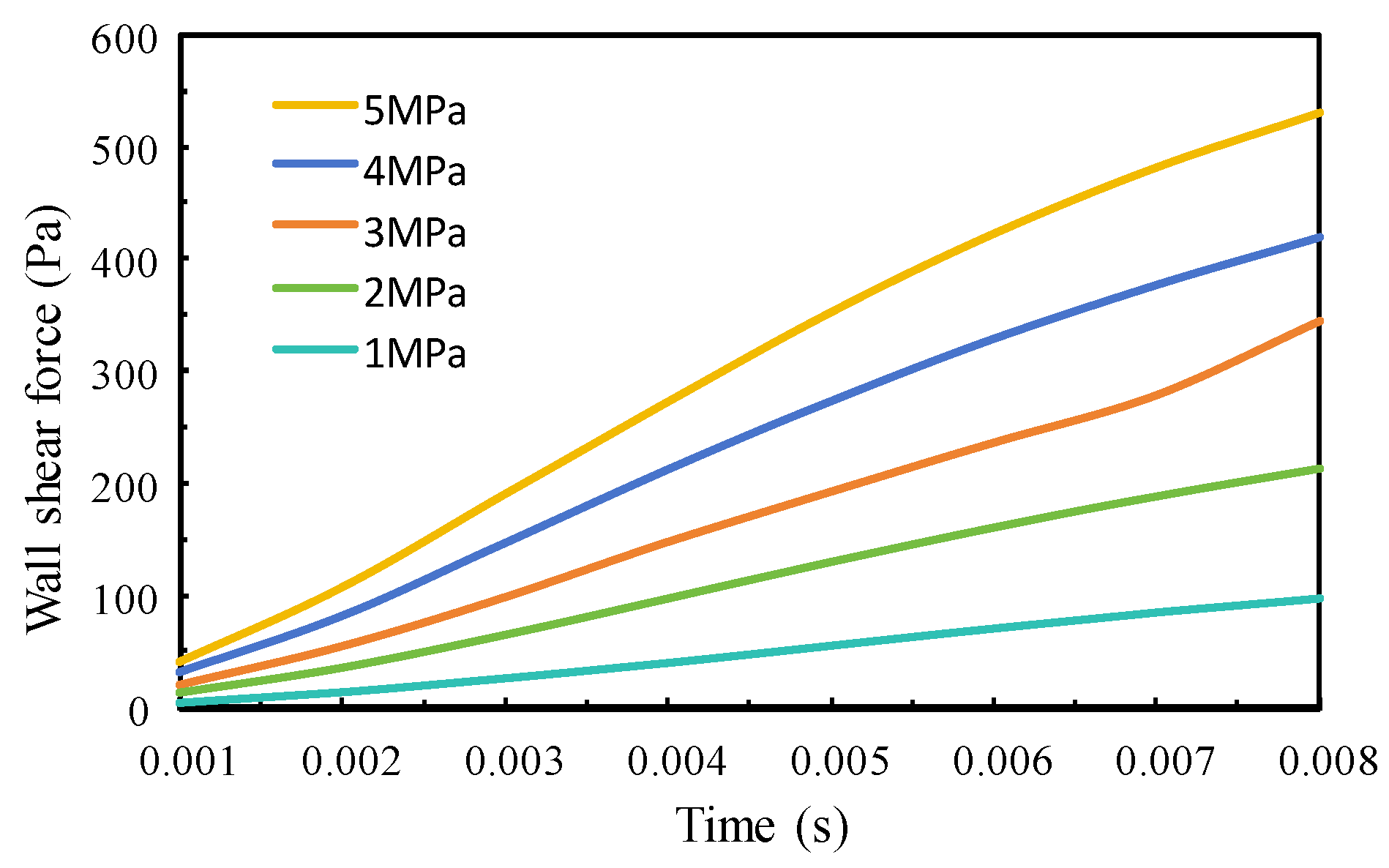
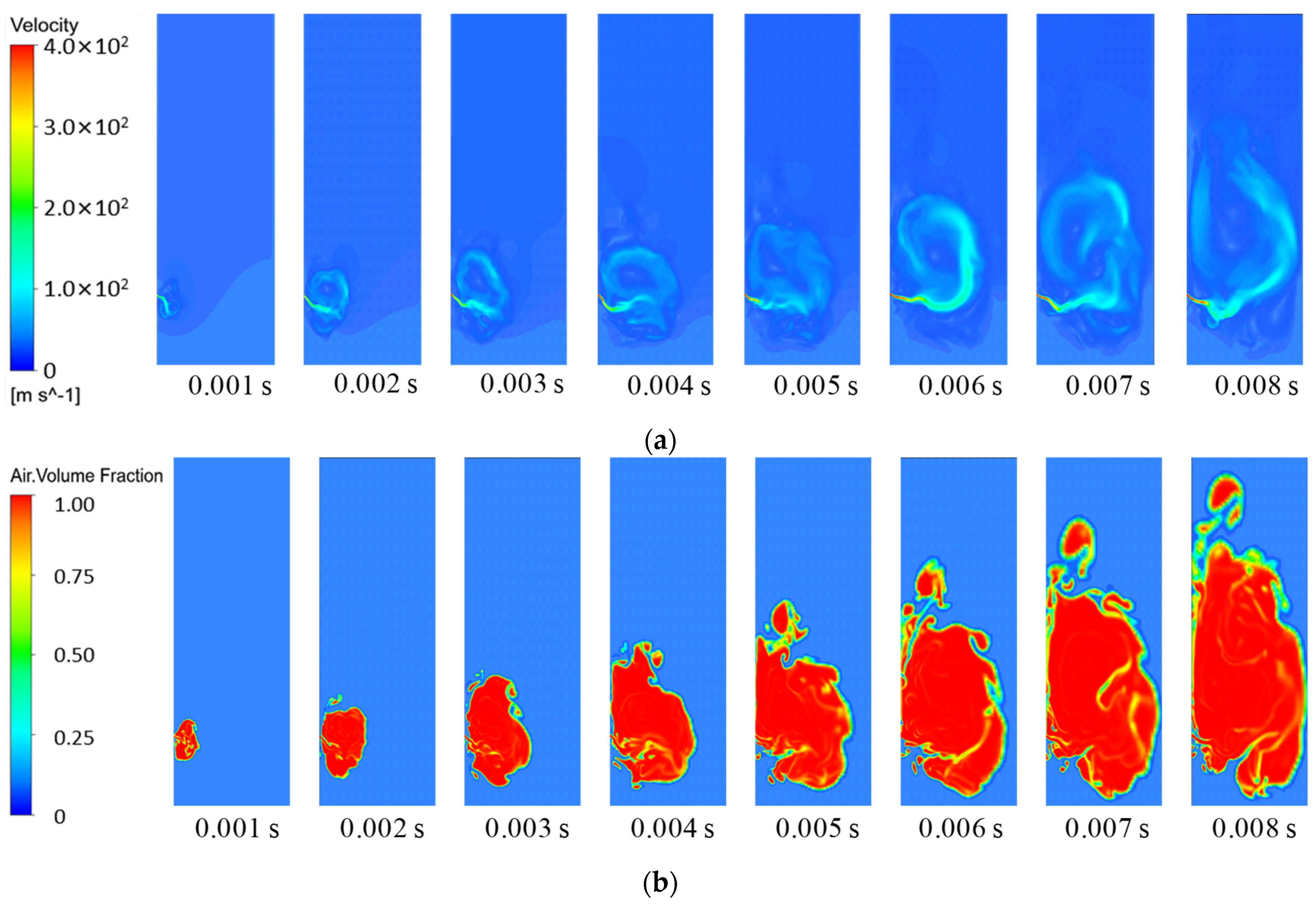
3.1. Simulation Analysis of Leakage Under Different Pressure Differential Conditions
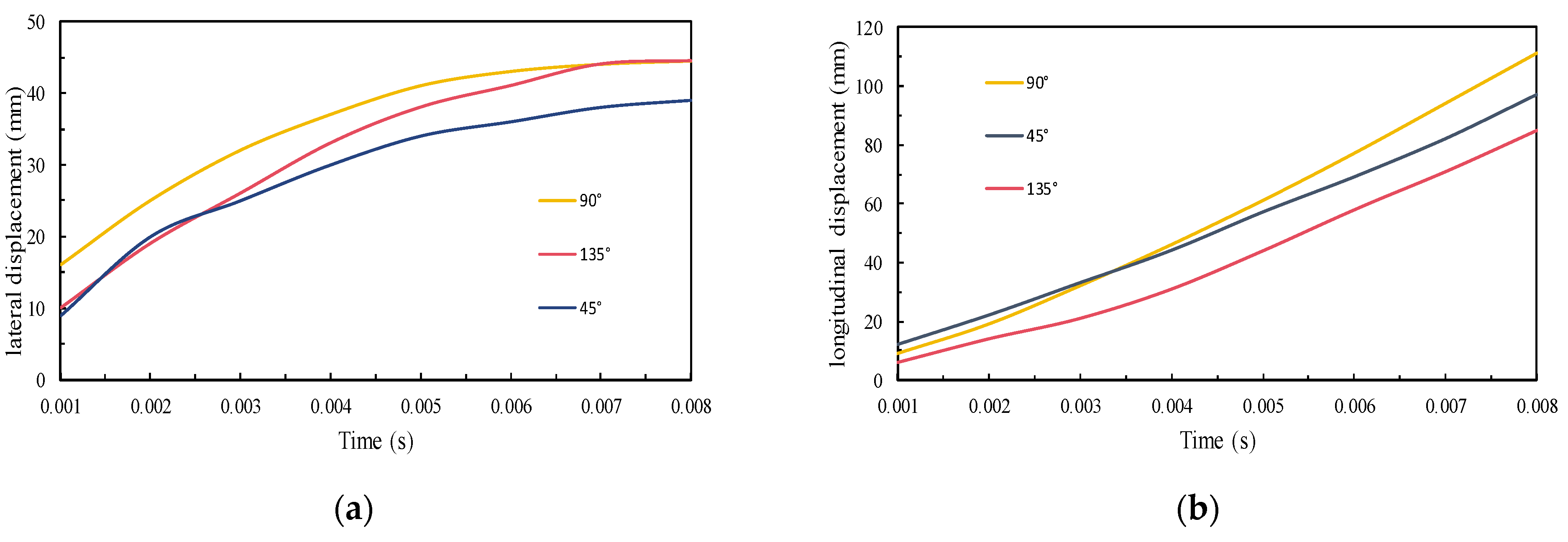
3.2. Leakage Simulation Analysis Under Different Leakage Directions
3.3. Leakage Simulation Analysis Under Different Leakage Times
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, B.; Xu, Z.; Lu, N.; Liu, H.; Liu, J.; Hu, Z.; Xie, J.; Wang, K. Characteristics of sustained annular pressure and fluid distribution in high pressure and high temperature gas wells considering multiple leakage of tubing string. J. Pet. Sci. Eng. 2021, 196, 108083. [Google Scholar] [CrossRef]
- Cao, L.; Sun, J.; Zhang, B.; Lu, N.; Xu, Y. Analysis of Multiple Annular Pressure in Gas Storage Well and High-Pressure Gas Well, Energy Engineering. J. Assoc. Energy Eng. 2023, 120, 35–48. [Google Scholar] [CrossRef]
- Martins, I.O.; da Silva, A.K.; Silva, E.C.C.M.; Hasan, A.R.; Barbosa, J.R. Predicting the annular pressure behavior during water injection in offshore wells with a transient, multiphysics model. J. Pet. Sci. Eng. 2022, 218, 110992. [Google Scholar] [CrossRef]
- Wei, L.; Fu, C.; Li, W.; Gao, Y.; Guo, L.; Liu, Y.; Liang, F.; Jia, A.; Guo, Q. Integrity assessment of shale gas wells in Changning Block based on hierarchical analysis method. J. Pet. Explor. Prod. 2024, 14, 2129–2142. [Google Scholar] [CrossRef]
- Zeng, D.; He, Q.; Yu, Z.; Jia, W.; Zhang, S.; Liu, Q. Risk assessment of sustained casing pressure in gas wells based on the fuzzy comprehensive evaluation method. J. Nat. Gas Sci. Eng. 2017, 46, 756–763. [Google Scholar] [CrossRef]
- Zeng, D.; Dong, B.; Zhang, S.; Yi, Y.; Huang, Z.; Tian, G.; Yu, H.; Sun, Y. Annular corrosion risk analysis of gas injection in CO2 flooding and development of oil-based annulus protection fluid. J. Pet. Sci. Eng. 2022, 208, 109526. [Google Scholar] [CrossRef]
- Dong, B.; Zeng, D.; Yu, Z.; Le Cai, L.; Yu, H.; Shi, S.Z.; Tian, G.; Yi, Y. Major corrosion influence factors analysis in the production well of CO2 flooding and the optimization of relative anti-corrosion measures. J. Pet. Sci. Eng. 2021, 200, 108052. [Google Scholar] [CrossRef]
- Qin, M.; Liao, K.; He, G.; Huang, Y.; Wang, M.; Zhang, S. Main control factors and prediction model of flow-accelerated CO2/H2S synergistic corrosion for X65 steel. Process Saf. Environ. Prot. 2022, 160, 749–762. [Google Scholar] [CrossRef]
- Hu, J.; Xiong, Q.; Chen, L.; Zhang, C.; Zheng, Z.; Geng, S.; Yang, Z.; Zhong, X. Corrosion inhibitor in CO2-O2-containing environment: Inhibition effect and mechanisms of Bis(2-ehylhexyl) phosphate for the corrosion of carbon steel. Corros. Sci. 2021, 179, 109173. [Google Scholar] [CrossRef]
- Zeng, D.; Dong, B.; Zeng, F.; Yu, Z.; Zeng, W.; Guo, Y.; Peng, Z.; Tao, Y. Analysis of corrosion failure and materials selection for CO2–H2S gas well. J. Nat. Gas Sci. Eng. 2021, 86, 103734. [Google Scholar] [CrossRef]
- Zhi, Z.; Jing, L.; Yushan, Z.; Cheng, Z.; Qingsheng, Z.; Dezhi, Z.; Xiankang, Z. Finite service life evaluation method of production casing for sour-gas wells. J. Pet. Sci. Eng. 2018, 165, 171–180. [Google Scholar] [CrossRef]
- Ha, H.Y.; Jang, J.H.; Lee, T.H.; Won, C.; Lee, C.H.; Moon, J.; Lee, C.G. Investigation of the localized corrosion and passive behavior of type 304 stainless steels with 0.2–1.8 wt % B. Materials 2018, 11, 2097. [Google Scholar] [CrossRef]
- Montiel, H.; Vílchez, J.A.; Casal, J.; Arnaldos, J. Mathematical modelling of accidental gas releases. J. Hazard. Mater. 1998, 59, 211–233. [Google Scholar] [CrossRef]
- Kostowski, W.J.; Skorek, J. Real gas flow simulation in damaged distribution pipelines. Energy 2012, 45, 481–488. [Google Scholar] [CrossRef]
- Liu, C.; Li, Y.; Meng, L.; Wang, W.; Zhao, F.; Fu, J. Computational fluid dynamic simulation of pressure perturbations generation for gas pipelines leakage. Comput. Fluids 2015, 119, 213–223. [Google Scholar] [CrossRef]
- Xinhong, L.; Guoming, C.; Renren, Z.; Hongwei, Z.; Jianmin, F. Simulation and assessment of underwater gas release and dispersion from subsea gas pipelines leak. Process Saf. Environ. Prot. 2018, 119, 46–57. [Google Scholar] [CrossRef]
- Oke, A.; Mahgerefteh, H.; Economou, I.; Rykov, Y. A transient outflow model for pipeline puncture. Chem. Eng. Sci. 2003, 58, 4591–4604. [Google Scholar] [CrossRef]
- Nouri-Borujerdi, A.; Ziaei-Rad, M. Simulation of compressible flow in high pressure buried gas pipelines. Int. J. Heat Mass Transf. 2009, 52, 5751–5758. [Google Scholar] [CrossRef]
- Moloudi, R.; Esfahani, J.A. Modeling of gas release following pipeline rupture: Proposing non-dimensional correlation. J. Loss Prev. Process. Ind. 2014, 32, 207–217. [Google Scholar] [CrossRef]
- Ebrahimi-Moghadam, A.; Farzaneh-Gord, M.; Deymi-Dashtebayaz, M. Correlations for estimating natural gas leakage from above-ground and buried urban distribution pipelines. J. Nat. Gas Sci. Eng. 2016, 34, 185–196. [Google Scholar] [CrossRef]
- Jing, J.; Tian, Y.; Zhu, X.; Zhou, Y.; Shi, C.; Lei, Q. Safety evaluation of offshore oil and gas well string based on corrosion rate prediction. J. Loss Prev. Process. Ind. 2024, 91, 105385. [Google Scholar] [CrossRef]
- Li, Y.Y.; Zhu, G.Y.; Hou, B.S.; Zhang, Q.H.; Zhang, G.A. A numerical model based on finite element method for predicting the corrosion of carbon steel under supercritical CO2 conditions. Process Saf. Environ. Prot. 2021, 149, 866–884. [Google Scholar] [CrossRef]
- Mubarak, G.; Elkhodbia, M.; Gadala, I.; Al Fantazi, A.; Barsoum, I. Failure analysis corrosion rate prediction, and integrity assessment of J55 downhole tubing in ultra-deep gas and condensate well. Eng. Fail. Anal. 2023, 151, 107381. [Google Scholar] [CrossRef]
- Zeng, D.; Dong, B.; Yu, Z.; Huang, Z.; Yi, Y.; Yu, H.; Li, J.; Tian, G. Design of water-based annulus protection fluid for CO2 flooding injection well. J. Pet. Sci. Eng. 2021, 205, 108726. [Google Scholar] [CrossRef]
- Liu, C.; An, J.; Xie, C.; Wu, H.; Zhang, Z. Numerical simulation-based pinhole leakage characteristics and hazard boundaries of buried natural gas risers. Process Saf. Environ. Prot. 2024, 184, 462–476. [Google Scholar] [CrossRef]
- Bu, F.; Liu, Y.; Liu, Y.; Xu, Z.; Chen, S.; Jiang, M.; Guan, B. Leakage diffusion characteristics and harmful boundary analysis of buried natural gas pipeline under multiple working conditions. J. Nat. Gas Sci. Eng. 2021, 94, 104047. [Google Scholar] [CrossRef]
- Bonnaud, C.; Cluzel, V.; Corcoles, P.; Dubois, J.P.; Louvet, V.; Maury, M.; Narbonne, A.; Orefice, H.; Perez, A.; Ranty, J.; et al. Experimental study and modelling of the consequences of small leaks on buried transmission gas pipeline. J. Loss Prev. Process. Ind. 2018, 55, 303–312. [Google Scholar] [CrossRef]
- Ayyildiz, B.; Sheriff, M.Z.; Rahman, M.A.; Delgado, A.; Hassan, I.; Nounou, H.; Nounou, M. Research on pinhole accidental gas release in pipelines: Statistical modeling, real gas CFD simulation, and validation. Process Saf. Environ. Prot. 2023, 176, 786–796. [Google Scholar] [CrossRef]

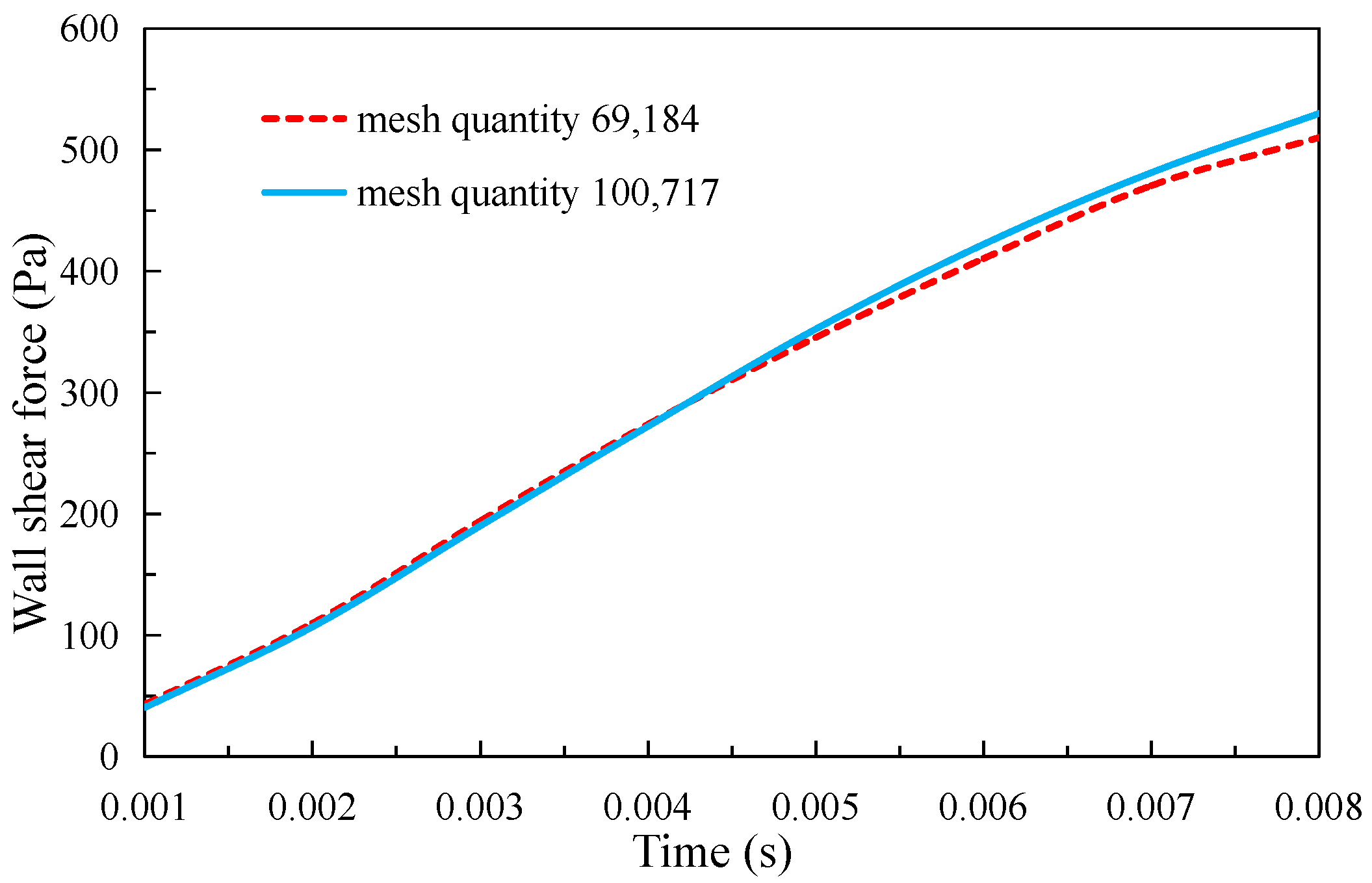




| Serial Number | Mesh Quantity | Mesh Quality |
|---|---|---|
| 1 | 69,184 | 0.97988 |
| 2 | 100,717 | 0.97832 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, Q.; Ke, R.; Bai, X.; Du, C.; Luo, Z.; Huang, Y.; Du, L.; Pei, S.; Zeng, D. Simulation Analysis of the Annular Liquid Disturbance Induced by Gas Leakage from String Seals During Annular Pressure Relief. Modelling 2024, 5, 1674-1686. https://doi.org/10.3390/modelling5040087
Du Q, Ke R, Bai X, Du C, Luo Z, Huang Y, Du L, Pei S, Zeng D. Simulation Analysis of the Annular Liquid Disturbance Induced by Gas Leakage from String Seals During Annular Pressure Relief. Modelling. 2024; 5(4):1674-1686. https://doi.org/10.3390/modelling5040087
Chicago/Turabian StyleDu, Qiang, Ruikang Ke, Xiangwei Bai, Cheng Du, Zhaoqian Luo, Yao Huang, Lang Du, Senqi Pei, and Dezhi Zeng. 2024. "Simulation Analysis of the Annular Liquid Disturbance Induced by Gas Leakage from String Seals During Annular Pressure Relief" Modelling 5, no. 4: 1674-1686. https://doi.org/10.3390/modelling5040087
APA StyleDu, Q., Ke, R., Bai, X., Du, C., Luo, Z., Huang, Y., Du, L., Pei, S., & Zeng, D. (2024). Simulation Analysis of the Annular Liquid Disturbance Induced by Gas Leakage from String Seals During Annular Pressure Relief. Modelling, 5(4), 1674-1686. https://doi.org/10.3390/modelling5040087





