Modeling Temperature and Moisture Dynamics in Corn Storage Silos: A Comparative 2D and 3D Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mathematical Model
2.2. Boundary Conditions with Environmental Conditions
2.3. Numerical Solution
2.4. Model Validation
3. Results
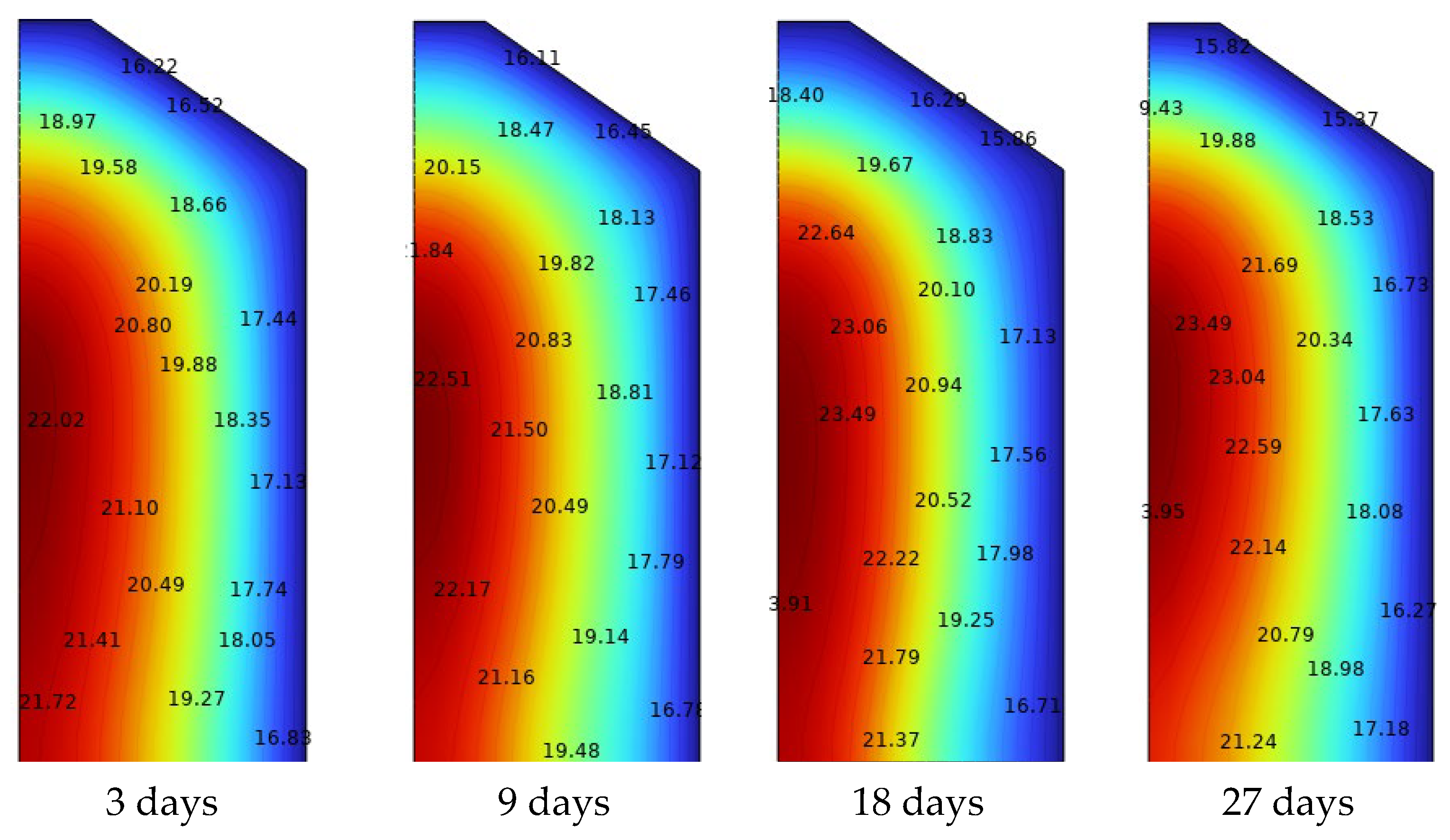
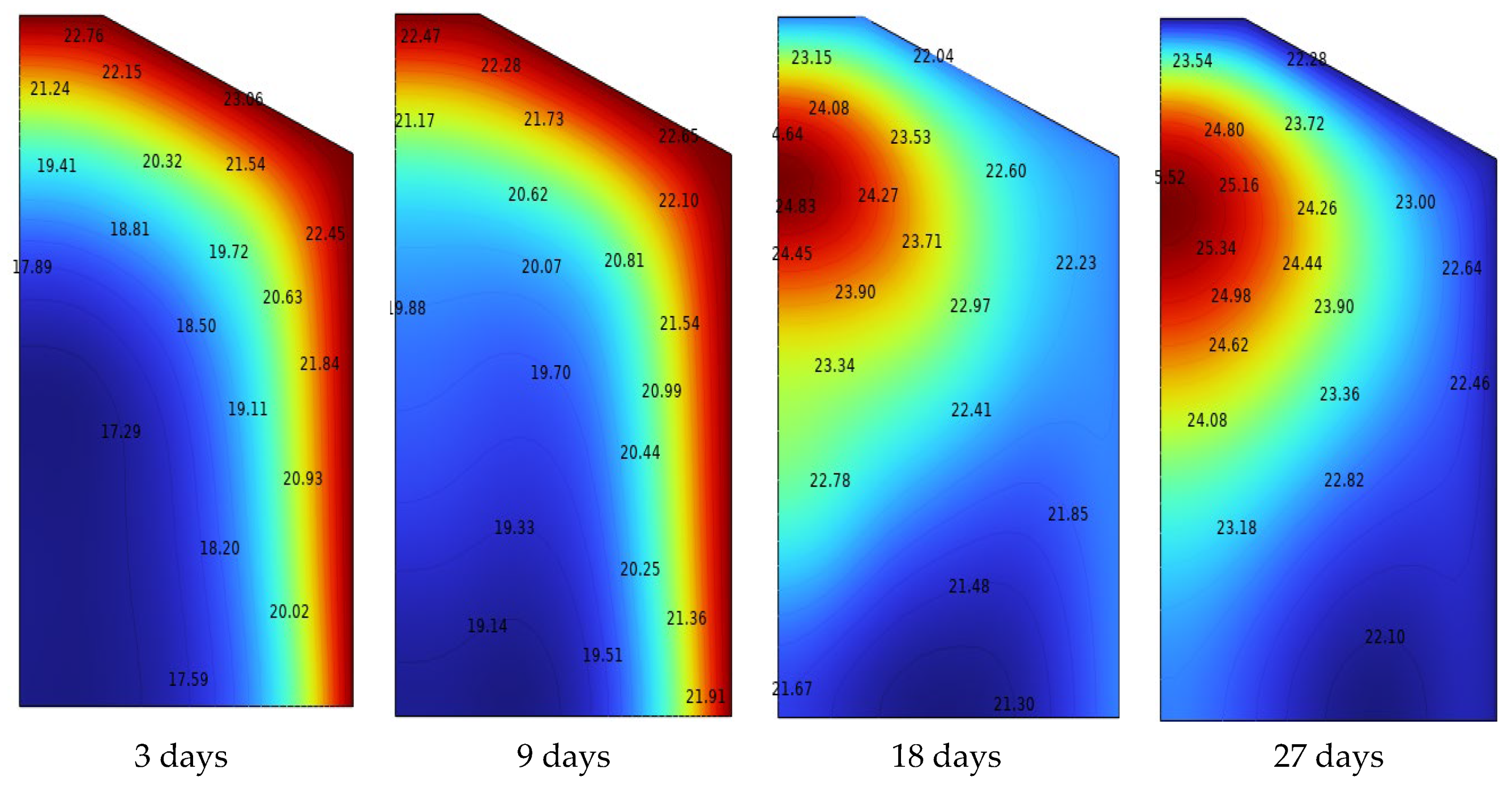
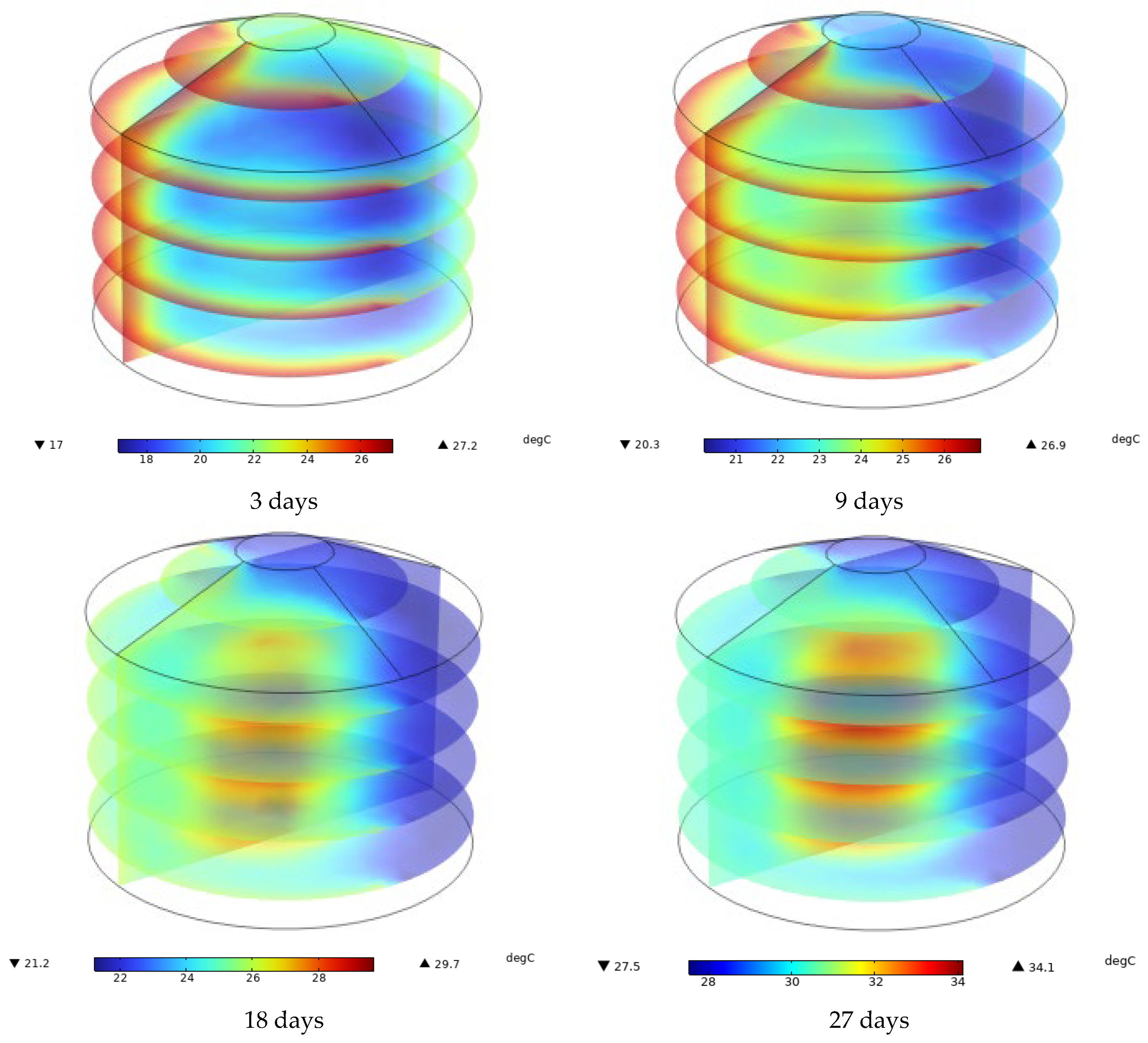
3.1. Temperature Profiles
3.2. Relative Humidity Profiles
3.3. Grain Moisture Profiles
3.4. Temperature Contours
3.5. Stream Function Contours
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| List of Symbols | ||
| Absorptivity of galvanized steel | ||
| Grain–air interfacial area, m2·m−3 | ||
| Water activity, dimensionless | ||
| Concentration of grain moisture, kg/m3 | ||
| Concentration of water vapor, kg/m3 | ||
| Specific heat, J/kg °C | ||
| Scalar diffusivity, m2/s | ||
| Solar radiation incident on the silo surface, W/m2 | ||
| Gravity acceleration, m/s2 | ||
| Heat transfer coefficient, W/m2 °C | ||
| Molecular mass of water | ||
| Molecular mass of air | ||
| Average molecular mass | ||
| Thermal conductivity of the porous media, W/m °C | ||
| Thermal conductivity of the silo wall, W/m °C | ||
| Mass transfer coefficient, m/s | ||
| Height of the cavity, m | ||
| Normal direction | ||
| Air pressure, mmHg | ||
| Volumetric generation of water by respiration, kg/m3·s | ||
| Vapor pressure, mmHg | ||
| Volumetric heat of respiration of cereal grain, J/m3·s | ||
| Radius of the cavity, m | ||
| Cylindrical coordinates, m | ||
| Time, hours | ||
| Fluid temperature, °C | ||
| Initial temperature of the grain, °C | ||
| Ambient temperature, °C | ||
| Sky temperature, °C | ||
| Moisture of the grain on dry basis, kg H2O/kg dry grain | ||
| Moisture of the grain on wet basis, kg H2O/kg grain | ||
| Initial moisture content, kg H2O/kg dry grain | ||
| Absolute humidity of the air, kg H2O/kg dry air | ||
| Initial absolute humidity, kgH2O/kg dry air | ||
| Absolute humidity of air in the grain-air interface, kg H2O/kg dry air | ||
| Greek Symbols | ||
| Volumetric coefficient of thermal expansion, K−1 | ||
| Volumetric coefficient of mass expansion, m3/kg | ||
| γ | continuous phase | |
| ε | Porosity | |
| Permeability, m2 | ||
| ᴦ | Boundary of the computational domain | |
| Sky emissivity | ||
| Steel emissivity | ||
| Latent heat of vaporization of water, J/kg | ||
| Air viscosity, kg/m·s | ||
| Density of dry air, kg/m3 | ||
| Density of the continuous phase, kg/m3 | ||
| σ | Stefan–Boltzmann constant, W/m2·K4 | |
| ω | Discontinuous phase | |
| Abbreviations | ||
| FEM | Finite element method | |
| FVM | Finite volume method | |
| PDEs | Partial differential equations | |
| RH | Relative humidity % | |
References
- Babangida, L.Y.; Yong, H. Design development and techniques for controlling grains post-harvest losses with metal silo for small and medium scale farmers. AJB 2011, 10, 14552–14561. [Google Scholar] [CrossRef]
- Sutton, A.O.; Strickland, D.; Norris, D.R. Food storage in a changing world: Implications of climate change for food-caching species. Clim. Change Responses 2016, 3, 12. [Google Scholar] [CrossRef]
- Jiménez-Islas, H.; Navarrete-Bolaños, J.L.; Botello-Álvarez, E. Numerical study of the natural convection of heat and 2-D mass of grain stored in cylindrical silos. Agrociencia 2004, 38, 325–342. [Google Scholar]
- Barreto, A.; Abalone, R.; Gastón, A. Mathematical modelling of momentum, heat and mass transfer in silos: Part I: Model development and validation. Lat. Am. Appl. Res. 2013, 43, 377–384. [Google Scholar]
- Lawrence, N.J.; Maier, N.D.E.; Stroshine, N.R.L. Three-dimensional transient heat, mass, momentum, and species transfer in the stored grain ecosystem: Part I. Model Development and Evaluation. Trans. ASABE 2013, 56, 179–188. [Google Scholar] [CrossRef]
- Barreto, A.A.; Abalone, R.; Gastón, A. Mathematical modelling of momentum, heat and mass transfer in grains stored in silos: Part II: Model application. Lat. Am. Appl. Res. 2013, 43, 385–391. [Google Scholar]
- Khankari, N.K.K.; Morey, N.R.V.; Patankar, N.S.V. Mathematical model for moisture diffusion in stored grain due to temperature gradients. Trans. ASABE 1994, 37, 1591–1604. [Google Scholar] [CrossRef]
- Khankari, N.K.K.; Morey, N.R.V.; Patankar, N.S.V. Application of a numerical model for prediction of moisture migration in stored grain. Trans. ASABE 1995, 38, 1789–1804. [Google Scholar] [CrossRef]
- Montross, M.D.; Maier, N.D.E.; Haghighi, K. Validation of a finite element stored grain ecosystem model. Trans. ASABE 2002, 45, 1465. [Google Scholar] [CrossRef]
- Montross, M.D.; Maier, D.E.; Haghighi, N.K. Development of a finite-element stored grain ecosystem model. Trans. ASABE 2002, 45, 1455. [Google Scholar] [CrossRef]
- Lawrence, N.J.; Maier, D.E.; Stroshine, N.R.L. Three-dimensional transient heat, mass, momentum, and species transfer in the stored grain ecosystem: Part II. Model Validation. Trans. ASABE 2013, 56, 189–201. [Google Scholar] [CrossRef]
- Quemada-Villagómez, L.I.; Molina-Herrera, F.I.; Carrera-Rodríguez, M.; Calderón-Ramírez, M.; Martínez-González, G.M.; Navarrete-Bolaños, J.; Jiménez-Islas, H. Numerical study to predict temperature and moisture profiles in unventilated grain silos at prolonged periods. Int. J. Thermophys. 2020, 41, 52. [Google Scholar] [CrossRef]
- Abbouda, N.S.K.; Chung, N.D.S.; Seib, N.P.A.; Song, N.A. Heat and mass transfer in stored milo. Part I. Heat Transfer Model. Trans. ASABE 1992, 35, 1569–1573. [Google Scholar] [CrossRef]
- Abbouda, N.S.K.; Seib, N.P.A.; Chung, N.D.S.; Song, N.A. Heat and mass transfer in stored milo. Part II. Mass Transfer Model. Trans. ASABE 1992, 35, 1575–1580. [Google Scholar] [CrossRef]
- Abalone, R.; Gastón, A.; Cassinera, R.; Lara, M. Modelización de la distribución de la temperatura y humedad en granos almacenados en silos. Mecánica Comput. 2006, 24, 233–247. [Google Scholar]
- Carrera-Rodríguez, M.; Martínez-González, G.M.; Navarrete-Bolaños, J.L.; Botello-Álvarez, J.E.; Rico-Martínez, R.; Jiménez-Islas, H. Transient numerical study of the effect of ambient temperature on 2-D cereal grain storage in cylindrical silos. J. Stored Prod. Res. 2011, 47, 106–122. [Google Scholar] [CrossRef]
- Jiang, N.S.; Jofriet, N.J.C. Finite element prediction of silage temperatures in tower silos. Trans. ASABE 1987, 30, 1744–1750. [Google Scholar] [CrossRef]
- Jofriet, J.C.; Jiang, S.; Tang, S. Finite element prediction of temperature gradients in walls of cylindrical concrete storage structures. Can. J. Civ. Eng. 1991, 18, 12–19. [Google Scholar] [CrossRef]
- Alagusundaram, N.K.; Jayas, N.D.S.; White, N.N.D.G.; Muir, N.W.E. Three-dimensional, finite element, heat transfer temperature distribution model in grain storage bins. Trans. ASABE 1990, 33, 0577–0584. [Google Scholar] [CrossRef]
- Rocha, K.S.O.; Martins, J.H.; Martins, M.A.; Saraz, J.A.O.; Filho, A.F.L. Three-Dimensional modeling and simulation of heat and mass transfer processes in porous media: An application for maize stored in a flat bin. Dry. Technol. 2013, 31, 1099–1106. [Google Scholar] [CrossRef]
- Bartosik, N.R.E.; Maier, N.D. Effect of airflow distribution on the performance of NA/LT in-bin drying of corn. Trans. ASABE 2006, 49, 1095–1104. [Google Scholar] [CrossRef]
- Novoa-Muñoz, F. Simulation of the temperature of barley during its storage in cylindrical silos. MATCOM 2019, 157, 1–14. [Google Scholar] [CrossRef]
- Markowski, M.; Bialobrzewski, I.; Bowszys, J.; Suchecki, S. Simulation of temperature distribution in stored wheat without aeration. Dry. Technol. 2007, 25, 1527–1536. [Google Scholar] [CrossRef]
- De Oliveira, G.H.; De Oliveira, A.P.L.R.; Correa, P.C. Use of the CFD tool to analyze the aeration compartment in a horizontal silo. Int. J. Agric. Technol. 2022, 2, 1–6. [Google Scholar] [CrossRef]
- Valle, F.J.M.; Gastón, A.; Abalone, R.M.; De la Torre, D.A.; Castellari, C.C.; Bartosik, R.E. Study and modelling the respiration of corn seeds (Zea mays L.) during hermetic storage. Biosyst. Eng. 2021, 208, 45–57. [Google Scholar] [CrossRef]
- Masud, A.; Khurram, R.A. Multiscale finite element method for the incompressible Navier–Stokes equations. Comput. Methods Appl. Mech. Eng. 2006, 195, 1750–1777. [Google Scholar] [CrossRef]
- Moukalled, F.; Mangani, L.; Darwish, M. The Finite Volume Method in Computational Fluid Dynamics: An Advanced Introduction with OpenFOAM® and MATLAB; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Jia, C.; Sun, D.; Cao, C. Finite element prediction of transient temperature distribution in a grain storage bin. J. Agric. Eng. Res. 2000, 76, 323–330. [Google Scholar] [CrossRef]
- Jia, C.; Sun, D.; Cao, C. Computer simulation of temperature changes in a wheat storage bin. J. Stored Prod. Res. 2001, 37, 165–177. [Google Scholar] [CrossRef]
- Gastón, A.; Abalone, R.; Cassinera, A.; Lara, M.A. Predicción de la distribución de temperatura de granos almacenados en silos. AVERMA 2005, 9, 13–18. [Google Scholar]
- Abe, T.; Basunia, M. Simulation of temperature and moisture changes during storage of rough rice in cylindrical bins owing to weather variability. J. Agric. Eng. Res. 1996, 65, 223–233. [Google Scholar] [CrossRef]
- Andrade, N.E.T.; Couto, N.S.M.; Queiroz, N.D.M.; Faroni, N.L.R.A.; De Sousa Damasceno, N.G. Three-Dimensional Simulation of the Temperature Variation in Corn Stored in Metallic Bin. In Proceedings of the 2002 ASAE Annual Meeting, Chicago, IL, USA, 28–31 July 2002. [Google Scholar] [CrossRef]
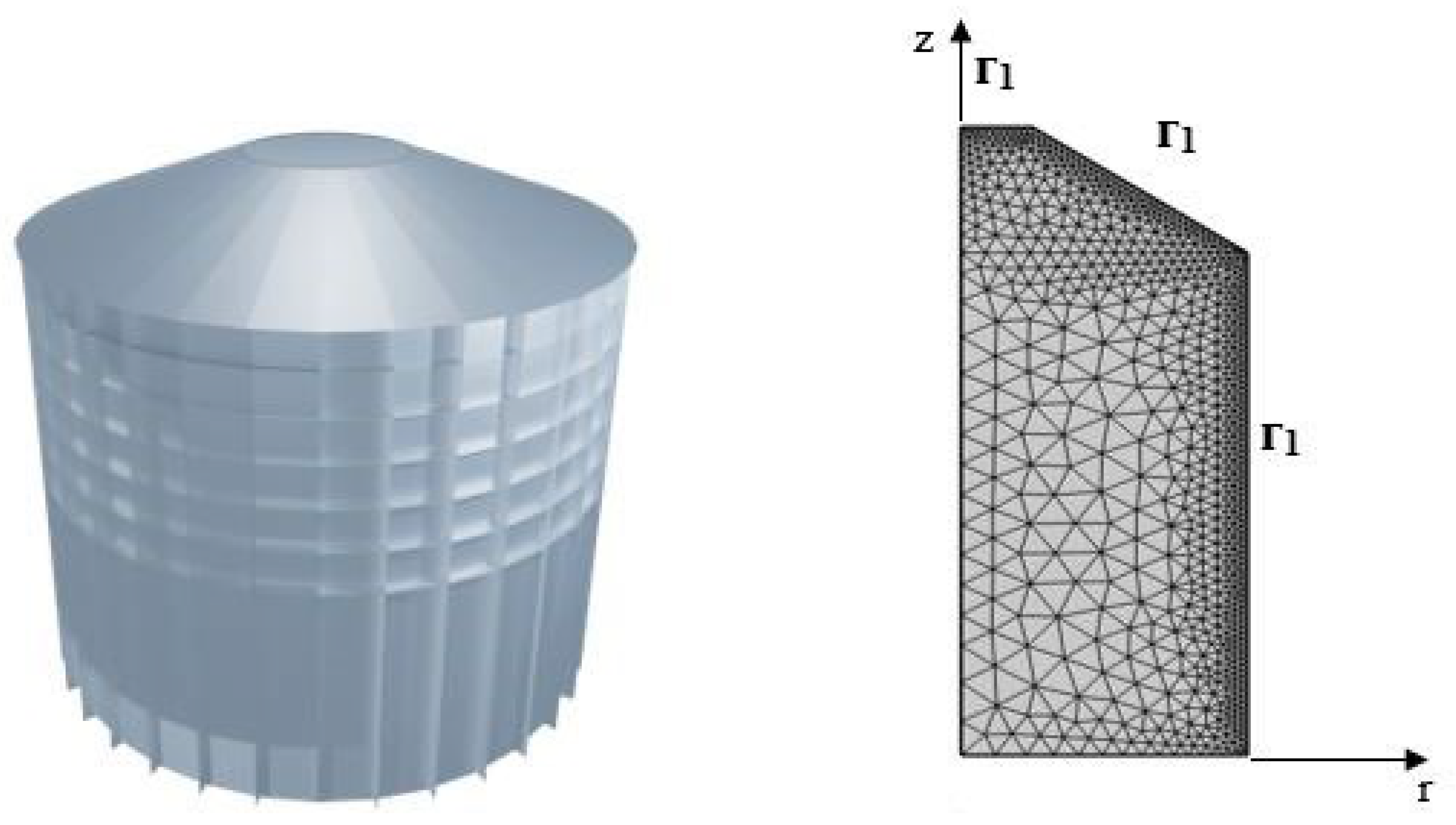
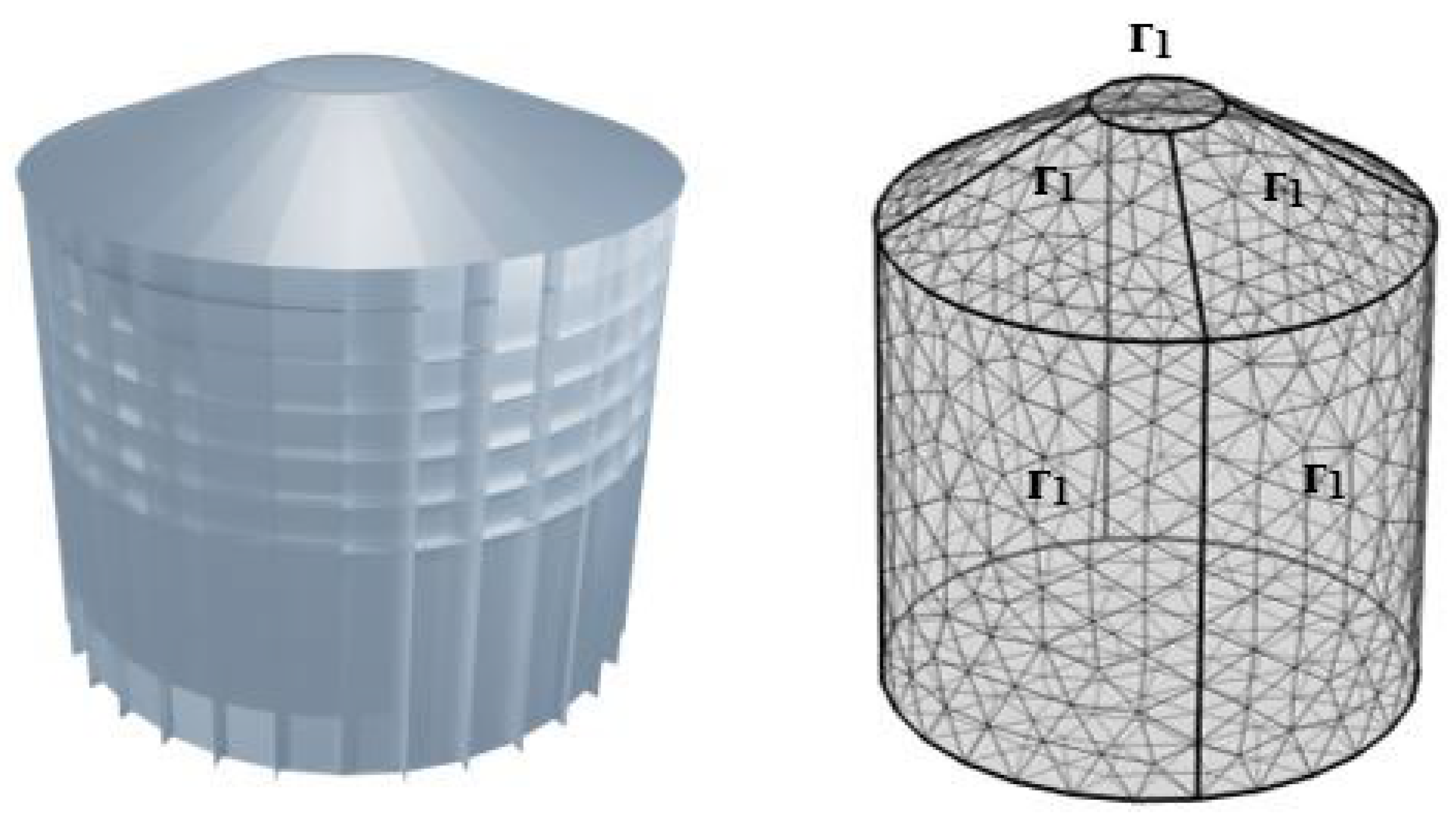

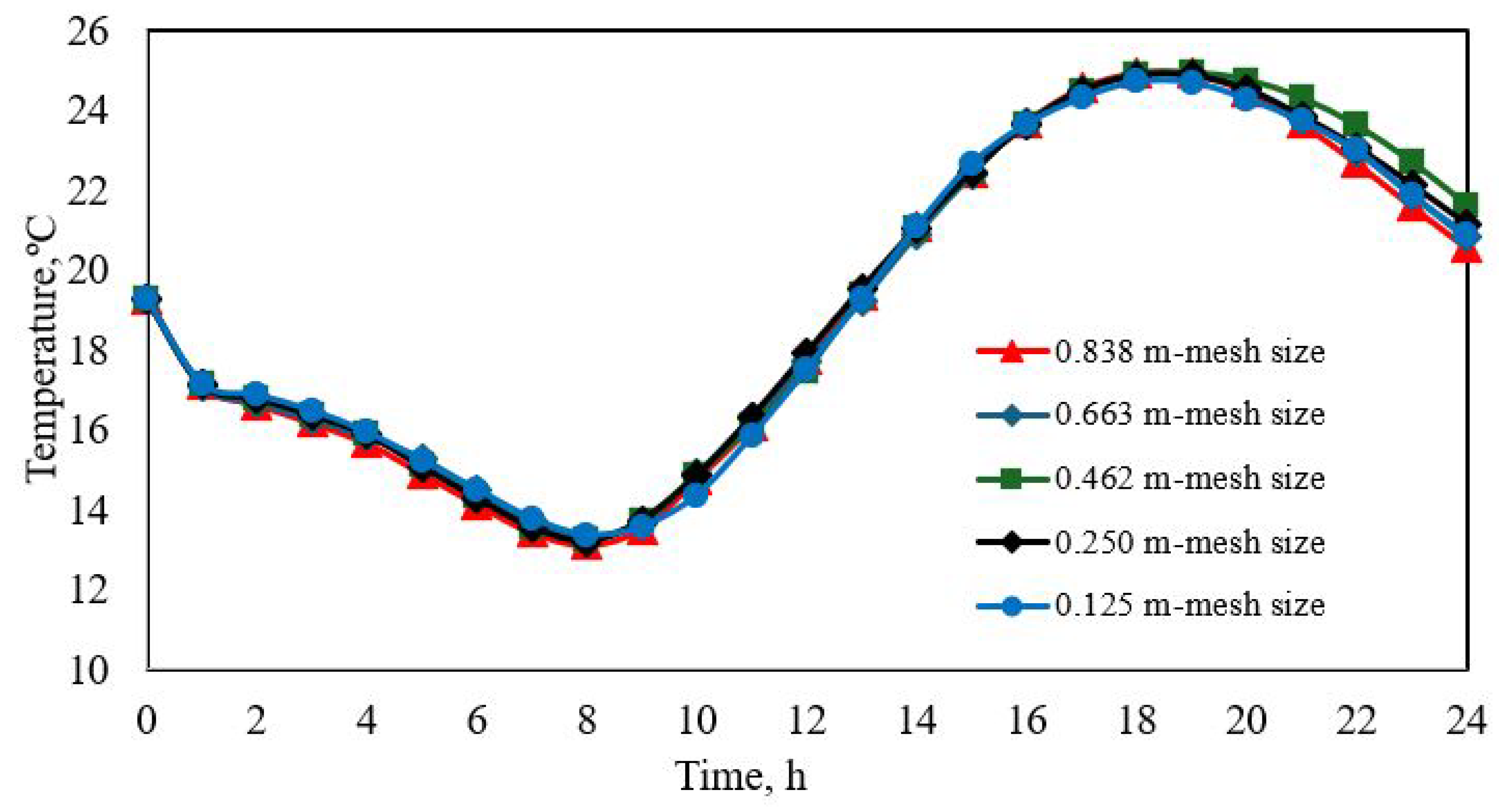







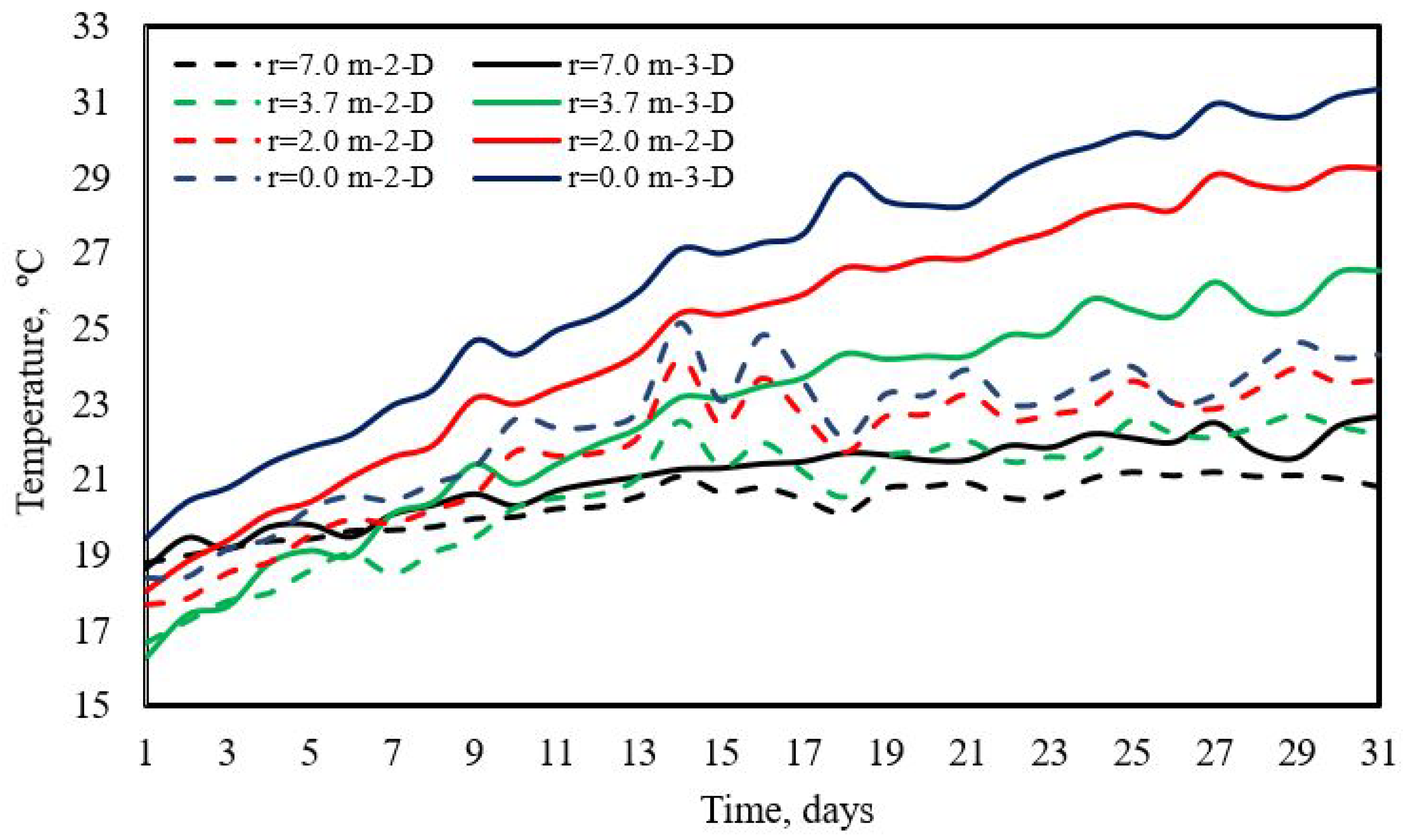

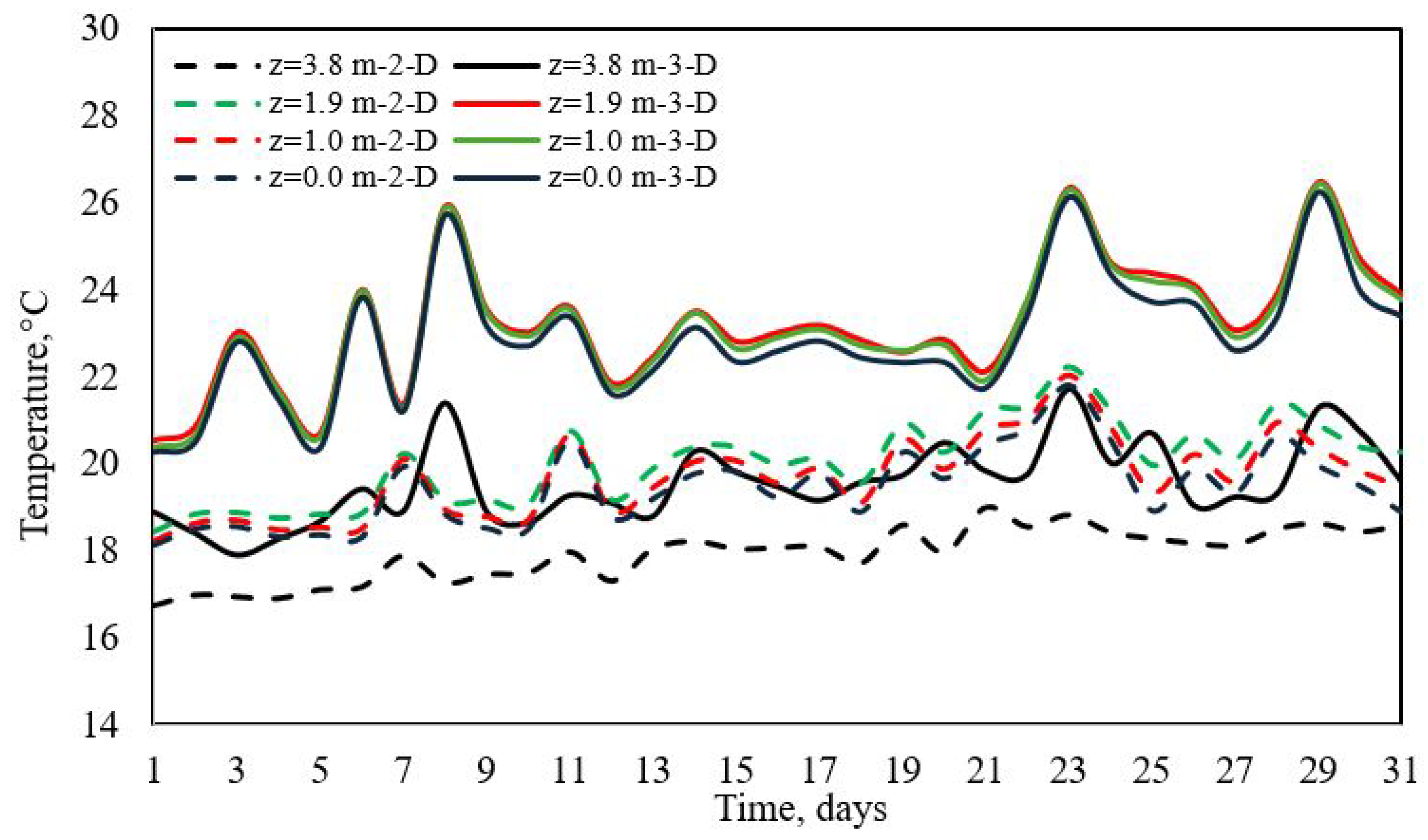
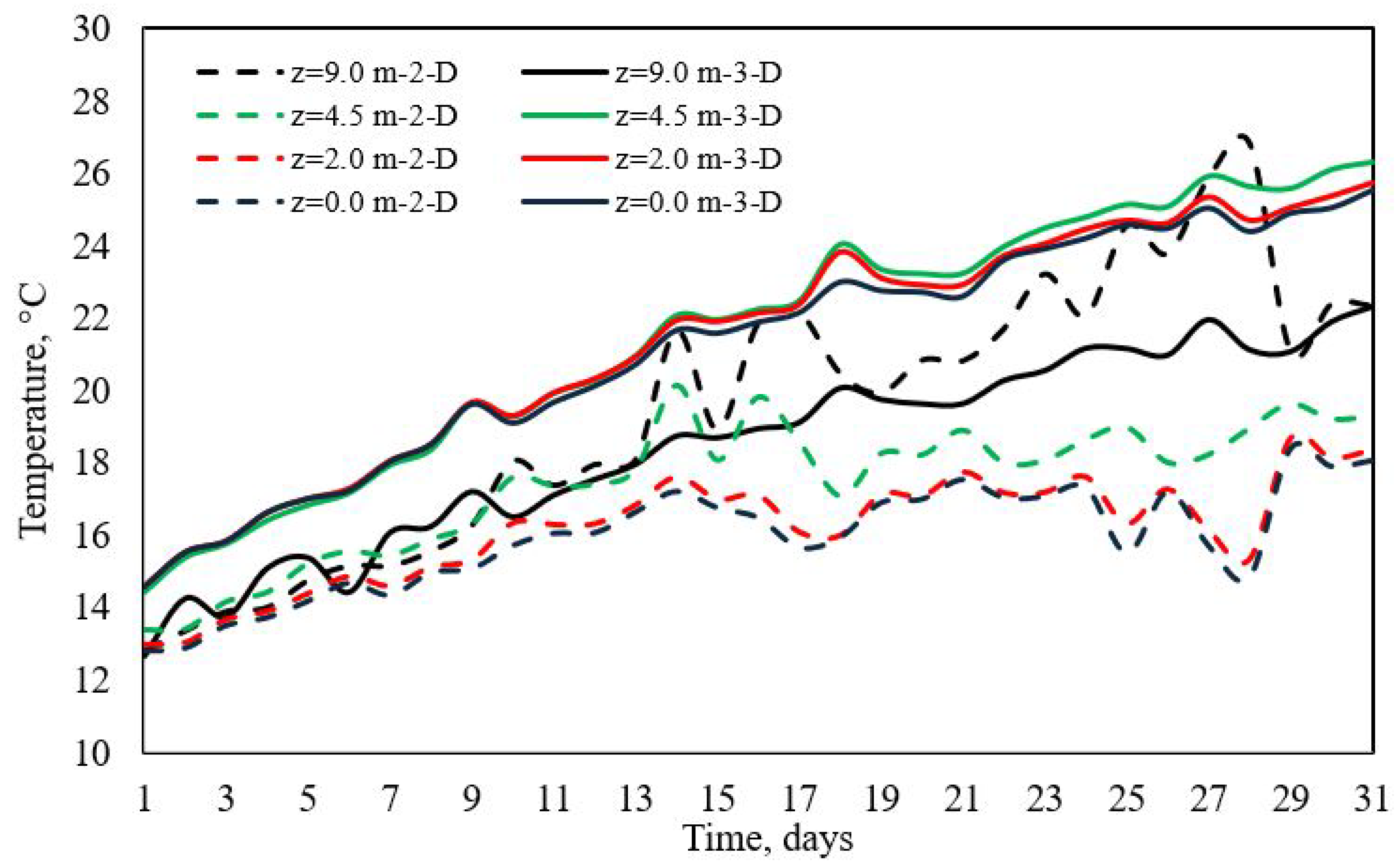



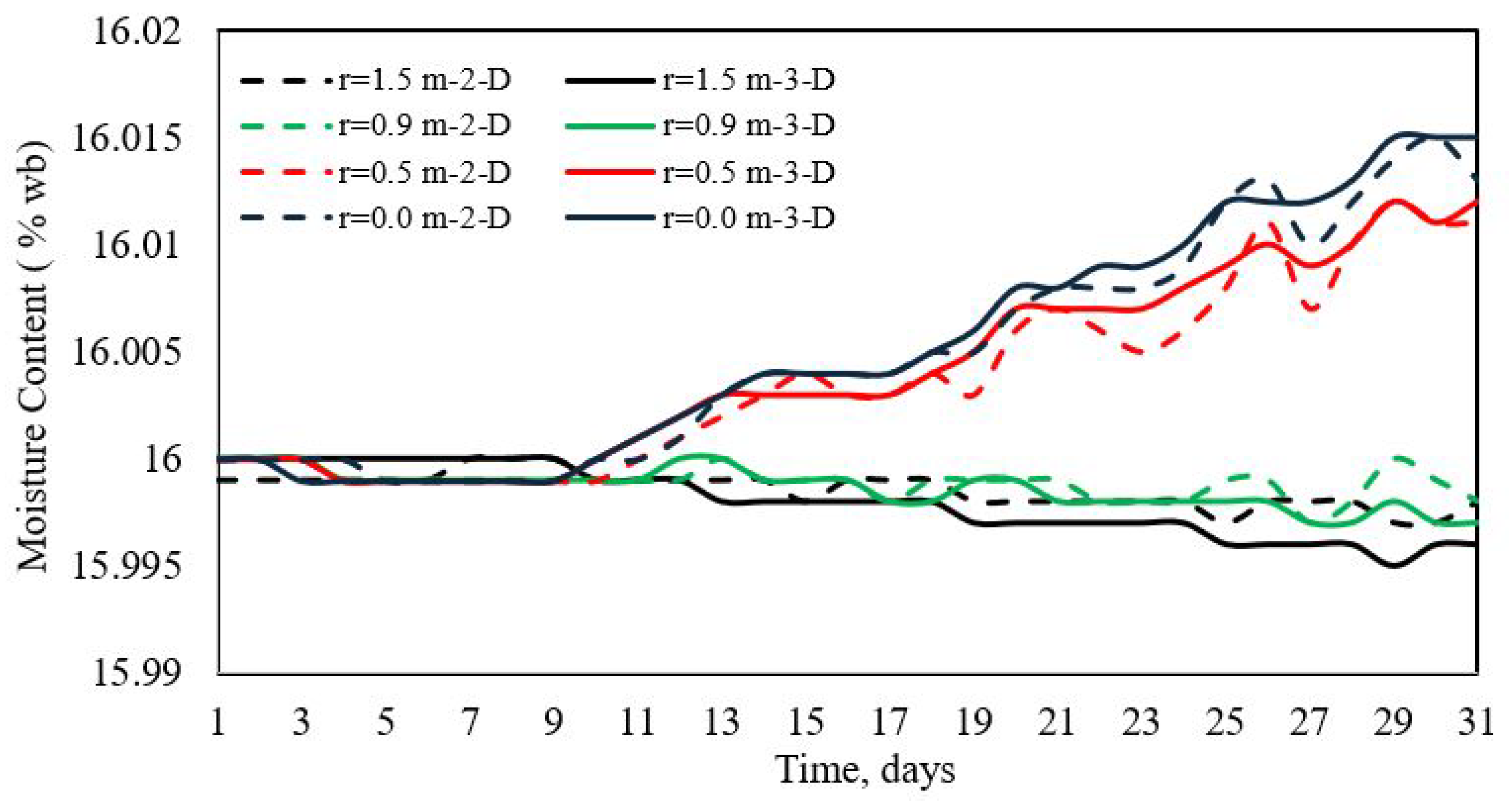
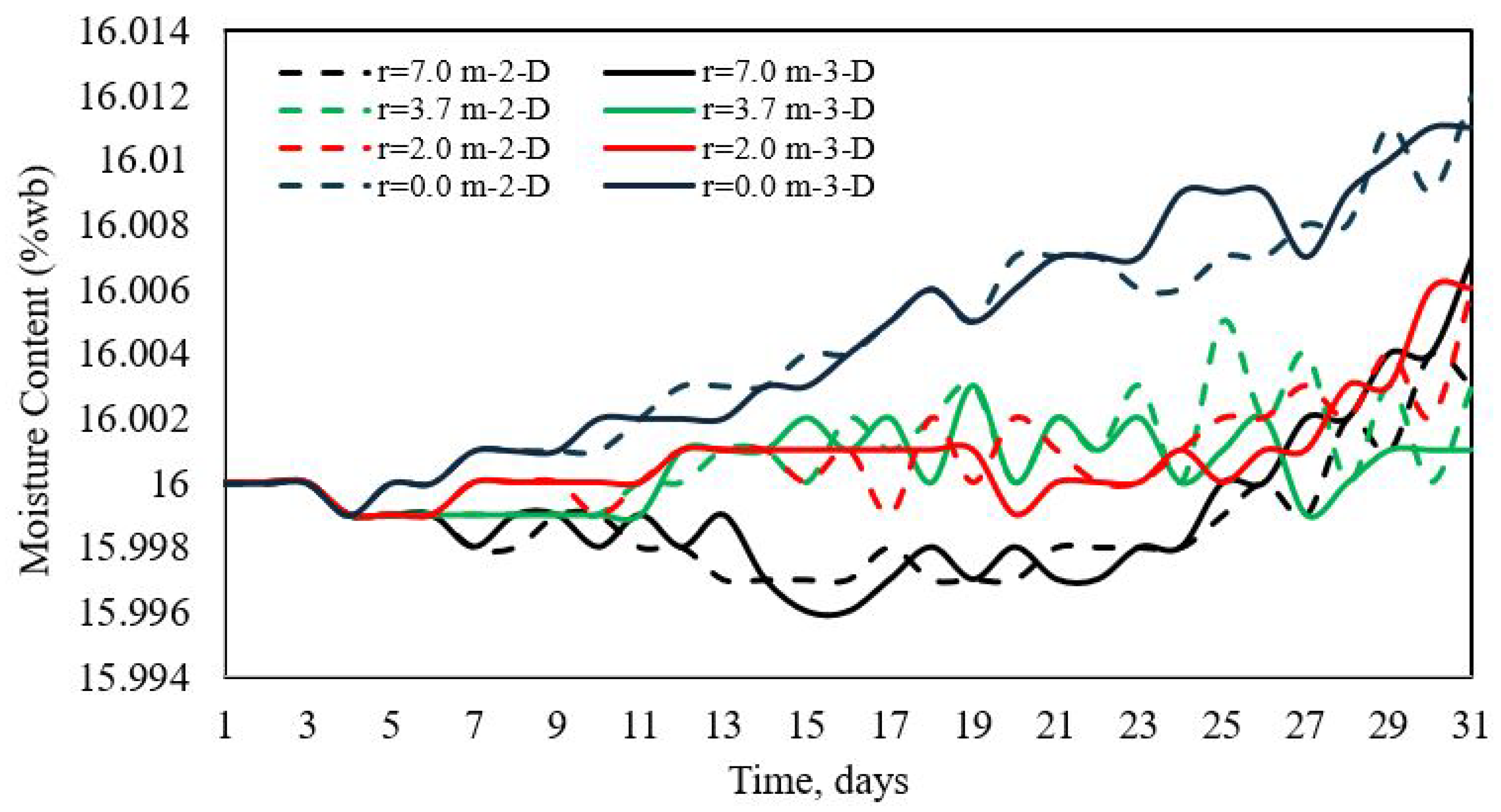




| Boussinesq approximation a | ||
| Heat generation a,b | ||
| Moisture generation a | ||
| Sorption isotherm b | ||
| Water vapor pressure a | ||
| Absolute humidity at the grain–air interface a |
| Variable | Value | |
|---|---|---|
| Corn parameters a | The initial moisture content of corn Initial temperature Bulk density Specific heat Thermal conductivity Effective thermal conductivity Permeability Porosity | 14.5% 20 °C 760 kg/m3 1780 kJ/kg K 0.13 W/m K 0.089 W/m K 3.5 × 10−9 m2 0.38 |
| Air parameters a | Reference temperature Specific heat Thermal conductivity Viscosity Heat transfer coefficient Mass transfer coefficient Interfacial area | 25 °C 972.92 kJ/kg K 0.023697 W/m K 1.7810−5 Pa-s 15 W/m2 K 1.00 × 10−4 m·s−1 760 m2·m−3 |
| Silo Size | Radius (m) | Height (m) | Cone Height (m) | Average Volumetric Capacity (kg) |
|---|---|---|---|---|
| Silo S Silo B | 1.83 7.5 | 3.81 9.00 | 0.95 1.82 | 32,000 1,350,000 |
| Parameters for the thermal model | |
| Convective heat transfer coefficient Sky temperature # Sky emissivity # Steel emissivity # Steel absorptivity # Stefan–Boltzmann constant | W·m2 K−1 σ = 5.670374419 × 10−8 W·m−2·K−4 |
| Parameters for the mass transfer model | |
| Water diffusivity in air * Water diffusivity in corn Mass transfer coefficient * Particle diameter Grain-air interfacial area * | 2.437 × 10−5 m2·s−1 2.8766 × 10−11 m2·s−1 1.00 × 10−4 m·s−1 0.005 m 744 m2·m3 |
| Silo S | |||
|---|---|---|---|
| Model 2D | Model 3D | ||
| Mesh size | Computation time (min) | Mesh size | Computation time (min) |
| 0.838 m 0.663 m 0.462 m 0.250 m 0.125 m | 0.75 0.70 0.73 1.11 2.71 | 0.476 m 0.381 m 0.262 m 0.167 m --------- | 37.20 18.85 29.32 43.86 ------ |
| Silo B | |||
| Mesh size | Computation time (min) | Mesh size | Computation time (min) |
| 0.838 m 0.663 m 0.462 m 0.250 m 0.125 m | 1.03 1.01 1.50 1.20 1.68 | 0.476 m 0.381 m 0.262 m 0.167 m ---------- | 25.58 40.65 54.48 67.43 ------- |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Molina-Herrera, F.I.; Quemada-Villagómez, L.I.; Calderón-Ramírez, M.; Martínez-González, G.M.; Jiménez-Islas, H. Modeling Temperature and Moisture Dynamics in Corn Storage Silos: A Comparative 2D and 3D Approach. Modelling 2025, 6, 7. https://doi.org/10.3390/modelling6010007
Molina-Herrera FI, Quemada-Villagómez LI, Calderón-Ramírez M, Martínez-González GM, Jiménez-Islas H. Modeling Temperature and Moisture Dynamics in Corn Storage Silos: A Comparative 2D and 3D Approach. Modelling. 2025; 6(1):7. https://doi.org/10.3390/modelling6010007
Chicago/Turabian StyleMolina-Herrera, Fernando Iván, Luis Isai Quemada-Villagómez, Mario Calderón-Ramírez, Gloria María Martínez-González, and Hugo Jiménez-Islas. 2025. "Modeling Temperature and Moisture Dynamics in Corn Storage Silos: A Comparative 2D and 3D Approach" Modelling 6, no. 1: 7. https://doi.org/10.3390/modelling6010007
APA StyleMolina-Herrera, F. I., Quemada-Villagómez, L. I., Calderón-Ramírez, M., Martínez-González, G. M., & Jiménez-Islas, H. (2025). Modeling Temperature and Moisture Dynamics in Corn Storage Silos: A Comparative 2D and 3D Approach. Modelling, 6(1), 7. https://doi.org/10.3390/modelling6010007






