Hydrodynamic Modeling of Unstretched Length Variations in Nonlinear Catenary Mooring Systems for Floating PV Installations in Small Indonesian Islands

Abstract

Floating photovoltaic (FPV) systems offer a promising renewable energy solution, particularly for coastal waters. This preliminary numerical study proposes a single-array pentamaran configuration designed to maximize panel installation and enhance stability by reducing rolling motion. The study investigates the effect of mooring length on the motion behavior of FPV systems and actual line tension using the Boundary Element Method (BEM) in both frequency and time domains under irregular wave conditions. The results demonstrate that the mooring system significantly reduces all horizontal motion displacements, with reductions exceeding 90%. Even with a reduction of up to 51% in the unstretched mooring length, from the original design (304.53 m) to the shortest alternative (154.53 m), the motion response shows minimal change. This is supported by RMSE values of only 0.01 m/m for surge, 0.02 m/m for sway, and 0.09 deg/m for yaw. In the time-domain response, the shortened mooring line demonstrates improved motion performance. This improvement comes with the consequence of stronger nonlinearity in restoring forces and stiffness, resulting in higher peak tensions of up to 15.79 kN. Despite this increase, all configurations remain within the allowable tension limit of 30.69 kN, indicating that the FPV’s system satisfies safety criteria.

1. Introduction

Solar energy, particularly photovoltaic (PV) technology, is an essential component of the global transition toward zero-emission energy systems. Its affordability has positioned it as a leading choice for electricity generation in many regions, with projections indicating it will soon dominate global electricity production, as illustrated in Figure 1. In developing countries, where access to electricity remains a persistent challenge for many communities, the adoption of PV systems provides a practical solution to address ongoing power shortages [1].

The transition from conventional land-based PV installations to more adaptable spatial configurations, such as Floating Photovoltaics (FPV), is becoming increasingly important. The cooling effect provided by water enhances the energy generated by FPV systems up to 30% [2]. When installed on open water, FPV systems help reduce dust accumulation on the panels [3].

By being installed on water surfaces, FPV technology eliminates the shading challenges typically caused by nearby buildings or geographic obstructions, ensuring more effective solar energy capture [4].

Figure 1. Global electricity generation by source 2010–2035, redrawn from IEA [5].

Figure 1. Global electricity generation by source 2010–2035, redrawn from IEA [5].

Therefore, nearshore areas provide an ideal location for FPV systems due to the vast and adaptable ocean spaces, which offer significantly greater installation capacity compared to the limited surface area of reservoirs and other inland water bodies. These systems are particularly suited for supplying energy to coastal regions, which are characterized by dense industrial, commercial, and residential activities [6].

This technology is particularly beneficial for countries with abundant solar resources, such as Indonesia. As depicted in Figure 2, the southern region of Indonesia, specifically Nusa Tenggara Timur, achieves a high Global Horizontal Irradiance (GHI) level of 6.0 kWh/m²/day. Similarly, the northern coastline of East Java records GHI levels of 5.4 kWh/m²/day.

Deploying FPV technology in Indonesia’s nearshore waters offers a significant opportunity, given the country’s vast ocean space compared to inland areas. This potential is further supported by Indonesia’s favourable environmental conditions, particularly the enclosed waters of the equatorial archipelago.

As shown in Figure 3, historical data from 1956 to 2021 show that tropical storms have had little impact on Indonesia, Malaysia, and Singapore. This suggests that these areas are relatively safe for installing FPV systems. The reason for this is Indonesia’s location along the equator, where the Coriolis effect is almost negligible, making the region less likely to experience cyclones.

Designing nearshore FPV systems requires careful consideration of the challenges posed by the ocean environment. These systems must be designed to endure strong winds and the forces resulting from wave-current interactions. Moreover, the high salinity of seawater can accelerate corrosion, which may shorten the lifespan of the support structures. To address this, it is crucial to use materials that are durable and resistant to corrosion.

Mooring systems play a critical role in mitigating substantial displacements and protecting essential components by restricting translational (surge and sway) and rotational (yaw) motions. Once installed at a specific site, the floating structures and mooring cables function as a coupled system, exhibiting dynamic responses influenced by prevailing environmental conditions.

Extensive research has focused on the coupling effects between floating structures and mooring systems. Among these studies, Oh et al. [9] developed a three-dimensional time-domain Indirect Boundary Integral Equation Method (IBIEM) to simulate the motion of floating bodies, which is coupled with a quasi-static mooring model. Validation against model tests and other established numerical techniques confirms the accuracy of the developed code in predicting the dynamic behavior of offshore structures. Similarly, Chang et al. [10] introduced an efficient frequency-domain approach for fully coupled analyses of floater-mooring systems, achieving results that strongly correlate with those from time-domain simulations.

In line with the research conducted by He and Wang [11], his study developed numerical procedures for the dynamic analysis of mooring lines in both the time and frequency domains. The lumped mass method was used to model the mooring lines in the time-domain analysis. A comparison of the results shows good agreement between the frequency domain and the nonlinear time-domain outcomes. This framework enables both time-domain and frequency-domain analyses, providing a comprehensive tool for understanding dynamic responses.

Therefore, the objective of this study was defined by several conditions within the area of investigation, as shown in

Table 1. Area of Investigation.

Independent Variables	Dependent Variables	Control Variable
Analysis condition ○ Free-floating (A1) ○ Mooring condition (B1–E1) Loading consideration Wave, wind, and current in both collinear and omnidirectional: ○ 0 degree [surge, heave and pitch] ○ 45 degree [yaw] ○ 90 degree [sway and roll] Effect of Touchdown Length ○ Original Design, B1 ○ Alternative 1, C1 ○ Alternative 2, D1 ○ Alternative 3, E1	RAOs in frequency domain Motion response in time domain Cable tension in time domain	JONSWAP with γ = 2.5 for irregular wave spectrum Mooring properties and configuration Main principal dimension floater design

. This study defined its scope through independent, dependent, and control variables. It investigated the influence of mooring lines on a floating system in generating external restoring forces. Both free-floating and moored conditions were analyzed in the frequency domain over a range of 0.05–3.00 rad/s (ω) to determine response amplitude operators (RAOs), considering the coupled interaction between the structure and mooring cables.

Additionally, variations in the unstretched length of a catenary mooring system were investigated to assess their influence on the performance of a FPV structure in terms of motion and line tension. These variations began with the original design (B1) and were systematically reduced, with the shortest length determined based on the touchdown length.

The numerical simulations were conducted under controlled conditions, including mooring properties, mooring configurations, and environmental loads (wave, wind and current loads). Wave energy was modeled using the JONSWAP spectrum from the Modified Pierson–Moskowitz (P-M) model, with a peak enhancement factor (γ) of 2.50. However, other aspects beyond the hydrodynamic effects, such as marine biofouling, long-term degradation, the water quality impact due to the shading effect of the floating PV system, and sedimentation effects related to the structure, are not further considered in this study.

Subsequently, this paper is structured as follows: Section 2 describes the proposed FPV design, including the mooring system arrangements and their variations. It also explains the governing equations for fluid environment and cable discretization used in the numerical simulation, followed by details of the case study involving a small island and its ocean water conditions, and closing with the grid convergence index parameters. Section 3 presents the key findings and discussions, which are divided into four sub-sections: numerical stability parameters, motion in regular waves (frequency domain), motion in irregular waves (time domain), and mooring tension analysis in the time domain. Section 4 concludes the paper by summarizing the numerical key findings. Finally, Section 5 outlines future investigations in FPV research.

2. Materials and Methods

The 3D panel diffraction method, utilizing the Boundary Element Method (BEM), serves as a reliable numerical approach for solving linear partial differential equations formulated as integral equations. This technique is highly effective for seakeeping analysis, as it accurately captures both first- and second-order effects in the frequency and time domains [12]. Additionally, the cable dynamics are integrated to account for the time-dependent forces acting on the cable, which often exhibit nonlinear behavior. This fully coupled solution ensures that the vessel’s motions and the cable’s tension are interdependent.

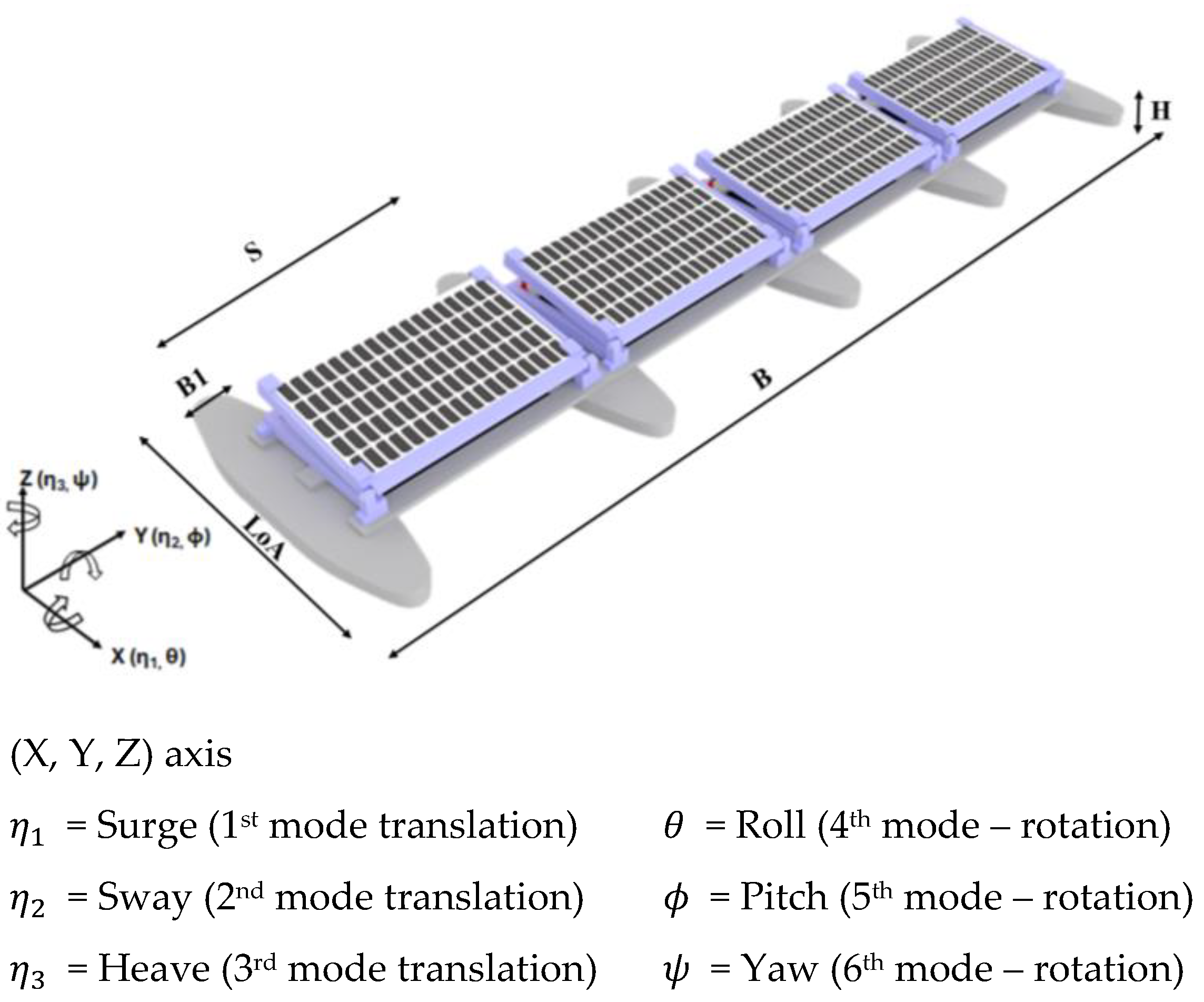
2.1. Model Description and Material Properties

In a previous study by Jifaturrohman et al. [13] numerical simulations were conducted for PV floater systems, including catamarans (two hulls), trimarans (three hulls), quadrimarans (four hulls), and pentamarans (five hulls), with hulls arranged by laterally duplicating from the demihull then investigated their effect on motion performance.

As shown in Figure 4a, the hydrostatic properties for all these configurations indicate that as the number of hulls increases, the transverse metacentric height (GM_T) also increases, while the longitudinal metacentric height (GM_L) remains constant. This increase in GM_T enhances transverse stability and improves roll damping, which is consistent with the study by Gong et al. [14].

The increase in GM_T affects the roll period. Therefore, floating structures with a larger GMT will have a shorter roll period, while those with a smaller GM_T will have a longer period [15]. Additionally, Figure 4b shows that the roll RAO transfer function for the pentamaran configuration is the smallest among the others, indicating a strong relationship between the reduction in roll RAO and the increase in GM_T for the pentamaran configuration. Consequently, this study selects the single-array pentamaran configuration for mounting solar panels.

Furthermore, Figure 5 illustrates the global coordinate system, which serves as a reference for identifying motion types in both seakeeping and station-keeping studies, as well as the notations for the main principal dimensions of the floating PV system. The floater of the FPV system is typically made of High-Density Polyethylene (HDPE) and consists of lightweight components and a modular design for easy assembly and quick installation.

Subsequently,

Table 2. Main dimensions of the single-array pentamaran-FPV platform.

Parameter	Values	Units
Length overall (LoA)	3.24	m
Breadth (B)	11.94	m
Height (H)	0.30	m
Draft Amidship (T)	0.12	m
Demihull Width (B1)	0.74	m
Spacing (S)	2.80	m
Hydrostatic values
Waterplane Area (AWP)	9.65	m2
Block coefficient (Cb)	0.75	-
Prismatic coefficient (Cp)	0.76	-
Keel to buoyancy (KB)	0.06	m
Longitudinal Center of Buoyancy (LCB)	1.62	m
Weight and inertia distribution without mooring
Displacement (Δ)	1094.17	kg
CoG	X = 1.62 Y = 0.00 Z = 0.26	m
Radius gyration–X-axis (Kxx)	3.69	m
Radius gyration–Y-axis (Kyy)	0.70	m
Radius gyration–Z-axis (Kzz)	3.75	m

provides the principal dimensions, hydrostatic properties, and weight distribution of the proposed floater design. The Canadian Solar Panel was adopted for the PV module [16], with its power output and characteristics detailed as follows: a capacity of 665 Wp, a module efficiency of 21.40%, and dimensions of 2.38 m × 1.30 m. The PV module weighs 34.40 kg.

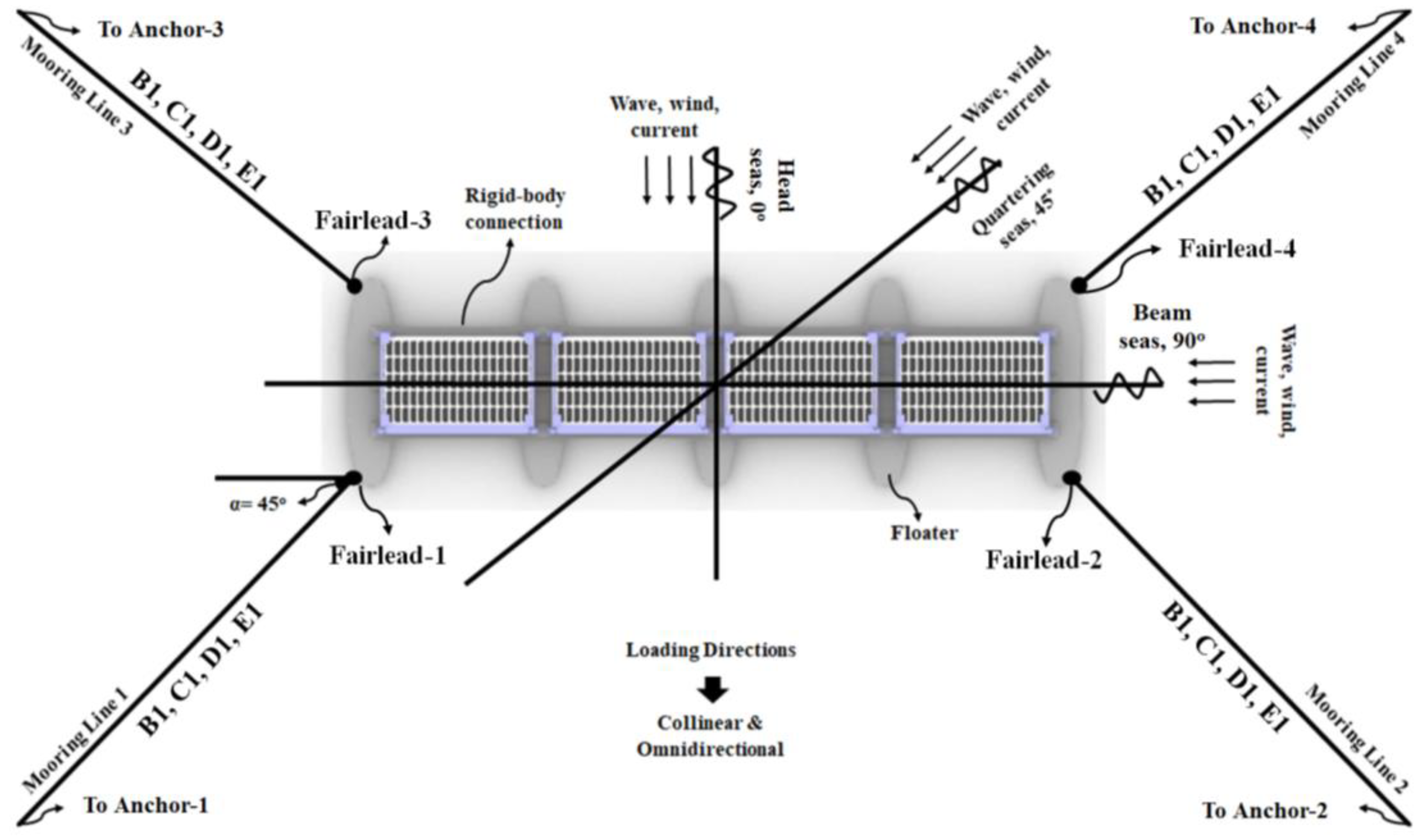
2.2. Mooring Properties and Arrangements

The mooring system arrangement consists of four mooring lines attached to the outer corners of the floater. The fairlead locations are positioned at the floater’s outer edges at the water surface draft elevation. Since the FPV system is designed for installation in shallow water, a catenary-type mooring system is employed, oriented at a 45-degree angle relative to the global Y-axis as shown in Figure 6.

Additionally, parameters related to mooring properties are detailed in

Table 3. Mooring properties.

Parameter	Symbol	Value	Unit
Mooring type	6 × 19 IWRC (independent wire rope core)
Nominal diameter	Ø	9.50	mm
Nominal strength	MBL	58.35	kN
Effective mass per unit length	Weff	0.39	kg/m
Modulus Young	E	190,000,000	kN/m2
Axial Stiffness	EA	13,467.62	kN
Allowable Tension Max	Tamax	30.69	kN
Catenary Weight	Ws*h	32.51	kg

, while variations in the unstretched length as a function of touchdown length, which is considered in this study, are provided in

Table 4. Independent variable of unstretched length.

Variations	Maximum Touchdown (m)	Unstretched Length (m)
B1	137.71	304.53
C1	88.44	254.53
D1	40.26	204.53
E1	9.83	154.53

.

2.3. Boundary Element Method Governing Equations

In numerical seakeeping analysis, hydrodynamic forces (added masses, damping coefficients, and wave-induced forces) are derived from potential flow theory. These forces are solved using the BEM and are based on linear wave theory for small wave amplitudes. Linear seakeeping methods are typically limited to small wave heights because they assume linear behavior, where the floating structure’s response is directly proportional to the wave height. However, despite this theoretical limitation, these methods are often applied to much larger waves in practice. This is because they are simpler to use and are frequently formulated in the frequency domain, making them more practical for engineering applications [17].

This methodology, as described by Faltinsen [18], assumes of an idealized fluid—inviscid, irrotational, and incompressible without surface tension. These assumptions facilitate the derivation of the potential velocity function for evaluating velocity and pressure. Then, the calculation of RAOs in frequency domain is detailed in ANSYS-AQWA 20.2 [19]. Equation (1) defines the potential velocity function, as shown below:

$$V={\displaystyle \frac{\partial \varphi }{\partial x}}i+{\displaystyle \frac{\partial \varphi }{\partial y}}j+{\displaystyle \frac{\partial \varphi }{\partial z}}k$$

(1)

The assumption of an incompressible fluid, indicating no change in mass as the fluid flows into or out of a control surface, necessitates that the velocity potential satisfies the Laplace equation. This relationship is mathematically represented in Equation (2), as follows:

$${{\nabla }^2}_{\varphi }={\displaystyle \frac{\partial u}{\partial x}}+{\displaystyle \frac{\partial v}{\partial y}}+{\displaystyle \frac{\partial w}{\partial z}}=0$$

(2)

Subsequently, this method is based on the principle of determining the Green’s function (G) rather than directly solving the governing equations, as described by Guha [20]. The approach involves distributing source points along a discretized boundary, with control points placed within each mesh segment to simultaneously satisfy the required boundary conditions. The resulting equation is fundamental for calculating the RAO, which describes the motion of the floating object. The coupled FPV motion equations can be solved to determine the complex motion amplitudes. The six degrees of freedom (6-DoF) motion equations are presented in Equation (3) below:

$$\sum _{j=1}^6\left[-{\omega }^2\left(M_{ij}+M_{ij}^{ad}\right)-i\omega B_{ij}+C_{ij}\right]{\eta }_j^{A\left(1\right)}=F_i+F_d$$

(3)

where $M_{ij}$ is vessel mass matrix, $M_{ij}^{ad}$ is vessel added mass matrix, $B_{ij}$ is radiation damping coefficient, $C_{ij}$ = hydrostatic stiffness coefficient, η_j = j-th vessel motion amplitude in j-th mode motion, F_i is incident wave forces, and F_d is diffraction forces.

2.4. Dynamic Catenary Cable Equations

The numerical modeling of a catenary mooring cable using the Lumped Mass Method (LMM) through the Finite Element Method (FEM) approach, is described by Du et al. [21]. This method involves dividing the mooring cable into discrete mass nodes connected by massless spring elements to replicate its mechanical behavior.

The numerical modeling of the mooring line is conducted using the Morison element approach, based on the theory from ANSYS-AQWA 20.2 [19] for assembly of the mass and applied or internal forces and moment. This approach models the mooring line as a circular slender cable influenced by various external forces. The equations governing the motion of a single mooring line element are presented in Equations (4) and (5) as follows:

$${\displaystyle \frac{\partial \overrightarrow{T}}{\partial s_e}}+{\displaystyle \frac{\partial \overrightarrow{V}}{\partial s_e}}+\overrightarrow{w}+\overrightarrow{F}h=m{\displaystyle \frac{{\partial }^2\overrightarrow{R}}{\partial t^2}}$$

(4)

$${\displaystyle \frac{\partial \overrightarrow{M}}{\partial s_e}}+{\displaystyle \frac{\partial \overrightarrow{R}}{\partial s_e}}\times \overrightarrow{V}=-\overrightarrow{q}$$

(5)

In this representation, $∆S_e$ and $D_e$ denote the element’s length and diameter, respectively, while $\overrightarrow{w}$ represents the element’s weight, and $\overrightarrow{F}h$ corresponds to the external hydrodynamic loading vectors per unit length. Then, $m$ represents the mass per unit length of the structural component, while $\overrightarrow{q}$ denotes the distributed moment loading applied per unit length. Additionally, $\overrightarrow{R}$ defines the position vector of the initial node in the cable element. Furthermore, $\overrightarrow{T}$, $\overrightarrow{M}$, and $\overrightarrow{V}$ indicate the tension force, bending moment vector, and shear force vector acting at the element’s first node.

The bending moment and tension in the cable are influenced by its bending stiffness ($EI$) and axial stiffness ($EA$), which are determined using Equations (6) and (7), as shown in the following expressions:

$$M=EI {\displaystyle \frac{\partial \overrightarrow{R}}{\partial s_e}}\times {\displaystyle \frac{{\partial }^2\overrightarrow{R}}{\partial s_e^2}}$$

(6)

$$T=EA\epsilon +EA{c}_j{\displaystyle \frac{\partial {∆S_e}_j}{\partial t}}{\displaystyle \frac{1}{{∆S_e}_j}}$$

(7)

where ${\epsilon }_i=({∆S_e}_j-{∆S_e}_{j0})/{∆S_e}_{j0}$ represents the axial strain, ${∆S_e}_j$ is the instantaneous length of the j-th segment, and ${∆S_e}_{j0}$ is the original length of the j-th segment. Additionally, $c_j$ denotes the damping coefficient of the j-th segment of the cable line.

Furthermore, based on Equations (8) and (9), pinned connection boundary conditions are applied at both the top (fairlead) and bottom (anchor) ends of the cable. Here, L denotes the total unstretched length of the cable, as expressed below.

$$\overrightarrow{R}\left(0\right)={\displaystyle \frac{{\partial }^2\overrightarrow{R}\left(0\right)}{\partial s_e^2}}=\overrightarrow{0}$$

(8)

$$\overrightarrow{R}\left(L\right)={\displaystyle \frac{{\partial }^2\overrightarrow{R}\left(L\right)}{\partial s_e^2}}=\overrightarrow{0}$$

(9)

The fluid force acting on the j-th node is determined using the Morison equation, as expressed in Equation (10):

$$f_j={\displaystyle \frac{1}{2}}\rho C_D{D}_e{∆S_e}_j\left|v_j\right|v_j+C_M\rho V_j{\displaystyle \frac{\partial \overrightarrow{u_j}}{\partial t}}$$

(10)

where $C_D$ is the drag force coefficient and $C_M$ is the inertia force coefficient, $v_j$ is the velocity of the j-th node, ${\displaystyle \frac{\partial \overrightarrow{u_j}}{\partial t}}$ is the acceleration of the j-th node, and $V_j$ is the volume of the j-th segment.

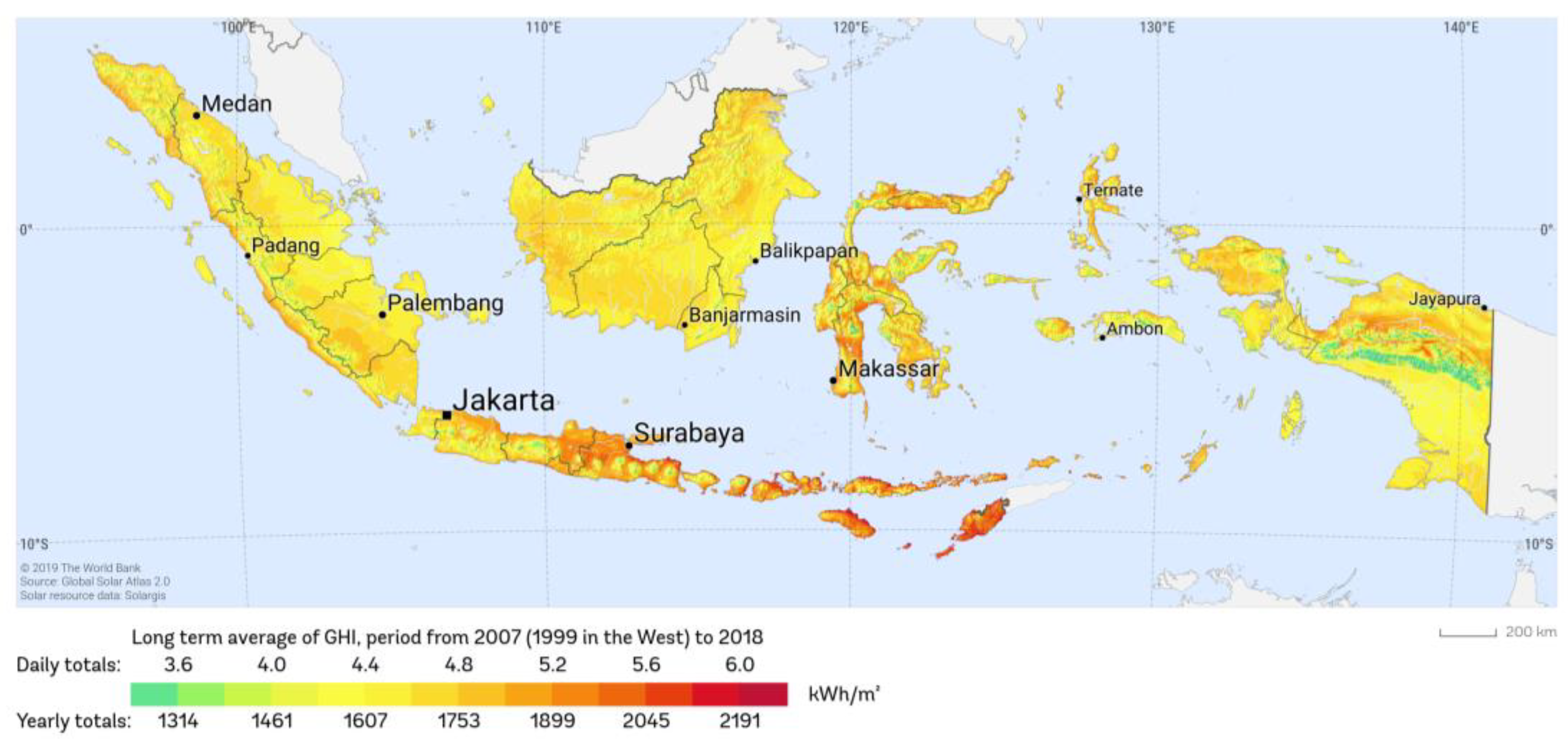
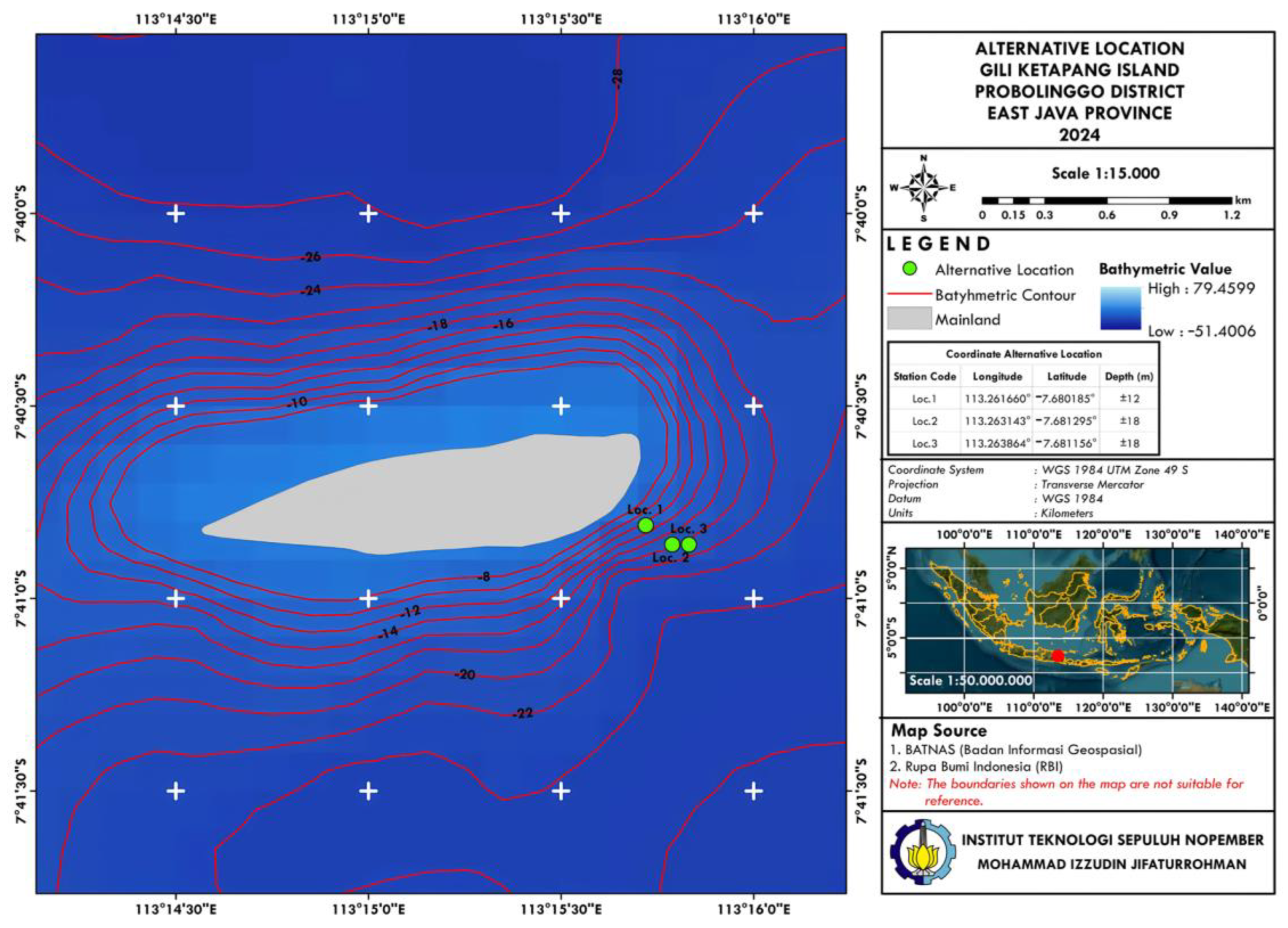
2.5. Case Study: Gili Ketapang Island

Several studies highlight Indonesia’s potential for developing FPV systems. Research by Untoro et al. [22] demonstrated FPV’s economic viability, while Silalahi et al. [23] identified Indonesia as a promising location for floating solar energy. Gili Ketapang Island was selected because it is a small island located about 5.6 km from the main island. Gili Ketapang’s electricity is not connected to the national grid, so it relies on diesel generators for power which are transported from the main island, as shown in Figure 7.

An important factor in site selection is designing a power system that is easily accessible to island residents, economically accessible to the villagers, and reduces the island’s dependence on diesel fuel. Several geographic details about Gili Ketapang Island are provided in

Table 5. General information for Gili Ketapang island.

Components	Description
Easting	113°15′26.9″
Northing	7°41′00.8″
Sub-District	Sumberasih
District	Probolinggo
State/Province	East Java
Surface area of the town	68 Ha
Road access	No main road on the island the road can be accessed by bicycle only
Length of coastline	Approx. 4.73 km
Access from main island	Traditional boat

, including its coordinates determined using the Global Positioning System (GPS) with the UTM WGS84 system and falling within the Western Indonesian Time zone.

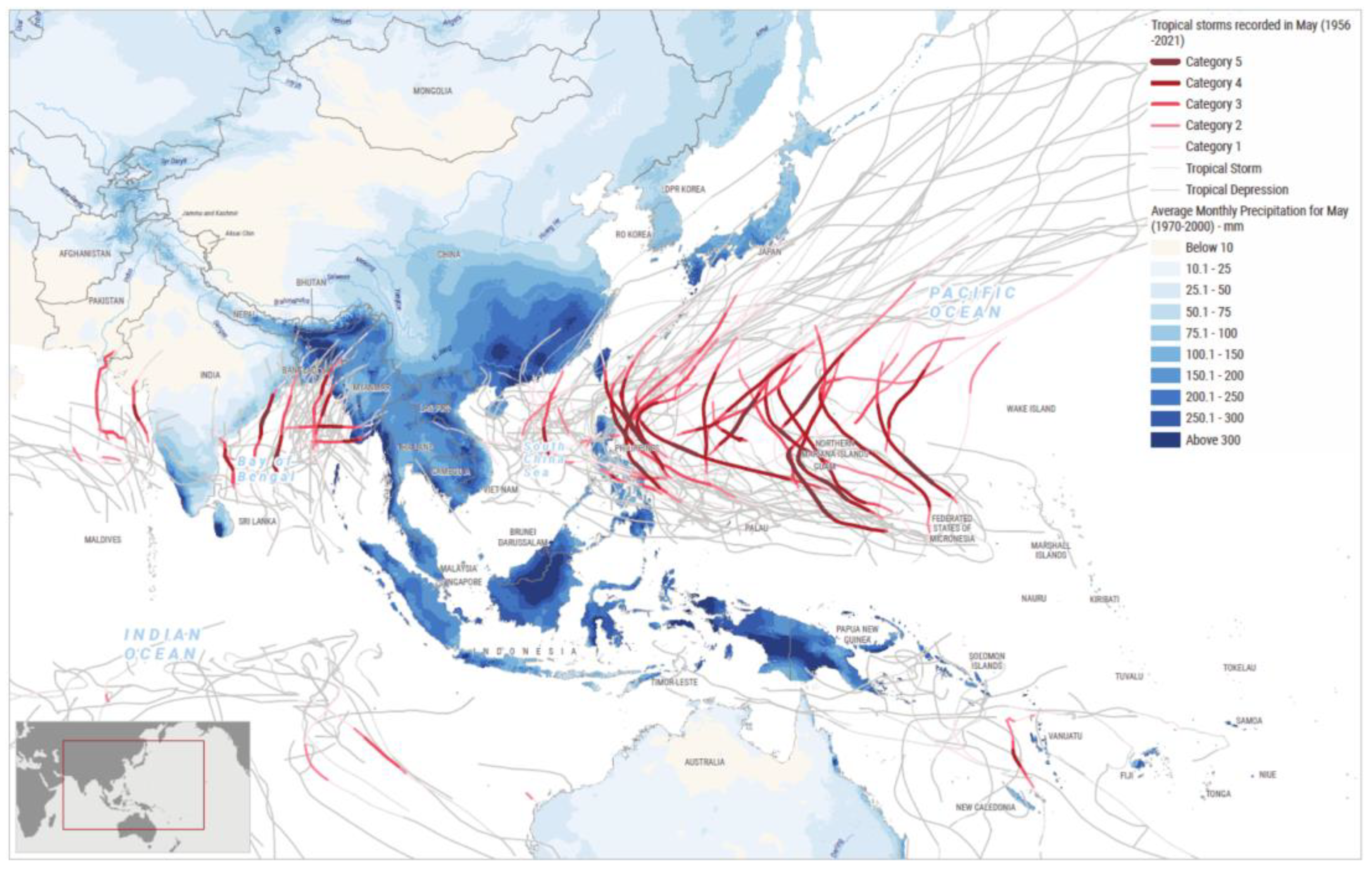
2.6. Bathymetry and Environmental Data in Gili Ketapang’s Water

Figure 8 illustrates the differences in water depth around Gili Ketapang between the northern and southern regions. The northern waters reach depths of up to 33 m, while the southern waters are shallower, with depths of approximately 25 m. Potential locations for installing FPV systems have been identified and are marked with green points, primarily in the southeastern region of the island.

The selected points (green point) in Gili Ketapang, with available environmental data, include measurements of water depth, wind speed, ocean current velocity, significant wave height, and tidal parameters calculated using the Admiralty method. These parameters presented in

Table 6. Environmental data in Gili Ketapang.

No.	Parameter	Value	Unit	Remark
1	Original water depth, (Wd−1)	18.00	m
2	Wind Speed at 10 m, Wv	7.44	m/s	Ref. [25]
3	Significant wave height, Hs	0.77	m
4	Peak period of waves, Tp	3.66	s
5	Ocean current velocity, Cv	0.52	m/s
Tidal parameters
6	Mean Sea Level, MSL (Z0)	1.60	m	Ref. [26]
7	Highest High Water Level, HHWL	+1.52	m
8	Lowest Low Water Level, LLWL	−1.52	m
9	Highest Astronomical Tide, HAT	+3.39	m
10	Lowest Astronomical Tide, LAT	−0.19	m
11	Conservative water depth, (Wd−2)	21.39	m
12	Formzahl number, F	0.91	-	Mixed, mainly semi-diurnal

.

In Indonesian waters, a smaller γ parameter, typically ranging from 2.0 to 2.5, is considered more suitable [27]. This lower value reduces the sharpness of the spectral peak, resulting in a broader distribution of wave energy across different frequencies. This adjustment better represents the mixed wind–sea and swell conditions commonly found in tropical, archipelagic environments. The JONSWAP wave spectrum equations and parameters, adapted for these localized conditions, are based on the recommended practice by Det Norske Veritas (DNV) [28] and presented in Equations (11)–(13):

$$S_J\left(\omega \right)=1-0.287\mathit{ln}\left(\gamma \right)·{\displaystyle \frac{5}{16}}·{H_s}^2{{\omega }_0}^4·{\omega }^{-5}exp\left[-{\displaystyle \frac{5}{4}}{\left({\displaystyle \frac{\omega }{{\omega }_0}}\right)}^{-4}\right]·{\gamma }^{exp\left[-0.5{\left({\displaystyle \frac{\omega -{\omega }_0}{\sigma {\omega }_0}}\right)}^2\right]}$$

(11)

$${\omega }_0={\displaystyle \frac{0.161g}{H_s}}$$

(12)

$$\sigma =0.07 \mathrm{f}\mathrm{o}\mathrm{r} \omega \le {\omega }_0 \mathrm{o}\mathrm{r} \sigma =0.09 \mathrm{f}\mathrm{o}\mathrm{r} \omega >{\omega }_0$$

(13)

Here, S_J (ω) represents the JONSWAP spectrum, ω₀ is the peak frequency, g denotes gravitational acceleration. H_s is the significant wave height, and σ is the spectral width parameter.

2.7. Grid Convergence Index

Grid Convergence Index (GCI) is a standardized method for evaluating convergence across different levels of mesh refinement. Although there is no universally accepted standard for GCI values, smaller GCI values generally indicate greater numerical stability. In this study, the analysis was performed on coarse, medium, and fine grids, focusing on the area under the heave and pitch RAO curves.

As stated by Celik et al. [29] the derived order of the method, $p_a$, and the grid refinement ratio $R_G$ are determined using Equations (14) and (15):

$$P_a={\displaystyle \frac{1}{\mathit{ln}\left(r_{21}\right)}}\left|\mathit{ln}\left|{\displaystyle \frac{{\epsilon }_{32}}{{\epsilon }_{21}}}\right|\right|$$

(14)

$$R_G={\displaystyle \raisebox{1ex}{${\epsilon }_{32}$}\!\left/ \!\raisebox{-1ex}{${\epsilon }_{21}$}\right.}$$

(15)

Here, ${\epsilon }_{21}=S_2-S_1$ represents the difference in the area under the heave and pitch RAO curves between the medium and fine grids, while ${\epsilon }_{32}=S_3-S_2$ denotes the difference between the coarse and medium grids. Then, the value of refinement factors $r_{21}$ and $r_{32}$ are calculated as ${\left({\displaystyle \frac{N_1}{N_2}}\right)}^{{\displaystyle \frac{1}{3}}}$ and ${\left({\displaystyle \frac{N_2}{N_3}}\right)}^{{\displaystyle \frac{1}{3}}}$, respectively, where N_i denotes t the number of cells in the numerical setup.

Convergence conditions are subsequently defined based on the grid refinement ratio ($R_G$), which is calculated using Richardson extrapolation [30]. The convergence conditions are categorized as follows:

(1)

$R_G>1$: Grid divergence

(2)

$R_G<0$: Oscillatory convergence

(3)

$0<R_G<1$: Monotonic convergence

Then, the extrapolated value ${\varphi }_{ext}^{21}$, approximate relative error $e_a^{21}$, and extrapolated relative error $e_{ext}^{21}$ are determined using Equations (16)–(18):

$${\varphi }_{ext}^{21}={\displaystyle \frac{r_{21 }^p{\mathrm{S}}_1-{\mathrm{S}}_2}{r_{21 }^p-1}}$$

(16)

$$e_a^{21}=\left|{\displaystyle \frac{{\mathrm{S}}_1-{\mathrm{S}}_2}{{\mathrm{S}}_1}}\right|$$

(17)

$$e_{ext}^{21}=\left|{\displaystyle \frac{{\varphi }_{ext}^{21}-{\mathrm{S}}_1}{{\varphi }_{ext}^{21}}}\right|$$

(18)

Finally, GCI index is determined using Equation (19) below:

$${\mathrm{G}\mathrm{C}\mathrm{I}}_{fine}^{32}={\displaystyle \frac{1.25·e_a^{21}}{r_{21}^p-1}}$$

(19)

3. Result and Discussion

3.1. Mesh Discretization and Numerical Stability

High-quality meshing is crucial for ensuring the accuracy of numerical computations. A critical procedure is achieving grid convergence, where further mesh refinement no longer significantly impacts the results. Figure 9 illustrates the mesh refinement process in a complex geometry. While a finer mesh enhances accuracy, it also increases computational cost. Conversely, inadequate mesh quality can lead to inaccuracies and reduced reliability in numerical simulations.

The GCI calculation in

Table 7. Spatial convergence and discretization error evaluation.

Parameter	Global Z, η3	Global RY, φ
N1 (Fine)	19,705	19,705
N2 (Medium)	9854	9854
N3 (Coarse)	4928	4928
r21	1.26	1.26
r32	1.26	1.26
S1 (Fine)	1.64	48.42
S2 (Medium)	1.64	48.37
S3 (Coarse)	1.64	48.34
ε32	−0.00	−0.03
ε21	−0.00	−0.05
RG	0.50	0.60
ea21	0.00	0.00
pa	3.00	2.16
φ21ext	1.65	48.50
e21ext	0.00	0.00
GCI21fine	0.15%	0.20%

shows that monotonic convergence is achieved for all simulation variables in heave and pitch motions, as the $R_G$ values are within the range of 0 to 1. The results further indicate that the calculations become increasingly stable as the grid size decreases.

The results of GCI²¹_fine indicate a value of 0.15% for the heave mode and 0.20% for the roll mode, demonstrating that there are no significant differences between using the medium and fine mesh sizes. Therefore, based on previous GCI considerations, 19,705 elements were selected instead of 39,405.

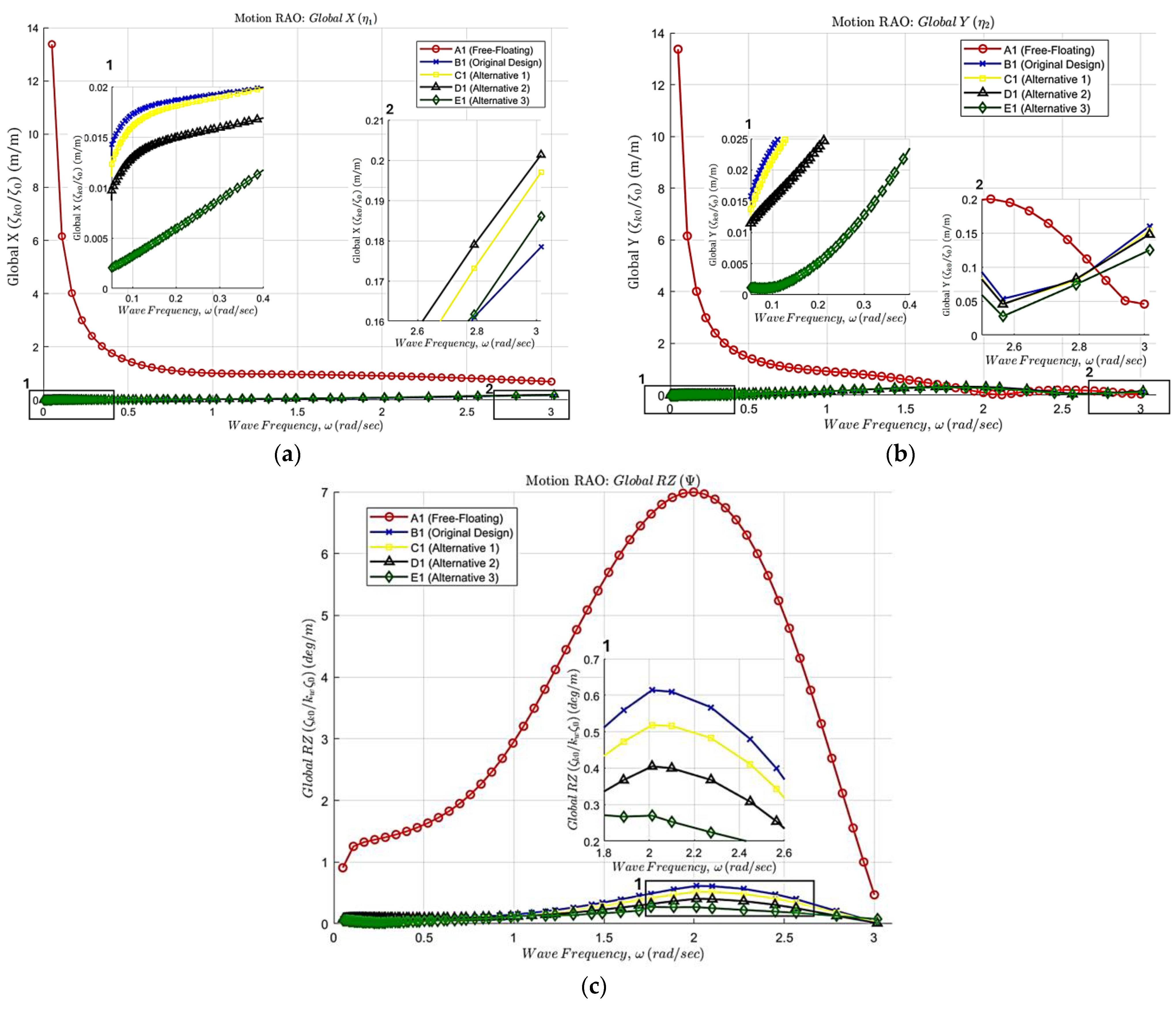
3.2. Structural Motions in Frequency Domain

3.2.1. Horizontal Motions in Regular Waves

Horizontal motion displacements, such as surge, sway, and yaw, can be mitigated by external restoring forces and moments generated by the mooring system. However, potential theory indicates that these motions inherently lack restoring forces and moments, so that in global practice, mooring mechanisms effectively restrict horizontal displacement. This is further illustrated in Figure 10, which highlights a substantial reduction of more than 80% under moored conditions in particular motion modes [31]. The effectiveness of the mooring system is further validated by the Mean Absolute Percentage Error (MAPE) values among these modes. The surge motion mode records a MAPE of 94.01%, while the sway motion mode exhibits the highest deviation at 99.78%. Similarly, the yaw motion mode reaches 96.19%.

The simulation results are supported by the findings of Ghafari and Dardel [32], demonstrating that mooring stiffness contributes to restoring forces that mitigate surge and sway movement caused by wave-induced motion excitation. Additionally, yaw motion follows a similar trend, showing a more significant distinction between the free-floating and moored conditions. This occurs due to the lack of a yaw-restoring moment around the Z-axis in hydrostatics [33].

Additionally, the effect of implementing unstretched length as a function of touchdown length on the transfer function results shows that a shorter unstretched length reduces motion excitation. However, the difference in motion response among the variations (B1–E1) is not particularly significant, even between the original design and Alternative 3. Despite Alternative 3 being approximately 0.51 times shorter than the original design, the reduction in motion response remains minimal, with Root Mean Square Error (RMSE) values of only 0.01 m/m (surge), 0.02 m/m (sway), and 0.09 deg/m (yaw). These findings align with the study conducted by Yan et al. [34].

3.2.2. Pure Oscillatory Motions in Regular Waves

For pure oscillatory motion modes, the hydrostatic restoring force for heave and the restoring moments for roll and pitch in floating structures are primarily determined by the structure’s dimensions and mass distribution. These motions are primarily restricted by hydrostatic-buoyancy and the structural gravity [33,35].

Figure 11 provides information on the differences between free-floating and station-keeping in moored conditions, specifically for Alternative 3, which has the shortest line configuration. In the heave motion mode, the difference is not particularly significant, as indicated by a MAPE value of approximately 7.96%. For roll motion mode, shows a slight difference, as indicated by an MAPE of 6.29% and finally, the most significant difference is observed in the pitch motion mode, with a MAPE of 28.16%.

The effects of external mooring restoring forces and moments, governed by hydrostatic restoring parameters such as A_WP, ∇, GM_T, and GM_L, show noticeable differences. However, when examining the magnitude of the percentage, they are less effective compared to the horizontal motion mode.

3.3. Structural Horizontal Motions Response in Time Domain

This subsection focuses on the time-domain responses of motions that depend on external restoring forces or moments to limit the displacement of the structure system, referred to as horizontal motion. These motions are governed by the stiffness of the mooring cables to maintain their position from drift loads. The performance of horizontal motion was evaluated over a simulation period of 10,800 s to capture the coupled dynamic interactions between the structure and the mooring system. Statistical parameters, including the maximum and minimum responses for each simulation condition (B1–E1), were analyzed to assess the effect of touchdown length, while the mooring properties, such as mass and EA parameters remained constant.

The simulation results presented in Figure 12a illustrate the surge motion mode. The main graph displays the surge response in meters, while the inset graphs provide detailed information on the global maximum surge responses during specific intervals. The global maximum surge response shows that condition B1 has the highest value at 1.78 m, while condition E1 has the lowest value at 1.70 m, occurring at 9214 s.

Subsequently, the sway response in meters shown in Figure 12b demonstrates the global maximum sway response reaches its highest value of 0.28 m under condition B1, while condition E1 exhibits the lowest value of 0.18 m, occurring at 4784 s.

The yaw response shown in Figure 12c indicates that the global maximum yaw response occurs under condition B1, reaching the highest value of 3.51°, while condition E1 exhibits the lowest value at 1.20°, both observed at 6317 s.

These results confirm that condition E1, characterized by the shortest touchdown length, effectively reduces horizontal motion amplitudes compared to other conditions (B1–D1). This trend is consistent across all global maximum motion responses. The reduction in motion amplitudes highlights improved performance in mooring stiffness as the mooring length decreases in stabilizing longitudinal (global X), lateral (global Y), and rotational (global RZ) motions [36].

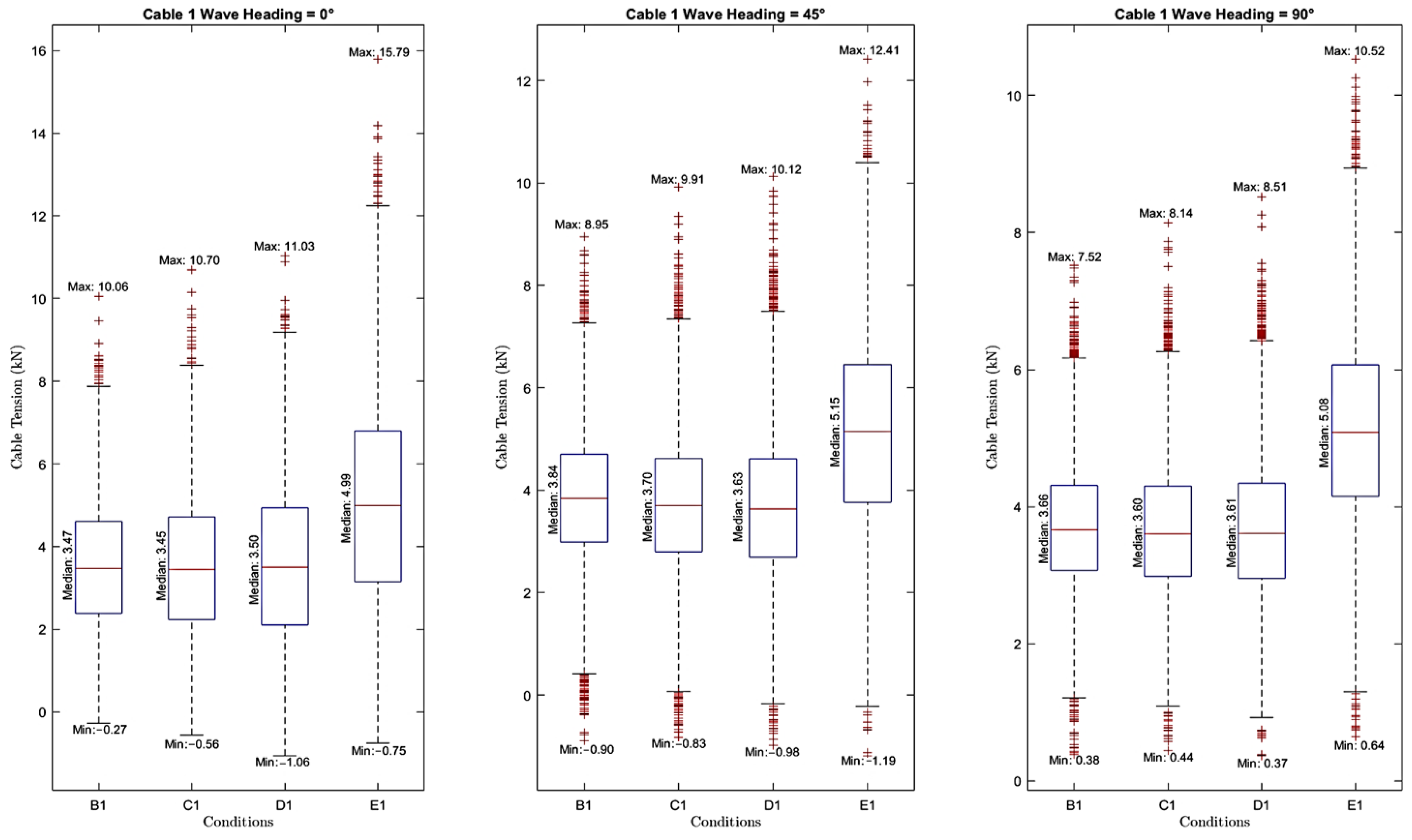
3.4. Time Domain in Mooring Line Tension

This subsection concludes by presenting the time-domain analysis of cable tension for mooring cables 1 through 4 under proposed load directions of 0°, 45°, and 90° for the single-array pentamaran-FPV structure. Visualization results are provided using statistical values illustrated in box plots. In each box plot, the lower and upper edges of the box represent the 25th (Q1) and 75th (Q3) percentiles of the data distribution, respectively. The dataset’s median is represented by a horizontal line within the box. The whiskers extend from the edges of the box to the smallest and largest values that are not considered outliers. Outliers are shown as red plus signs and represent data points that are more than 1.5 times the interquartile range (IQR) beyond the first or third quartile. The IQR itself is a measure of statistical dispersion that shows the range of the middle 50% of a dataset.

Figure 13 provides several insights. First, the shortest touchdown as a function of the mooring line length is associated with an increase in mooring tension. This is reflected in an upward shift of the box plot distribution. Furthermore, under condition E1, the dataset exhibits significant variability and a wide distribution of values. Both the long box and whisker indicate the possible presence of extreme values in the dynamic mooring line behavior. For safety considerations, the maximum tension is conservatively defined as the maximum outlier value.

For further clarification, the differences in mooring tension for each alternative moored condition from C1 through E1 were quantified as percentage deviations relative to the baseline of the original design (B1). The baseline tension value for the original design (B1) was 10.06 kN under head seas loading direction. This indicates that in condition C1, the tension increased to 10.70 kN (a 6.34% increase), in condition D1, the tension increased to 11.03 kN (a 9.62% increase), and finally in condition E1, the tension climbed significantly to 15.79 kN (a 56.91% increase).

A similar approach was applied to calculate the tension changes in quartering seas and beam seas conditions. In these conditions, the baseline mooring tension for the original design was 8.95 kN and 7.52 kN, respectively. Consequently, in the quartering seas, the mooring tension increased by 10.72%, 13.00%, and 38.62% as the unstretched mooring line length decreased. Meanwhile, in beam seas, the mooring tension increased by 8.16%, 13.17%, and 39.91%. Based on these findings, it can be concluded that for mooring line-1, the highest tension occurs under 0-degree loading conditions (head seas). Although the maximum mooring tension values were 15.79 kN, 12.41 kN, and 10.52 kN for the three wave headings considered, these values remain within the allowable tension limit of approximately 30.69 kN, indicating that the system is still considered safe from an engineering perspective.

Following a similar trend to mooring line-1, Figure 14 provides several insights into the box plots illustrating the distribution of mooring line-2 tension under different loading conditions, comparing four conditions: B1 through E1. Under head seas, the median tension in B1 to D1 remains relatively stable, while E1 shows a noticeable increase, with a median of 4.99 kN. The maximum tension values progressively increase from 10.06 kN (B1) to 15.78 kN (E1), with E1 experiencing the highest tension and the largest number of outliers.

Under quartering seas, the median tension remains consistent across B1 to D1, but E1 exhibits a slight increase to 4.93 kN. The maximum tension is lower compared to the previous loading direction, but the number of outliers is higher, particularly in B1 and E1. This indicates a wider spread of tension data compared to head seas.

In beam seas, the trend is similar, with B1 (3.39 kN), C1 (3.37 kN), and D1 (3.42 kN) showing stable median values, whereas E1 again exhibits a significantly higher median of 4.87 kN. The maximum tension values range from 7.37 kN (B1) to 10.19 kN (E1). The number of outliers increases further, indicating that beam seas induce more frequent extreme tension values.

The results demonstrate that a reduction in the unstretched mooring line length leads to an increase in mooring tension. Nevertheless, the maximum tension values recorded for each wave heading, measured at 15.78 kN, 11.69 kN, and 10.19 kN, remain within acceptable safety limits. The corresponding ratios between the recorded tension and the allowable tension are 0.51, 0.38, and 0.33, respectively. However, it is crucial to consider that if the mooring tension ratio approaches 1, the risk of exceeding the mooring system’s capacity increases and potentially compromising safety.

The box plots in Figure 15 present findings on mooring line tension distribution. In head seas conditions, the median tension values for B1 to D1 show slight variations. However, differences in the IQR indicate that as the unstretched mooring line length decreases, the box plots become taller, indicating an increase in overall tension and a wider data distribution. In the E1 condition, the box plot shows a significant shift, with a higher median tension of 5.15 kN. Additionally, the maximum tension progressively increases, reaching 15.73 kN, further showing that E1 experiences the highest loading conditions compared to the other cases.

Under quartering seas, the median values remain relatively stable across B1 to D1, while E1 shows an increase of approximately 38.14% compared to the previous average median values. The maximum tension remains high but does not reach the extreme values observed in head seas, with a value of 12.49 kN. However, the number of outliers increases significantly, particularly in B1 and E1, indicating greater variation in tension distribution. This suggests that quartering seas introduce more variability in mooring response.

In the beam seas scenario, the median tension values remain closely aligned across B1 to D1, while E1 consistently shows the highest median and peak tension values across all wave headings, with values of approximately 5.08 kN and 10.53 kN, respectively. Although the maximum tension in this wave heading is lower compared to the other two conditions, the number of extreme values (outliers) increases significantly, indicating more frequent fluctuations in tension.

Regarding safety requirements, cable 3 in the E1 condition, which shows the highest maximum tension compared to conditions B1 through D1 across all wave headings, remains below the allowable tension limit of 30.69 kN. Therefore, this condition is considered to meet safety requirements.

Finally, for mooring line-4 in Figure 16, the box plot illustrates the variation in tension. Under head seas conditions, the median tension values for B1 (3.73 kN), C1 (3.66 kN), and D1 (3.65 kN) are relatively close. However, E1 exhibits a higher median tension of 5.15 kN, and the maximum tension values gradually increase from 11.47 kN (B1) to 15.73 kN (E1).

Under quartering seas, the distribution follows a similar pattern. The median values for B1 to D1 (3.81 kN, 3.69 kN, and 3.63 kN, respectively) remain stable, while E1 increases to 5.08 kN. The maximum recorded tension in E1 (12.61 kN) is higher than in the previous loading direction, suggesting that quartering seas induce more pronounced tension variations.

In beam seas, a different trend emerges. The median values for B1 (3.39 kN), C1 (3.37 kN), and D1 (3.42 kN) remain closely aligned, while E1 shows an increased median of 4.87 kN. The maximum tension in E1 reaches 10.19 kN, which is lower than in head and quartering seas. However, the number of extreme values (outliers) rises significantly, particularly in D1 (102 outliers) and C1 (98 outliers), indicating a broader distribution of fluctuating tension data. It can be observed that under all E1 conditions for cable 4, all actual tension values remain below the allowable limit of 30.69 kN, indicating that this condition can be considered safe.

Overall, across all mooring cables (1 through 4), the results indicate that E1 consistently experiences the highest median and maximum tension values across all wave headings. Head seas generate the highest peak tension, quartering seas increase tension variability, and beam seas cause frequent fluctuations but lower tension amplitudes. These findings highlight that the unstretched mooring line length influences both motion performance and line tension, which are important for ensuring safe operations.

This study identifies an important relationship between motion response and line tension. Reducing motion response to improve stability often leads to higher line tension. On the other hand, lowering line tension may result in increased motion response, which can compromise stability. To manage this balance, standards such as those from DNV [37] and American Bureau of Shipping (ABS) [38] recommend applying a suitable Factor of Safety (FoS) to keep floating structures both stable and safe in various environmental conditions.

4. Conclusions

This preliminary numerical study investigates the effect of touchdown length as a function of dynamic catenary mooring length configurations on the non-linear response performance of pentamaran-FPV. The study was conducted in the waters of Gili Ketapang, a small island, to analyze the motion characteristics of the proposed FPV design under specific environmental conditions.

The analysis was conducted using a BEM-based potential theory solver in an inviscid fluid environment. The study examined motion transfer functions, specifically RAOs for each mode, comparing behavior under free-floating and moored conditions. Various catenary mooring lengths, ranging from the original design to alternative configurations, were examined. A frequency and time-domain simulation were conducted to evaluate dynamic motion responses in irregular waves within different loading directions, considering both collinear and omnidirectional conditions. Based on the analysis in this study, the following conclusions can be drawn:

• Achieving numerical stability involved conducting a GCI calculation between the medium and fine grid sizes. The results showed that both variables, heave and pitch RAO, had differences of less than 1%, indicating no significant differences between the medium and fine mesh sizes. Therefore, this study employed the medium grid size (19,705 elements) to reduce computation time.
• External restoring forces and moments generated by the mooring system significantly reduce horizontal motion displacements (surge, sway, and yaw). The reduction exceeds 90%, with the MAPE in RAO calculations showing reductions of 94.01% in surge, 99.78% in sway, and 96.19% in yaw between free-floating and moored conditions. Furthermore, a shortened in unstretched mooring length leads to a decrease in motion excitation in RAO, though the effect is not highly significant. Even with a length reduction of up to 51% of the original design, the motion response remains relatively stable. This is evidenced by the RMSE values, which indicate minimal differences in motion between the longest and shortest mooring configurations: 0.01 m/m for surge, 0.02 m/m for sway, and 0.09 deg/m for yaw.
• For pure oscillatory motion, which is governed by natural hydrostatic restoring forces and moments, the addition of a mooring system has a combined effect in restricting motion. The MAPE values for heave, roll, and pitch RAOs are 7.96%, 6.29%, and 28.16%, respectively. This indicates that although the mooring system contributes to motion reduction, its effect is less significant compared to the reduction observed in horizontal displacements.
• The time-domain response for horizontal motion shows a declining trend in motion, indicating improved performance in mooring stiffness as the mooring length decreases. Additionally, of the three motion responses, the most significant reduction occurs in rotational motion (yaw), rather than in translational motions (surge and sway).
• In the time domain, mooring lines with the same properties and configurations show stronger nonlinearity in restoring forces and stiffness as the mooring length decreases. This increased nonlinearity causes a wider distribution of line tension data, resulting in larger maximum mooring tensions. Nevertheless, all mooring cables across all wave headings still meet the safety requirements, as all actual tension values remain below the allowable limit of 30.69 kN.

5. Future Work

The integration of floating structures and anchoring systems currently contributes to a Levelized Cost of Energy (LCOE) that is approximately 20% higher than traditional ground-mounted PV systems [39]. However, significant cost reductions can be achieved by scaling up FPV installations into multi-array modular designs. For instance, energy costs can decrease by 85% when FPV capacity increases from 52 kilowatts (kW) to 2 megawatts (MW) [40].

Modular design is crucial in this process, as breaking down large floating structures into smaller units helps mitigate hydro-elastic issues, enhancing safety and long-term reliability, even under harsh ocean conditions [41]. Additionally, modular FPV systems offer substantial cost savings in manufacturing, transportation, and installation.

In line with this, there is a growing trend in the FPV industry to adopt standardized, lightweight floating modules that are connected by semi-rigid or flexible connectors, rather than using fully integrated FPV structures [42,43].

Among the various connection types, hinge connections are increasingly recognized as the most suitable for FPV applications due to their ability to provide greater flexibility and resilience, allowing adjacent modules to move relative to each other in response to wave-induced forces [44]. The modeling of the hinge connection between structures in this future study is shown in Figure 17.

Additionally, marine growth on mooring lines should be incorporated into the long-term mooring system analysis. The thickness of the marine growth should be determined based on survey data for the actual depth. This growth is accounted for by increasing the weight of the line segments and the drag coefficient. For detailed calculations and considerations regarding the impact of marine growth on the drag coefficient, the reader shall refer to DNV-OS-E301 Offshore Standard ‘Position mooring’ [37].

Considering these multiple factors, this study requires further validation through seakeeping experiments to compare the numerical simulations with the motion characteristics of a single-array pentamaran floater in real-life fluid dynamics conditions. Subsequently, further investigation into motion excitation should be conducted in a multi-array configuration, incorporating a hinged connection between modules in the FPV multi-body system, as well as the design of the mooring system, taking into account the effects of marine growth in dynamic nearshore environments.