Modeling the Coal Tar Pitch Primary Carbonization Process
Abstract
:1. Introduction
2. Materials and Methods
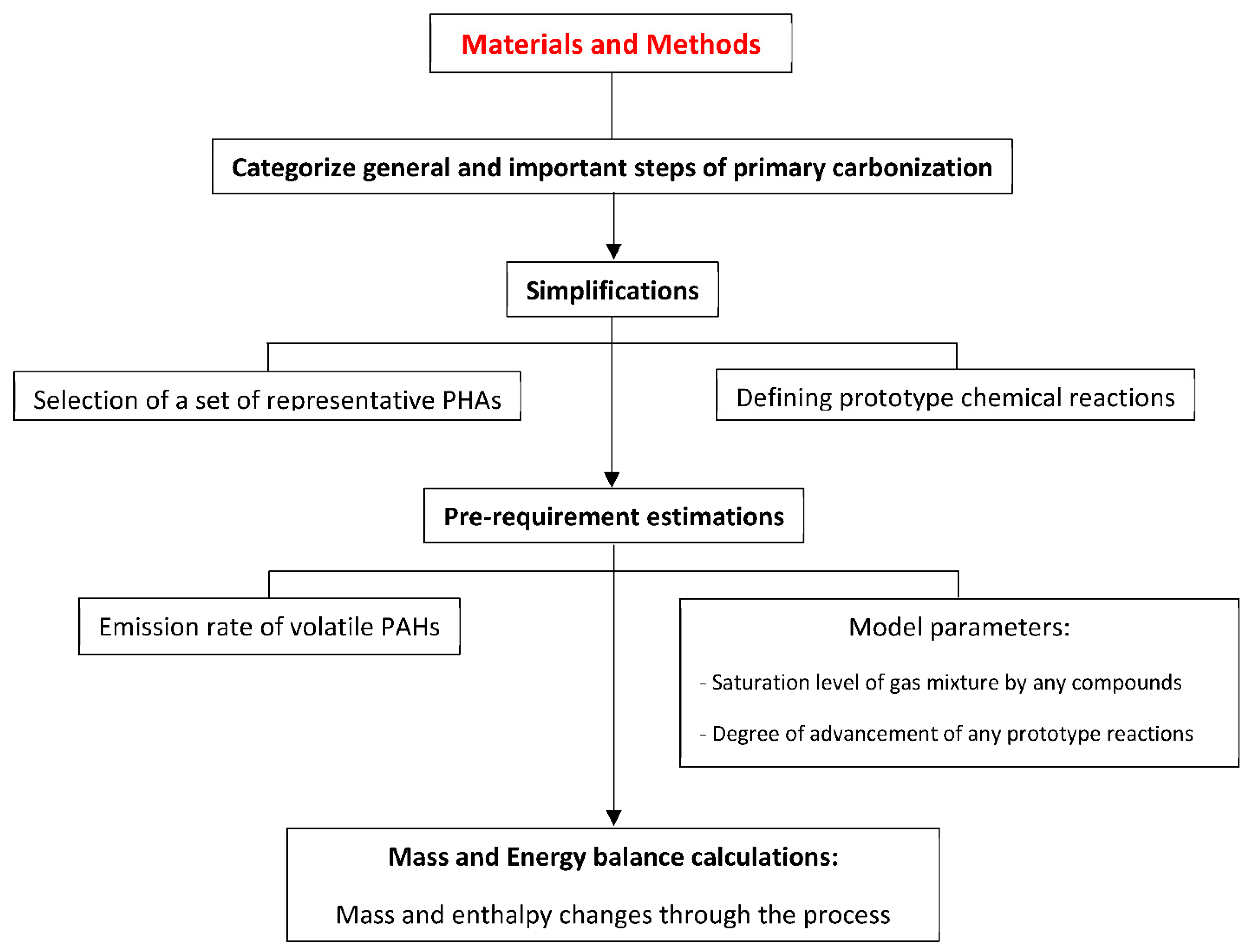
2.1. Overview of General Steps of Primary Carbonization Process
2.2. Simplified Approach for Modeling of Internal Phenomena Occurring in Coal Tar Pitch Primary Carbonization
2.2.1. Selection of a Set of Representative PAH Compounds Appearing during CTP Primary Carbonization
2.2.2. Estimation of Volatile PAHs Emission during CTP Heat Treatment
2.2.3. Defining Prototype Chemical Reactions as a Reduced Description of the Mesophase and Semi-Coke Formation Steps
2.2.4. Estimation of the Model Parameters
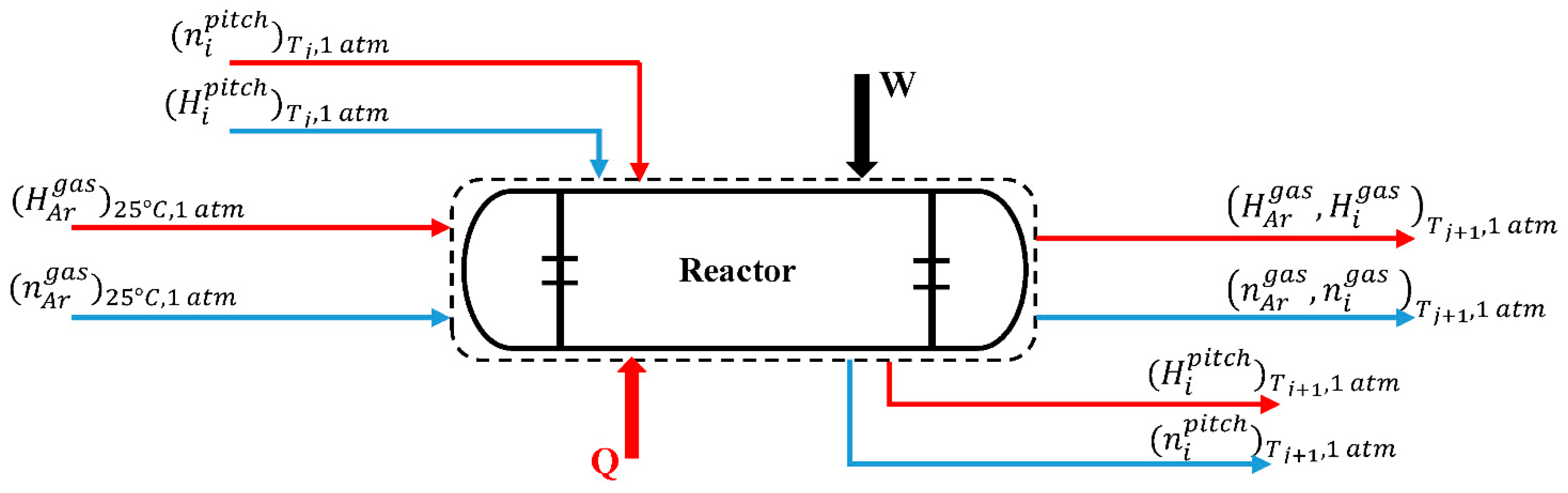
2.3. Mass and Energy Balance through the Process
2.4. Integrating the Model Equations for Estimation of Mass and Enthalpy Changes through the Primary Carbonization Process
3. Results and Discussion
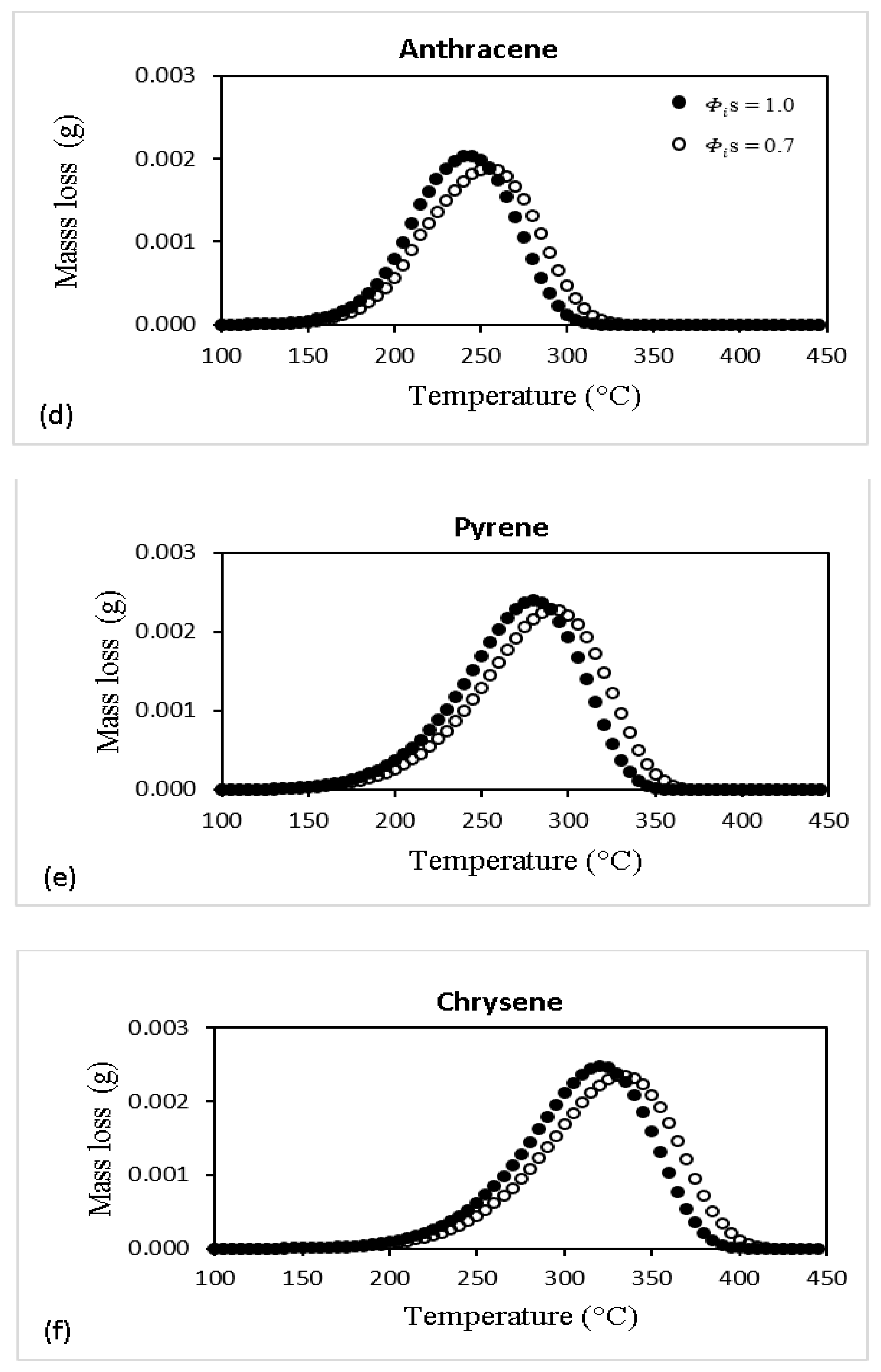
3.1. General Prediction of Gas Emission Rate during Heat Treatment of Coal Tar Pitch (below 350 °C)
3.2. Application to Bouchard’s Experiments
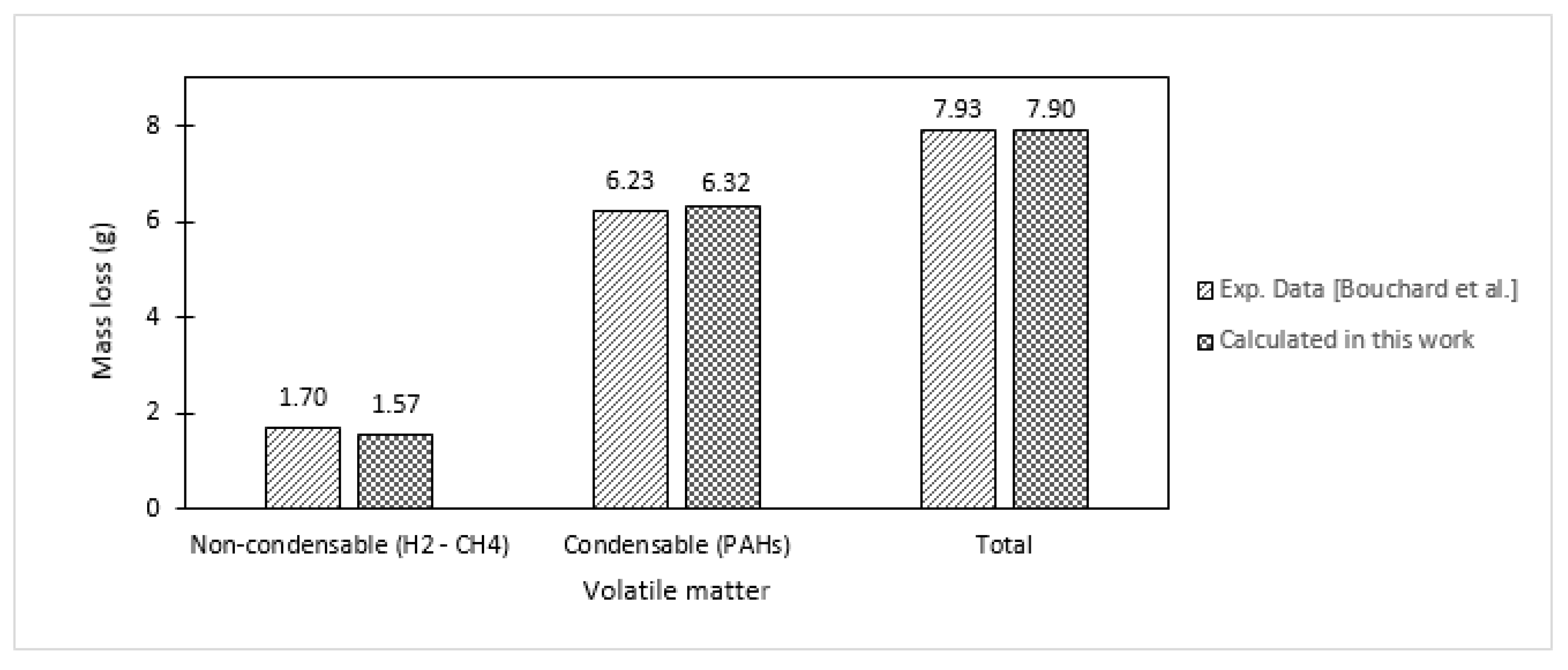
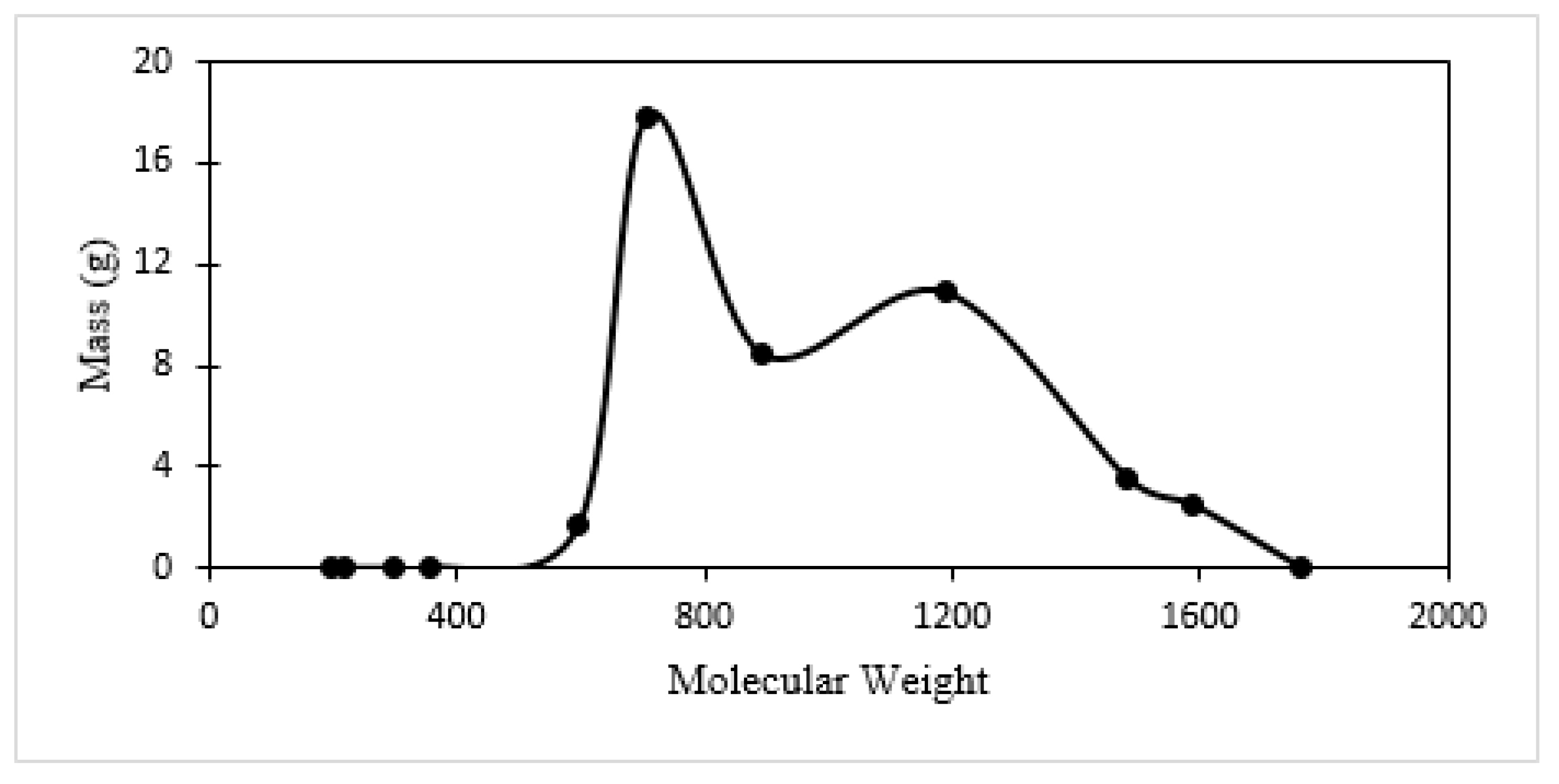
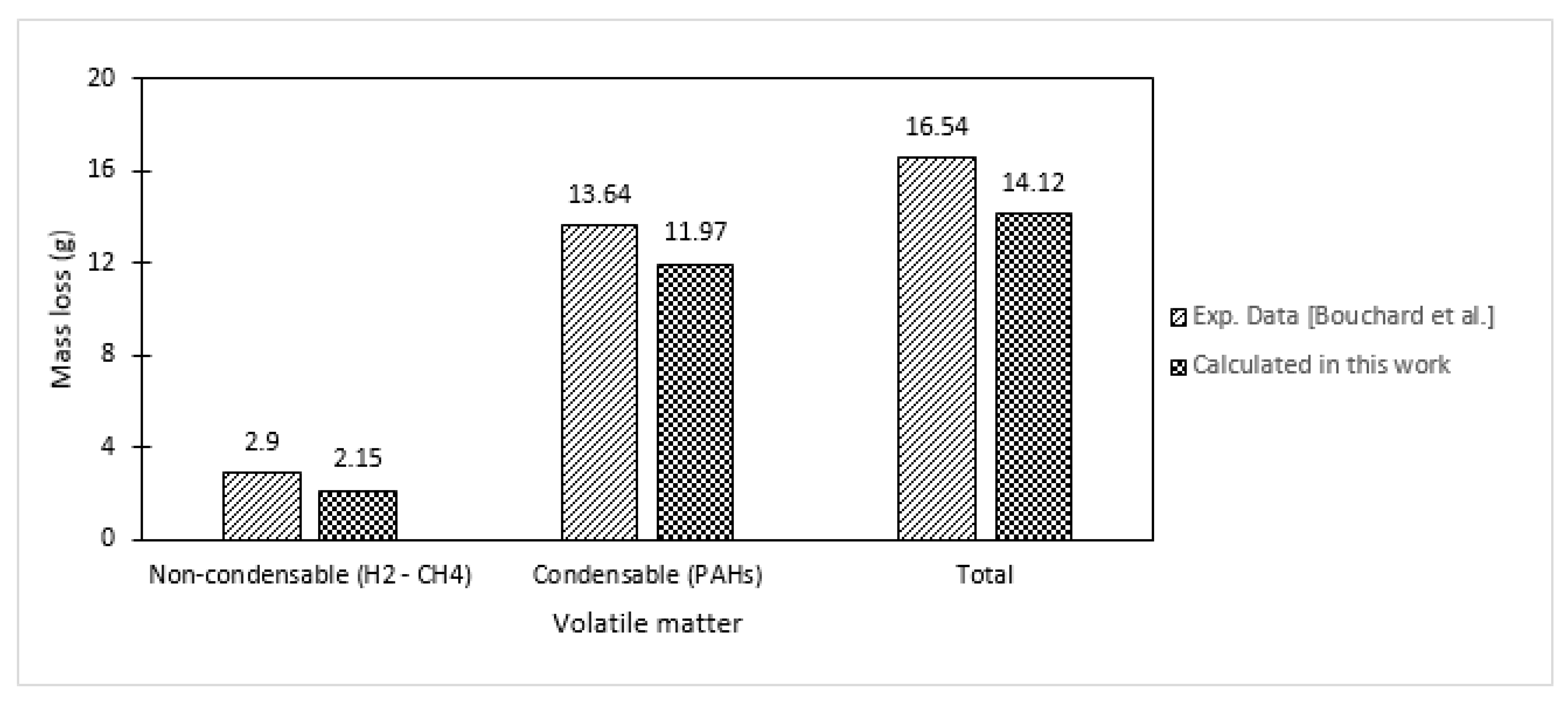
3.2.1. Estimation of Mass Changes of CTP (during Heat Treatment)
3.2.2. Estimation of Energy Requirement of Different Steps of CTP Primary Carbonization
- −
- In the present work, estimation of the enthalpies of any PAHs is based on critical assessment presented in our previous work [67]. In this reference, due to the lack of experimental data, the application of the developed model to estimate the thermodynamic properties of PAH oligomers has only been justified for a limited number of PAH oligomers.
- −
- As was proposed in Section 2.3, the enthalpy of semi-coke crystallite (needed for the required energy calculation in semi-coke formation step in temperature range 450–550 °C) can be estimated by applying the model developed for coke by Ouzilleau et al. In their model, perfectly parallel planes (shown in Figure 4) with enthalpy of stacking of zero are assumed in Gibbs energy calculations. However, some issues have to be taken into account in switching from the formalism of estimation of enthalpy of the large planes of oligomer PAHs (established in ref. [67]) in mesophase formation step to Ouzilleau’s formalism for enthalpy estimation of the idealized crystallite structure in the semi-coke formation step. In other words, transforming such a large plane of high MW PAH oligomers to idealized semi-coke crystallite (satisfying Ouzilleau’s model) requires energies to bring them to the configuration shown in Figure 4 and to parallelize them.
4. Conclusions
- −
- The first limitation relates to neglecting the role played by impurities, such as sulfur, nitrogen, and oxygen, as well as non-PAHs (heterocyclic compounds) which are usually found in CTP, in the carbonization process. It has been well established that the intermediate and final products of the primary carbonization, i.e., mesophase and semi-coke, are composed of polyaromatic molecules mutually cross-linked by a medium composed of carbon functions containing heteroatoms (e.g., sulfur and oxygen) which enter the process through impurities and (or) heterocyclic compounds in the pitches [37]. Indeed, in the present model the effect of the ratio of cross-linking heteroatoms (e.g., sulfur, nitrogen and oxygen) to hydrogen atoms of precursor carbon materials (CTP in this work) on the efficiency of the primary carbonization and the quality of the final product was ignored by neglecting the presence of the impurities and heterocyclic compounds in coal tar pitch. Hence, one aspect that will be treated in future work is development of a more appropriate model to predict the physical and chemical evolutions occurring during primary carbonization of any source of CTP containing heteroatoms.
- −
- In the mass and energy balance calculations, the temperature of the condensed pitch was assumed to become equal and uniform in all directions instantaneously at each iteration after increasing the temperature of the pitch by a heat treatment. This assumption is not compatible with what really happens in industrial processes. Thus, it is recommended to improve the predictive capacity of the present model by considering adequate heat transfer equations for the calculation of temperature gradients in condensed pitch.
- −
- Only one set of experimental data (Bouchard’s experiments) was found in the literature to calibrate the model. Although the model developed seems to be versatile enough to reproduce the experimental data for the heat treatment of different types of CTP in different operating conditions, it is recommended to design and run a certain number of experiments reporting the changes of both the mass of pitch residue and the composition of volatile species throughout CTP primary carbonization in order to extend the application of the proposed model to predict different experimental data sets.
- −
- The paucity of experimental data made it difficult to assess the uncertainties associated with the process energy requirement calculations in the 25–350 °C temperature range. Performing some CTP heat treatment experiments in order to generate a data set including energy consumption of different steps of the primary carbonization process for model justification purposes is recommended.
- −
- The discussion in Section 3.2.2 presented the weakness of the present model as regards estimation of the enthalpy changes of residual pitch during the mesophase and semi-coke formation steps of the primary carbonization process. Hence, another important aspect of future work is to extend the present model so that it can be applied to calculate the required energy for heat treatment of CTP beyond 350 °C.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Banerjee, C.; Chandaliya, V.K.; Dash, P.S. Recent advancement in coal tar pitch-based carbon fiber precursor development and fiber manufacturing process. J. Anal. Appl. Pyrolysis 2021, 158, 105272. [Google Scholar] [CrossRef]
- Barbouche, M.; Hajji, M.; Ezzaouia, H. Electric arc furnace design and construction for metallurgical and semiconductor research. Int. J. Adv. Manuf. Technol. 2016, 82, 997–1006. [Google Scholar] [CrossRef]
- Chen, Z.; Ma, W.; Li, S.; Wu, J.; Wei, K.; Yu, Z.; Ding, W. Influence of carbon material on the production process of different electric arc furnaces. J. Clean. Prod. 2018, 174, 17–25. [Google Scholar] [CrossRef]
- Edwards, L. The history and future challenges of calcined petroleum coke production and use in aluminum smelting. JOM 2015, 67, 308–321. [Google Scholar] [CrossRef] [Green Version]
- Fitzer, E. The future of carbon-carbon composites. Carbon 1987, 25, 163–190. [Google Scholar] [CrossRef]
- García, R.; Crespo, J.L.; Martin, S.C.; Snape, C.E.; Moinelo, S.R. Development of mesophase from a low-temperature coal tar pitch. Energy Fuels 2003, 17, 291–301. [Google Scholar] [CrossRef]
- Gasik, M.M.; Gasik, M.I. Smelting of Aluminum. In Handbook of Aluminum; Marcel Dekker, Inc.: New York, NY, USA, 2003; pp. 47–79. [Google Scholar]
- Jin, S.; Jiang, Y.; Ji, H.; Yu, Y. Advanced 3D current collectors for lithium-based batteries. Adv. Mater. 2018, 30, 1802014. [Google Scholar] [CrossRef]
- Radenovic, A. Properties of carbon anode components for aluminium production. NAFATA 2012, 63, 111–114. [Google Scholar]
- Kvande, H. The aluminum smelting process. J. Occup. Environ. Med. 2014, 56 (Suppl. 5), S2. [Google Scholar] [CrossRef] [Green Version]
- Kvande, H.; Drabløs, P.A. The aluminum smelting process and innovative alternative technologies. J. Occup. Environ. Med. 2014, 56 (Suppl. 5), S23. [Google Scholar] [CrossRef] [Green Version]
- Lavin, J.G. Chemical reactions in the stabilization of mesophase pitch-based carbon fiber. Carbon 1992, 30, 351–357. [Google Scholar] [CrossRef]
- Liu, J.; Chen, X.; Liang, D.; Xie, Q. Development of pitch-based carbon fibers: A review. Energy Sources Part A Recovery Util. Environ. Eff. 2020, 1–21. [Google Scholar] [CrossRef]
- Martín, Y.; García, R.; Keating, P.; Snape, C.E.; Moinelo, S.R. A study of the polymerization and condensation reactions during the heat treatment of pitches under gas-blowing conditions. Energy Fuels 2000, 14, 380–392. [Google Scholar] [CrossRef]
- Reverdy, M.; Potocnik, V. History of Inventions and innovations for aluminum production. In TMS 2020 149th Annual Meeting & Exhibition Supplemental Proceedings; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Song, C.; Schobert, H.H. Opportunities for developing specialty chemicals and advanced materials from coals. Fuel Process. Technol. 1993, 34, 157–196. [Google Scholar] [CrossRef]
- Tabereaux, A.T.; Peterson, R.D. Aluminum production. In Treatise on Process Metallurgy; Elsevier: Amsterdam, The Netherlands, 2014; pp. 839–917. [Google Scholar]
- Tajik, A.R.; Shamim, T.; Al-Rub, R.K.A.; Zaidani, M. Performance analysis of a horizontal anode baking furnace for aluminum production. In Proceedings of the ICTEA: International Conference on Thermal Engineering, Muscat, Oman, 26–28 February 2017. [Google Scholar]
- Tajik, A.R.; Shamim, T.; Ghoniem, A.F.; Abu Al-Rub, R.K. The impact of critical operational parameters on the performance of the aluminum anode baking furnace. J. Energy Resour. Technol. 2021, 143, 062103. [Google Scholar] [CrossRef]
- Vohler, O. Carbon and graphite in future markets. Erdöl Kohle Erdgas Petrochem. 1986, 39, 561. [Google Scholar]
- Wang, Y.; Chen, K. Low-cost, lightweight electrodes based on carbon fibers as current collectors for aluminum-ion batteries. J. Electroanal. Chem. 2019, 849, 113374. [Google Scholar] [CrossRef]
- Wazir, A.H.; Kakakhel, L. Preparation and characterization of pitch-based carbon fibers. New Carbon Mater. 2009, 24, 83–88. [Google Scholar] [CrossRef]
- Wilson, W.S.; Guichelaar, P.J. Electric arc furnace processes. In Carbide, Nitride and Boride Materials Synthesis and Processing; Springer: Dordrecht, Germany, 1997; pp. 131–136. [Google Scholar]
- Winter, M.; Wrodnigg, G.H.; Besenhard, J.O.; Biberacher, W.; Novák, P. Dilatometric investigations of graphite electrodes in nonaqueous lithium battery electrolytes. J. Electrochem. Soc. 2000, 147, 2427. [Google Scholar] [CrossRef]
- Zhu, J.; Park, S.W.; Joh, H.I.; Kim, H.C.; Lee, S. Preparation and characterization of isotropic pitch-based carbon fiber. Carbon Lett. 2013, 14, 94–98. [Google Scholar] [CrossRef] [Green Version]
- Lewis, I. Chemistry of pitch carbonization. Fuel 1987, 66, 1527–1531. [Google Scholar] [CrossRef]
- Lewis, I.; Singer, L. Carbonization of aromatic hydrocarbons. [18 refs]. Am. Chem. Soc. Div. Fuel Chem. Prepr. 1969, 13, 86–100. [Google Scholar]
- Bouchard, N. Pyrolyse de Divers Brais Utilisés Dans la Technologie Söderberg et Analyse des Matières Volatiles; Université du Québec à Chicoutimi: Quebec, QC, Canada, 1998. [Google Scholar] [CrossRef]
- Dumont, M.; Dourges, M.A.; Bourrat, X.; Pailler, R.; Naslain, R.; Babot, O.; Birot, M.; Pillot, J.P. Carbonization behaviour of modified synthetic mesophase pitches. Carbon 2005, 43, 2277–2284. [Google Scholar] [CrossRef]
- Oumarou, N.; Kocaefe, D.; Kocaefe, Y.; Morais, B. Transient process model of open anode baking furnace. Appl. Therm. Eng. 2016, 107, 1253–1260. [Google Scholar] [CrossRef]
- Lewis, I. Thermal polymerization of aromatic hydrocarbons. Carbon 1980, 18, 191–196. [Google Scholar] [CrossRef]
- Lewis, I. Chemistry of carbonization. Carbon 1982, 20, 519–529. [Google Scholar] [CrossRef]
- Lewis, I. Chemistry and development of mesophase in pitch. J. Chim. Phys. 1984, 81, 751–758. [Google Scholar] [CrossRef]
- Lewis, I.; Singer, L. Carbonization of Aromatic Hydrocarbons. In Abstracts of Papers of the American Chemical Society; American Chemical Society: Washington, DC, USA, 1969; p. 20036. [Google Scholar]
- Lewis, I.; Singer, L. Thermal Conversion of Polynuclear Aromatic Compounds to Carbon. In Advances in Chemistry; ACS Publications: Washington, DC, USA, 1988. [Google Scholar]
- Oberlin, A. Carbonization and graphitization. Carbon 1984, 22, 521–541. [Google Scholar] [CrossRef]
- Oberlin, A.; Bonnamy, S. Colloidal and Supramolecular Aspects. Chem. Phys. Carbon 1999, 26, 1. [Google Scholar]
- Oberlin, A.; Bonnamy, S. Carbonization and graphitization. In Graphite and Precursors; CRC Press: Boca Raton, FL, USA, 2001; pp. 199–220. [Google Scholar]
- Oshida, K.; Bonnamy, S. Primary carbonization of an anisotropic ‘mesophase’pitch compared to conventional isotropic pitch. Carbon 2002, 40, 2699–2711. [Google Scholar] [CrossRef]
- Brooks, J.; Taylor, G. The formation of graphitizing carbons from the liquid phase. Carbon 1965, 3, 185–193. [Google Scholar] [CrossRef]
- Brooks, J.D.; Taylor, G. The formation of some graphitizing carbons. Chem. Phys. Carbon 1968, 4, 243–286. [Google Scholar]
- Taylor, G. Development of optical properties of coke during carbonization. Fuel 1961, 40, 465–472. [Google Scholar]
- Marsh, H. Carbonization and liquid-crystal (mesophase) development: Part 1. The significance of the mesophase during carbonization of coking coals. Fuel 1973, 52, 205–212. [Google Scholar] [CrossRef]
- Franklin, R.E. The structure of graphitic carbons. Acta Crystallogr. 1951, 4, 253–261. [Google Scholar] [CrossRef]
- Franklin, R.E. Crystallite growth in graphitizing and non-graphitizing carbons. Proc. R. Soc. London Ser. A Math. Phys. Sci. 1951, 209, 196–218. [Google Scholar]
- Cottinet, D.; Couderc, P.; Saint Romain, J.L.; Dhamelincourt, P. Raman microprobe study of heat-treated pitches. Carbon 1988, 26, 339–344. [Google Scholar] [CrossRef]
- Greinke, R. Kinetics of petroleum pitch polymerization by gel permeation chromatography. Carbon 1986, 24, 677–686. [Google Scholar] [CrossRef]
- Greinke, R. Early Stages of Petroleum Pitch Carbonization—Kinetics and Mechanisms. Chem. Phys. Carbon 1994, 24, 1. [Google Scholar]
- Greinke, R.; Lewis, I. Carbonization of naphthalene and dimethylnaphthalene. Carbon 1984, 22, 305–314. [Google Scholar] [CrossRef]
- Greinke, R.; Singer, L. Constitution of coexisting phases in mesophase pitch during heat treatment: Mechanism of mesophase formation. Carbon 1988, 26, 665–670. [Google Scholar] [CrossRef]
- Tillmanns, H. Carbonization and coke characterization. In ACS Symposium Series; American Chemical Society: Washington, DC, USA, 1986. [Google Scholar] [CrossRef]
- Ouzilleau, P.; Gheribi, A.E.; Chartrand, P.; Soucy, G.; Monthioux, M. Why some carbons may or may not graphitize? The point of view of thermodynamics. Carbon 2019, 149, 419–435. [Google Scholar] [CrossRef]
- Riggs, D.; Diefendorf, R. A phase diagram for pitches. Carbon 1980, 80, 326–329. [Google Scholar]
- Shishido, M.; Inomata, H.; Arai, K.; Saito, S. Application of liquid crystal theory to the estimation of mesophase pitch phase transition behavior. Carbon 1997, 35, 797–799. [Google Scholar] [CrossRef]
- Ragan, S.; Marsh, H. Science and technology of graphite manufacture. J. Mater. Sci. 1983, 18, 3161–3176. [Google Scholar] [CrossRef]
- Gray, G.W.; Winsor, P.A. Liquid Crystals & Plastic Crystals; Ellis Horwood Ltd.: Chichester, UK, 1974; Volume 1, p. 314. [Google Scholar]
- Zhang, W.; Andersson, J.T.; Räder, H.J.; Müllen, K. Molecular characterization of large polycyclic aromatic hydrocarbons in solid petroleum pitch and coal tar pitch by high resolution MALDI ToF MS and insights from ion mobility separation. Carbon 2015, 95, 672–680. [Google Scholar] [CrossRef]
- Lauzon-Gauthier, J. Multivariate Latent Variable Modelling of the Pre-Baked Anode Manufacturing Process Used in Alu-minum Smelting. Master’s Thesis, Laval University, Québec City, QC, Canada, 2011. [Google Scholar]
- Shoko, L.; Beukes, J.P.; Strydom, C.A.; Larsen, B.; Lindstad, L. Predicting the toluene-and quinoline insoluble contents of coal tar pitches used as binders in Söderberg electrodes. Int. J. Miner. Process. 2015, 144, 46–49. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, K.; Huo, X.; Xu, X. International Perspectives: Sources, Distribution, and Toxicity of Polycyclic Aromatic Hydrocarbons. J. Environ. Health 2011, 73, 22–25. [Google Scholar]
- Farant, J.-P.; Gariépy, M. Relationship between benzo [a] pyrene and individual polycyclic aromatic hydrocarbons in a Söderberg primary aluminum smelter. Am. Ind. Hyg. Assoc. J. 1998, 59, 758–765. [Google Scholar] [CrossRef]
- Zhou, Y.M.; Tian, L.; Xie, G.; Li, R.X.; Yu, X.H. A New Ecofriendly Cold Ramming Paste for the Aluminum Electrolysis Cell. In Advanced Materials Research; Trans Tech Publications Ltd.: Bäch, Switzerland, 2012. [Google Scholar] [CrossRef]
- Allard, B.; Paulus, R.; Billat, G. A new ramming paste with improved potlining working conditions. In Light Metals 2011; Springer: Cham, Switzerland, 2011; pp. 1091–1096. [Google Scholar]
- Ouzilleau, P.; Gheribi, A.E.; Erikson, G.; Lindberg, D.K.; Chartrand, P. A size-dependent thermodynamic model for coke crystallites: The carbon–hydrogen system up to 2500 K. Carbon 2015, 85, 99–118. [Google Scholar] [CrossRef]
- Hu, Y.; Hurt, R.H. Thermodynamics of carbonaceous mesophase: II. General theory for nonideal solutions. Carbon 2001, 39, 887–896. [Google Scholar] [CrossRef]
- Hosseini, M.S.; Chartrand, P. Thermodynamics and phase relationship of carbonaceous mesophase appearing during coal tar pitch carbonization. Fuel 2020, 275, 117899. [Google Scholar] [CrossRef]
- Hosseini, M.S.; Chartrand, P. Critical assessment of thermodynamic properties of important polycyclic aromatic hydrocarbon compounds (PAHs) in coal tar pitch at typical temperature ranges of the carbonization process. Calphad 2021, 74, 102278. [Google Scholar] [CrossRef]
- Bale, C.W.; Bélisle, E.; Chartrand, P.; Decterov, S.A.; Eriksson, G.; Hack, K.; Jung, I.-H.; Kang, Y.-B.; Melançon, J.; Pelton, A.D.; et al. FactSage thermochemical software and databases—Recent developments. Calphad 2009, 33, 295–311. [Google Scholar] [CrossRef]
- Bale, C.W.; Chartrand, P.; Degterov, S.A.; Eriksson, G.; Hack, K.; Mahfoud, R.B.; Melançon, J.; Pelton, A.D.; Petersen, S. FactSage thermochemical software and databases. Calphad 2002, 26, 189–228. [Google Scholar] [CrossRef]
- About Coal Tar and Polycyclic Aromatic Hydrocarbons (PAHs). Available online: http://www.truthaboutcoaltar.com/aboutcoaltar.html (accessed on 1 July 2020).
- Shoko, L. Effects of the Chemical Composition of Coal Tar Pitch on Dimensional Changes during Graphitization. Doctoral Thesis, North-West University, Potchefstroom, South Africa, 2014. [Google Scholar]
- Kuznetsov, P.N.; Kamenskiy, E.S.; Kuznetsova, L.I. Comparative study of the properties of the coal extractive and commercial pitches. Energy Fuels 2017, 31, 5402–5410. [Google Scholar] [CrossRef]
- Chamam, Y.; Kocaefe, D.; Kocaefe, Y.; Bhattacharyay, D.; Morais, B. Effect of heating rate during baking on the properties of carbon anodes used in aluminum industry. In Light Metals 2016; Springer: Cham, Switzerland, 2016; pp. 947–951. [Google Scholar]
- Fischer, W.K.; Keller, F.; Perruchoud, R.C.; Oderbolz, S. Baking parameters and the resulting anode quality. Light Metals 1993, 1993, 683–689. [Google Scholar]


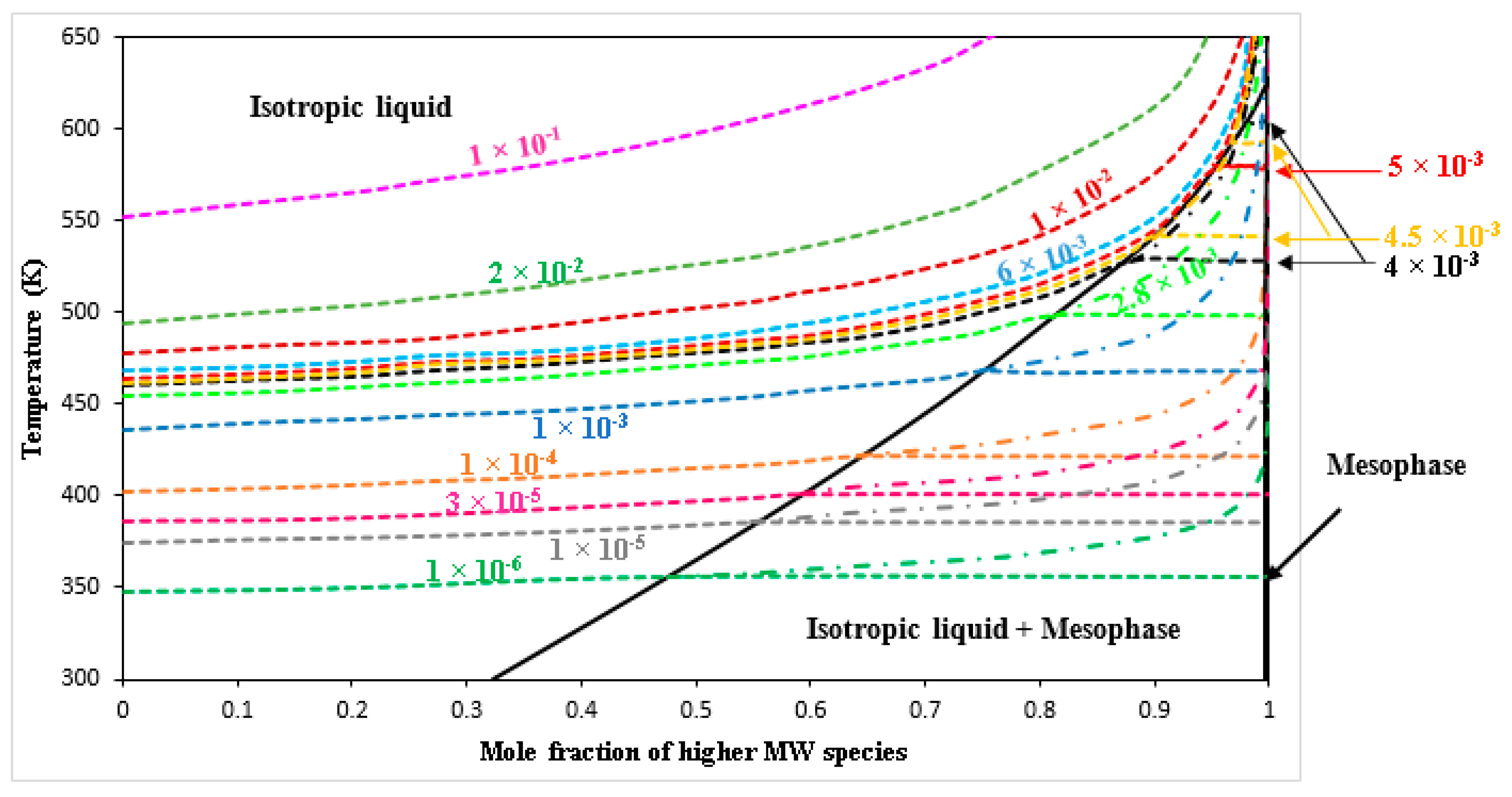
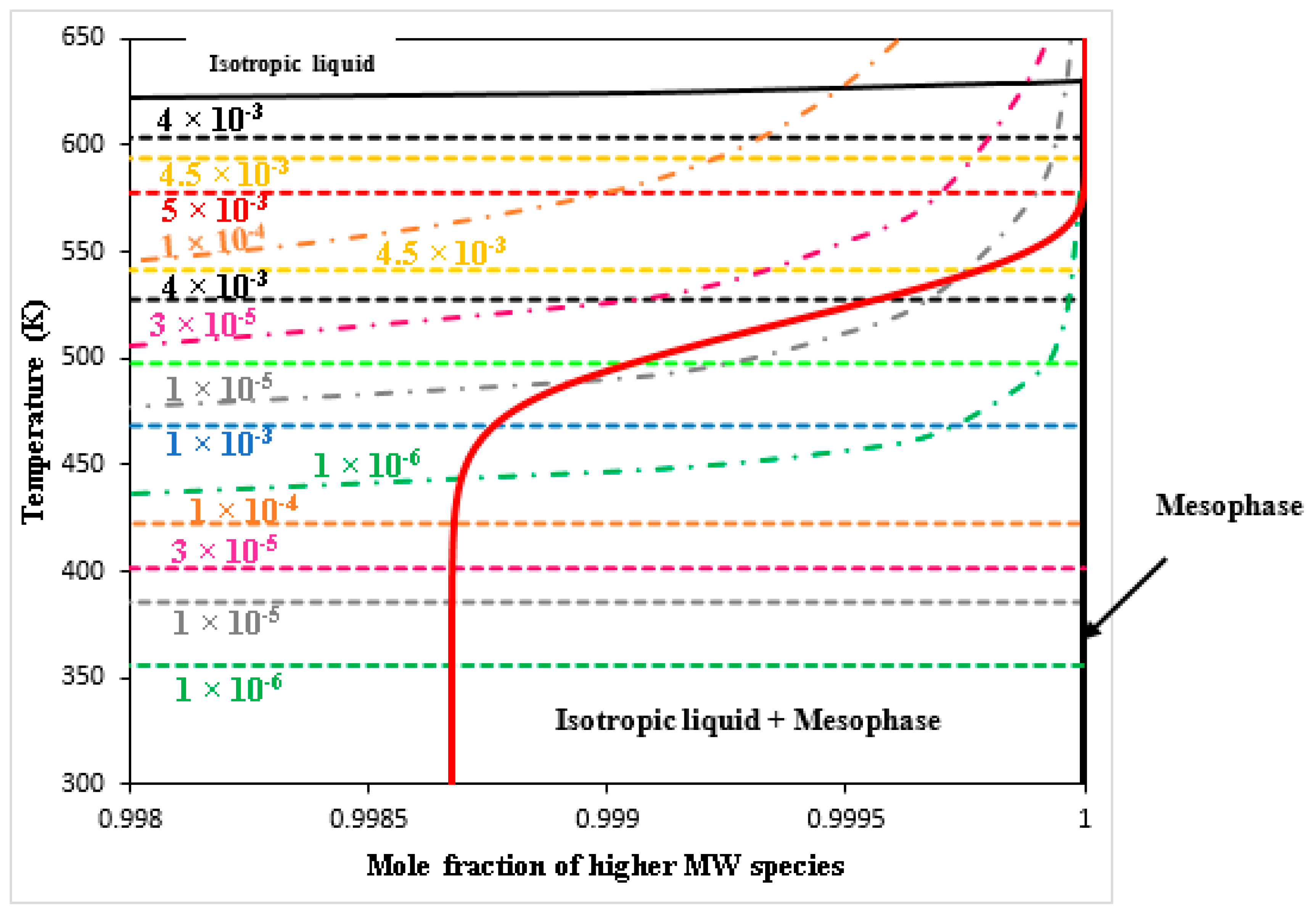

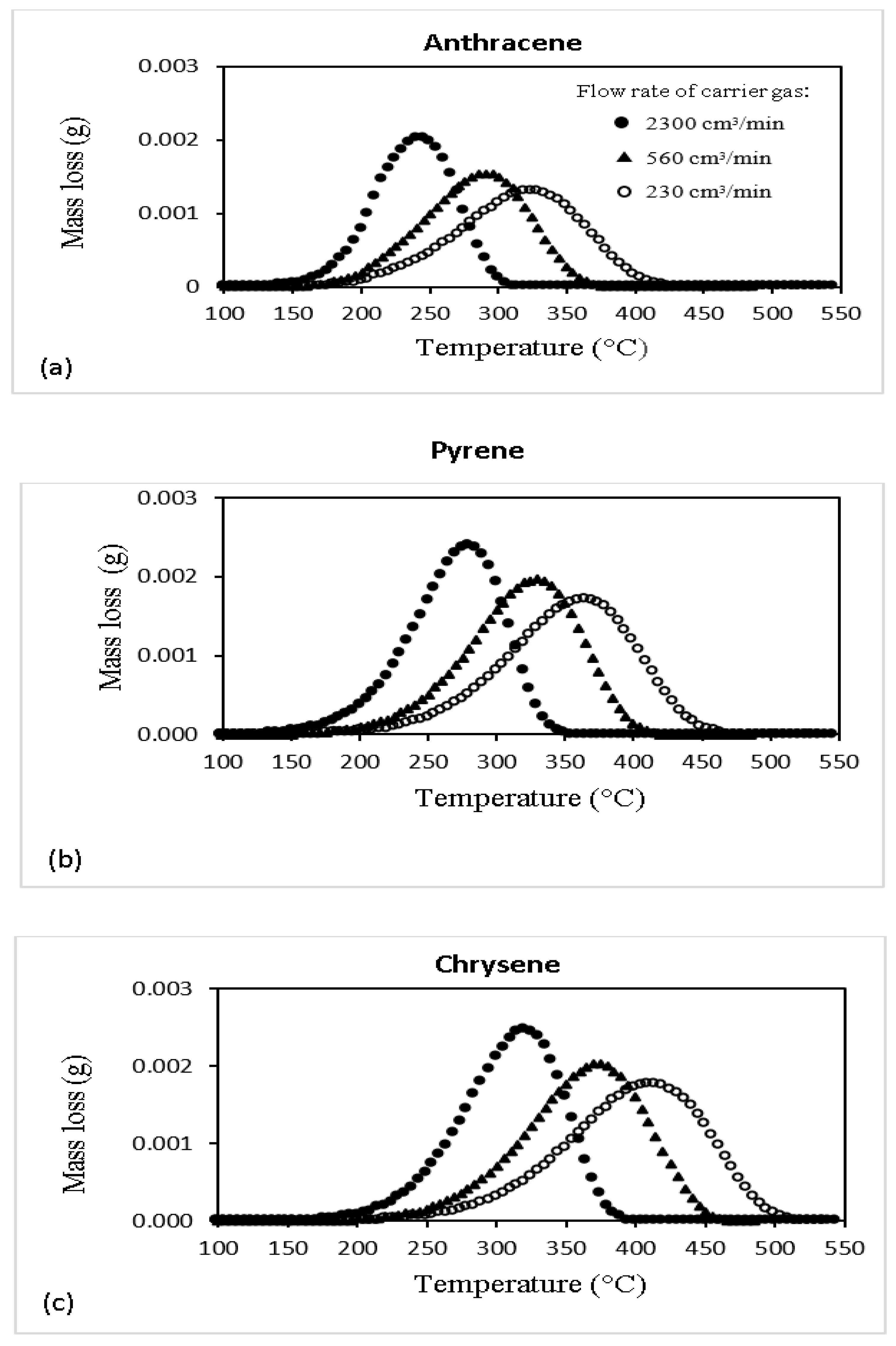

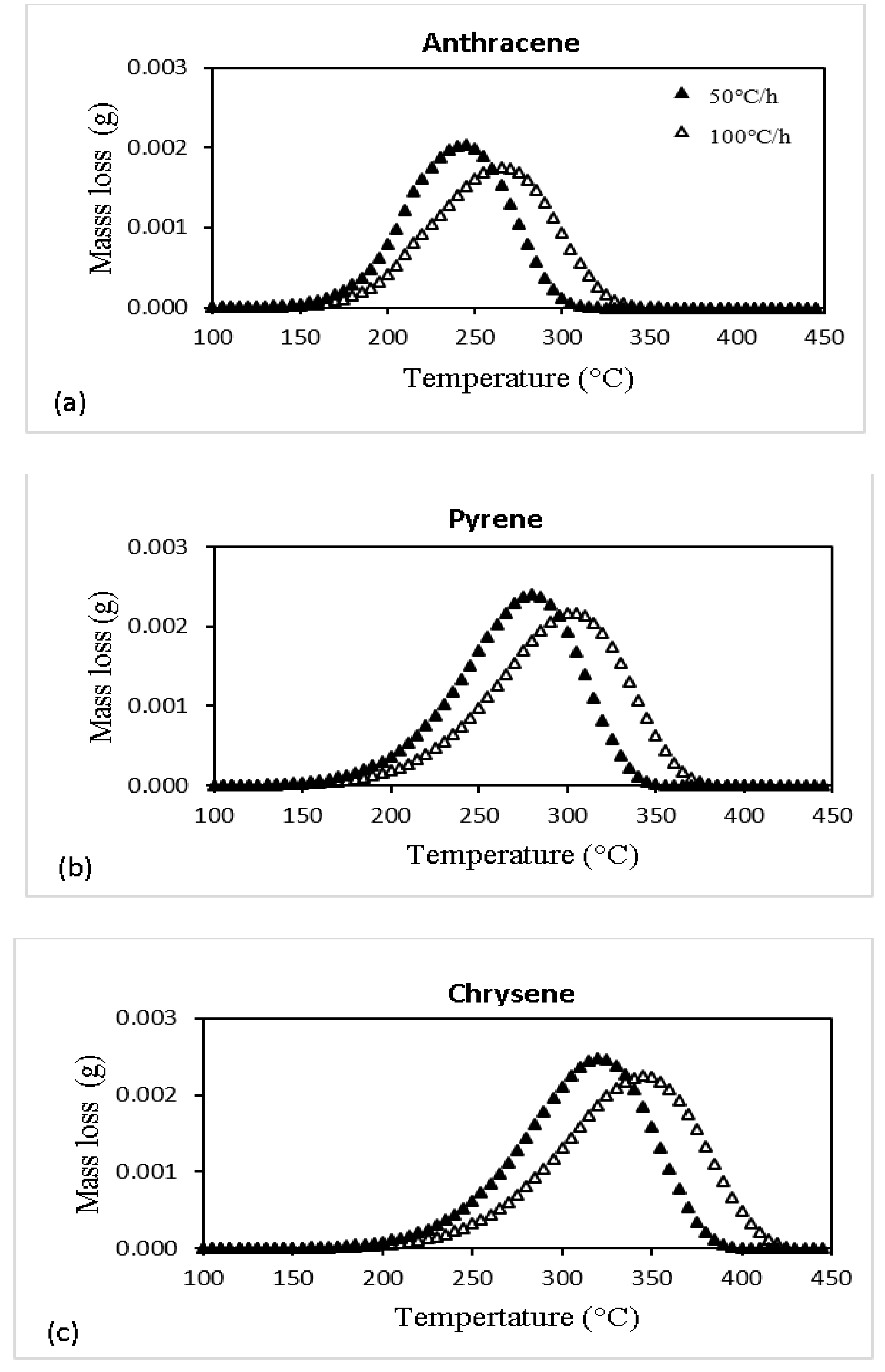
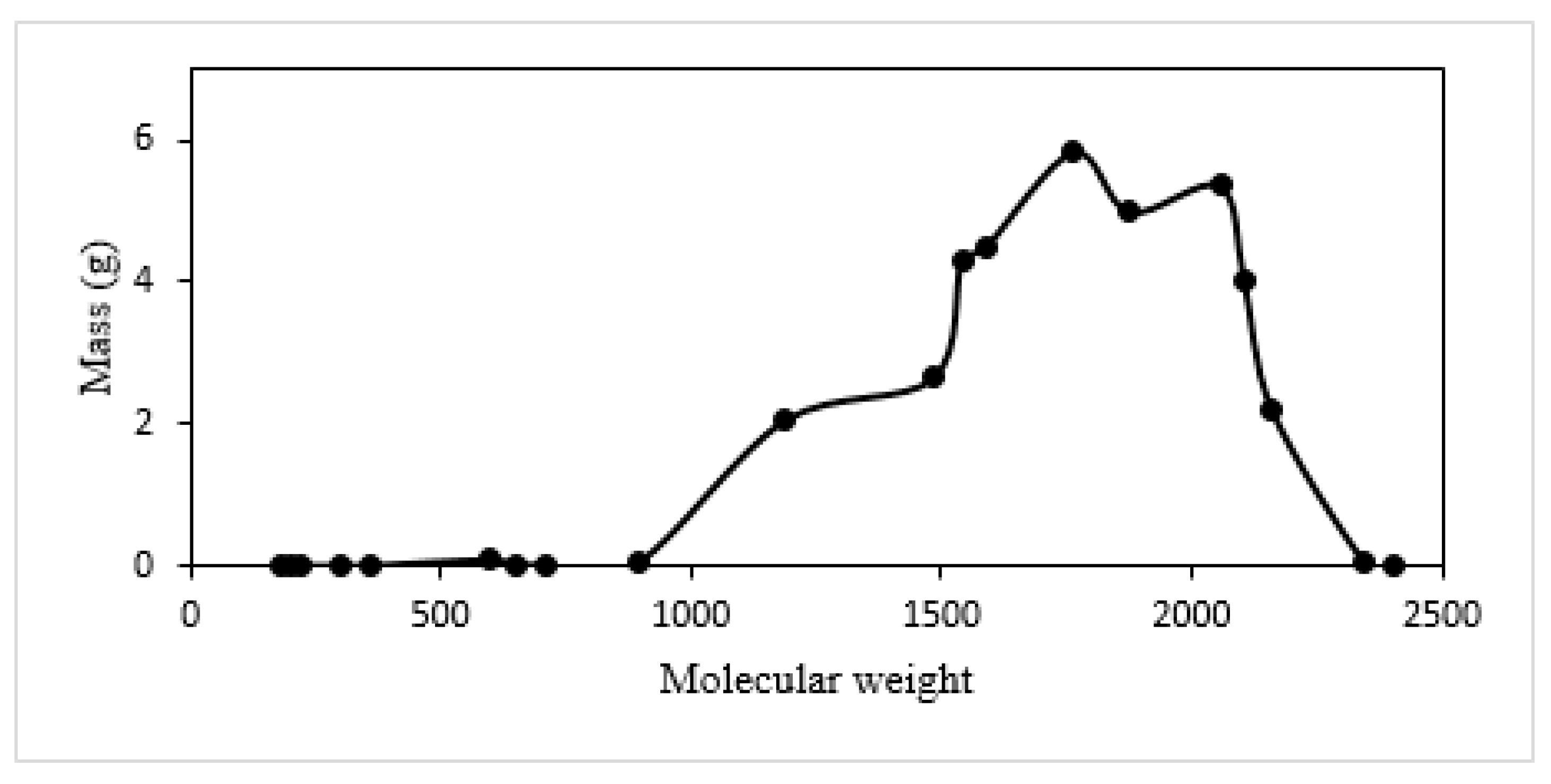
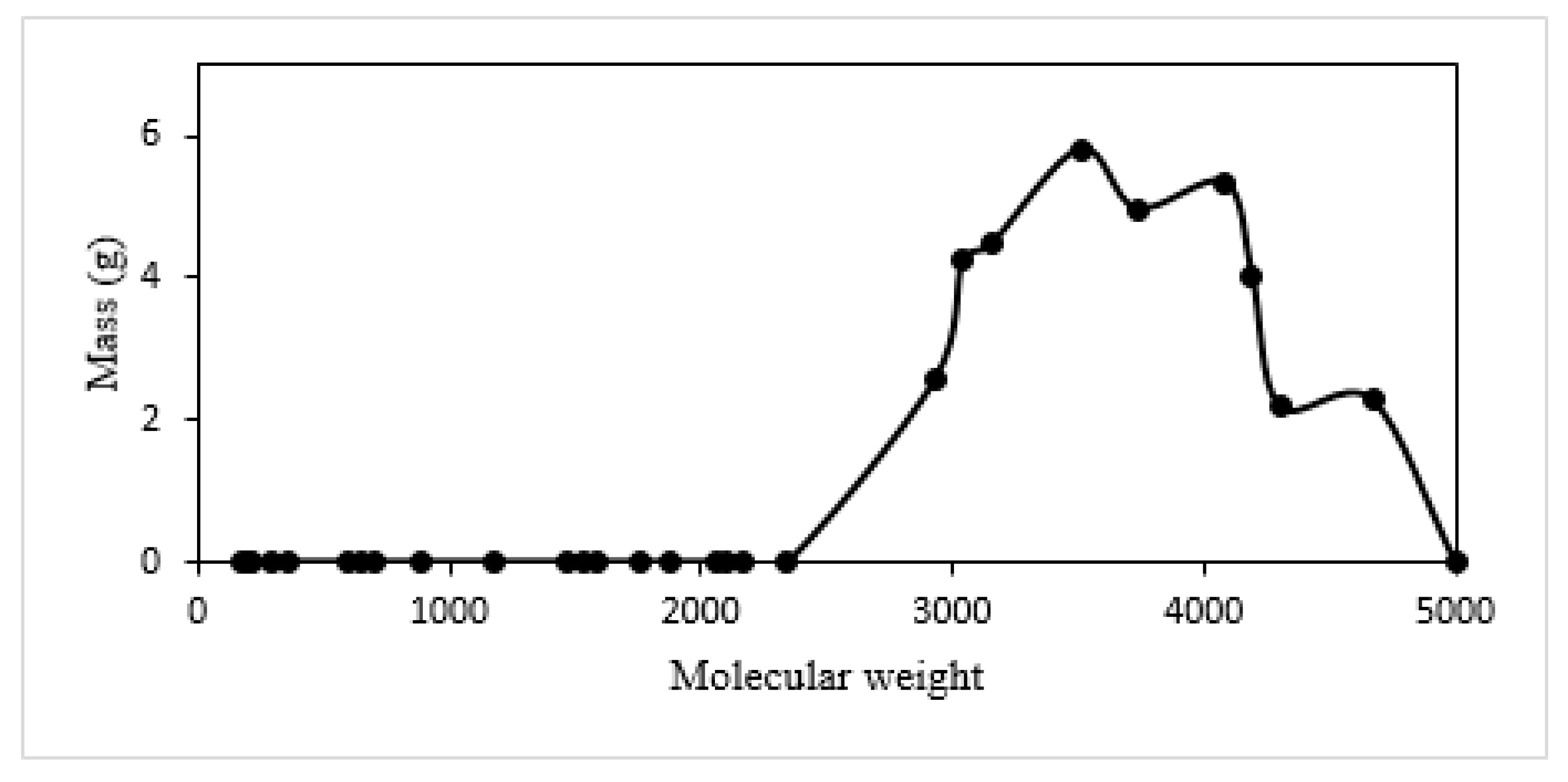
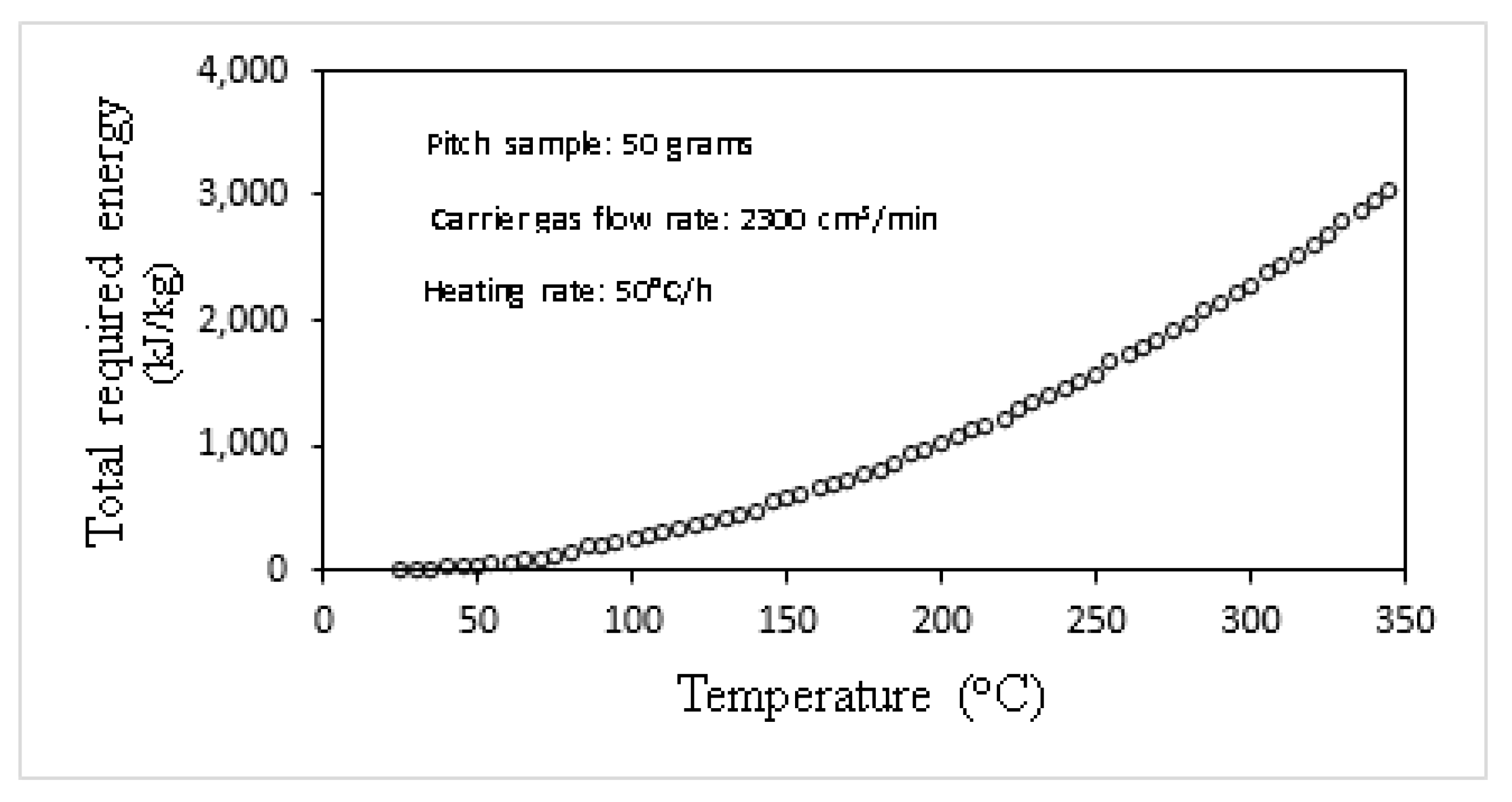
| Specie No. | Name | Chemical Formula | MW |
|---|---|---|---|
| 1 | Hydrogen | H2 | 2 |
| 2 | Methane | CH4 | 16 |
| 3 | Anthracene | C14H10 | 178 |
| 4 | Pyrene | C16H10 | 200 |
| 5 | Chrysene | C18H12 | 220 |
| 6 | Coronene | C24H12 | 300 |
| 7 | Tetra-methyl-coronene | C28H20 | 356 |
| 8 | Bi-coronene | C48H20 | 596 |
| 9 | Tri-coronene | C72H28 | 892 |
| 10 | Tetra-coronene | C96H36 | 1188 |
| 11 | Penta-coronene | C120H44 | 1484 |
| 12 | Penta.tmc * | C128H52 | 1588 |
| 13 | Hexa-coronene | C144H36 | 1764 |
| 14 | Hexa-tmc * | C152H52 | 1876 |
| 15 | Hepta-coronene | C168H36 | 2052 |
| 16 | Hepta-tmc * | C176H48 | 2160 |
| 17 | Octa-coronene | C192H40 | 2344 |
| 18 | Deca-coronene | C240H48 | 2928 |
| 19 | 12-coronene | C288H52 | 3508 |
| 20 | 12-tmc * | C304H84 | 3732 |
| 21 | 14-coronene | C336H52 | 4084 |
| 22 | 14-tmc * | C352H76 | 4300 |
| 23 | 16-coronene | C384H60 | 4668 |
| Reaction | Type of Reaction | Chemical Reaction |
|---|---|---|
| R1 | Oligomerization/Polymerization | 2C24H12 = C48H20 + 2H2 |
| R2 | Oligomerization/Polymerization | 3C24H12 = C72H28 + 4H2 |
| R3 | Oligomerization/Polymerization | 2C48H20 = C96H36 + 2H2 |
| R4 | Oligomerization/Polymerization | C24H12 + C48H20 = C72H28 + 2H2 |
| R5 | Oligomerization/Polymerization | C48H20 + C72H28 = C120H44 + 2H2 |
| R6 | Oligomerization/Polymerization | 2C28H20 = C56H36 + 2H2 |
| R7 | Oligomerization/Polymerization | C56H36 + C72H28 = C128H52 + 6H2 |
| R8 | Oligomerization/Polymerization | C56H36 + C72H28 = C120H52 + 6H2 |
| R9 | Cracking | C28H20 + 4H2 = C24H12 + 4CH4 |
| R10 | Cracking | C56H36 + 8H2 = C48H20 + 8CH4 |
| R11 | Cracking | C48H20 + 2H2 = 2C24H12 |
| R12 | Cracking | C56H36 + 2H2 = 2C28H20 |
| Reaction | Type of Reaction | Chemical Reaction |
|---|---|---|
| R1 | Oligomerization/Polymerization | 2C72H28 = C144H36 + 10H2 |
| R2 | Oligomerization/Polymerization | C48H20 + C96H36 = C144H36 + 6H2 |
| R3 | Oligomerization/Polymerization | C72H28 + C96H36 = C168H36 + 14H2 |
| R4 | Oligomerization/Polymerization | C56H36 + C96H36 = C152H52 + 10H2 |
| R5 | Oligomerization/Polymerization | C56H36 + C120H44 = C176H48 + 16H2 |
| R6 | Oligomerization/Polymerization | 2C96H36 = C192H40 + 16H2 |
| R7 | Oligomerization/Polymerization | 2C120H44 = C240H48 + 20H2 |
| R8 | Oligomerization/Polymerization | 2C144H36 = C288H52 + 10H2 |
| R9 | Oligomerization/Polymerization | 2C152H52 = C304H60 + 10H2 |
| R10 | Oligomerization/Polymerization | 2C168H36 = C336H52 + 10H2 |
| R11 | Oligomerization/Polymerization | 2C176H48 = C352H76 + 10H2 |
| R12 | Oligomerization/Polymerization | 2C192H40 = C384H60 + 10H2 |
| R13 | Cracking | C48H20 + 2H2 = 2C24H12 |
| R14 | Cracking | C56H36 + 2H2 = 2C28H20 |
| R15 | Cracking | C56H36 + 8H2 = C48H20 + 8CH4 |
| Temperature Range | |||
|---|---|---|---|
| 25–350 °C | 0, i = 1,2 , i = 3,4,…N | 0, i = 1,2 , i = 3,4,…N | 0, i = 1,2, and 8, 9,…N , i = 3,4,…,7 |
| 350–450 °C | 0, i = 1,2,…5 , i = 6,7,…N | 0, i = 1,2,…7 , i = 8,9,…N | 0, i = 8,9,…N , i = 1,2,…,7 |
| 450–550 °C | 0, i = 1, 2,…7 , i = 8,9,…N | 0, i = 1,2,…7 , i = 8,9,…N | 0, i = 8, 9,…N , i = 1,2,…,7 |
| Temperature Range | |||
|---|---|---|---|
| 25–350 °C | (i = 3,4,…N) | (i = 3,4,…N) | (i = 3,4,…,7) |
| 350–450 °C | (i = 6,7,…N) | (i = 8,9,…N) | (i = 1,2,…,7) |
| 450–550 °C | (i = 8,9,…N) | (i = 8,9,…N) | (i = 1,2,…,7) |
| Name | Chemical Formula | MW | Mass (g) |
|---|---|---|---|
| Anthracene | C14H10 | 178 | 0.03 |
| Pyrene | C16H10 | 200 | 0.04 |
| Chrysene | C18H12 | 220 | 0.044 |
| Coronene | C24H12 | 300 | 9 |
| Tetra-methyl-coronene | C28H20 | 356 | 27 |
| Bi-coronene | C48H20 | 596 | 10 |
| Tri-coronene | C72H28 | 892 | 3 |
| Tetra-coronene | C96H28 | 1180 | 0.886 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosseini, M.S.; Chartrand, P. Modeling the Coal Tar Pitch Primary Carbonization Process. Fuels 2022, 3, 698-729. https://doi.org/10.3390/fuels3040042
Hosseini MS, Chartrand P. Modeling the Coal Tar Pitch Primary Carbonization Process. Fuels. 2022; 3(4):698-729. https://doi.org/10.3390/fuels3040042
Chicago/Turabian StyleHosseini, Mahnaz Soltani, and Patrice Chartrand. 2022. "Modeling the Coal Tar Pitch Primary Carbonization Process" Fuels 3, no. 4: 698-729. https://doi.org/10.3390/fuels3040042
APA StyleHosseini, M. S., & Chartrand, P. (2022). Modeling the Coal Tar Pitch Primary Carbonization Process. Fuels, 3(4), 698-729. https://doi.org/10.3390/fuels3040042





