Symmetric Keys for Lightweight Encryption Algorithms Using a Pre–Trained VGG16 Model
Abstract
:1. Introduction
- Introduce a new method that leverages the pre–trained VGG16 approach for generating lengthy symmetric keys. Reduce the number of keys required for long inputs, resulting in a shorter time for key generation.
- The key length depends on the number of features in the two images.
- The proposed methodology offers flexibility in key generation by not restricting it to a specific type of image.
- Incorporating feature extraction into key generation increases randomness and unpredictability.
- By creating exceptionally long keys, it improves defenses against brute force attacks.
2. Theoretical Background
2.1. Symmetric Key
2.1.1. Advanced Encryption Standard (AES)
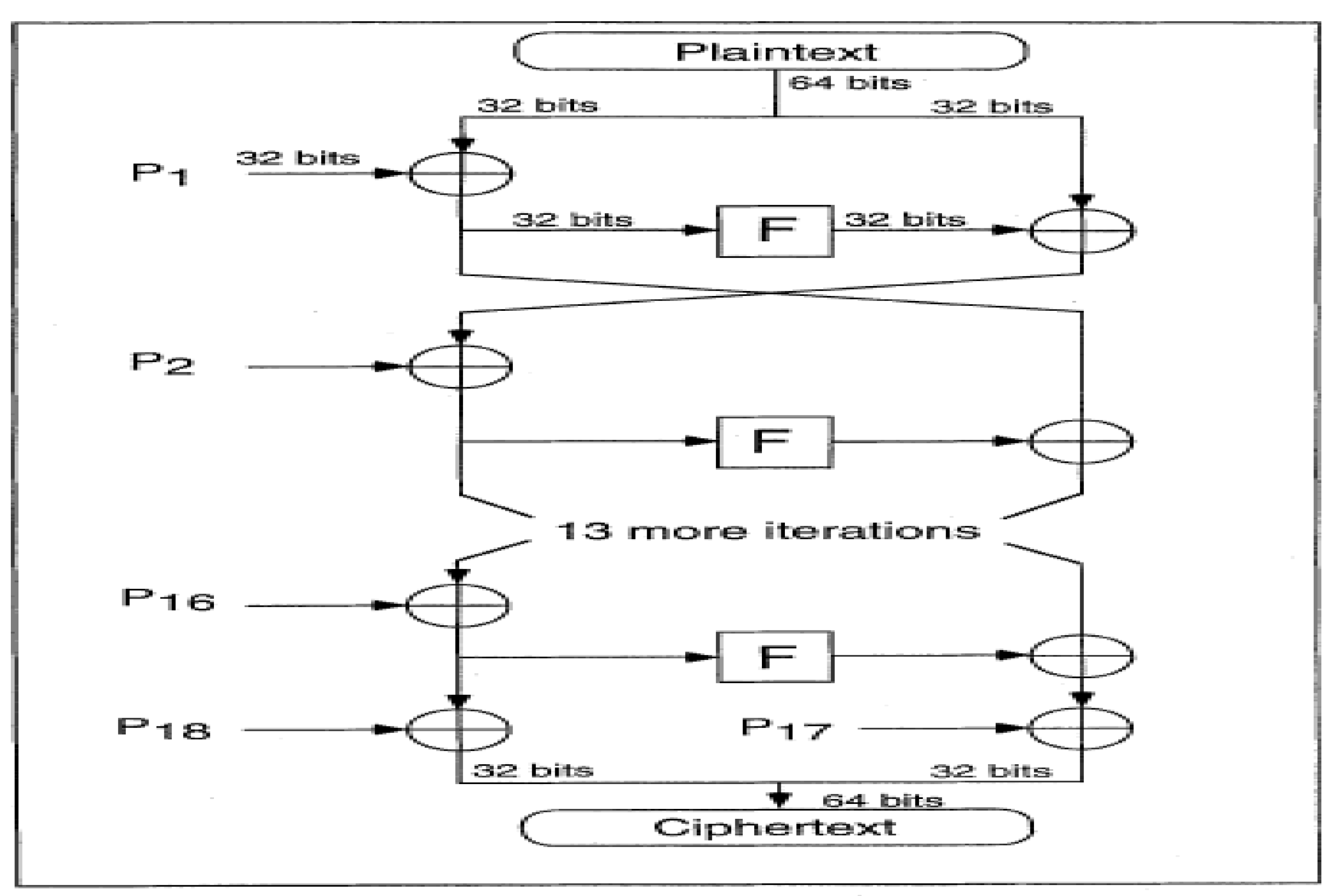
2.1.2. Data Encryption Standard (DES)
2.1.3. Blowfish
2.2. Transfer Learning
2.3. Feature Extraction Using VGG16 Architecture
- ✓
- The initial two convolutional layers contain 64 feature kernel filters, each sized at 3 × 3. Upon passing an RGB image input (with a depth of 3) through these layers, the dimensions transform to 224 × 224 × 64. Subsequently, the output undergoes a max pooling layer with a stride of 2.
- ✓
- Following are the third and fourth convolutional layers with 128 feature kernel filters, each also sized at 3 × 3. These layers are succeeded by a max pooling layer with a stride of 2, resulting in output dimensions of 56 × 56 × 128.
- ✓
- The fifth, sixth, and seventh layers are convolutional layers with 256 feature maps, each with a kernel size of 3 × 3. These layers are followed by a max pooling layer with a stride of 2.
- ✓
- The eighth through thirteenth layers are two sets of convolutional layers with 512 kernel filters, each with a size of 3 × 3. These layers are followed by a max pooling layer with a stride of 1.
- ✓
- The fourteenth and fifteenth layers are fully connected hidden layers with 4096 units each, followed by a softmax output layer (the sixteenth layer) with 1000 units.
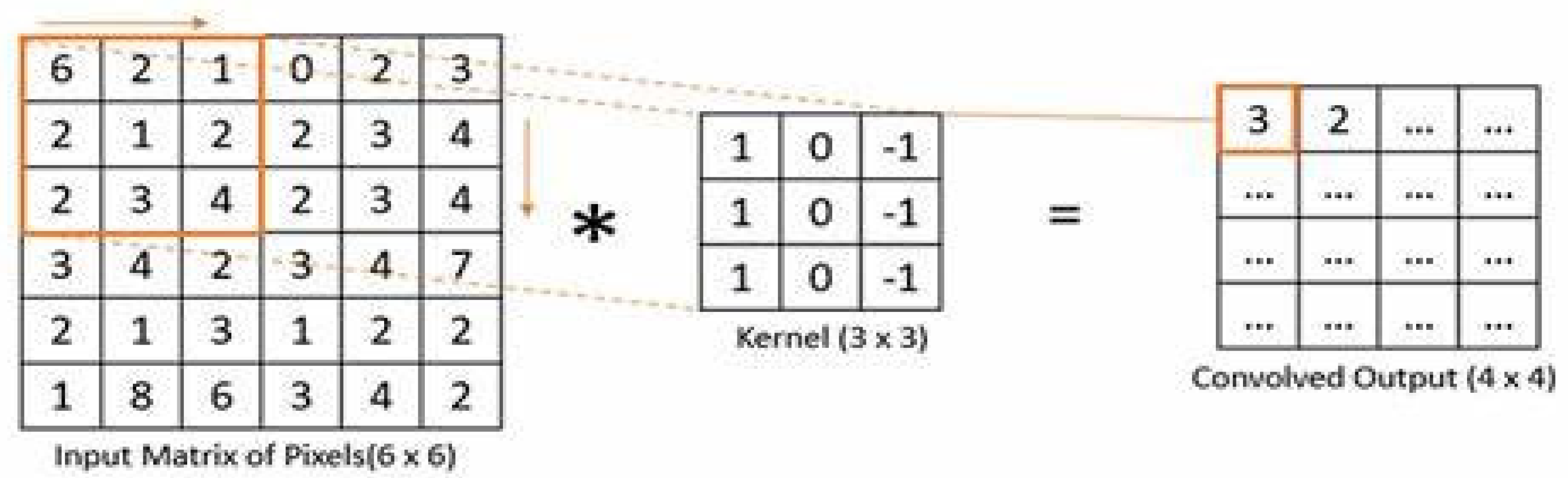
- Convolution layer: The convolutional layer process entails using a kernel matrix to generate a feature map from the input matrix, achieved through the mathematical operation of convolution [20]. This linear operation involves sliding the kernel matrix across the input matrix, performing element-wise matrix multiplication at each position, and accumulating the results onto the feature map, as shown in Figure 7 [21]. Convolution is widely utilized in various fields like image processing, statistics, and physics [22]. The calculation of the convoluted image follows this procedure:where I is a 2-dimensional image input, k is a 2-dimensional kernel filter, and S is a 2-dimensional output feature map.
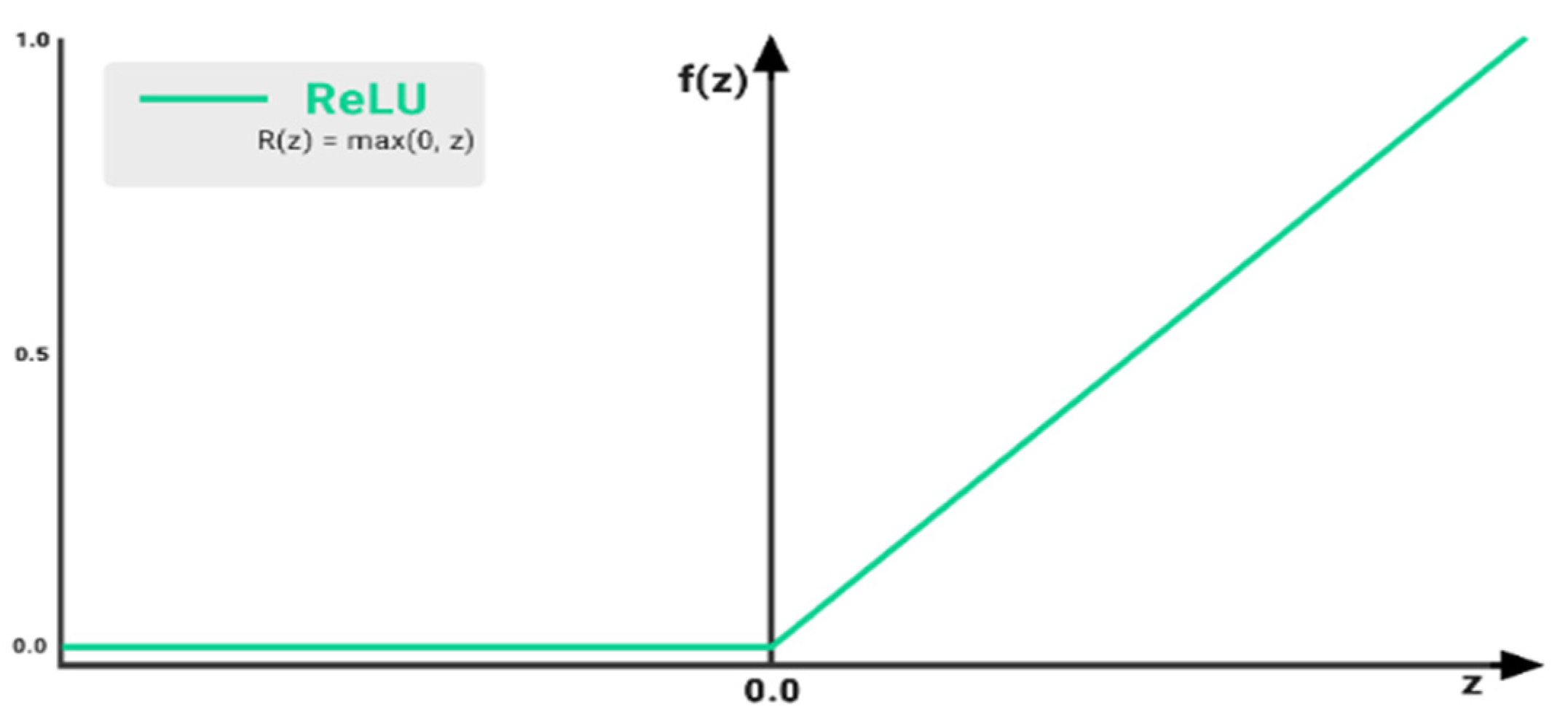
- Non-linear activation functions, such as the Rectified Linear Unit (ReLU), serve as nodes in a neural network that follow the convolutional layer. These functions are responsible for introducing nonlinearity to the input signal through a piecewise linear transformation. In the case of ReLU, the function outputs the input if it is positive and outputs zero if it is negative, as shown in Figure 8 [23].
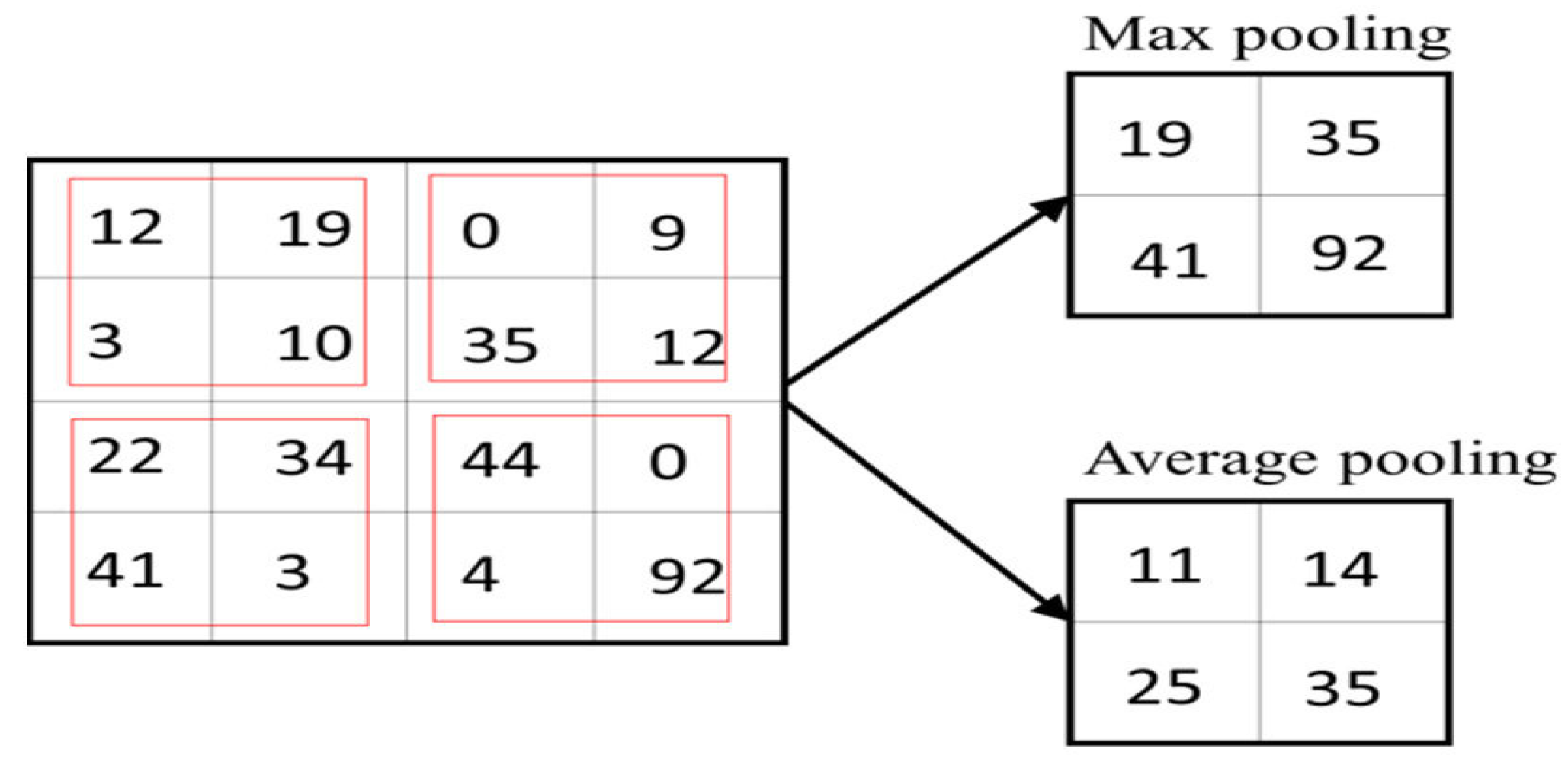
- Pooling layer: The convolutional layer’s feature map output is limited because it preserves the exact location of features in the input, making it sensitive to minor changes like cropping or rotation [24]. To address this issue, we can introduce down–sampling in the convolutional layers by adding a pooling layer after the nonlinearity layer [25]. This pooling helps to make the representation insensitive to small translations of the input, ensuring that most of the pooled outputs remain unchanged even with slight adjustments to the input [26]. The max-pooling unit extracts the maximum value from a set of four values, as illustrated in Figure 9. Average pooling is an alternative option for pooling layers [27].
3. The Proposed Method
| Algorithm 1. Symmetric Key Generation Using Pre–trained VGG16 |
| Input: Two images (randomly) Output: Symmetric key (binary) Begin
|
3.1. Example
- The user randomly chooses the first image

- The user randomly chooses the second image

- The features are extracted from the first image. The result appears as a 3D array since the image is in color, as shown below.
- The features are extracted from the second image. The result appears as a 3D array since the image is in color, as shown below.
- We eliminated all instances of 0.0 from the extracted features in the first image. The first image contains 2832 features, as shown below.
- We eliminated all instances of 0.0 from the extracted features in the second image. The second image contains 3644 features, as shown below.
- Remove decimal points from all the resulting features for the first image, then convert them into a binary string. The output is a binary string of 150,728 bits.
| Feature | Remove the Dot (.) | Convert to Binary |
| 6.903665065765381 | 6903665065765381 | 11000100001101101100011000111111001001010101000000101 |
| 34.10573196411133 | 3410573196411133 | 1100000111011110010111110011110110100100000011111101 |
| 67.41827392578125 | 6741827392578125 | 10111111100111010100000000010110111110010001001001101 |
| 31.747112274169922 | 31747112274169922 | 1110000110010011101010010010101101111110001000001000010 |
| 15.003043174743652 | 15003043174743652 | 110101010011010011000000110010111110101111111001100100 |
| … | … | … |
- Remove decimal points from all the resulting features for the second image, then convert them into a binary string. The output is a binary string of 193,752 bits.
| Feature | Remove the Dot (.) | Convert to Binary |
| 24.223085403442383 | 24223085403442383 | 1010110000011101100010010010000110101100000110011001111 |
| 10.136581420898438 | 10136581420898438 | 100100000000110010101011000110110101000101100010000110 |
| 9.996827125549316 | 9996827125549316 | 100011100001000000111110110001101100110000100100000100 |
| 43.26572036743164 | 4326572036743164 | 1111010111101111111010001101010110000101111111111100 |
| 9.374469757080078 | 9374469757080078 | 100001010011100000011111010011110101000001001000001110 |
| … | … | … |
- To equalize the two binary strings, truncate them to the length of the shorter one and perform an XOR operation between the binary string of the first image and the binary string of the second image. The output is a binary string of 150,728 bits, as shown below.
3.2. The Sensitivity of the Symmetric Key to Any Alterations Made to One of the Reference Images
| Base image | single bit in the base image is changed |
 |  |
- The features are extracted from the base image. The result appears as a 3D array since the image is in color, as shown below.
- The features are extracted from the base image after a single bit is changed. The result appears as a 3D array since the image is in color, as shown below.
4. Randomness Testing
4.1. Basic Five Statistical Tests
4.2. NIST SP 800-22 Statistical Test Suite
5. Symmetric Key Length
6. Time Complexity
7. Brute Force Attack
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abd Zaid, M.M.; Hassan, S. Proposal Framework to Lightweight Cryptography Primitives. Eng. Technol. J. 2022, 40, 516–526. [Google Scholar] [CrossRef]
- Khudhair, A.T.; Maolood, A.T. Towards Generating a New Strong key for AES Encryption Method Depending on 2D Henon Map. Diyala J. Pure Sci. 2019, 15, 53–69. [Google Scholar] [CrossRef]
- Jamil, A.S.; Azeez, R.A.; Hassan, N.F. An Image Feature Extraction to Generate a Key for Encryption in Cyber Security Medical Environments. Int. J. Online Biomed. Eng. 2023, 19, 93–106. [Google Scholar] [CrossRef]
- Khudhair, A.T.; Maolood, A.T. Towards Generating Robust Key Based on Neural Networks and Chaos Theory. Iraqi J. Sci. 2018, 59, 1518–1530. [Google Scholar] [CrossRef]
- Siddique, M.F.; Ahmad, Z.; Ullah, N.; Ullah, S.; Kim, J.-M. Pipeline Leak Detection: A Comprehensive Deep Learning Model Using CWT Image Analysis and an Optimized DBN-GA-LSSVM Framework. Sensors 2024, 24, 4009. [Google Scholar] [CrossRef]
- Alawi, A.R.; Hassan, N.F. A Proposal Video Encryption Using Light Stream Algorithm. Eng. Technol. J. 2021, 39, 184–196. [Google Scholar] [CrossRef]
- Stamp, M. Information Security Principles and Practice, 2nd ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Abd Aljabar, R.W.; Hassan, N.F. Encryption VoIP based on Generated Biometric Key for RC4 Algorithm. Eng. Technol. J. 2021, 39, 209–221. [Google Scholar] [CrossRef]
- Maolood, A.T.; Gbashi, E.K.; Mahmood, E.S. Novel lightweight video encryption method based on ChaCha20 stream cipher and hybrid chaotic map. Int. J. Electr. Comput. Eng. 2022, 12, 4988–5000. [Google Scholar] [CrossRef]
- Gbashi, E.K.; Maolood, A.T.; Jurn, Y.N. Privacy Security System for Video Data Transmission in Edge-Fog-cloud Environment. Int. J. Intell. Eng. Syst. 2023, 16, 307–318. [Google Scholar] [CrossRef]
- Khudhair, A.T.; Maolood, A.T.; Gbashi, E.K. Symmetry Analysis in Construction Two Dynamic Lightweight S-Boxes Based on the 2D Tinkerbell Map and the 2D Duffing Map. Symmetry 2024, 16, 872. [Google Scholar] [CrossRef]
- Raza, M.S.; Sheikh, M.N.A.; Hwang, I.-S.; Ab-Rahman, M.S. Feature-Selection-Based DDoS Attack Detection Using AI Algorithms. Telecom 2024, 5, 333–346. [Google Scholar] [CrossRef]
- Mewada, H. Extended Deep-Learning Network for Histopathological Image-Based Multiclass Breast Cancer Classification Using Residual Features. Symmetry 2024, 16, 507. [Google Scholar] [CrossRef]
- Keawin, C.; Innok, A.; Uthansakul, P. Optimization of Signal Detection Using Deep CNN in Ultra-Massive MIMO. Telecom 2024, 5, 280–295. [Google Scholar] [CrossRef]
- Sekhar, K.S.R.; Babu, T.R.; Prathibha, G.; Ming, K.V.L.C. Dermoscopic image classification using CNN with Handcrafted features. J. King Saud Univ.–Sci. 2021, 33, 101550. [Google Scholar] [CrossRef]
- Tammina, S. Transfer learning using VGG-16 with Deep Convolutional Neural Network for Classifying Images. Int. J. Sci. Res. Publ. 2019, 9, 143–150. [Google Scholar] [CrossRef]
- Peixoto, J.; Sousa, J.; Carvalho, R.; Santos, G.; Mendes, J.; Cardoso, R.; Reis, A. Development of an Analog Gauge Reading Solution Based on Computer Vision and Deep Learning for an IoT Application. Telecom 2022, 3, 564–580. [Google Scholar] [CrossRef]
- Rana, S.; Mondal, M.R.H.; Parvez, A.H.M.S. A New Key Generation Technique based on Neural Networks for Lightweight Block Ciphers. Int. J. Adv. Comput. Sci. Appl. 2021, 12, 208–216. [Google Scholar] [CrossRef]
- Alshehri, A.; AlSaeed, D. Breast Cancer Diagnosis in Thermography Using Pre-Trained VGG16 with Deep Attention Mechanisms. Symmetry 2023, 15, 582. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar] [CrossRef]
- Akhand, M.A.H.; Roy, S.; Siddique, N.; Kamal, M.A.S.; Shimamura, T. Facial Emotion Recognition Using Transfer Learning in the Deep CNN. Electronics 2021, 10, 1036. [Google Scholar] [CrossRef]
- Hashem, M.I.; Kuban, K.H. Key generation method from fingerprint image based on deep convolutional neural network model. Nexo Rev. Cient. 2023, 36, 906–925. [Google Scholar] [CrossRef]
- Jumaah, M.A.; Ali, Y.H.; Rashid, T.A.; Vimal, S. FOXANN: A Method for Boosting Neural Network Performance. Journal of Soft Comput. Comput. Appl. 2024, 1, 1001. [Google Scholar]
- Erkan, U.; Toktas, A.; Enginoğlu, S.; Enver Akbacak, E.; Dang, N.H.T. An image encryption scheme based on chaotic logarithmic map and key generation using deep CNN. Multimed. Tools Appl. 2022, 81, 7365–7391. [Google Scholar] [CrossRef]
- Patgiri, R. symKrypt: A Lightweight Symmetric-Key Cryptography for Diverse Applications. Comput. Inf. Sci. 2022, 1055, 1–30. [Google Scholar] [CrossRef]
- Socasi, F.Q.; Vera, L.Z.; Chang, O. A Deep Learning Approach for Symmetric-Key Cryptography System. In Proceedings of the Future Technologies Conference, Xi’an, China, 24–25 October 2020; pp. 539–552. [Google Scholar] [CrossRef]
- Wang, Y.; Bing, L.; Zhang, Y.; Jiaxin, W.; Qianya, M. A Secure Biometric Key Generation Mechanism via Deep Learning and Its Application. Appl. Sci. 2021, 11, 8497. [Google Scholar] [CrossRef]
- Kuznetsov, O.; Zakharov, D.; Frontoni, E. Deep learning-based biometric cryptographic key generation with post-quantum security. Multimed. Tools Appl. 2024, 83, 56909–56938. [Google Scholar] [CrossRef]






| Tests | Freedom Degree | 18,750,723 Bits | |
|---|---|---|---|
| Frequency Test | Must be <= 3.84 | Pass = 0.490 | |
| Run Test | T0 | Must be <= 32.386 | Pass = 23.280 |
| T1 | Must be <= 31.126 | Pass = 30.734 | |
| Poker Test | Must be <= 11.1 | Pass = 2.871 | |
| Serial Test | Must be <= 7.81 | Pass = 2.524 | |
| Auto Correlation Test | Shift No. 1 | Must be <= 3.84 | Pass = 0.559 |
| Shift No. 2 | Pass = 1.294 | ||
| Shift No. 3 | Pass = 1.023 | ||
| Shift No. 4 | Pass = 2.721 | ||
| Shift No. 5 | Pass = 1.906 | ||
| Shift No. 6 | Pass = 1.907 | ||
| Shift No. 7 | Pass = 0.457 | ||
| Shift No. 8 | Pass = 3.536 | ||
| Shift No. 9 | Pass = 1.010 | ||
| Shift No. 10 | Pass = 0.054 | ||
| Test Name | Assess: 387,840 | Assess: 387,840 | Assess: 435,671 | |||
|---|---|---|---|---|---|---|
| Number of Bits: 30 Bits | Number of Bits: 41 Bits | Number of Bits: 43 Bits | ||||
| p-Value | Pass Rate | p-Value | Pass Rate | p-Value | Pass Rate | |
| Frequency | 0.468595 | 29/30 | 0.559523 | 40/41 | 0.611108 | 43/43 |
| Block Frequency | 0.671779 | 30/30 | 0.460664 | 41/41 | 0.460664 | 43/43 |
| Cumulative Sums | 0.804337 | 30/30 | 0.811993 | 41/41 | 0.927083 | 42/43 |
| Runs | 0.671779 | 29/30 | 0.663130 | 40/41 | 0.764655 | 41/43 |
| Longest Run | 0.671779 | 29/30 | 0.258961 | 40/41 | 0.151616 | 42/43 |
| Rank | 0.602458 | 29/30 | 0.414525 | 39/41 | 0.559523 | 43/43 |
| Discrete Fourier Transform | 0.976060 | 30/30 | 0.663130 | 41/41 | 0.258961 | 43/43 |
| Non- Overlapping Templates | 0.999896 | 30/30 | 0.986869 | 41/41 | 0.953553 | 43/43 |
| Overlapping Templates | 0.602458 | 28/30 | 0.811993 | 39/41 | 0.811993 | 41/43 |
| Universal | 0.602458 | 30/30 | 0.227773 | 41/41 | 0.811993 | 43/43 |
| Approximate Entropy | 0.534146 | 30/30 | 0.460664 | 41/41 | 0.509162 | 43/43 |
| Random Excursions | 0.739918 | 20/20 | 0.534146 | 24/24 | 0.875539 | 23/23 |
| Random Excursions Variant | 0.991468 | 19/20 | 0.964295 | 24/24 | 0.941144 | 23/23 |
| Serial | 0.253551 | 30/30 | 0.764655 | 41/41 | 0.559523 | 43/43 |
| Linear Complexity | 0.213309 | 30/30 | 0.258961 | 41/41 | 0.371101 | 43/43 |
| Image 1 | Image 2 | Key Length in Bits |
|---|---|---|
 |  | 106,970 bits |
 |  | 148,424 bits |
 |  | 150,728 bits |
 |  | 157,597 bits |
| Cipher Name | Key Size (Bits) | Time | Basic Components | |
|---|---|---|---|---|
| AES | 128 | 0.053 | Key expansion from a master key | |
| DES | 56 | 0.152 | Key scheduling from a master key | |
| Blowfish | 32–448 | 0.054 | Key expansion from a master key | |
| Speck | 64 | 0.097 | Key expansion from a master key | |
| 128 | 0.130 | |||
| LBlock | 80 | 0.180 | derived from the original 80-bit master key | |
| Proposed method | Depending on the number of features | 106,970 | 0.3858 | Feature extraction by pre–trained VGG16 |
| 148,424 | 0.4016 | |||
| 150,728 | 0.4018 | |||
| 157,597 | 0.4171 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khudhair, A.T.; Maolood, A.T.; Gbashi, E.K. Symmetric Keys for Lightweight Encryption Algorithms Using a Pre–Trained VGG16 Model. Telecom 2024, 5, 892-906. https://doi.org/10.3390/telecom5030044
Khudhair AT, Maolood AT, Gbashi EK. Symmetric Keys for Lightweight Encryption Algorithms Using a Pre–Trained VGG16 Model. Telecom. 2024; 5(3):892-906. https://doi.org/10.3390/telecom5030044
Chicago/Turabian StyleKhudhair, Ala’a Talib, Abeer Tariq Maolood, and Ekhlas Khalaf Gbashi. 2024. "Symmetric Keys for Lightweight Encryption Algorithms Using a Pre–Trained VGG16 Model" Telecom 5, no. 3: 892-906. https://doi.org/10.3390/telecom5030044
APA StyleKhudhair, A. T., Maolood, A. T., & Gbashi, E. K. (2024). Symmetric Keys for Lightweight Encryption Algorithms Using a Pre–Trained VGG16 Model. Telecom, 5(3), 892-906. https://doi.org/10.3390/telecom5030044






