Assessment of the Current and Voltage Ripples of a Buck Converter as a Driver for LEDs Using a Non-Resistive Model
Abstract
:1. Introduction
2. Materials and Methods
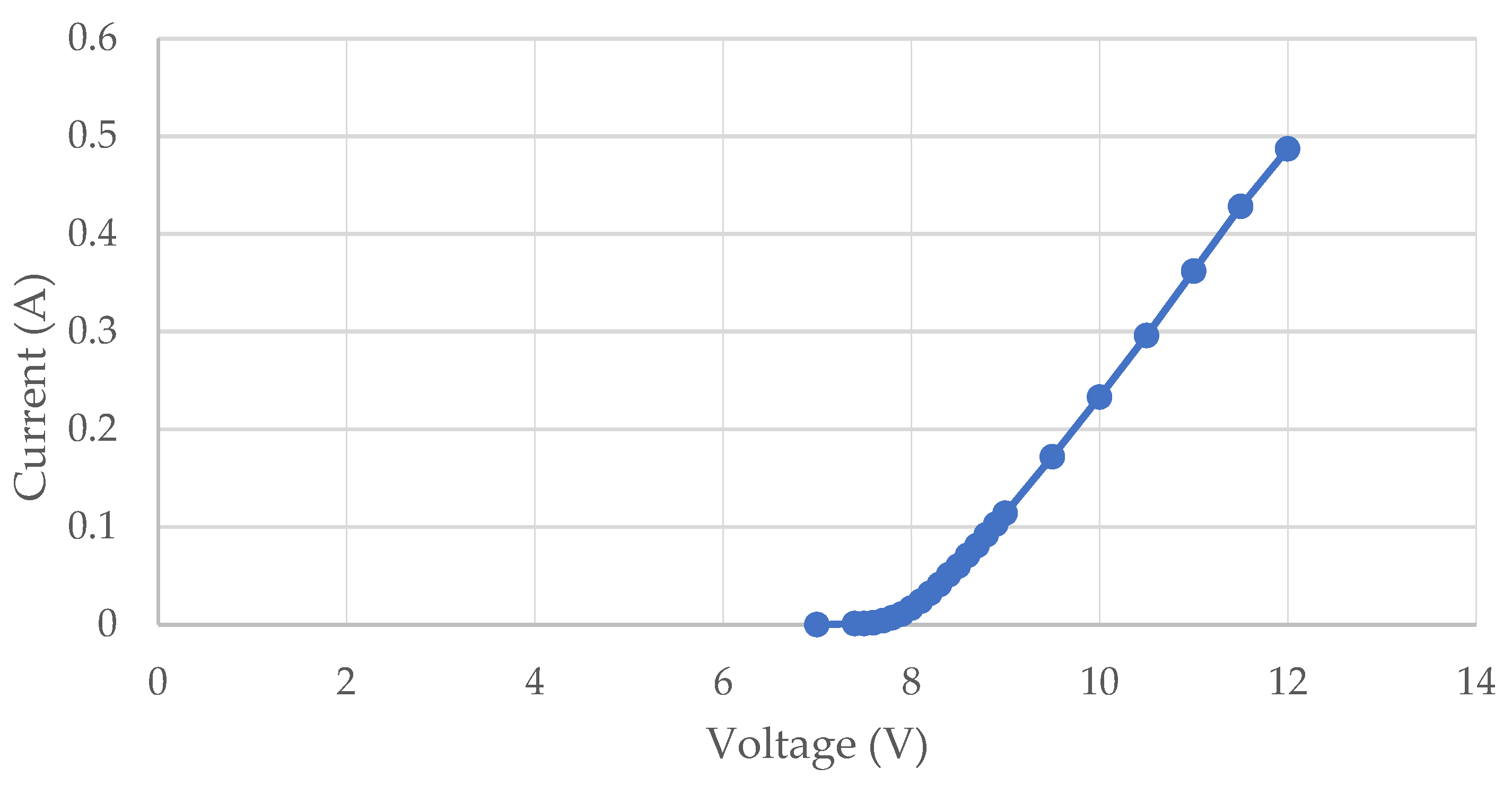
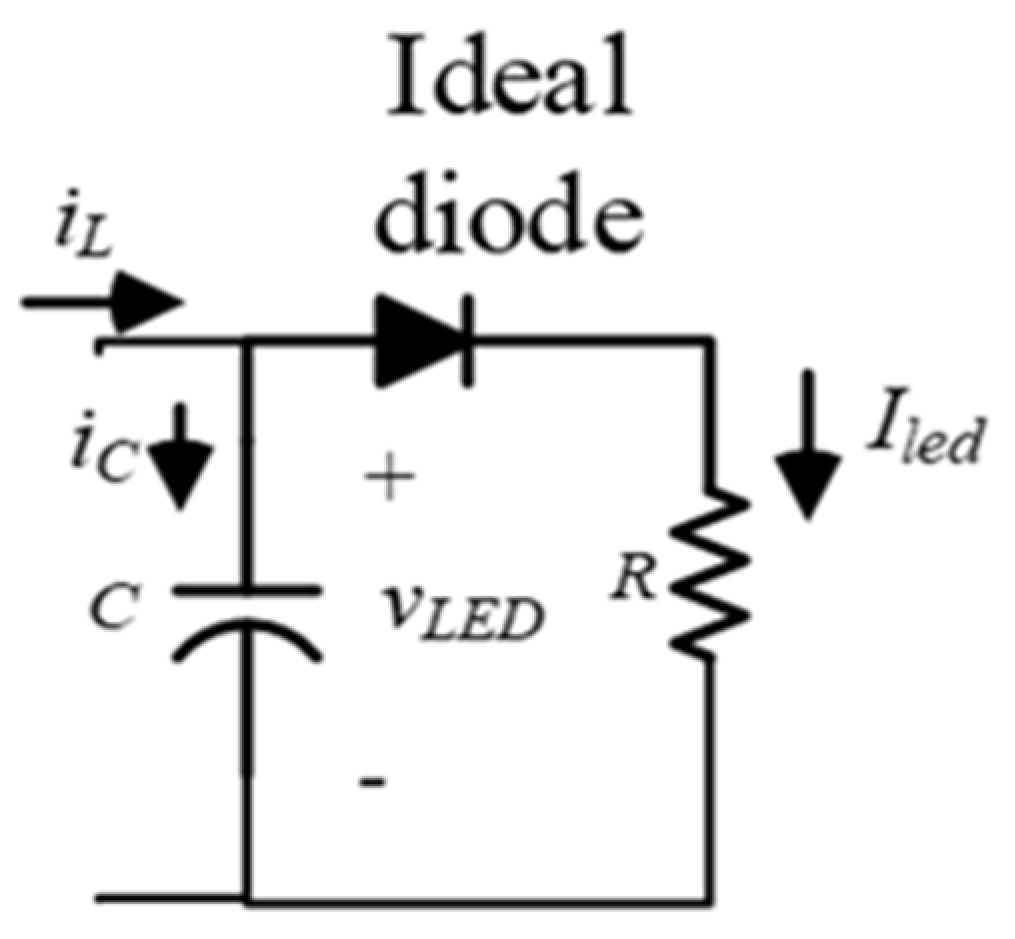
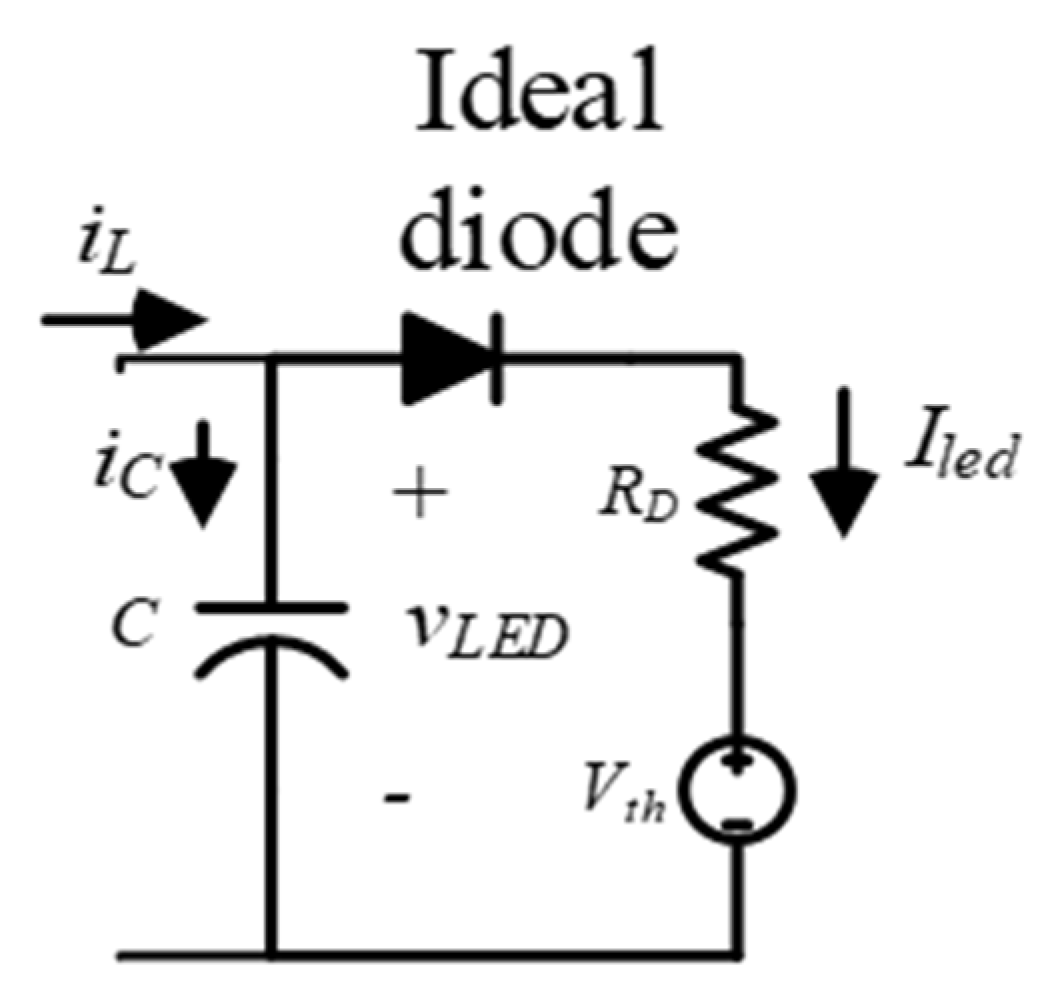
2.1. Model of a Load LED
2.2. LED Linear Modeling
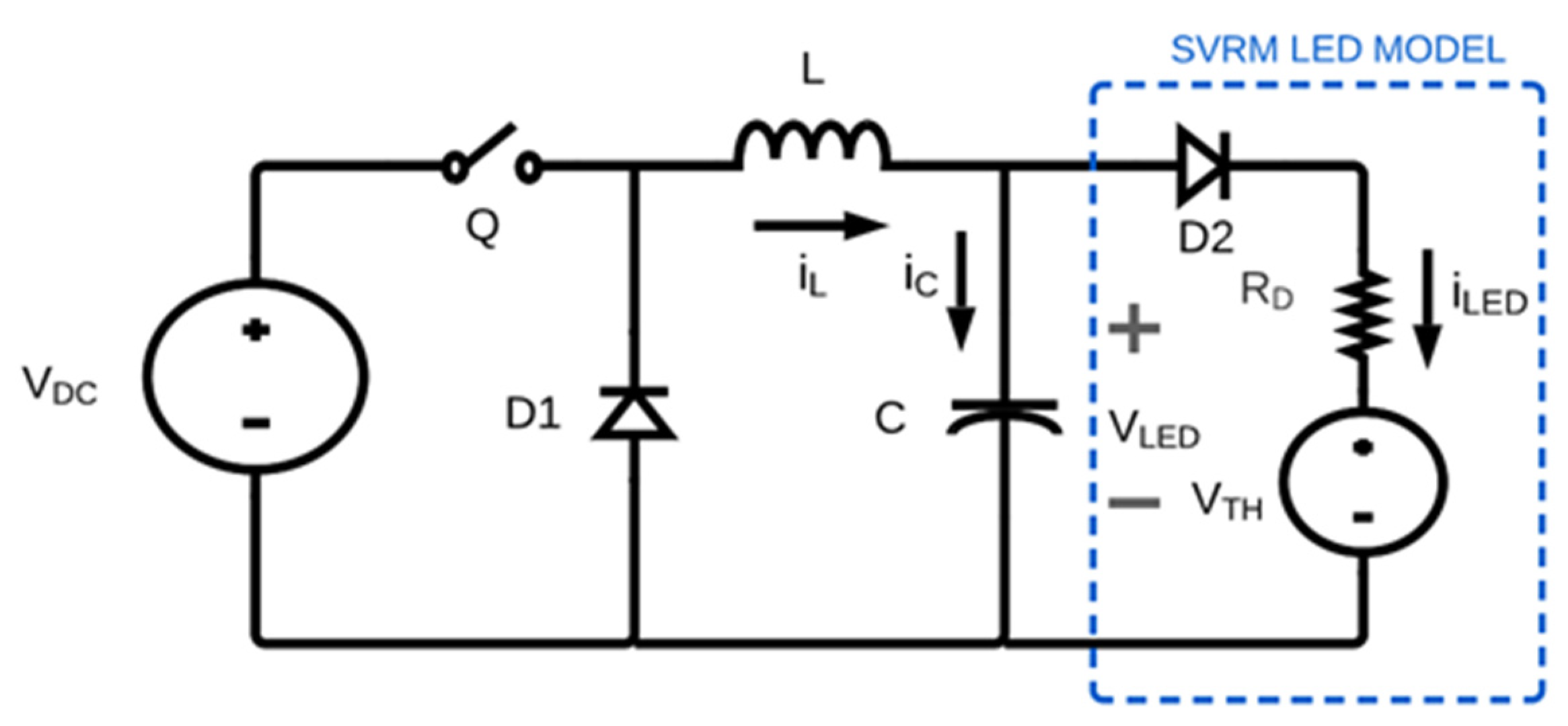
2.3. Analysis of the Equation for Buck Converter with LED Load
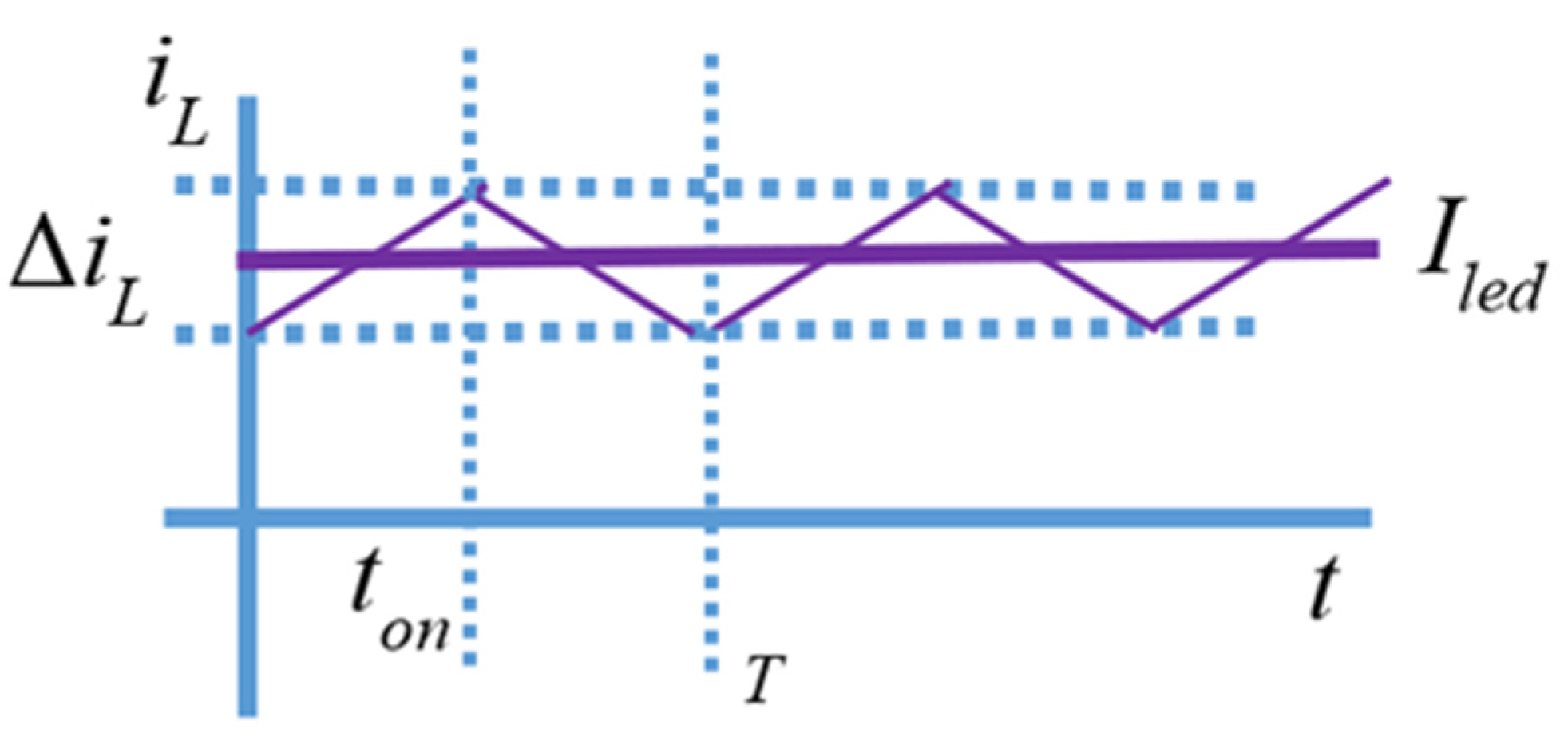
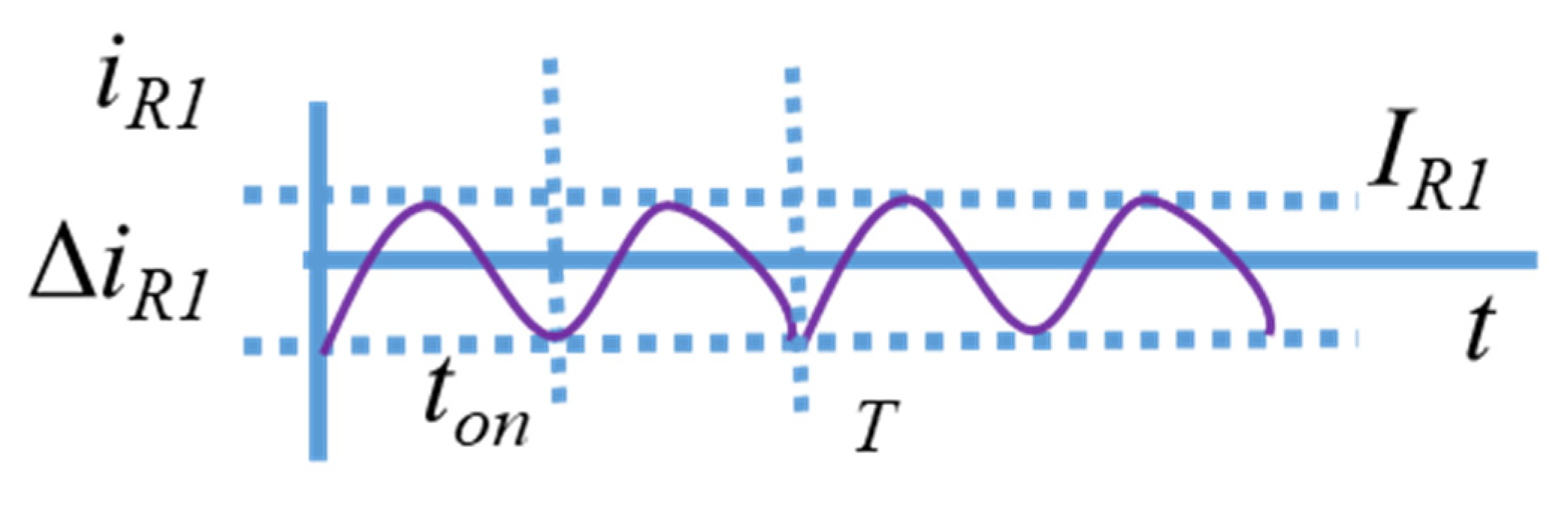
2.3.1. Inductor Equation Analysis
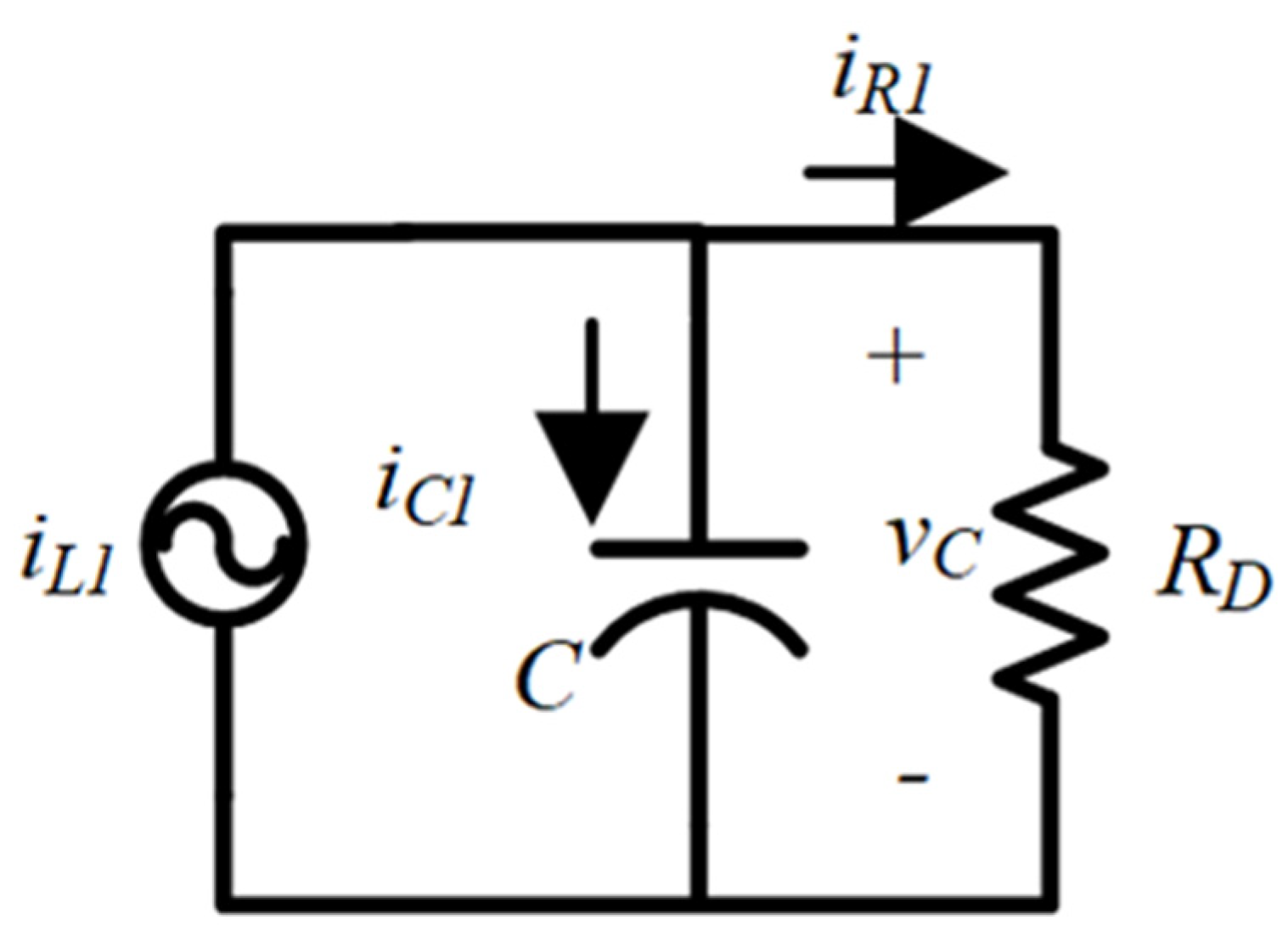
2.3.2. Capacitor Equation Analysis
2.3.3. Relationship between Voltage and Current Ripples in the LED
2.3.4. Component Selection from Conduction Losses
3. Results
3.1. Design Specifications
3.2. Equations for the Buck Converter
Relationship between Current Ripple and Voltage in the LED
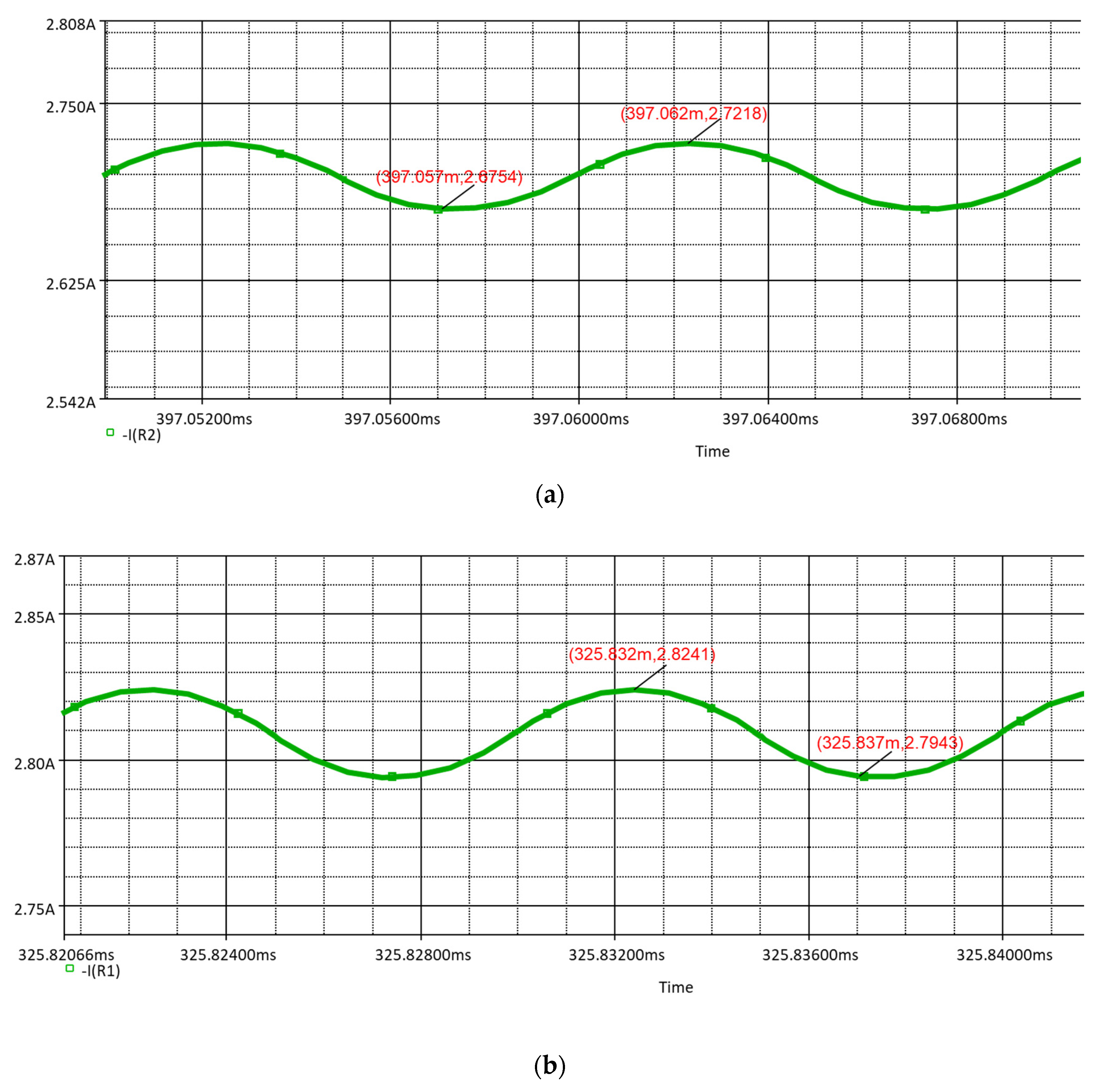
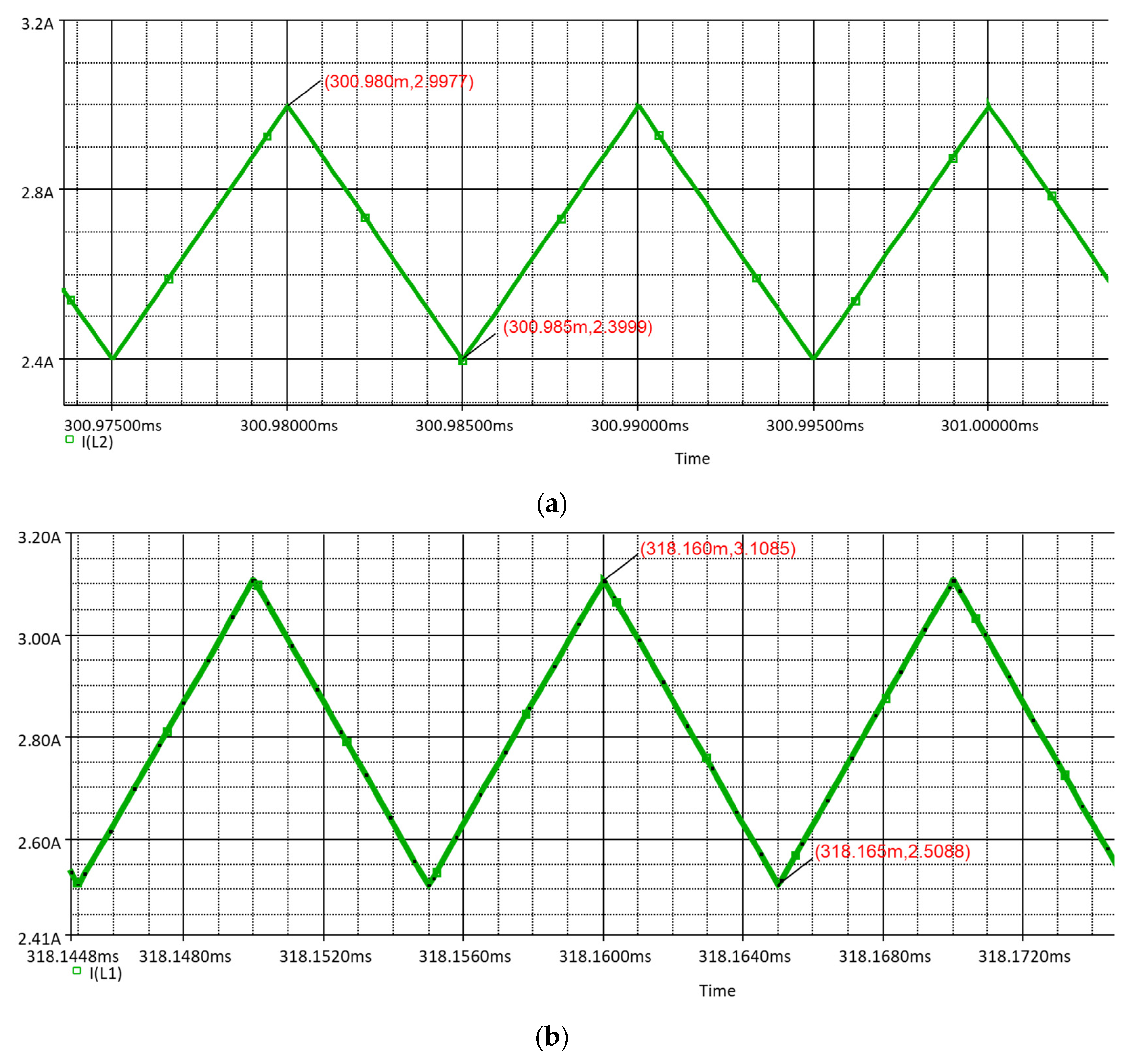
3.3. Circuit Analysis in PSPICE
4. Discussion
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Wang, S.; Ruan, X.; Yao, K.; Tan, S.C.; Yang, Y.; Ye, Z. A Flicker-Free Electrolytic Capacitor-Less AC–DC LED Driver. IEEE Trans. Power Electron. 2012, 27, 4540–4548. [Google Scholar] [CrossRef]
- Alonso, J.M.; Vina, J.; Vaquero, D.G.; Martinez, G.; Osorio, R. Analysis and Design of the Integrated Double Buck–Boost Converter as a High-Power-Factor Driver for Power-LED Lamps. IEEE Trans. Ind. Electron. 2012, 59, 1689–1697. [Google Scholar] [CrossRef]
- Pai, N.; Kini, S.G. Design and Prototyping of Dimmable LED Driver for General Lighting Application. In Proceedings of the 2018 Second International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 29–31 March 2018; pp. 1–6. [Google Scholar]
- Agrawal, A.; Jana, K.C.; Shrivastava, A. A review of different DC/DC converters for power quality improvement in LED lighting load. In Proceedings of the 2015 International Conference on Energy Economics and Environment (ICEEE), Greater Noida, India, 27–28 March 2015; pp. 1–6. [Google Scholar]
- Wang, Y.; Alonso, J.M.; Ruan, X. A Review of LED Drivers and Related Technologies. IEEE Trans. Ind. Electron. 2017, 64, 5754–5765. [Google Scholar] [CrossRef]
- Mrabet, B.M.; Chammam, A.; Nsibi, W. Constant-Current LEDs driver based on DC-DC buck converter with dimming capability. In Proceedings of the 2020 6th IEEE International Energy Conference (ENERGYCon), Gammarth, Tunisia, 28 September–1 October 2020; pp. 204–209. [Google Scholar]
- Papenfuss, F.; Timmermann, D. Alias-Free Periodic Signal Analysis using Efficient Rate Nonuniform Sampling Sets. In Proceedings of the 2007 IEEE International Conference on Acoustics, Speech and Signal Processing—ICASSP ‘07, Honolulu, HI, USA, 15–20 April 2007; Volume 3, pp. III-1497–III-1500. [Google Scholar]
- Saad, H.; Peralta, J.; Dennetière, S.; Mahseredjian, J.; Jatskevich, J.; Martinez, J.A.; Davoudi, A.; Saeedifard, M.; Sood, V.; Wang, X.; et al. Dynamic Averaged and Simplified Models for MMC-Based HVDC Transmission Systems. IEEE Trans. Power Deliv. 2013, 28, 1723–1730. [Google Scholar] [CrossRef]
- Cheng, C.-A.; Chang, C.-H.; Cheng, H.-L.; Chang, E.-C.; Chung, T.-Y.; Chang, M.-T. A Single-Stage LED Streetlight Driver with Soft-Switching and Interleaved PFC Features. Electronics 2019, 8, 911. [Google Scholar] [CrossRef]
- Abdelmlek, K.B.; Araoud, Z.; Canale, L.; Nejma, F.B.; Charrada, K.; Zissis, G. Thermal management of LEDs packages within inclined enclosures for lighting applications. In Proceedings of the 2021 IEEE Industry Applications Society Annual Meeting (IAS), Vancouver, BC, Canada, 10–14 October 2021; pp. 1–6. [Google Scholar]
- Salazar-Pérez, D.; Ponce-Silva, M.; Aqui, J.; García-Guzmán, J.; Pérez-Cruz, J. Effects of the LED modelling on the output capacitance of power converters. IET Power Electron. 2020, 13, 3467–3474. [Google Scholar] [CrossRef]
- Górecki, K.; Ptak, P. Modelling LED lamps in SPICE with thermal phenomena taken into account. Microelectron. Reliab. 2017, 79, 440–447. [Google Scholar] [CrossRef]
- Salazar-Pérez, D.; Ponce-Silva, M.; Alonso, J.M.; Aquí-Tapia, J.A.; Cortés-García, C. A Novel High-Power-Factor Electrolytic-Capacitorless LED Driver Based on Ripple Port. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 6248–6258. [Google Scholar] [CrossRef]
- Shockley, W. The theory of p-n junctions in semiconductors and p-n junction transistors. Bell Syst. Tech. J. 1949, 28, 435–489. [Google Scholar] [CrossRef]
- Lam, J.C.W.; Jain, P.K. A High Power Factor, Electrolytic Capacitor-Less AC-Input LED Driver Topology With High Frequency Pulsating Output Current. IEEE Trans. Power Electron. 2015, 30, 943–955. [Google Scholar] [CrossRef]
- Wang, B.; Ruan, X.; Yao, K.; Xu, M. A Method of Reducing the Peak-to-Average Ratio of LED Current for Electrolytic Capacitor-Less AC–DC Drivers. IEEE Trans. Power Electron. 2010, 25, 592–601. [Google Scholar] [CrossRef]
- Yan, L.; Chen, B. New developments in dimmable LED driver controllers. In Proceedings of the 2014 11th China International Forum on Solid State Lighting (SSLCHINA), Guangzhou, China, 6–8 November 2014; pp. 92–96. [Google Scholar]
- Ang, S.; Oliva, A. Power-Switching Converters, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]



| Parameter | Symbol | Value |
|---|---|---|
| Voltage on the LED | VLED | 12 V |
| Threshold Voltage | Vth | 9.1 V |
| LED Resistance | RD | 7.76 Ω |
| Power | P | 5.84 W |
| Switching frequency | 100 kHz | |
| Supply voltage | VDC | 24 V |
| Normalized voltage ripple | 0.01 | |
| Normalized current ripple | 0.2 |
| Parameter | Equation | Value |
|---|---|---|
| LED Current | ||
| LED Resistance | ||
| Duty Cycle | ||
| Inductor | ||
| Capacitor | ||
| The losses in transistor |
| Parameter | Resistive LED Model [18] | Value | SVRM Model | Value |
|---|---|---|---|---|
| Inductor | ||||
| Capacitor | ||||
| Resistor |
| Parameter | Resistive LED Model | SVRM Model |
|---|---|---|
| Output current | ||
| Ripple voltage | ||
| Ripple current | ||
| Ratio between voltage and current ripple |
| Value | Theoretical | Simulation | Error % |
|---|---|---|---|
| Vavg, V | 12 | 11.8 | 1.66% |
| IL, mA | 97.4 | 101.03 | 3.69% |
| % RiL | 20% | 20.73% | 0.73% |
| % RV LED | 1% | 0.8% | 0.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alvarado-Maldonado, R.C.; Ponce-Silva, M.; Olivar-Castellanos, G.S. Assessment of the Current and Voltage Ripples of a Buck Converter as a Driver for LEDs Using a Non-Resistive Model. Eng 2023, 4, 1377-1392. https://doi.org/10.3390/eng4020080
Alvarado-Maldonado RC, Ponce-Silva M, Olivar-Castellanos GS. Assessment of the Current and Voltage Ripples of a Buck Converter as a Driver for LEDs Using a Non-Resistive Model. Eng. 2023; 4(2):1377-1392. https://doi.org/10.3390/eng4020080
Chicago/Turabian StyleAlvarado-Maldonado, Roberto Carlos, Mario Ponce-Silva, and Gregorio Saúl Olivar-Castellanos. 2023. "Assessment of the Current and Voltage Ripples of a Buck Converter as a Driver for LEDs Using a Non-Resistive Model" Eng 4, no. 2: 1377-1392. https://doi.org/10.3390/eng4020080
APA StyleAlvarado-Maldonado, R. C., Ponce-Silva, M., & Olivar-Castellanos, G. S. (2023). Assessment of the Current and Voltage Ripples of a Buck Converter as a Driver for LEDs Using a Non-Resistive Model. Eng, 4(2), 1377-1392. https://doi.org/10.3390/eng4020080







