Gasification of Lignocellulosic Waste in Supercritical Water: Study of Thermodynamic Equilibrium as a Nonlinear Programming Problem
Abstract
:1. Introduction
2. Methodology
2.1. Thermodynamic Approach
2.1.1. Chemical and Phase Equilibrium Formulated as a Gibbs Energy Minimization Problem: Calculation of Isothermal Reactor
2.1.2. Chemical and Phase Equilibrium Formulated as an Entropy Maximization Problem: Calculation of an Adiabatic Reactor
2.2. Calculation of Fugacity Coefficients Using the Peng-Robinson Equation
2.3. Mathematical Formulation and Solution of the Equilibrium Problem
| Components | Tc (K) | Pc (bar) | Vc (m3/kmol) | ω | ∆Hf (cal/mol) | ∆Gf (cal/mol) |
|---|---|---|---|---|---|---|
| H2O | 647.14 | 220.64 | 0.056 | 0.344 | −5.78 × 104 | −5.46 × 104 |
| H2 | 32.98 | 12.93 | 0.064 | −0.217 | 0 | 0 |
| CH4 | 190.56 | 45.99 | 0.099 | 0.011 | −1.78 × 104 | −1.21 × 104 |
| CO2 | 304.15 | 73.74 | 0.094 | 0.225 | −9.41 × 104 | −9.43 × 104 |
| CO | 132.85 | 34.94 | 0.093 | 0.045 | −2.64 × 104 | −3.28 × 104 |
| O2 | 154.58 | 50.43 | 0.073 | 0.022 | 0 | 0 |
| N2 | 126.20 | 33.98 | 0.090 | 0.037 | 0 | 0 |
| CH4O | 512.64 | 80.97 | 0.118 | 0.565 | −4.80 × 104 | −3.88 × 104 |
| C2H6 | 305.32 | 48.72 | 0.146 | 0.099 | −2.00 × 104 | −7.61 × 103 |
| C3H8 | 369.83 | 42.48 | 0.200 | 0.152 | −2.50 × 104 | −5.81 × 103 |
| NH3 | 405.40 | 113.53 | 0.072 | 0.257 | −1.10 × 104 | −3.92 × 103 |
| C2H4 | 282.34 | 50.41 | 0.131 | 0.087 | 1.25 × 104 | 1.64 × 104 |
3. Results and Discussion
3.1. Methodology Validation
3.1.1. Methodology Validation for Isothermal Systems Using Gibbs Energy Minimization
3.1.2. Methodology Validation for Adiabatic Systems Using Entropy Maximization
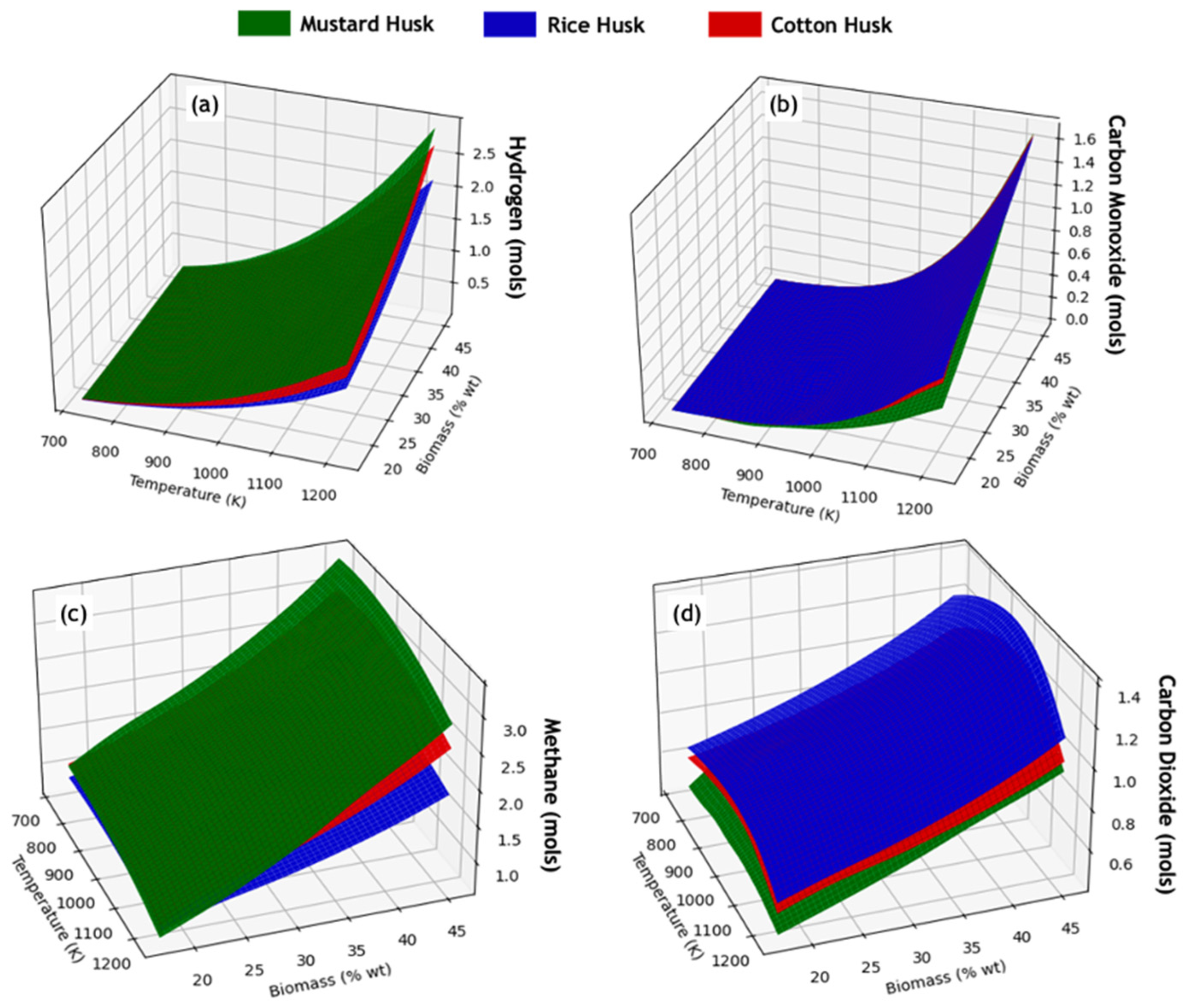
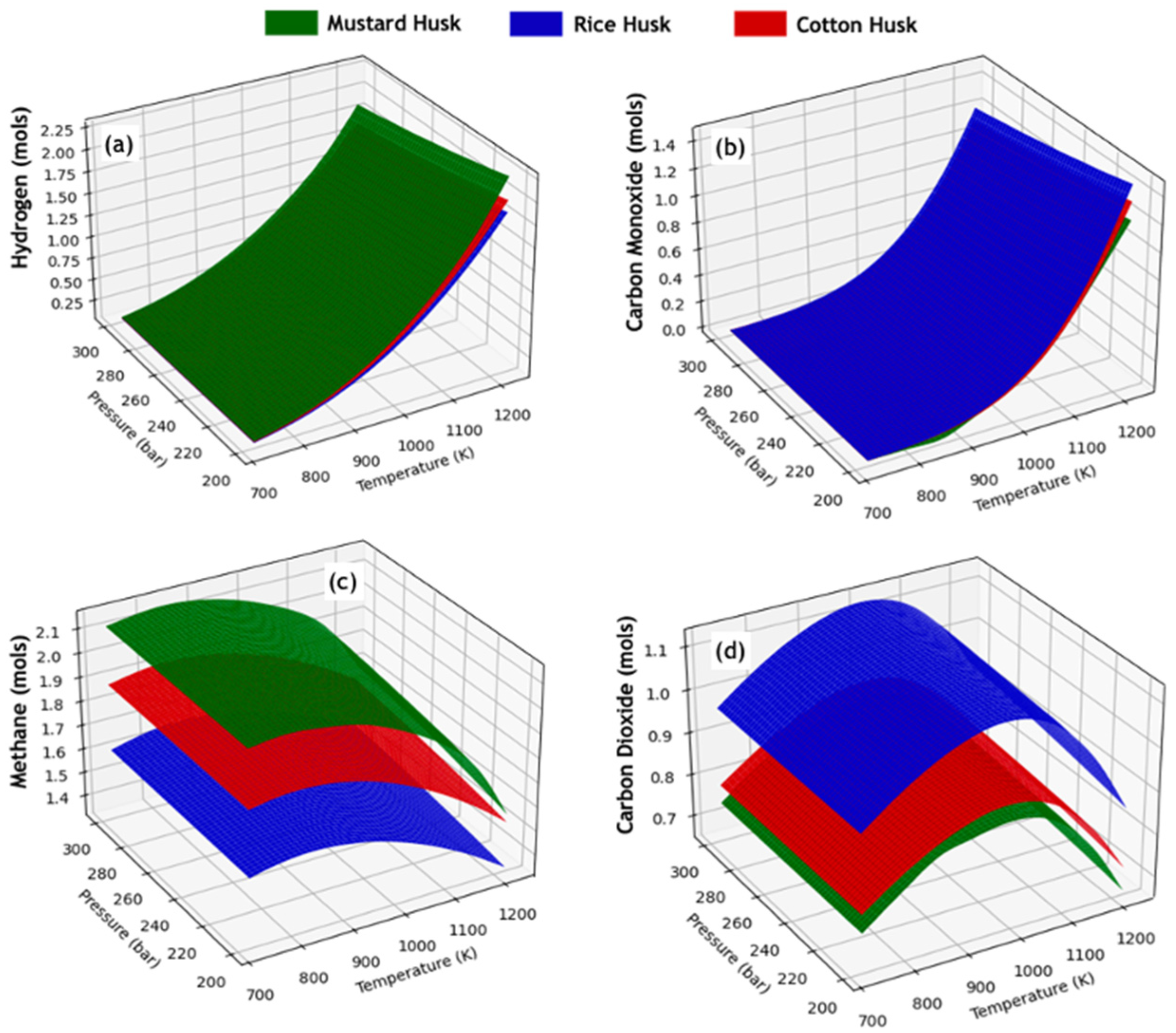
3.2. Study of Equilibrium Compositions of SCWG Processes of Lignocellulosic Waste
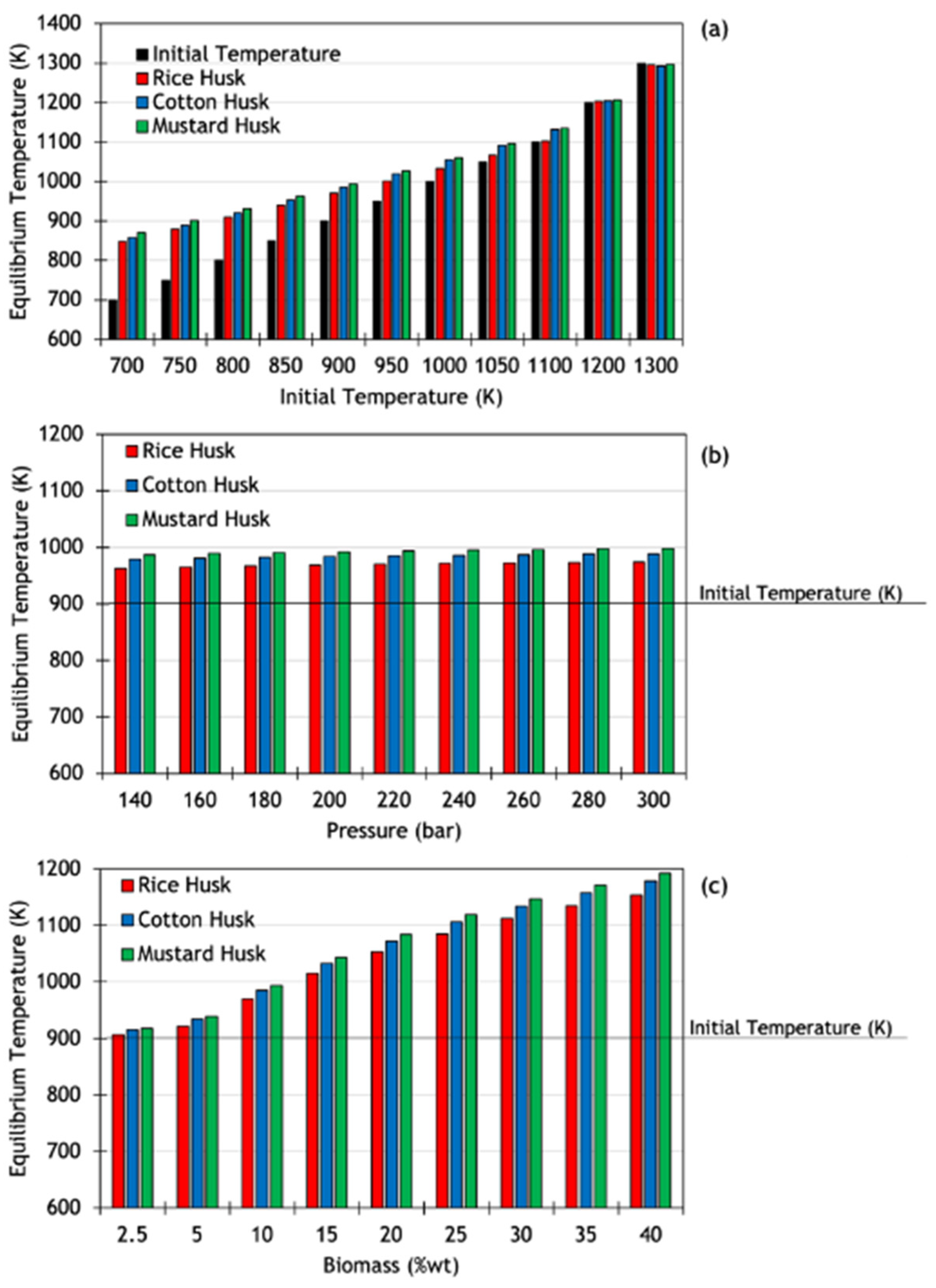
3.3. Thermal Behavior of SCWG Processes of Lignocellulosic Waste
4. Conclusions
5. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| G | Total Gibbs energy | P | Pressure |
| l | Liquid phase | n | Number of moles |
| s | Solid phase | NC | Number of components |
| v | Vapor phase | NF | Number of phases |
| NC | Number of components | T | Temperature |
| NF | Number of phases | R | Universal gas constant |
| Fugacity of component i in phase k | Number of atoms of element i in component m | ||
| Fugacity of pure species i in a standard reference state | Number of moles in standard state | ||
| Enthalpy of component i in phase k | H0 | Total enthalpy | |
| Enthalpy of component i in the standard state | Chemical potential of component i in a standard reference state | ||
| Mole fraction of component i in the vapor phase | Component saturation pressure i | ||
| Molar fraction of component i in the liquid phase | Zi | Compressibility factor | |
| am | Attraction parameter for mixtures | kij | Binary interaction parameter |
| bm | Repulsion parameter for mixtures | A, B, u, w | Parameters of the cubic equation of state |
| M | Constant for Kamath, Biegler, and Grossmann constraints | ||
| σk | Slack variables for Kamath, Biegler, and Grossmann constraints | ||
| Tc,I | Critical component temperature i | ||
| Pc,i | Critical component pressure i | ||
| wi | Acentric factor | ||
| Number of moles of component i in phase k; i = [1, 2, 3, …, NC]; k = [v, l, s] | |||
| µik | Chemical potential of component i in phase k; i = [1, 2, 3, …, NC]; k = [v, l, s] | ||
| Coefficient of fugacity of component i in phase k; i = [1, 2, 3, …, NC]; k = [v, l] | |||
References
- Dechamps, P. The IEA World Energy Outlook 2022—A brief analysis and implications. Eur. Energy Clim. J. 2023, 11, 100–103. [Google Scholar] [CrossRef]
- Virmond, E.; De Sena, R.F.; Albrecht, W.; Althoff, C.A.; Moreira, R.F.P.M.; José, H.J. Characterisation of agroindustrial solid residues as biofuels and potential application in thermochemical processes. Waste Manag. 2012, 32, 1952–1961. [Google Scholar] [CrossRef] [PubMed]
- Araújo, D.J.C.; Machado, A.V.; Vilarinho, M.C.L.G. Availability and Suitability of Agroindustrial Residues as Feedstock for Cellulose-Based Materials: Brazil Case Study. Waste Biomass Valorization 2019, 10, 2863–2878. [Google Scholar] [CrossRef]
- Saravanan, A.; Kumar, P.S.; Aron, N.S.M.; Jeevanantham, S.; Karishma, S.; Yaashikaa, P.R.; Chew, K.W.; Show, P.L. A review on bioconversion processes for hydrogen production from agro-industrial residues. Int. J. Hydrogen Energy 2022, 47, 37302–37320. [Google Scholar] [CrossRef]
- Khandelwal, K.; Nanda, S.; Boahene, P.; Dalai, A.K. Conversion of biomass into hydrogen by supercritical water gasification: A review. Environ. Chem. Lett. 2023, 21, 2619–2638. [Google Scholar] [CrossRef]
- Gomes, J.G.; Mitoura, J.; Guirardello, R. Thermodynamic analysis for hydrogen production from the reaction of subcritical and supercritical gasification of the C. vulgaris microalgae. Energy 2022, 260, 125030. [Google Scholar] [CrossRef]
- Osada, M.; Sato, T.; Watanabe, M.; Shirai, M.; Arai, K. Catalytic gasification of wood biomass in subcritical and supercritical water. Combust. Sci. Technol. 2006, 178, 537–552. [Google Scholar] [CrossRef]
- Guo, L.; Jin, H. Boiling coal in water: Hydrogen production and power generation system with zero net CO2 emission based on coal and supercritical water gasification. Int. J. Hydrogen Energy 2013, 38, 12953–12967. [Google Scholar] [CrossRef]
- Thiruvenkadam, S.; Izhar, S.; Yoshida, H.; Danquah, M.K.; Harun, R. Process application of Subcritical Water Extraction (SWE) for algal bio-products and biofuels production. Appl. Energy 2015, 154, 815–828. [Google Scholar] [CrossRef]
- Freitas, A.C.D.; Guirardello, R. Use of CO2 as a co-reactant to promote syngas production in supercritical water gasification of sugarcane bagasse. J. CO2 Util. 2015, 9, 66–73. [Google Scholar] [CrossRef]
- Mitoura dos Santos Junior, J.; Gomes, J.G.; de Freitas, A.C.D.; Guirardello, R. An Analysis of the Methane Cracking Process for CO2-Free Hydrogen Production Using Thermodynamic Methodologies. Methane 2022, 1, 243–261. [Google Scholar] [CrossRef]
- Freitas, A.C.D.; Guirardello, R. Comparison of several glycerol reforming methods for hydrogen and syngas production using Gibbs energy minimization. Int. J. Hydrogen Energy 2014, 39, 17969–17984. [Google Scholar] [CrossRef]
- Castello, D.; Fiori, L. Supercritical water gasification of biomass: Thermodynamic constraints. Bioresour. Technol. 2011, 102, 7574–7582. [Google Scholar] [CrossRef] [PubMed]
- Ciuffi, B.; Chiaramonti, D.; Rizzo, A.M.; Frediani, M.; Rosi, L. A critical review of SCWG in the context of available gasification technologies for plastic waste. Appl. Sci. 2020, 10, 6307. [Google Scholar] [CrossRef]
- Rossi, C.C.R.S.; Berezuk, M.E.; Cardozo-Filho, L.; Guirardello, R. Simultaneous calculation of chemical and phase equilibria using convexity analysis. Comput. Chem. Eng. 2011, 35, 1226–1237. [Google Scholar] [CrossRef]
- Sandler, S.I. Chemical, Biochemical, and Engineering Thermodynamics; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Barros, T.V.; Carregosa, J.D.; Wisniewski, A.W., Jr.; Freitas, A.C.; Guirardello, R.; Ferreira-Pinto, L.; Bonfim-Rocha, L.; Jegatheesan, V.; Cardozo-Filho, L. Assessment of black liquor hydrothermal treatment under sub- and supercritical conditions: Products distribution and economic perspectives. Chemosphere 2022, 286, 131774. [Google Scholar] [CrossRef] [PubMed]
- Louw, J.; Schwarz, C.E.; Knoetze, J.H.; Burger, A.J. Thermodynamic modelling of supercritical water gasification: Investigating the effect of biomass composition to aid in the selection of appropriate feedstock material. Bioresour. Technol. 2014, 174, 11–23. [Google Scholar] [CrossRef] [PubMed]
- Hantoko, D.; Yan, M.; Prabowo, B.; Susanto, H.; Li, X.; Chen, C. Aspen Plus Modeling Approach in Solid Waste Gasification. Current Developments in Biotechnology and Bioengineering; Elsevier: Amsterdam, The Netherlands, 2019; pp. 259–281. [Google Scholar] [CrossRef]
- Dowling, A.W.; Balwani, C.; Gao, Q.; Biegler, L.T. Optimization of sub-ambient separation systems with embedded cubic equation of state thermodynamic models and complementarity constraints. Comput. Chem. Eng. 2015, 81, 323–343. [Google Scholar] [CrossRef]
- Peng, D.-Y.; Robinson, D.B. A New Two-Constant Equation of State. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Kamath, R.S.; Biegler, L.T.; Grossmann, I.E. An equation-oriented approach for handling thermodynamics based on cubic equation of state in process optimization. Comput. Chem. Eng. 2010, 34, 2085–2096. [Google Scholar] [CrossRef]
- Tang, H.; Kitagawa, K. Supercritical water gasification of biomass: Thermodynamic analysis with direct Gibbs free energy minimization. Chem. Eng. J. 2005, 106, 261–267. [Google Scholar] [CrossRef]
- Basu, P.; Mettanant, V. Biomass Gasification in Supercritical Water—A Review. Int. J. Chem. React. Eng. 2009, 7. [Google Scholar] [CrossRef]
- Kang, Q.; Appels, L.; Tan, T.; Dewil, R. Bioethanol from Lignocellulosic Biomass: Current Findings Determine Research Priorities. Sci. World J. 2014, 2014, 298153. [Google Scholar] [CrossRef]
- Vassilev, S.V.; Baxter, D.; Andersen, L.K.; Vassileva, C.G. An overview of the chemical composition of biomass. Fuel 2010, 89, 913–933. [Google Scholar] [CrossRef]
- Poling, B.E.; Prausnitz, J.M.; O’connell, J.P. Properties of Gases and Liquids; McGraw-Hill Education: New York, NY, USA, 2001. [Google Scholar]
- Ćalasan, M.P.; Nikitović, L.; Mujović, S. CONOPT solver embedded in GAMS for optimal power flow. J. Renew. Sustain. Energy 2019, 11, 046301. [Google Scholar] [CrossRef]
- Rocha, S.A.; Guirardello, R. An approach to calculate solid–liquid phase equilibrium for binary mixtures. Fluid. Phase Equilib. 2009, 281, 12–21. [Google Scholar] [CrossRef]
- Voll, F.; Rossi, C.; Silva, C.; Guirardello, R.; Souza, R.; Cabral, V.; Cardozo-Filho, L. Thermodynamic analysis of supercritical water gasification of methanol, ethanol, glycerol, glucose and cellulose. Int. J. Hydrogen Energy 2009, 34, 9737–9744. [Google Scholar] [CrossRef]
- Chakinala, A.G.; Brilman, D.W.F.; van Swaaij, W.P.; Kersten, S.R.A. Catalytic and Non-catalytic Supercritical Water Gasification of Microalgae and Glycerol. Ind. Eng. Chem. Res. 2010, 49, 1113–1122. [Google Scholar] [CrossRef]
- Lopez-Echeverry, J.S.; Reif-Acherman, S.; Araujo-Lopez, E. Peng-Robinson equation of state: 40 years through cubics. Fluid. Phase Equilib. 2017, 447, 39–71. [Google Scholar] [CrossRef]
- Dos Santos, J.M.; De Sousa, G.F.B.; Vidotti, A.D.S.; De Freitas, A.C.D.; Guirardello, R. Optimization of glycerol gasification process in supercritical water using thermodynamic approach. Chem. Eng. Trans. 2021, 86, 847–852. [Google Scholar] [CrossRef]
- De Blasio, C.; Järvinen, M. Supercritical Water Gasification of Biomass. Encyclopedia of Sustainable Technologies; Elsevier: Amsterdam, The Netherlands, 2017; pp. 171–195. [Google Scholar] [CrossRef]
- Rodriguez Correa, C.; Kruse, A. Supercritical water gasification of biomass for hydrogen production—Review. J. Supercrit. Fluids 2018, 133, 573–590. [Google Scholar] [CrossRef]
- Yan, Q.; Guo, L.; Lu, Y. Thermodynamic analysis of hydrogen production from biomass gasification in supercritical water. Energy Convers. Manag. 2006, 47, 1515–1528. [Google Scholar] [CrossRef]
- Ding, W.; Shi, J.; Wei, W.; Cao, C.; Jin, H. A molecular dynamics simulation study on solubility behaviors of polycyclic aromatic hydrocarbons in supercritical water/hydrogen environment. Int. J. Hydrogen Energy 2021, 46, 2899–2904. [Google Scholar] [CrossRef]
- Withag, J.A.M.; Smeets, J.R.; Bramer, E.A.; Brem, G. System model for gasification of biomass model compounds in supercritical water—A thermodynamic analysis. J. Supercrit. Fluids 2012, 61, 157–166. [Google Scholar] [CrossRef]
- Ferreira-Pinto, L.; Silva Parizi, M.P.; Carvalho de Araújo, P.C.; Zanette, A.F.; Cardozo-Filho, L. Experimental basic factors in the production of H2 via supercritical water gasification. Int. J. Hydrogen Energy 2019, 44, 25365–25383. [Google Scholar] [CrossRef]
- Luyben, W.L. Control of parallel dry methane and steam methane reforming processes for Fischer–Tropsch syngas. J. Process Control 2016, 39, 77–87. [Google Scholar] [CrossRef]
- Cheng, C.K.; Foo, S.Y.; Adesina, A.A. H2-rich synthesis gas production over Co/Al2O3 catalyst via glycerol steam reforming. Catal. Commun. 2010, 12, 292–298. [Google Scholar] [CrossRef]
- Lundgren, J.; Ekbom, T.; Hulteberg, C.; Larsson, M.; Grip, C.-E.; Nilsson, L.; Tunå, P. Methanol production from steel-work off-gases and biomass based synthesis gas. Appl. Energy 2013, 112, 431–439. [Google Scholar] [CrossRef]
- Saad, J.M.; Williams, P.T. Manipulating the H2/CO ratio from dry reforming of simulated mixed waste plastics by the addition of steam. Fuel Process. Technol. 2017, 156, 331–338. [Google Scholar] [CrossRef]
- Rostrup-Nielsen, J.; Christiansen, L.J. Concepts in Syngas Manufacture; World Scientific: Singapore, 2011; Volume 10. [Google Scholar]
- Rahimpour, M.R.; Arab Aboosadi, Z.; Jahanmiri, A.H. Synthesis gas production in a novel hydrogen and oxygen perm-selective membranes tri-reformer for methanol production. J. Nat. Gas. Sci. Eng. 2012, 9, 149–159. [Google Scholar] [CrossRef]
- Jia, D.; Liang, J.; Liu, J.; Chen, D.; Evrendilek, F.; Wen, T.; Cao, H.; Zhong, S.; Yang, Z.; He, Y. Insights into pyrolysis of ginger via TG-FTIR and Py-GC/MS analyses: Thermochemical behaviors, kinetics, evolved gas, and products. J. Anal. Appl. Pyrolysis 2024, 179, 106442. [Google Scholar] [CrossRef]




| Biomass | C | H | N | O | H/C * | O/C * | Reference |
|---|---|---|---|---|---|---|---|
| Rice husk | 49.3 | 6.1 | 0.8 | 43.7 | 1.48 | 0.59 | [25] |
| Soy husk | 45.4 | 6.7 | 0.9 | 46.9 | 1.77 | 0.69 | [25] |
| Mustard husk | 45.8 | 9.2 | 0.4 | 44.4 | 2.41 | 0.65 | [25] |
| Cotton husk | 50.4 | 8.4 | 1.4 | 39.8 | 2.00 | 0.53 | [26] |
| Temperature Deviation (%) | |||
|---|---|---|---|
| Initial Temperature (K) | Rice Husk | Cotton Husk | Mustard Husk |
| 700 | +17.5 | +18.4 | +19.6 |
| 750 | +14.7 | +15.7 | +16.8 |
| 800 | +12.0 | +13.1 | +14.1 |
| 850 | +9.6 | +10.8 | +11.7 |
| 900 | +7.2 | +8.6 | +9.4 |
| 950 | +5.1 | +6.8 | +7.4 |
| 1000 | +3.2 | +5.2 | +5.7 |
| 1050 | +1.6 | +3.8 | +4.2 |
| 1100 | +0.27 | +2.8 | +3.0 |
| 1200 | +0.25 | +0.34 | +0.57 |
| 1300 | −0.33 | −0.56 | −0.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
dos Santos Junior, J.M.; Mariano, A.P. Gasification of Lignocellulosic Waste in Supercritical Water: Study of Thermodynamic Equilibrium as a Nonlinear Programming Problem. Eng 2024, 5, 1096-1111. https://doi.org/10.3390/eng5020060
dos Santos Junior JM, Mariano AP. Gasification of Lignocellulosic Waste in Supercritical Water: Study of Thermodynamic Equilibrium as a Nonlinear Programming Problem. Eng. 2024; 5(2):1096-1111. https://doi.org/10.3390/eng5020060
Chicago/Turabian Styledos Santos Junior, Julles Mitoura, and Adriano Pinto Mariano. 2024. "Gasification of Lignocellulosic Waste in Supercritical Water: Study of Thermodynamic Equilibrium as a Nonlinear Programming Problem" Eng 5, no. 2: 1096-1111. https://doi.org/10.3390/eng5020060
APA Styledos Santos Junior, J. M., & Mariano, A. P. (2024). Gasification of Lignocellulosic Waste in Supercritical Water: Study of Thermodynamic Equilibrium as a Nonlinear Programming Problem. Eng, 5(2), 1096-1111. https://doi.org/10.3390/eng5020060






