Development of a Methodology for Railway Bolster Beam Design Enhancement Using Topological Optimization and Manufacturing Constraints
Abstract
:1. Introduction
2. Materials and Methods
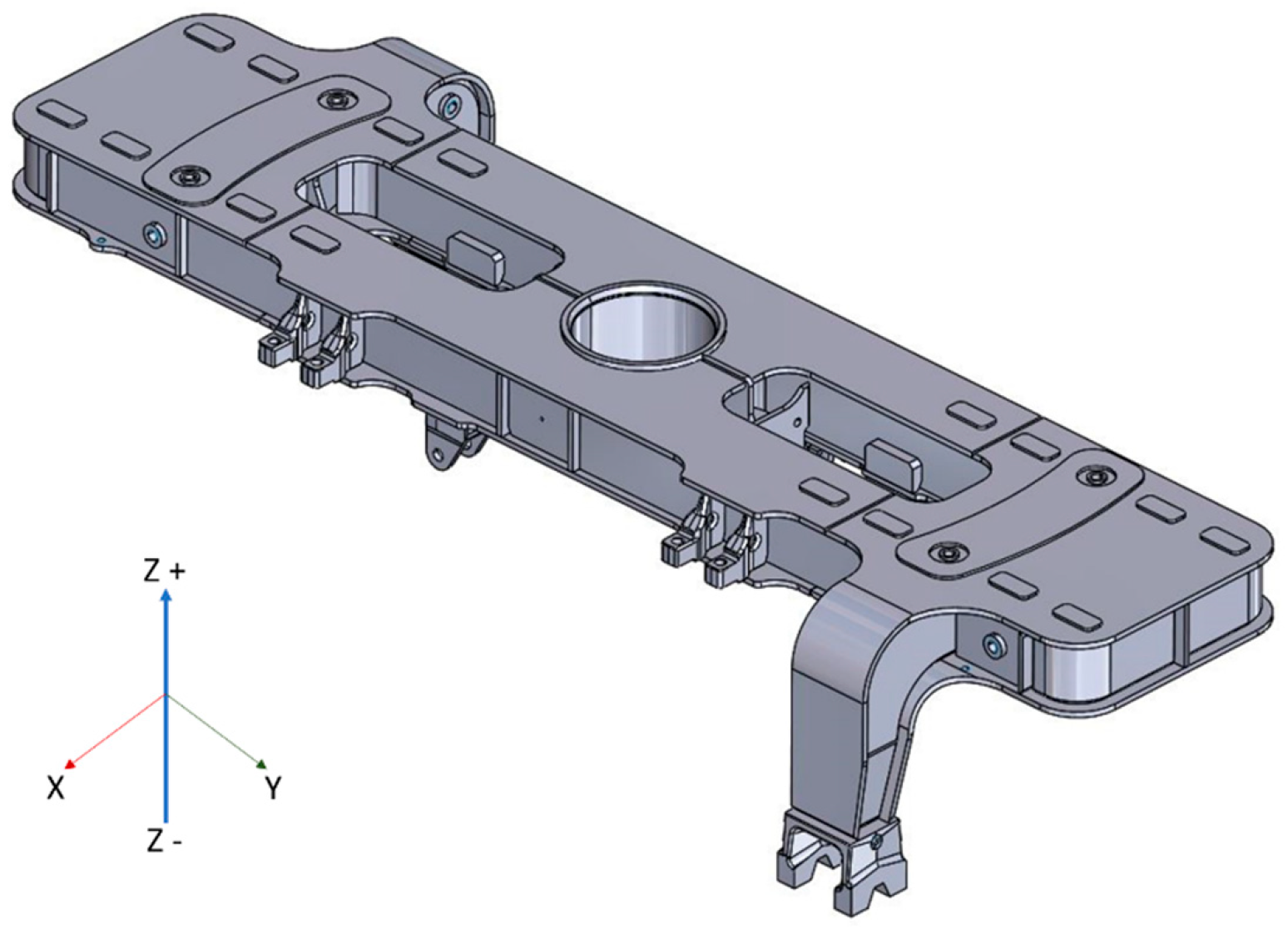
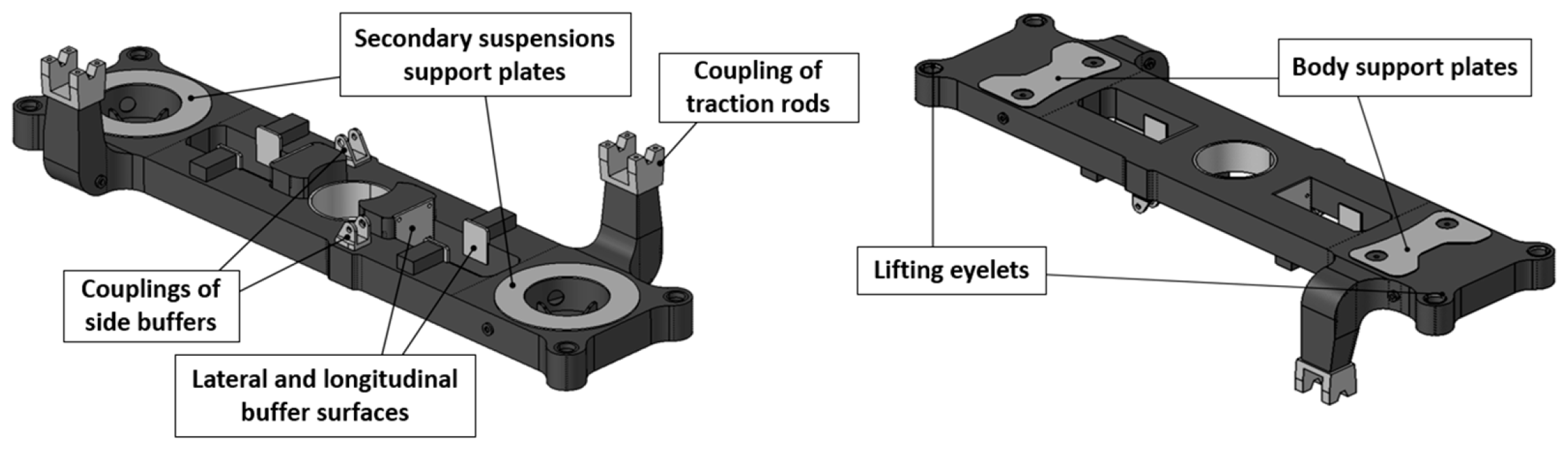
2.1. Model Description: The Bolster Beam
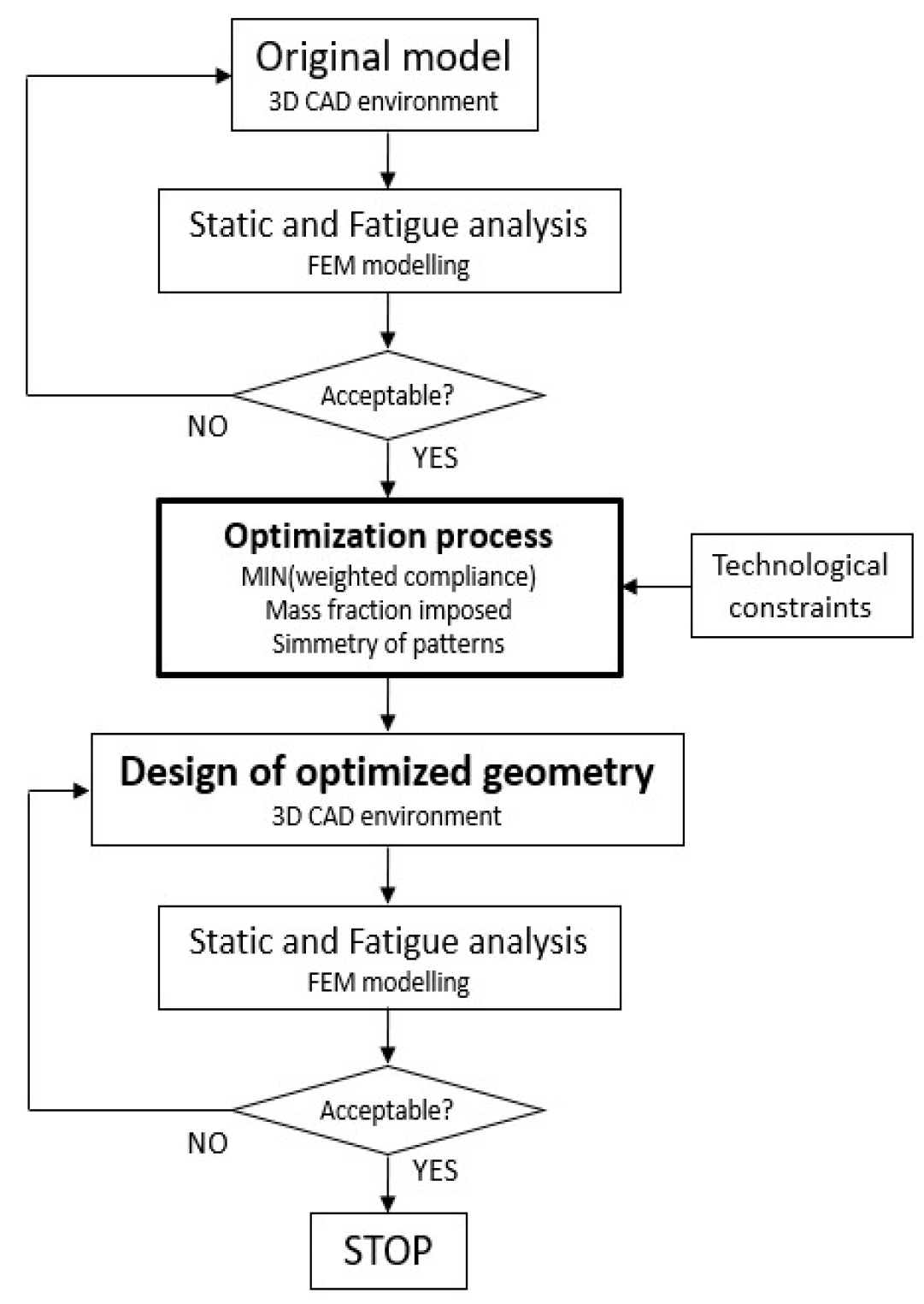
2.2. Methodology
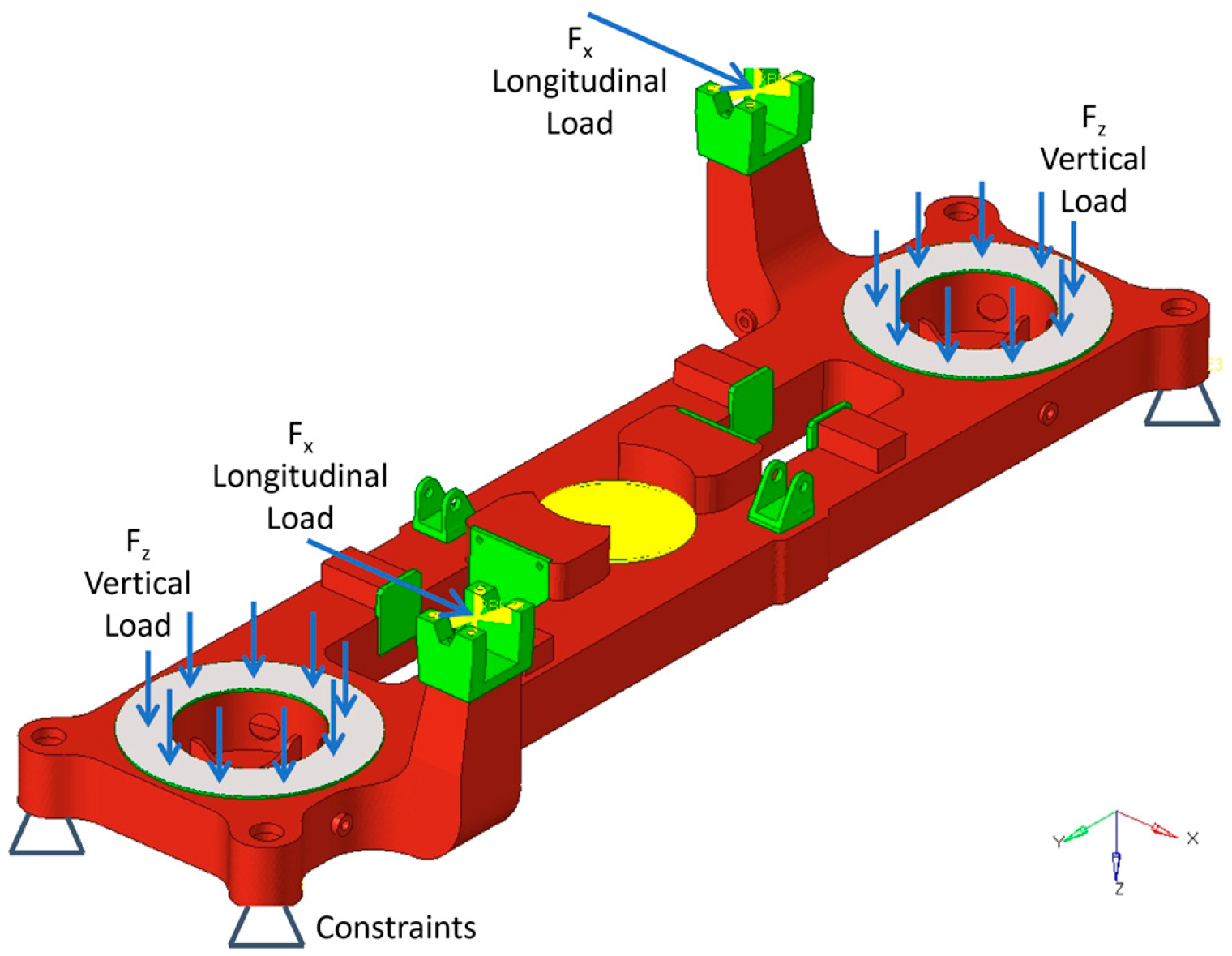
2.3. Optimization Settings and Load Cases
- Longitudinal load on the bogie bolster to carbody connection;
- Transversal load on the bogie bolster to carbody connection;
- Truck lifting;
- Truck twist (with also the completing unloading of one wheel);
- Braking forces;
- Internal pressure of the air springs;
- Longitudinal lozenging forces.
3. Topological Optimization and FEA Results
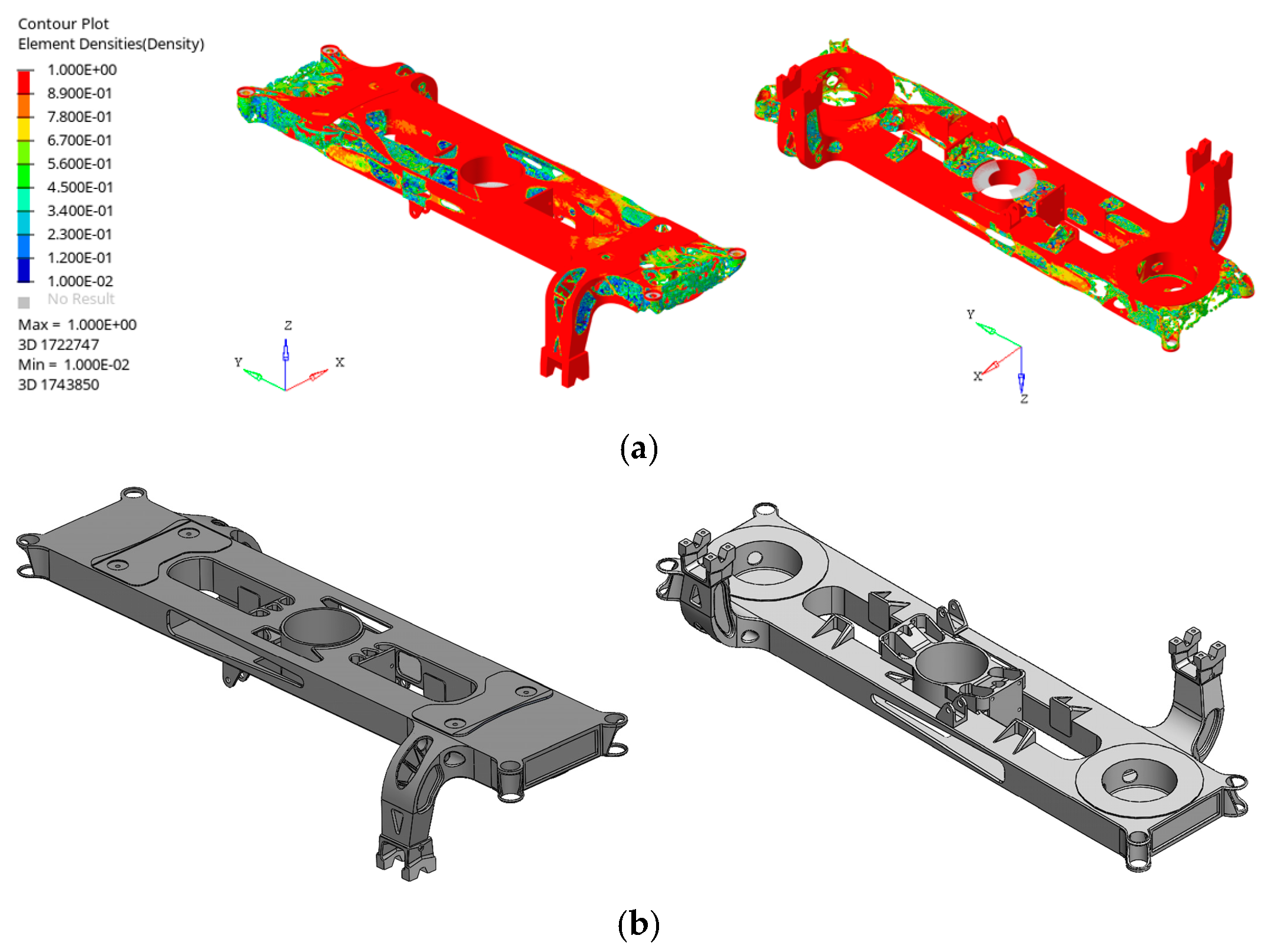
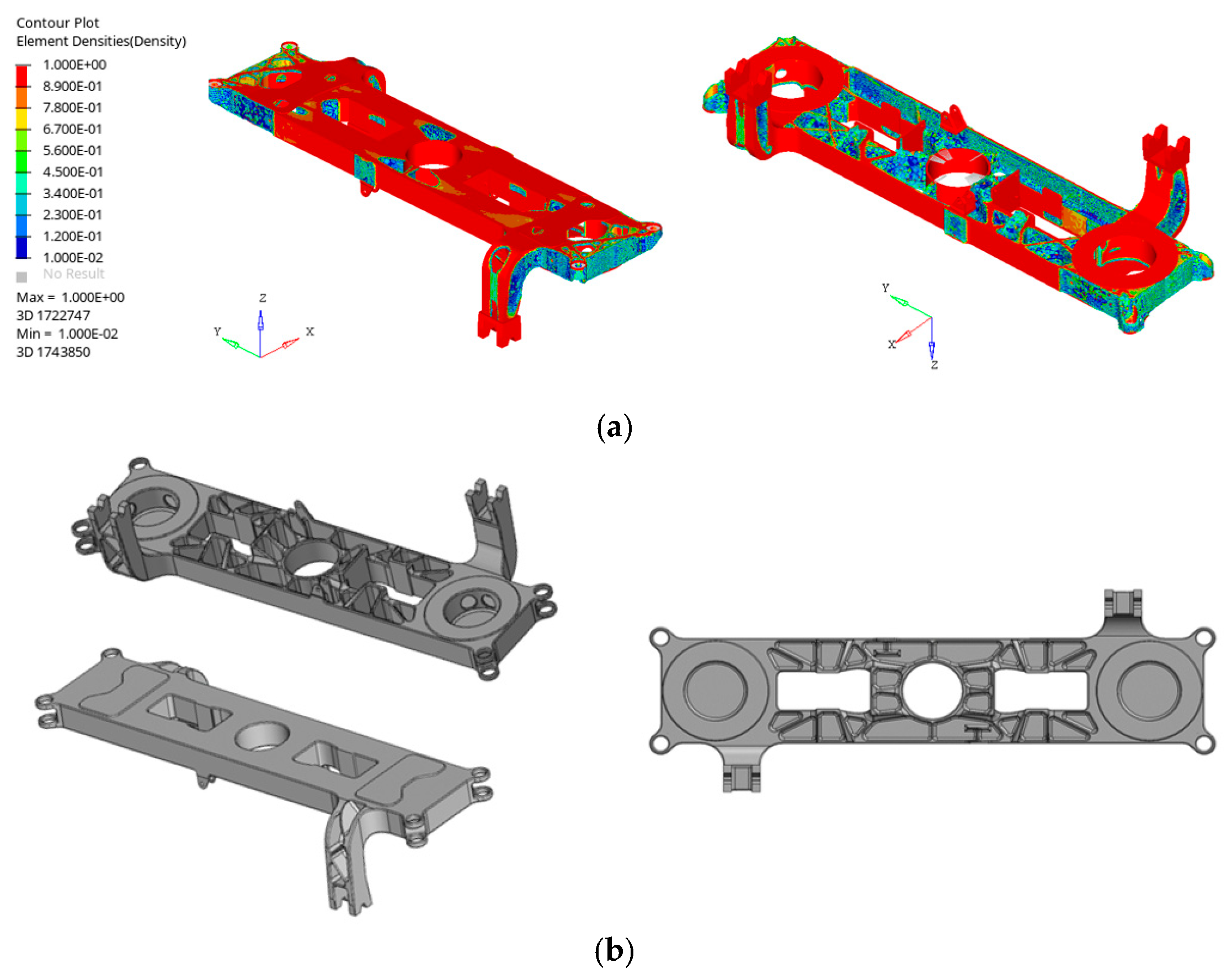
3.1. Topological Optimization Results
3.1.1. Topology Optimization Results—Case 1
3.1.2. Topology Optimization—Case 2
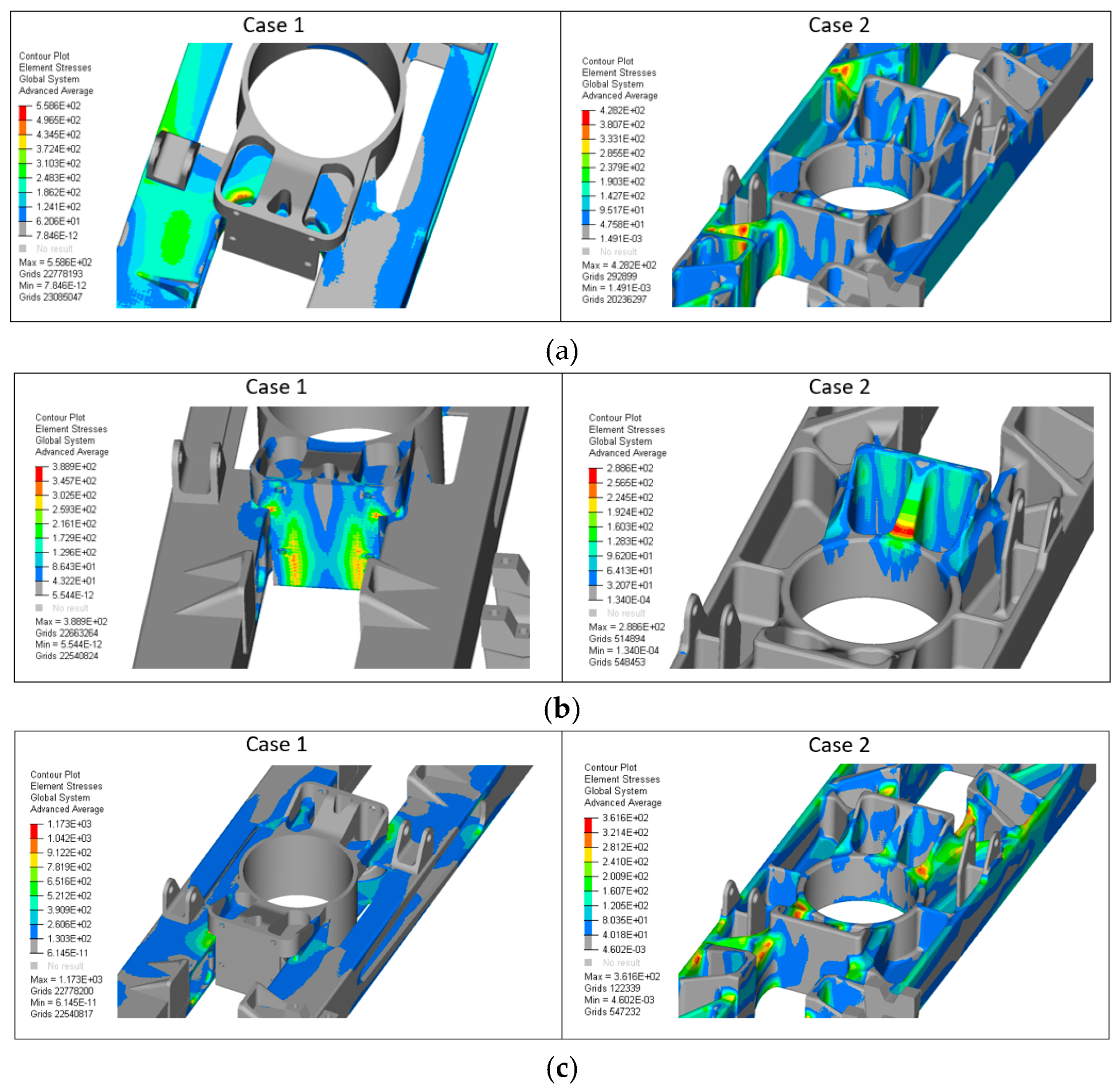
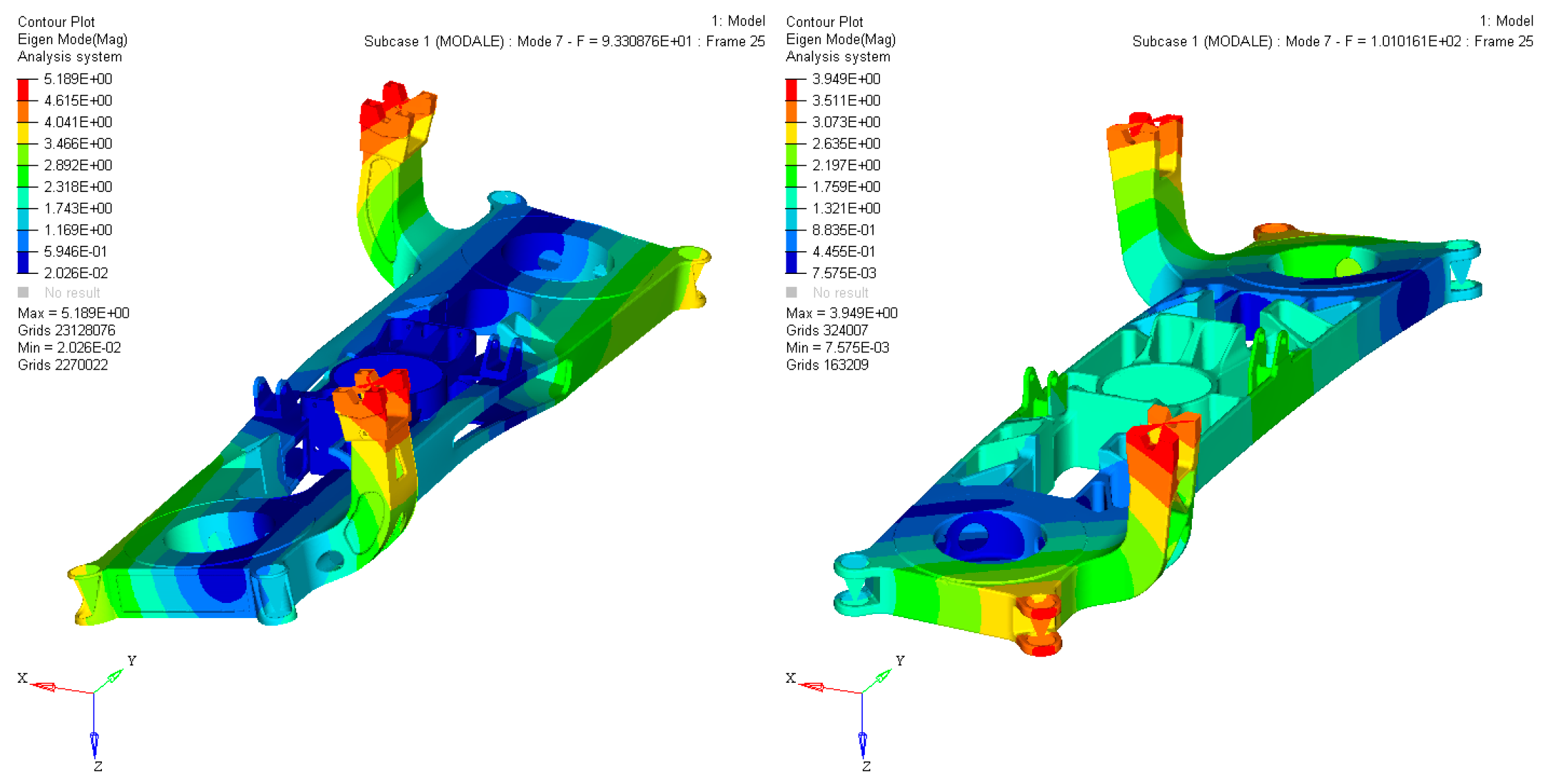
3.2. FEA Verification Results
4. Results and Discussion
5. Conclusions and Future Developments
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; Kang, Z. Structural shape and topology optimization of cast parts using level set method: Structural shape and topology optimization of cast parts using level set method. Int. J. Numer. Meth. Eng. 2017, 111, 1252–1273. [Google Scholar] [CrossRef]
- Allaire, G.; Jouve, F.; Michailidis, G. Casting Constraints in Structural Optimization via a Level-Set Method. Orlando, United States. 2013, p. 10. Available online: https://hal.science/hal-01088775 (accessed on 28 May 2024).
- Xia, Q.; Shi, T.; Wang, M.Y.; Liu, S. A level set based method for the optimization of cast part. Struct. Multidisc. Optim. 2010, 41, 735–747. [Google Scholar] [CrossRef]
- Xia, Q.; Shi, T.; Wang, M.Y.; Liu, S. Simultaneous optimization of cast part and parting direction using level set method. Struct. Multidisc. Optim. 2011, 44, 751–759. [Google Scholar] [CrossRef]
- Liu, J.; Ma, Y. A survey of manufacturing oriented topology optimization methods. Adv. Eng. Softw. 2016, 100, 161–175. [Google Scholar] [CrossRef]
- Gersborg, A.R.; Andreasen, C.S. An explicit parameterization for casting constraints in gradient driven topology optimization. Struct. Multidisc. Optim. 2011, 44, 875–881. [Google Scholar] [CrossRef]
- Liu, S.; Li, Q.; Chen, W.; Hu, R.; Tong, L. H-DGTP—A Heaviside-function based directional growth topology parameterization for design optimization of stiffener layout and height of thin-walled structures. Struct. Multidisc. Optim. 2015, 52, 903–913. [Google Scholar] [CrossRef]
- Guest, J.K.; Prévost, J.H.; Belytschko, T. Achieving minimum length scale in topology optimization using nodal design variables and projection functions. Int. J. Numer. Meth. Eng. 2004, 61, 238–254. [Google Scholar] [CrossRef]
- Schmitt, O.; Friederich, J.; Riehl, S.; Steinmann, P. On the formulation and implementation of geometric and manufacturing constraints in node–based shape optimization. Struct. Multidisc. Optim. 2016, 53, 881–892. [Google Scholar] [CrossRef]
- Harzheim, L.; Graf, G. A review of optimization of cast parts using topology optimization: I—Topology optimization without manufacturing constraints. Struct. Multidisc. Optim. 2005, 30, 491–497. [Google Scholar] [CrossRef]
- Bhosale, G.H.; Sapkal, S.U. Re-engineering of Cast Product by Topology Optimization. IJETER 2021, 9, 1211–1216. [Google Scholar]
- Luo, Y.; Peng, Y. Topology optimization design of the suspension arm of a certain type of train battery system. JMESS 2021, 7, 4059–4061. [Google Scholar]
- Hoosain, S.E.; Tshabalala, L.; Bester, D.; Chetty, D.; Mukwevho, G. Additive Manufacturing Case Study in the Railway Industry; Rapid Product Development Association of South Africa: Pretoria, South Africa, 2020. [Google Scholar]
- Koenig, J. Integral Consideration of the Lightweight Design for Railway Vehicles; Technical University of Denmark: Lyngby, Denmark, 2011. [Google Scholar]
- Cascino, A.; Meli, E.; Rindi, A. Dynamic size optimization approach to support railway carbody lightweight design process. Proc. Inst. Mech. Eng. Part F: J. Rail Rapid Transit 2023, 237, 871–881. [Google Scholar] [CrossRef]
- Cascino, A.; Meli, E.; Rindi, A. A strategy for lightweight designing of a railway vehicle car body including composite material and dynamic structural optimization. Rail. Eng. Sci. 2023, 31, 340–350. [Google Scholar] [CrossRef]
- Kirkayak, L.; Krüger, D.; Malzacher, G.; Gomes Alves, C.; Schmauder, N.; Kopp, G. Lightweight Design Concept Methodology of the Extended Market Wagon: A Shift2Rail Project; WCRR: Birmingham, UK, 2022; p. 6. [Google Scholar]
- Li, X.; Peng, F.; Yang, Z.; Peng, Y.; Zhou, J. Structural optimization design of a bolster based on simulation driven design method. Transp. Saf. Environ. 2023, 5, tdac075. [Google Scholar] [CrossRef]
- Srivastava, P.K.; Shukla, S. Topology Optimization: Weight Reduction of Indian Railway Freight Bogie Side Frame. Int. J. Mech. Eng. 2021, 6, 4374–4383. [Google Scholar]
- Park, B.H.; Lee, K.Y. Bogie frame design in consideration of fatigue strength and weight reduction. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit. 2006, 220, 201–206. [Google Scholar] [CrossRef]
- Krishnakumar, K. Micro-Genetic Algorithms For Stationary And Non-Stationary Function Optimization. In Intelligent Control and Adaptive Systems; Rodriguez, G., Ed.; SPIE: Bellingham, WA, USA, 1990; pp. 289–296. [Google Scholar]
- Park, B.H.; Kim, N.P.; Kim, J.S.; Lee, K.Y. Optimum design of tilting bogie frame in consideration of fatigue strength and weight. Veh. Syst. Dyn. 2006, 44, 887–901. [Google Scholar] [CrossRef]
- Yamamoto, M. Non-parametric optimization of railway wheel web shape based on fatigue design criteria. Int. J. Fatigue 2020, 134, 105463. [Google Scholar] [CrossRef]
- Abid, M. Analysis and Redesign of Bolster Beam of the Bogie Frame of a Locomotive. J. Eng. Res. 2013, 1, 271–287. [Google Scholar]
- Cetin, M.H.; Alvali, G.T.; Korkmaz, S. Parameter Optimization with Multi-criteria Decision-Making Methods in Rail Transport: A Case Study of Freight Wagon Bogie. Arab. J. Sci. Eng. 2021, 46, 10059–10076. [Google Scholar] [CrossRef]
- EN 13749:2021; Railway Applications—Wheelsets and Bogies—Method of Specifying the Structural Requirements of Bogie Frames. iTeh, Inc.: Newark, DE, USA, 2021.
- Jameson, A. Gradient Based Optimization Methods; MAE Technical Report No (2057); Princeton University: Princeton, NJ, USA, 1995. [Google Scholar]
| Parameters | Case 1 | Case 2a | Case 2b | |
|---|---|---|---|---|
| General settings | Material | Spheroidal graphite cast iron EN-GJS-450-10 | ||
| Symmetry constraint | Cyclic around Z axis | |||
| Optimization constraint | Mass fraction < 0.4 | |||
| Optimization objective | Min. weighted compliance | |||
| Load cases considered | Static and fatigue | |||
| Technological constraints | Extraction from mold | - | Z positive | Z negative |
| Minimum feature size | - | 20 mm | 20 mm | |
| Load Case | [MPa] | Case 1 | Case 2 | ||
|---|---|---|---|---|---|
| [MPa] | U [-] | [MPa] | U [-] | ||
| Longitudinal | 310 | 559 | 1.80 | 428 | 1.38 |
| Transversal | 390 | 1.26 | 289 | 0.93 | |
| Lifting | 1173 | 3.78 | 362 | 1.17 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cascino, A.; Meli, E.; Rindi, A. Development of a Methodology for Railway Bolster Beam Design Enhancement Using Topological Optimization and Manufacturing Constraints. Eng 2024, 5, 1485-1498. https://doi.org/10.3390/eng5030079
Cascino A, Meli E, Rindi A. Development of a Methodology for Railway Bolster Beam Design Enhancement Using Topological Optimization and Manufacturing Constraints. Eng. 2024; 5(3):1485-1498. https://doi.org/10.3390/eng5030079
Chicago/Turabian StyleCascino, Alessio, Enrico Meli, and Andrea Rindi. 2024. "Development of a Methodology for Railway Bolster Beam Design Enhancement Using Topological Optimization and Manufacturing Constraints" Eng 5, no. 3: 1485-1498. https://doi.org/10.3390/eng5030079
APA StyleCascino, A., Meli, E., & Rindi, A. (2024). Development of a Methodology for Railway Bolster Beam Design Enhancement Using Topological Optimization and Manufacturing Constraints. Eng, 5(3), 1485-1498. https://doi.org/10.3390/eng5030079








