Accuracy of Mathematical Models and Process Simulators for Predicting the Performance of Gas-Separation Membranes
Abstract
1. Introduction
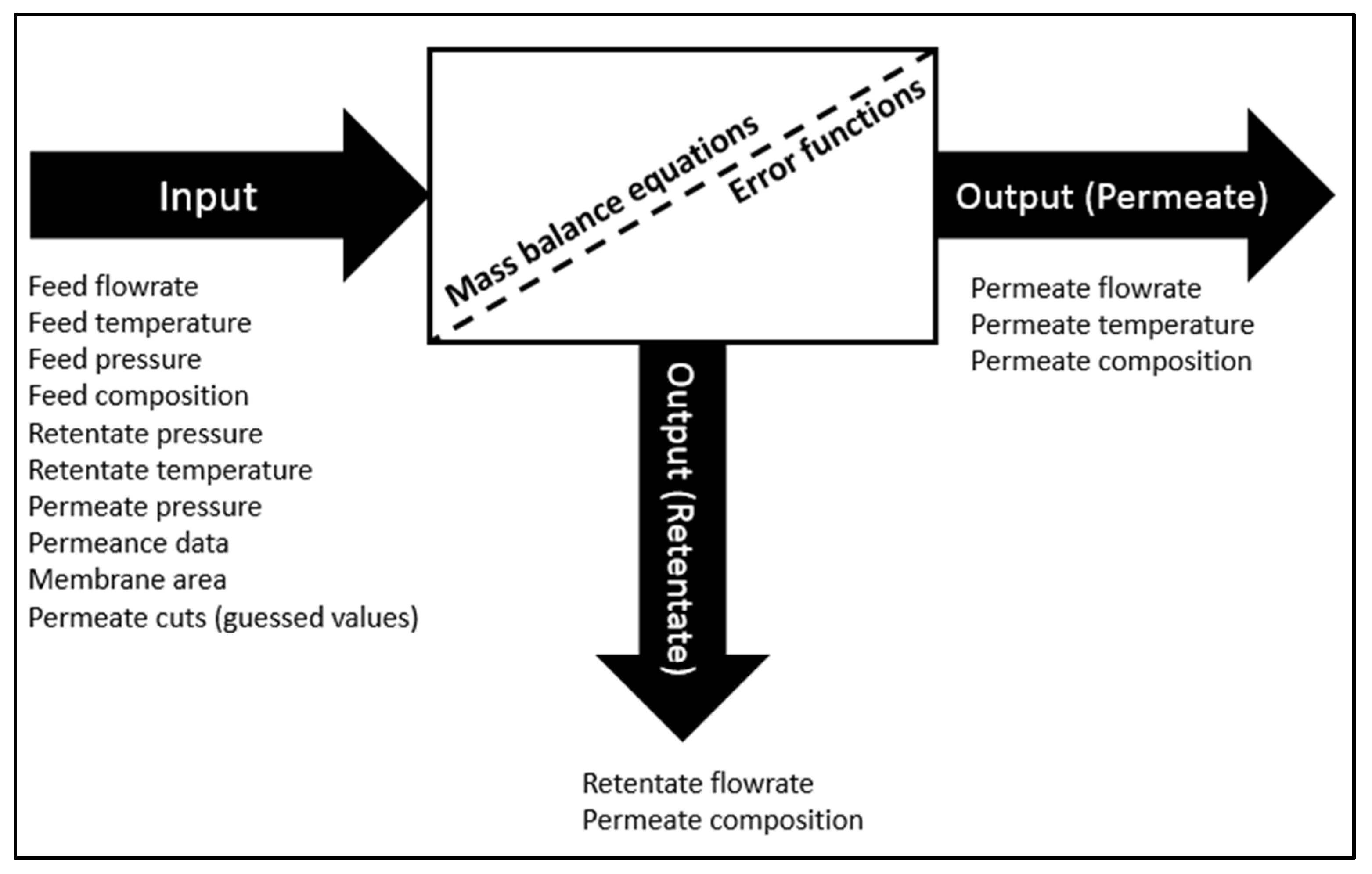
2. Methodology
2.1. Membrane Development in UniSIM®
2.2. Membrane Development in COCO
3. Results and Discussion
4. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gkotsis, P.; Peleka, E.; Zouboulis, A. Membrane-based technologies for post-combustion CO2 capture from flue gases: Recent progress in commonly employed membrane materials. Membranes 2023, 13, 898. [Google Scholar] [CrossRef] [PubMed]
- Basile, A.; Favvas, E. Current Trends and Future Developments on (Bio-) Membranes; Elsevier: Amsterdam, The Netherlands, 2024; pp. 3–28. [Google Scholar]
- He, X.; Lie, J.; Sheridan, E.; Hägg, M.-B. CO2 capture by hollow fibre carbon membranes: Experiments and process simulations. Energy Procedia 2009, 1, 261–268. [Google Scholar] [CrossRef]
- Offord, G.; Armstrong, S.; Freeman, B.; Baer, E.; Hiltner, A.; Paul, D. Gas transport in coextruded multilayered membranes with alternating dense and porous polymeric layers. Polym 2014, 55, 1259–1266. [Google Scholar] [CrossRef]
- Lahiri, S. Profit Maximization Techniques for Operating Chemical Plants; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar]
- Du, Z.; Li, C.; Sun, W.; Wang, J. A simulation of diesel hydrotreating process with real component method. Chin. J. Chem. Eng. 2015, 23, 780–788. [Google Scholar] [CrossRef]
- Oyegoke, T. COCO, a process simulator: Methane oxidation simulation & its agreement with commercial simulator’s predictions. Chem. Prod. Process Model. 2023, 18, 995–1004. [Google Scholar]
- Chemmangattuvalappil, N.; Chong, C.H.; Foo, D.C.Y.; Ng, D.K.S.; Elyas, R.; Chen, C.-L.; Chien, I.; Elms, R.D.; Lee, H.-Y.; Chong, S. Chemical Engineering Process Simulation; Elsevier Science: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Yeom, C.; Kim, J.; Park, H.; Lee, J.; Park, S.; Gu, B. Simulation model for prediction of gas separation in membrane contactor process. Membranes 2022, 12, 158. [Google Scholar] [CrossRef] [PubMed]
- Mirzaee, H.; Mirzaee, F. Modeling and simulation gas separation by membrane of poly dimethyl siloxane. J. King Saud Univ.-Eng. Sci. 2012, 24, 35–43. [Google Scholar] [CrossRef]
- Baker, R.; Hofmann, T.; Jariwala, A. Field Demonstration of a Membrane Process to Recover Heavy Hydrocarbons and to Remove Water From Natural Gas; United States Department of Energy: Washington, DC, USA, 2007. [Google Scholar]
- Sethi, S.; Wiesner, M. Simulated cost comparisons of hollow-fiber and integrated nanofiltration configurations. Water Res. 2000, 34, 2589–2597. [Google Scholar] [CrossRef]
- Wenten, I.; Recent Development in Membrane and Its Industrial Applications. Membrane Technology in Oil and Gas Industry; 2005, Indonesia 2005. Available online: https://www.researchgate.net/publication/281257916_Recent_Development_in_Membrane_and_Its_Industrial_Applications_Membrane_Technology_in_Oil_and_Gas_Industry (accessed on 19 October 2024).
- Davis, R. Simple gas permeation and pervaporation membrane unit operation models for process simulators. Chem. Eng. Technol. 2002, 25, 717–722. [Google Scholar] [CrossRef]
- Ahmad, Z. Recent Trends in Processing and Degradation of Aluminium Alloys; IntechOpen: London, UK, 2011. [Google Scholar]
- Triantafyllidis, T. Holistic Simulation of Geotechnical Installation Processes: Numerical and Physical Modelling; Springer International Publishing: Manhattan, NY, USA, 2015. [Google Scholar]
- Bafleur, M.; Caignet, F.; Nolhier, N. ESD Protection Methodologies: From Component to System; Elsevier Science: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Koh, H.; Teh, S. Ecological Modeling for Mitigating Environmental and Climate Shocks: Achieving the UNSDGs; World Scientific Publishing Company: Singapore, 2021. [Google Scholar]
- Drioli, E.; Barbieri, G.; Peter, L.M. Membrane Engineering for the Treatment of Gases: Gas-Separation Problems with Membranes; Royal Society of Chemistry: London, UK, 2011. [Google Scholar]
- Ismail, A.; Khulbe, K.; Matsuura, T. Gas Separation Membranes: Polymeric and Inorganic; Springer International Publishing: Manhattan, NY, USA, 2015. [Google Scholar]
- Conn, A.; Gould, N.; Toint, P. Trust Region Methods; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2000. [Google Scholar]
- Marsland, S. Machine Learning: An Algorithmic Perspective; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]


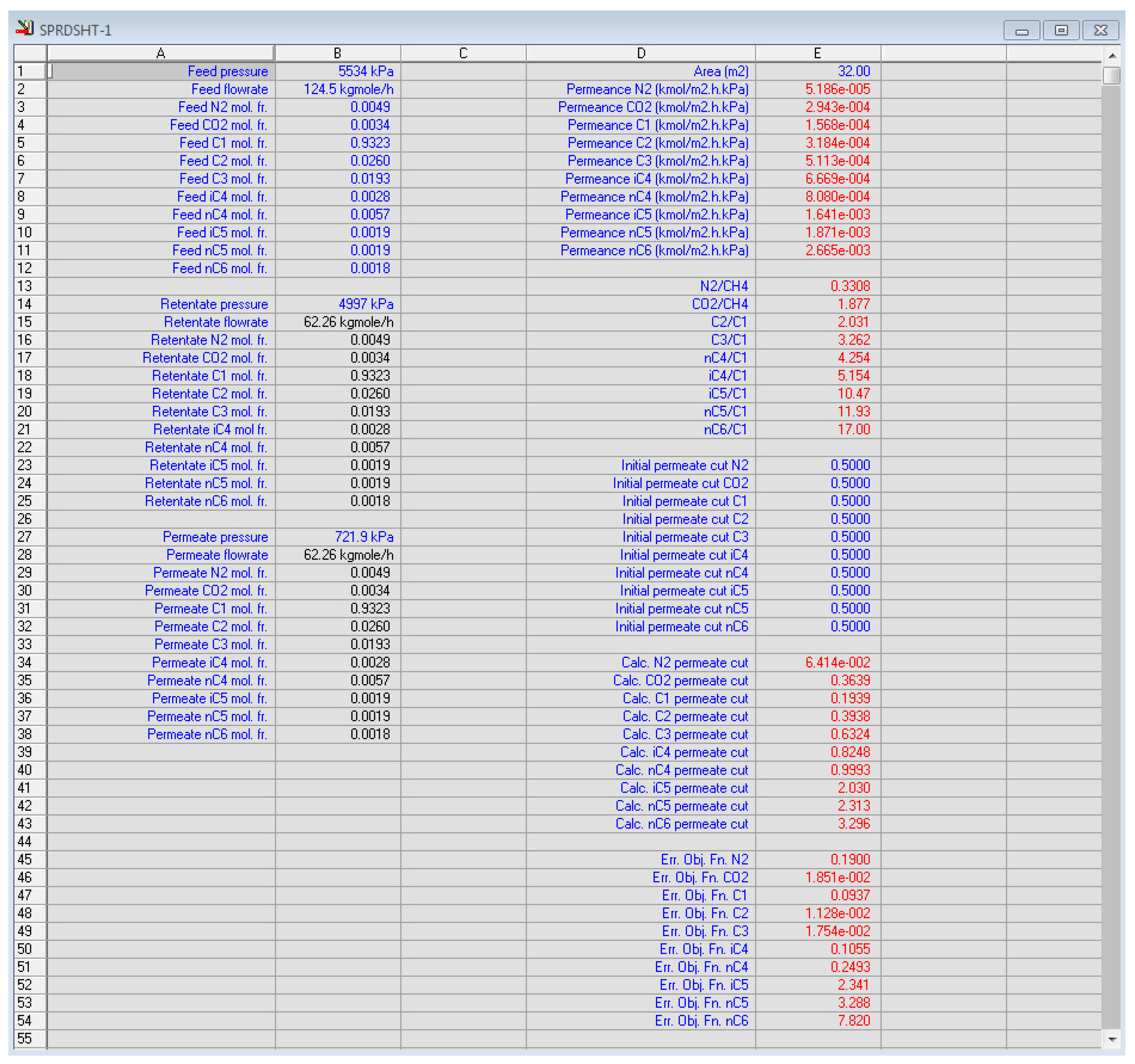



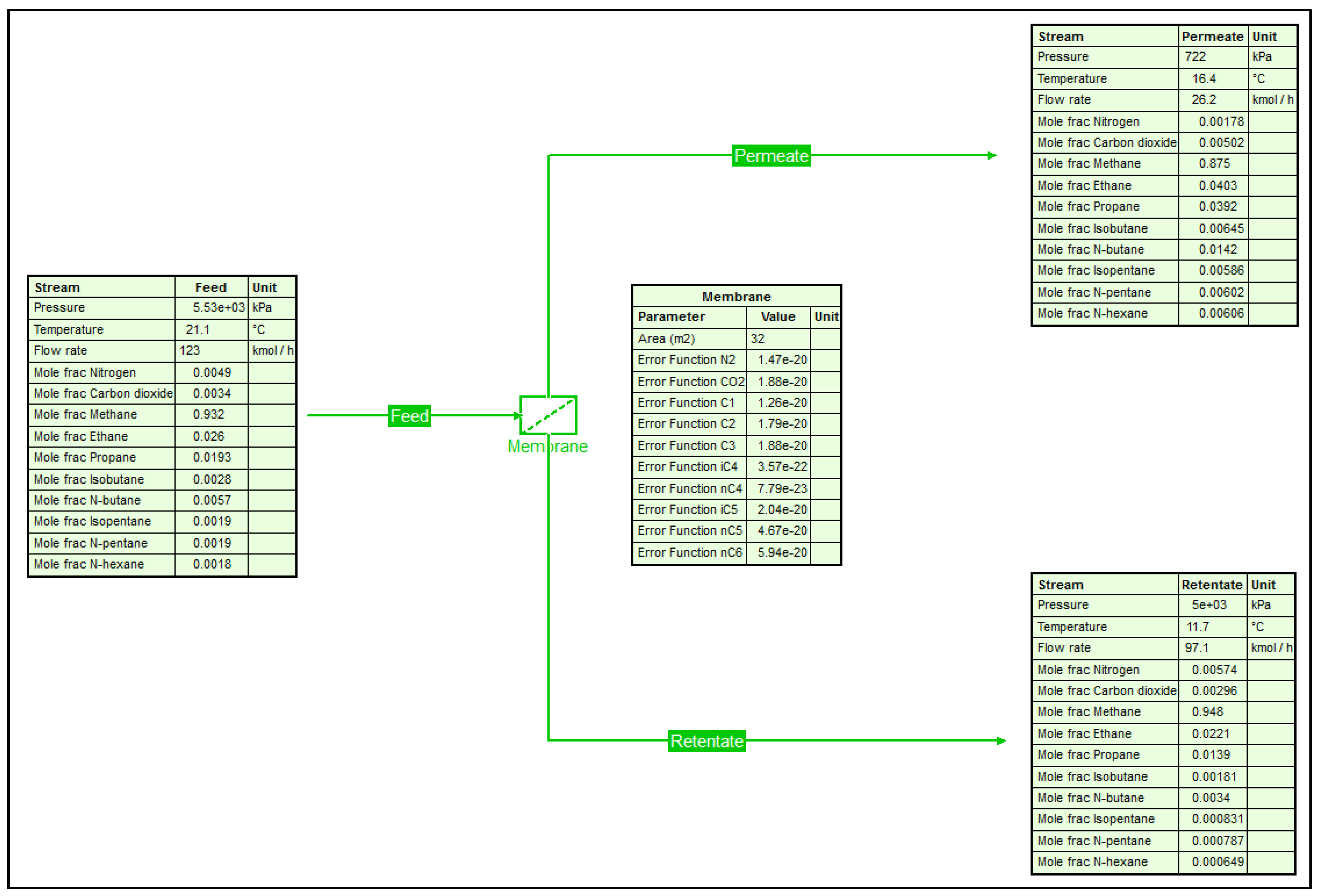
| Property | Feed | Retentate (Product) | Permeate | Permeance (GPU a) |
|---|---|---|---|---|
| Flowrate (MMSCFD *) | 2.50 | 2.00 | 0.50 | – |
| Temperature (°C) | 21.11 | 11.67 | – | – |
| Pressure (kPa) | 5534 | 4997 | 721.9 | – |
| N2 (mol%) | 0.49 | 0.51 | 0.76 | 43 b |
| CO2 (mol%) | 0.34 | 0.28 | 0.48 | 244 |
| C1 (mol%) | 93.23 | 94.3 | 85.9 | 130 |
| C2 (mol%) | 2.60 | 2.43 | 4.13 | 264 |
| C3 (mol%) | 1.93 | 1.46 | 3.91 | 424 |
| iC4 (mol%) | 0.28 | 0.21 | 0.67 | 553 |
| nC4 (mol%) | 0.57 | 0.41 | 1.51 | 670 |
| iC5 (mol%) | 0.19 | 0.13 | 0.70 | 1361 |
| nC5 (mol%) | 0.19 | 0.14 | 0.76 | 1551 |
| nC6 (mol%) | 0.18 | 0.13 | 1.18 | 2210 b |
| Property | Field Data [11] | UniSIM® | COCO |
|---|---|---|---|
| Permeate stream | |||
| Temperature (°C) | – | 16.6 | 16.4 |
| Flowrate (MMSCFD) | 0.50 | 0.53 | 0.50 |
| N2 (mol%) | 0.76 | 0.18 | 0.18 |
| CO2 (mol%) | 0.48 | 0.49 | 0.50 |
| C1 (mol%) | 85.9 | 87.64 | 87.50 |
| C2 (mol%) | 4.13 | 3.97 | 4.03 |
| C3 (mol%) | 3.91 | 3.88 | 3.92 |
| iC4 (mol%) | 0.67 | 0.64 | 0.64 |
| nC4 (mol%) | 1.51 | 1.41 | 1.42 |
| iC5 (mol%) | 0.70 | 0.58 | 0.59 |
| nC5 (mol%) | 0.76 | 0.60 | 0.60 |
| nC6 (mol%) | 1.18 | 0.60 | 0.61 |
| Retentate stream | |||
| Flowrate (MMSCFD) | 2.0 | 2.0 | 2.0 |
| N2 (mol%) | 0.51 | 0.57 | 0.57 |
| CO2 (mol%) | 0.28 | 0.30 | 0.30 |
| C1 (mol%) | 94.30 | 94.75 | 94.78 |
| C2 (mol%) | 2.43 | 2.23 | 2.21 |
| C3 (mol%) | 1.46 | 1.40 | 1.39 |
| iC4 (mol%) | 0.21 | 0.18 | 0.18 |
| nC4 (mol%) | 0.41 | 0.34 | 0.34 |
| iC5 (mol%) | 0.13 | 0.08 | 0.08 |
| nC5 (mol%) | 0.14 | 0.08 | 0.08 |
| nC6 (mol%) | 0.13 | 0.07 | 0.06 |
| Average Error (%) | – | 17.4 | 17.1 |
| Parameter | UniSIM® | COCO |
|---|---|---|
| Software license | Commercial | Free |
| Membrane unit elements | Component splitter Spreadsheet Adjust functions | Scilab plugin Program coding |
| Time to build unit | Short | Long |
| Units conversion | Automatically | Manually for feed flowrate |
| Mass balance | Need to add equations | Need to add equations |
| Heat balance | Automatically | Need to add equations |
| Need initial guesses to solve | Yes | Yes |
| Solved from first guess * | No | Yes |
| Solving time ** | Few minutes (depending on initial guesses) | Few seconds |
| Error from field data | Higher | Lower |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alqaheem, Y. Accuracy of Mathematical Models and Process Simulators for Predicting the Performance of Gas-Separation Membranes. Eng 2024, 5, 3137-3147. https://doi.org/10.3390/eng5040164
Alqaheem Y. Accuracy of Mathematical Models and Process Simulators for Predicting the Performance of Gas-Separation Membranes. Eng. 2024; 5(4):3137-3147. https://doi.org/10.3390/eng5040164
Chicago/Turabian StyleAlqaheem, Yousef. 2024. "Accuracy of Mathematical Models and Process Simulators for Predicting the Performance of Gas-Separation Membranes" Eng 5, no. 4: 3137-3147. https://doi.org/10.3390/eng5040164
APA StyleAlqaheem, Y. (2024). Accuracy of Mathematical Models and Process Simulators for Predicting the Performance of Gas-Separation Membranes. Eng, 5(4), 3137-3147. https://doi.org/10.3390/eng5040164






