Computational Analysis of Blended Winglet Designs to Reduce the Wake Turbulence on the Airbus A380 Wingtip
Abstract
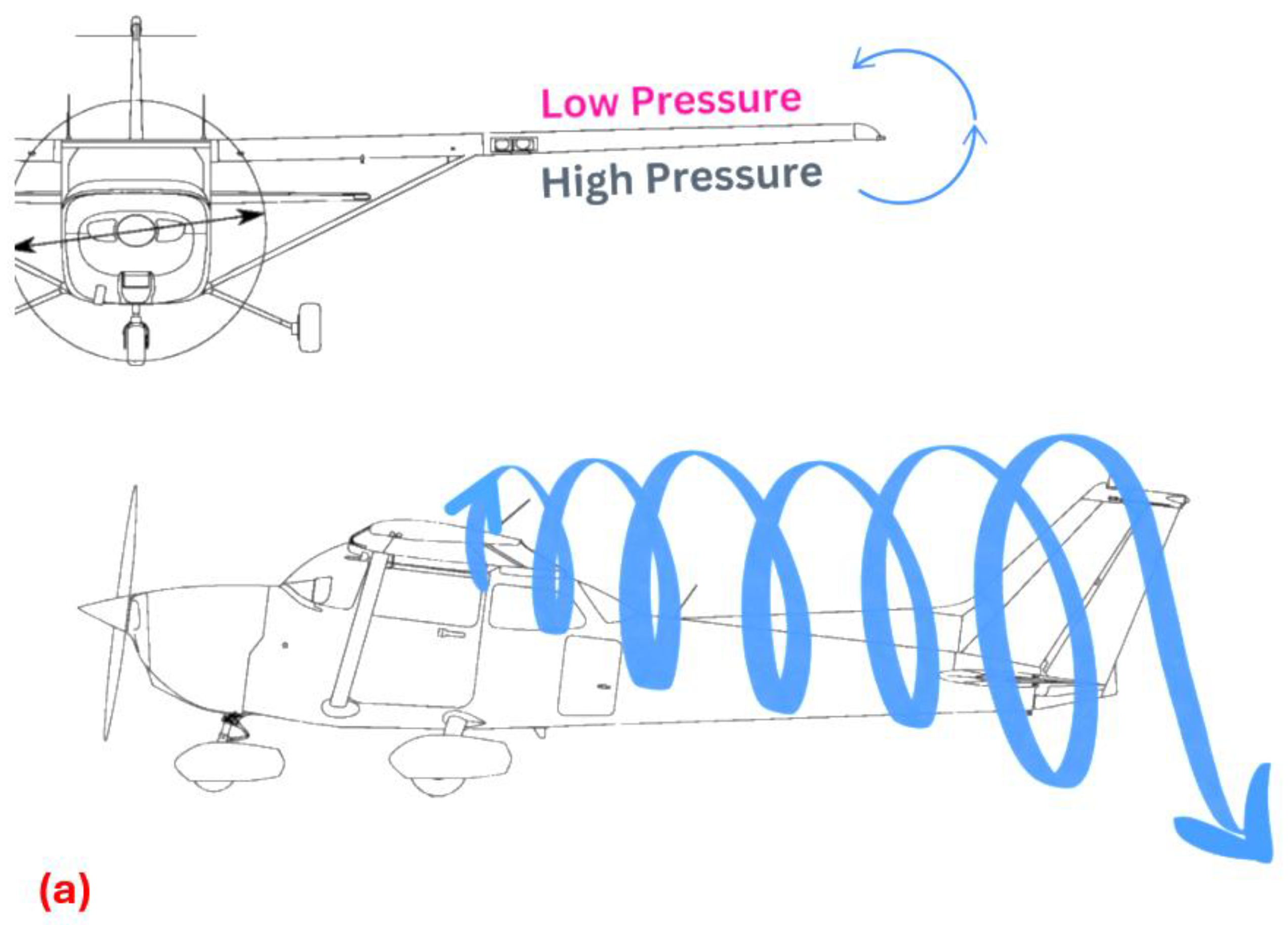
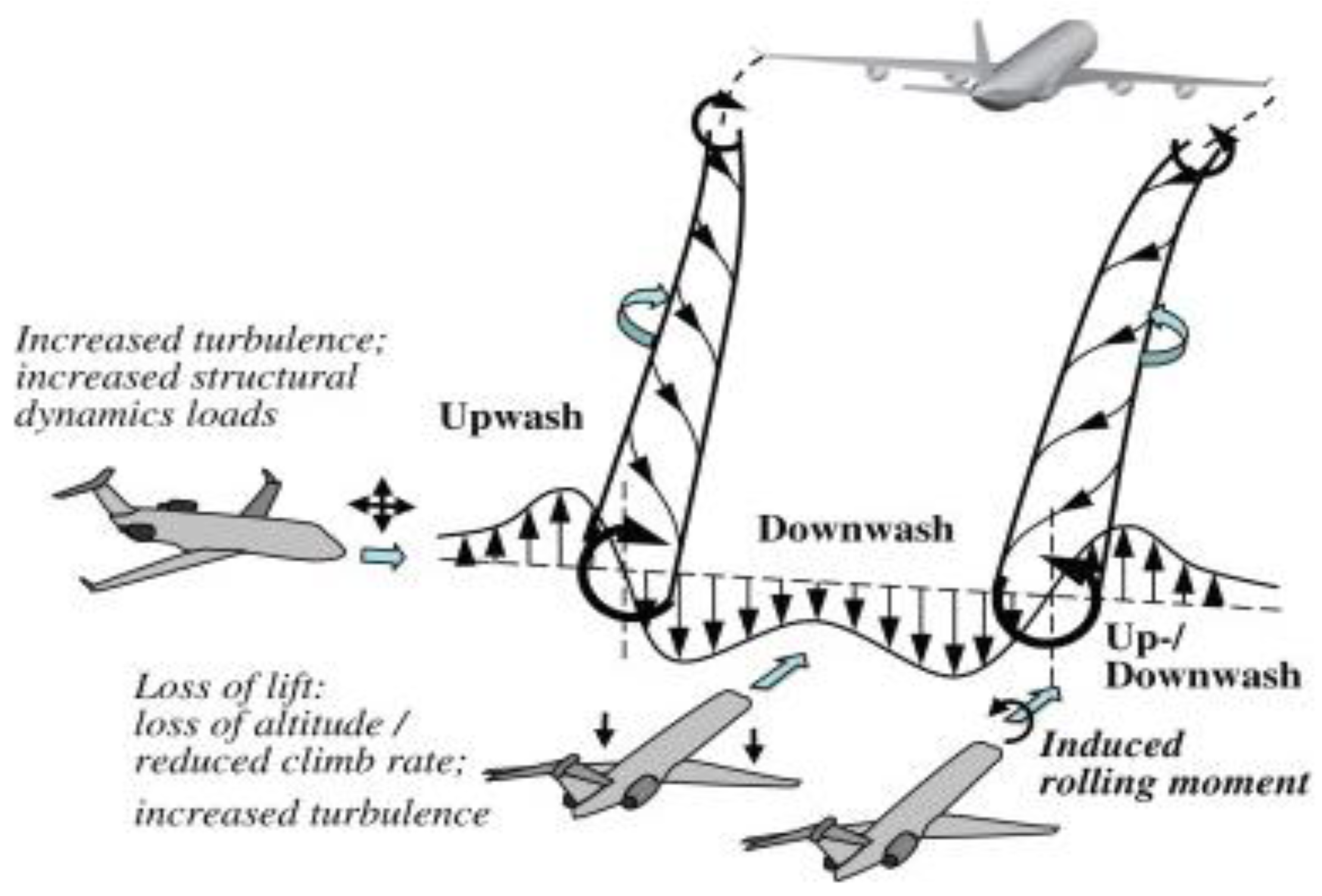
:1. Introduction
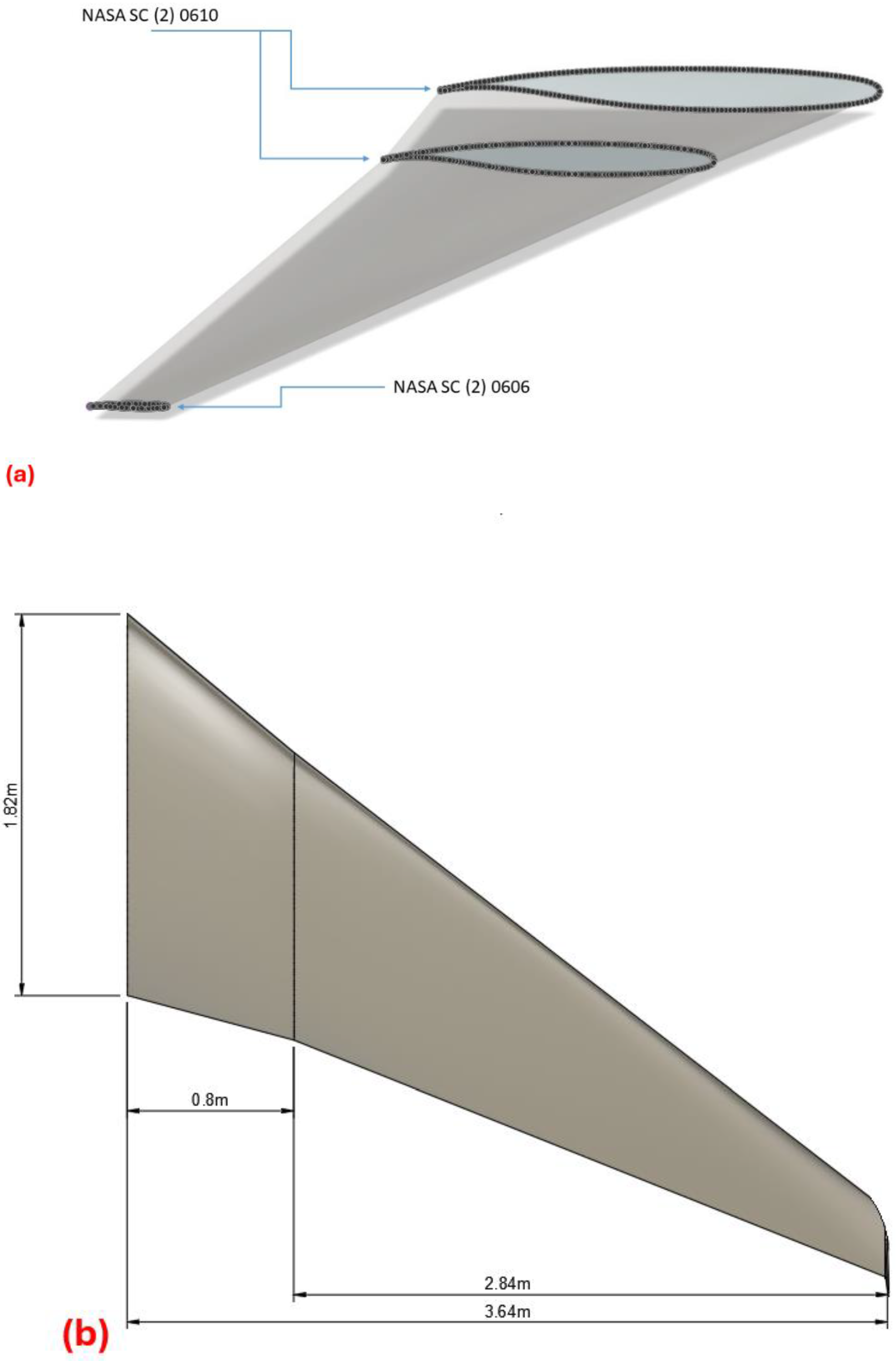
2. Computational Design
3. Computational Simulations
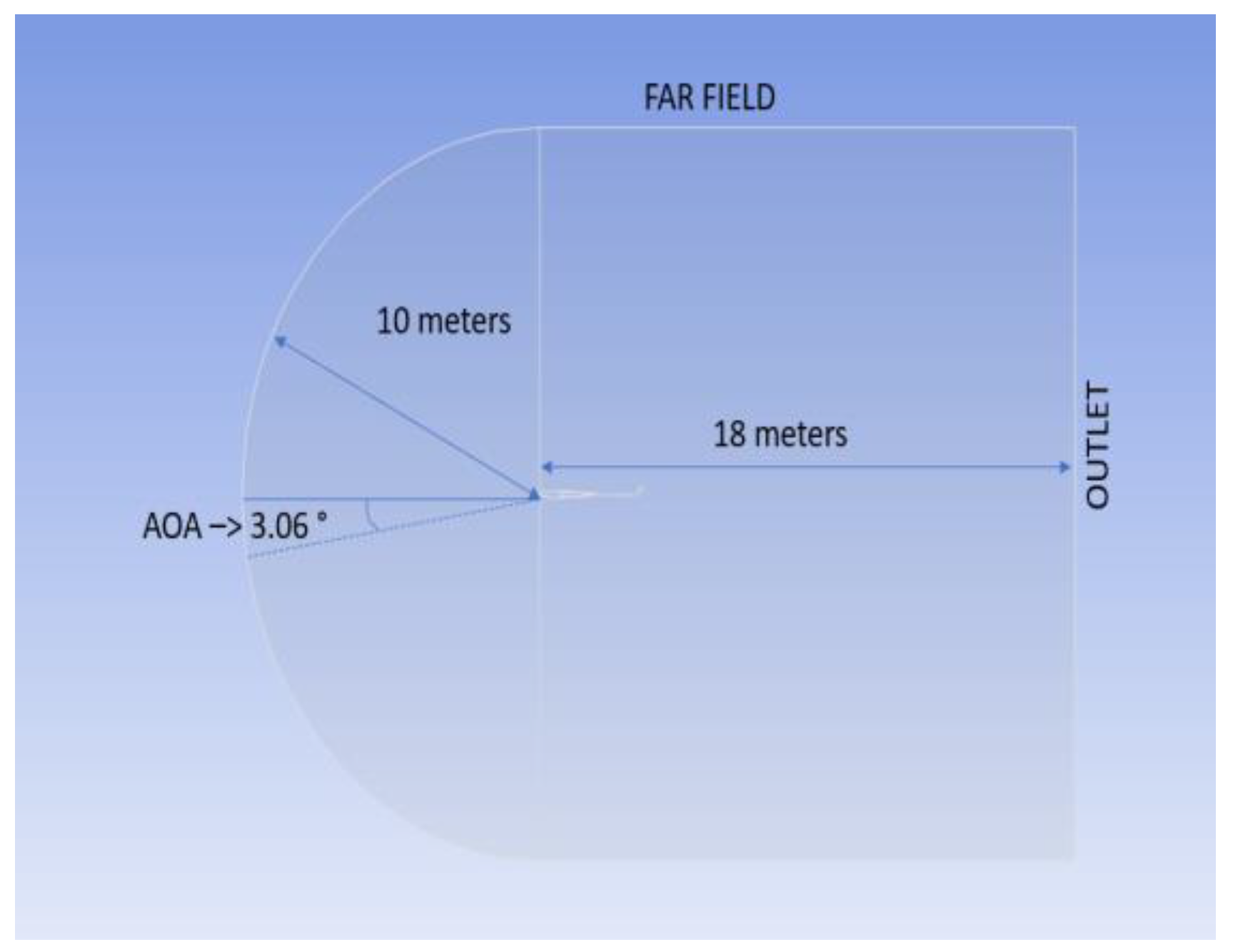
3.1. Computational Domain
3.2. Computational Mesh
3.3. Computational Analysis
4. Result Analysis and Discussion
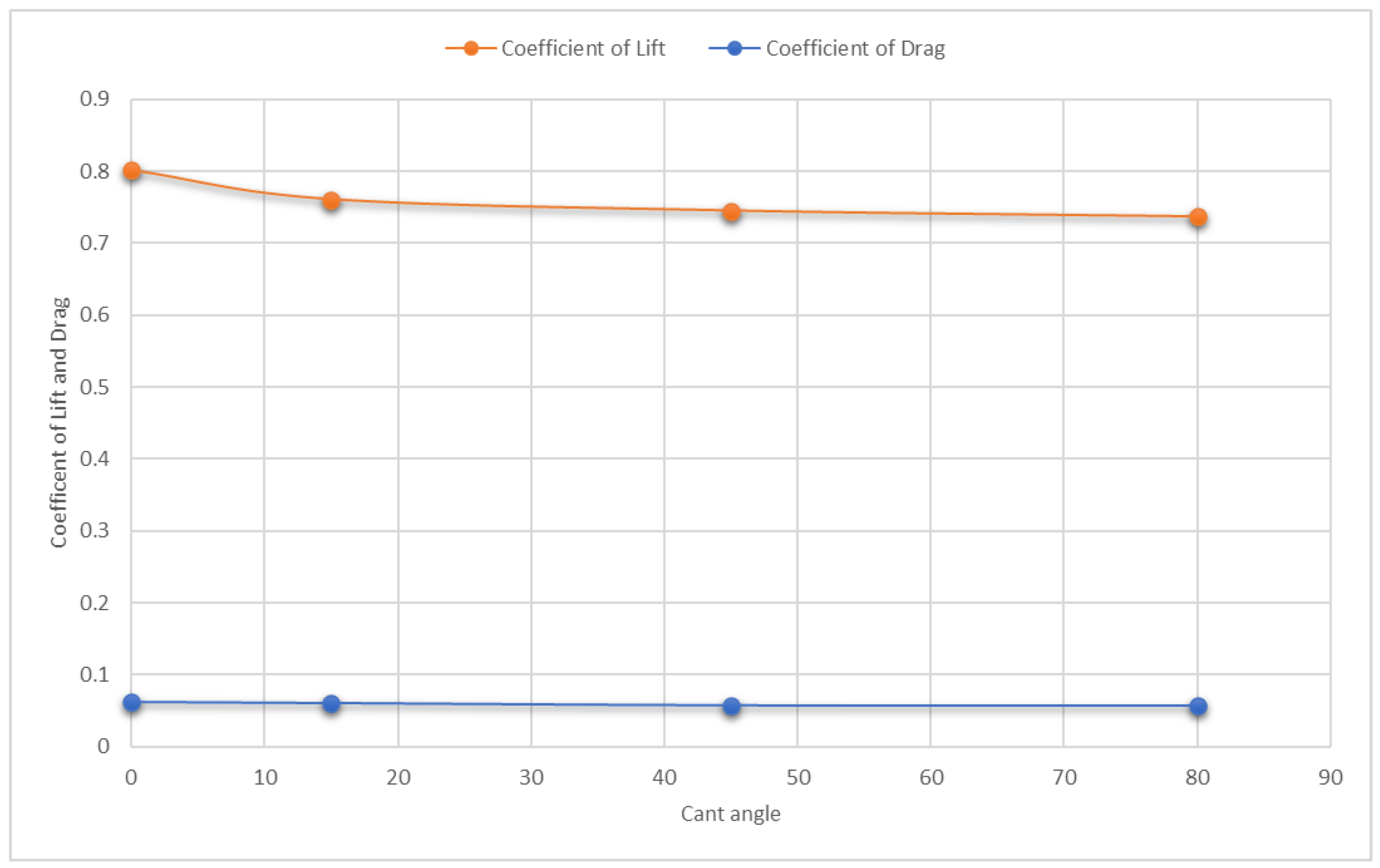
4.1. Lift Coefficient
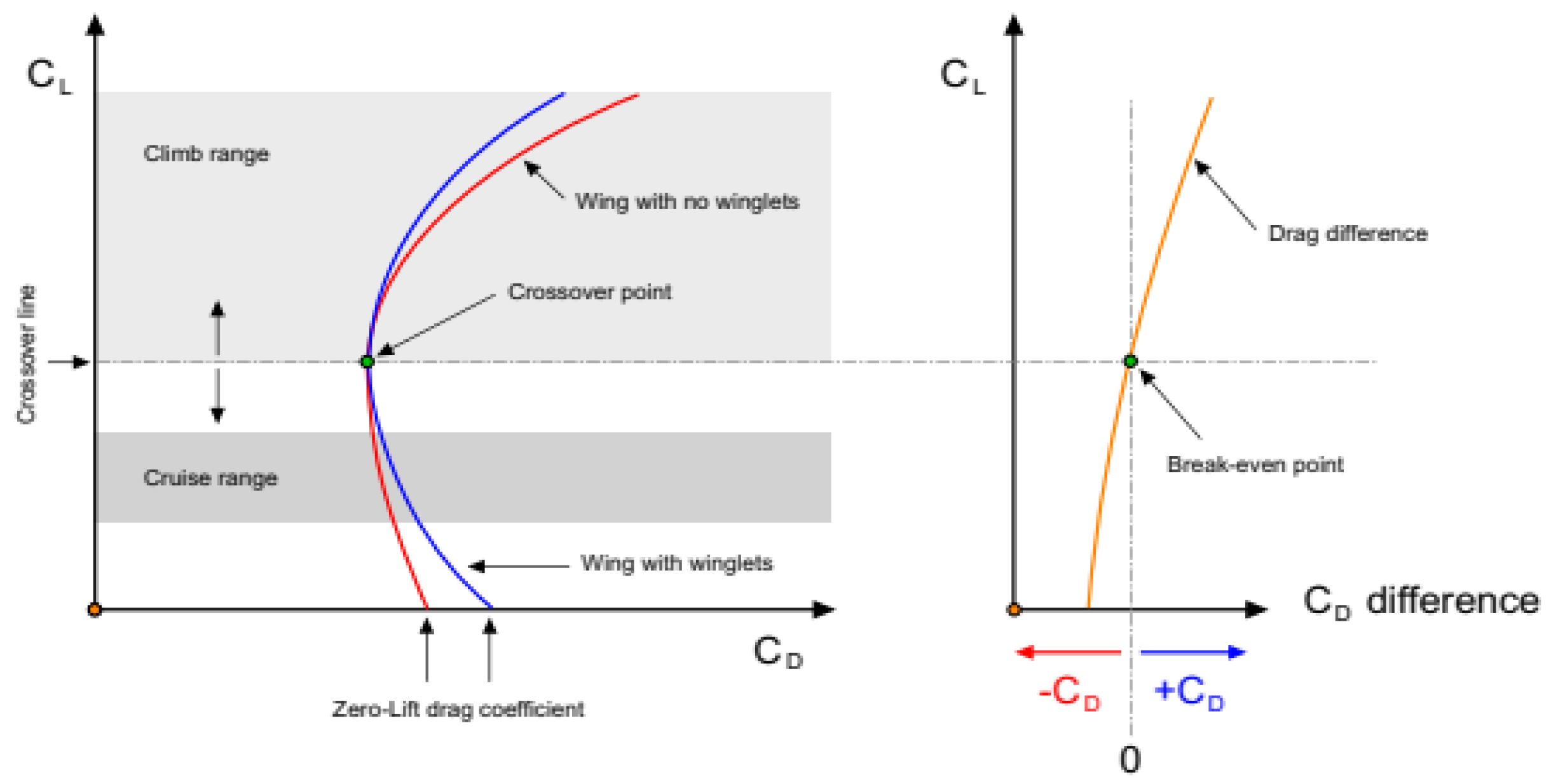
4.2. Drag Coefficient
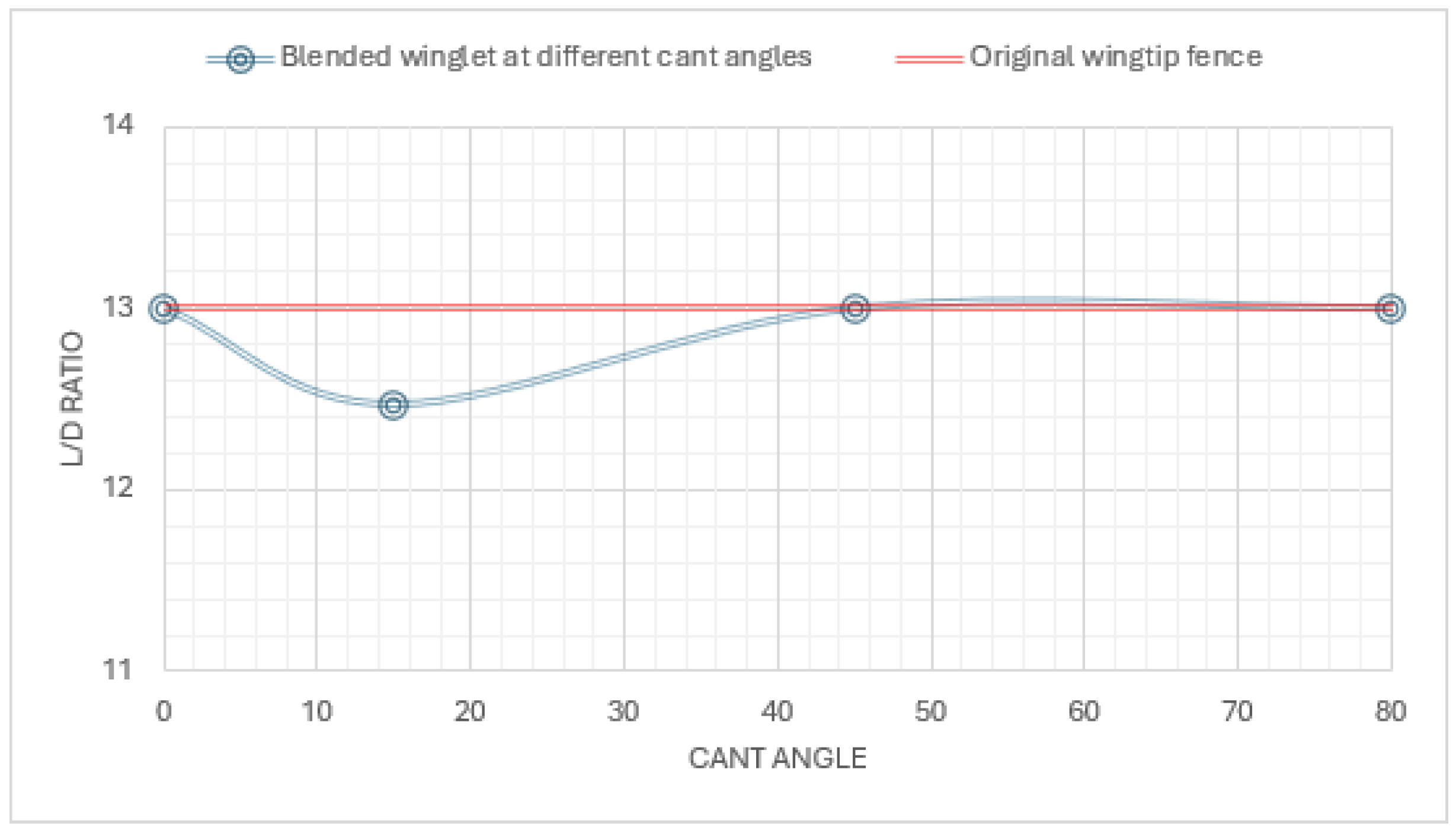
4.3. Lift to Drag Ratio
4.4. Alternative Wingtip for A380
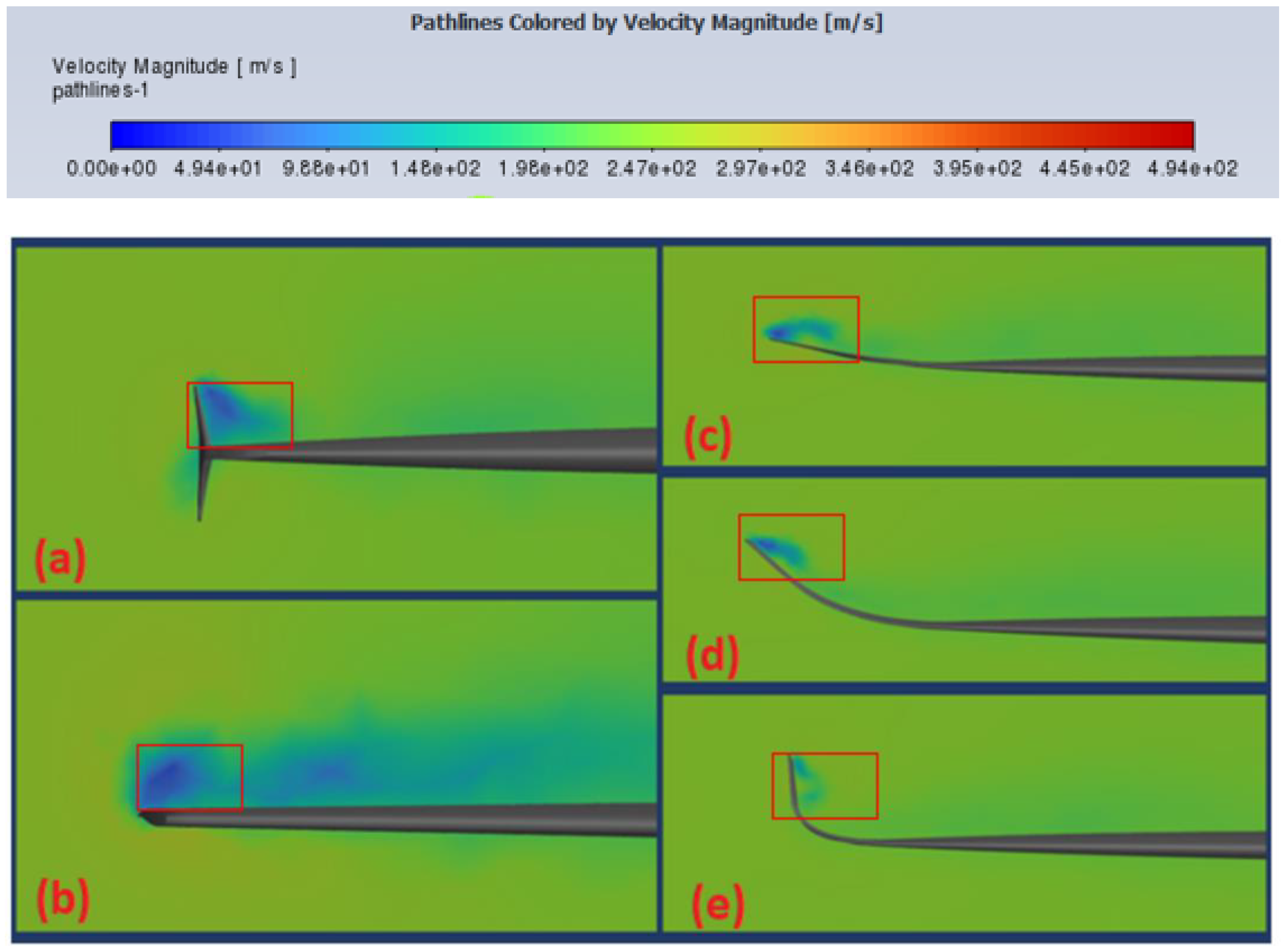
4.5. Wingtip Vortex Elevation
4.6. Downstream Wake Reduction
4.7. Discussion
5. Validation
5.1. Method Validation
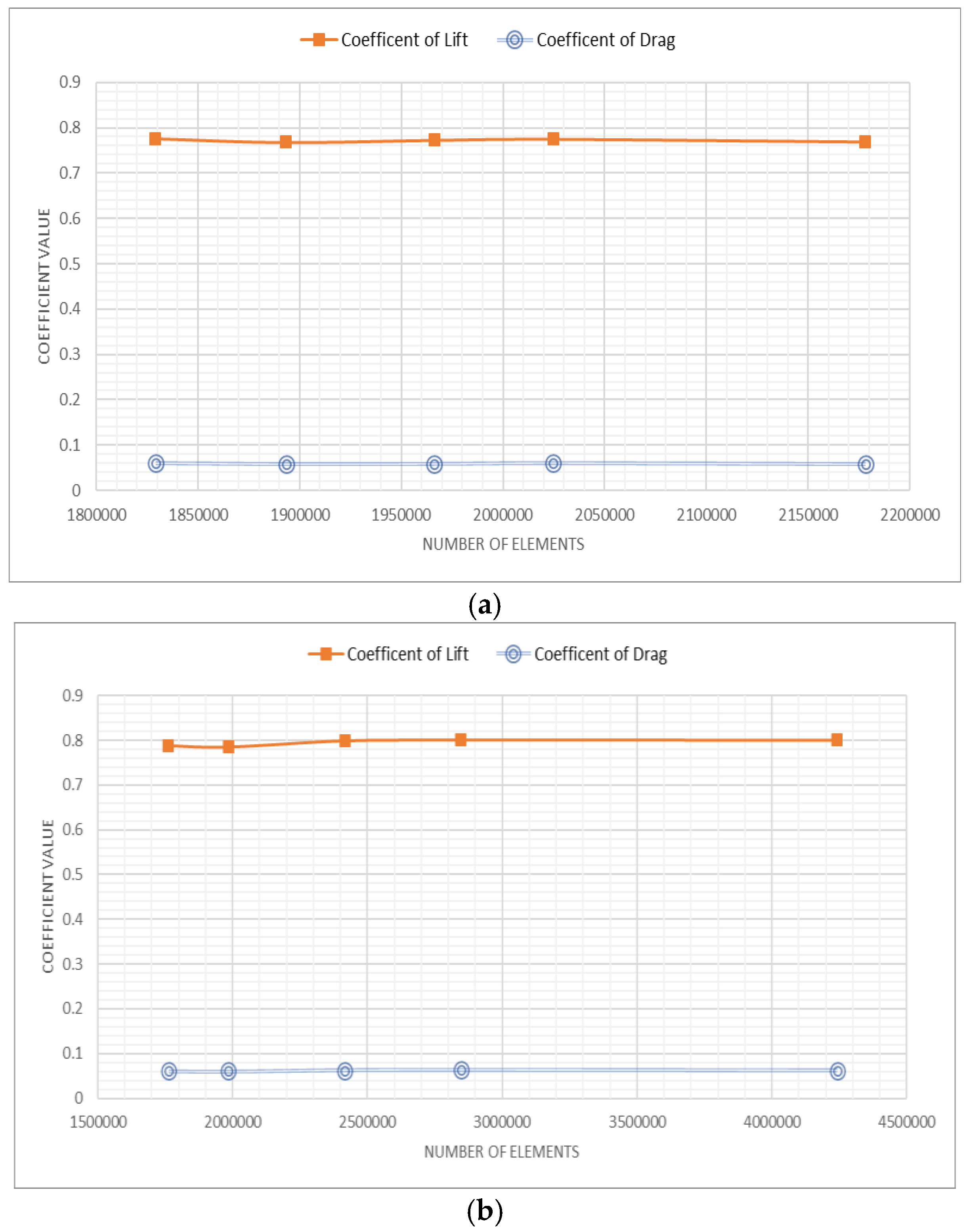
5.2. Mesh Validation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Department for Transport. Jet Zero Strategy, Jet Zero Strategy Delivering Net Zero Aviation by 2050. 2022. Available online: https://assets.publishing.service.gov.uk/media/62e931d48fa8f5033896888a/jet-zero-strategy.pdf (accessed on 23 August 2024).
- Kim, H.; Teter, J. International Energy Agency. Available online: https://www.iea.org/energy-system/transport/aviation (accessed on 26 March 2024).
- Price, D. The Impact of Winglets on Fuel Consumption and Aircraft Emissions, Cirium Aviation Analytics. 2022. Available online: https://www.cirium.com/thoughtcloud/impact-winglets-on-fuel-consumption-and-aircraft-emissions/ (accessed on 23 August 2024).
- Benson, T. What Is Lift? NASA: Washington, DC, USA, 2021. Available online: https://www.grc.nasa.gov/www/k-12/VirtualAero/BottleRocket/airplane/lift1.html (accessed on 23 August 2024).
- Anderson, J.D. Fundamentals of Aerodynamics, 6th ed.; McGraw-Hill Publishing Co.: New York, NY, USA, 2017. [Google Scholar]
- Houghton, E.L.; Carpenter, P.W.; Collicott, S.H.; Valentine, D.T. Aerodynamics for Engineering Students; Butterworth-Heinemann: Kidlington, UK, 2017. [Google Scholar]
- Narayan, G.; John, B. Effect of winglets induced tip vortex structure on the performance of subsonic wings. Aerosp. Sci. Technol. 2016, 58, 328–340. [Google Scholar] [CrossRef]
- Hrúz, M.; Pecho, P.; Bugaj, M.; Rostáš, J. Investigation of vortex structure behavior induced by different drag reduction devices in the near field. Transp. Res. Procedia 2022, 65, 318–328. [Google Scholar] [CrossRef]
- Pilot Institute, Induced Drag. 2023. Available online: https://pilotinstitute.com/induced-drag-explained/ (accessed on 23 August 2024).
- Maaz, A. The Dangers of Wake Turbulence and How It’s Managed by Pilots. 2022. Available online: https://simpleflying.com/the-dangers-of-wake-turbulence-and-how-its-managed-by-pilots/ (accessed on 23 August 2024).
- Kroo, I. Drag due to lift: Concepts for prediction and reduction. Annu. Rev. Fluid Mech. 2001, 33, 587–617. [Google Scholar]
- Abramowski, T. Numerical investigation of an airfoil in ground proximity. J. Theor. Appl. Mech. 2007, 45, 425–436. [Google Scholar]
- Breitsamter, C. Wake vortex characteristics of transport aircraft. Prog. Aerosp. Sci. 2011, 47, 89–134. [Google Scholar] [CrossRef]
- Regional Aviation Safety Group—Middle East, Wake Turbulence Separation in RVSM Airspace; International Civil Aviation Organization: Manama, Bahrain, 2017.
- Airbus, A380. Available online: https://www.airbus.com/en/products-services/commercial-aircraft/passenger-aircraft/a380 (accessed on 29 August 2024).
- SKYBRARY: ICAO, Wake Turbulence Category. Available online: https://skybrary.aero/articles/icao-wake-turbulence-category (accessed on 2 April 2024).
- Benson, T. L/D Ratio, NASA. Available online: https://www.grc.nasa.gov/www/k-12/VirtualAero/BottleRocket/airplane/ldrat.html#:~:text=Lift%20and%20drag%20are%20aerodynamic,aerodynamic%20efficiency%20of%20the%20airplane (accessed on 25 April 2024).
- Guzelbey, I.H.; Eraslan, Y.; Doğru, M.H. Effects of taper ratio on aircraft wing aerodynamic parameters: A comperative study. Eur. Mech. Sci. 2019, 3, 18–23. [Google Scholar] [CrossRef]
- Free Online Course Materials, Wing Taper Considerations, Massachusetts Institute of Technology. Available online: https://ocw.mit.edu/courses/16-01-unified-engineering-i-ii-iii-iv-fall-2005-spring-2006/67bd719047babb2159b4d6460250d66d_spl8a.pdf (accessed on 24 April 2024).
- Marimuthu, S.; Chinnathambi, D. Computational analysis of biomimetic butterfly valve. Bioinspired Biomim. Nanobiomater. 2020, 9, 223–232. [Google Scholar] [CrossRef]
- Marimuthu, S.; Chinnathambi, D. Computational analysis to enhance the compressible flow over an aerofoil surface. Aircr. Eng. Aerosp. Technol. 2021, 93, 925–934. [Google Scholar]
- Marimuthu, S.; Al-Rabeei, S.; Boha, H.A. Three-dimensional analysis of biomimetic aerofoil in transonic flow. Biomimetics 2022, 7, 20. [Google Scholar] [CrossRef] [PubMed]
- Marimuthu, S.; Natarajan, M.; Ramesh, R.; Murugesan, R. Hollow three-dimensional model for fuel reduction in aviation industry. Int. J. Interact. Des. Manuf. 2022. [Google Scholar] [CrossRef]
- Marimuthu, S.; Murugan, M.A.; Sivasathya, U.; Dharmalingham, S. Biomimetic in turbulence reduction-recent developments. J. Appl. Sci. Res. 2015, 11, 123–134. [Google Scholar]
- Selvanose, S.M.; Marimuthu, S.; Awan, A.W.; Daniel, K. NACA 2412 drag reduction using V-shaped riblets. Eng 2024, 5, 944–957. [Google Scholar] [CrossRef]
- Boldmethod, B. How Does Aspect Ratio Affect Your Wing? Online Flight Training Courses and CFI Tools 2022. Available online: https://www.boldmethod.com/learn-to-fly/aircraft-systems/how-does-aspect-ratio-affect-aircraft-wings/ (accessed on 23 August 2024).
- Leishman, J.G. Wing Shapes & Nomenclature, Introduction to Aerospace Flight Vehicles 2023. Available online: https://eaglepubs.erau.edu/introductiontoaerospaceflightvehicles/chapter/wing-shapes-and-nomenclature/ (accessed on 23 August 2024).
- Guerrero, J.; Sanguineti, M.; Wittkowski, K. CFD study of the impact of variable cant angle winglets on total drag reduction. Aerospace 2018, 5, 126. [Google Scholar] [CrossRef]
- Newman, D.M. Lift & Drag Effects of a Variable-Angle Winglet System. Bachelor’s Thesis, University of Vermont, Burlington, VT, USA, 2020. [Google Scholar]
- NASA. Winglets Save Billions of Dollars in Fuel Costs. Available online: https://spinoff.nasa.gov/Spinoff2010/t_5.html (accessed on 23 August 2024).
- Ghaith, F.A.; Haque, M.F. Elastodynamic Modeling and Simulation of the Airbus A380 Wing. In Proceedings of the 26th Conference on Mechanical Vibration and Noise, Buffalo, NY, USA, 17–20 August 2014; Volume 8. [Google Scholar]
- NASA, Supercritical Airfoils, A Matrix of Family-Related Airfoils. Available online: https://ntrs.nasa.gov/api/citations/19900007394/downloads/19900007394.pdf (accessed on 28 April 2024).
- Airbus Aircraft, Autocad 3-View Aircraft Drawings. Available online: https://aircraft.airbus.com/en/customer-care/fleet-wide-care/airport-operations-and-aircraft-characteristics/autocad-3-view-aircraft-drawings (accessed on 23 April 2024).
- Lutton, M.J. Comparison of C- and O-Grid Generation Methods Using a NACA 0012 Airfoil, Defense Technical Information Center. 1989. Available online: https://apps.dtic.mil/sti/citations/ADA216375 (accessed on 11 April 2024).
- Sijal, A. Understanding Y+ for CFD Simulations. 2019. Available online: https://www.linkedin.com/pulse/understanding-y-cfd-simulation-sijal-ahmed (accessed on 23 August 2024).
- Cadence, Hexahedral Mesh vs. Tetrahedral: Comparing high-Quality Meshing, 2022. Available online: https://resources.system-analysis.cadence.com/blog/msa2022-hexahedral-mesh-vs-tetrahedral-comparing-high-quality-meshing (accessed on 23 August 2024).
- Fatchurrohman, N.; Chia, S.T. Performance of hybrid nano-micro reinforced MG metal matrix composites brake calliper: Simulation approach. IOP Conf. Ser. Mater. Sci. Eng. 2017, 257, 012060. [Google Scholar] [CrossRef]
- Hall, N. Navier-Stokes Equations; NASA: Washington, DC, USA, 2021. Available online: https://www.grc.nasa.gov/www/k-12/airplane/nseqs.html (accessed on 9 April 2024).
- Andersson, B.; Andersson, R.; Hakansson, L. Computational Fluid Dynamics for Engineers; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Wilcox, D.C. Turbulence Modelling for CFD; DCW Industries: La Canada, CA, USA, 2006. [Google Scholar]
- Goyal, S.G. Selection of Turbulence Model for Analysis of Airfoil Wing using CFD. Int. Res. J. Eng. Technol. 2021, 8, 2608. [Google Scholar]
- Kamaraj, A. Pressure Based vs. Density Based Solver. 2018. Available online: https://www.linkedin.com/pulse/pressure-based-vs-density-solver-aravinth-kamaraj/ (accessed on 6 April 2024).
- The Emirates A380 Fleet, Our Fleet: The Emirates Experience, Emirates United Kingdom, The Emirates A380. Available online: https://www.emirates.com/uk/english/experience/our-fleet/a380/ (accessed on 6 April 2024).
- Reynolds Number; NASA: Washington, DC, USA. Available online: https://www.grc.nasa.gov/www/k-12/airplane/reynolds.html (accessed on 7 January 2024).
- Guerrero, J.E.; Sanguineti, M.; Wittkowski, K. Variable cant angle winglets for improvement of aircraft flight performance. Meccanica 2020, 55, 1917–1947. [Google Scholar] [CrossRef]
- Gasparini, R. Mesh Sensitivity Study for CFD Projects: Knowledge Base, SimScale. 2022. Available online: https://www.simscale.com/knowledge-base/mesh-sensitivity-cfd/#:~:text=A%20mesh%20sensitivity%20study%20(also,solution%20changes%20with%20each%20mesh (accessed on 22 April 2024).





| Class | Maximum Take-Off Weight (Kilograms) | Name of the Aircraft |
|---|---|---|
| J (Super) | 560,000 | Airbus A380 |
| H (Heavy) | ≥136,000 | Boeing 747-8 |
| M (Medium) | <136,000 >7000 | Airbus A320 |
| L (Light) | ≤7000 | Embraer Phenom 100 |
| Wing/Winglet | Cant Angle (Degree) | Length (m) |
|---|---|---|
| Wing (1:10 ratio) | N/A | 3.637 |
| Winglet 1 | 0 | 0.5455 |
| Winglet 2 | 15 | 0.4561 |
| Winglet 3 | 45 | 0.3954 |
| Winglet 4 | 80 | 0.2013 |
| Cant Angle | Lift Coefficient | Change in Lift (%) |
|---|---|---|
| 0 | 0.802 | 3.886 |
| 15 | 0.761 | −1.425 |
| 45 | 0.745 | −3.497 |
| 80 | 0.737 | −4.533 |
| Wingtip Fence (A380 Wing) | 0.772 | - |
| Cant Angle | Drag Coefficient | Change in Drag (%) |
|---|---|---|
| 0 | 0.063 | 8.621 |
| 15 | 0.061 | 5.172 |
| 45 | 0.058 | 0.000 |
| 80 | 0.057 | −1.724 |
| Wingtip Fence (A380 Wing) | 0.058 | - |
| Model | Lift Coefficient | Drag Coefficient |
|---|---|---|
| Guerrero’s ONERA wing | 0.2608 | 0.01863 |
| Redesigned ONERA wing | 0.2647 | 0.01805 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinto, J.C.; Marimuthu, S.; Rajendran, P.; Natarajan, M.; Murugesan, R. Computational Analysis of Blended Winglet Designs to Reduce the Wake Turbulence on the Airbus A380 Wingtip. Eng 2025, 6, 68. https://doi.org/10.3390/eng6040068
Pinto JC, Marimuthu S, Rajendran P, Natarajan M, Murugesan R. Computational Analysis of Blended Winglet Designs to Reduce the Wake Turbulence on the Airbus A380 Wingtip. Eng. 2025; 6(4):68. https://doi.org/10.3390/eng6040068
Chicago/Turabian StylePinto, Joseph Ciano, Siva Marimuthu, Parvathy Rajendran, Manikandan Natarajan, and Rajadurai Murugesan. 2025. "Computational Analysis of Blended Winglet Designs to Reduce the Wake Turbulence on the Airbus A380 Wingtip" Eng 6, no. 4: 68. https://doi.org/10.3390/eng6040068
APA StylePinto, J. C., Marimuthu, S., Rajendran, P., Natarajan, M., & Murugesan, R. (2025). Computational Analysis of Blended Winglet Designs to Reduce the Wake Turbulence on the Airbus A380 Wingtip. Eng, 6(4), 68. https://doi.org/10.3390/eng6040068