Lurie Control Systems Applied to the Sudden Cardiac Death Problem Based on Chua Circuit Dynamics
Abstract
:1. Introduction
- The demonstration in Section 3.1 that the Chua circuit is a particular case of a Lurie control system;
- The main contribution of this work is the presentation, demonstration, and validation of Theorem 3 via the Chua circuit. This theorem introduces a novel approach for controller synthesis based on the mixed sensitivity technique for time-delay systems. Furthermore, the theorem is not limited to the control of Chua’s circuits with or without delay but extends to a broader class of dynamical systems, specifically Lurie-type SISO systems with or without delay and nonlinearities mapped by sector conditions. This generalization significantly expands the applicability of the proposed method, enabling its use in various systems beyond the Osaka model, thereby reinforcing its originality and contribution to the field of robust control of chaotic or nonlinear systems;
- Controller design via Matlab for Chua circuits with and without delay that simulate the dynamics between SNA, HR, and BP in SCD.
2. Problem Statement
3. Theoretical Basis
3.1. Lurie Control System
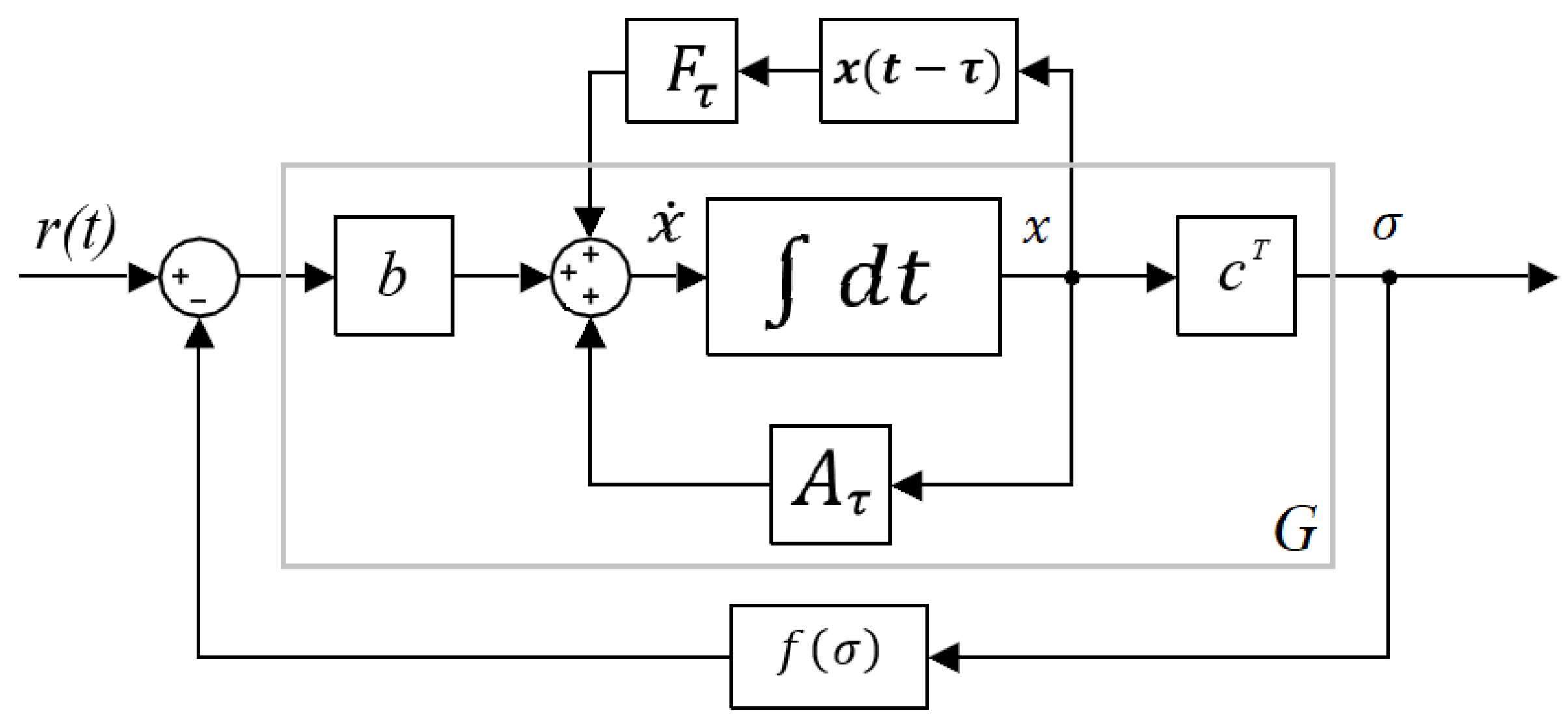
3.2. Mixed-Sensitivity for Lurie Control Systems
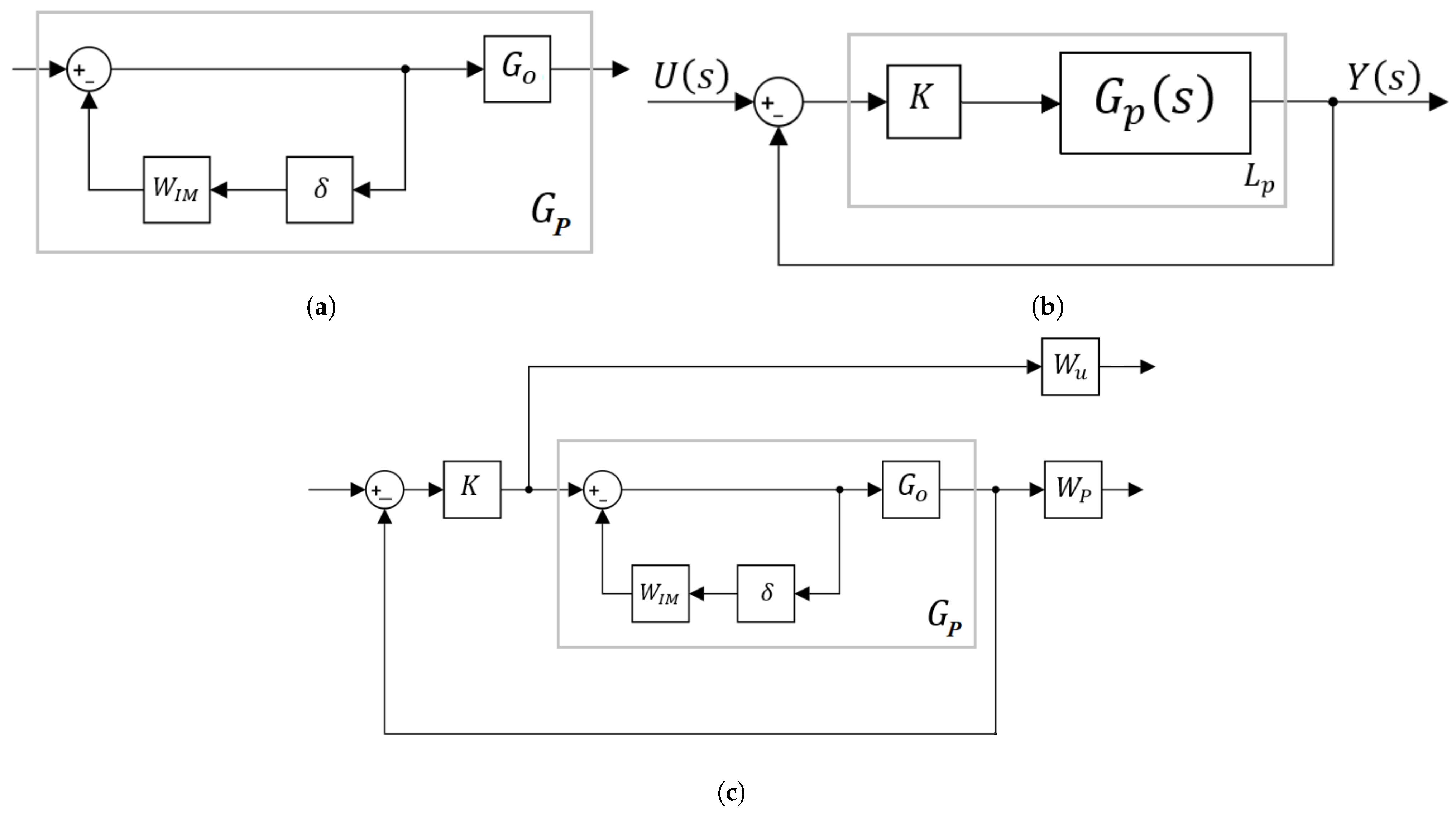
3.3. Padé Approximations
4. Main Results
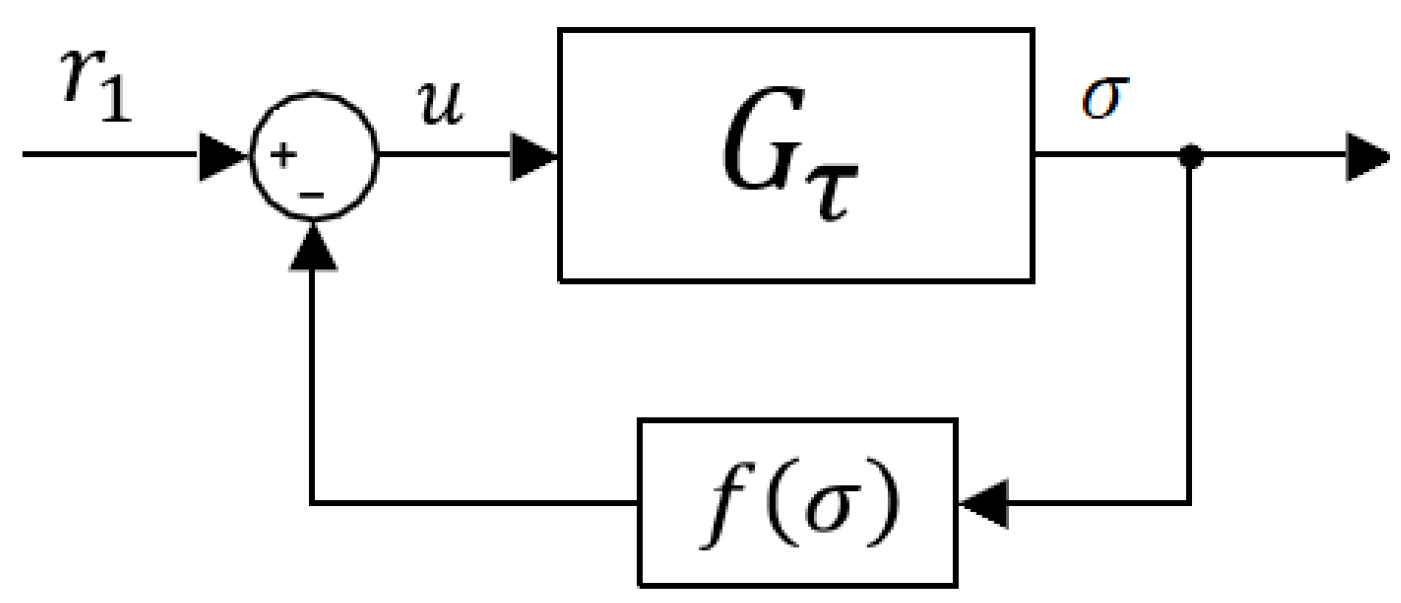
4.1. Theorem for the Synthesis of Lurie SISO Control Systems with Delay
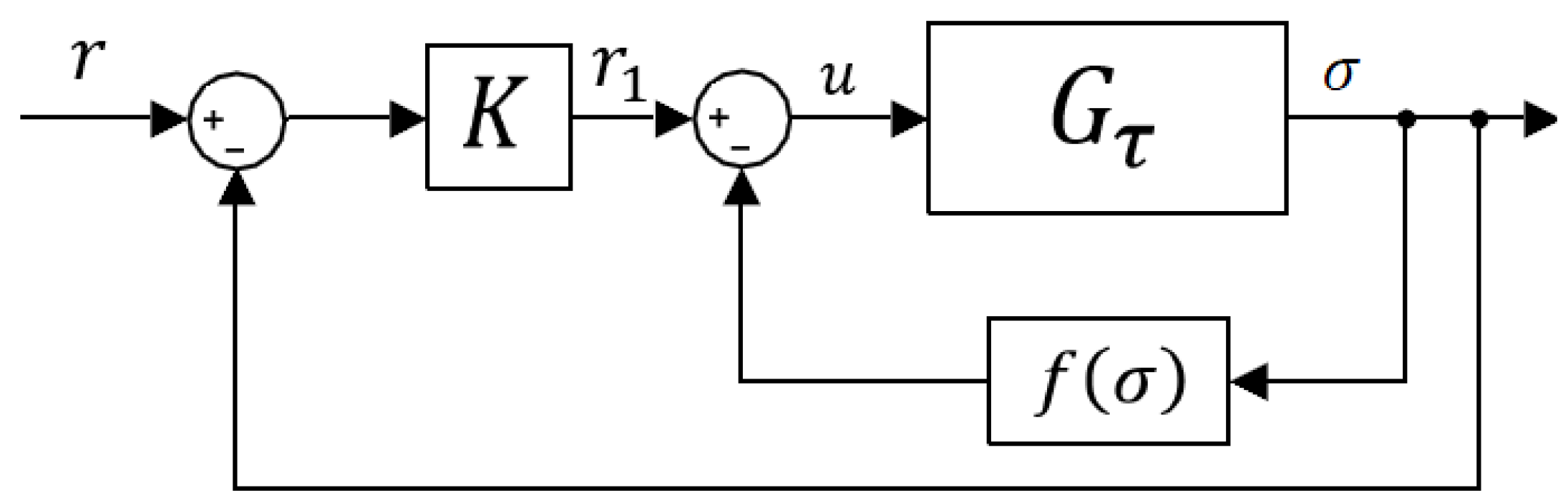
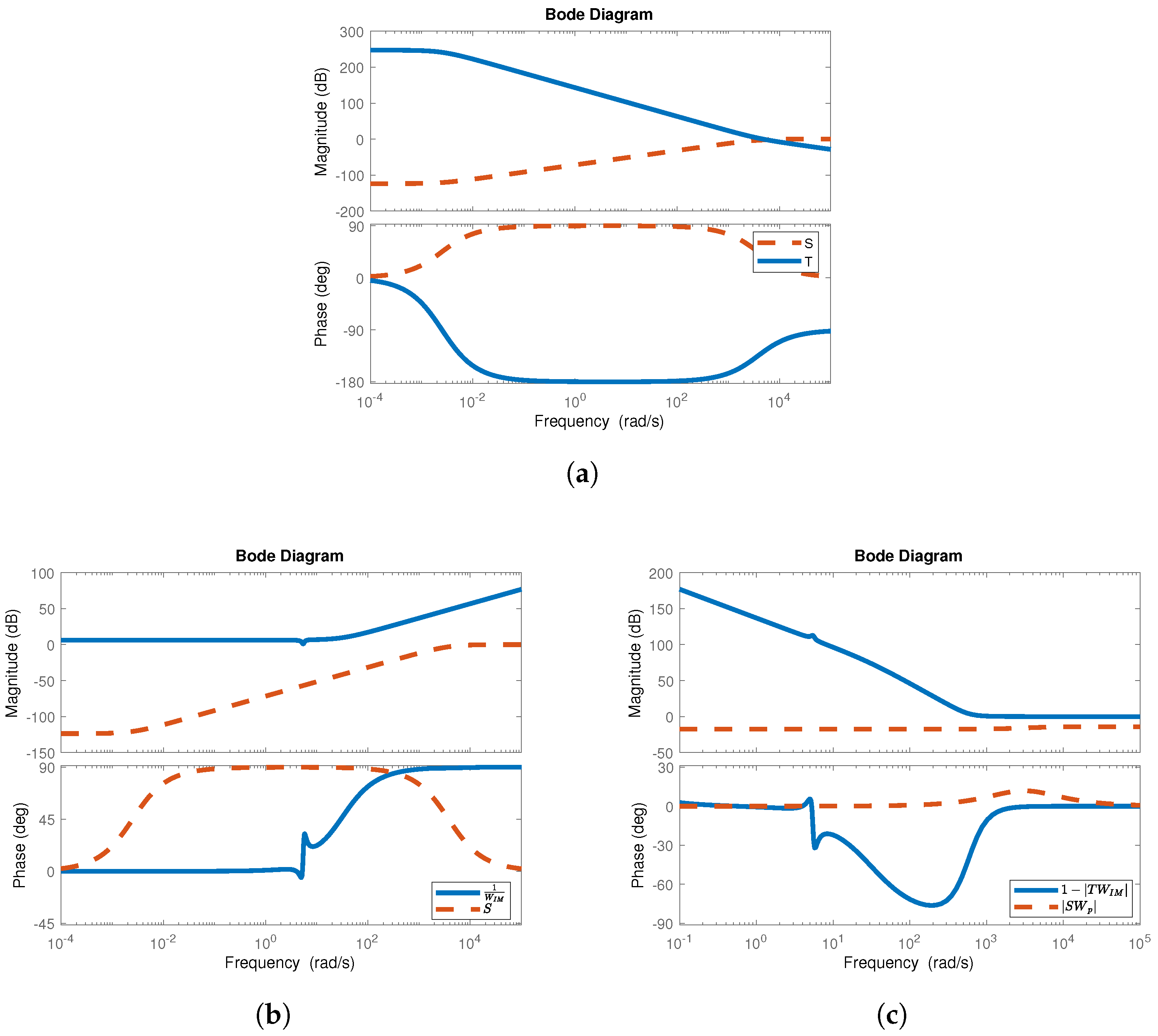
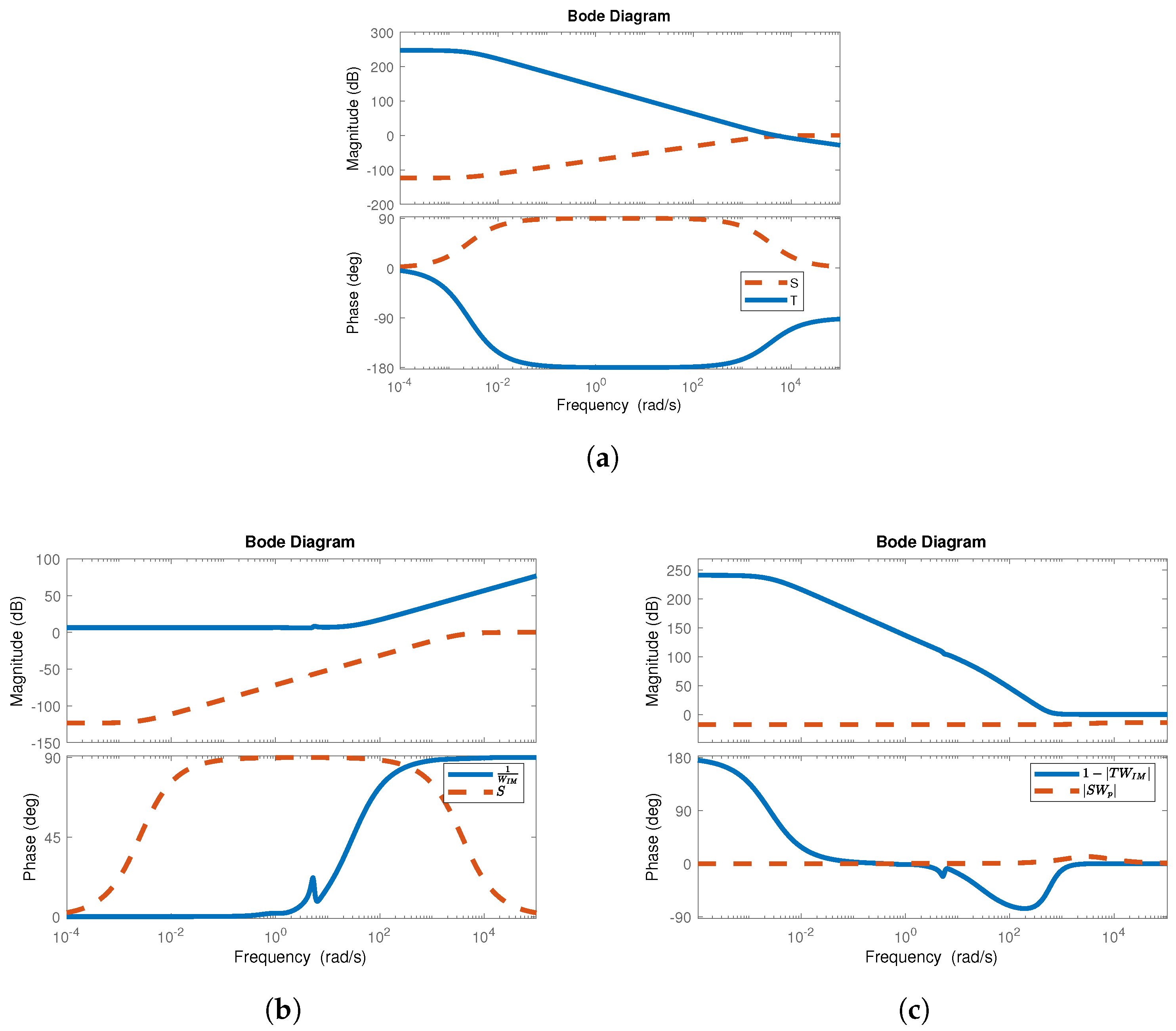
4.2. Controller Design and Simulations
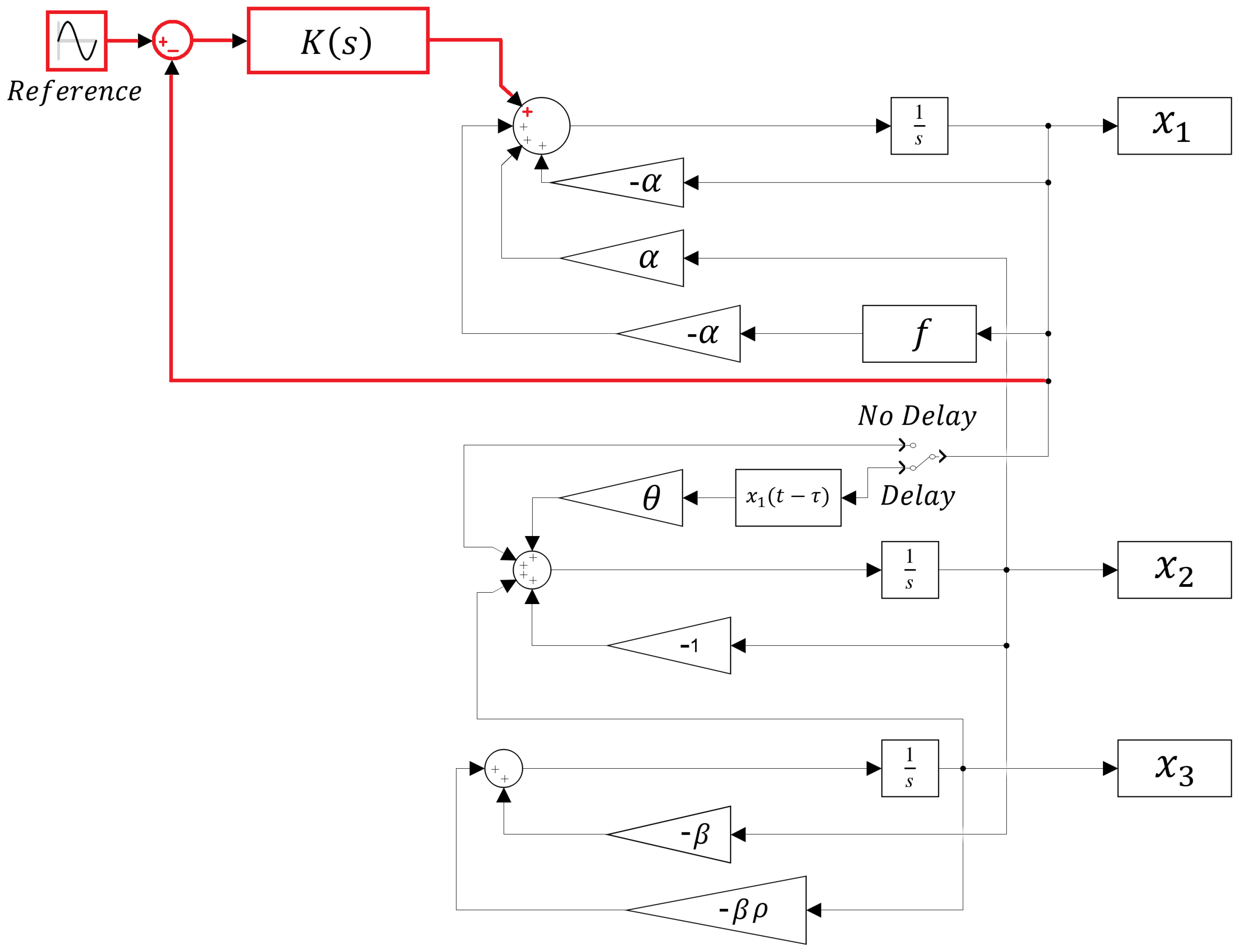
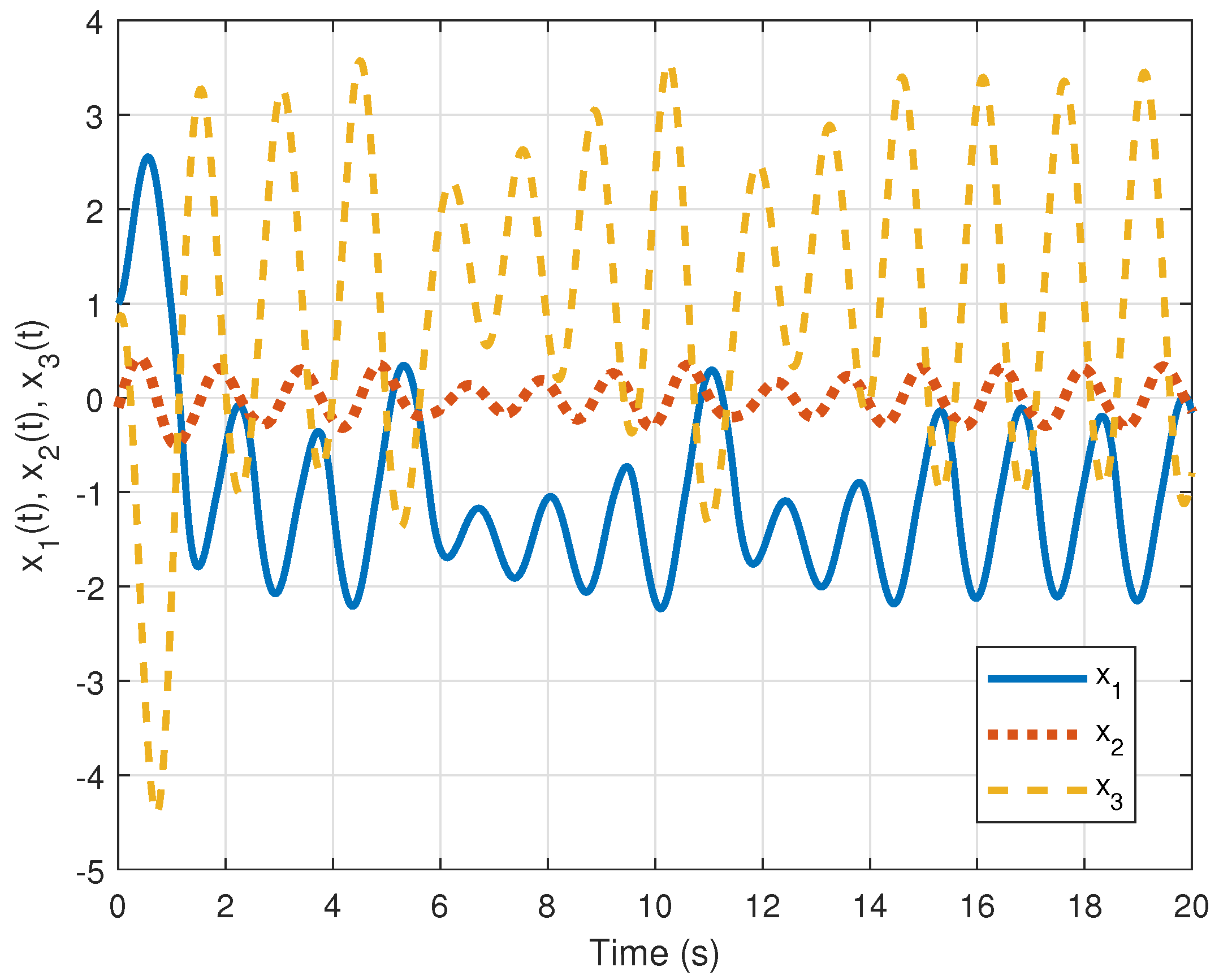
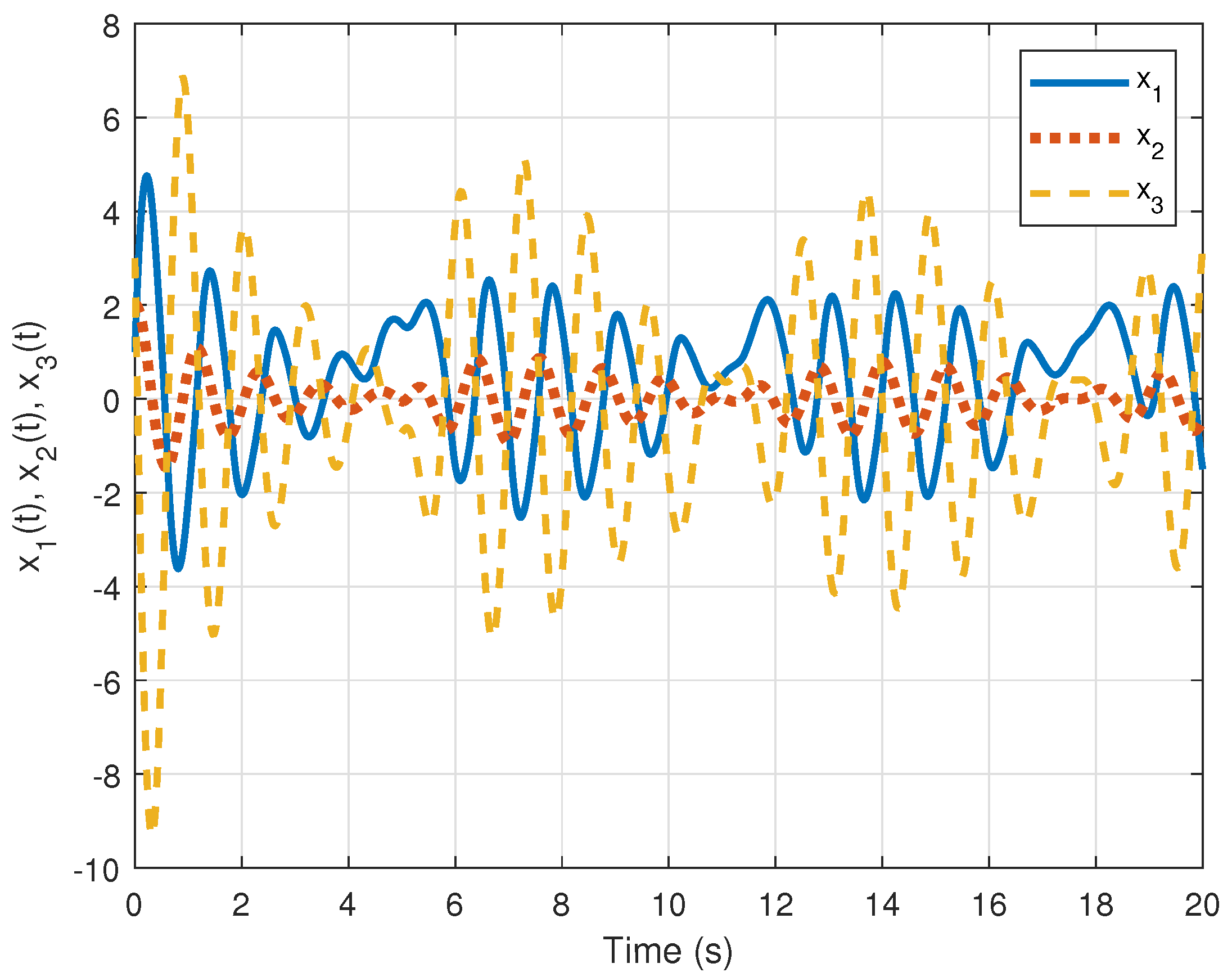
4.2.1. Controller for the Chua Circuit (1) That Models HR, SNA, and BP in the SCD
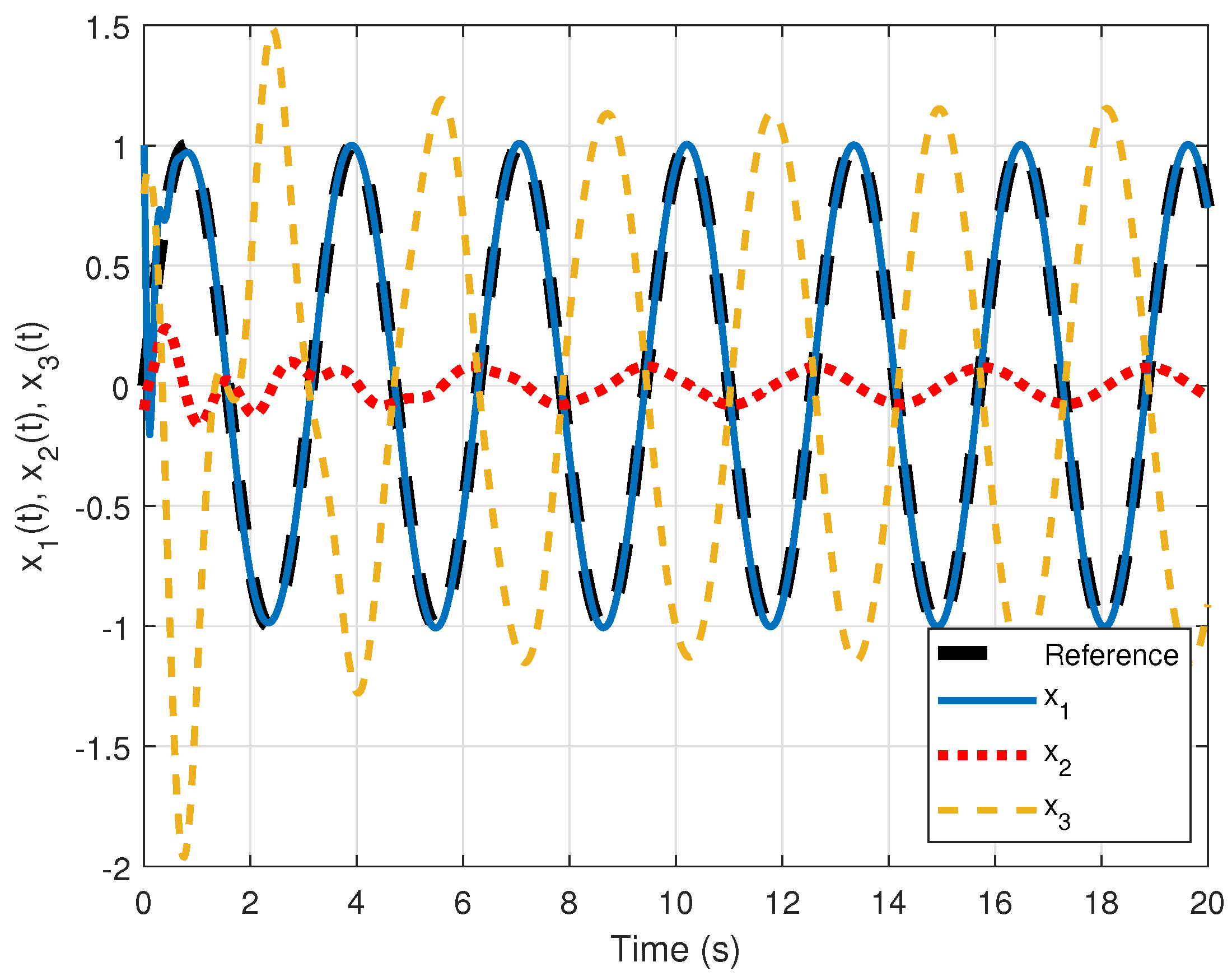
4.2.2. Controller for the Delayed Chua Circuit (3)
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BP | Blood pressure |
| ICD | Implantable cardioverter defibrillator |
| HR | Heart rate |
| ODE | Ordinary differential equations |
| SCD | Sudden cardiac death |
| SISO | Single-input–single-output |
| SNA | Sympathetic nerve activity |
References
- Zhao, S.; Ching, C.K.; Huang, D.; Liu, Y.B.; Rodriguez-Guerrero, D.A.; Hussin, A. Improve SCA Investigators. Regional disparities and risk factors of mortality among patients at high risk of sudden cardiac death in emerging countries: A nonrandomized controlled trial. BMC Med. 2024, 22, 130. [Google Scholar] [CrossRef] [PubMed]
- Zipes, D.P.; Wellens, H.J. Sudden cardiac death. Circulation 1998, 98, 2334–2351. [Google Scholar] [CrossRef] [PubMed]
- Zadok, O.I.B.; Agmon, I.N.; Neiman, V.; Eisen, A.; Golovchiner, G.; Bental, T.; Barsheshet, A. Implantable cardioverter defibrillator for the primary prevention of sudden cardiac death among patients with cancer. Am. J. Cardiol. 2023, 191, 32–38. [Google Scholar] [CrossRef]
- Cavalcanti, R.; Aboul-Hosn, N.; Morales, G.; Abdel-Latif, A. Implantable cardioverter defibrillator for the primary prevention of sudden cardiac death in patients with nonischemic cardiomyopathy. Angiology 2018, 69, 297–302. [Google Scholar] [CrossRef]
- Philippon, F.; Domain, G.; Sarrazin, J.F.; Nault, I.; O’Hara, G.; Champagne, J.; Steinberg, C. Evolution of devices to prevent sudden cardiac death: Contemporary clinical impacts. Can. J. Cardiol. 2022, 38, 515–525. [Google Scholar] [CrossRef]
- Osaka, M. A modified chua circuit simulates a v-shaped trough in autonomic activity as a precursor of sudden cardiac death. Int. J. Bifurc. Chaos 2011, 21, 2713–2722. [Google Scholar] [CrossRef]
- Vrana, M.; Pokorny, J.; Marcian, P.; Fejfard, Z. Class I and III antiarrhythmic drugs for prevention of sudden cardiac death and management of postmyocardial infarction arrhythmias. A review. Biomed. Pap. Med. Fac. Palacky Univ. Olomouc 2013, 157, 114–124. [Google Scholar] [CrossRef]
- Osaka, M. Sudden Cardiac Death from the Perspective of Nonlinear Dynamics. J. Nippon. Med. Sch. 2018, 85, 11–17. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Rasappan, S. Global chaos synchronization of n-scroll Chua circuit and Lur’e system using backstepping control design with recursive feedback. Arab. J. Sci. Eng. 2014, 39, 3351–3364. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, H.; Zhang, J.; Wang, L. Event-based predefined-time anti-synchronization for unified chaotic systems and the application to Chua’s circuit. Chaos Solitons Fractals 2024, 188, 115534. [Google Scholar] [CrossRef]
- Amiri, S.; Seyed Moosavi, S.M.; Forouzanfar, M.; Aghajari, E. Addressing asymmetric saturation in chaotic Chua’s circuit switched system: A combined adaptive sliding mode strategy. Int. J. Adapt. Control Signal Process. 2024, 38, 968–985. [Google Scholar] [CrossRef]
- Xing, X. Fixed-time Lyapunov criteria of stochastic impulsive time-delay systems and its application to synchronization of Chua’s circuit networks. Neurocomputing 2025, 616, 128943. [Google Scholar] [CrossRef]
- Pinheiro, R.F.; Colón, D. Controller by H∞ mixed-sensitivity design (S/KS/T) for Lurie type systems. In Proceedings of the 24th ABCM International Congress of Mechanical Engineering, Curitiba, Brazil, 3–8 December 2017. [Google Scholar]
- Pinheiro, R.F.; Colón, D.; Reinoso, L.L.R. Relating Lurie’s problem, Hopfield’s network and Alzheimer’s disease. In Congresso Brasileiro de Automática-CBA; Sociedade Brasileira de AUTOMATICA: Campinas, Brazil, 2020; Volume 2, pp. 1–8. [Google Scholar]
- Pinheiro, R.F.; Colón, D. On the μ-analysis and synthesis of MIMO Lurie-type systems with application in complex networks. Circuits Syst. Signal Process. 2021, 40, 193–232. [Google Scholar] [CrossRef]
- Pinheiro, R.F. The Lurie Problem and Its Relationships with Artificial Neural Networks and Alzheimer-like Disease. Ph.D. Thesis, University of São Paulo, São Paulo, Brazil, 2021. [Google Scholar]
- Pinheiro, R.F.; Colón, D. Robust digital controllers via H∞ design for Lurie type systems. J. Appl. Instrum. Control 2022, 10, 9–18. [Google Scholar]
- Pinheiro, R.F.; Colón, D. Analysis and synthesis of single-input-single-output Lurie type systems via H∞ mixed-sensitivity. Trans. Inst. Meas. Control 2022, 44, 133–143. [Google Scholar] [CrossRef]
- Pinheiro, R.F.; Colón, D.; Fonseca-Pinto, R. An improved Alzheimer-like disease computational model via delayed Hopfield network with Lurie control system for healing. TechRxiv 2023. [Google Scholar] [CrossRef]
- Pinheiro, R.F.; Colón, D. On the μ-analysis and synthesis for uncertain time-delay systems with Padé approximations. J. Frankl. Inst. 2024, 361, 106643. [Google Scholar] [CrossRef]
- Pinheiro, R.F.; Fonseca-Pinto, R.; Colón, D. A review of the Lurie problem and its applications in the medical and biological fields. AIMS Math. 2024, 9, 32962–32999. [Google Scholar] [CrossRef]
- Doyle, J. Analysis of feedback systems with structured uncertainties. IEE Proc. D (Control Theory Appl.) 1982, 129, 242–250. [Google Scholar] [CrossRef]
- Doyle, J. Structured uncertainty in control system design. In Proceedings of the 1985 24th IEEE Conference on Decision and Control, Fort Lauderdale, FL, USA, 11–13 December 1985; pp. 260–265. [Google Scholar]
- Zhou, K.; Doyle, J.C.; Glover, K. Robust and Optimal Control; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and Design, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Lurie, A.I.; Postnikov, V.N. On the theory of stability of control systems. Prikl. Mat. Mekh. 1944, 8, 246–248. [Google Scholar]
- Kazemy, A.; Farrokhi, M. Synchronization of chaotic Lur’e systems with state and transmission line time delay: A linear matrix inequality approach. Trans. Inst. Meas. Control 2017, 39, 1703–1709. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Tan, Y. Hidden extreme multistability with hyperchaos and transient chaos in a Hopfield neural network affected by electromagnetic radiation. Nonlinear Dyn. 2020, 99, 2369–2386. [Google Scholar] [CrossRef]
- Venkatesh, Y.V. Frequency-domain stability criteria for SISO and MIMO nonlinear feedback systems with constant and variable time-delays. Control Theory Technol. 2016, 14, 347–368. [Google Scholar] [CrossRef]
- Abtahi, S.F.; Yazdi, E.A. Robust control synthesis using coefficient diagram method and µ-analysis: An aerospace example. Int. J. Dyn. Control 2019, 7, 595–606. [Google Scholar] [CrossRef]
- Lee, C.M.; Juang, J.C. A novel approach to stability analysis of multivariable Lurie systems. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Niagara Falls, ON, Canada, 29 July–1 August 2005; pp. 199–203. [Google Scholar]
- Tan, N.; Atherton, D.P. Robustness analysis of control systems with mixed perturbations. Trans. Inst. Meas. Control 2003, 25, 163–184. [Google Scholar] [CrossRef]
- Sun, Z. Recent advances on analysis and design of switched linear systems. Control Theory Technol. 2017, 15, 242–244. [Google Scholar] [CrossRef]
- Imani, A. A multi-loop switching controller for aircraft gas turbine engine with stability proof. Int. J. Control. Autom. Syst. 2019, 17, 1359–1368. [Google Scholar] [CrossRef]
- Duan, W.; Du, B.; Li, Y.; Shen, C.; Zhu, X.; Li, X.; Chen, J. Improved sufficient LMI conditions for the robust stability of time-delayed neutral-type Lur’e systems. Int. J. Control Autom. Syst. 2018, 16, 2343–2353. [Google Scholar] [CrossRef]
- Wang, W.; Zeng, H.B. A looped functional method to design state feedback controllers for Lurie networked control systems. IEEE/CAA J. Autom. Sin. 2023, 10, 1093–1095. [Google Scholar] [CrossRef]
- Baker, G.; Grave-Morris, P.R. Padé Approximants; Addison-Wesley Publishing Company: Boston, MA, USA, 1981. [Google Scholar]
- MathWorks. mixsyn (Robust Control Toolbox). MathWorks. Available online: https://www.mathworks.com/help/robust/ref/dynamicsystem.mixsyn.html (accessed on 19 December 2024).
- Koleff, L.; Matakas, L.; Pellini, E. H-infinity current control of the LC coupled voltage source inverter. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 5347–5354. [Google Scholar]
- Zeng, H.B.; Zhai, Z.L.; He, Y.; Teo, K.L.; Wang, W. New insights on stability of sampled-data systems with time-delay. Appl. Math. Comput. 2020, 374, 125041. [Google Scholar] [CrossRef]
- Wang, W.; Liang, J.M.; Zeng, H.B. Sampled-data-based stability and stabilization of Lurie systems. Appl. Math. Comput. 2025, 501, 129455. [Google Scholar] [CrossRef]
- Gaspar, J.F.; Pinheiro, R.F.; Mendes, M.J.; Kamarlouei, M.; Soares, C.G. Review on hardware-in-the-loop simulation of wave energy converters and power take-offs. Renew. Sustain. Energy Rev. 2024, 191, 114144. [Google Scholar] [CrossRef]


| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | |||
| 1 | |||
| 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinheiro, R.F.; Colón, D.; Antunes, A.; Fonseca-Pinto, R. Lurie Control Systems Applied to the Sudden Cardiac Death Problem Based on Chua Circuit Dynamics. Eng 2025, 6, 89. https://doi.org/10.3390/eng6050089
Pinheiro RF, Colón D, Antunes A, Fonseca-Pinto R. Lurie Control Systems Applied to the Sudden Cardiac Death Problem Based on Chua Circuit Dynamics. Eng. 2025; 6(5):89. https://doi.org/10.3390/eng6050089
Chicago/Turabian StylePinheiro, Rafael F., Diego Colón, Alexandre Antunes, and Rui Fonseca-Pinto. 2025. "Lurie Control Systems Applied to the Sudden Cardiac Death Problem Based on Chua Circuit Dynamics" Eng 6, no. 5: 89. https://doi.org/10.3390/eng6050089
APA StylePinheiro, R. F., Colón, D., Antunes, A., & Fonseca-Pinto, R. (2025). Lurie Control Systems Applied to the Sudden Cardiac Death Problem Based on Chua Circuit Dynamics. Eng, 6(5), 89. https://doi.org/10.3390/eng6050089







