Did Maxwell Dream of Electrical Bacteria?
Abstract
:1. Introduction
2. Materials and Methods
- (1)
- In the first step, the potential V of each node and the energy of the whole network is computed. For the l-th node, the potential and its energy, are, respectively:where N = Lx × Ly is the network size and is the Euclidean distance between the two nodes l and j. The energy of the network is computed by evaluating the Coulomb interactionBoth the potentials and the energy change with the iteration step (time).
- (2)
- Nodes (bacteria) establish contacts with nodes having a lower potential. Furthermore, the probability of establishing a contact is higher for nodes with mutually closer energy values. This implements the idea that nodes with higher activity send AIs toward nodes with lower activity. Thus, for any pair of nodes with labels n and m, we first sort them in order to have > and then a connection n-m is activated with probability:which is chosen in order to favor the nodes closest in normalized energy.The choice of a Boltzmann-like linking probability is not stringent. Generally speaking, it can be replaced by similar functions without changing qualitatively the outcome of the evolution. In our simulations, we take = 1.
- (3)
- A pair of extended ideal electrical contacts is put at the ends of the network [21,22]. When a contact is established between nodes n and m, we assign to the link a resistance in the interval [, ] according to the formula:where the interpolating functions are taken to have a Hill-like shape [11,13]:The parameter g controls the steepness of the interpolation and, in our simulations, will be fixed at the value g = 0.01. Other choices for f(n,m) are with the constraint of being unified for the large activation product . The Hill form in (5) is just the simplest possibility. The change in the resistance represents the QS signal. As a matter of fact, the resistance reduction means that an electrical current is flowing between a couple of nodes, thus accounting for the transfer of information among those nodes (AI exchange) [21,22]. The opening of conduction channels, due to the interpolation effect of the function (Equation (5)), becomes even more sharp at an increasing value of activity and mimics the autocatalytic effects observed in colony growth [18]. The role of is that of implementing the cooperative action of different AIs and assuring a smooth evolution of the network with iteration time too.
- (4)
- For each node n, the number of activations produces a score which is added to the node activity Q(n). A certain amount of charge is distributed among the nodes that are connected. In particular:where 1 < is a real number whose value determines the efficiency of activation, and links(n) is the number of nodes connected to the n-th node.
- (5)
- In this step, for each (parent) node, we consider migration/duplication transitions. First, we choose one empty node out of the 8 nearest neighbors. This choice, as highlighted in the remarkable paper [15], is not purely random. It is driven by utilitarian reasons like the reach of regions with a higher amount of food or different bacterium concentration. The selected node is called the target node. The choice is done by first sorting the neighbors in order of increasing potential. Then, the k-th node in the list is selected with probabilityThis formula corresponds to choosing the minimum potential node (k = 1) with probability 1–1/9 and otherwise, with probability 1/9, choosing the second (k = 2) with probability 1–2/9, and so on.If the parent node has the minimum nonzero value Q = 1, it will migrate to the target node that inherits Q = 1 while the parent node is set to Q = 0.If instead the parent node has Q 2, a daughter–daughter reproduction is implemented and the parent node gives half of its charge to the target. The daughter–daughter reproduction is almost similar to the binary fission, in which the original cell splits into two equal parts, and is the most credited framework for bacteria replication [23].
- (6)
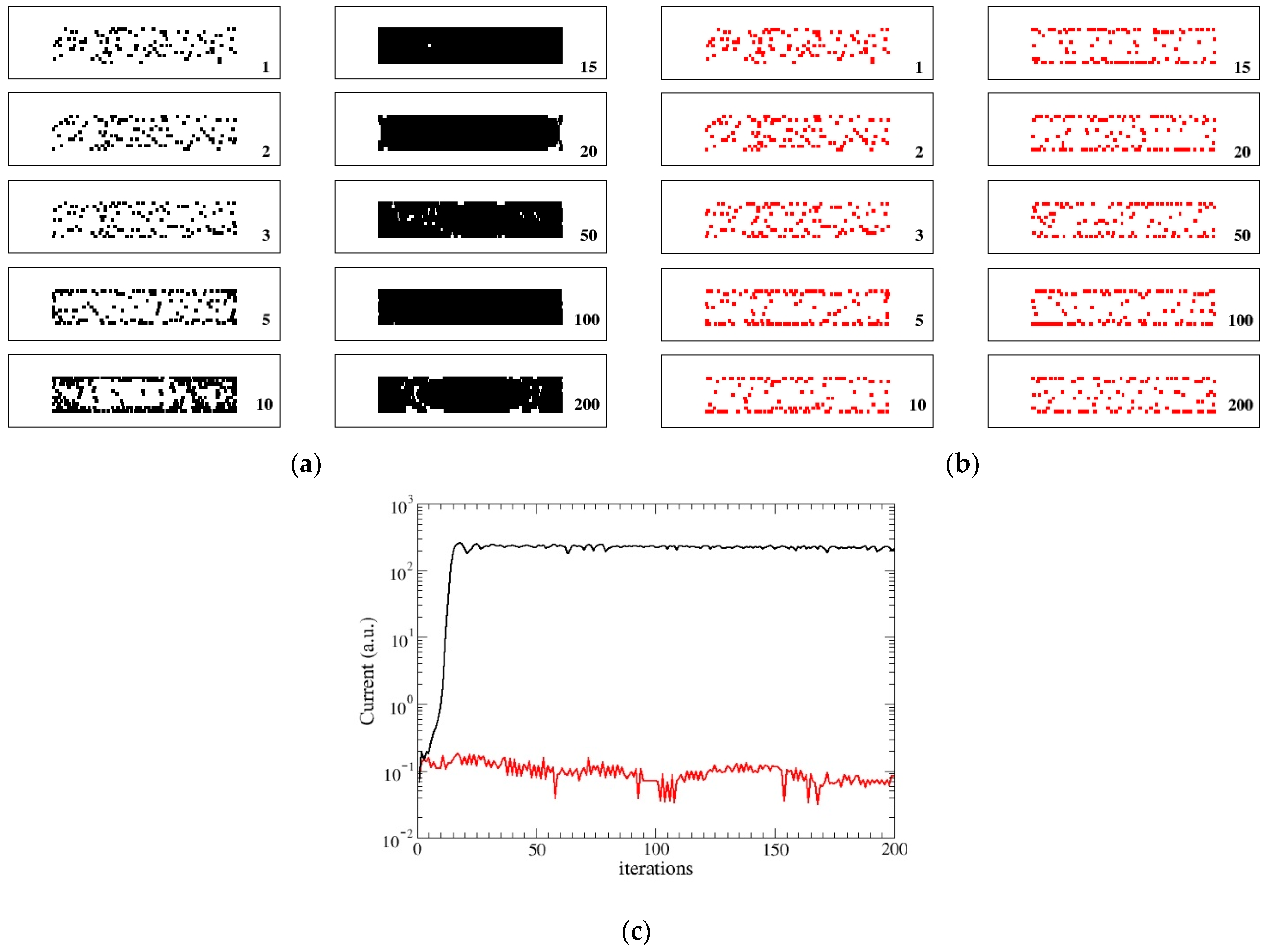
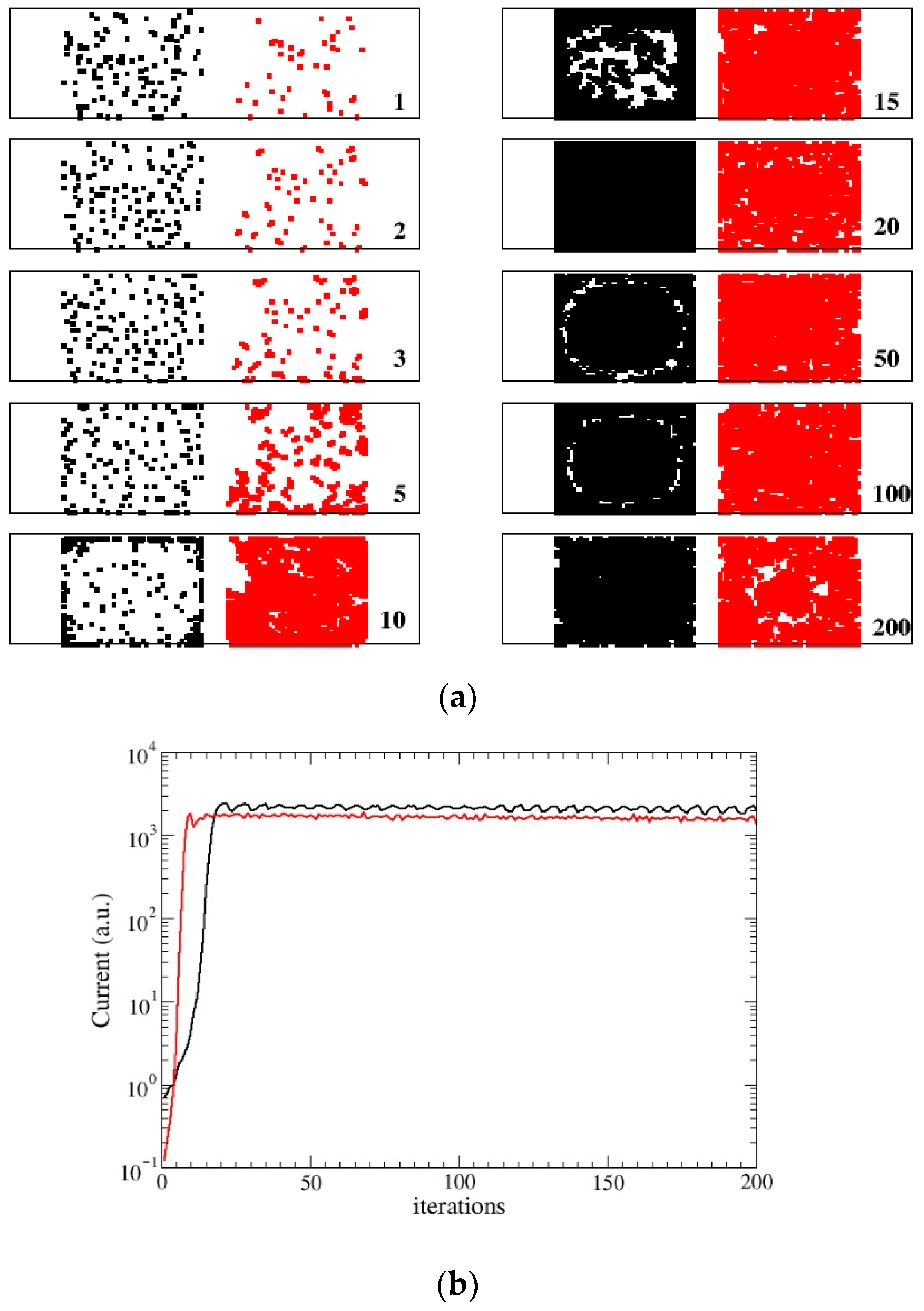
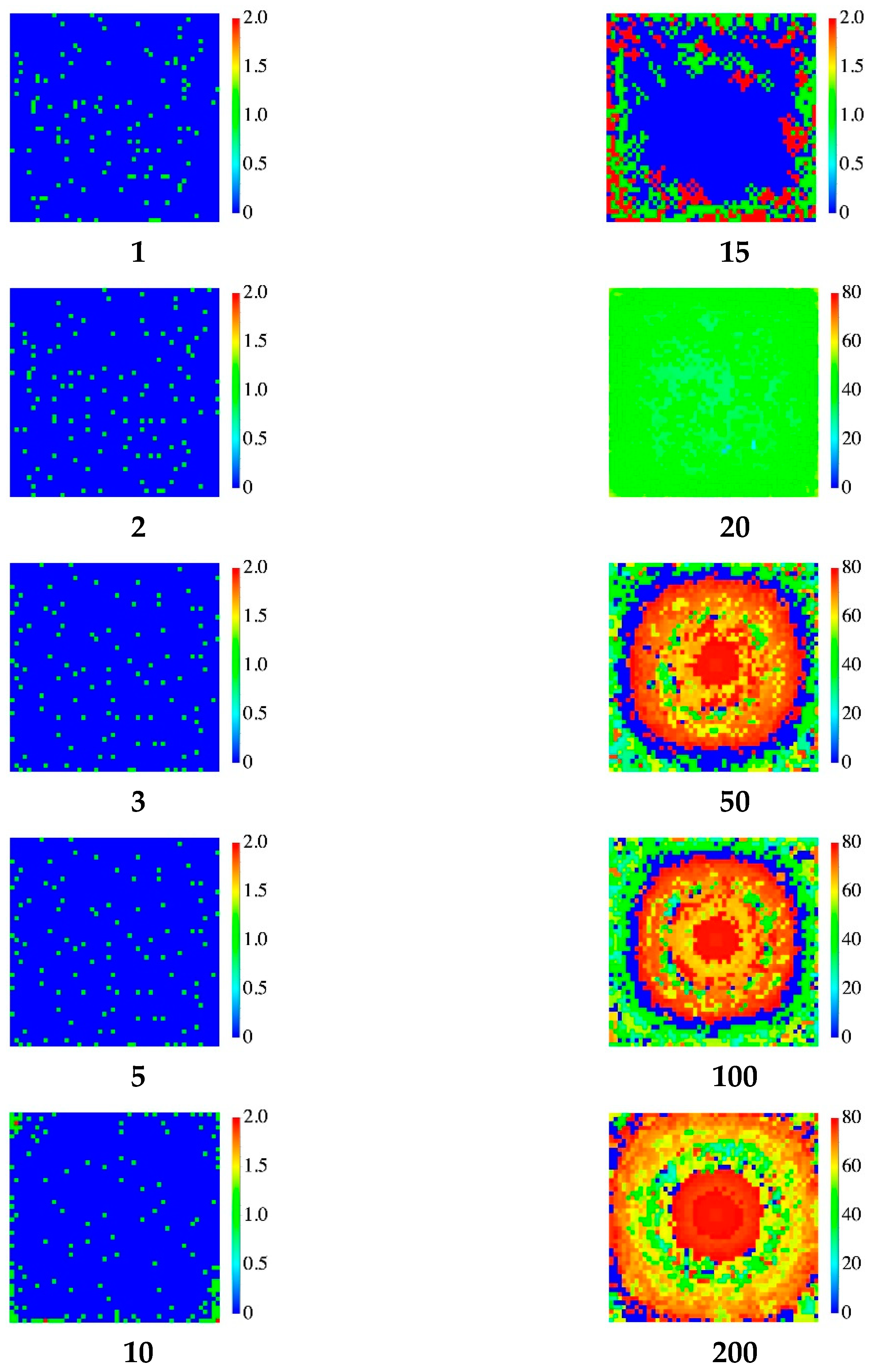
- When Q(n) reaches the assigned maximum value , we consider again two possible rules. In the first rule (DYING), the node dies, i.e., Q(n)= 0. In the second one (STATIC), it evolves toward a static form with Q(n) = −1 (spore-biofilm). The value of the maximum allowed charge , can be tuned and when it is increased, the evolution time becomes longer. In all our simulations it will be fixed at the value = 80.In the DYING scheme, the final exit of the bacterium evolution is death and its activity returns to the network and can be reused and the bacterium replaced. The network reaches a stationary state with a final mean energy and some nodes which are continuously reborn. This condition mimics the formation of a swimming colony (flocks) [3] which behaves in a cooperative manner. In the STATIC scheme, the node becomes inactive and cannot be substituted. In this case, its activity remains trapped and the network reaches a quasi-static state with few alive nodes. This condition mimics the formation of a stationary colony (biofilm) in which few cells or micro-colonies are encased in a polymeric matrix.Notice that, in this version, interactions among faraway sites describe the exchange of signaling AIs among bacteria, therefore, they happen only between active nodes. Steps (1–2), (4–6) pertain to the colony dynamics (AIs diffusion, gene regulation of reproduction, colony formation) while step (3) describes the QS signal.
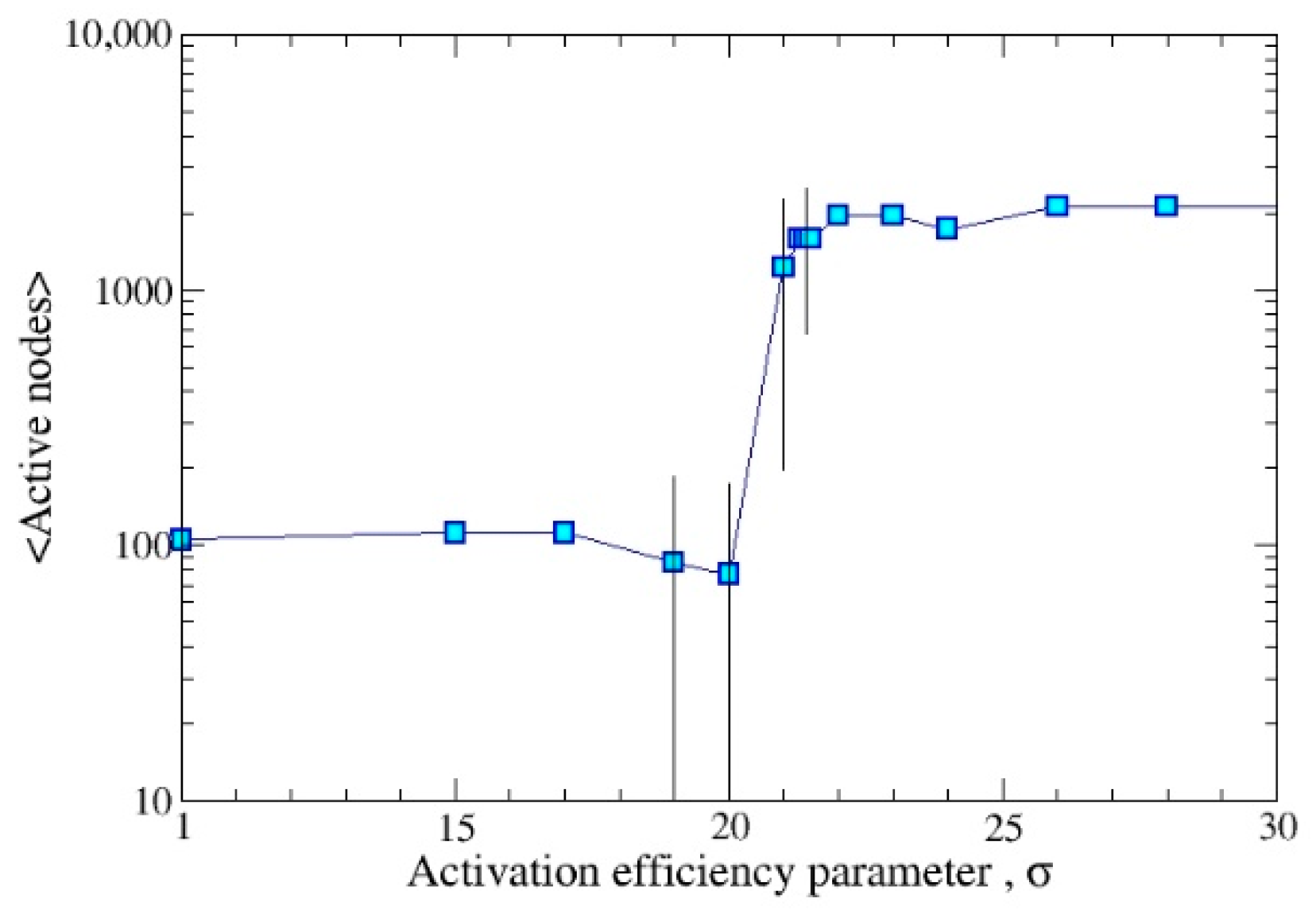
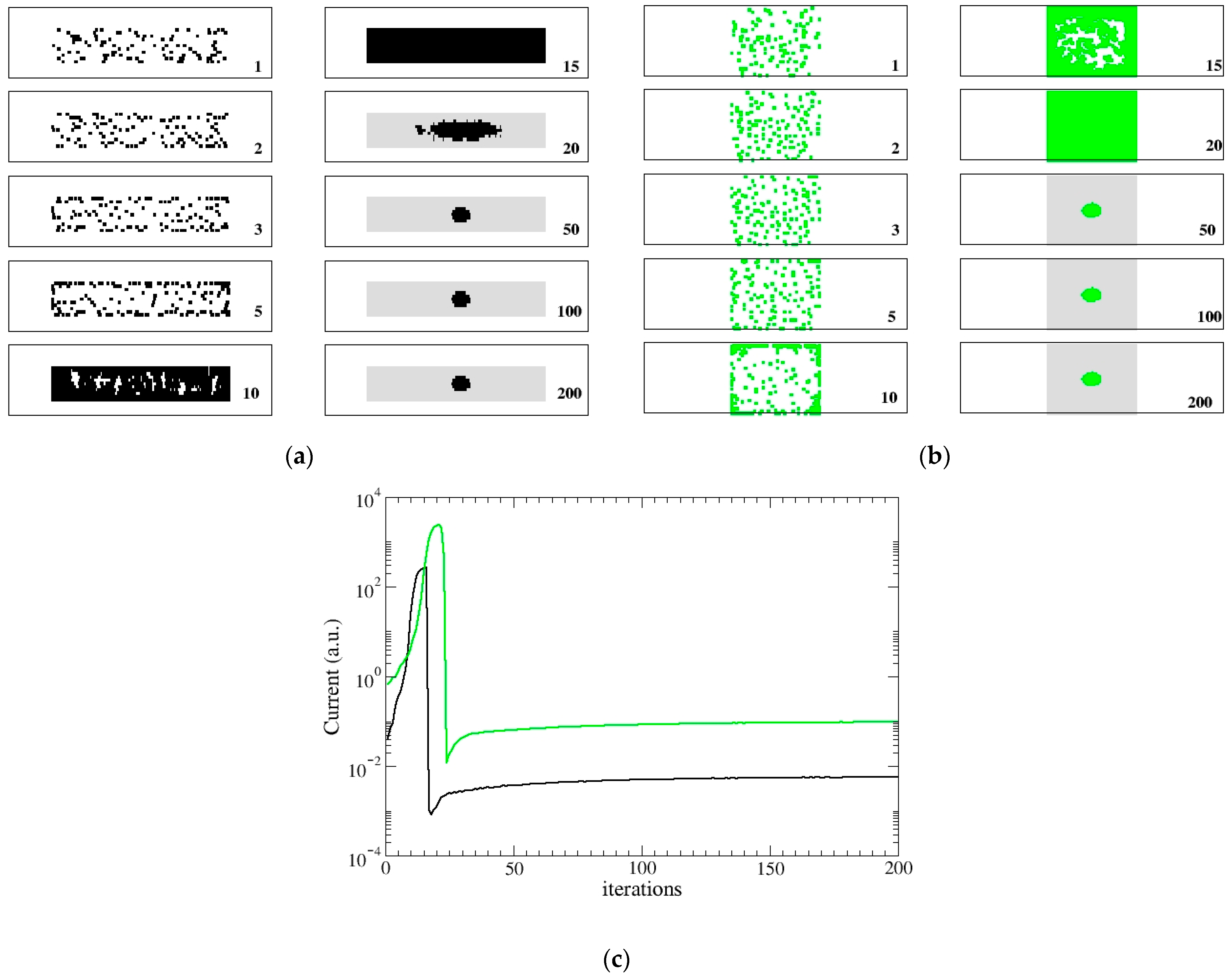
3. Results
3.1. DYING Model
3.2. STATIC Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alfinito, E.; Cataldo, R.; Reggiani, L. A pH-based bio-rheostat: A proof-of-concept. APL 2022, 120, 013701. [Google Scholar] [CrossRef]
- Flemming, H.C.; Wingender, J.; Szewzyk, U.; Steinberg, P.; Rice, S.A.; Kjelleberg, S. Biofilms: An emergent form of bacterial life. Nat. Rev. Microbiol. 2016, 14, 563–575. [Google Scholar] [CrossRef] [PubMed]
- Sokolov, A.; Aranson, I.S.; Kessler, J.O.; Goldstein, R.E. Concentration dependence of the collective dynamics of swimming bacteria. Phys. Rev. Lett. 2007, 98, 158102. [Google Scholar] [CrossRef] [PubMed]
- Resch, A.; Rosenstein, R.; Nerz, C.; Götz, F. Differential gene expression profiling of Staphylococcus aureus cultivated under biofilm and planktonic conditions. Appl. Environ. Microbiol. 2005, 71, 2663–2676. [Google Scholar] [CrossRef]
- Jefferson, K.K. What drives bacteria to produce a biofilm? FEMS Microbiol. Lett. 2004, 236, 163–173. [Google Scholar] [CrossRef]
- Sabass, B.; Koch, M.D.; Liu, G.; Stone, H.A.; Shaevitz, J.W. Force generation by groups of migrating bacteria. Proc. Natl. Acad. Sci. USA 2017, 114, 7266–7271. [Google Scholar] [CrossRef]
- Fuqua, W.C.; Winans, S.C.; Greenberg, E.P. Quorum sensing in bacteria: The LuxR-LuxI family of cell density-responsive transcriptional regulators. J. Bacterial. 1994, 176, 269–275. [Google Scholar] [CrossRef]
- Ng, W.L.; Bassler, B.L. Bacterial quorum-sensing network architectures. Annu. Rev. Genet. 2009, 43, 197–222. [Google Scholar] [CrossRef]
- Miller, M.B.; Bassler, B.L. Quorum sensing in bacteria. Annu. Rev. Microbiol. 2001, 55, 165–199. [Google Scholar] [CrossRef]
- Chopp, D.L.; Kirisits, M.J.; Moran, B.; Parsek, M.R. A mathematical model of quorum sensing in a growing bacterial biofilm. J. Ind. Microbiol. Biotechnol. 2002, 29, 339–346. [Google Scholar] [CrossRef]
- Eberl, H.J.; Parker, D.F.; Vanloosdrecht, M.C. A new deterministic spatio-temporal continuum model for biofilm development. Comput. Math. Methods Med. 2001, 3, 161–175. [Google Scholar] [CrossRef]
- Kreft, J.U.; Picioreanu, C.; Wimpenny, J.W.; van Loosdrecht, M.C. Individual-based modelling of biofilms. Microbiology 2001, 147, 2897–2912. [Google Scholar] [CrossRef] [PubMed]
- Dilanji, G.E.; Langebrake, J.B.; De Leenheer, P.; Hagen, S.J. Quorum activation at a distance: Spatiotemporal patterns of gene regulation from diffusion of an autoinducer signal. J. Am. Chem. Soc. 2012, 134, 5618–5626. [Google Scholar] [CrossRef] [PubMed]
- Kosakowski, J.; Verma, P.; Sengupta, S.; Higgs, P.G. The evolution of antibiotic production rate in a spatial model of bacterial competition. PLoS ONE 2018, 13, e0205202. [Google Scholar]
- Ben-Jacob, E.; Schochet, O.; Tenenbaum, A.; Cohen, I.; Czirok, A.; Vicsek, T. Generic modelling of cooperative growth patterns in bacterial colonies. Nature 1994, 368, 46–49. [Google Scholar] [CrossRef]
- Goryachev, A.B.; Toh, D.J.; Wee, K.B.; Lee, T.; Zhang, H.B.; Zhang, L.H. Transition to quorum sensing in an Agrobacterium population: A stochastic model. PLoS Comput. Biol. 2005, 1, e37. [Google Scholar] [CrossRef]
- Abadal, S.; Akyildiz, I.F. Automata modeling of quorum sensing for nanocommunication networks. Nano Commun. Netw. 2011, 2, 74–83. [Google Scholar] [CrossRef]
- Roy, A.; Goberman, D.; Pugatch, R. A unifying autocatalytic network-based framework for bacterial growth laws. Proc. Natl. Acad. Sci. USA 2021, 118, e2107829118. [Google Scholar] [CrossRef]
- Dockery, J.D.; Keener, J.P. A mathematical model for quorum sensing in Pseudomonas aeruginosa. Bull. Math. Biol. 2001, 63, 95–116. [Google Scholar] [CrossRef]
- Williams, P.; Camara, M.; Hardman, A.; Swift, S.; Milton, D.; Hope, V.J.; Bycroft, B.W. Quorum sensing and the population-dependent control of virulence. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2000, 355, 667–680. [Google Scholar] [CrossRef]
- Alfinito, E.; Reggiani, L. Mechanisms responsible for the photocurrent in bacteriorhodopsin. Phys. Rev. E 2015, 91, 032702. [Google Scholar] [CrossRef] [PubMed]
- Alfinito, E.; Reggiani, L. Opsin vs opsin: New materials for biotechnological applications. J. Appl. Phys. 2014, 116, 064901. [Google Scholar] [CrossRef]
- Angert, E.R. Alternatives to binary fission in bacteria. Nat. Rev. Microbiol. 2005, 3, 214–224. [Google Scholar] [CrossRef] [PubMed]
- Alfinito, E.; Beccaria, M.; Macorini, G. Critical behavior in a stochastic model of vector mediated epidemics. Sci. Rep. 2016, 6, 27202. [Google Scholar] [CrossRef]
- Alfinito, E.; Beccaria, M.; Fachechi, A.; Macorini, G. Reactive immunization on complex networks. Eur. Lett. 2017, 117, 18002. [Google Scholar] [CrossRef]
- Doh, I.J.; Kim, H.; Sturgis, J.; Rajwa, B.; Robinson, J.P.; Bae, E. Optical multi-channel interrogation instrument for bacterial colony characterization. PLoS ONE 2021, 16, e0247721. [Google Scholar] [CrossRef]
- Talà, A.; Delle Side, D.; Buccolieri, G.; Tredici, S.M.; Velardi, L.; Paladini, F.; De Stefano, M.; Nassisi, V.; Alifano, P. Exposure to static magnetic field stimulates quorum sensing circuit in luminescent Vibrio strains of the Harveyi clade. PLoS ONE 2014, 9, e100825. [Google Scholar] [CrossRef]
- Borole, A.P.; Reguera, G.; Ringeisen, B.; Wang, Z.W.; Feng, Y.; Kim, B.H. Electroactive biofilms: Current status and future research needs. Energy Environ. Sci. 2011, 4, 4813–4834. [Google Scholar] [CrossRef]
- Chen, S.; Jing, X.; Tang, J.; Fang, Y.; Zhou, S. Quorum sensing signals enhance the electrochemical activity and energy recovery of mixed-culture electroactive biofilms. Biosens. Bioelectron. 2017, 97, 369–376. [Google Scholar] [CrossRef]
| Lx, Ly | Dimensions of the rectangular grid | variable |
| f0 | Initial fraction of occupied nodes | variable |
| Parameter entering the linking probability | 1 | |
| Resistance values entering the link resistance formula | = 1 | |
| Parameter in the Hill-like function, controlling the resistance interpolation | 0.01 | |
| σ | Parameter controlling the activation efficiency | variable |
| Maximum value of the activity triggering death or biofilm formation | 80 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alfinito, E.; Cesaria, M.; Beccaria, M. Did Maxwell Dream of Electrical Bacteria? Biophysica 2022, 2, 281-291. https://doi.org/10.3390/biophysica2030026
Alfinito E, Cesaria M, Beccaria M. Did Maxwell Dream of Electrical Bacteria? Biophysica. 2022; 2(3):281-291. https://doi.org/10.3390/biophysica2030026
Chicago/Turabian StyleAlfinito, Eleonora, Maura Cesaria, and Matteo Beccaria. 2022. "Did Maxwell Dream of Electrical Bacteria?" Biophysica 2, no. 3: 281-291. https://doi.org/10.3390/biophysica2030026
APA StyleAlfinito, E., Cesaria, M., & Beccaria, M. (2022). Did Maxwell Dream of Electrical Bacteria? Biophysica, 2(3), 281-291. https://doi.org/10.3390/biophysica2030026










