RBL-2H3 Mast Cell Receptor Dynamics in the Immunological Synapse

Abstract

The RBL-2H3 mast cell immunological synapse dynamics is often simulated with reaction–diffusion and Fokker–Planck equations. The equations focus on how the cell synapse captures receptors following an immune response, where the receptor capture at the immunological site appears to be a delayed process. This article investigates the physical nature and mathematics behind such time-dependent delays. Using signal processing methods, convolution and cross-correlation-type delay capture simulations give a χ-squared range of 22 to 60, in good agreement with experimental results. The cell polarization event is offered as a possible explanation for these capture delays, where polarizing rates measure how fast the cell polarization event occurs. In the case of RBL-2H3 mast cells, polarization appears to be associated with cytoskeletal rearrangement; thus, both cytoskeletal and diffusional components are considered. From these simulations, a maximum polarizing rate ranging from 0.0057 s⁻² to 0.031 s⁻² is obtained. These results indicate that RBL-2H3 mast cells possess both temporal and spatial memory, and cell polarization is possibly linked to a Turing-type pattern formation.

1. Introduction

The RBL-2H3 mast cell signaling pathway plays an important role in human inflammatory and allergic responses. Mast cells signal by an immunological synapse that forms upon receptor contact with antigens [1,2]. In a synapse, receptors that have been activated by binding usually form clusters all over the cell, but eventually aggregate in a central patch at the point of first contact. The tracking of single receptors within these clusters reveals what appears outwardly to be a diffusion-mediated reaction process [3]. To quantify this process mathematically, various forms of the reaction–diffusion equation, i.e., the Smoluchowski equation, were solved both analytically and numerically by several authors [4,5,6]. Each form of the Smoluchowski equation employed a slightly different capture mechanism for the central patch aggregate, yet the results of their simulations had significant differences. Capture mechanisms used include those of infinite (perfect) absorption, finite absorption, and enhanced diffusion at the capture site. Infinite absorption resulted in a standard Gaussian probability distribution that moves from initial location (Dirac Delta initial condition) toward the capture site, while finite absorption produced a slower overall concentration decrease that can be controlled by a capture rate constant, making it ideal for fitting to real experimental data. Capture rate constants can also be used in enhanced diffusion, where a capture potential gathers the probability density distribution into an energy minimum at the capture site, rather than absorbing them out of the system. In a harmonic potential, probability density is Gaussian as usual, but its dynamics differ from that of finite absorption. With a linear V-potential, probability density is no longer Gaussian. The boundary conditions used to solve these differential equations also contribute to differences in the results. Thus, by choosing the appropriate capture term, boundary condition, and initial condition, these diffusion–reaction equations could have a wide range of applications in molecular systems such as excitons, photosynthetic units, crystal aggregates, and receptor clusters [4].

In the case of receptor clusters, very specific capture conditions are required. In a recent experiment [7], receptors in an immunological synapse on mast cells were observed. Receptors form initial clusters spread over the area of contact, followed by a slower movement towards the point of first contact to form the central patch. While the mechanism for RBL-2H3 mast cell synapse cluster formation has not been directly found, evidence [1] supports the theory of cytoskeletal rearrangement that occurs during cell contact with antigens. This cluster formation causes a delay in the aggregate of the central patch, since the central patch must compete with other clusters for free receptors. However, cytoskeletal rearrangement favors the point of initial contact, and all receptors in the clusters eventually diffuse into the central patch. Therefore, according to these observations, the initial probability distribution is uniform throughout the cell, Neumann boundary conditions are given by the boundary of the contact area, and the capture process at the central patch is delayed by peripheral clusters, where the radius of the central patch increases over time.

A study of mast cell receptor dynamics using some of these conditions is given in reference [7]. The authors improve upon previous theories by incorporating a dynamic radius, R(t), for the central patch, which increases its area (radius) in proportion to the amount of free receptors remaining outside the central patch,

$$\frac{R^2\left(t\right)-R^2\left(0\right)}{R^2(\infty )-R^2\left(0\right)}=\frac{Q\left(0\right)-Q\left(t\right)}{Q\left(0\right)-Q(\infty )}$$

(1)

where $R\left(0\right)$ is the initial central patch radius, $R(\infty )$ the final radius; $Q\left(0\right)$ the initial fraction of total receptors remaining outside of the central patch, $Q(\infty )$ the final fraction. $Q\left(t\right)$ is calculated by integrating (in polar coordinates) the probability density function, $P\left(r,\theta ,t\right)$, of receptors over the area outside the central patch, thus giving an equation for $R\left(t\right)$ once the probability density is found.

Using Laplace transform, $P\left(r,\theta ,t\right)$ is then calculated from the solution to the Smoluchowski equation with a specific capture term,

$$\frac{dP\left(r,\theta ,t\right)}{dt}=\mathrm{D} {\nabla }^{2}P\left(r,\theta ,t\right)-\frac{2 \pi }{r} \delta \left(r-R\right) {{\displaystyle \int }}_0^{t}ds C\left(t-s\right)P\left(r,\theta ,s\right),$$

(2)

where the Laplacian term represents the diffusion process with diffusion coefficient D, and the Dirac Delta term represents the reaction process, or the capture, with discrete point traps at radius R from the origin. In polar coordinates, the delta function forms the boundary of the central patch, and the integral from time zero to t is the convolution-type memory function which will be discussed below. Since the delta function represents infinite capture and is thus unphysical in this case (the Dirac Delta representation is used in quantum systems, which is not the case here), the authors replace the infinite delta function solution with a finite reaction rate obtained from their previous work [5]. The result is an analytical solution $Q\left(\epsilon ,r_0,R\left(0\right)\right)$, where $\epsilon$ is the Laplace variable, and $r_0$ refers to an initial condition of receptors laying along a ring of radius $r_0$. Then, approximating the peripheral clusters by circular rings outside the central patch and integrating $Q\left(\epsilon ,r_0,R\left(0\right)\right)$ over the area outside the central patch, the authors obtain a solution for $Q\left(\epsilon \right)$ subject to absorption at a stationary central patch boundary, with an initial condition of concentric circular receptor rings. The combined effect of the central patch capture and peripheral cluster distribution on the quantity $Q\left(\epsilon \right)$ is described by

$$Q\left(\epsilon \right)=N{{\displaystyle \int }}_{R\left(0\right)}^{r{0}^{\prime }}Q\left(\epsilon ,r_0,R\left(0\right)\right) r_0 d{r}_0,$$

(3)

where $N$ is the normalization factor that normalizes the maximum of $Q\left(\epsilon \right)$ to one, $r{0}^{\prime }$ the entire contact area radius, and $Q\left(\epsilon ,r_0,R\left(0\right)\right)$ is an analytical solution that not only depends on the Laplace variable $\epsilon$ but also on the initial central patch radius $R\left(0\right)$.

However, we note that the central patch boundary is a dynamic quantity, with the radius increase described by $R\left(t\right)$ in Equation (1). Increasing the central patch size over time is equivalent to dynamically increasing the overall absorption rate. Replacing $R\left(0\right)$ in Equation (3) with $R\left(t\right)$ drastically increases the complexity of the integral, making it less attainable by analytical methods. Therefore, we suggest the use of numerical approaches to solve such problems.

Additionally, the convolution-type function in the capture term reflects and quantifies the physical situation of the delayed central patch aggregation caused by peripheral clusters competing for free receptors. This convolution-type function has deep physical meanings not only in signal processing but also in quantitative studies of memory and learning [8,9]. In reference [7], the authors refer to these types of functions as memory functions to approach this problem from a cell recollection point of view. With this approach, a cell is able to “learn” from what happened to it in the past, in this case its past history of free receptors. This memory term also makes it possible to study signals that cause the cluster formation and, therefore, illuminate possible underlying mechanisms. However, using memory capture, the theory was fitted to experimental data and a polarizing time constant of 10⁻¹² s⁻¹ was obtained. The inverse of this number, 10¹² s, far exceeds the time duration of most cellular processes.

Nevertheless, in a related field of study [10], it is shown that cells are able to communicate through local polarization and depolarization upon contact, providing a new insight into the inner workings of the mast cell immunological synapse. In fact, polarization plays an important role in the immunological synapse of many cells [11,12]. It is also known that polarization in different types of cells is stimuli-specific. Most cell types respond to chemical stimuli, but some will respond to mechanical and other types of contact. Moreover, different cell types also react to polarization stimuli in different ways: some cell types rearrange their cytoskeletal components, while others alter their cytosolic signaling molecules [13]. In the case of RBL-2H3 mast cell, polarization appears to be initiated by antigen binding and is mediated by actin and myosin, resulting in cytoskeletal rearrangement [14]. Thus, in the present study, we continue to build into this theory a capture term that consists of both convolution-type and cross-correlation-type signals, which corresponds to the depolarization and polarization event, respectively. Additionally, to transition from polarization to depolarization, we build into the theory a time-delayed Fokker–Planck potential term. Using these theories, we then obtain polarizing time constants ranging from 0.022 s⁻¹ to 0.031 s⁻¹, and maximum polarization is reached approximately 112 s after polarization initiation. This is consistent with experimental observations in the literature [13], where cell polarization can take seconds to minutes, depending on the cell type.

2. Materials and Methods

Due to high symmetry, the 2-D Smoluchowski equation, Equation (2), can be reduced to 1-D when the center of the capturing trap is located at the origin. The only asymmetric component in this problem would be the initial distribution of receptor clusters around the central patch. When these clusters are approximated as circular rings, as was carried out in the previous study, the problem can still be reduced to 1-D. Reducing the problem to 1-D or to 2-D circular rings saves both computational memory and time, although doing so does not allow details of the 2-D solution such as movement speed of independent clusters toward the central patch to be simulated. With 1-D capture, such features are then hidden in the capture term’s delay-type memory function, i.e., $C\left(t\right)$ in Equation (2).

The memory function in reference [7] is an important improvement over previous diffusion reaction capture terms, without the use of such functions the central patch aggregation delay could not be properly simulated in 1-D. Illustrations in Figure 1 and Figure 2 show two major types of memory functions used in this study.

Figure 1 shows convolution-type capture delay. The convolution-type capture memory function, $C\left(t\right)=c_2\alpha Exp\left(-\alpha t\right)$ is shown in Figure 1a, while an idealized rectangular probability density function for free receptors is shown in Figure 1b. Variable $c_2$ is the capture strength, $\alpha$ the polarizing time constant, and $x_0$ represents an arbitrary point in the 1-D probability density function, $P\left(x_0,s\right)$, in terms of convolution time $s$. The rectangular shape is used here for illustrative purposes only and does not depict the real density profile of free receptors. Figure 2 follows the same format for cross-correlation-type capture delay, with $C\left(t\right)$ replaced by a piecewise function of $c_2\alpha Exp\left(\alpha t\right)$. Using the rectangular probability density function, differences in convolution and cross-correlation results can be seen clearly in Figure 1c and Figure 2c. Assuming the upward increase in capture rate (Figure 1c) is caused by mast cell polarization upon contact with antigens and the downward curve by depolarization, the convolution-type capture gives fast initial polarization and depolarization. The same reasoning in Figure 2c gives cross-correlation-type capture slow initial polarization and depolarization.

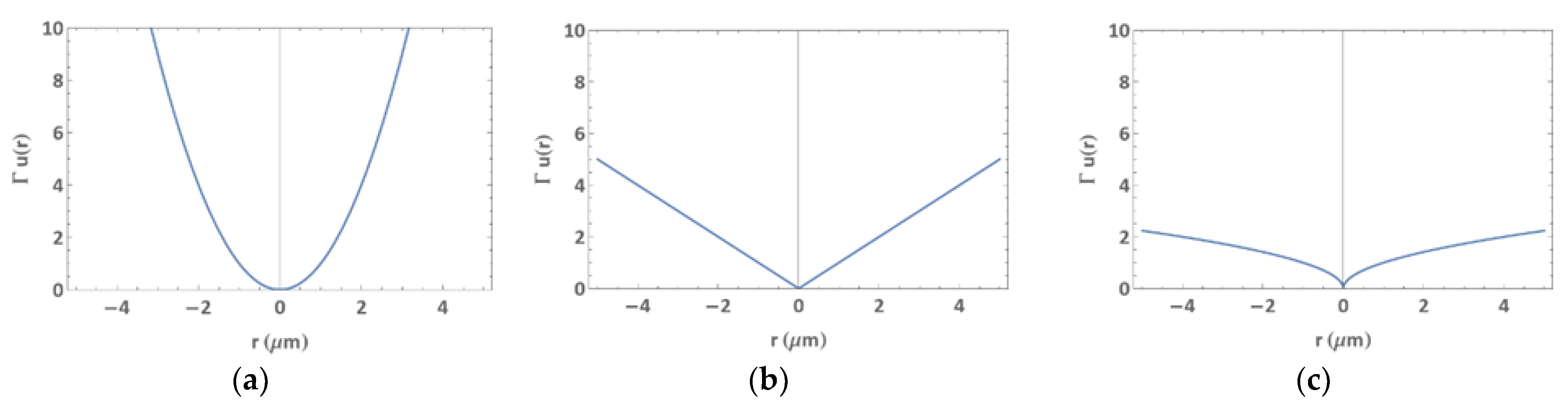
Convolution and cross-correlation provide a physical way to distinguish between polarization and depolarization events, but the Dirac Delta function in front of the capture term in Equation (2) is still unphysical because it represents an infinite capture rate. Thus, replacing the Dirac Delta function with a rescaled normal distribution, $n\left(t\right)=Exp\left(-\frac{r^2}{{\left(R\left(t\right)/2\right)}^2}\right)$, we obtain a capture trap size of height one, with the radius $R\left(t\right)$ set to 2√2 standard deviations away from the center of trap (see Figure 3).

Lastly, we note that, in Figure 1b, $P\left(x_0,t\right)$ drops to zero at $t=400$ s, yet the capture process in Figure 1c does not stop until $t=800$ s. This effectively gives a negative $P\left(x_0,t\right)$ for times greater than $t=400$ s and is again unphysical. The same is true for Figure 2. Therefore, we rescale the capture term with the probability function itself at time $t$, i.e., multiply the capture term in Equation (2) by $P\left(x_0,t\right)/P\left(x_0,0\right)$, to obtain the physical capture results for convolution in Figure 4a and cross-correlation in Figure 4b.

Altogether, the 1-D Smoluchowski equation now reads:

$$\frac{dP\left(r,t\right)}{dt}=\mathrm{D} {\nabla }^{2}P\left(r,t\right)-Exp\left(-\frac{{\mathrm{r}}^2}{{\left(\frac{\mathrm{R}\left(\mathrm{t}\right)}{2}\right)}^2}\right) \frac{P\left(r,t\right)}{P\left(r,0\right)} {{\displaystyle \int }}_0^{t}ds C\left(t-s\right)P\left(r,s\right),$$

(4)

with initial condition $P\left(r,0\right)=1$ μm⁻¹ uniform throughout the surface of the cell (the initial peripheral clusters are now taken into account by the delay memory functions, instead of being built into the initial condition as 2-D circular rings) and Neumann conditions at the cell contact boundary $r=\pm r{0}^{\prime }$.

Moreover, evidence shows that the RBL-2H3 mast cell synapse receptor dynamics is affected by their distance from the central patch, where the peripheral receptor cluster average 2-D speeds are faster when they are further away from the central patch [6]. Assuming the radial 1-D speeds of the peripheral clusters are also faster than the central region and the clusters’ overall movement is toward the center, this results in an enhanced absorption where peripheral clusters are pulled into the central patch. Such movements appear to be due to an underlying cytoskeleton rearrangement [14] associated with cell polarization. Representing this cytoskeletal rearrangement by a specific 1-D diffusional potential and linking it to the transition from polarization to depolarization, we add a Fokker–Planck potential term to Equation (4), obtaining

$$\frac{dP\left(r,t\right)}{dt}=\mathrm{D} {\nabla }^{2}P\left(r,t\right)-\frac{d}{dr}\left(P\left(r,t\right)\frac{d}{dr}u\left(r\right)\right)\frac{P\left(r,t\right)}{P\left(r,0\right)} {{\displaystyle \int }}_0^{t}ds \Pi \left(t-s\right)P\left(r,s\right)-Exp\left(-\frac{{\mathrm{r}}^2}{{\left(\frac{\mathrm{R}\left(\mathrm{t}\right)}{2}\right)}^2}\right) \frac{P\left(r,t\right)}{P\left(r,0\right)} {{\displaystyle \int }}_0^{t}ds C\left(t-s\right)P\left(r,s\right),$$

(5)

where $\Pi \left(t\right)$ is equal to $\Gamma \alpha Exp\left(-\alpha t\right)$ for convolution, and a piecewise function of $\Gamma \alpha Exp\left(\alpha t\right)$ for cross-correlation. $\Pi \left(t\right)$ has the same time delay dynamics (same polarizing time constant $\alpha$) as $C\left(t\right)$, and, similar to how $c_2$ describes the capture strength, $\Gamma$ describes the strength of the potential. Thus, the capture term would describe the external receptor aggregation of the central patch, while the potential term describes the internal cytoskeleton rearrangement of the cell. Here, the V-potential is used, $u\left(r\right)=\left|r\right|$. This V-potential is chosen not only because it creates a richer motion than the harmonic potential [6], but also it is the median of 3 possible potential configurations (see Figure 5). Note that, due to the delays caused by $C\left(t\right)$ and $\Pi \left(t\right)$, the effect of both capture and potential is most prominent around the time of maximum capture, $t_{max}$ (see Figure 1c and Figure 2c). This $t_{max}$ also marks the transition from polarization to depolarization, so the memory function is in fact a mathematical representation of such transitions.

To determine $Q\left(t\right)$, which represents the fraction of total free receptors remaining at time $t$, we integrate the fraction $P\left(r,t\right)/P\left(r,0\right)$ over the cell contact area,

$$Q\left(t\right)={{\displaystyle \int }}_0^{r{0}^{\prime }}dr \frac{P\left(r,t\right)}{P\left(r,0\right)}.$$

(6)

Equations (4) and (5), together with their initial and boundary conditions, are solved numerically by Wolfram Mathematica version 13. Memory-function-type equations such as these are called delay partial differential equations (DPDE) [15]. The quantity $R\left(t\right)$ is an equation that depends on $Q\left(t\right)$, which is a function that depends on the solution $P\left(r,t\right)$ itself. More importantly, $P\left(r,s\right)$ is a memory-linked function that depends on the history of $P\left(r,t\right)$. These features make it difficult to solve the equations analytically, so numerical approximation methods are usually used [16]. One effective strategy, documented in the Python language [17], uses what is known as “history functions”. The history function represents a function that holds the approximate value of the solution $P\left(r,t\right)$ while the differential solver slowly corrects and pushes it towards the true solution. This strategy employs solving an initial partial differential equation (PDE) that is similar to the task at hand, using that solution as an initial history function for $P\left(r,s\right)$ in the DPDE, and then repeatedly solving the DPDE in a loop, each time updating the history function $P\left(r,s\right)$, until the history function becomes almost identical to the solution $P\left(r,t\right)$. The Mathematica NDSolve function currently does not support non-constant delays [18], so users must implement these loops manually (see accompanying code). Here, we have chosen Mathematica for this study due to our familiarity and experience with the language.

3. Results

To compare experiments with Mathematica simulations, observed mean data on the central patch radius in the RBL-2H3 mast cell synapse is taken from reference [7] and fitted with an arctan curve that resembles the experimental data points (Figure 6). This is carried out to provide visual comparisons with simulation curves and also to obtain better estimates for the initial central patch radius $R\left(0\right)$ and the final central patch radius $R(\infty )$. This estimate is necessary because the initial and final mean radius data points do not appear to lie on the same curve as the rest of the data. If the initial and final mean data points were used directly as $R\left(0\right)$ and $R(\infty )$, simulation results on central patch radius would deviate greatly from a large number of the data points. The source of this error might be due to the difficulty in estimating polarization initiation and end times when these measurements were made.

The shifted and scaled arctan curve thus obtained achieves a high-accuracy fit with an χ-Squared value of 61.2542. The choice of this arctan fit is arbitrary, as any sigmoidal curve with a sufficiently high $R^2$ and low ${\chi }^2$ values can be used. Thus, the arctan function is not the only sigmoidal curve that can be used to fit the data, but we note that other sigmoidal curves do not produce any ${\chi }^2$ values that are significantly different. We then compare the arctan curve with our simulation results using the same initial and final central patch radii as the arctan curve in our simulations.

From the arctan curve, $R_{arc}\left(t\right)$, we determine an initial central patch radius of 1.31 μm and a final central patch radius (by taking the arctan limit to ∞) of 3.15 μm. We also calculate the approximate time when maximum capture rate is achieved, $t_{max}$, from $R_{arc}\left(t\right)$, by setting its second derivative to zero. This gives a $t_{max}$ value of 112 s, and, as we shall see below, this value is important for estimating cross-correlation-type capture delay.

Then, taking experimental values from [7], we use an initial $Q\left(0\right)$ of 1, a final $Q(\infty )$ of 0.26, a cell contact radius of 5.75 μm, and a diffusion constant of 0.011 μm² s⁻¹ to numerically solve variations in Equation (4) for $P\left(r,t\right)$ and determine $Q\left(t\right)$ from Equation (6). Finally, we plot the corresponding $R\left(t\right)$ using Equation (1) for several different cases of capture in the subsequent results.

To see the effect of un-delayed capture, Equation (4) is modified using an un-delayed constant capture rate $c_0=0.4$ μm⁻¹ s⁻¹, as in Equation (7). The equation is then solved numerically, and the resulting central patch radius, $R_{uc}\left(t\right)$, is plotted in Figure 7.

$$\frac{dP\left(r,t\right)}{dt}=\mathrm{D} {\nabla }^{2}P\left(r,t\right)-Exp\left(-\frac{r^2}{{\left(\frac{R\left(t\right)}{2}\right)}^2}\right) c_0 \frac{P\left(r,t\right)}{P\left(r,0\right)}$$

(7)

To see the effects of delayed capture, $C\left(t\right)$ in Equation (4) needs to be defined for both cross-correlation and convolution. From the shape of the delayed captures, Figure 1c and Figure 2c, one could see that the experimental curve in Figure 6 must be due to a cross-correlation-type polarization before $t_{max}$, and a convolution-type depolarization afterward. Additionally, unlike convolution, cross correlation memory function must be constructed in pieces. Thus, we define a piecewise function for cross-correlation (Equation (8)) and a non-piecewise function for convolution (Equation (9)),

$$C\left(t\right)=\{\begin{array}{cc} c_2 {\alpha }^2 Exp\left(\alpha t\right)& ,0\le t\le t_{max}\\ 0& ,elsewhere\end{array}$$

(8)

and

$$C\left(t\right)=c_2 \alpha Exp\left(-\alpha t\right)$$

(9)

where the extra dimensionless $\alpha$ factor in cross-correlation is due to its integration form (see Figure 2c). Then, by setting $\alpha Exp\left(\alpha t_{max}\right)$ to $c_2$, adjusting the value of $c_2$ and solving for $\alpha$, we obtain $c_2=0.3$ s⁻¹ and $\alpha =0.0229$ s⁻¹ for the cross-correlation type. Convolution values for $c_2$ and $\alpha$ are similarly obtained, with values $c_2=1$ s⁻¹ and $\alpha =0.031$ s⁻¹. The cross-correlation and convolution values are then used to numerically solve Equation (4) using Equation (8) and Equation (9), respectively, and the results of their central patch radii, $R_{cc}\left(t\right)$ for cross-correlation and $R_{co}\left(t\right)$ for convolution, are plotted in Figure 8. Both $R_{cc}\left(t\right)$ and $R_{co}\left(t\right)$ are more accurate (lower χ²) than $R_{arc}\left(t\right)$ in their respective time intervals ($t$ < 112 for cross correlation and $t$ > 160 for convolution).

Finally, to see the effect of a time-dependent V-potential, Equation (5) is numerically solved for the case of cross correlation, where $\Pi \left(t\right)$ is described by $C\left(t\right)$ in Equation (8), with $c_2$ replaced by $\Gamma$. Using the values $\Gamma =0.185$ μm²s⁻¹, $c_2=0.26$ s⁻¹, and $\alpha =0.022$ s⁻¹, the resulting radius, $R_{ccv}\left(t\right)$, is plotted in Figure 9, where $R_{ccv}\left(t\right)$ is, again, more accurate than $R_{arc}\left(t\right)$.

The resulting time and strength constants from the above simulations are summarized in

Table 1. Time and strength constants for different types of capture delays.

	${\mathit{c}}_2$ (s−1)	$\mathit{\alpha }$ (s−1)	${\mathit{c}}_2\mathit{\alpha }$ (s−2)	$\mathit{\Gamma }$ (μm2 s−1)
Cross-Correlation	0.30	0.023	0.0069	0
Convolution	1	0.031	0.031	0
Cross-Correlation and Potential	0.26	0.022	0.0057	0.19

, where $c_2$ is the capture strength in units of s⁻¹, $\alpha$ the polarizing time constant in s⁻¹, $c_2 \alpha$ the maximum polarizing rate in s⁻², and $\Gamma$ the potential strength in μm² s⁻¹.

4. Discussion

As expected, the un-delayed capture radius does not match experimental data points (Figure 7). However, the latter part of $R_{uc}\left(t\right)$ in Figure 7 does coincide with the data points and the arctan curve. Physically, this is due to the receptors being absorbed out of the system (into the central patch) naturally, which has nothing to do with depolarization. This reflects the fact that, unlike polarization, depolarization is simply not observed in many systems due to the natural decline of the primary cellular process. In Figure 8, the central patch radius increase is well-described by cross correlation for $t<112$ s, and by convolution for $t>160$ s. This corresponds to a slow initial polarization and a fast initial depolarization in the RBL-2H3 mast cell, although it remains unclear whether the decrease in the capture rate for times $t>160$ s is due to depolarization or the natural decrease in the number of free receptors. The maximum polarizing rate, $c_2 \alpha$, is 0.0069 s⁻² for the cross-correlation type, and 0.031 s⁻² for the convolution type. The fact that these values are different for polarization and depolarization suggest that these processes are controlled by separate events in the RBL-2H3 mast cell.

Additionally, the transition from polarization to depolarization, from time $t=112$ s to $t=160$ s, is not well-described by either the cross-correlation or the convolution-type capture delay, so we suspect some kind of phase change has occurred in the mast cell during this time. This phase change can be simulated by adding a diffusional potential delay, i.e., by considering cytoskeleton rearrangement. The result of this is shown in Figure 9, where experimental data are well-described by using a cross-correlation-type delay in both the capture and potential terms in our simulations (Equation (5)). Thus, the receptor clusters are dynamically attracted to the center of the trap, which is also consistent with experimental observations [6]. The maximum polarizing rate obtained with the inclusion of the V-potential is 0.0057 s⁻².

The key features of Equation (5) are the memory function, $C\left(t\right)$, and the V-potential, $u\left(r\right)$. We note that if the V-potential is replaced by the Y-potential (Figure 5c), slower radial diffusion speeds would bring the latter part of the cross-correlation curve, $R_{ccv}\left(t\right)$ in Figure 9, slightly closer to a plateau, which could make the curve even more accurate. The success of this equation has deep physical implications. It means that the cell has not only a temporal memory from $C\left(t\right)$, but also a spatial memory from $u\left(r\right)$, especially in the case of the Y-potential. The cell can “remember” the exact location at $r=0$, the point of initial contact, throughout the entire process of immunological synapse polarization. The application of the potential and memory functions here is especially crucial, since it could be the first of many types of cell memory that can be represented mathematically.

The mechanism behind the cluster formations that caused these capture and potential delays has to do with polarization and cytoskeleton rearrangement, and perhaps some insights can be gathered from the famous Turing patterns [20]. The Turing patterns are formed by a system of two reaction–diffusion equations, each describing the 2-D diffusion of a different molecule, one inhibiting the other. The pattern thus formed describes the color pigment formation of spots on animal coats. We suspect something similar occurs in the cluster formation on mast cells, where the stability of the diffusion field that forms the peripheral clusters is broken and disturbed by the increase in the central patch. This breaking point then marks the beginning of the transition from polarization to depolarization. If this was the case, then a molecule that inhibits polarization as well as a molecule that causes it would have to be simulated at the same time in 2-D. Thus, what appears to be delayed captures and potentials in 1-D would then be equivalent to the Turing pattern formation in 2-D with a central patch that increases in time but captures receptors at a constant rate at its boundary.

The idea of using 2-D pattern formation to describe polarization is not new, and much work has been conducted in this area [13,21]. The Turing-type diffusion reaction equations are widely used to form polarization patterns in these works, which consist of both simulations and experiments [22,23]. Specifically, polarization activators are represented by the active form of either cytosolic or cytoskeletal proteins, while polarization inhibitors by the inactive form [24,25]. Thus, it is the interplay between the active and inactive form that shapes the stable regions in the Turing-type diffusion field. Mathematical theories on polarization go beyond Turing-type simulations when intracellular dynamics is involved, however. Monte Carlo and phase fields are both effective tools when intracellular regions greatly affect the overall polarization [13].

In summary, the choice between delay function and Turing-type simulation has to do with simulation time and biological background considerations. The disadvantage of simulating delayed functions is that it requires an extremely long run time, even for 1-D models. With most common hardware specifications, 1-D simulations take approximately 1 h, while 2-D simulations take significantly longer, anywhere from days to weeks depending on how efficiently the code is programmed and what language is used. With Turing-type simulations, the delay functions are not required since the delay emergence can be built into the Turing-type diffusion field dynamics. Without the delay functions, the 2-D Turing-type reaction–diffusion equations take mere minutes to simulate.

The advantage of simulating delayed functions in 1-D is that it gives numerical values for capture strength and polarization time constants that would not be so readily acquired in Turing-type simulations. These constants can provide a basis for comparison between two different types of cells. For example, one can compare the capture strength of normal cells with that of cancer cells, if a difference in polarization is suspected. On the other hand, Turing-type simulations provide more information on cluster formation, but it does so at the expense of making the assumption that the polarization event is based on a two-component reaction–diffusion system (inactive and active proteins). Making such assumptions requires the researcher to have in-depth knowledge on the polarization mechanism of the interested cell type. Such assumptions are not necessary for delay function simulations. Thus, the choice of 1-D delay function vs. 2-D Turing-type simulation depends on how much experimental biological information the researcher has on the interested cell and whether polarization capture strength and time constants are required for comparison purposes.

5. Conclusions

Using convolution and cross-correlation from signal processing, we can characterize the polarization and depolarization speed of a mast cell synapse formation in 1-D. We found that polarization follows a cross-correlation-type signature, while depolarization follows a convolution-type signature, giving the mast cell a slow initial polarization and a fast initial depolarization. When transition effects are simulated by a time dependent potential term, cross-correlational delay alone is enough to describe the data points to a high degree of accuracy. Two-dimensional simulations of these events could reveal much more interesting details about the nature of cluster formation and possible cellular phase changes, and that might provide a way to link these events to molecular changes in RBL-2H3 mast cells.