Neuronal Cultures: Exploring Biophysics, Complex Systems, and Medicine in a Dish
Abstract
:1. Introduction
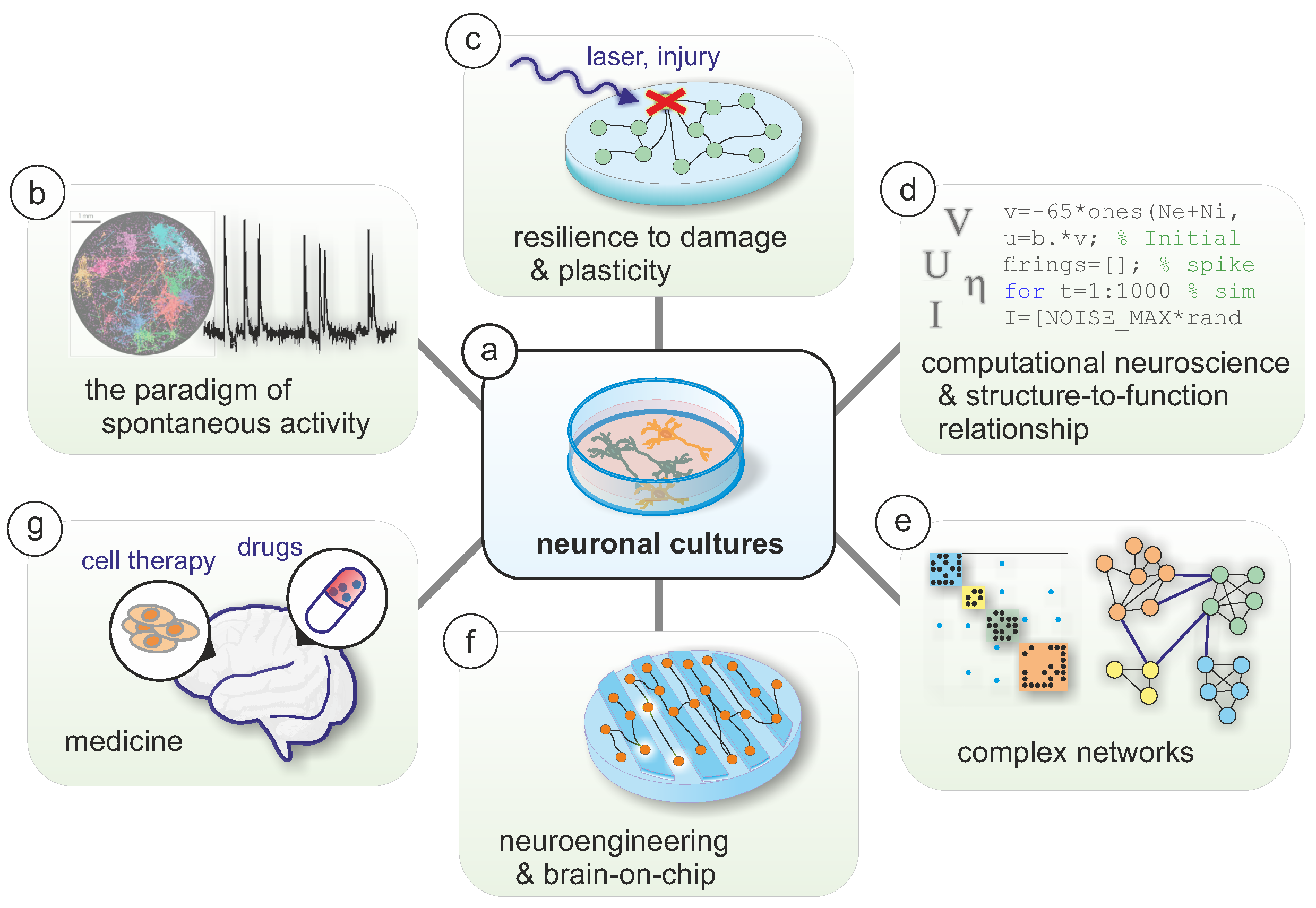
2. An Overview of Neuronal Cultures
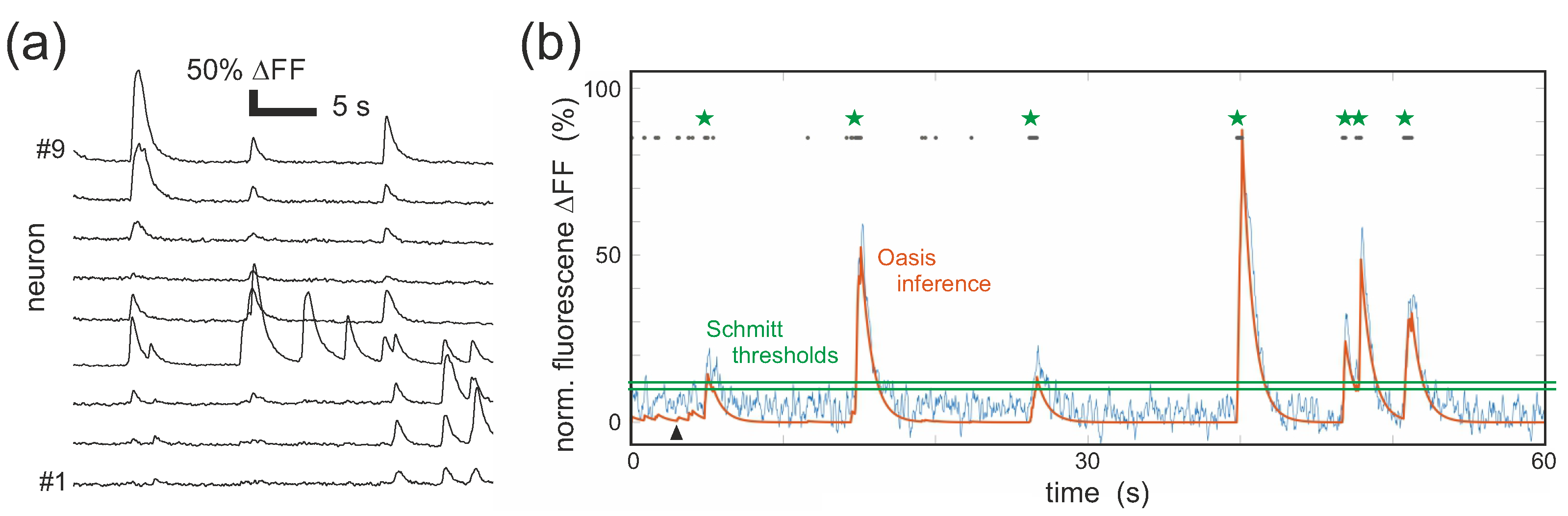
3. Data Acquisition and Analysis
4. Spontaneous Activity in Cultures and the Importance of In Silico Modeling
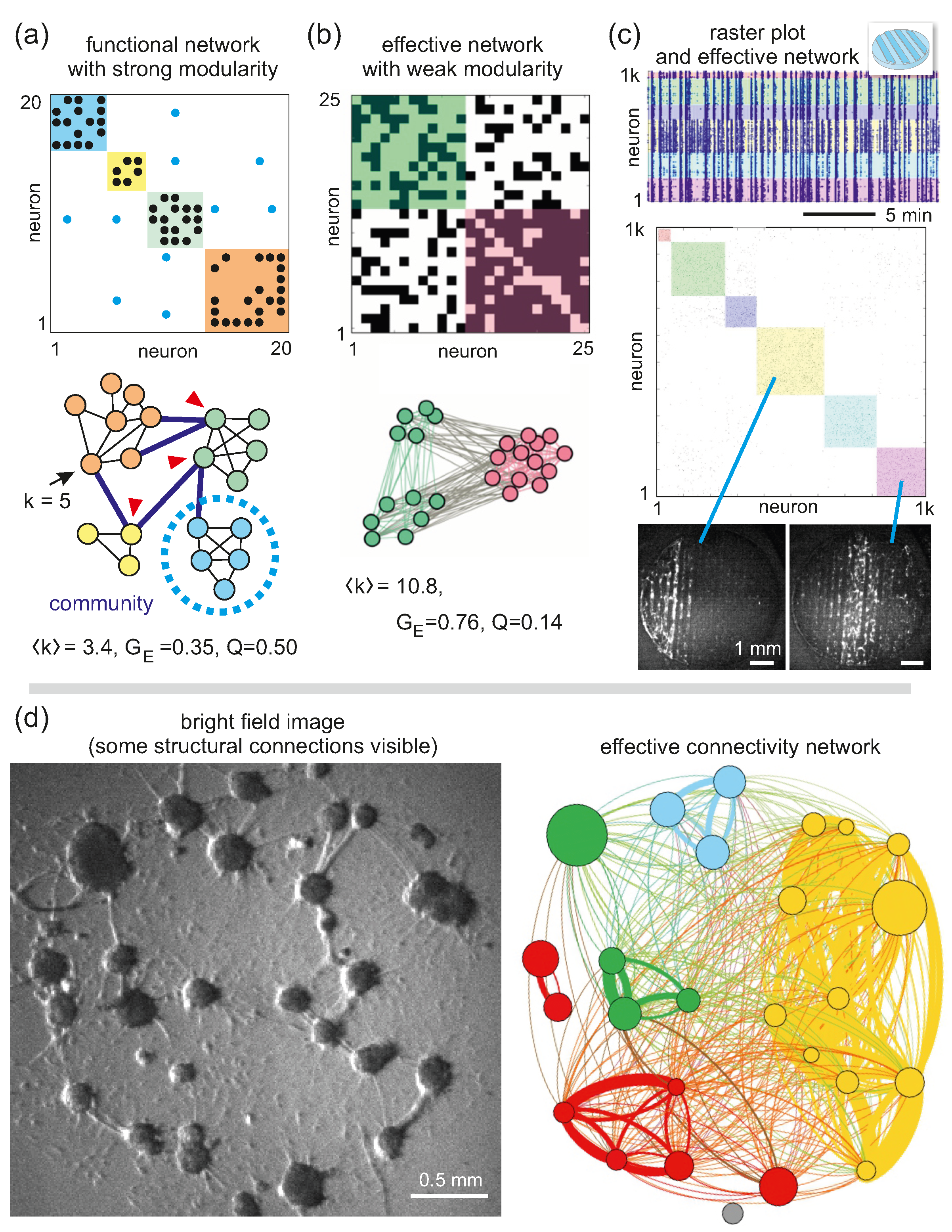
5. Complex Networks in Neuroscience and Neuronal Cultures
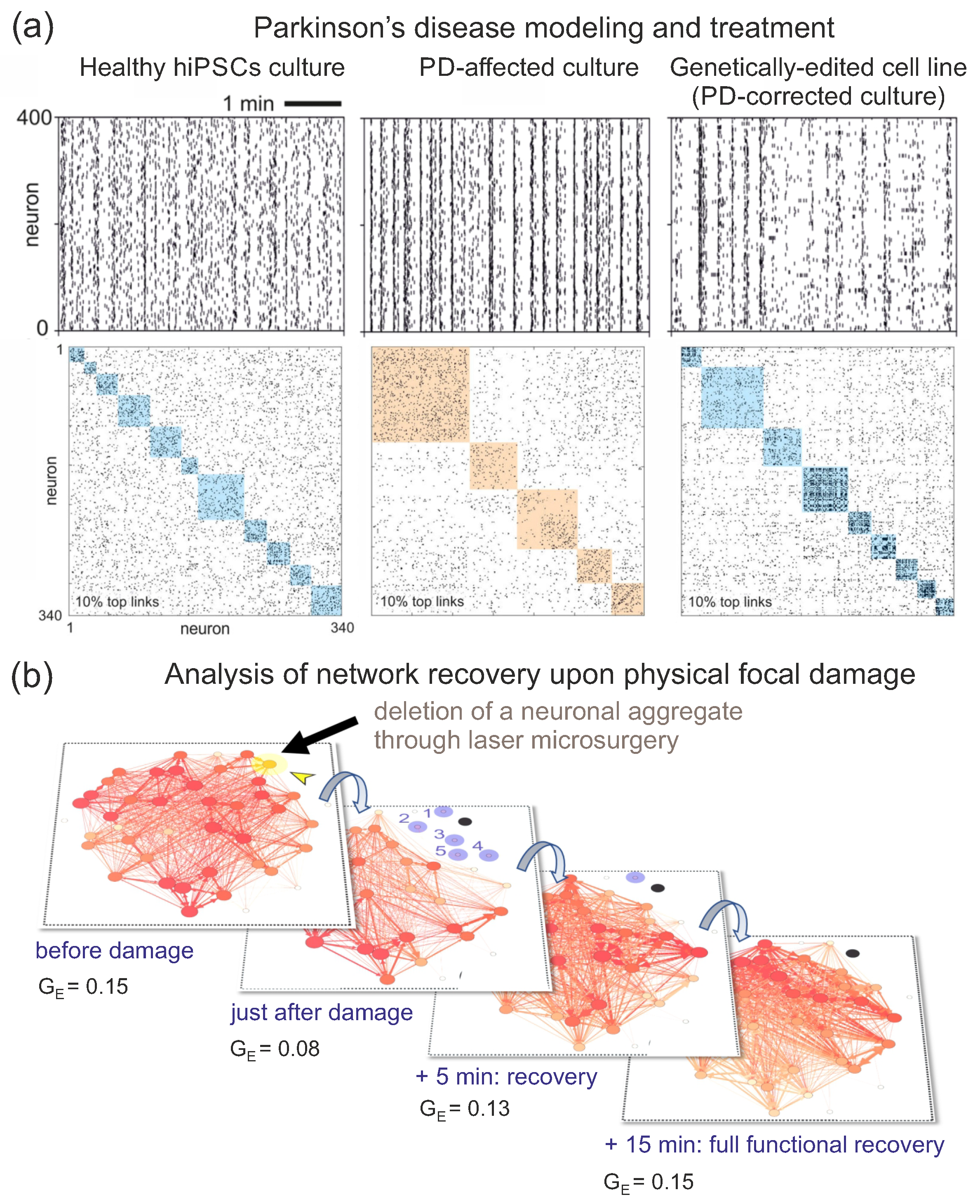
6. The Study of Neurological Disorders In Vitro
7. Towards Brain-on-Chip Systems
8. Limitations and Challenges of Neuronal Cultures
9. Future Directions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ramón y Cajal, S. Neuron Theory or Reticular Theory (1935); Purkiss, M.U., Fox, C.A., Eds.; Consejo Superior de Investigaciones Cientificas, Instituto Ramon y Cajal: Madrid, Spain, 1954. [Google Scholar]
- Guillery, R. Observations of synaptic structures: Origins of the neuron doctrine and its current status. Philos. Trans. R. Soc. B Biol. Sci. 2005, 360, 1281–1307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saceleanu, V.M.; Mohan, A.G.; Covache-Busuioc, R.A.; Costin, H.P.; Ciurea, A.V. Wilhelm von Waldeyer: Important Steps in Neural Theory, Anatomy and Citology. Brain Sci. 2022, 12, 224. [Google Scholar] [CrossRef] [PubMed]
- Yuste, R. From the neuron doctrine to neural networks. Nat. Rev. Neurosci. 2015, 16, 487–497. [Google Scholar] [CrossRef] [PubMed]
- Millet, L.J.; Gillette, M.U. Over a century of neuron culture: From the hanging drop to microfluidic devices. Yale J. Biol. Med. 2012, 85, 501–521. [Google Scholar] [PubMed]
- Tibau, E.; Valencia, M.; Soriano, J. Identification of neuronal network properties from the spectral analysis of calcium imaging signals in neuronal cultures. Front. Neur. Circ. 2013, 7, 199. [Google Scholar] [CrossRef]
- Orlandi, J.G.; Soriano, J.; Alvarez-Lacalle, E.; Teller, S.; Casademunt, J. Noise focusing and the emergence of coherent activity in neuronal cultures. Nat. Phys. 2013, 9, 582–590. [Google Scholar] [CrossRef]
- Hernández-Navarro, L.; Faci-Lázaro, S.; Orlandi, J.G.; Feudel, U.; Gómez-Gardeñes, J.; Soriano, J. Noise-driven amplification mechanisms governing the emergence of coherent extreme events in excitable systems. Phys. Rev. Res. 2021, 3, 023133. [Google Scholar] [CrossRef]
- Faci-Lázaro, S.; Soriano, J.; Gómez-Gardeñes, J. Impact of targeted attack on the spontaneous activity in spatial and biologically-inspired neuronal networks. Chaos 2019, 29, 083126. [Google Scholar] [CrossRef]
- Hernández-Navarro, L.; Orlandi, J.G.; Cerruti, B.; Vives, E.; Soriano, J. Dominance of Metric Correlations in Two-Dimensional Neuronal Cultures Described through a Random Field Ising Model. Phys. Rev. Lett. 2017, 118, 208101. [Google Scholar] [CrossRef] [Green Version]
- Ayasreh, S.; Jurado, I.; López-León, C.; Montalà-Flaquer, M.; Soriano, J. Dynamic and Functional Alterations of Neuronal Networks In Vitro upon Physical Damage: A Proof of Concept. Micromachines 2022, 13, 2259. [Google Scholar] [CrossRef]
- Estévez-Priego, E.; Teller, S.; Granell, C.; Arenas, A.; Soriano, J. Functional strengthening through synaptic scaling upon connectivity disruption in neuronal cultures. Netw. Neurosci. 2020, 4, 1160–1180. [Google Scholar] [CrossRef]
- Teller, S.; Estévez-Priego, E.; Granell, C.; Tornero, D.; Andilla, J.; Olarte, O.E.; Loza-Alvarez, P.; Arenas, A.; Soriano, J. Spontaneous functional recovery after focal damage in neuronal cultures. eNeuro 2020, 7, 0254-19.2019. [Google Scholar] [CrossRef] [PubMed]
- Teller, S.; Tahirbegi, I.B.; Mir, M.; Samitier, J.; Soriano, J. Magnetite-Amyloid-β deteriorates activity and functional organization in an in vitro model for Alzheimer’s disease. Sci. Rep. 2015, 5, 17261. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tibau, E.; Ludl, A.A.; Rudiger, S.; Orlandi, J.G.; Soriano, J. Neuronal Spatial Arrangement Shapes Effective Connectivity Traits of in vitro Cortical Networks. IEEE Trans. Netw. Sci. Eng. 2020, 7, 435–448. [Google Scholar] [CrossRef] [Green Version]
- Ludl, A.A.; Soriano, J. Impact of Physical Obstacles on the Structural and Effective Connectivity of in silico Neuronal Circuits. Front. Comput. Neurosci. 2020, 14, 77. [Google Scholar] [CrossRef]
- Stetter, O.; Battaglia, D.; Soriano, J.; Geisel, T. Model-free reconstruction of excitatory neuronal connectivity from calcium imaging signals. PLoS Comput. Biol. 2012, 8, e1002653. [Google Scholar] [CrossRef] [Green Version]
- Orlandi, J.G.; Stetter, O.; Soriano, J.; Geisel, T.; Battaglia, D. Transfer entropy reconstruction and labeling of neuronal connections from simulated calcium imaging. PLoS ONE 2014, 9, e98842. [Google Scholar] [CrossRef] [Green Version]
- Montalà-Flaquer, M.; López-León, C.F.; Tornero, D.; Houben, A.M.; Fardet, T.; Monceau, P.; Bottani, S.; Soriano, J. Rich dynamics and functional organization on topographically designed neuronal networks in vitro. iScience 2022, 25, 105680. [Google Scholar] [CrossRef]
- Carola, G.; Malagarriga, D.; Calatayud, C.; Pons-Espinal, M.; Blasco-Agell, L.; Richaud-Patin, Y.; Fernandez-Carasa, I.; Baruffi, V.; Beltramone, S.; Molina, E.; et al. Parkinson’s disease patient-specific neuronal networks carrying the LRRK2 G2019S mutation unveil early functional alterations that predate neurodegeneration. npj Parkinson’s Dis. 2021, 7, 1–14. [Google Scholar] [CrossRef]
- Estévez-Priego, E.; Moreno-Fina, M.; Monni, E.; Kokaia, Z.; Soriano, J.; Tornero, D. Long-term calcium imaging reveals functional development in hiPSC-derived cultures comparable to human but not rat primary cultures. Stem Cell Rep. 2023, 18, 1–15. [Google Scholar] [CrossRef]
- Yamamoto, H.; Moriya, S.; Ide, K.; Hayakawa, T.; Akima, H.; Sato, S.; Kubota, S.; Tanii, T.; Niwano, M.; Teller, S.; et al. Impact of modular organization on dynamical richness in cortical networks. Sci. Adv. 2018, 4, eaau4914. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Crowe, J.A.; El-Tamer, A.; Nagel, D.; Koroleva, A.V.; Madrid-Wolff, J.; Olarte, O.E.; Sokolovsky, S.; Estevez-Priego, E.; Ludl, A.A.; Soriano, J.; et al. Development of two-photon polymerised scaffolds for optical interrogation and neurite guidance of human iPSC-derived cortical neuronal networks. Lab Chip 2020, 20, 1792–1806. [Google Scholar] [CrossRef] [PubMed]
- Koroleva, A.; Deiwick, A.; El-Tamer, A.; Koch, L.; Shi, Y.; Estévez-Priego, E.; Ludl, A.A.; Soriano, J.; Guseva, D.; Ponimaskin, E.; et al. In Vitro Development of Human iPSC-Derived Functional Neuronal Networks on Laser-Fabricated 3D Scaffolds. ACS Appl. Mater. Interfaces 2021, 13, 7839–7853. [Google Scholar] [CrossRef] [PubMed]
- Comella-Bolla, A.; Orlandi, J.G.; Miguez, A.; Straccia, M.; García-Bravo, M.; Bombau, G.; Galofré, M.; Sanders, P.; Carrere, J.; Segovia, J.C.; et al. Human Pluripotent Stem Cell-Derived Neurons Are Functionally Mature In Vitro and Integrate into the Mouse Striatum Following Transplantation. Mol. Neurobiol. 2020, 57, 2766–2798. [Google Scholar] [CrossRef]
- Fernández-García, S.; Orlandi, J.G.; Barriga, G.A.G.D.; Rodríguez, M.J.; Masana, M.; Soriano, J.; Alberch, J. Deficits in coordinated neuronal activity and network topology are striatal hallmarks in Huntington’s disease. BMC Biol. 2020, 18, 58. [Google Scholar] [CrossRef]
- di Domenico, A.; Carola, G.; Calatayud, C.; Pons-Espinal, M.; Muñoz, J.P.; Richaud-Patin, Y.; Fernandez-Carasa, I.; Gut, M.; Faella, A.; Parameswaran, J.; et al. Patient-Specific iPSC-Derived Astrocytes Contribute to Non-Cell-Autonomous Neurodegeneration in Parkinson’s Disease. Stem Cell Rep. 2019, 12, 213–229. [Google Scholar] [CrossRef] [Green Version]
- Fernández-Santiago, R.; Carballo-Carbajal, I.; Castellano, G.; Torrent, R.; Richaud, Y.; Sánchez-Danés, A.; Vilarrasa-Blasi, R.; Sánchez-Pla, A.; Mosquera, J.L.; Soriano, J.; et al. Aberrant epigenome in iPSC--derived dopaminergic neurons from Parkinson’s disease patients. EMBO Mol. Med. 2015, 7, 1529–1546. [Google Scholar] [CrossRef]
- Calatayud, C.; Carola, G.; Fernández-Carasa, I.; Valtorta, M.; Jiménez-Delgado, S.; Díaz, M.; Soriano-Fradera, J.; Cappelletti, G.; García-Sancho, J.; Raya, Á.; et al. CRISPR/Cas9-mediated generation of a tyrosine hydroxylase reporter iPSC line for live imaging and isolation of dopaminergic neurons. Sci. Rep. 2019, 9, 6811. [Google Scholar] [CrossRef] [Green Version]
- Canals, I.; Soriano, J.; Orlandi, J.G.; Torrent, R.; Richaud-Patin, Y.; Jiménez-Delgado, S.; Merlin, S.; Follenzi, A.; Consiglio, A.; Vilageliu, L.; et al. Activity and high-order effective connectivity alterations in sanfilippo C patient-specific neuronal networks. Stem Cell Rep. 2015, 5, 546–557. [Google Scholar] [CrossRef] [Green Version]
- Barriga, G.G.D.; Giralt, A.; Anglada-Huguet, M.; Gaja-Capdevila, N.; Orlandi, J.G.; Soriano, J.; Canals, J.M.; Alberch, J. 7,8-dihydroxyflavone ameliorates cognitive and motor deficits in a Huntington’s disease mouse model through specific activation of the PLCγ1 pathway. Hum. Mol. Genet. 2017, 26, 3144–3160. [Google Scholar] [CrossRef]
- Matamoros-Angles, A.; Hervera, A.; Soriano, J.; Martí, E.; Carulla, P.; Llorens, F.; Nuvolone, M.; Aguzzi, A.; Ferrer, I.; Gruart, A.; et al. Analysis of co-isogenic prion protein deficient mice reveals behavioral deficits, learning impairment, and enhanced hippocampal excitability. BMC Biol. 2022, 20, 17. [Google Scholar] [CrossRef] [PubMed]
- Cobb, M. The Idea of the Brain: The Past and Future of Neuroscience; Hachette: London, UK, 2020. [Google Scholar]
- Wellbourne-Wood, J.; Chatton, J.Y. From Cultured Rodent Neurons to Human Brain Tissue: Model Systems for Pharmacological and Translational Neuroscience. ACS Chem. Neurosci. 2018, 9, 1975–1985. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shi, Y.; Inoue, H.; Wu, J.C.; Yamanaka, S. Induced pluripotent stem cell technology: A decade of progress. Nature Reviews Drug Discovery 2017, 16, 115–130. [Google Scholar] [CrossRef] [PubMed]
- Nikolakopoulou, P.; Rauti, R.; Voulgaris, D.; Shlomy, I.; Maoz, B.M.; Herland, A. Recent progress in translational engineered in vitro models of the central nervous system. Brain 2021, 143, 3181–3213. [Google Scholar] [CrossRef]
- Salazar, I.; Mele, M.; Caldeira, M.; Costa, R.; Correia, B.; Frisari, S.; Duarte, C. Preparation of Primary Cultures of Embryonic Rat Hippocampal and Cerebrocortical Neurons. Bio-protocol 2017, 7, 1–11. [Google Scholar] [CrossRef]
- Spanu, A.; Tedesco, M.; Martinoia, S.; Bonfiglio, A. In Vitro Neuronal Networks; Advances in Neurobiology; Springer International Publishing: Berlin, Germany, 2019; Volume 22, pp. 155–167. [Google Scholar] [CrossRef]
- Allen, N.J.; Barres, B.A. Glia—More than just brain glue. Nature 2009, 457, 675–677. [Google Scholar] [CrossRef]
- Shi, M.; Majumdar, D.; Gao, Y.; Brewer, B.M.; Goodwin, C.R.; McLean, J.A.; Li, D.; Webb, D.J. Glia co-culture with neurons in microfluidic platforms promotes the formation and stabilization of synaptic contacts. Lab. Chip. 2013, 13, 3008–3021. [Google Scholar] [CrossRef] [Green Version]
- Teller, S.; Granell, C.; De Domenico, M.; Soriano, J.; Gómez, S.; Arenas, A. Emergence of Assortative Mixing between Clusters of Cultured Neurons. PLoS Comput. Biol. 2014. [Google Scholar] [CrossRef] [Green Version]
- Cohen, E.; Ivenshitz, M.; Amor-Baroukh, V.; Greenberger, V.; Segal, M. Determinants of spontaneous activity in networks of cultured hippocampus. Brain Res. 2008, 1235, 21–30. [Google Scholar] [CrossRef]
- Takahashi, K.; Yamanaka, S. Induction of Pluripotent Stem Cells from Mouse Embryonic and Adult Fibroblast Cultures by Defined Factors. Cell 2006, 126, 663–676. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, K.; Tanabe, K.; Ohnuki, M.; Narita, M.; Ichisaka, T.; Tomoda, K.; Yamanaka, S. Induction of Pluripotent Stem Cells from Adult Human Fibroblasts by Defined Factors. Cell 2007, 131, 861–872. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nishikawa, S.i.; Goldstein, R.A.; Nierras, C.R. The promise of human induced pluripotent stem cells for research and therapy. Nat. Rev. Mol. Cell Biol. 2008, 9, 725–729. [Google Scholar] [CrossRef] [PubMed]
- Idelson, M.S.; Ben-Jacob, E.; Hanein, Y. Innate Synchronous Oscillations in Freely-Organized Small Neuronal Circuits. PLoS ONE 2010, 5, e14443. [Google Scholar] [CrossRef] [PubMed]
- Breskin, I.; Soriano, J.; Moses, E.; Tlusty, T. Percolation in living neural networks. Phys. Rev. Lett. 2006, 97, 188102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eckmann, J.P.; Feinerman, O.; Gruendlinger, L.; Moses, E.; Soriano, J.; Tlusty, T. The physics of living neural networks. Phys. Rep. 2007, 449, 54–76. [Google Scholar] [CrossRef] [Green Version]
- Soriano, J.; Martínez, M.R.; Tlusty, T.; Moses, E. Development of input connections in neural cultures. Proc. Natl. Acad. Sci. USA 2008, 105, 13758–13763. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- le Feber, J.; Dummer, A.; Hassink, G.C.; van Putten, M.J.A.M.; Hofmeijer, J. Evolution of Excitation–Inhibition Ratio in Cortical Cultures Exposed to Hypoxia. Front. Cell. Neurosci. 2018, 12. [Google Scholar] [CrossRef]
- Grienberger, C.; Konnerth, A. Imaging Calcium in Neurons. Neuron 2012, 73, 862–885. [Google Scholar] [CrossRef] [Green Version]
- Paredes, R.M.; Etzler, J.C.; Watts, L.T.; Zheng, W.; Lechleiter, J.D. Chemical calcium indicators. Methods 2008, 46, 143–151. [Google Scholar] [CrossRef] [Green Version]
- Knöpfel, T. Genetically encoded optical indicators for the analysis of neuronal circuits. Nat. Rev. Neurosci. 2012, 13, 687–700. [Google Scholar] [CrossRef]
- Grewe, B.F.; Langer, D.; Kasper, H.; Kampa, B.M.; Helmchen, F. High-speed in vivo calcium imaging reveals neuronal network activity with near-millisecond precision. Nat. Methods 2010, 7, 399–405. [Google Scholar] [CrossRef] [PubMed]
- Lütcke, H.; Gerhard, F.; Zenke, F.; Gerstner, W.; Helmchen, F. Inference of neuronal network spike dynamics and topology from calcium imaging data. Front. Neural Circuits 2013, 7, 201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deneux, T.; Kaszas, A.; Szalay, G.; Katona, G.; Lakner, T.; Grinvald, A.; Rózsa, B.; Vanzetta, I. Accurate spike estimation from noisy calcium signals for ultrafast three-dimensional imaging of large neuronal populations in vivo. Nat. Commun. 2016, 7, 12190. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Friedrich, J.; Zhou, P.; Paninski, L.; Staneva, V.; Chklovskii, D.; Pnevmatikakis, E. Fast online deconvolution of calcium imaging data. PLoS Comput. Biol. 2017, 13, e1005423. [Google Scholar] [CrossRef] [Green Version]
- Pnevmatikakis, E.A.; Soudry, D.; Gao, Y.; Machado, T.A.; Merel, J.; Pfau, D.; Reardon, T.; Mu, Y.; Lacefield, C.; Yang, W.; et al. Simultaneous Denoising, Deconvolution, and Demixing of Calcium Imaging Data. Neuron 2016, 89, 285–299. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wei, Z.; Lin, B.J.; Chen, T.W.; Daie, K.; Svoboda, K.; Druckmann, S. A comparison of neuronal population dynamics measured with calcium imaging and electrophysiology. PLoS Comput. Biol. 2020, 16, 1–29. [Google Scholar] [CrossRef]
- Orlandi, J.G.; Fernández-García, S.; Comella-Bolla, A.; Masana, M.; Barriga, G.G.D.; Yaghoubi, M.; Kipp, A.; Canals, J.M.; Colicos, M.A.; Davidsen, J.; et al. NETCAL: An interactive platform for large-scale, NETwork and population dynamics analysis of CALcium imaging recordings. Zenodo 2017. [Google Scholar] [CrossRef]
- Zamora-López, G.; Chen, Y.; Deco, G.; Kringelbach, M.L.; Zhou, C. Functional complexity emerging from anatomical constraints in the brain: The significance of network modularity and rich-clubs. Sci. Rep. 2016, 6, 38424. [Google Scholar] [CrossRef] [Green Version]
- Jacobi, S.; Soriano, J.; Moses, E. BDNF and NT-3 increase velocity of activity front propagation in unidimensional hippocampal cultures. J. Neurophysiol. 2010, 104, 2932–2939. [Google Scholar] [CrossRef]
- Chiappalone, M.; Bove, M.; Vato, A.; Tedesco, M.; Martinoia, S. Dissociated cortical networks show spontaneously correlated activity patterns during in vitro development. Brain Res. 2006, 1093, 41–53. [Google Scholar] [CrossRef]
- Wagenaar, D.A.; Pine, J.; Potter, S.M. An extremely rich repertoire of bursting patterns during the development of cortical cultures. BMC Neurosci. 2006, 7, 11. [Google Scholar] [CrossRef] [PubMed]
- Mazzoni, A.; Broccard, F.D.; Garcia-Perez, E.; Bonifazi, P.; Ruaro, M.E.; Torre, V. On the dynamics of the spontaneous activity in neuronal networks. PLoS ONE 2007, 2, e439. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pasquale, V.; Massobrio, P.; Bologna, L.; Chiappalone, M.; Martinoia, S. Self-organization and neuronal avalanches in networks of dissociated cortical neurons. Neuroscience 2008, 153, 1354–1369. [Google Scholar] [CrossRef] [PubMed]
- Ham, M.I.; Bettencourt, L.M.; McDaniel, F.D.; Gross, G.W. Spontaneous coordinated activity in cultured networks: Analysis of multiple ignition sites, primary circuits, and burst phase delay distributions. J. Comput. Neurosci. 2008, 24, 346–357. [Google Scholar] [CrossRef] [Green Version]
- Okujeni, S.; Kandler, S.; Egert, U. Mesoscale architecture shapes initiation and richness of spontaneous network activity. J. Neurosci. 2017, 37, 3972–3987. [Google Scholar] [CrossRef] [Green Version]
- Spitzer, N.C. Electrical activity in early neuronal development. Nature 2006, 444, 707–712. [Google Scholar] [CrossRef]
- Blankenship, A.G.; Feller, M.B. Mechanisms underlying spontaneous patterned activity in developing neural circuits. Nat. Rev. Neurosci. 2010, 11, 18–29. [Google Scholar] [CrossRef]
- Soto, F.; Ma, X.; Cecil, J.L.; Vo, B.Q.; Culican, S.M.; Kerschensteiner, D. Spontaneous Activity Promotes Synapse Formation in a Cell-Type-Dependent Manner in the Developing Retina. J. Neurosci. 2012, 32, 5426–5439. [Google Scholar] [CrossRef] [Green Version]
- Warp, E.; Agarwal, G.; Wyart, C.; Friedmann, D.; Oldfield, C.S.; Conner, A.; Bene, F.D.; Arrenberg, A.B.; Baier, H.; Isacoff, E.Y. Emergence of patterned activity in the developing zebrafish spinal cord. Curr. Biol. CB 2012, 22, 93–102. [Google Scholar] [CrossRef] [Green Version]
- Buzsáki, G.; Draguhn, A. Neuronal oscillations in cortical networks. Science 2004, 304, 1926–1929. [Google Scholar] [CrossRef] [Green Version]
- Cohen, O.; Keselman, A.; Moses, E.; Martínez, M.R.; Soriano, J.; Tlusty, T. Quorum percolation in living neural networks. Europhys. Lett. 2010, 89, 18008. [Google Scholar] [CrossRef] [Green Version]
- Izhikevich, E.M. Simple model of spiking neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Izhikevich, E.M. Which model to use for cortical spiking neurons? IEEE Trans. Neural Netw. 2004, 15, 1063–1070. [Google Scholar] [CrossRef]
- Tsodyks, M.; Markram, H. The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability. Proc. Natl. Acad. Sci. USA 1997, 94, 719–723. [Google Scholar] [CrossRef] [Green Version]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef] [Green Version]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Rubinov, M.; Sporns, O. Complex network measures of brain connectivity: Uses and interpretations. NeuroImage 2010, 52, 1059–1069. [Google Scholar] [CrossRef]
- Sporns, O. Structure and function of complex brain networks. Dialogues Clin. Neurosci. 2013, 15, 247–262. [Google Scholar] [CrossRef]
- Bassett, D.S.; Sporns, O. Network neuroscience. Nat. Neurosci. 2017, 20, 353–364. [Google Scholar] [CrossRef] [Green Version]
- Friston, K.J. Functional and Effective Connectivity: A Review. Brain Connect. 2011, 1, 13–36. [Google Scholar] [CrossRef]
- Wang, H.E.; Bénar, C.G.; Quilichini, P.P.; Friston, K.J.; Jirsa, V.K.; Bernard, C. A systematic framework for functional connectivity measures. Front. Neurosci. 2014, 8, 405. [Google Scholar] [CrossRef] [PubMed]
- Valdes-Sosa, P.A.; Roebroeck, A.; Daunizeau, J.; Friston, K. Effective connectivity: Influence, causality and biophysical modeling. NeuroImage 2011, 58, 339–361. [Google Scholar] [CrossRef] [PubMed]
- Vicente, R.; Wibral, M.; Lindner, M.; Pipa, G. Transfer entropy-a model-free measure of effective connectivity for the neurosciences. J. Comput. Neurosci. 2011, 30, 45–67. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schreiber, T. Measuring Information Transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wibral, M.; Vicente, R.; Lindner, M. Transfer Entropy in Neuroscience. In Directed Information Measures in Neuroscience; Wibral, M., Vicente, R., Lizier, J.T., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 3–36. [Google Scholar] [CrossRef]
- Barthélemy, M. Spatial networks. Physics Reports 2011, 499, 1–101. [Google Scholar] [CrossRef] [Green Version]
- Bullmore, E.; Sporns, O. The economy of brain network organization. Nat. Rev. Neurosci. 2012, 13, 336–349. [Google Scholar] [CrossRef]
- Stiso, J.; Bassett, D.S. Spatial Embedding Imposes Constraints on Neuronal Network Architectures. Trends Cogn. Sci. 2018, 22, 1127–1142. [Google Scholar] [CrossRef] [PubMed]
- Latora, V.; Marchiori, M. Efficient behavior of small-world networks. Phys. Rev. Lett. 2001, 87, 198701. [Google Scholar] [CrossRef] [Green Version]
- Variano, E.A.; McCoy, J.H.; Lipson, H. Networks, dynamics, and modularity. Phys. Rev. Lett. 2004, 92, 188701. [Google Scholar] [CrossRef] [Green Version]
- Fortunato, S. Community detection in graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef] [Green Version]
- Sporns, O.; Honey, C.J.; Kötter, R. Identification and classification of hubs in brain networks. PLoS ONE 2007, 2, e1049. [Google Scholar] [CrossRef] [PubMed]
- van den Heuvel, M.P.; Sporns, O. Network hubs in the human brain. Trends Cogn. Sci. 2013, 17, 683–696. [Google Scholar] [CrossRef] [PubMed]
- Battaglia, D.; Guyon, I.; Lemaire, V.; Orlandi, J.; Ray, B.; Soriano, J. Neural Connectomics Challenge; Springer: Berlin, Germany, 2017. [Google Scholar]
- Stam, C.J. Modern network science of neurological disorders. Nat. Rev. Neurosci. 2014, 15, 683–695. [Google Scholar] [CrossRef] [PubMed]
- Medaglia, J.D.; Bassett, D.S. Network Analyses and Nervous System Disorders; Oxford University Press: Oxford, UK, 2018. [Google Scholar] [CrossRef] [Green Version]
- Bassett, D.S.; Bullmore, E.T. Human brain networks in health and disease. Curr. Opin. Neurol. 2009, 22, 340–347. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Evans, A. Graph theoretical modeling of brain connectivity. Curr. Opin. Neurol. 2010, 23, 341–350. [Google Scholar] [CrossRef] [Green Version]
- Griffa, A.; Baumann, P.S.; Thiran, J.P.; Hagmann, P. Structural connectomics in brain diseases. NeuroImage 2013, 80, 515–526. [Google Scholar] [CrossRef]
- Meunier, D.; Lambiotte, R.; Bullmore, E.T. Modular and hierarchically modular organization of brain networks. Front. Neurosci. 2010, 4, 200. [Google Scholar] [CrossRef] [Green Version]
- Sporns, O.; Betzel, R.F. Modular Brain Networks. Annu. Rev. Psychol. 2016, 67, 613–640. [Google Scholar] [CrossRef] [Green Version]
- Alexander-Bloch, A.F.; Vértes, P.E.; Stidd, R.; Lalonde, F.; Clasen, L.; Rapoport, J.; Giedd, J.; Bullmore, E.T.; Gogtay, N. The Anatomical Distance of Functional Connections Predicts Brain Network Topology in Health and Schizophrenia. Cereb. Cortex 2013, 23, 127–138. [Google Scholar] [CrossRef] [Green Version]
- Buckner, R.L.; Sepulcre, J.; Talukdar, T.; Krienen, F.M.; Liu, H.; Hedden, T.; Andrews-Hanna, J.R.; Sperling, R.A.; Johnson, K.A. Cortical hubs revealed by intrinsic functional connectivity: Mapping, assessment of stability, and relation to Alzheimer’s disease. J. Neurosci. 2009, 29, 1860–1873. [Google Scholar] [CrossRef] [Green Version]
- Ruaro, M.; Bonifazi, P.; Torre, V. Toward the Neurocomputer: Image Processing and Pattern Recognition With Neuronal Cultures. IEEE Trans. Biomed. Eng. 2005, 52, 371–383. [Google Scholar] [CrossRef] [PubMed]
- Novellino, A.; D’Angelo, P.; Cozzi, L.; Chiappalone, M.; Sanguineti, V.; Martinoia, S. Connecting Neurons to a Mobile Robot: An In Vitro Bidirectional Neural Interface. Comput. Intell. Neurosci. 2007, 2007, 012725. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- George, R.; Chiappalone, M.; Giugliano, M.; Levi, T.; Vassanelli, S.; Partzsch, J.; Mayr, C. Plasticity and Adaptation in Neuromorphic Biohybrid Systems. iScience 2020, 23, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Kagan, B.J.; Kitchen, A.C.; Tran, N.T.; Habibollahi, F.; Khajehnejad, M.; Parker, B.J.; Bhat, A.; Rollo, B.; Razi, A.; Friston, K.J. In vitro neurons learn and exhibit sentience when embodied in a simulated game-world. Neuron 2022, 110, 3952–3969.e8. [Google Scholar] [CrossRef]
- Pelt, J.V.; Corner, M.; Wolters, P.; Rutten, W.; Ramakers, G. Longterm stability and developmental changes in spontaneous network burst firing patterns in dissociated rat cerebral cortex cell cultures on multielectrode arrays. Neurosci. Lett. 2004, 361, 86–89. [Google Scholar] [CrossRef]
- Kuebler, E.S.; Tauskela, J.S.; Aylsworth, A.; Zhao, X.; Thivierge, J.P. Burst predicting neurons survive an in vitro glutamate injury model of cerebral ischemia. Sci. Rep. 2015, 5, 17718. [Google Scholar] [CrossRef] [Green Version]
- Downes, J.H.; Hammond, M.W.; Xydas, D.; Spencer, M.C.; Becerra, V.M.; Warwick, K.; Whalley, B.J.; Nasuto, S.J. Emergence of a Small-World Functional Network in Cultured Neurons. PLoS Comput. Biol. 2012, 8, e1002522. [Google Scholar] [CrossRef] [Green Version]
- Okujeni, S.; Egert, U. Self-organization of modular network architecture by activity-dependent neuronal migration and outgrowth. eLife 2019, 8, 1–29. [Google Scholar] [CrossRef]
- Antonello, P.C.; Varley, T.F.; Beggs, J.; Porcionatto, M.; Sporns, O.; Faber, J. Self-organization of in vitro neuronal assemblies drives to complex network topology. eLife 2022, 11. [Google Scholar] [CrossRef]
- Wagenaar, D.A.; Madhavan, R.; Pine, J.; Potter, S.M. Controlling Bursting in Cortical Cultures with Closed-Loop Multi-Electrode Stimulation. J. Neurosci. 2005, 25, 680–688. [Google Scholar] [CrossRef] [Green Version]
- Bisio, M.; Pimashkin, A.; Buccelli, S.; Tessadori, J.; Semprini, M.; Levi, T.; Colombi, I.; Gladkov, A.; Mukhina, I.; Averna, A.; et al. Closed-Loop Systems and In Vitro Neuronal Cultures: Overview and Applications. In In Vitro Neuronal Networks; Springer: Berlin, Germany, 2019; pp. 351–387. [Google Scholar] [CrossRef]
- le Feber, J.; Stegenga, J.; Rutten, W.L.C. The Effect of Slow Electrical Stimuli to Achieve Learning in Cultured Networks of Rat Cortical Neurons. PLoS ONE 2010, 5, e8871. [Google Scholar] [CrossRef] [PubMed]
- Kirwan, P.; Turner-Bridger, B.; Peter, M.; Momoh, A.; Arambepola, D.; Robinson, H.P.C.; Livesey, F.J. Development and function of human cerebral cortex neural networks from pluripotent stem cells in vitro. Development 2015, 142, 3178–3187. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hyvärinen, T.; Hyysalo, A.; Kapucu, F.E.; Aarnos, L.; Vinogradov, A.; Eglen, S.J.; Ylä-Outinen, L.; Narkilahti, S. Functional characterization of human pluripotent stem cell-derived cortical networks differentiated on laminin-521 substrate: Comparison to rat cortical cultures. Sci. Rep. 2019, 9, 17125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perea, G.; Araque, A. Glial calcium signaling and neuron–glia communication. Cell Calcium 2005, 38, 375–382. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sancho, L.; Contreras, M.; Allen, N.J. Glia as sculptors of synaptic plasticity. Neurosci. Res. 2021, 167, 17–29. [Google Scholar] [CrossRef] [PubMed]
- Keck, T.; Hübener, M.; Bonhoeffer, T. Interactions between synaptic homeostatic mechanisms: An attempt to reconcile BCM theory, synaptic scaling, and changing excitation/inhibition balance. Curr. Opin. Neurobiol. 2017, 43, 87–93. [Google Scholar] [CrossRef]
- Zierenberg, J.; Wilting, J.; Priesemann, V. Homeostatic Plasticity and External Input Shape Neural Network Dynamics. Phys. Rev. X 2018, 8. [Google Scholar] [CrossRef] [Green Version]
- Fenno, L.; Yizhar, O.; Deisseroth, K. The Development and Application of Optogenetics. Annu. Rev. Neurosci. 2011, 34, 389–412. [Google Scholar] [CrossRef]
- Emiliani, V.; Entcheva, E.; Hedrich, R.; Hegemann, P.; Konrad, K.R.; Lüscher, C.; Mahn, M.; Pan, Z.H.; Sims, R.R.; Vierock, J.; et al. Optogenetics for light control of biological systems. Nat. Rev. Methods Prim. 2022, 2, 55. [Google Scholar] [CrossRef]
- Lonardoni, D.; Amin, H.; Zordan, S.; Boi, F.; Lecomte, A.; Angotzi, G.N.; Berdondini, L. Active High-Density Electrode Arrays: Technology and Applications in Neuronal Cell Cultures. In In Vitro Neuronal Networks; Springer: Berlin, Germany, 2019; pp. 253–273. [Google Scholar] [CrossRef]
- Chen, Z.; Liang, Q.; Wei, Z.; Chen, X.; Shi, Q.; Yu, Z.; Sun, T. An Overview of In Vitro Biological Neural Networks for Robot Intelligence. Cyborg Bionic Syst. 2023, 4, 0001. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soriano, J. Neuronal Cultures: Exploring Biophysics, Complex Systems, and Medicine in a Dish. Biophysica 2023, 3, 181-202. https://doi.org/10.3390/biophysica3010012
Soriano J. Neuronal Cultures: Exploring Biophysics, Complex Systems, and Medicine in a Dish. Biophysica. 2023; 3(1):181-202. https://doi.org/10.3390/biophysica3010012
Chicago/Turabian StyleSoriano, Jordi. 2023. "Neuronal Cultures: Exploring Biophysics, Complex Systems, and Medicine in a Dish" Biophysica 3, no. 1: 181-202. https://doi.org/10.3390/biophysica3010012
APA StyleSoriano, J. (2023). Neuronal Cultures: Exploring Biophysics, Complex Systems, and Medicine in a Dish. Biophysica, 3(1), 181-202. https://doi.org/10.3390/biophysica3010012





