Single-Molecule Tracking in Live Cell without Immobilization or without Hydrodynamic Flow by Simulations: Thermodynamic Jitter †
Abstract
:1. Introduction
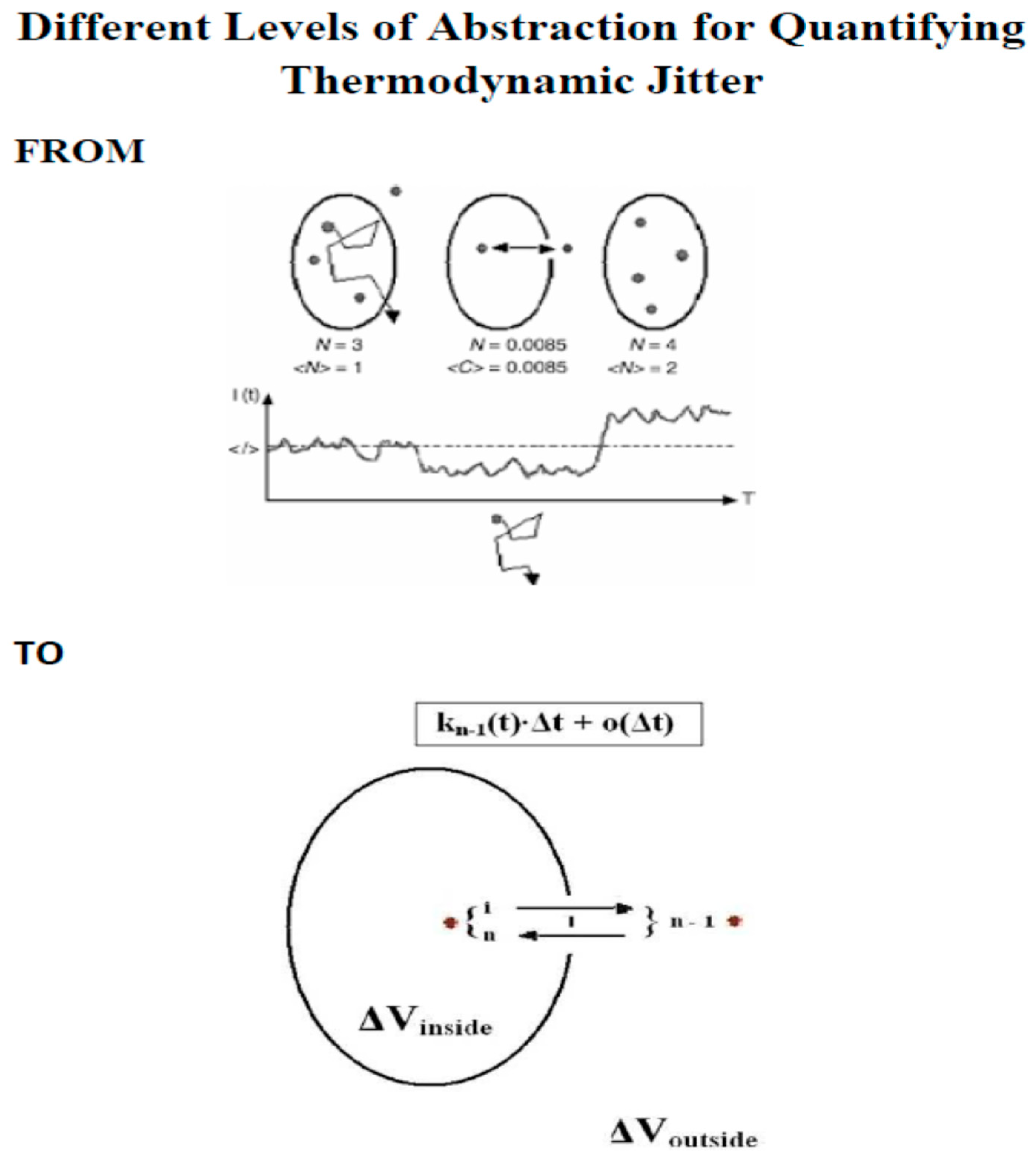

2. Methods
3. Results
3.1. Evaluation of Single-Molecule Detection: A Brief Narrative on the Motivation of the Simulation Experiments and Their Design as an Experimental Starting Point for the Obtained Results
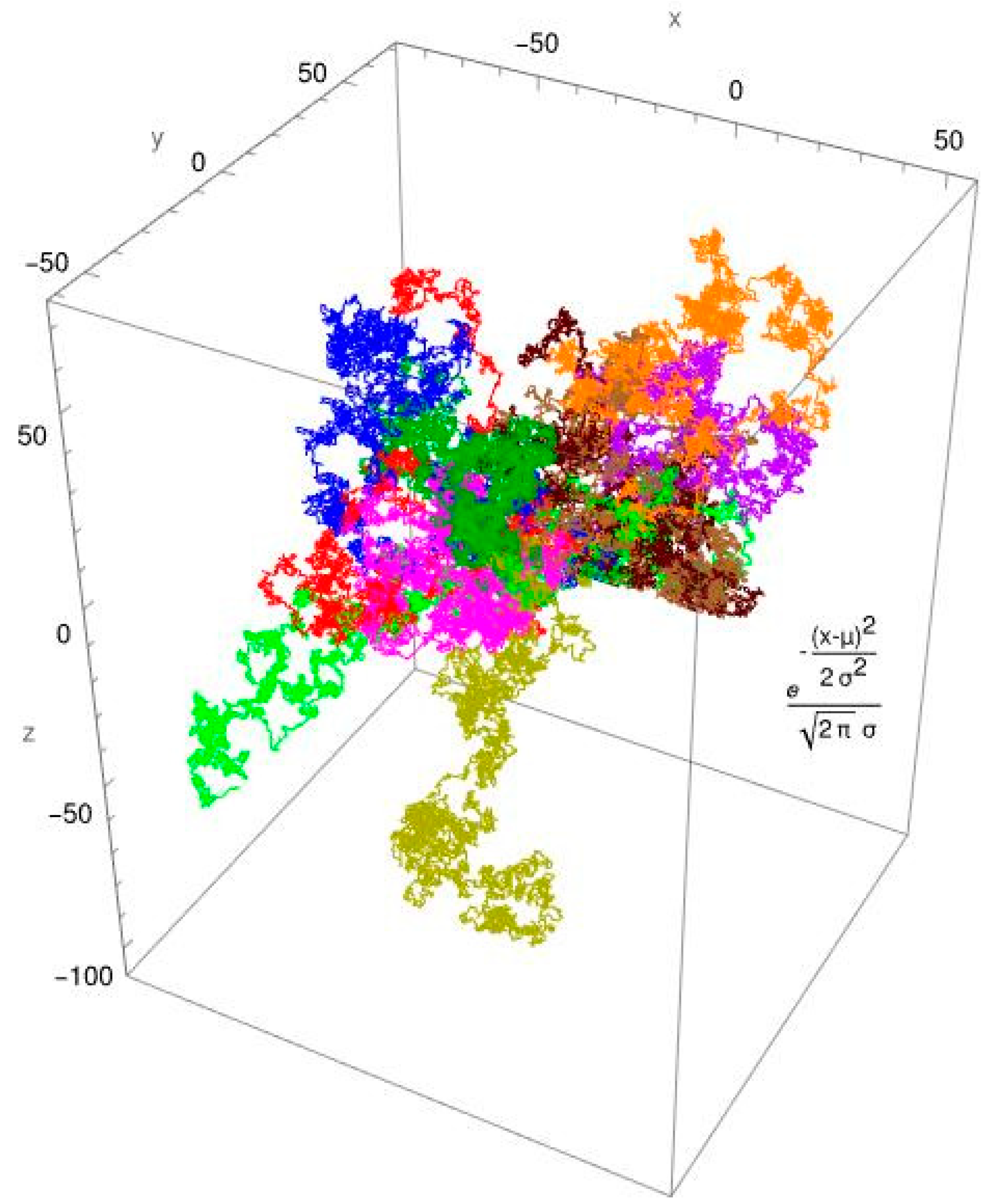
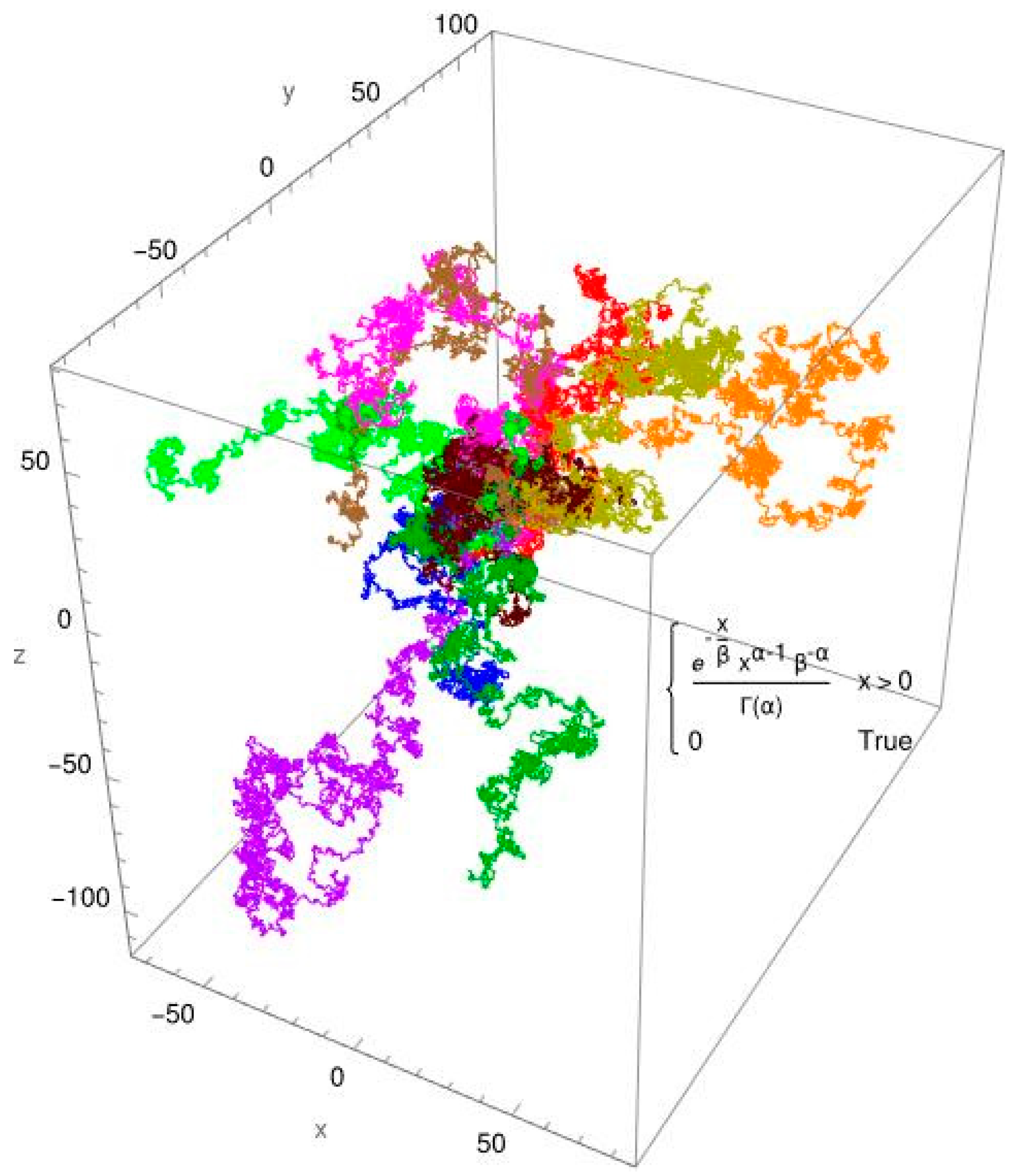
3.2. Single-Molecule Tracking
4. Discussion
- the meaningful time as single-molecule/single-particle time resolution is discussed here (for mathematical details see: ref. [12]),
5. Conclusions
6. Addendum
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- D’Este, E.; Lukinavičius, G.; Lincoln, R.; Opazo, F.; Fornasiero, E.F. Advancing cell biology with nanoscale fluorescence imaging: Essential practical considerations. Trends Cell Biol. 2024, 34, 671–684. [Google Scholar] [CrossRef] [PubMed]
- Loidolt-Krueger, M. New Confocal Microscope for quantitative fluorescence lifetime imaging with improved reproducibility. Microsc. Today 2023, 31, 24–31. [Google Scholar] [CrossRef]
- Harms, G.S.; Cognet, L.; Lommerse, P.H.; Blab, G.A.; Schmidt, T. Autofluorescent proteins in single-molecule research: Applications to live cell imaging microscopy. Biophys. J. 2001, 80, 2396–2408. [Google Scholar] [CrossRef] [PubMed]
- White, J.; Stelzer, E. Photobleaching GFP reveals protein dynamics inside live cells. Trends Cell Biol. 1999, 9, 61–65. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Exell, J.; Lin, H.; Zhang, C.; Welsher, K.D. Hour-long, kilohertz sampling Rate three-dimensional single-virus tracking in live cells enabled by StayGold fluorescent protein fusions. J. Phys. Chem. B 2024, 128, 5590–5600. [Google Scholar] [CrossRef] [PubMed]
- Foote, A.K.; Ishii, K.; Cullinane, B.; Tahara, T.; Goldsmith, R.H. Quantifying microsecond solution-phase conformational dynamics of a DNA hairpin at the single-molecule level. ACS Phys. Chem. 2024, 4, 408–419. [Google Scholar] [CrossRef] [PubMed]
- Földes-Papp, Z. Fluorescence fluctuation spectroscopic approaches to the study of a single molecule diffusing in solution and a live cell without systemic drift or convection: A theoretical study. Curr. Pharm. Biotechnol. 2007, 8, 261–273. [Google Scholar] [CrossRef] [PubMed]
- Földes-Papp, Z. ‘True’ single-molecule molecule observations by fluorescence correlation spectroscopy and two-color fluorescence cross-correlation spectroscopy. Exp. Mol. Pathol. 2007, 82, 147–155. [Google Scholar] [CrossRef] [PubMed]
- Földes-Papp, Z.; Baumann, G.; Kinjo, M.; Tamura, M. Single-Phase Single-Molecule Fluorescence Correlation Spectroscopy (SPSM-FCS). In Encyclopedia of Medical Genomics & Proteomics; Fuchs, J., Podda, M., Eds.; Taylor & Francis: New York, NY, USA, 2005; pp. 1–7. [Google Scholar]
- Földes-Papp, Z. What it means to measure a single molecule in a solution by fluorescence fluctuation spectroscopy. Exp. Mol. Pathol. 2006, 80, 209–218. [Google Scholar] [CrossRef] [PubMed]
- Földes-Papp, Z. Single-molecule time resolution in dilute liquids and live cells at the molecular scale: Constraints on the measurement time. Am. J. Transl. Med. 2021, 5, 154–165. [Google Scholar]
- Földes-Papp, Z. Measurements of Single Molecules in Solution and Live Cells Over Longer Observation Times Than Those Currently Possible: The Meaningful Time. Curr. Pharm. Biotechnol. 2013, 14, 441–444. [Google Scholar] [CrossRef] [PubMed]
- Baumann, G.; Földes-Papp, Z. Study on Single-Molecule Biophysics and Biochemistry in dilute liquids and live cells without immobilization or significant hydrodynamic flow: The thermodynamic Single-Molecule DEMON. Curr. Pharm. Biotechnol. 2022, 23, 1750–1757. [Google Scholar] [PubMed]
- Földes-Papp, Z. The thermodynamic signature of a single molecule or a single particle in dilute liquids and live cells: Single-Molecule Biophysics & Biochemistry based on the stochastic nature of diffusion. Am. J. Transl. Med. 2023, 7, 74–77. [Google Scholar]
- Baumann, G.; Place, R.F.; Földes-Papp, Z. Meaningful interpretation of subdiffusive measurements in living cells (crowded environment) by fluorescence fluctuation microscopy. Curr. Pharm. Biotechnol. 2010, 11, 527–543. [Google Scholar] [CrossRef] [PubMed]
- Földes-Papp, Z. Individual macromolecule motion in a crowded living cell. Curr. Pharm. Biotechnol. 2015, 16, 1–2. [Google Scholar] [CrossRef] [PubMed]
- Földes-Papp, Z.; Baumann, G.; Li, L.-C. Visualization of subdiffusive sites in a live single cell. J. Biol. Methods 2021, 8, e142. [Google Scholar] [CrossRef] [PubMed]
- Digman, M.A.; Gratton, E. Lessons in fluctuation correlation spectroscopy. Annu. Rev. Phys. Chem. 2011, 62, 645–668. [Google Scholar] [CrossRef] [PubMed]
- Földes-Papp, Z.; Baumann, G. Fluorescence molecule counting for single-molecule studies in crowded environment of living cells without and with broken ergodicity. Curr. Pharm. Biotechnol. 2011, 12, 824–833. [Google Scholar] [CrossRef] [PubMed]
- Földes-Papp, Z.; Herold, A.; Seliger, H.; Kleinschmidt, A.K. Error propagation theory of chemically solid phase synthesized oligonucleotides and DNA sequences for biomedical application. In Fractals in Biology and Medicine; Nonnenmacher, T.F., Losa, G.A., Weibel, E.R., Eds.; Springer: Boston, MA, USA, 1994; Volume 1, pp. 165–173. [Google Scholar]
- Gaire, S.K.; Daneshkhah, A.; Flowerday, E.; Gong, R.; Frederick, J.; Backman, V. Deep learning-based spectroscopic single-molecule localization microscopy. J. Biomed. Opt. 2024, 29, 066501. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Gao, C.; Emusani, R.; Jia, C.; Xiang, D. Toward Practical Single-Molecule/Atom Switches. Adv. Sci. 2024, e2400877. [Google Scholar] [CrossRef] [PubMed]
| Experimental Criteria | Formulas |
|---|---|
| Criterion 1: N is the absolute number of the specific molecules/particles (labeled, studied) in the observation/detection volume. | , which is the Poisson probability of detecting single molecules/single particles of the same kind in the observation/detection volume. |
| Criterion 2: C denotes the (true) mean value of the population (subpopulation) of specific (e.g. fluorescent) molecules/particles of the same kind (the average molecule/particle number) in the observation/detection volume. | , which describes the analytical sensitivity that the observation/detection volume contains a single molecule/a single particle of the same kind. |
| Criterion 3: denotes the selfsame molecule likelihood estimators which are the probabilities that a second molecule/a second particle of the same kind (e.g., a second fluorescent molecule) is outside a boundary at time , meaning outside the lower limit of distance, for example of the observation/detection volume. | , which is the likelihood to really see (measure) the selfsame molecule that is the individual molecule/the individual particle in the observation/detection volume. is the meaningful time for measuring just one molecule at a time that is the individual molecule/individual particle (see Scheme 2), D stands for the diffusion coefficient of the molecule/particle. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baumann, G.; Földes-Papp, Z. Single-Molecule Tracking in Live Cell without Immobilization or without Hydrodynamic Flow by Simulations: Thermodynamic Jitter. Biophysica 2024, 4, 442-452. https://doi.org/10.3390/biophysica4030028
Baumann G, Földes-Papp Z. Single-Molecule Tracking in Live Cell without Immobilization or without Hydrodynamic Flow by Simulations: Thermodynamic Jitter. Biophysica. 2024; 4(3):442-452. https://doi.org/10.3390/biophysica4030028
Chicago/Turabian StyleBaumann, Gerd, and Zeno Földes-Papp. 2024. "Single-Molecule Tracking in Live Cell without Immobilization or without Hydrodynamic Flow by Simulations: Thermodynamic Jitter" Biophysica 4, no. 3: 442-452. https://doi.org/10.3390/biophysica4030028
APA StyleBaumann, G., & Földes-Papp, Z. (2024). Single-Molecule Tracking in Live Cell without Immobilization or without Hydrodynamic Flow by Simulations: Thermodynamic Jitter. Biophysica, 4(3), 442-452. https://doi.org/10.3390/biophysica4030028





