Proximal Policy Optimization for Radiation Source Search
Abstract
:1. Introduction
1.1. Machine Learning (ML)
1.2. Related Work
1.3. Contributions
2. Materials and Methods
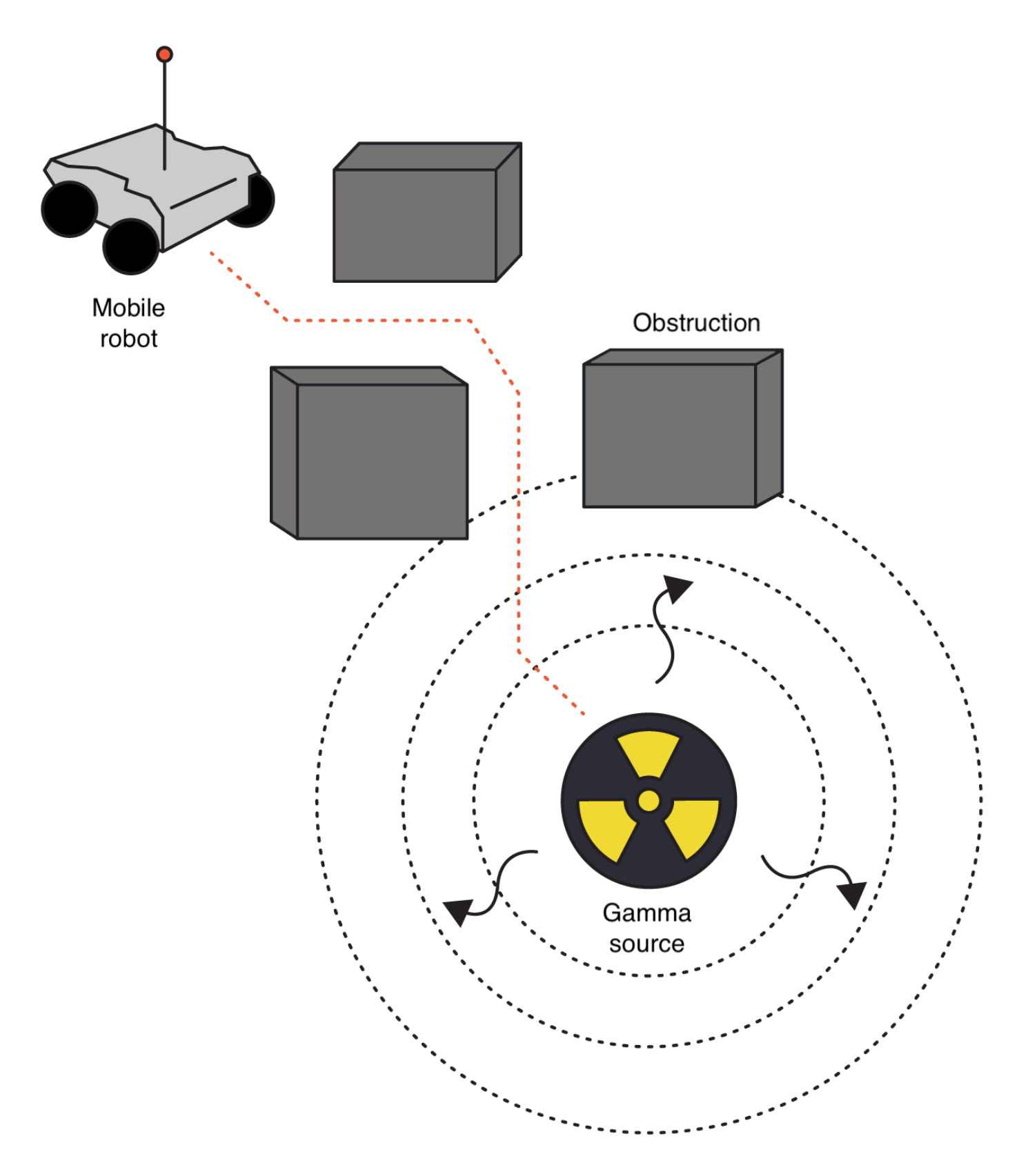
2.1. Radiation Source Search Environment
2.1.1. Partial Observability
2.1.2. Gamma Radiation Model
2.1.3. Reward Function
2.1.4. Configuration
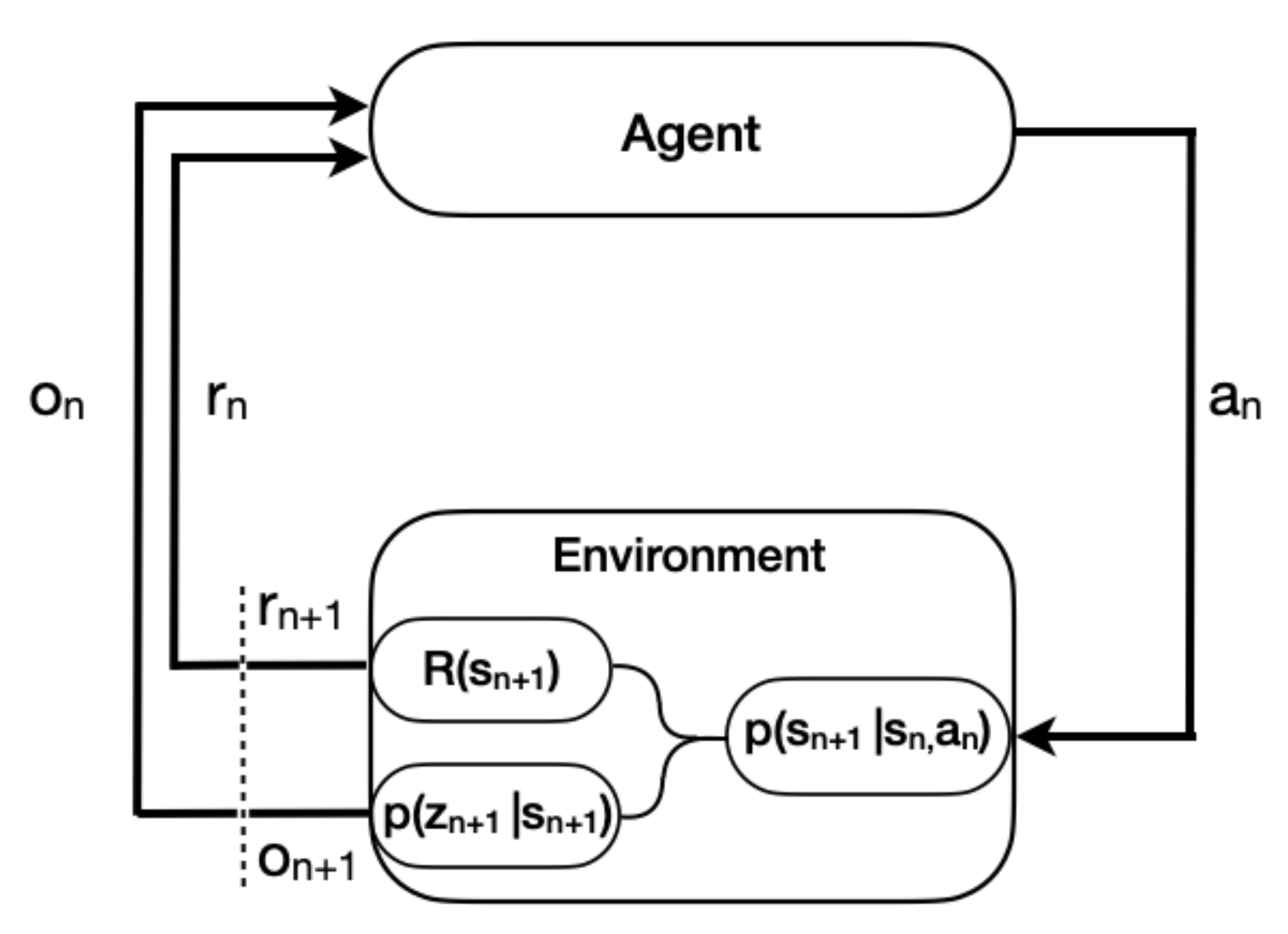
2.2. Reinforcement Learning (RL)
2.2.1. Background
2.2.2. Proximal Policy Optimization (PPO)
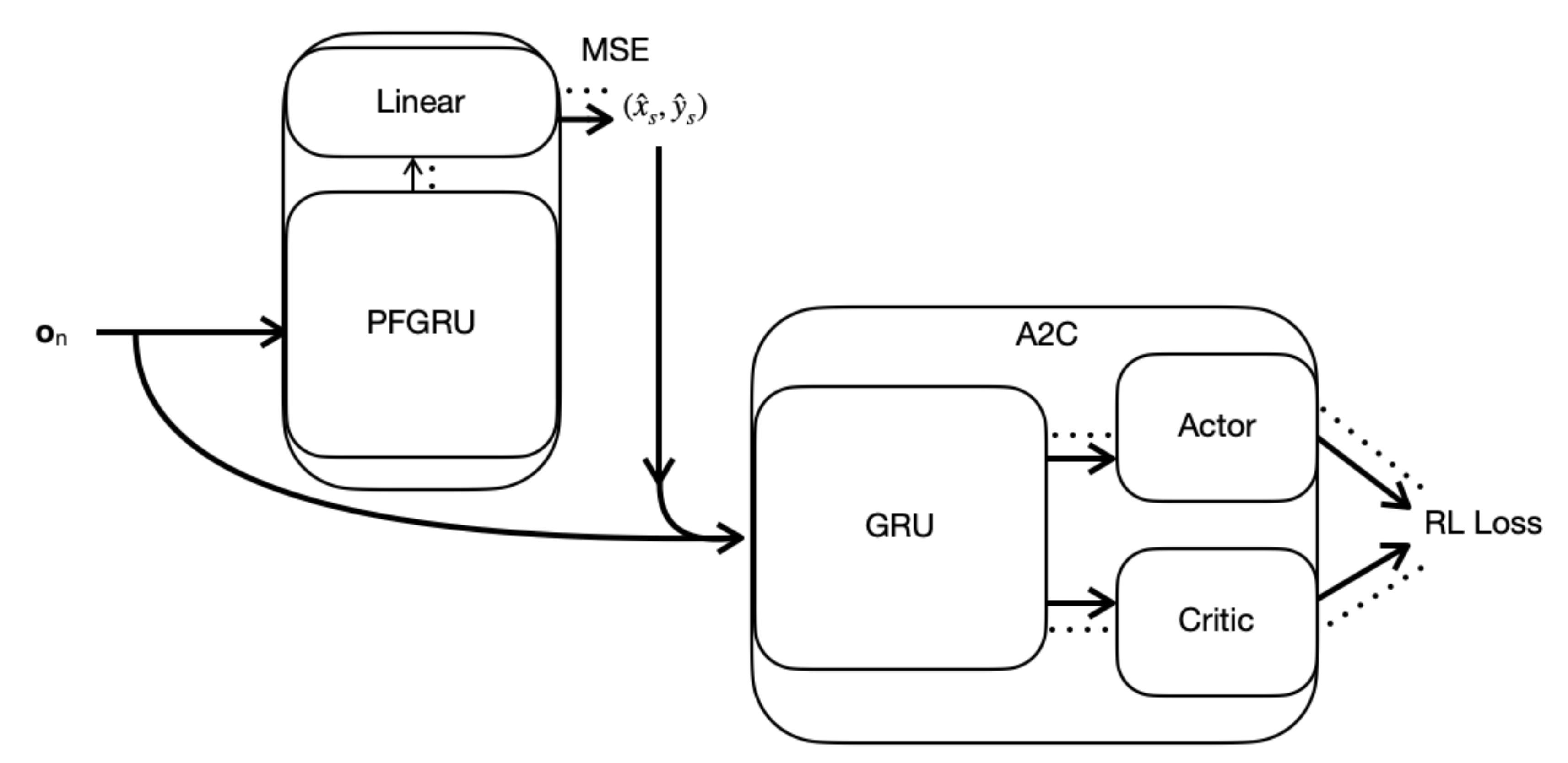
2.3. RAD-A2C
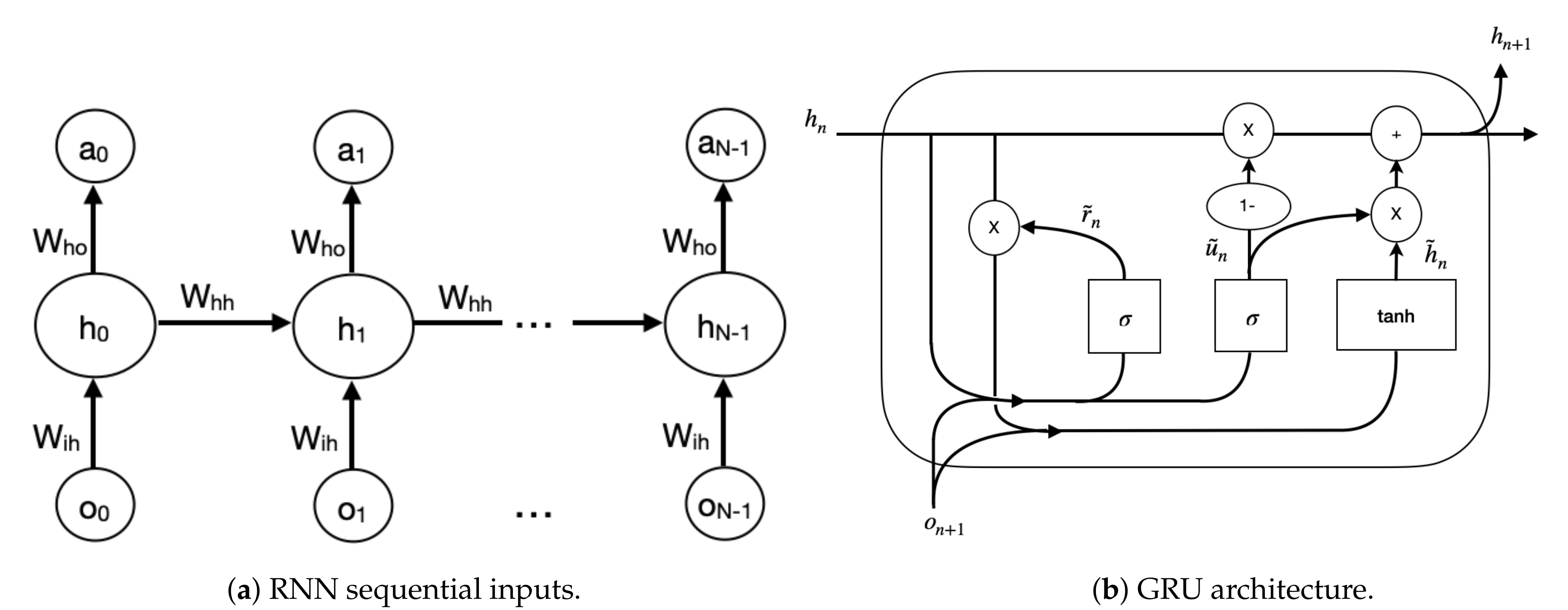
2.3.1. Gated Recurrent Unit (GRU)
2.3.2. Architecture
2.4. Evaluation
2.4.1. Metrics
2.4.2. Experiments
3. Results and Discussion
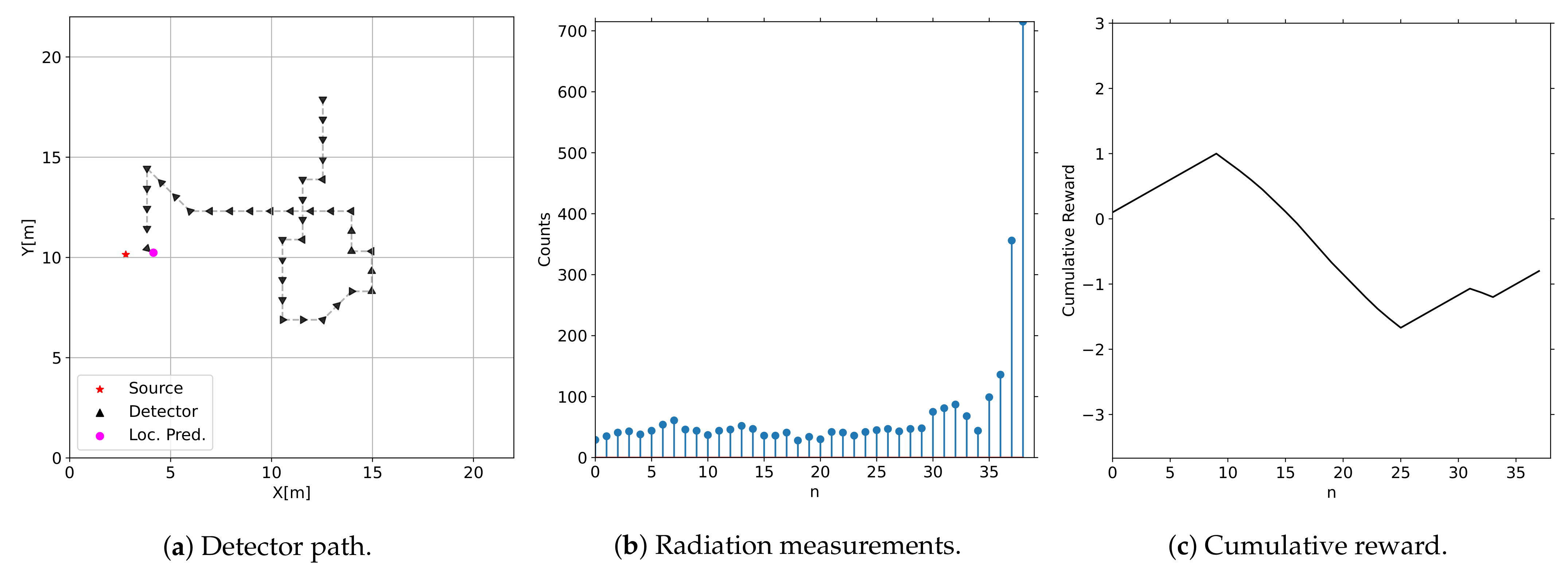
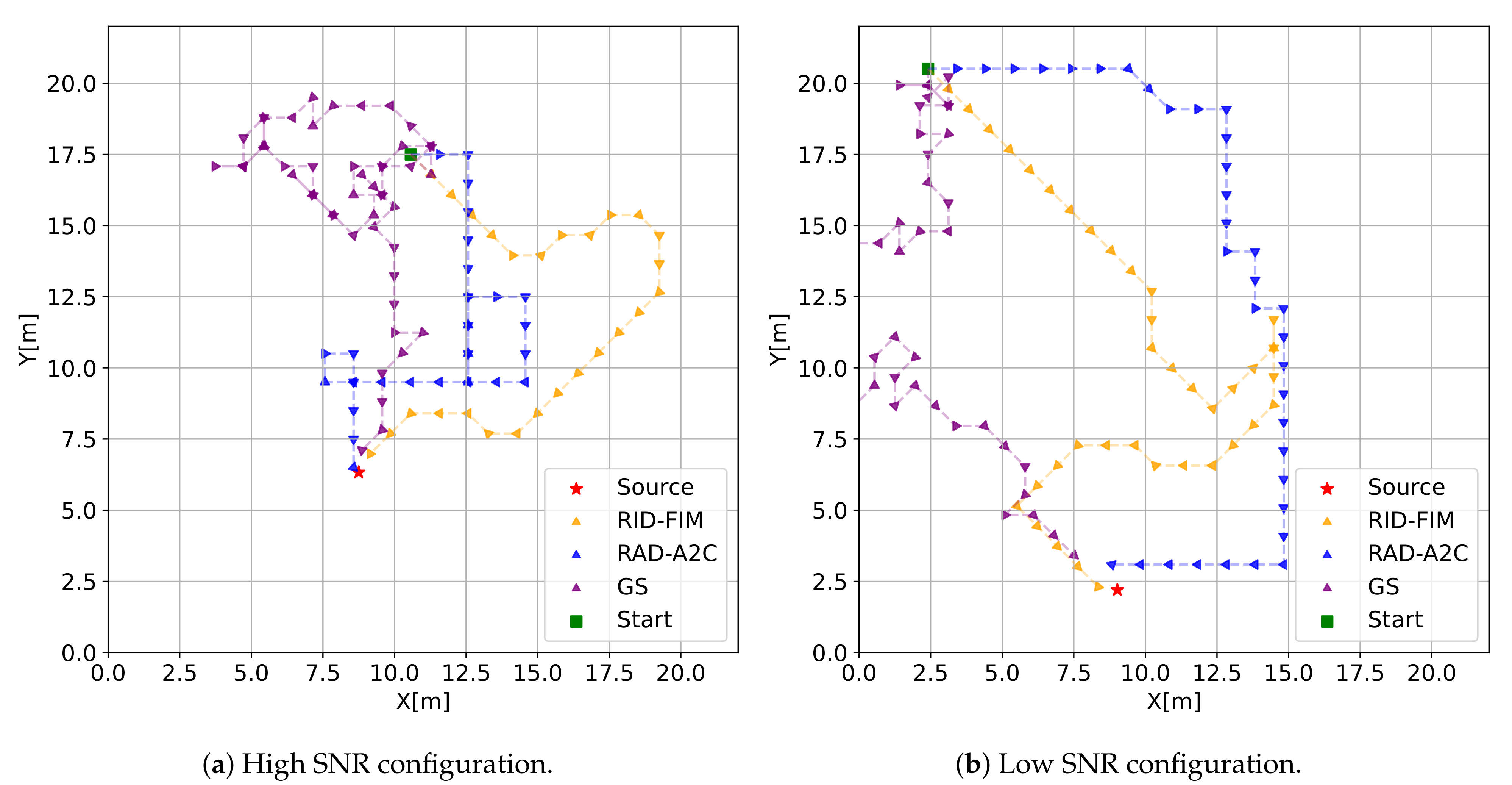
3.1. Convex Environment
Detector Path Examples
3.2. Performance
3.3. Discussion
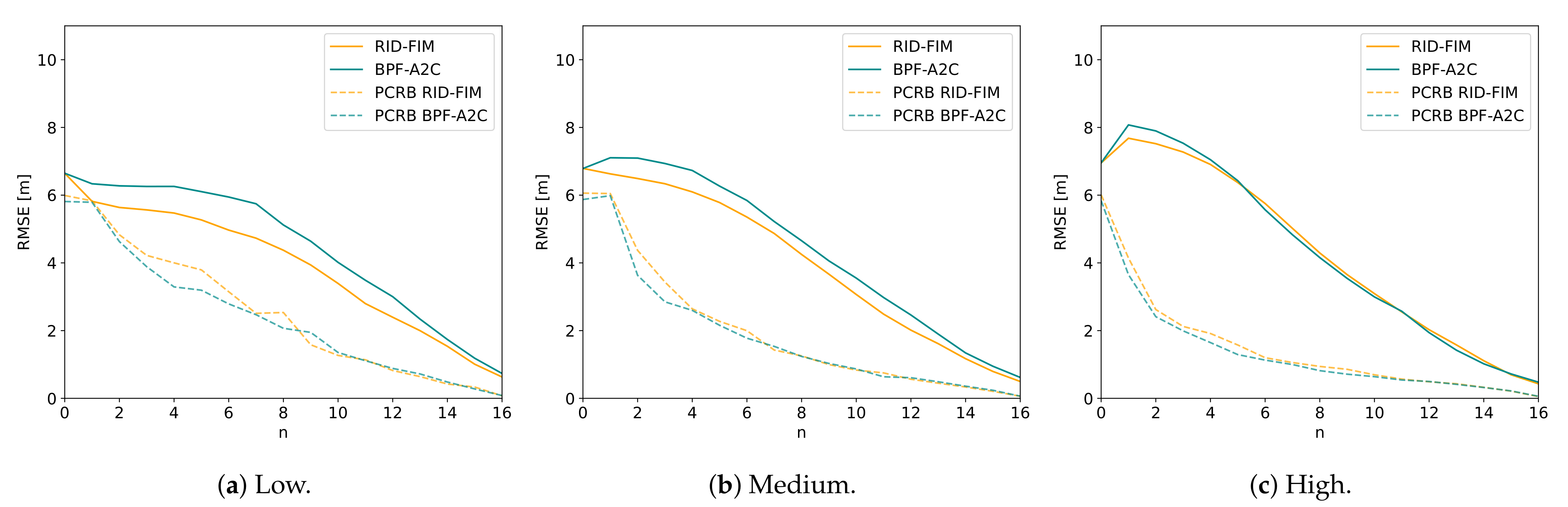
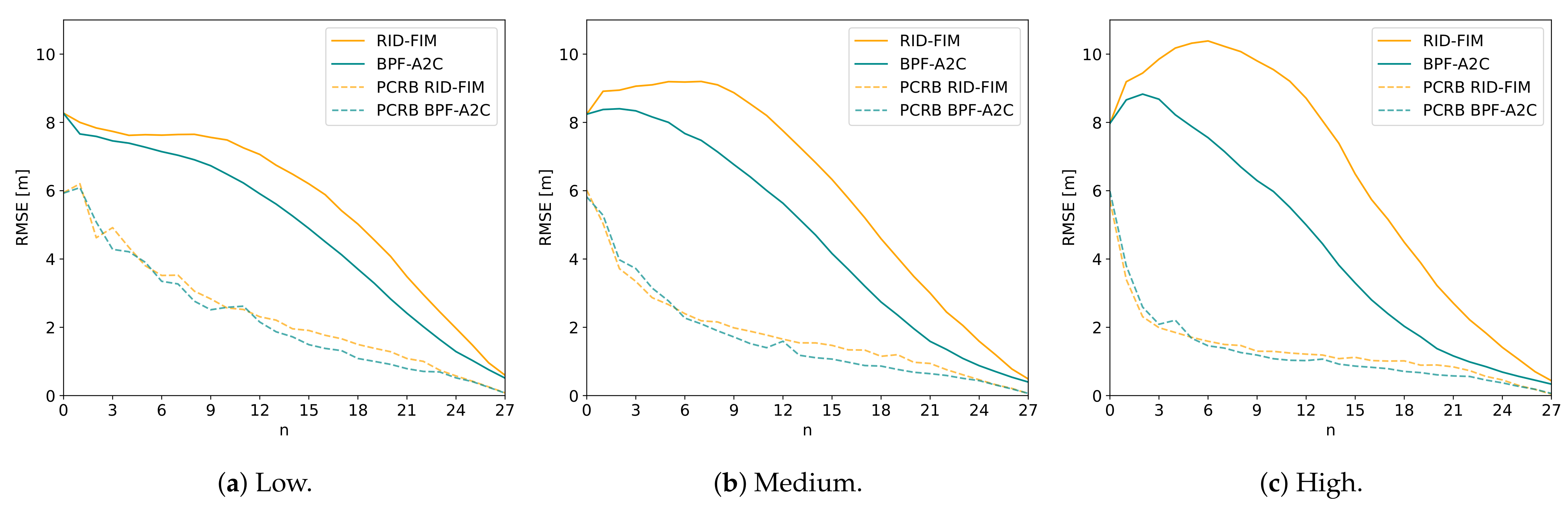
3.4. BPF Comparison
3.5. Discussion
3.6. Non-Convex Environment
Detector Path Examples
3.7. Performance
3.8. Non-Convex Environment
4. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| A2C | Advantage actor-critic |
| BPF | Bootstrap particle filter |
| BPF-A2C | Bootstrap particle filter and actor-critic |
| CRB | Cramér-Rao lower bound |
| DRL | Deep reinforcement learning |
| DL | Deep learning |
| FIM | Fisher information matrix |
| GRU | Gated recurrent unit |
| GS | Gradient search |
| LOS | Line-of-sight |
| NLOS | No line-of-sight |
| ML | Machine learning |
| PCRB | Posterior Cramér-Rao lower bound |
| PFGRU | Particle filter gated recurrent unit |
| PPO | Proximal policy optimization |
| RAD-A2C | Our proposed actor-critic architecture |
| RNN | Recurrent neural network |
| RID | Rényi information divergence |
| RID-FIM | Hybrid information-driven controller that uses RID and FIM |
| RL | Reinforcement learning |
| SNR | Signal-to-noise ratio |
Appendix A. RAD-A2C
Appendix A.1. Particle Filter Gated Recurrent Unit (PFGRU)
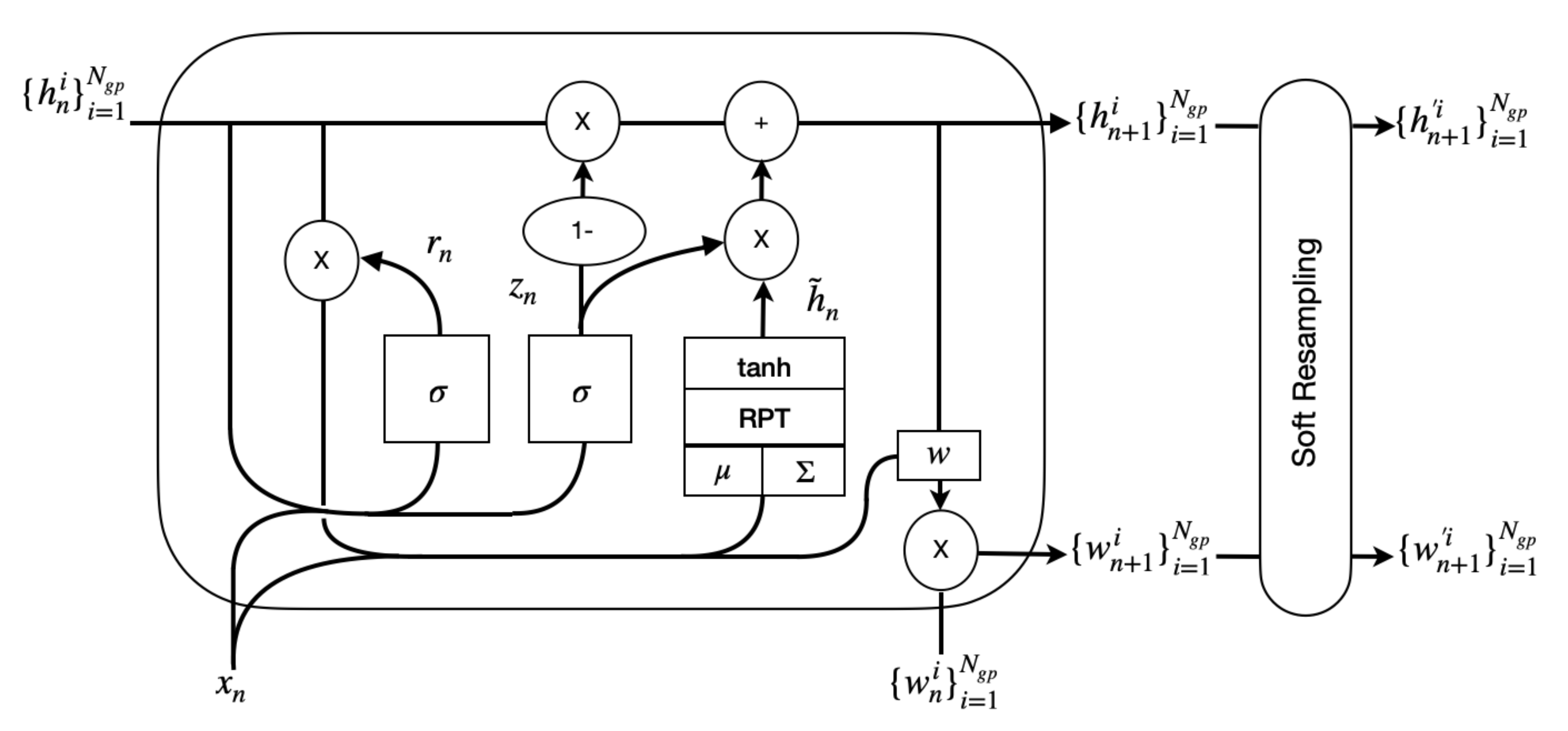
Appendix A.2. Training
| Parameter | Value |
|---|---|
| Epochs | 3000 |
| Episodes per epoch | 4 |
| Num. cores | 10 |
| Tot. weights & biases | 7443 |
| GRU hidden size | 24 |
| PFGRU hidden size | 24 |
| PFGRU particles | 40 |
| Learning Rate A2C | |
| Learning Rate PFGRU | |
| Optimizer | Adam |
| c | 0.01 |
| (,,) |

Appendix A.3. Standardization
Appendix B. Information-Driven Controller
Appendix B.1. Bootstrap Particle Filter (BPF)
Appendix B.2. Fisher Information Matrix (FIM)
Appendix B.3. Rényi Information Divergence (RID)
Appendix B.4. Hybrid RID-FIM Controller
| Algorithm A1 RID-FIM Controller. |
| Input:, set RID FLAG to 1, switch threshold , effective particles threshold , measurement interval Receive init. measurement, , perform prediction and filtering of particles while episode not terminated do if RID FLAG then Calculate RID according to Equation (A16) over if RID > then Set RID FLAG to 0 end if else Calculate FIM according to Equation (A13) end if Select action that maximizes information metric Receive , perform prediction and filtering of particles if then Resample and reweight particles end if end while |
| Parameter | Value |
|---|---|
| 6000 | |
| 6000 | |
| Process noise XY | m |
| Process noise | gps |
| Prior XY | m |
| Prior | gps |
| Resampling threshold, | |
| Lookahead, L | 1 |
| Order, | |
| Switch threshold, | |
| Meas. interval | cps |
Appendix B.5. Posterior Cramér-Rao Lower Bound (PCRB)
Appendix C. Gradient Search
References
- Sieminski, A. International energy outlook. Energy Inf. Adm. (EIA) 2014, 18, 2. [Google Scholar]
- The United Nations Scientific Committee on the Effects of Atomic Radiation. Sources and Effects of Ionizing Radiation; United Nations Publications: New York City, NY, USA, 2008; Volume 1. [Google Scholar]
- Nagatani, K.; Kiribayashi, S.; Okada, Y.; Otake, K.; Yoshida, K.; Tadokoro, S.; Nishimura, T.; Yoshida, T.; Koyanagi, E.; Fukushima, M.; et al. Emergency response to the nuclear accident at the Fukushima Daiichi Nuclear Power Plants using mobile rescue robots. J. Field Robot. 2013, 30, 44–63. [Google Scholar] [CrossRef]
- Knoll, G.F. Radiation Detection and Measurement; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Curto, C.; Gross, E.; Jeffries, J.; Morrison, K.; Omar, M.; Rosen, Z.; Shiu, A.; Youngs, N. What makes a neural code convex? SIAM J. Appl. Algebra Geom. 2017, 1, 222–238. [Google Scholar] [CrossRef] [Green Version]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of Go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef] [PubMed]
- Morelande, M.; Ristic, B.; Gunatilaka, A. Detection and parameter estimation of multiple radioactive sources. In Proceedings of the 2007 10th International Conference on Information Fusion, Quebec, QC, Canada, 9–12 July 2007; pp. 1–7. [Google Scholar]
- Hite, J.; Mattingly, J. Bayesian Metropolis methods for source localization in an urban environment. Radiat. Phys. Chem. 2019, 155, 271–274. [Google Scholar] [CrossRef]
- Hellfeld, D.; Joshi, T.H.; Bandstra, M.S.; Cooper, R.J.; Quiter, B.J.; Vetter, K. Gamma-ray point-source localization and sparse image reconstruction using Poisson likelihood. IEEE Trans. Nucl. Sci. 2019, 66, 2088–2099. [Google Scholar] [CrossRef]
- Cortez, R.; Papageorgiou, X.; Tanner, H.; Klimenko, A.; Borozdin, K.; Priedhorsk, W. Experimental implementation of robotic sequential nuclear search. In Proceedings of the 2007 Mediterranean Conference on Control & Automation, Athens, Greece, 27–29 June 2007; pp. 1–6. [Google Scholar]
- Ristic, B.; Gunatilaka, A. Information driven localisation of a radiological point source. Inf. Fusion 2008, 9, 317–326. [Google Scholar] [CrossRef]
- Ristic, B.; Morelande, M.; Gunatilaka, A. Information driven search for point sources of gamma radiation. Signal Process. 2010, 90, 1225–1239. [Google Scholar] [CrossRef]
- Ristic, B.; Morelande, M.; Gunatilaka, A. A controlled search for radioactive point sources. In Proceedings of the 2008 11th International Conference on Information Fusion, Cologne, Germany, 30 June–3 July 2008; pp. 1–5. [Google Scholar]
- Anderson, R.B.; Pryor, M.; Abeyta, A.; Landsberger, S. Mobile Robotic Radiation Surveying With Recursive Bayesian Estimation and Attenuation Modeling. IEEE Trans. Autom. Sci. Eng. 2020, 1–15. [Google Scholar] [CrossRef]
- Landgren, P.C. Distributed Multi-Agent Multi-Armed Bandits. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 2019. [Google Scholar]
- Liu, Z.; Abbaszadeh, S. Double Q-learning for radiation source detection. Sensors 2019, 19, 960. [Google Scholar] [CrossRef] [Green Version]
- Tobin, J.; Fong, R.; Ray, A.; Schneider, J.; Zaremba, W.; Abbeel, P. Domain randomization for transferring deep neural networks from simulation to the real world. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 23–30. [Google Scholar]
- Wierstra, D.; Förster, A.; Peters, J.; Schmidhuber, J. Recurrent policy gradients. Log. J. IGPL 2010, 18, 620–634. [Google Scholar] [CrossRef]
- Beigzadeh, A.M.; Vaziri, M.R.R.; Soltani, Z.; Afarideh, H. Design and improvement of a simple and easy-to-use gamma-ray densitometer for application in wood industry. Measurement 2019, 138, 157–161. [Google Scholar] [CrossRef]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. OpenAI gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]
- Henderson, P.; Islam, R.; Bachman, P.; Pineau, J.; Precup, D.; Meger, D. Deep reinforcement learning that matters. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Tesauro, G. Temporal difference learning and TD-Gammon. Commun. ACM 1995, 38, 58–68. [Google Scholar] [CrossRef]
- Schulman, J.; Moritz, P.; Levine, S.; Jordan, M.; Abbeel, P. High-dimensional continuous control using generalized advantage estimation. arXiv 2015, arXiv:1506.02438. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Andrychowicz, M.; Raichuk, A.; Stańczyk, P.; Orsini, M.; Girgin, S.; Marinier, R.; Hussenot, L.; Geist, M.; Pietquin, O.; Michalski, M.; et al. What matters in on-policy reinforcement learning? A large-scale empirical study. arXiv 2020, arXiv:2006.05990. [Google Scholar]
- Cho, K.; Van Merriënboer, B.; Bahdanau, D.; Bengio, Y. On the properties of neural machine translation: Encoder-decoder approaches. arXiv 2014, arXiv:1409.1259. [Google Scholar]
- Olah, C. Understanding LSTM Networks. 2015. Available online: http://colah.github.io/posts/2015-08-Understanding-LSTMs/ (accessed on 20 April 2021).
- Ma, X.; Karkus, P.; Hsu, D.; Lee, W.S. Particle filter recurrent neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 5101–5108. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. Adv. Neural Inf. Process. Syst. 2019, 32, 8026–8037. [Google Scholar]
- Bergman, N. Recursive Bayesian Estimation: Navigation and Tracking Applications. Ph.D. Thesis, Linköping University, Linköping, Sweden, 1999. [Google Scholar]
- Baca, T.; Stibinger, P.; Doubravova, D.; Turecek, D.; Solc, J.; Rusnak, J.; Saska, M.; Jakubek, J. Gamma Radiation Source Localization for Micro Aerial Vehicles with a Miniature Single-Detector Compton Event Camera. arXiv 2020, arXiv:2011.03356. [Google Scholar]
- Koenig, N.; Howard, A. Design and Use Paradigms for Gazebo, An Open-Source Multi-Robot Simulator. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Sendai, Japan, 28 September–2 October 2004; pp. 2149–2154. [Google Scholar]
- Téllez, R.; Ezquerro, A.; Rodríguez, M.Á. ROS Manipulation in 5 Days: Entirely Practical Robot Operating System Training; Independently Published: Barcelona, Spain, 2017. [Google Scholar]
- Welford, B. Note on a method for calculating corrected sums of squares and products. Technometrics 1962, 4, 419–420. [Google Scholar] [CrossRef]
- Stone, L.D. OR Forum—What’s Happened in Search Theory Since the 1975 Lanchester Prize? Oper. Res. 1989, 37, 501–506. [Google Scholar] [CrossRef] [Green Version]
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Process. 2002, 50, 174–188. [Google Scholar] [CrossRef] [Green Version]
- Gerber, M.; Chopin, N.; Whiteley, N. Negative association, ordering and convergence of resampling methods. Ann. Stat. 2019, 47, 2236–2260. [Google Scholar] [CrossRef] [Green Version]
- Srinivasan, A. Distributions on level-sets with applications to approximation algorithms. In Proceedings of the 42nd IEEE Symposium on Foundations of Computer Science, Newport Beach, CA, USA, 8–11 October 2001; pp. 588–597. [Google Scholar]
- Hammel, S.; Liu, P.; Hilliard, E.; Gong, K. Optimal observer motion for localization with bearing measurements. Comput. Math. Appl. 1989, 18, 171–180. [Google Scholar] [CrossRef] [Green Version]
- Van Trees, H.L. Detection, Estimation, and Modulation Theory, Part I: Detection, Estimation, and Linear Modulation Theory; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Helferty, J.P.; Mudgett, D.R. Optimal observer trajectories for bearings only tracking by minimizing the trace of the Cramér-Rao lower bound. In Proceedings of the 32nd IEEE Conference on Decision and Control, San Antonio, TX, USA, 15–17 December 1993; pp. 936–939. [Google Scholar]
- Pronzato, L. Optimal experimental design and some related control problems. Automatica 2008, 44, 303–325. [Google Scholar] [CrossRef] [Green Version]
- Kreucher, C.; Kastella, K.; Hero Iii, A.O. Sensor management using an active sensing approach. Signal Process. 2005, 85, 607–624. [Google Scholar] [CrossRef]
- Tichavsky, P.; Muravchik, C.H.; Nehorai, A. Posterior Cramér-Rao bounds for discrete-time nonlinear filtering. IEEE Trans. Signal Process. 1998, 46, 1386–1396. [Google Scholar] [CrossRef] [Green Version]






| Parameter | Value |
|---|---|
| Area Dimensions | |
| Src., det. initial positions | [0, 20] m |
| Src. rate | gps |
| Background rate | [10, 50] cps |
| State space | 11 |
| Action space | 8 |
| Max. search time | 120 samples |
| Velocity | 1 m/sample |
| Termination dist. | 1.1 m |
| Min. src.-det. initial dist. | 10 m |
| Number of obstructions | [1, 5] |
| Obstruction dim. | [2, 5] m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Proctor, P.; Teuscher, C.; Hecht, A.; Osiński, M. Proximal Policy Optimization for Radiation Source Search. J. Nucl. Eng. 2021, 2, 368-397. https://doi.org/10.3390/jne2040029
Proctor P, Teuscher C, Hecht A, Osiński M. Proximal Policy Optimization for Radiation Source Search. Journal of Nuclear Engineering. 2021; 2(4):368-397. https://doi.org/10.3390/jne2040029
Chicago/Turabian StyleProctor, Philippe, Christof Teuscher, Adam Hecht, and Marek Osiński. 2021. "Proximal Policy Optimization for Radiation Source Search" Journal of Nuclear Engineering 2, no. 4: 368-397. https://doi.org/10.3390/jne2040029
APA StyleProctor, P., Teuscher, C., Hecht, A., & Osiński, M. (2021). Proximal Policy Optimization for Radiation Source Search. Journal of Nuclear Engineering, 2(4), 368-397. https://doi.org/10.3390/jne2040029







