Model Reduction of Discrete-Time Index-3 Second-Order Form Systems for Limited Frequency Intervals †
Abstract
:1. Introduction
2. Proposed Technique
2.1. Discrete-Time Index-3 Second-Order System
2.2. Limited Frequency Interval Gramians
2.3. Balance Truncation for Frequency Limited Second-Order System
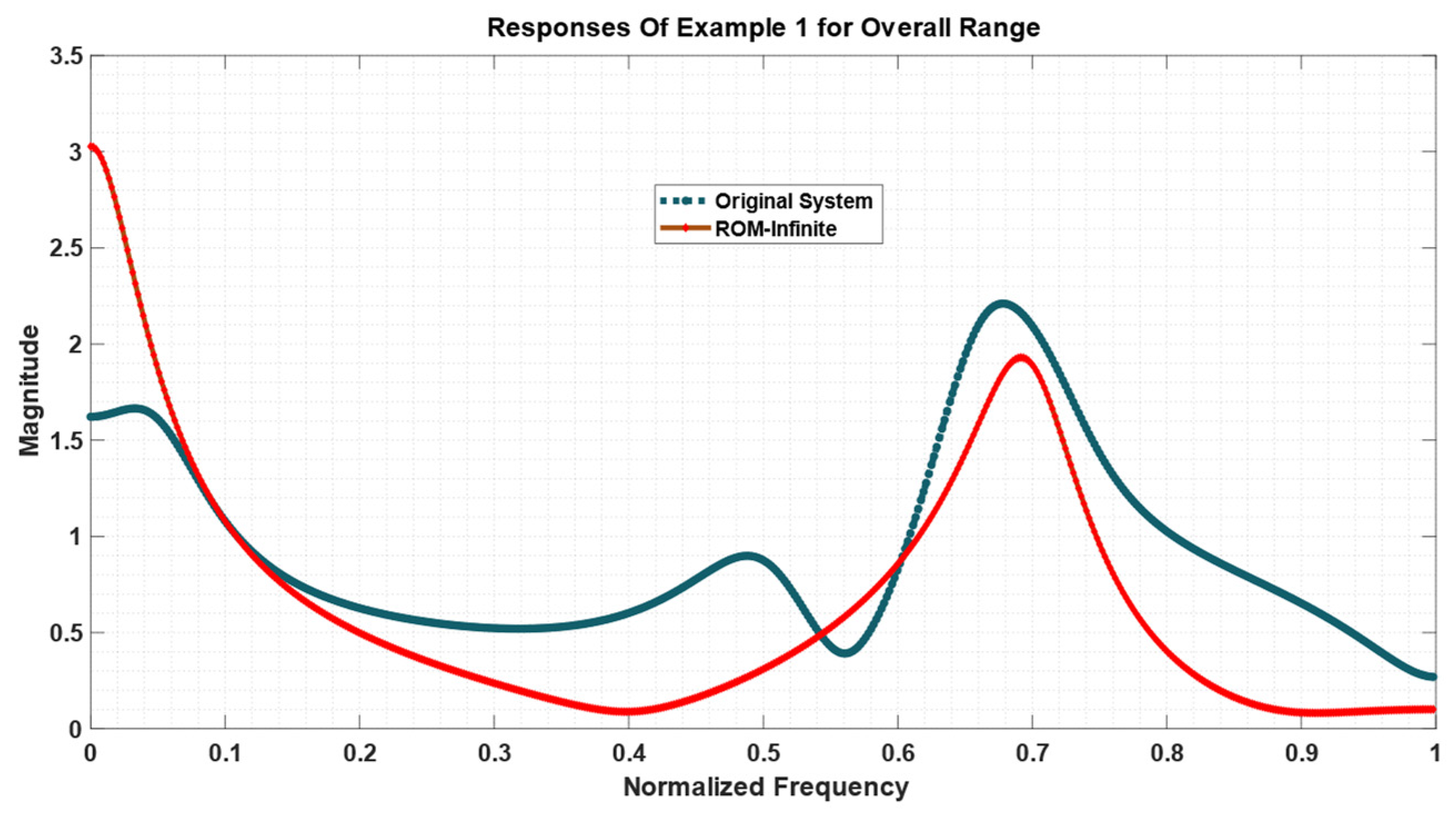
3. Numerical Results with Example
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Uddin, M.M. Structure preserving model order reduction of a class of second-order descriptor systems via balanced truncation. Appl. Numer. Math. 2020, 152, 185–198. [Google Scholar] [CrossRef]
- Hammarling, S.J. Numerical solution of the stable, non-negative definite lyapunov equation lyapunov equation. IMA J. Numer. Anal. 1982, 2, 303–323. [Google Scholar] [CrossRef] [Green Version]
- Uddin, M.M. Computational Methods for Model Reduction of Large-Scale Sparse Structured Descriptor Systems. Ph.D. Thesis, Otto-von-Guericke Universität Magdeburg, Magdeburg, Germany, 2015. [Google Scholar]
- Hossain, M.S.; Omar, S.G.; Tahsin, A.; Khan, E.H. Efficient system reduction modeling of periodic control systems with application to circuit problems. In Proceedings of the 2017 4th International Conference on Advances in Electrical Engineering (ICAEE), Dhaka, Bangladesh, 28–30 September 2017. [Google Scholar]
- Mullis, C.; Richard, R. Synthesis of minimum roundoff noise fixed point digital filters. IEEE Trans. Circuits Syst. 1976, 23, 551–562. [Google Scholar] [CrossRef]
- Gawronski, W.; Juang, J.-N. Model reduction in limited time and frequency intervals. Int. J. Syst. Sci. 1990, 21, 349–376. [Google Scholar] [CrossRef]
- Stykel, T. Gramian-based model reduction for descriptor systems. Math. Control. Signals Syst. 2004, 16, 297–319. [Google Scholar] [CrossRef]
- Monir Uddin, M. Gramian-based Model Order Reduction of a constrained Structural Dynamic Systems. IET Control Theory Appl. 2018, 12, 2337–2346. [Google Scholar] [CrossRef]
- Imran, M.; Abdul, G. Stability preserving model reduction technique and error bounds using frequency-limited Gramians for discrete-time systems. IEEE Trans. Circuits Syst. II Express Briefs 2014, 61, 716–720. [Google Scholar] [CrossRef]
- Omar, S.G.; Hossain, M.S.; Khan, E.H.; Tahsin, A. An efficient model reduction strategy for discrete-time index-2 descriptor control systems. In Proceedings of the 2019 International Conference on Electrical, Computer, and Communication Engineering (ECCE), Cox’sBazar, Bangladesh, 7–9 February 2019. [Google Scholar]
- Haider, S.; Ghafoor, A.; Imran, M.; Malik, F.M. Frequency interval Gramians based structure preserving model order reduction for second order systems. Asian J. Control. 2018, 20, 790–801. [Google Scholar] [CrossRef]
- Haider, S.; Ghafoor, A.; Imran, M.; Malik, F.M. Time-limited Gramians-based model order reduction for second order form systems. Trans. Inst. Meas. Control. 2019, 41, 2310–2318. [Google Scholar] [CrossRef]
- Benner, P.; Du, X.; Yang, G.; Ye, D. Balanced truncation of linear time-invariant systems over finite-frequency ranges. Adv. Comput. Math. 2020, 46, 1–34. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qazi, H.R.; Haider, S.; Huda, A.B.; Saqlain, M.; Arif, A.R. Model Reduction of Discrete-Time Index-3 Second-Order Form Systems for Limited Frequency Intervals. Eng. Proc. 2022, 20, 40. https://doi.org/10.3390/engproc2022020040
Qazi HR, Haider S, Huda AB, Saqlain M, Arif AR. Model Reduction of Discrete-Time Index-3 Second-Order Form Systems for Limited Frequency Intervals. Engineering Proceedings. 2022; 20(1):40. https://doi.org/10.3390/engproc2022020040
Chicago/Turabian StyleQazi, Humaira Rauf, Shafiq Haider, Aamina Bintul Huda, Muhammad Saqlain, and Ahmed Roohullah Arif. 2022. "Model Reduction of Discrete-Time Index-3 Second-Order Form Systems for Limited Frequency Intervals" Engineering Proceedings 20, no. 1: 40. https://doi.org/10.3390/engproc2022020040





