Abstract
In general, the parallel machine scheduling problem that minimizes maximum completion time is NP-hard in a strong sense; a lot of heuristics have been proposed for this kind of problem. In this paper, the unrelated parallel machine scheduling problem with maintainability (UPMSPM) is studied, in which the reliability of machines obeys exponential distribution. A hybrid algorithm HDSMO, which combines the discrete spider monkey algorithm (SMO) with the crossover and mutation operation, is proposed to solve UPMSPM. In view of the lack of local search capability in the later iteration of the traditional SMO algorithm, inertial weights are introduced to update the local leader and the global leader. Computational experiments with randomly generated instances demonstrate that the proposed HDSMO algorithm can obtain significantly better solutions in a shorter time than GA and SMO algorithms.
1. Introduction
UPMSP is an important branch of production scheduling. In the real-world production system, long-term running wear and performance degradation of the machines can easily lead to production interruptions, requiring preventive maintenance (PM) to keep machines running [1]. Therefore, it is of great significance to consider the joint optimization of maintenance and scheduling for UPMSP [2]. UPMSP studies considering maintenance are relatively rare, and several classic studies are as follows [3].
Cheng et al. studied UPMSP with degradation and maintenance and proved that the problem could be optimally solved in polynomial time [4]. Avalos-Rosales et al. studied unrelated parallel machines and considered preventive maintenance activities and setup times by order and by machine [5]. Luo J et al. proposed a predictable scheduling and rescheduling and accounting for machine failures and consistency in unrelated machine environments, where work separations include printed circuit boards (PCB) [6].
Comparatively speaking, the research on UPMSP based on the Spider Monkey Optimization (SMO) algorithm is rare. Aiming at the optimization problem of unrelated parallel machine maintenance and scheduling integration, this paper proposes a hybrid spider monkey algorithm, and compares it with classical algorithms to provide the foundation for solving UPMSP [7].
2. Problem Formulation
The problem studies in this paper can be described as follows: jobs are to be processed on unrelated parallel machines; in most situations, we assume m is less than n, and these jobs are non-preemptive and can all be processed at time 0. Maintenance performed on the machine may depend on the state of the machine (e.g., running time). The state of a machine is determined by reliability, which decreases with the cumulative processing time of the workpiece or degradation of the machine. Once the reliability of the machine falls below the threshold , PM must be implemented. The reliability of the machine does not change during operation.
Using the three-field notation α|β|γ for describing scheduling problems, we denote our problem by , where denotes those jobs are non-resumable; “” denotes variable PM; the objective is to minimize the maximum completion time. The decision is to determine the allocation and sequence of jobs on machines and the maintenance time of the machines. Since problem has been proved to be an NP-Hard problem, it can be concluded that problem is an NP-Hard problem by comparison. Thus, the approximate methods are needed to solve real-size instances.
3. HDSMO Algorithm
3.1. Basic Flow of the HDSMO Algorithm
SMO is a proposed global optimization algorithm; the main feature is that it can improve the ability to search for optimal solutions. However, in the traditional SMO algorithm, the spider monkey individual completely inherits the old location information of the individual in the updating process, which makes the algorithm lack the local search ability in the late iteration. An HDSMO algorithm considering inertia weight aims at the above problems and shortcomings. and represent the local leader counter and limit, respectively, while and represents the global leader counter and limit. The process of the proposed HDSMO algorithm is shown in Figure 1.
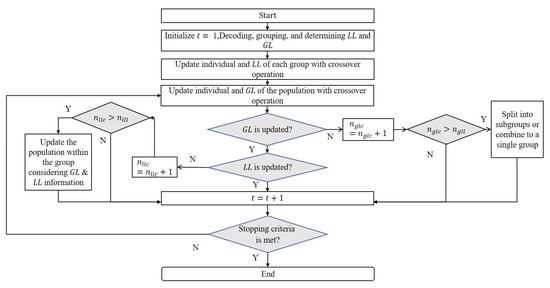
Figure 1.
Flow chart of the proposed HDSMO.
3.2. Local Leader Phase (LLP) Update with the Inertia Weight
The position update process in the local leader stage of the SMO algorithm is shown in Equation (1): the population is first divided into different groups, is the mutation operation added to enhance the local search ability according to inertia weight . For the individuals of the first 50% generation population and the last 50% generation population, the mutation operation methods of reverse order and two-point exchange can be used respectively, which can effectively improve the diversity of the population and further improve the local search ability of the algorithm. The mutation method is shown in Figure 2, where 0 represents the machine, and the remaining numbers represent the job.

Figure 2.
Two mutation operations (a) reverse order (b) exchange.
and represent crossover operations. The mutant individuals cross with according to crossover rate , and the generated new individuals cross with random individuals according to crossover rate . In this paper, two crossover methods are designed based on whether there are identical parts between individuals, as shown in Figure 3.

Figure 3.
Two kinds of crossover operation (a) with the same parts; (b) without the same parts.
3.3. Global Leader Phase (GLP) Update with the Inertia Weight
At this phase, individual mutates according to crossover rate inertia weight , and then crosses with according to crossover rate , and the generated new individuals cross with random individuals according to crossover rate . The same method is shown in Section 3.2.
4. Numerical Example and Analysis
4.1. Parameters Setting
The experimental data include the number of machines , the number of jobs , the processing time , the PM parameters including the threshold , and the maintenance time . For each combination of problem instance size, Generate 10 random problem instances. The instances and the range of experimental parameters are shown in Table 1, the parameters of the GA algorithm and the DSMO algorithm are experimentally analyzed, and the algorithm parameter values under different problem scales are determined as shown in Table 2.

Table 1.
Experimental problem scale and parameter range.

Table 2.
Parameter values for algorithms.
4.2. Computational Experiments and Discussion
The computational experiments result for the different algorithms are given in Table 3. Each algorithm calculates the average relative percentage deviation () from the optimal solution, i.e., the value . There is also the average computed time in seconds ().

Table 3.
The performance of the algorithms.
It can be concluded from Table 3 that HDSMO is superior to DSMO and GA in average relative percentage deviation for three scale problems. However, in terms of computation time, the DSMO algorithm outperforms GA and HDSMO for the small problems, and the needed computation time of HDSMO is decreased with the increase in the problem size. The HDSMO algorithm is a recommended method for solving large and medium-sized problems because it can give approximate optimal solutions in a short computing time.
5. Conclusions
According to the property of the addressed problem and the decision-making method of “job-grouping batch and allocating”, a hybrid discrete SMO algorithm is proposed in this paper. Experimental results demonstrate that HDSMO is superior to GA and DSMO in solving quality and effectiveness.
Author Contributions
Conceptualization, Y.C.; methodology, K.K.; software, K.K.; validation, K.K.; formal analysis, K.K.; investigation, K.K.; resources, Y.C.; data—curation, K.K.; writing—original draft preparation, K.K., writing—review and editing, K.K.; visualization, K.K.; supervision, Y.C., project administration, Y.C.; funding acquisition: Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China grant number [No.51705370].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mumtaz, J.; Guan, Z.; Yue, L.; Zhang, L.; He, C. Hybrid Spider Monkey Optimisation Algorithm for Multi-Level Planning and Scheduling Problems of Assembly Lines. Int. J. Prod. Res. 2020, 58, 6252–6267. [Google Scholar] [CrossRef]
- Lei, D.; Liu, M. An Artificial Bee Colony with Division for Distributed Unrelated Parallel Machine Scheduling with Preventive Maintenance. Comput. Ind. Eng. 2020, 141, 106320. [Google Scholar] [CrossRef]
- Mirabedini, S.N.; Iranmanesh, H. A Scheduling Model for Serial Jobs on Parallel Machines with Different Preventive Maintenance (PM). Int. J. Adv. Manuf. Technol. 2014, 70, 1579–1589. [Google Scholar] [CrossRef]
- Cheng, T.C.E.; Hsu, C.J.; Yang, D.L. Unrelated Parallel-Machine Scheduling with Deteriorating Maintenance Activities. Comput. Ind. Eng. 2011, 60, 602–605. [Google Scholar] [CrossRef]
- Avalos-Rosales, O.; Angel-Bello, F.; Álvarez, A.; Cardona-Valdés, Y. Including Preventive Maintenance Activities in an Unrelated Parallel Machine Environment with Dependent Setup Times. Comput. Ind. Eng. 2018, 123, 364–377. [Google Scholar] [CrossRef]
- Luo, J.; Liu, J.; Hu, Y. An MILP Model and a Hybrid Evolutionary Algorithm for Integrated Operation Optimisation of Multi-Head Surface Mounting Machines in PCB Assembly. Int. J. Prod. Res. 2017, 55, 145–160. [Google Scholar] [CrossRef]
- Lei, D.; Yang, H. Scheduling Unrelated Parallel Machines with Preventive Maintenance and Setup Time: Multi-Sub-Colony Artificial Bee Colony. Appl. Soft Comput. 2022, 125, 109154. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).