Artificial Neural Networks Multicriteria Training Based on Graphics Processors †
Abstract
:1. Introduction
2. Problem Statement
3. GPU-Based Parallel Implementation of the Hierarchical Evolutionary MCOU Algorithm
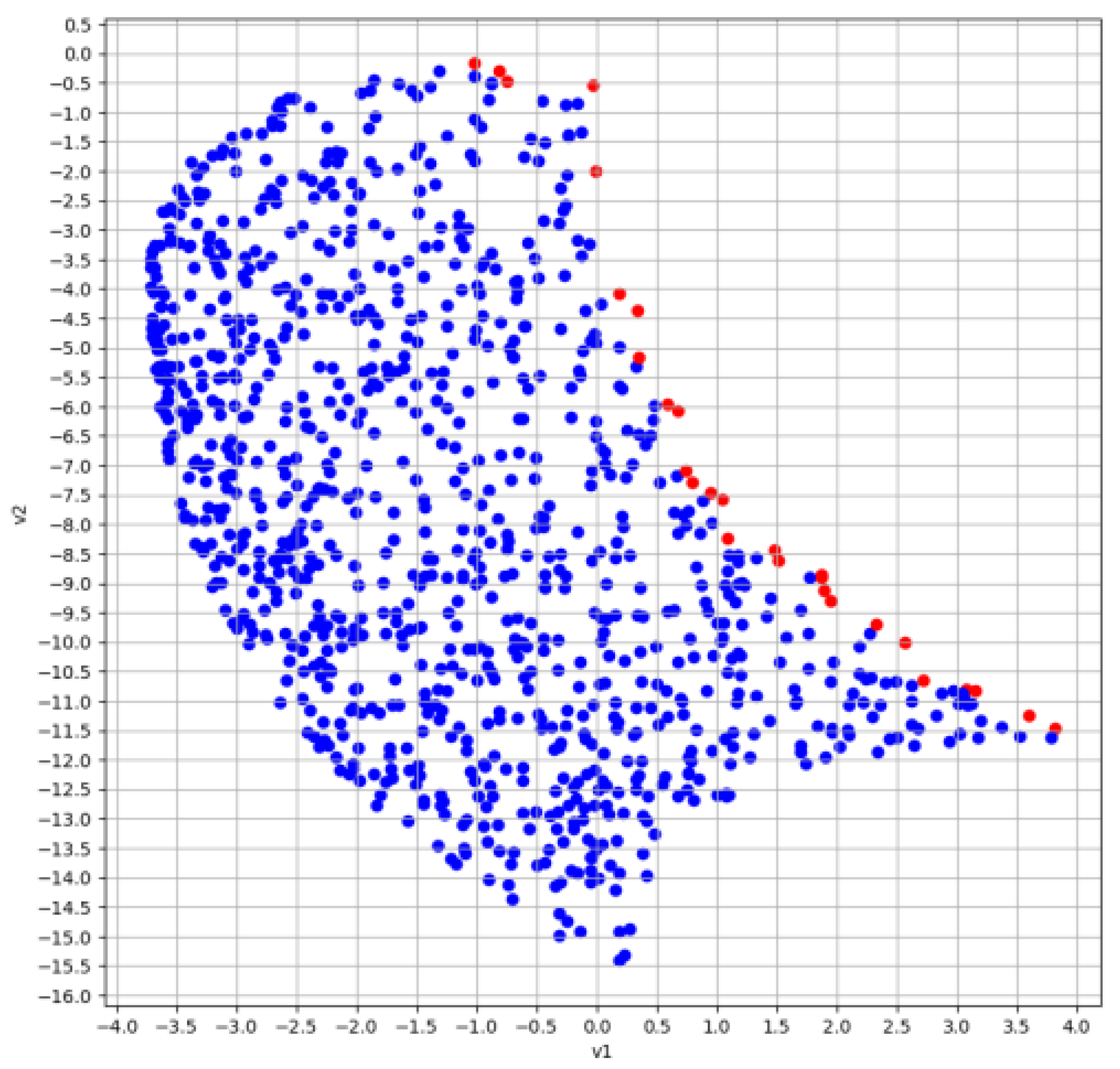
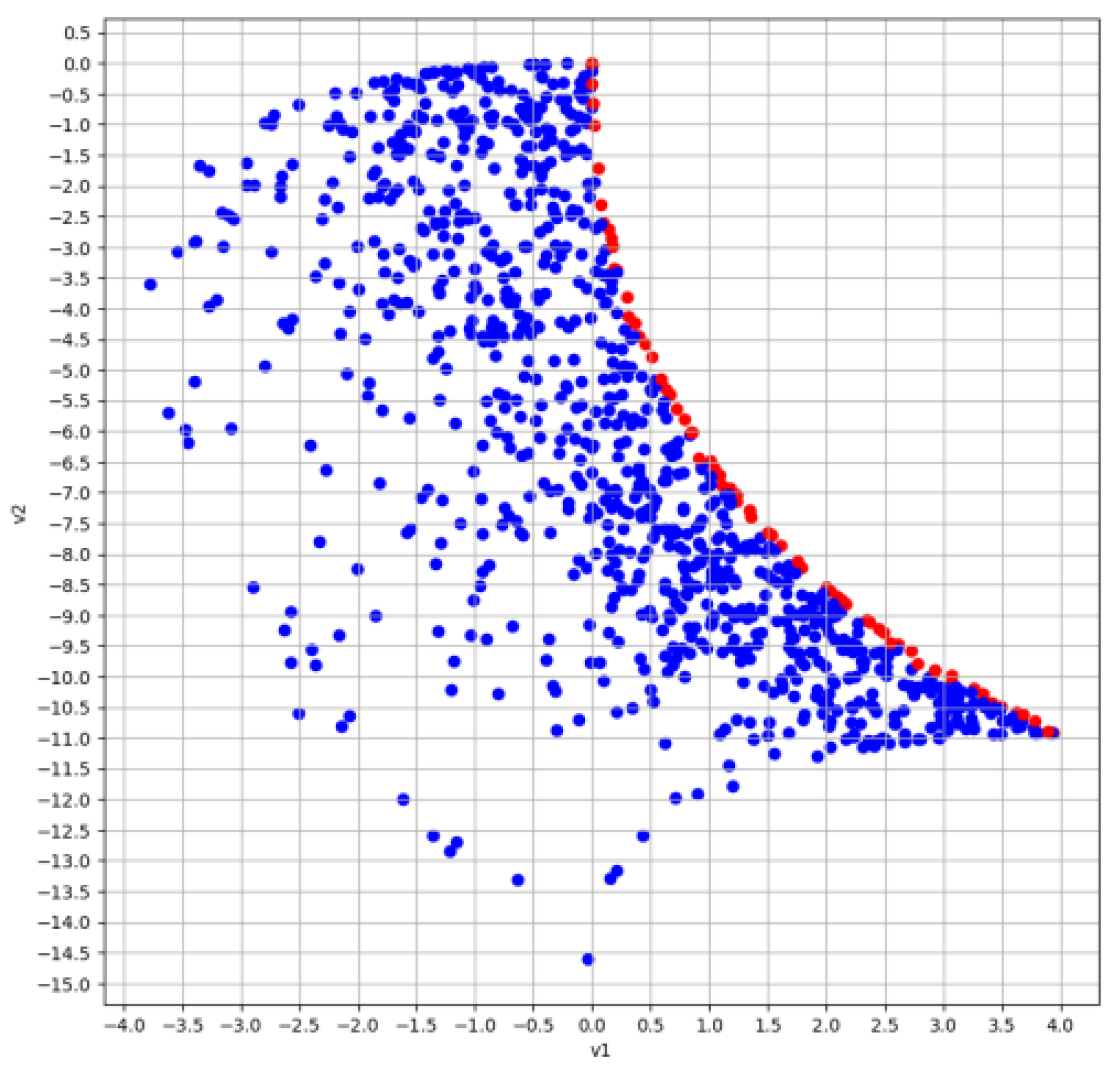
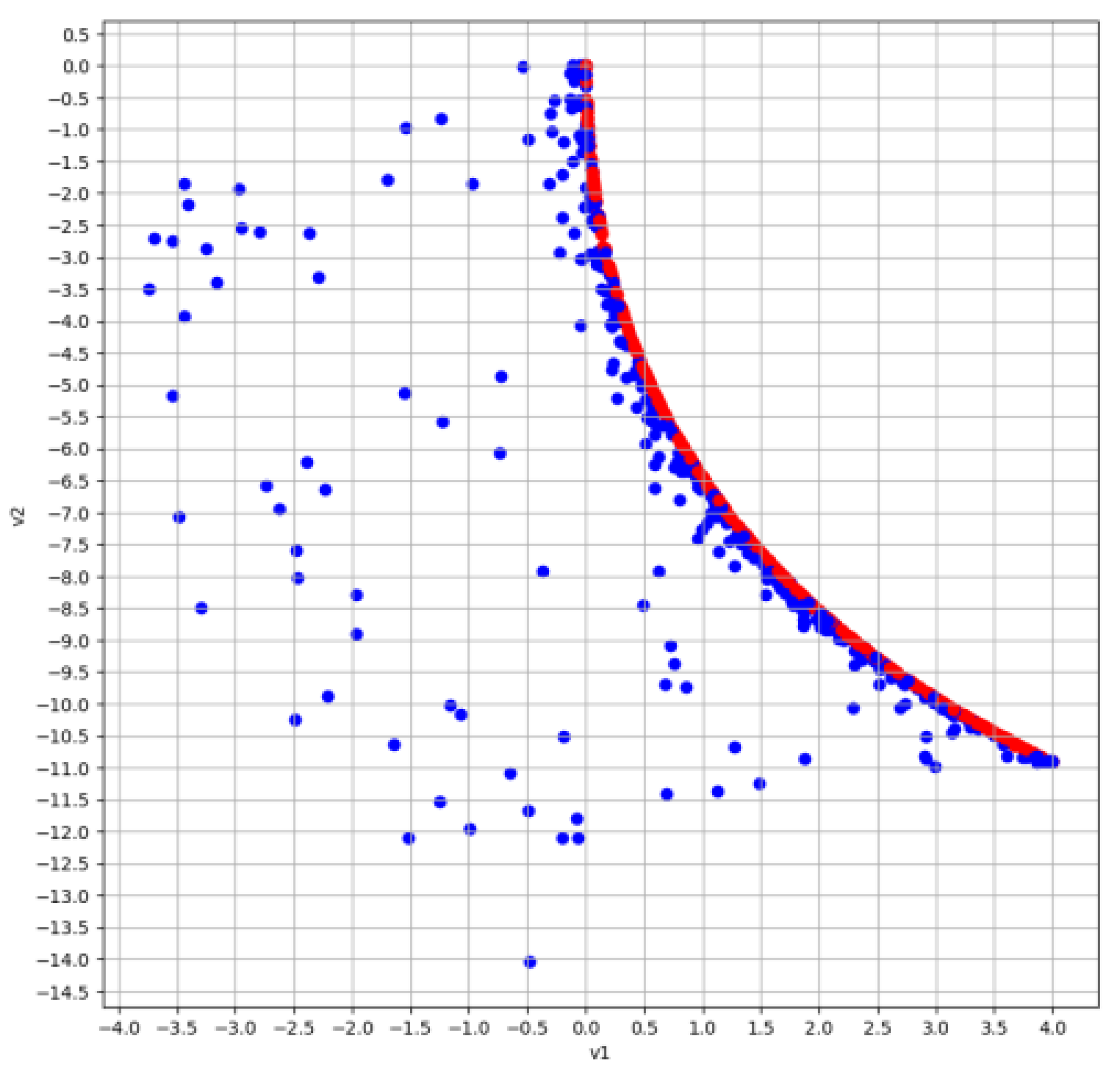
4. Computational Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, E.J.; Perez, R.E. Neuroevolutionary Control for Autonomous Soaring. Aerospace 2021, 8, 267. [Google Scholar] [CrossRef]
- Bernas, M.; Płaczek, B.; Smyła, J. A Neuroevolutionary Approach to Controlling Traffic Signals Based on Data from Sensor Network. Sensors 2019, 19, 1776. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salichon, M.; Tumer, K. A neuro-evolutionary approach to micro aerial vehicle control. In Proceedings of the 12th Annual Genetic and Evolutionary Computation Conference (GECCO’10), Portland, OR, USA, 7–11 July 2010; pp. 1123–1130. [Google Scholar] [CrossRef]
- Serov, V.A.; Voronov, E.M.; Kozlov, D.A. A neuroevolutionary synthesis of coordinated stable-effective compromises in hierarchical systems under conflict and uncertainty. Procedia Comput. Sci. 2021, 186, 257–268. [Google Scholar] [CrossRef]
- Serov, V.A.; Voronov, E.M.; Kozlov, D.A. Hierarchical Neuro-Game Model of the FANET based Remote Monitoring System Resources Balancing. In Studies in Systems, Decision and Control. Smart Electromechanical Systems. Situational Control; Gorodetskiy, A., Tarasova, I., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; Volume 261, pp. 117–130. [Google Scholar] [CrossRef]
- Serov, V.A.; Voronov, E.M.; Kozlov, D.A. Hierarchical Population Game Models of Machine Learning in Control Problems Under Conflict and Uncertainty. In Studies in Systems, Decision and Control. Smart Electromechanical Systems. Recognition, Identification, Modeling, Measurement Systems, Sensors; Gorodetskiy, A.E., Tarasova, I.L., Eds.; Springer: Cham, Switzerland, 2022; Volume 419, pp. 125–145. [Google Scholar] [CrossRef]
- Serov, V.A. Hierarchical Population Game Models of Coevolution in Multi-Criteria Optimization Problems under Uncertainty. Appl. Sci. 2021, 11, 6563. [Google Scholar] [CrossRef]
- Andión, J.M.; Arenaz, M.; Bodin, F.; Rodríguez, G.; Tourino, J. Locality-aware automatic parallelization for GPGPU with OpenHMPP directives. Int. J. Parallel Program. 2016, 44, 620–643. [Google Scholar] [CrossRef]
- Chandrashekhar, B.N.; Sanjay, H.A. Performance Study of OpenMP and Hybrid Programming Models on CPU–GPU Cluster. In Emerging Research in Computing, Information, Communication and Applications; Springer: Singapore, 2019; pp. 323–337. [Google Scholar]
- Chandrashekhar, B.N.; Sanjay, H.A.; Srinivas, T. Performance Analysis of Parallel Programming Paradigms on CPU-GPU Clusters. In Proceedings of the 2021 International Conference on Artificial Intelligence and Smart Systems (ICAIS), Coimbatore, India, 25–27 March 2021; pp. 646–651. [Google Scholar]
- Soyata, T. GPU Parallel Program Development Using CUDA; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Karovič, V.; Kaźmierczakb, M.; Pankivb, O.; Górkiewiczb, M.; Zakharchukc, M.; Stolyarchukc, R. OpenCL and CUDA Comparison of MapReduce Performance on Distributed Heterogeneous Platform through Integration with Hadoop Cluster. In Proceedings of the CEUR Workshop Proceedings, IT&AS’2021: Symposium on Information Technologies & Applied Sciences, Bratislava, Slovakia, 5 March 2021; pp. 202–208. [Google Scholar]


| Population Size | Running Time of the Parallel Algorithm s | Running Time of the Sequential Algorithm s |
|---|---|---|
| 10 | 0.1353302 | 0.0003806 |
| 50 | 0.1354179 | 0.0049311 |
| 100 | 0.1397946 | 0.0129666 |
| 500 | 0.1476841 | 0.2834744 |
| 1000 | 0.1611041 | 1.0414738 |
| 5000 | 0.2373939 | 26.2836442 |
| 10,000 | 0.3495695 | 104.6257208 |
| 50,000 | 0.3617121 | 2623.5825713 |
| 100,000 | 0.6700136 | 10,134.2378412 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serov, V.A.; Dolgacheva, E.L.; Kosyuk, E.Y.; Popova, D.L.; Rogalev, P.P.; Tararina, A.V. Artificial Neural Networks Multicriteria Training Based on Graphics Processors. Eng. Proc. 2023, 33, 57. https://doi.org/10.3390/engproc2023033057
Serov VA, Dolgacheva EL, Kosyuk EY, Popova DL, Rogalev PP, Tararina AV. Artificial Neural Networks Multicriteria Training Based on Graphics Processors. Engineering Proceedings. 2023; 33(1):57. https://doi.org/10.3390/engproc2023033057
Chicago/Turabian StyleSerov, Vladimir A., Evgenia L. Dolgacheva, Elizaveta Y. Kosyuk, Daria L. Popova, Pavel P. Rogalev, and Anastasia V. Tararina. 2023. "Artificial Neural Networks Multicriteria Training Based on Graphics Processors" Engineering Proceedings 33, no. 1: 57. https://doi.org/10.3390/engproc2023033057
APA StyleSerov, V. A., Dolgacheva, E. L., Kosyuk, E. Y., Popova, D. L., Rogalev, P. P., & Tararina, A. V. (2023). Artificial Neural Networks Multicriteria Training Based on Graphics Processors. Engineering Proceedings, 33(1), 57. https://doi.org/10.3390/engproc2023033057






