Precipitation Time Series Analysis and Forecasting for Italian Regions †
Abstract
1. Introduction
- (1)
- For each Italian region, we apply the non-parametric Mann–Kendall (MK) test and Sen’s slope estimator to estimate the gradient of the precipitation time series corresponding to each calendar month since 2000.
- (2)
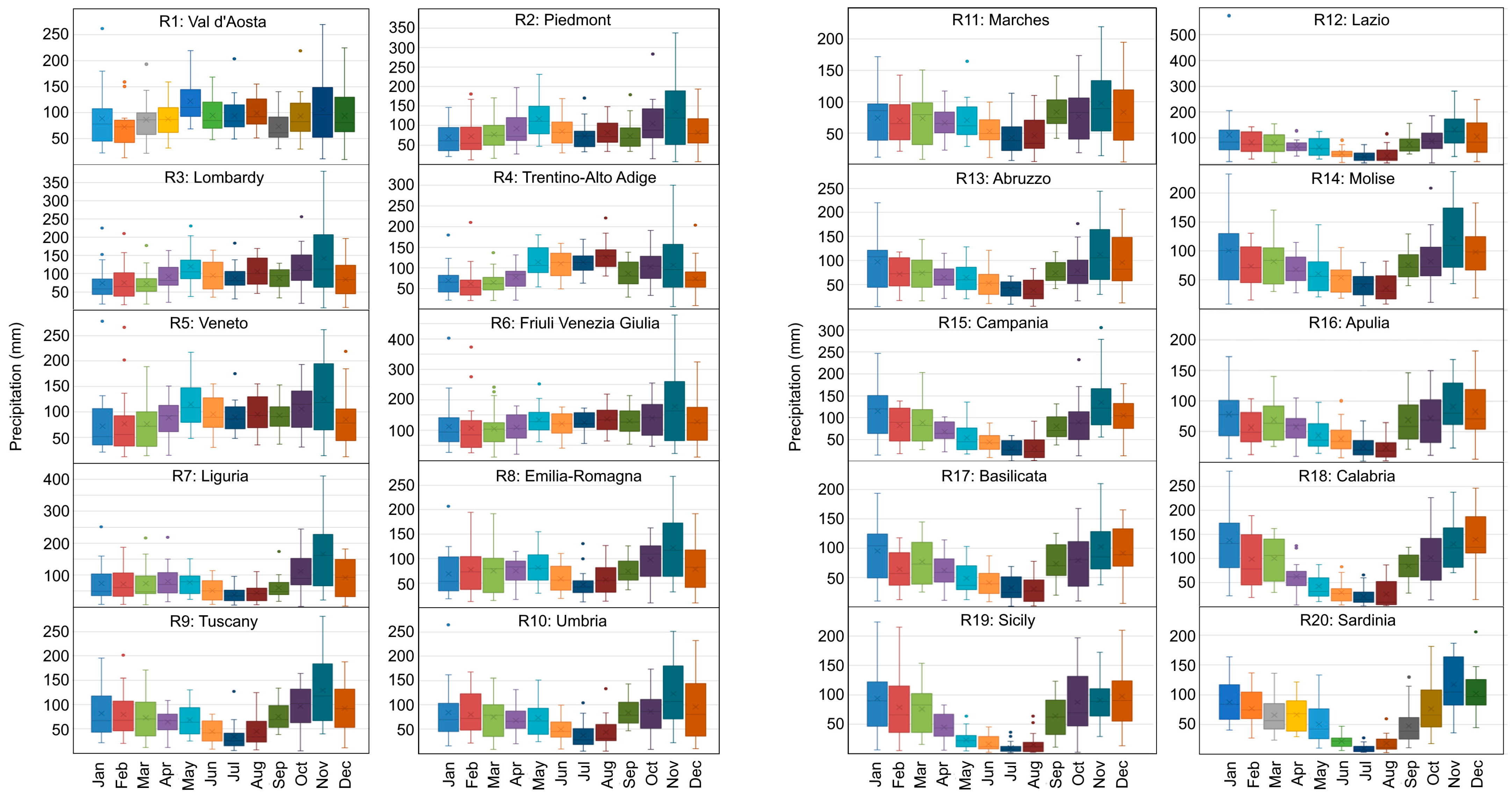
- For each Italian region, we produce the monthly box plots to better visualize the annual variation of precipitation.
- (3)
- We apply the antileakage least-squares spectral analysis (ALLSSA) to estimate the season and trend components of the 21-year-long monthly GPM time series for each Italian region.
- (4)
- We compare the performance of time series forecasting methods on the monthly precipitation time series. These methods are auto-regressive integrated moving average (ARIMA), ARIMA with eXogenous factors (ARIMAX), ARIMAX with seasonal terms (SARIMAX), and ALLSSA.
2. Materials and Methods
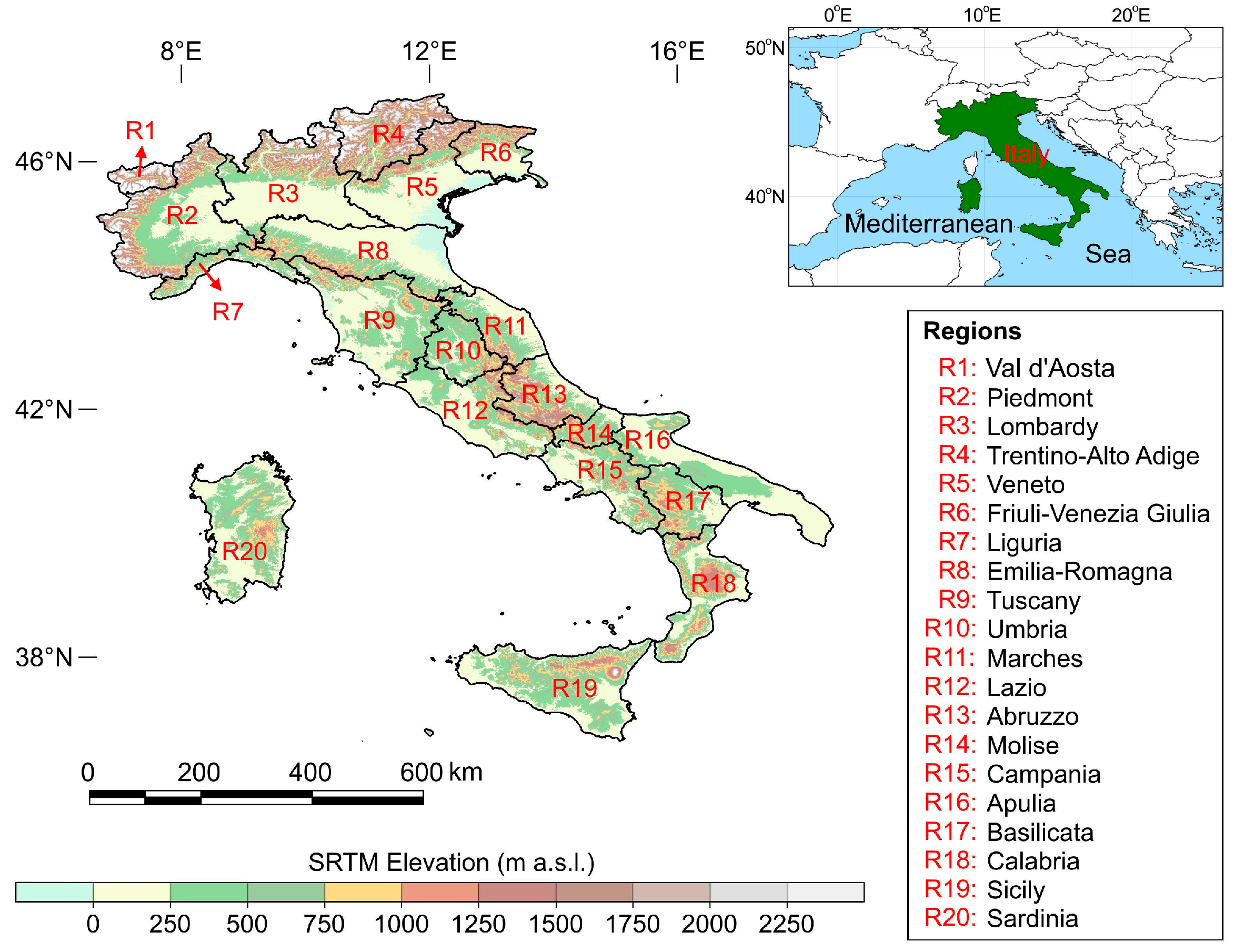
2.1. Study Region and Datasets
2.2. Methods
2.2.1. The Mann–Kendall (MK) Method and Sen’s Slope Estimator
2.2.2. Boxplots
2.2.3. The Antileakage Least-Squares Spectral Analysis (ALLSSA)
2.2.4. The Auto-Regressive Integrated Moving Average (ARIMA) and Its Extensions
3. Results and Discussion
3.1. The MK and Sen’s Slope Results
3.2. The Boxplots for Monthly Precipitation
3.3. The ALLSSA Season-Trend Results
3.4. The ARIMA, ARIMAX, SARIMAX, and ALLSSA Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gentilucci, M.; Materazzi, M.; Pambianchi, G. Statistical Analysis of Landslide Susceptibility, Macerata Province (Central Italy). Hydrology 2021, 8, 5. [Google Scholar] [CrossRef]
- Mazzanti, P.; Bozzano, F.; Cipriani, I.; Prestininzi, A. New insights into the temporal prediction of landslides by a terrestrial SAR interferometry monitoring case study. Landslides 2015, 12, 55–68. [Google Scholar] [CrossRef]
- Koehler, J.; Dietz, A.J.; Zellner, P.; Baumhoer, C.A.; Dirscherl, M.; Cattani, L.; Vlahović, Ž.; Alasawedah, M.H.; Mayer, K.; Haslinger, K.; et al. Drought in Northern Italy: Long Earth Observation Time Series Reveal Snow Line Elevation to Be Several Hundred Meters Above Long-Term Average in 2022. Remote Sens. 2022, 14, 6091. [Google Scholar] [CrossRef]
- Malandra, F.; Vitali, A.; Morresi, D.; Garbarino, M.; Foster, D.E.; Stephens, S.L.; Urbinati, C. Burn Severity Drivers in Italian Large Wildfires. Fire 2022, 5, 180. [Google Scholar] [CrossRef]
- Marino, D.; Palmieri, M.; Marucci, A.; Soraci, M.; Barone, A.; Pili, S. Linking Flood Risk Mitigation and Food Security: An Analysis of Land-Use Change in the Metropolitan Area of Rome. Land 2023, 12, 366. [Google Scholar] [CrossRef]
- Marchesini, I.; Ardizzone, F.; Alvioli, M.; Rossi, M.; Guzzetti, F. Non-susceptible landslide areas in Italy and in the Mediterranean region. Nat. Hazards Earth Syst. Sci. 2014, 12, 2215–2231. [Google Scholar] [CrossRef]
- Lombardi, A.; Gallicchio, D.; Tomassetti, B.; Raparelli, E.; Tuccella, P.; Lidori, R.; Verdecchia, M.; Colaiuda, V. Evaluating the Response of Hydrological Stress Indices Using the CHyM Model over a Wide Area in Central Italy. Hydrology 2022, 9, 139. [Google Scholar] [CrossRef]
- Alessi, D.; Bozzano, F.; Di Lisa, A.; Esposito, C.; Fantini, A.; Loffredo, A.; Martino, S.; Mele, F.; Moretto, S.; Noviello, A.; et al. Geological risks in large cities: The landslides triggered in the city of Rome (Italy) by the rainfall of 31 January–2 February 2014. Ital. J. Eng. Geol. Environ. 2014, 1, 15–34. [Google Scholar]
- Shawky, M.; Moussa, A.; Hassan, Q.K.; El-Sheimy, N. Performance Assessment of Sub-Daily and Daily Precipitation Estimates Derived from GPM and GSMaP Products over an Arid Environment. Remote Sens. 2019, 11, 2840. [Google Scholar] [CrossRef]
- Huffman, G.J.; Stocker, E.F.; Bolvin, D.T.; Nelkin, E.J.; Tan, J. GPM IMERG Final Precipitation L3 1 month 0.1 degree x 0.1 degree V06 (GPM_3IMERGM). 2019. [Google Scholar] [CrossRef]
- Pradhan, R.K.; Markonis, Y.; Godoy, M.R.V.; Villalba-Pradas, A.; Andreadis, K.M.; Nikolopoulos, E.I.; Papalexiou, S.M.; Rahim, A.; Tapiador, F.J.; Hanel, M. Review of GPM IMERG performance: A global perspective. Remote Sens. Environ. 2022, 268, 112754. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Mazzanti, P.; Scarascia Mugnozza, G.; Bozzano, F. Coherency and phase delay analyses between land cover and climate across Italy via the least-squares wavelet software. Int. J. Appl. Earth Obs. Geoinf. 2023, 118, 103241. [Google Scholar] [CrossRef]
- Shawky, M.; Ahmed, M.R.; Ghaderpour, E.; Gupta, A.; Dewan, A.; Hassan, Q.K. Remote sensing-derived land surface temperature trends over South Asia. Ecol. Inform. 2023, 74, 101969. [Google Scholar] [CrossRef]
- Zaghloul, M.S.; Ghaderpour, E.; Dastour, H.; Farjad, B.; Gupta, A.; Eum, H.; Achari, G.; Hassan, Q.K. Long Term Trend Analysis of River Flow and Climate in Northern Canada. Hydrology 2022, 9, 197. [Google Scholar] [CrossRef]
- McGill, R.; Tukey, J.; Larsen, W. Variations of box plots. Am. Stat. 1978, 32, 12–16. [Google Scholar]
- Ghaderpour, E. JUST: MATLAB and Python software for change detection and time series analysis. GPS Solut. 2021, 25, 85. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Vujadinovic, T.; Hassan, Q.A. Application of the Least-Squares Wavelet software in hydrology: Athabasca River Basin. J. Hydrol. Reg. Stud. 2021, 36, 100847. [Google Scholar] [CrossRef]
- McKenzie, E.D. General exponential smoothing and the equivalent ARMA process. J. Forecast. 1984, 3, 333–344. [Google Scholar] [CrossRef]
- Barba, P.; Rosado, B.; Ramírez-Zelaya, J.; Berrocoso, M. Comparative Analysis of Statistical and Analytical Techniques for the Study of GNSS Geodetic Time Series. Eng. Proc. 2021, 5, 21. [Google Scholar]
- Jalalkamali, A.; Moradi, M.; Moradi, N. Application of several artificial intelligence models and ARIMAX model for forecasting drought using the Standardized Precipitation Index. Int. J. Environ. Sci. Technol. 2015, 12, 1201–1210. [Google Scholar] [CrossRef]
- Manigandan, P.; Alam, M.S.; Alharthi, M.; Khan, U.; Alagirisamy, K.; Pachiyappan, D.; Rehman, A. Forecasting Natural Gas Production and Consumption in United States-Evidence from SARIMA and SARIMAX Models. Energies 2021, 14, 6021. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Vujadinovic, T. The Potential of the Least-Squares Spectral and Cross-Wavelet Analyses for Near-Real-Time Disturbance Detection within Unequally Spaced Satellite Image Time Series. Remote Sens. 2020, 12, 2446. [Google Scholar] [CrossRef]
- Song, Q.; Chissom, B.S. Fuzzy time series and its models. Fuzzy Sets Syst. 1993, 54, 269–277. [Google Scholar] [CrossRef]
- Zhang, Y.; Qu, H.; Wang, W.; Zhao, J. A novel fuzzy time series forecasting model based on multiple linear regression and time series clustering. Math. Probl. Eng. 2020, 2020, 9546792. [Google Scholar] [CrossRef]
- Novák, V.; Perfilieva, I.; Dvorak, A. Insight into Fuzzy Modeling; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]


| R | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.15 | 0.39 | −0.67 | −0.19 | 1.17 | 0.12 | −0.87 | −1.03 | −2.14 ** | 0.80 | 1.75 | 2.85 |
| 2 | 0.34 | −0.19 | −0.11 | 0.48 | 0.30 | 0.20 | −0.42 | −0.76 | −2.75 ** | 0.63 | 0.80 | 0.63 |
| 3 | 0.08 | −0.22 | −0.29 | 0.05 | 0.70 | 1.77 | −2.07 | −0.16 | −1.01 | 1.72 | −2.22 | 1.75 |
| 4 | 0.89 | 0.36 | −0.95 | −0.44 | 1.09 | 0.83 | −1.56 | 0.94 | 0.142 | 0.68 | −2.39 | 1.14 |
| 5 | −0.48 | 1.30 | −0.54 | −1.34 | 1.30 | 0.54 | −1.17 | 0.26 | −1.23 | 0.56 | −2.12 | 0.96 |
| 6 | 0.59 | 1.89 | −1.16 | −1.48 | 2.37 | 0.94 | −1.37 | 0.46 | −0.44 | 0.17 | −1.97 | 1.34 |
| 7 | −0.20 | 0.22 | 0.16 | 0.19 | −0.35 | 0.86 | 0.07 | −0.21 | −1.08 | −0.47 | 0.60 | 0.58 |
| 8 | −0.34 | 0.92 | −0.20 | −1.14 | 0.70 | 0.50 | −0.52 | −0.33 | −0.81 | 0.27 | −0.29 | 0.42 |
| 9 | 0.35 | 1.49 | −0.52 | −0.91 | 0.47 | 0.19 | −0.52 | −0.25 | −0.49 | 0.46 | −0.44 | −1.15 |
| 10 | −0.35 | 1.17 | 1.24 | −1.16 | 0.29 | 1.11 | 0.15 | 0.05 | −0.04 | 0.31 | 0.84 | −1.64 |
| 11 | −0.08 | 2.06 | 1.47 | −1.98 ** | 1.12 | 1.15 | 0.02 | −0.69 | −0.83 | −0.40 | 0.24 | −2.13 |
| 12 | −0.75 | 0.72 | 0.93 | −1.06 | −0.03 | 0.53 | 0.20 | −0.41 | 0.14 | −0.58 | 0.55 | −1.82 |
| 13 | −0.04 | −0.81 | 1.12 | −1.23 | −0.10 | 0.36 | 0.30 | −0.62 | −0.86 | −0.71 | −0.24 | −2.89 |
| 14 | −0.62 | −0.31 | 0.35 | −1.32 | 0.46 | 0.09 | 0.64 | 0.08 | 0.63 | −0.49 | 2.95 | −2.52 |
| 15 | −0.37 | 0.22 | 0.33 | −1.41 * | 0.59 | 0.71 | −0.02 | 0.19 | 0.38 | 0.52 | 2.07 | −1.41 |
| 16 | −0.27 | 0.42 | 0.50 | −1.17 | 0.39 | 0.52 | 0.16 | 0.38 | −0.68 | 0.42 | 2.52 | −3.11 ** |
| 17 | 0.02 | 0.00 | 0.37 | −1.60 | −0.04 | 0.75 | 0.24 | 0.16 | −0.87 | 0.03 | 1.96 | −3.64 ** |
| 18 | −0.47 | 0.27 | 0.30 | −1.86 ** | −0.06 | 0.32 | 0.44 | 0.08 | −0.87 | 1.31 | 2.68 | −2.83 |
| 19 | −2.07 | 0.47 | 2.27 | −1.98 ** | −0.55 | −0.32 | 0.12 | 0.14 | −0.26 | 1.34 | 2.66 | −4.12 *** |
| 20 | −0.23 | −0.05 | 0.62 | −1.25 | −0.03 | 0.33 | 0.01 | 0.31 | 1.00 | −1.32 | 0.36 | −1.48 |
| Lazio (R12) | Calabria (R18) | |||||||
|---|---|---|---|---|---|---|---|---|
| ARIMA | ARIMAX | SARIMAX | ALLSSA | ARIMA | ARIMAX | SARIMAX | ALLSSA | |
| (1,1,1) | (6,1,1) | (3,1,6) (0,1,1) [12] | (1,1,1) | (6,1,1) | (3,1,6) (0,1,1) [12] | |||
| MAE (mm) | 71.97 | 72.66 | 68.54 | 65.17 | 43.11 | 37.15 | 33.57 | 23.39 |
| MAPE (%) | 84.96 | 90.97 | 50.24 | 42.73 | 76.32 | 107.05 | 61.18 | 51.34 |
| RMSE (mm) | 153.39 | 153.23 | 150.25 | 145.71 | 57.49 | 50.20 | 39.10 | 27.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghaderpour, E.; Dadkhah, H.; Dabiri, H.; Bozzano, F.; Scarascia Mugnozza, G.; Mazzanti, P. Precipitation Time Series Analysis and Forecasting for Italian Regions. Eng. Proc. 2023, 39, 23. https://doi.org/10.3390/engproc2023039023
Ghaderpour E, Dadkhah H, Dabiri H, Bozzano F, Scarascia Mugnozza G, Mazzanti P. Precipitation Time Series Analysis and Forecasting for Italian Regions. Engineering Proceedings. 2023; 39(1):23. https://doi.org/10.3390/engproc2023039023
Chicago/Turabian StyleGhaderpour, Ebrahim, Hanieh Dadkhah, Hamed Dabiri, Francesca Bozzano, Gabriele Scarascia Mugnozza, and Paolo Mazzanti. 2023. "Precipitation Time Series Analysis and Forecasting for Italian Regions" Engineering Proceedings 39, no. 1: 23. https://doi.org/10.3390/engproc2023039023
APA StyleGhaderpour, E., Dadkhah, H., Dabiri, H., Bozzano, F., Scarascia Mugnozza, G., & Mazzanti, P. (2023). Precipitation Time Series Analysis and Forecasting for Italian Regions. Engineering Proceedings, 39(1), 23. https://doi.org/10.3390/engproc2023039023









