Abstract
A solution method based on the ant colony optimization (ACO) algorithm is established for the hybrid flow shop scheduling problem with the objective of minimizing the maximum completion time and the number of fixtures. By using the linear weighting method, the dual-objective optimization problem can be effectively converted into a single-objective optimization. Taking the scheduling problem of an automated production line of precision parts as an example, the feasibility of the proposed algorithm is verified, and the integrated optimization of fixture resource allocation and production scheduling is realized.
1. Introduction
The hybrid flow-shop scheduling problem (HFSP) is a classical problem in the field of production scheduling. In automated production lines, the cost of fixture resources is high due to the fact that each fixture system can only hold one job at a time. Therefore, in this paper, an ant colony algorithm is used to simultaneously consider minimizing the maximum completion time and the number of fixtures for hybrid flow shop scheduling.
Some classic studies on ACO are as follows. Qin et al. studied the dynamic hybrid flow shop scheduling problem with uncertain processing time and proposed a rescheduling method based on the ant colony algorithm [1]. Zhao analyzed the objective function and boundary conditions of the emergency distribution routes based on the ant colony algorithm and solved the optimal routes based on the pheromone content of each route [2]. Jiang et al. proposed to guide the optimization approach by improving the pheromone update rule based on the experience of the global optimum [3]. Li et al. improved the pheromone updating method by improving the path selection strategy and path transfer probability function and utilizing a max–min ant colony system [4].
2. Problem Formulation
The problem can be described as jobs are to be processed in an automated production line with processes and the same processing sequence for each job. is the set of parallel machines on each process. Process can be processed on any . Scheduling decisions are made to determine the sequencing of all jobs for each process and the selection of machines for each process. The goal of scheduling is to minimize the maximum completion time and reduce the number of fixtures.
The basic assumptions include: (1) jobs on automated production lines must be processed using fixtures, each fixture follows a job until the end of processing, and the number of fixtures is limited; (2) only one job can be processed per machine at any one time without interruption; (3) if the machine required for the processing of the job is in operation, the job waits at the caching station; (4) negligible movement of the robot arm as well as disassembly and clamping time of jobs.
3. ACO Algorithm with Consideration of Fixture Resources
3.1. Flow of the ACO Algorithm
The ACO algorithm is a heuristic bionic algorithm based on positive feedback of information [5]. By transforming the scheduling process into the search path of an ant colony, a feasible and effective ant colony algorithm model is constructed to solve the complex automatic production line shop scheduling problem. The ACO algorithm flow is shown in Figure 1. represents maximum completion time. represents the current number of iterations. represents the maximum number of iterations.

Figure 1.
ACO algorithm flow.
3.2. Feasible Process Table for the ACO Algorithm
represents the serial number of the process that is processing indicates that the job started processing but not finished processing and will occupy a fixture until the last process is completed. The number of jobs that meet is equal to . represents the number of fixtures currently occupied. represents the maximum number of fixtures on a production line.
If , the table of feasible process includes the first process of a raw job and the tightening process of the job has begun. If , the table of feasible process includes the tightening process of the job has begun.
3.3. Optional Process Probabilities for the ACO Algorithm
The probability of optional processes is calculated as shown in Equation (1). is one of the optional processes, is any of the optional processes, is the set of optional processes. represents the probability that an ant’s current process is and the next process is chosen as , represents its pheromone concentration, represents the value of its heuristic function value.
3.4. Feasible Solution Generation for the ACO Algorithm
Use an array of to represent a feasible scheduling solution to the problem, is the total number of processes. The first layer is the total process gene and the second layer is the machine gene. Randomly generate an integer in the range 1 to as the first process chosen by an ant. After generating the corresponding feasible process table, all optional processes and their selection probabilities are determined. Update the feasible process table and recalculate the selection probabilities for all available processes after determining the next process by means of the roulette method, until all processes have been selected. This is the step by step for the ACO algorithm to generate feasible solutions. A feasible solution for case is shown in Figure 2.
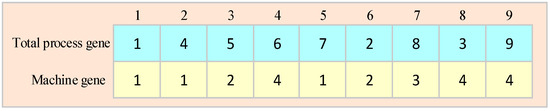
Figure 2.
Feasible solution example.
3.5. Pheromone Update for the ACO Algorithm
Two adjacent processes in the feasible solution are considered as a process path. The increment of pheromones on the path is inversely proportional to the maximum completion time, as shown in Equation (2). represents the pheromone constant factor. represents the maximum completion time of ant . represents the pheromone increment of each ant on its own path through the process.
Renewal of pheromones includes addition and volatilization as shown in Equation (3). represents pheromone volatile factor. represents the pheromone increment of all ants on the process path to .
4. Numerical Example and Analysis
4.1. Parameter Settings
Based on the automated production line for precision parts, the experimental parameter obtained through Taguchi’s experiments are shown in Table 1.

Table 1.
Experimental parameter.
4.2. Computational Experiments and Discussion
Normalization is performed by Equation (4) to determine the fitness of each solution. represents the minimum value of the target r. represents the minimum value of the target r.
A linear weighting method is used to convert the optimization objective into a single-objective problem, as shown in Equation (5). Weighting factors determined by multiple qualified experts with extensive experience and expertise. The weights of and the weights of fixtures number are set to and .
According to Table 2, achieves the minimum value when the = 3, and the corresponding production line scheduling Gantt chart is shown in Figure 3. Compared with , the number of fixtures is reduced by 7, and is increased by 53. Compared to heuristic rules, the ACO algorithm gives better results.

Table 2.
Correspondence table between and .

Figure 3.
Gantt chart of automated production line scheduling for .
5. Conclusions
In this paper, the ant colony algorithm is applied to the hybrid flow-shop scheduling problem with integrated consideration of fixture resources, and the experimental results show that it is feasible. More complex cases for HFSP are to be further studied and considered.
Author Contributions
Conceptualization, J.G.; methodology, J.G., L.X., and L.Z.; software, L.X.; validation, L.X.; formal analysis, L.Z.; investigation, L.X.; writing—original draft preparation, L.X.; writing—review and editing, J.G.; funding acquisition, J.G. All authors have read and agreed to the published version of the manuscript.
Funding
The National Natural Science Foundation of China, grant number [No. 51705370].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Qin, W.; Zhang, J.; Song, D. An improved ant colony algorithm for dynamic hybrid flow shop scheduling with uncertain processing time. J. Intell. Manuf. 2018, 29, 891–904. [Google Scholar] [CrossRef]
- Zhao, L. Research on Emergency Distribution Route Planning Based on the Ant Colony Algorithm. In Proceedings of the ISMHI 2019, Paris, France, 21–23 November 2019; Francis Academic Press: London, UK, 2019; p. 5. [Google Scholar]
- Jiang, X.; Tao, Q. Multi-objective flexible job shop schedule based on ant colony algorithm. In Proceedings of the DCABES 2015, Guiyang, China, 18–24 August 2015; p. 4. [Google Scholar]
- Li, X.; Li, Q.; Zhang, J. Research on global path planning of unmanned vehicles based on improved ant colony algorithm in the complex road environment. Meas. Control 2022, 55, 945–959. [Google Scholar] [CrossRef]
- Qin, W.; Zhuang, Z.; Liu, Y.; Tang, O. A two-stage ant colony algorithm for hybrid flow shop scheduling with lot sizing and calendar constraints in printed circuit board assembly. Comput. Ind. Eng. 2019, 138, 106115. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).