Impact of Fear on a Crowley–Martin Eco-Epidemiological Model with Prey Harvesting ^†

Abstract

In this paper, we develop a three-species food web model that incorporates the use of interactions between diseased predator–prey models. The logistically growing prey populations are susceptible and diseased prey. Prey populations are assumed to grow logistically in the absence of predators. We investigate the effect of fear on susceptible prey through infected prey populations. In Crowley–Martin-type interactions, it is assumed that interdependence between predators happens regardless of whether an individual predator is searching for prey or handling prey at the time. Also, the prey harvesting of susceptible and infected prey has been considered. The existence of all possible equilibrium points for biological systems has been established. The criteria for the local and global stability of equilibrium points are examined. Additionally, we look at Hopf-bifurcation analysis for the suggested model in relation to the existence of harvesting rate $\left(h_1\right)$. Numerical simulations are provided in order to explain the phenomenon and comprehend the complex interactions between predators and prey.

1. Introduction

The predator–prey models developed by Lotka [1] and Volterra [2] are regarded as the earliest developments in contemporary mathematical ecology in coupled systems of non-linear differential equations. Since Kermack and Mckendrick’s pioneering work on SIRS, [3], epidemiological models have attracted much interest from researchers. Mathematical modeling of predator–prey interactions, known as “functional response,” is among the most important factors in predator–prey population modeling. Crowley–Martin functional responses take into account both prey and predators. In the recent era, some eminent authors, [4,5,6,7], have studied to understand the importance and interactions of prey. To make the model system more realistic and feasible in the ecosystem, they incorporated some functional responses, i.e., Crowley–Martin-type functional responses. Kadhim and Azhar [8] use a type II Holling function to represent two disease types in a predator population model with a linear functional response. In [9], a nonlinear analysis of a discrete effects predator–prey model is investigated. Prey refuge and prey harvest [10,11], with ratio-dependent and Holling type II functional responses. Several investigations have been conducted on the dynamic behavior of Crowley–Martin diseased predator–prey models. To our knowledge, only a few researchers have looked into three-species prey–predator models that take into account species interactions, including Crowley–Martin disease in prey populations. This study examines how fear affects a Crowley–Martin eco-epidemiological model with prey harvesting. The rest of the paper is structured as follows: In Section 2, we describe how the study’s model formation was created. In Section 3 and Section 4, we talk about boundary equilibrium points and their stability. In Section 5, the Hopf-bifurcation is the positive equilibrium point $E^{*}(u^{*},v^{*},w^{*})$. Numerical simulations of the suggested model are examined in Section 6. The paper is concluded in Section 7, which also discusses the biological consequences of our mathematical findings.

2. Mathematical Model Formation

The model explains the relationship between the structure of the infected prey and the following equations. The proposed framework was used to discover a non-linear prey–predator mathematical model.

$$\begin{array}{c}\hfill \left.\begin{array}{ccc}\frac{dS}{dT}& =& \frac{RS}{1+\rho I}(1-\frac{S+I}{K})-\frac{{\alpha }_{1}SI}{a_1+S}-\frac{{\beta }_{1}SP}{(1+{\eta }_{1}S)(1+{\mu }_{1}P)}-H_1{E}_{1}S,\\ \frac{dI}{dT}& =& \frac{{\alpha }_{1}SI}{a_1+S}-D_{1}I-\frac{b_{1}IP}{(1+{\eta }_{1}I)(1+{\mu }_{1}P)}-H_2{E}_{2}I,\\ \frac{dP}{dT}& =& -D_{2}P+\frac{c{b}_{1}IP}{(1+{\eta }_{1}I)(1+{\mu }_{1}P)}+\frac{c{\beta }_{1}SP}{(1+{\eta }_{1}S)(1+{\mu }_{1}P)},\end{array}\right\}\end{array}$$

(1)

and the positive conditions are described as $S_0\ge 0,I_0\ge 0$ and $P_0\ge 0$.

The Table 1 displays the specific biological meanings of the parameters.

Table 1. Biological representation of the model.

Parameters	Biological Representation
$R,K$	Intrinsic rate of prey population increase, Ecological carrying capacity.
$\rho ,{\alpha }_1$	Level of fear, Infection rate.
$S,I,P$	Susceptible Prey, Prey with infection, Predator.
$a_1,{\beta }_1$	The constant for half-saturation, Vulnerable prey to predator’s consumption rate.
${\eta }_1,{\mu }_1$	Time for handling a predator, Interaction between predators on a large scale.
$H_1,H_2,E$	The catchability coefficient of the susceptible prey, Infected prey, Harvesting effort.
$D_1,D_2$	Diseased prey, Predator population death rate.
$b_1,c$	Capture rate by predator, Prey to predator consumption rate.

The condition for the impact of fear is $F(\rho ,i)$$=\frac{1}{1+\rho i}$. This refers to the infected’s fear effect on susceptible prey. Here, f is the amount of fear. It is appropriate to modify the variables as follows in order to decrease the number of systems (1) variables $s=\frac{S}{K},i=\frac{I}{K},p=\frac{P}{K}$, and to consider the dimension time $t=\lambda KT$. Now, we apply the following transformations. $r=\frac{R}{\lambda K},\alpha =\frac{{\alpha }_1}{\lambda K},a=\frac{a_1}{K},\beta =\frac{{\beta }_1}{\lambda },\eta ={\eta }_{1}K,\mu ={\mu }_{1}K,b=\frac{b_1}{\lambda },h_1=\frac{H_1{E}_1}{\lambda K},h_2=\frac{H_2{E}_2}{\lambda K},d=\frac{D_1}{\lambda K},\delta =\frac{D_2}{\lambda K}.$ Equation (1) can be represented in dimensionless form using the above transformations.

$$\begin{array}{c}\hfill \left.\begin{array}{ccc}\frac{ds}{dt}& =& \frac{rs}{1+\rho i}(1-s-i)-\frac{\alpha si}{a+s}-\frac{\beta sp}{(1+\eta s)(1+\mu p)}-h_{1}s,s\left(0\right)\ge 0,\\ \frac{di}{dt}& =& \frac{\alpha si}{a+s}-di-\frac{bip}{(1+\eta i)(1+\mu p)}-h_{2}i,i\left(0\right)\ge 0,\\ \frac{dp}{dt}& =& -\delta p+\frac{cbip}{(1+\eta i)(1+\mu p)}+\frac{c\beta sp}{(1+\eta s)(1+\mu p)},p\left(0\right)\ge 0,\end{array}\right\}\end{array}$$

(2)

3. Existence of Equilibrium Points

The model (2) exhibits the following equilibrium points based on observation:

• $E_0(0,0,0)$ is the trivial equilibrium point.
• $E_1(s,0,0)$ is the boundary equilibrium point exists if $h_1<r$, where $s=\frac{r-h_1}{r}$.
• $E_2(\widehat{s},\widehat{i},0)$ is the without predator equilibrium point, where $\widehat{s}=\frac{a(d+h_2)}{\alpha -d-h_2},\widehat{i}=\frac{-{\mathcal{R}}_2\pm \sqrt{{\mathcal{R}}_2^2-4{\mathcal{R}}_1{\mathcal{R}}_3}}{2{\mathcal{R}}_1}.$ Here, $\widehat{i}$ is the unique positive root of the equation
  ${\mathcal{R}}_1{\widehat{i}}^2+{\mathcal{R}}_2\widehat{i}+{\mathcal{R}}_3=0$, with ${\mathcal{R}}_1=\rho {(\alpha -d-h_2)}^2,{\mathcal{R}}_2=(\alpha -d-h_2)[a(r+h_1\rho )+(\alpha -d-h_2)],{\mathcal{R}}_3=a[ar(d+h_2)-(r-h_1)(\alpha -d-h_2)].$
  It is observed that $\widehat{i}$ is the unique positive root if $d+h_2<\alpha ,h_1<r$ and $\alpha -(d+h_2)<\frac{ar(d+h_2)}{r-h_1}$. $E_2$ exists for $d+h_2<\alpha ,h_1<r$.
• The infection-free equilibrium point $E_3(\overline{s},0,\overline{p})$, where $\overline{s}=\frac{\delta (1+\mu p)}{c\beta -\delta \eta (1+\mu p)},\overline{p}=\frac{(1+\eta s)(r(1-s)-h_1)}{\beta -\mu (1+\eta s)(r(1-s)-h_1)}.$ Thus, the conditions must exist for the infection-free equilibrium point $E_3$ are $\frac{\delta \eta (1+\mu p)}{c}<\beta$ and $r(1-s)-h_1<\frac{\beta }{\mu (1+\eta s)}$ (assume $h_1<r(1-s)$ and $s<1)$.
• The endemic equilibrium point $E^{*}(s^{*},i^{*},p^{*})$, where $s^{*}=\frac{\delta (1+\eta i^{*})(1+\mu p^{*})-bc{i}^{*}}{bc\eta i^{*}+(1+\eta i^{*})(c\beta -\delta \eta (1+\mu p^{*}))},i^{*}=\frac{b(a+s^{*})p^{*}-(1+\mu p^{*})[\alpha s^{*}-(d+h_2)(a+s^{*})]}{\eta (1+\mu p^{*})[\alpha s^{*}-(d+h_2)(a+s^{*})]},p^{*}=\frac{(1+\eta s^{*})[\frac{r(1-s^{*}-i^{*})}{1+\rho i^{*}}-\frac{\alpha i^{*}}{a+s^{*}}-h_1]}{\beta -\mu (1+\eta s^{*})[\frac{r(1-s^{*}-i^{*})}{1+\rho i^{*}}-\frac{\alpha i^{*}}{a+s^{*}}-h_1]}.$ Thus, the conditions must exist for the endemic equilibrium point $E^{*}$ are $\frac{\delta \eta (1+\mu p^{*})}{c}<\beta$, $d+h_2<\frac{\alpha s^{*}}{a+s^{*}}$, $\frac{r(1-s^{*}-i^{*})}{1+\rho i^{*}}<\frac{\alpha i^{*}}{a+s^{*}}+h_1+\frac{\beta }{\mu (1+\eta s^{*})}$.

4. Stability Analysis

In order to determine local stability around various equilibrium points, we compute the Jacobian matrix. At each given point $(s,i,p)$, the Jacobian matrix is given by

$$J\left(E\right)=\left[\begin{array}{ccc}{\mathcal{L}}_{11}& {\mathcal{L}}_{12}& {\mathcal{L}}_{13}\\ {\mathcal{L}}_{21}& {\mathcal{L}}_{22}& {\mathcal{L}}_{23}\\ {\mathcal{L}}_{31}& {\mathcal{L}}_{32}& {\mathcal{L}}_{33}\end{array}\right].$$

where, ${\mathcal{L}}_{11}=\frac{r}{1+\rho i}(1-2s-i)-\frac{a\alpha i}{{(a+s)}^2}-\frac{\beta p}{{(1+\eta s)}^2(1+\mu p)}-h_1,{\mathcal{L}}_{12}=-\frac{rs\left(\rho \right(1-s)+1)}{{(1+\rho i)}^2}-\frac{\alpha s}{a+s},{\mathcal{L}}_{13}=\frac{-\beta s}{(1+\eta s){(1+\mu p)}^2},{\mathcal{L}}_{21}=\frac{\alpha ai}{{(a+s)}^2},{\mathcal{L}}_{22}=\frac{\alpha s}{a+s}-\frac{bp}{(1+\mu p){(1+\eta i)}^2}-d-h_2,{\mathcal{L}}_{23}=-\frac{bi}{(1+\eta i){(1+\mu p)}^2},{\mathcal{L}}_{31}=\frac{\beta cp}{{(1+\eta s)}^2(1+\mu p)},{\mathcal{L}}_{32}=\frac{bcp}{{(1+\eta i)}^2(1+\mu p)},{\mathcal{L}}_{33}=-\delta +\frac{bci}{(1+\eta i){(1+\mu p)}^2}+\frac{\beta cs}{(1+\eta s){(1+\mu p)}^2}.$

Theorem 1.

The trivial equilibrium point $E_0(0,0,0)$ is always unstable.

Proof. 

$$J\left(E_0\right)=\left[\begin{array}{ccc}r-h_1& 0& 0\\ 0& -d-h_2& 0\\ 0& 0& -\delta \end{array}\right].$$

Here, the eigenvalues of $J\left(E_0\right)$ are $r-h_1$, $-d-h_2$, $-\delta$. Hence, $E_0$ is locally asymptotically stable only if $r<h_1$ and unstable otherwise. □

Theorem 2.

$E_1(\frac{r-h_1}{r},0,0)$ is locally asymptotically stable if $\alpha (r-h_1)<(d+h_2)(ar+(r-h_1))$ and $\beta c(r-h_1)<\delta (r+\eta (r-h_1))$.

Proof. 

$$J\left(E_1\right)=\left[\begin{array}{ccc}{\mathcal{M}}_1& {\mathcal{M}}_2& {\mathcal{M}}_3\\ 0& {\mathcal{M}}_4& 0\\ 0& 0& {\mathcal{M}}_5\end{array}\right].$$

where ${\mathcal{M}}_1=-r+h_1,{\mathcal{M}}_2=-\frac{rs(1+\rho (1-s\left)\right)}{{(1+\rho i)}^2}-\frac{\alpha s}{a+s},{\mathcal{M}}_3=-\frac{\beta s}{1+\eta s},{\mathcal{M}}_4=\frac{\alpha (r-h_1)}{ar+(r-h_1)}-d-h_2,{\mathcal{M}}_5=-\delta +c\beta \left[\frac{r-h_1}{r+\eta (r-h_1)}\right].$ Therefore, eigenvalues of $J\left(E_1\right)$ are $h_1-r,\frac{\alpha (r-h_1)}{ar+(r-h_1)}-(d+h_2),\mathrm{and}-\delta +c\beta \left[\frac{r-h_1}{r+\eta (r-h_1)}\right]$. If ${\lambda }_1<0$ i.e., $r<h_1$, ${\lambda }_2<0$, i.e., $\alpha (r-h_1)<(d+h_2)(ar+(r-h_1))$ and ${\lambda }_3<0$, i.e., $\beta c(r-h_1)<\delta (r+\eta (r-h_1))$. Thus, $E_1$ is locally asymptotically stable if $\alpha (r-h_1)<(d+h_2)(ar+(r-h_1))$ and $\beta c(r-h_1)<\delta (r+\eta (r-h_1))$. □

Theorem 3.

$E_2(\widehat{s},\widehat{i},0)$ is locally asymptotically stable if ${\mathcal{X}}_{11}>0$, ${\mathcal{X}}_{12}>0$ and $\delta >\frac{bc\widehat{i}}{1+\eta \widehat{i}}+\frac{\beta c\widehat{s}}{1+\eta \widehat{s}}$.

Proof. 

$$J\left(E_2\right)=\left[\begin{array}{ccc}{\mathcal{N}}_1& {\mathcal{N}}_2& {\mathcal{N}}_3\\ {\mathcal{N}}_4& {\mathcal{N}}_5& {\mathcal{N}}_6\\ 0& 0& {\mathcal{N}}_7\end{array}\right].$$

where, ${\mathcal{N}}_1=\frac{r(1-2\widehat{s}-\widehat{i})}{1+\rho \widehat{i}}-\frac{a\alpha \widehat{i}}{{(a+\widehat{s})}^2}-h_1,{\mathcal{N}}_2=-\frac{r\widehat{s}(1+\rho (1-\widehat{s}))}{{(1+f\widehat{i})}^2}-\frac{\alpha \widehat{s}}{a+\widehat{s}},{\mathcal{N}}_3=-\frac{\beta \widehat{s}}{1+\eta \widehat{s}},{\mathcal{N}}_4=\frac{\alpha a\widehat{i}}{{(a+\widehat{s})}^2},N_5=\frac{\alpha \widehat{s}}{a+\widehat{s}}-(d+h_2),{\mathcal{N}}_6=-\frac{b\widehat{i}}{1+\eta \widehat{i}},{\mathcal{N}}_7=-\delta +\frac{bc\widehat{i}}{1+\eta \widehat{i}}+\frac{\beta c\widehat{s}}{1+\eta \widehat{s}}.$

Therefore, the characteristic equation of $J\left(E_2\right)$ is $({\mathcal{N}}_7-\lambda )({\lambda }^2+{\mathcal{X}}_{11}\lambda +{\mathcal{X}}_{12})=0$, where ${\mathcal{X}}_{11}=-({\mathcal{N}}_1+{\mathcal{N}}_5)$ and ${\mathcal{X}}_{12}={\mathcal{N}}_1{\mathcal{N}}_5-{\mathcal{N}}_2{\mathcal{N}}_4$.

In the above characteristic equation, we obtain one of the eigenvalue is ${\mathcal{N}}_7$, which is negative as $\delta >\frac{bc\widehat{i}}{1+\eta \widehat{i}}+\frac{\beta c\widehat{s}}{1+\eta \widehat{s}}$ and the other two eigenvalues should be negative if ${\mathcal{X}}_{11}>0$ and ${\mathcal{X}}_{12}>0$.

Hence, $E_2$ is locally asymptotically stable if ${\mathcal{X}}_{11}>0$, ${\mathcal{X}}_{12}>0$ and $\delta >\frac{bc\widehat{i}}{1+\eta \widehat{i}}+\frac{\beta c\widehat{s}}{1+\eta \widehat{s}}$. □

Theorem 4.

The diseased-prey free equilibrium point $E_3(\overline{s},0,\overline{p})$ is locally asymptotically stable if ${\mathcal{Y}}_{11}>0$, ${\mathcal{Y}}_{12}>0$ and $d+h_2>\frac{\alpha \overline{s}}{a+\overline{s}}-\frac{b\overline{p}}{1+\mu \overline{p}}$.

Proof. 

$$J\left(E_3\right)=\left[\begin{array}{ccc}{\mathcal{P}}_1& {\mathcal{P}}_2& {\mathcal{P}}_3\\ 0& {\mathcal{P}}_4& 0\\ {\mathcal{P}}_5& {\mathcal{P}}_6& {\mathcal{P}}_7\end{array}\right].$$

where ${\mathcal{P}}_1=r(1-2\overline{s})-\frac{\beta \overline{p}}{{(1+\eta \overline{s})}^2(1+\mu \overline{p})}-h_1,{\mathcal{P}}_2=-r\overline{s}(1+f(1-\overline{s}))-\frac{\alpha \overline{s}}{a+\overline{s}},{\mathcal{P}}_3=-\frac{\beta \overline{s}}{(1+\eta \overline{s}){(1+\mu \overline{p})}^2},{\mathcal{P}}_4=\frac{\alpha \overline{s}}{a+\overline{s}}-\frac{b\overline{p}}{1+\mu \overline{p}}-(d+h_2),{\mathcal{P}}_5=\frac{\beta c\overline{p}}{{(1+\eta \overline{s})}^2(1+\mu \overline{p})},{\mathcal{P}}_6=\frac{bc\overline{p}}{1+\mu \overline{p}},{\mathcal{P}}_7=-\delta +\frac{\beta c\overline{s}}{(1+\eta \overline{s}){(1+\mu \overline{p})}^2}.$ Now, the characteristic equation for $J\left(E_3\right)$ is

$({\mathcal{P}}_4-\lambda )({\lambda }^2+{\mathcal{Y}}_{11}\lambda +{\mathcal{Y}}_{12})=0$, where ${\mathcal{Y}}_{11}=-({\mathcal{P}}_1+{\mathcal{P}}_7)\mathrm{and}{\mathcal{Y}}_{12}={\mathcal{P}}_1{\mathcal{P}}_7-{\mathcal{P}}_3{\mathcal{P}}_5.$

In the above characteristic equation, we obtain one if the eigenvalue is ${\mathcal{P}}_4$, which is negative as $d+h_2>\frac{\alpha \overline{s}}{a+\overline{s}}-\left(\frac{b\overline{p}}{1+\mu \overline{p}}\right)$ and the other two eigenvalues should be negative if ${\mathcal{Y}}_{11}>0$ and ${\mathcal{Y}}_{12}>0$. Therefore, $E_3(\overline{s},0,\overline{p})$ is locally asymptotically stable if $d+h_2>\frac{\alpha \overline{s}}{a+\overline{s}}-\left(\frac{b\overline{p}}{1+\mu \overline{p}}\right)$, ${\mathcal{Y}}_{11}>0$, ${\mathcal{Y}}_{12}>0$, otherwise the system (2) will be unstable. □

Theorem 5.

$E^{*}$ is locally asymptotically stable if ${\mathcal{Z}}_1>0$, ${\mathcal{Z}}_3>0$, and ${\mathcal{Z}}_1{\mathcal{Z}}_2-{\mathcal{Z}}_3>0$.

Proof. 

$$J\left(E^{*}\right)=\left[\begin{array}{ccc}{\mathcal{Q}}_{11}& {\mathcal{Q}}_{12}& {\mathcal{Q}}_{13}\\ {\mathcal{Q}}_{21}& {\mathcal{Q}}_{22}& {\mathcal{Q}}_{23}\\ {\mathcal{Q}}_{31}& {\mathcal{Q}}_{32}& {\mathcal{Q}}_{33}\end{array}\right].$$

where, ${\mathcal{Q}}_{11}=-\frac{r{s}^{*}}{1+\rho i^{*}}+\frac{\alpha s^{*}{i}^{*}}{{(a+s^{*})}^2}+\frac{\eta \beta s^{*}{p}^{*}}{{(1+\eta s^{*})}^2(1+\mu p^{*})},{\mathcal{Q}}_{12}=-\frac{r{s}^{*}(1+\rho (1-s^{*}))}{{(1+\rho i^{*})}^2}-\frac{\alpha s^{*}}{a+s^{*}},{\mathcal{Q}}_{13}=-\frac{\beta s^{*}}{(1+\eta s^{*}){(1+\mu p^{*})}^2},{\mathcal{Q}}_{21}=\frac{\alpha a{i}^{*}}{{(a+s^{*})}^2},{\mathcal{Q}}_{22}=\frac{\eta b{i}^{*}{p}^{*}}{{(1+\eta i^{*})}^2(1+\mu p^{*})},{\mathcal{Q}}_{23}=-\frac{b{i}^{*}}{(1+\eta i^{*}){(1+\mu p^{*})}^2},{\mathcal{Q}}_{31}=\frac{\beta c{p}^{*}}{{(1+\eta s^{*})}^2(1+\mu p^{*})},{\mathcal{Q}}_{32}=\frac{bc{p}^{*}}{{(1+\eta i^{*})}^2(1+\mu p^{*})},{\mathcal{Q}}_{33}=-\frac{\mu bc{i}^{*}{p}^{*}}{(1+\eta i^{*}){(1+\mu p^{*})}^2}-\frac{\mu \beta c{s}^{*}{p}^{*}}{(1+\eta s^{*}){(1+\mu p^{*})}^2}.$

The characteristic equation is

$$\begin{array}{cc}\hfill & Z_3+Z_2\lambda +Z_1{\lambda }^2+{\lambda }^3=0.\end{array}$$

(3)

where $Z_1=-({\mathcal{Q}}_{11}+{\mathcal{Q}}_{22}+{\mathcal{Q}}_{33}),Z_2=-({\mathcal{Q}}_{12}{\mathcal{Q}}_{21}+{\mathcal{Q}}_{13}{\mathcal{Q}}_{31}+{\mathcal{Q}}_{23}{\mathcal{Q}}_{32}-{\mathcal{Q}}_{11}{\mathcal{Q}}_{22}-{\mathcal{Q}}_{11}{\mathcal{Q}}_{33}-{\mathcal{Q}}_{22}{\mathcal{Q}}_{33}),Z_3=-({\mathcal{Q}}_{11}{\mathcal{Q}}_{22}{\mathcal{Q}}_{33}+{\mathcal{Q}}_{12}{\mathcal{Q}}_{23}{\mathcal{Q}}_{31}+{\mathcal{Q}}_{13}{\mathcal{Q}}_{21}{\mathcal{Q}}_{32}-{\mathcal{Q}}_{13}{\mathcal{Q}}_{31}{Q}_{22}-Q_{12}{Q}_{21}{\mathcal{Q}}_{33}-{\mathcal{Q}}_{11}{\mathcal{Q}}_{23}{\mathcal{Q}}_{32}).$

According to the Routh–Hurwitz criterion, $Z_1$, $Z_3$, and $Z_1{Z}_2-Z_3$ must all be positive, and the characteristic of all the roots must be negative. Hence, $E^{*}$ is locally asymptotically stable. □

Global Stability Analysis

Theorem 6.

If $E^{*}$ is the endemic equilibrium point is globally asymptotically stable in $G=\{(s,i,p):s>s^{*},i>i^{*}andp>p^{*})ors<s^{*},i<i^{*}andp<p^{*}\}$.

Proof. 

A positive Lyapunov function is defined as ${\displaystyle L_1(s,i,p)=(s-s^{*}-s^{*}ln\frac{s}{s^{*}})+L_2(i-i^{*}-i^{*}ln\frac{i}{i^{*}})+L_3(p-p^{*}-p^{*}ln\frac{p}{p^{*}}),}$ where $L_2,L_3$ are positive constants. Here, $L_1(s,i,p)\ge 0$ since $\psi -1\ge ln\psi$ for $\psi >0$ and $L_1(s^{*},i^{*},p^{*})=0$.

Differentiating $L_1$ with respect to t, we obtain

$$\begin{array}{cc}\hfill \frac{d{L}_1}{dt}=& (\frac{s-s^{*}}{s})\frac{ds}{dt}+L_2(\frac{i-i^{*}}{i})\frac{di}{dt}+L_3(\frac{p-p^{*}}{p})\frac{dp}{dt}\Rightarrow (s-s^{*})[\frac{r(1-s-i)}{1+\rho i}-\frac{\alpha i}{a+s}-\frac{\beta p}{(1+\eta s)(1+\mu p)}-h_1]\hfill \\ \hfill & +(i-i^{*})L_2[\frac{\alpha s}{a+s}-d-h_2-\frac{bp}{(1+\eta i)(1+\mu p)}]+(p-p^{*})L_3[-\delta +\frac{cbi}{(1+\eta i)(1+\mu p)}+\frac{c\beta s}{(1+\eta s)(1+\mu p)}].\hfill \\ \hfill \frac{d{L}_1}{dt}=& -(s-s^{*})[r(\frac{s+i}{1+\rho i}-\frac{s^{*}+i^{*}}{1+\rho i^{*}})+\alpha (\frac{i}{a+s}-\frac{i^{*}}{a+s^{*}})+\beta (\frac{p}{(1+\eta s)(1+\mu p)}-\frac{p^{*}}{(1+\eta s^{*})(1+\mu p^{*})})]\hfill \\ \hfill & -L_2(i-i^{*})[b(\frac{p}{(1+\eta i)(1+\mu p)}-\frac{p^{*}}{(1+\eta i^{*})(1+\mu p^{*})})-\alpha (\frac{s}{a+s}-\frac{s^{*}}{a+s^{*}})]-L_3(p-p^{*})c\hfill \\ \hfill & [b(\frac{\eta \mu (i^{*}p-i^{*}{p}^{*})-\mu (i{p}^{*}-i^{*}p)-(i-i^{*})}{(1+\eta i)(1+\mu p)(1+\eta i^{*})(1+\mu p^{*})})+\beta (\frac{\eta \mu (s^{*}p-s^{*}{p}^{*})-\mu (s{p}^{*}-s^{*}p)-(s-s^{*})}{(1+\eta s)(1+\mu p)(1+\eta s^{*})(1+\mu p^{*})})].\hfill \end{array}$$

Now, we see that $\frac{d{L}_1}{dt}\le 0$. Whenever $G=\{(s,i,p):s>s^{*},i>i^{*}\mathrm{and}p>p^{*})ors<s^{*},i<i^{*}\mathrm{and}p<p^{*}\}$ and Consequently, for all solutions in G, L is a Lyapunov function. □

5. Hopf-Bifurcation Analysis

Theorem 7.

If the critical value for the bifurcation parameter $h_1$ is exceeded, the model (2) will experience the Hopf-bifurcation. The following Hopf-bifurcation requirements are present for $h_1=h_1^{*}$,

1. 

$\mathcal{U}\left(h_1^{*}\right)\mathcal{V}\left(h_1^{*}\right)-\mathcal{W}\left(h_1^{*}\right)=0,$

2. 

$\frac{d}{d{h}_1}\left(Re\left(\mathcal{S}\left(h_1\right)\right)\right){|}_{h_1=h_1^{*}}\ne 0,$ where $\mathcal{S}$ is the zeros of the characteristic equation corresponding to the non-negative equilibrium point.

Proof. 

For $h_1=h_1^{*}$, let the characteristic Equation (3)

$$\begin{array}{ccc}\hfill & \Rightarrow & ({\mathcal{S}}^2\left(h_1^{*}\right)+\mathcal{V}\left(h_1^{*}\right))(\mathcal{S}\left(h_1^{*}\right)+\mathcal{U}\left(h_1^{*}\right))=0.\hfill \end{array}$$

(4)

$$\begin{array}{ccc}& \Rightarrow & \pm i\sqrt{\mathcal{V}\left(h_1^{*}\right)}\mathrm{and}-\mathcal{U}\left(h_1^{*}\right).\hfill \end{array}$$

(5)

The following transversality requirement must be satisfied in order to achieve the Hopf-bifurcation at $h_1^{*}=h_1$. $\frac{d}{d{h}_1}\left(Re\left(\mathcal{S}\left(h_1\right)\right)\right){|}_{h_1=h_1^{*}}\ne 0.$ For every $h_1$, the general roots of the form ${\mathcal{S}}_1\left(h_1\right)=a\left(h_1\right)+ib\left(h_1\right)$, ${\mathcal{S}}_2\left(h_1\right)=a\left(h_1\right)-ib\left(h_1\right),$ and ${\mathcal{S}}_3\left(h_1\right)=-\mathcal{U}\left(h_1\right).$ Now, we check the condition $\frac{d}{d{h}_1}\left(Re\left({\mathcal{S}}_j\left(h_1\right)\right)\right){|}_{h_1=h_1^{*}}\ne 0,j=1,2.$ Let ${\mathcal{S}}_1\left(h_1\right)$= $a\left(h_1\right)+ib\left(h_1\right)$ in (4), we obtain ${\zeta }_1\left(h_1\right)+i{\zeta }_2\left(h_1\right)=0$, where ${\zeta }_1\left(h_1\right)=a^3\left(h_1\right)+a^2\left(h_1\right)\mathcal{U}\left(h_1\right)-3a\left(h_1\right)b^2\left(h_1\right)-b^2\left(h_1\right)\mathcal{U}\left(h_1\right)+a\left(h_1\right)\mathcal{V}\left(h_1\right)+\mathcal{U}\left(h_1\right)\mathcal{V}\left(h_1\right),{\zeta }_2\left(h_1\right)=3a^2\left(h_1\right)b\left(h_1\right)+2a\left(h_1\right)b\left(h_1\right)\mathcal{U}\left(h_1\right)-b^3\left(h_1\right)+b\left(h_1\right)\mathcal{V}\left(h_1\right).$

$$\begin{array}{cc}\hfill & \frac{d{\zeta }_1}{d{h}_1}={\mathsf{\Psi }}_1\left(h_1\right)a^{\prime }\left(h_1\right)-{\mathsf{\Psi }}_2\left(h_1\right)b^{\prime }\left(h_1\right)+{\mathsf{\Psi }}_3\left(h_1\right)=0,\end{array}$$

(6)

$$\begin{array}{cc}\hfill & \frac{d{\zeta }_2}{d{h}_1}={\mathsf{\Psi }}_2\left(h_1\right)a^{\prime }\left(h_1\right)+{\mathsf{\Psi }}_1\left(h_1\right)b^{\prime }\left(h_1\right)+{\mathsf{\Psi }}_4\left(h_1\right)=0,\end{array}$$

(7)

where ${\mathsf{\Psi }}_1\left(h_1\right)=3a^2\left(h_1\right)+2a\left(h_1\right)\mathcal{U}\left(h_1\right)-3b^2\left(h_1\right)+\mathcal{V}\left(h_1\right),{\mathsf{\Psi }}_2\left(h_1\right)=6a\left(h_1\right)b\left(h_1\right)+2b\left(h_1\right)\mathcal{U}\left(h_1\right),{\mathsf{\Psi }}_3\left(h_1\right)=a^2\left(h_1\right){\mathcal{U}}^{\prime }\left(h_1\right)-b^2\left(h_1\right){\mathcal{U}}^{\prime }\left(h_1\right)+{\mathcal{W}}^{\prime }\left(h_1\right)+{\mathcal{V}}^{\prime }\left(h_1\right)a\left(h_1\right),{\mathsf{\Psi }}_4\left(h_1\right)=2a\left(h_1\right)b\left(h_1\right){\mathcal{U}}^{\prime }\left(h_1\right)+b\left(h_1\right){\mathcal{V}}^{\prime }\left(h_1\right).$ By multiplying (6) and (7) in ${\mathsf{\Psi }}_1\left(h_1\right)$ and ${\mathsf{\Psi }}_2\left(h_1\right)$, respectively,

$$\begin{array}{cc}\hfill & a^{\prime }\left(h_1\right)=-\frac{{\mathsf{\Psi }}_1\left(h_1\right){\mathsf{\Psi }}_3\left(h_1\right)+{\mathsf{\Psi }}_2\left(h_1\right){\mathsf{\Psi }}_4\left(h_1\right)}{{\mathsf{\Psi }}_1^2\left(h_1\right)+{\mathsf{\Psi }}_2^2\left(h_1\right)}.\end{array}$$

(8)

Substituting $a\left(h_1\right)=0$ and $b\left(h_1\right)=\sqrt{\mathcal{V}\left(h_1\right)}$ at $h_1=h_1^{*}$ on ${\mathsf{\Psi }}_1\left(h_1\right),{\mathsf{\Psi }}_2\left(h_1\right),{\mathsf{\Psi }}_3\left(h_1\right)$ and ${\mathsf{\Psi }}_4\left(h_1\right)$ we obtain ${\mathsf{\Psi }}_1\left(h_1^{*}\right)=-2\mathcal{V}\left(h_1^{*}\right),{\mathsf{\Psi }}_2\left(h_1^{*}\right)=2\sqrt{\mathcal{V}\left(h_1^{*}\right)}\mathcal{U}\left(h_1^{*}\right),{\mathsf{\Psi }}_3\left(h_1^{*}\right)=-\mathcal{V}\left(h_1^{*}\right){\mathcal{U}}^{\prime }\left(h_1^{*}\right)+{\mathcal{W}}^{\prime }\left(h_1^{*}\right),{\mathsf{\Psi }}_4\left(h_1^{*}\right)=\sqrt{\mathcal{V}\left(h_1^{*}\right)}{\mathcal{V}}^{\prime }\left(h_1^{*}\right).$ Equation (8), implies

$$\begin{array}{cc}\hfill & a^{\prime }\left(h_1^{*}\right)=\frac{{\mathcal{W}}^{\prime }\left(h_1^{*}\right)-(\mathcal{U}\left(h_1^{*}\right){\mathcal{V}}^{\prime }\left(h_1^{*}\right)+\mathcal{V}\left(h_1^{*}\right){\mathcal{U}}^{\prime }\left(h_1^{*}\right))}{2({\mathcal{V}}^2\left(h_1^{*}\right)+{\mathcal{U}}^2\left(h_1^{*}\right))},\end{array}$$

(9)

if ${\mathcal{W}}^{\prime }\left(h_1^{*}\right)-(\mathcal{U}\left(h_1^{*}\right){\mathcal{V}}^{\prime }\left(h_1^{*}\right)+\mathcal{V}\left(h_1^{*}\right){\mathcal{U}}^{\prime }{h}_1^{*}))\ne 0,$ which implies that $\frac{d}{d{h}_1}\left(Re\left({\mathcal{S}}_j\left(h_1\right)\right)\right){|}_{h_1=h_1^{*}}=a^{\prime }\left(h_1^{*}\right)\ne 0.$$j=1,2,$ and ${\mathcal{S}}_3\left(h_1^{*}\right)=-\mathcal{U}\left(h_1^{*}\right)\ne 0$. If ${\mathcal{W}}^{\prime }\left(h_1^{*}\right)-(\mathcal{U}\left(h_1^{*}\right){\mathcal{V}}^{\prime }\left(h_1^{*}\right)+\mathcal{V}\left(h_1^{*}\right){\mathcal{U}}^{\prime }\left(h_1^{*}\right))\ne 0$, is ensured if the transversality criterion holds, and at this point, the model (2) enters the Hopf-bifurcation at $h_1=h_1^{*}.$ □

6. Numerical Analysis

We show some numerical simulations of the model (2) in this section. To accomplish this, we use Diethelm et al.’s predictor–corrector approach to solve the proposed model. The system (2) parameter values are $r=2,\alpha =0.7,a=0.6,\beta =0.2,\eta =0.1,\mu =0.1,d=0.1,b=0.55,h_2=0.1,\delta =0.1,c=0.5,\rho =0.2,h_1=0.08$. From Theorem 5, the positive equilibrium point $E^{*}(0.698622,0.13125,0.336204)$ exists for $0.01<h_1<0.3$, and is locally asymptotically stable.

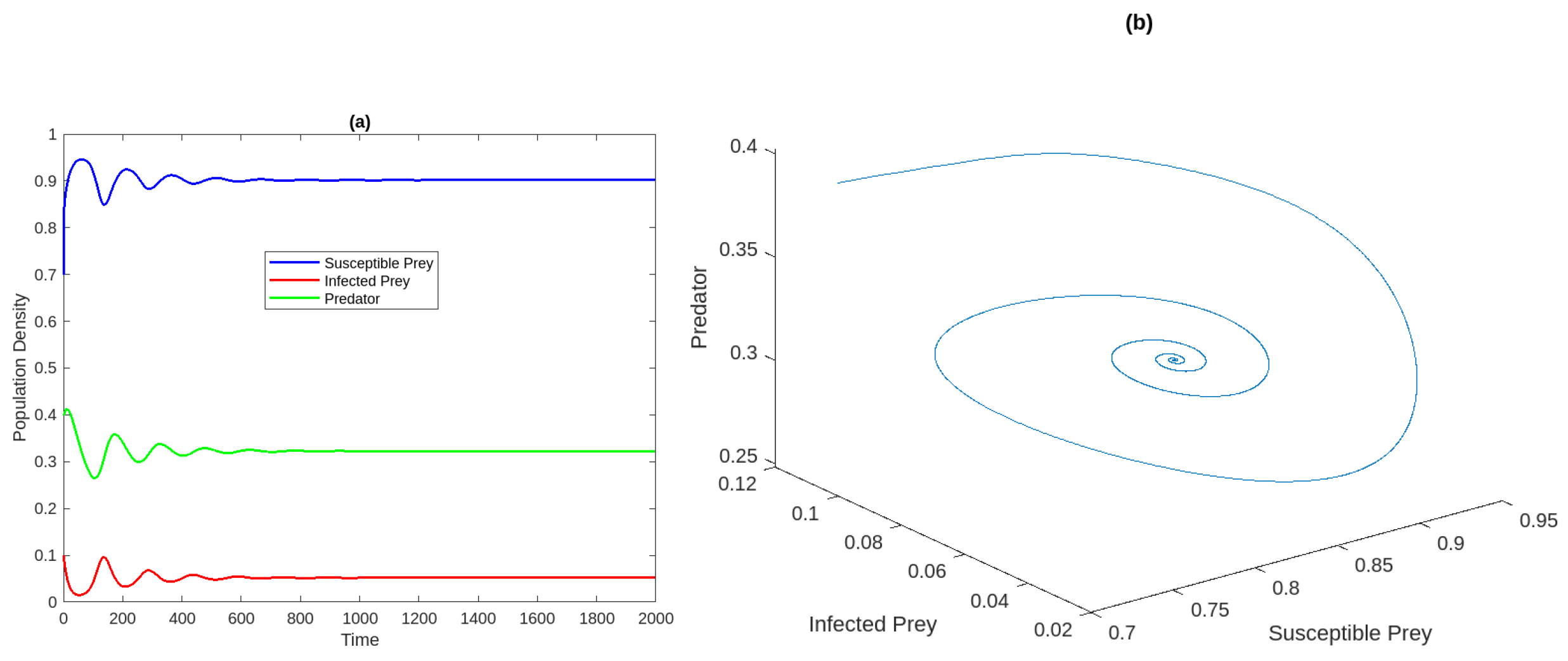
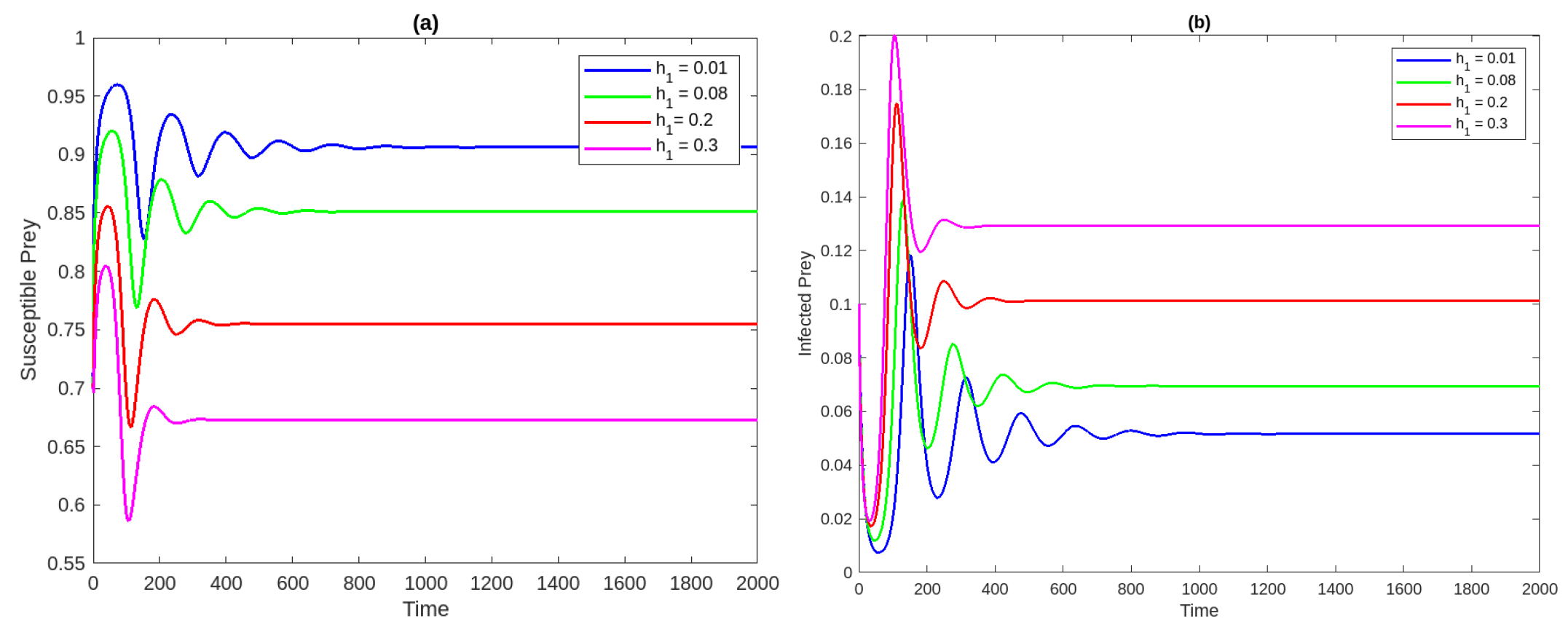
Figure 1a Time analysis for the system (2) for $h_1=0.08$. Figure 1b Phase portrait of the system at $E^{*}$. Figure 2a,b Susceptible and infected prey populations with different values for $h_1=0.01,0.08,0.2,0.3.$ It shows that increasing the harvesting rate of susceptible prey leads to a decrease in the population of vulnerable prey and predators while increasing the population of diseased prey.

Figure 1. (a) Time analysis for the system (2) for $h_1=0.08$. (b) Phase diagram of the model system $E^{*}$.

Figure 2. The population concentrations of susceptible prey (a) and infected prey (b) populations with different values for $h_1=0.01,0.08,0.2,0.3.$

7. Conclusions

We investigated a three-species food-web model that involved the use of the interactions between diseased prey–predator model. The local and global stability of (2) is used for each set of biologically possible equilibrium points in the model. It is used to modify the harvesting rate $\left(h_1\right)$ and the level of fear $\left(\rho \right)$ as control parameters. In addition, we investigated the stability analysis of the model (2) and studied the Hopf-bifurcation phenomenon. As a result, we found that modifying the harvesting rate $h_1$ significantly affects the stability of the system (2). The analytical and numerical findings demonstrate that the harvesting rate has a significant impact on every population. A decrease in the population of susceptible prey and an increase in infected prey population density are the effects of increasing the harvesting rate. This study shows the complex behavior of the proposed model.