Towards Resolving the Ambiguity in Low-Field, All-Optical Magnetic Field Sensing with High NV-Density Diamonds †
Abstract
:1. All-Optical Magnetic Field Sensing with NV Centers
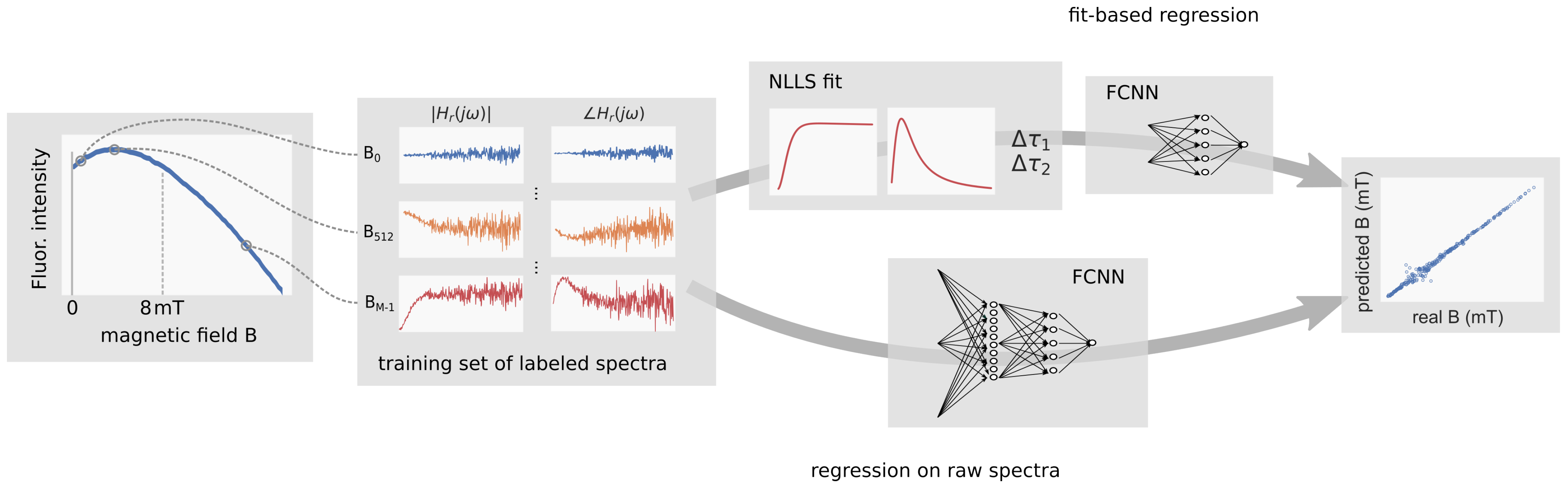
2. Materials and Methods
2.1. Frequency Domain Measurement Setup
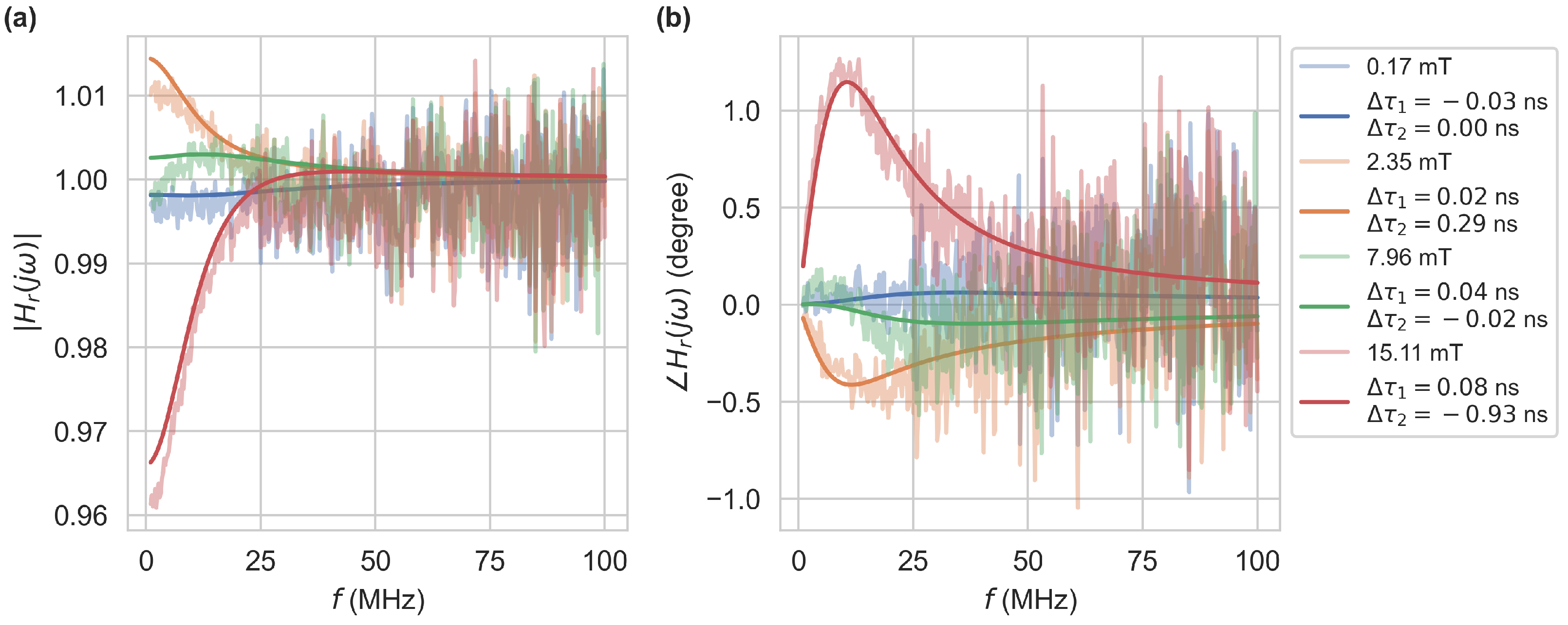
2.2. Fit-Based Regression
2.3. Regression on Raw Spectra
3. Results and Discussion
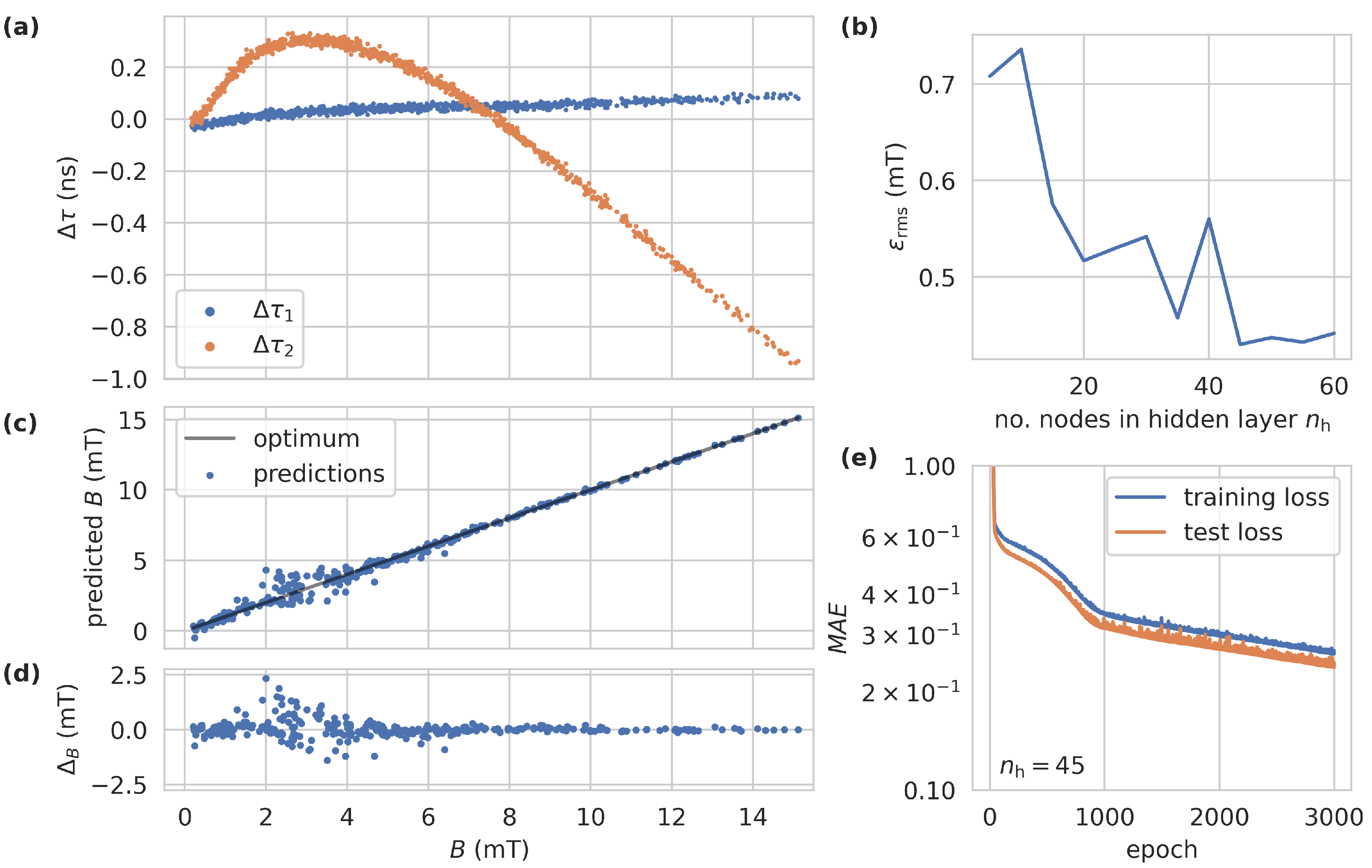
3.1. Fit-Based Regression
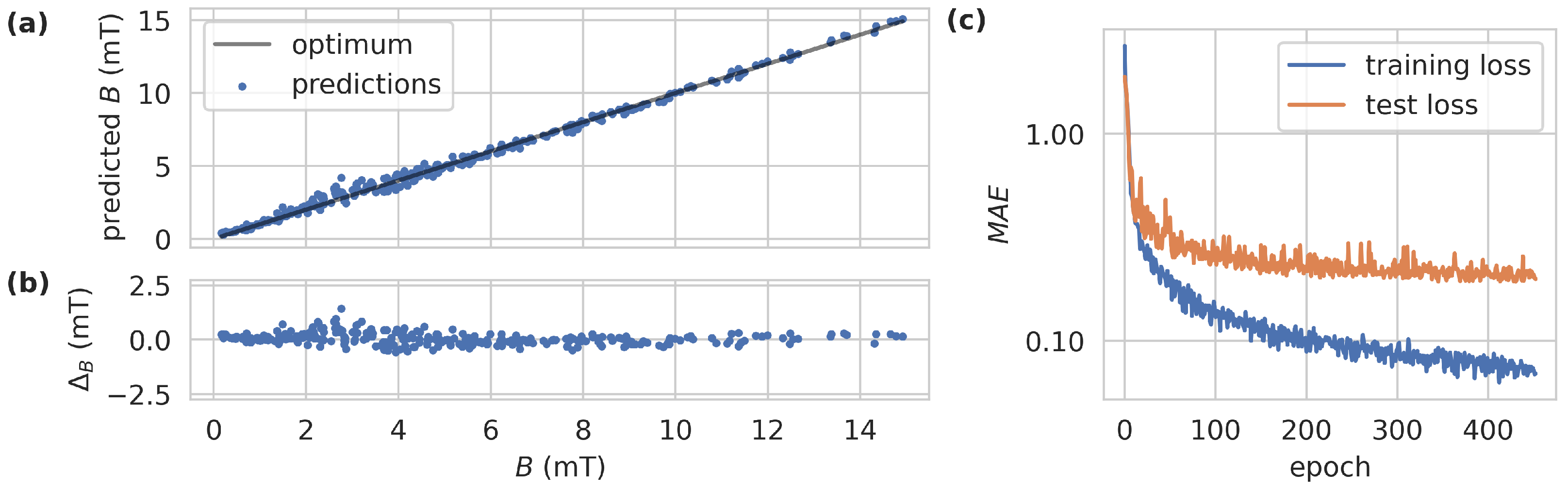
3.2. Regression on Raw Spectra
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NV | Nitrogen vacancy |
| MW | Microwave |
| NLLS | Non-linear least squares |
| VNA | Vector network analyzer |
| FCNN | Fully connected neural network |
| ReLU | Rectified linear unit |
| RMS | Root-mean-square |
| MAE | Mean average error |
References
- Fedotov, I.; Amitonova, L.; Sidorov-Biryukov, D.; Safronov, N.; Blakley, S.; Levchenko, A.; Zibrov, S.; Fedotov, A.; Kilin, S.; Scully, M.; et al. Fiber-optic magnetic-field imaging. Opt. Lett. 2014, 39, 6954–6957. [Google Scholar] [CrossRef] [PubMed]
- Duan, D.; Du, G.X.; Kavatamane, V.K.; Arumugam, S.; Tzeng, Y.K.; Chang, H.C.; Balasubramanian, G. Efficient nitrogen-vacancy centers’ fluorescence excitation and collection from micrometer-sized diamond by a tapered optical fiber in endoscope-type configuration. Opt. Express 2019, 27, 6734. [Google Scholar] [CrossRef] [PubMed]
- Chatzidrosos, G.; Rebeirro, J.S.; Zheng, H.; Omar, M.; Brenneis, A.; Stürner, F.M.; Fuchs, T.; Buck, T.; Rölver, R.; Schneemann, T.; et al. Fiberized Diamond-Based Vector Magnetometers. Front. Photonics 2021, 2, 732748. [Google Scholar] [CrossRef]
- Wunderlich, R.; Staacke, R.; Knolle, W.; Abel, B.; Meijer, J. Magnetic field and angle-dependent photoluminescence of a fiber-coupled nitrogen vacancy rich diamond. J. Appl. Phys. 2021, 130, 124901. [Google Scholar] [CrossRef]
- Wickenbrock, A.; Zheng, H.; Bougas, L.; Leefer, N.; Afach, S.; Jarmola, A.; Acosta, V.M.; Budker, D. Microwave-free magnetometry with nitrogen-vacancy centers in diamond. Appl. Phys. Lett. 2016, 109, 053505. [Google Scholar] [CrossRef]
- Zheng, H.; Chatzidrosos, G.; Wickenbrock, A.; Bougas, L.; Lazda, R.; Berzins, A.; Gahbauer, F.H.; Auzinsh, M.; Ferber, R.; Budker, D. Level anti-crossing magnetometry with color centers in diamond. arXiv 2017, arXiv:701.06838. [Google Scholar] [CrossRef]
- Zheng, H.; Sun, Z.; Chatzidrosos, G.; Zhang, C.; Nakamura, K.; Sumiya, H.; Ohshima, T.; Isoya, J.; Wrachtrup, J.; Wickenbrock, A.; et al. Microwave-Free Vector Magnetometry with Nitrogen-Vacancy Centers along a Single Axis in Diamond. Phys. Rev. Appl. 2020, 13, 044023. [Google Scholar] [CrossRef]
- Staacke, R.; John, R.; Wunderlich, R.; Horsthemke, L.; Knolle, W.; Laube, C.; Glösekötter, P.; Burchard, B.; Abel, B.; Meijer, J. Isotropic Scalar Quantum Sensing of Magnetic Fields for Industrial Application. Adv. Quantum Technol. 2020, 3, 2000037. [Google Scholar] [CrossRef]
- Horsthemke, L.; Pogorzelski, J.; Stiegekötter, D.; Hoffmann, F.; Langguth, L.; Staacke, R.; Laube, C.; Knolle, W.; Gregor, M.; Glösekötter, P. Excited-State Lifetime of NV Centers for All-Optical Magnetic Field Sensing. Sensors 2024, 24, 2093. [Google Scholar] [CrossRef] [PubMed]
- Lakowicz, J.R. Principles of Fluorescence Spectroscopy, 3rd ed.; corrected at 4. printing ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Lai, N.D.; Zheng, D.; Jelezko, F.; Treussart, F.; Roch, J.F. Influence of a static magnetic field on the photoluminescence of an ensemble of nitrogen-vacancy color centers in a diamond single-crystal. Appl. Phys. Lett. 2009, 95, 133101. [Google Scholar] [CrossRef]
- Tetienne, J.P.; Rondin, L.; Spinicelli, P.; Chipaux, M.; Debuisschert, T.; Roch, J.F.; Jacques, V. Magnetic-field-dependent photodynamics of single NV defects in diamond: An application to qualitative all-optical magnetic imaging. New J. Phys. 2012, 14, 103033. [Google Scholar] [CrossRef]
- Anishchik, S.V.; Vins, V.G.; Yelisseyev, A.P.; Lukzen, N.N.; Lavrik, N.L.; Bagryansky, V.A. Low-field feature in the magnetic spectra of N-V centers in diamond. New J. Phys. 2015, 17, 023040. [Google Scholar] [CrossRef]
- Akhmedzhanov, R.; Gushchin, L.; Nizov, N.; Nizov, V.; Sobgayda, D.; Zelensky, I.; Hemmer, P. Microwave-free magnetometry based on cross-relaxation resonances in diamond nitrogen-vacancy centers. Phys. Rev. A 2017, 96, 013806. [Google Scholar] [CrossRef]
- Sun, H.; Huang, S.; Peng, L. High-Current Sensing Technology for Transparent Power Grids: A Review. IEEE Open J. Ind. Electron. Soc. 2024, 5, 326–358. [Google Scholar] [CrossRef]
- Wee, T.L.; Tzeng, Y.K.; Han, C.C.; Chang, H.C.; Fann, W.; Hsu, J.H.; Chen, K.M.; Yu, Y.C. Two-photon Excited Fluorescence of Nitrogen-Vacancy Centers in Proton-Irradiated Type Ib Diamond. J. Phys. Chem. A 2007, 111, 9379–9386. [Google Scholar] [CrossRef] [PubMed]
- Magaletti, S.; Mayer, L.; Roch, J.F.; Debuisschert, T. A quantum radio frequency signal analyzer based on nitrogen vacancy centers in diamond. Commun. Eng. 2022, 1, 19. [Google Scholar] [CrossRef]
- Homrighausen, J.; Horsthemke, L.; Pogorzelski, J.; Trinschek, S.; Glösekötter, P.; Gregor, M. Edge-Machine-Learning-Assisted Robust Magnetometer Based on Randomly Oriented NV-Ensembles in Diamond. Sensors 2023, 23, 1119. [Google Scholar] [CrossRef] [PubMed]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. arXiv 2015, arXiv:1603.04467. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Horsthemke, L.; Pogorzelski, J.; Stiegekötter, D.; Hoffmann, F.; Bülter, A.-S.; Trinschek, S.; Gregor, M.; Glösekötter, P. Towards Resolving the Ambiguity in Low-Field, All-Optical Magnetic Field Sensing with High NV-Density Diamonds. Eng. Proc. 2024, 68, 8. https://doi.org/10.3390/engproc2024068008
Horsthemke L, Pogorzelski J, Stiegekötter D, Hoffmann F, Bülter A-S, Trinschek S, Gregor M, Glösekötter P. Towards Resolving the Ambiguity in Low-Field, All-Optical Magnetic Field Sensing with High NV-Density Diamonds. Engineering Proceedings. 2024; 68(1):8. https://doi.org/10.3390/engproc2024068008
Chicago/Turabian StyleHorsthemke, Ludwig, Jens Pogorzelski, Dennis Stiegekötter, Frederik Hoffmann, Ann-Sophie Bülter, Sarah Trinschek, Markus Gregor, and Peter Glösekötter. 2024. "Towards Resolving the Ambiguity in Low-Field, All-Optical Magnetic Field Sensing with High NV-Density Diamonds" Engineering Proceedings 68, no. 1: 8. https://doi.org/10.3390/engproc2024068008
APA StyleHorsthemke, L., Pogorzelski, J., Stiegekötter, D., Hoffmann, F., Bülter, A.-S., Trinschek, S., Gregor, M., & Glösekötter, P. (2024). Towards Resolving the Ambiguity in Low-Field, All-Optical Magnetic Field Sensing with High NV-Density Diamonds. Engineering Proceedings, 68(1), 8. https://doi.org/10.3390/engproc2024068008






