Hydraulic Transient Data Assimilation in Pipe Networks Using the Kalman Filter ^†

Abstract

Hydraulic transient data assimilation in pipe networks plays a critical role in monitoring the network’s behaviours, thereby ensuring the efficiency and reliability of water supply systems. However, the existing Kalman filter-based methods integrated with traditional numerical models face a severe computational burden with a significant number of state variables due to the need to discretise pipes into multiple pipe segments. This paper presents a novel Kalman filter approach that implements an efficient hydraulic transient model that requires fewer pipe segments and is particularly suited when the frequency of the transient fluctuation is low. As the number of state variables is reduced, a faster estimation of the system hydraulic states is enabled, as is an enhanced accuracy of transient predictions. The proposed method was tested in two pipe network simulations with user demands: a 7-pipe network and a 51-pipe network. The results indicate that the method provides accurate transient predictions and robust estimation of transient states in real time, and has high performance and efficiency for large pipe networks.

1. Introduction

The modern management of water supply systems is increasingly dependent on the ability to accurately monitor and control the flow and pressure of water throughout the distribution network [1].

In recent years, hydraulic transient data assimilation has emerged as a vital tool, leveraging the power of real-time data and advanced modelling techniques to offer a more nuanced understanding and control of water distribution processes [2,3,4]. Despite its apparent benefits, the current implementation of transient data assimilation in water supply systems is significantly limited by the requirements of robust hydraulic models, advanced data assimilation techniques, and sufficient computational resources available for real-time processing and analysis.

This study introduces an innovative approach for real-time pressure and flow data assimilation within pipe networks, leveraging the extended Kalman filter (EKF) and the elastic water column (EWC) model. By integrating real-time data assimilation with advanced hydraulic modelling, the proposed approach provides a robust, computationally efficient solution capable of accurately predicting transient pressure and flow data in real time, offering a promising tool for improving the resilience and efficiency of water distribution systems.

2. Hydraulic Transient Data Assimilation

2.1. Elastic Water Column (EWC) Model

Assuming the flow is one-dimensional and slightly compressible in a pressurized pipe having linear elastic walls, the EWC model converts the continuity and momentum equations into a set of ordinary differential equations (ODEs). The final governing equations for hydraulic transients in pipe networks are presented in Equation (1), and a detailed mathematical derivation has been given in [5]:

$$\left\{\begin{array}{c}{\displaystyle \frac{d\mathbf{q}}{dt}}=-{\mathbf{L}}^{-1}\mathbf{R}\left|\mathbf{q}\right|\mathbf{q}+{\mathbf{L}}^{-1}{\mathbf{A}}_I^T{\mathbf{h}}_I+{\mathbf{L}}^{-1}{\mathbf{A}}_R^T{\mathbf{h}}_R\\ {\displaystyle \frac{d{\mathbf{h}}_I}{dt}}=\left({\displaystyle \frac{1}{2}}\left|{\mathbf{A}}_I\right|\mathbf{C}{)}^{-1}\right({\mathbf{A}}_I\mathbf{q}-{\mathit{D}}_{\mathit{I}}\sqrt{{\mathbf{h}}_I})\end{array}\right.$$

(1)

2.2. Extend Kalman Filter (EKF) for Pressure and Flow Prediction

The EKF is implemented for the direct estimation of transient pressure and flow in this paper. Unlike the standard Kalman filter, which is designed for systems with linear equations, the EKF is capable of handling nonlinearities in both the process and measurement models.

Defining the transient state space $\widehat{\mathbf{X}}$ = [${\widehat{\mathbf{q}}}^T$, ${\widehat{\mathbf{h}}}_{\mathit{I}}^{\mathit{T}}$]^T, the system equations (Equation (1)) can be simplified as follows:

$$d\mathbf{X}/dt=\mathbf{M}·\mathbf{X}+\mathbf{B}$$

(2)

in which $\mathbf{M}$ is a matrix involving parameters L, R, C, and A, and B is a matrix involving demands and reservoir levels.

The EKF process involves two main steps: prediction and update.

• Prediction step

This step estimates the transient state space in the next time step k by linearizing the nonlinear EWC model (Equation (1)) around the current estimate:

$${\mathbf{X}}_{\mathit{k}}={\displaystyle \frac{\left(\mathbf{I}+0.5∆t·\mathbf{M}\right)}{\left(\mathbf{I}-0.5∆t·\mathbf{M}\right)}}·{\mathbf{X}}_{\mathit{k}-1}+{\displaystyle \frac{∆t·\mathbf{B}}{\left(\mathbf{I}-0.5∆t·\mathbf{M}\right)}}$$

(3)

Simplifying Equation (3) yields:

$${\mathbf{X}}_{\mathit{k}}^{-}={\mathbf{F}}_{\mathit{k}}·{\widehat{\mathbf{X}}}_{\mathit{k}-1}+{\mathbf{G}}_{\mathit{k}}$$

(4)

where ${\mathbf{F}}_{\mathit{k}}$ is the transfer matrix of the linearized system equations using the second-order Taylor series expansion; ${\mathbf{G}}_{\mathit{k}}$ is the external inference (e.g., demand change). The error covariance ${\widehat{\mathbf{P}}}_{\mathit{k}}$ is also estimated as follows:

$${\mathbf{P}}_{\mathit{k}}^{-}={\mathbf{F}}_{\mathit{k}}·{\mathbf{P}}_{\mathit{k}-1}·{\mathbf{F}}_{\mathit{k}}^{\mathit{T}}+{\mathbf{Q}}_{\mathit{k}}$$

(5)

where ${\mathbf{Q}}_{\mathit{k}}$ is the process noise covariance and is set to zero in the numerical cases.

• Update step

The update step calculates the Kalman gain ${\mathbf{K}}_{\mathit{k}}$ first, which determines how much the predictions should be adjusted based on the measurements and noise levels:

$${\mathbf{K}}_{\mathit{k}}={\mathbf{P}}_{\mathit{k}}^{-}{\mathbf{H}}_{\mathit{k}}^{\mathit{T}}{({\mathbf{H}}_{\mathit{k}}{\mathbf{P}}_{\mathit{k}}^{-}{\mathbf{H}}_{\mathit{k}}^{\mathit{T}}+\mathbf{R})}^{-1}$$

(6)

where ${\mathbf{H}}_{\mathit{k}}$ is the observation matrix and $\mathbf{R}$ is the measurement noise covariance. Once new measurements ${\mathit{z}}_{\mathit{k}}$ are available, the EKF updates its estimates and the corresponding error covariance to reflect the new information:

$${\widehat{\mathbf{X}}}_{\mathit{k}}={\widehat{\mathit{x}}}_{\mathit{k}}^{-}+{\mathbf{K}}_{\mathit{k}}({\mathit{z}}_{\mathit{k}}-{\mathbf{H}}_{\mathit{k}}{\mathbf{X}}_{\mathit{k}}^{-})$$

(7)

$${\mathbf{P}}_{\mathit{k}}=(\mathit{I}-{\mathbf{K}}_{\mathit{k}}{\mathbf{H}}_{\mathit{k}}){\mathbf{P}}_{\mathit{k}}^{-}$$

(8)

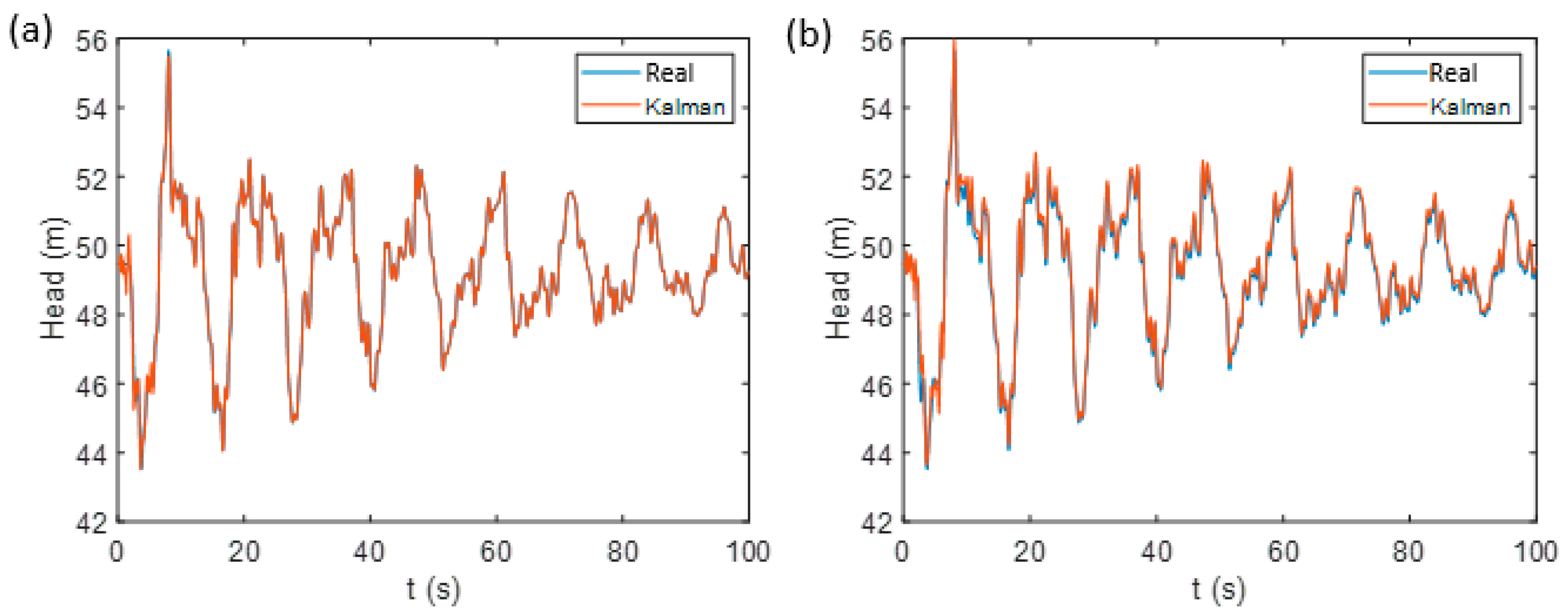
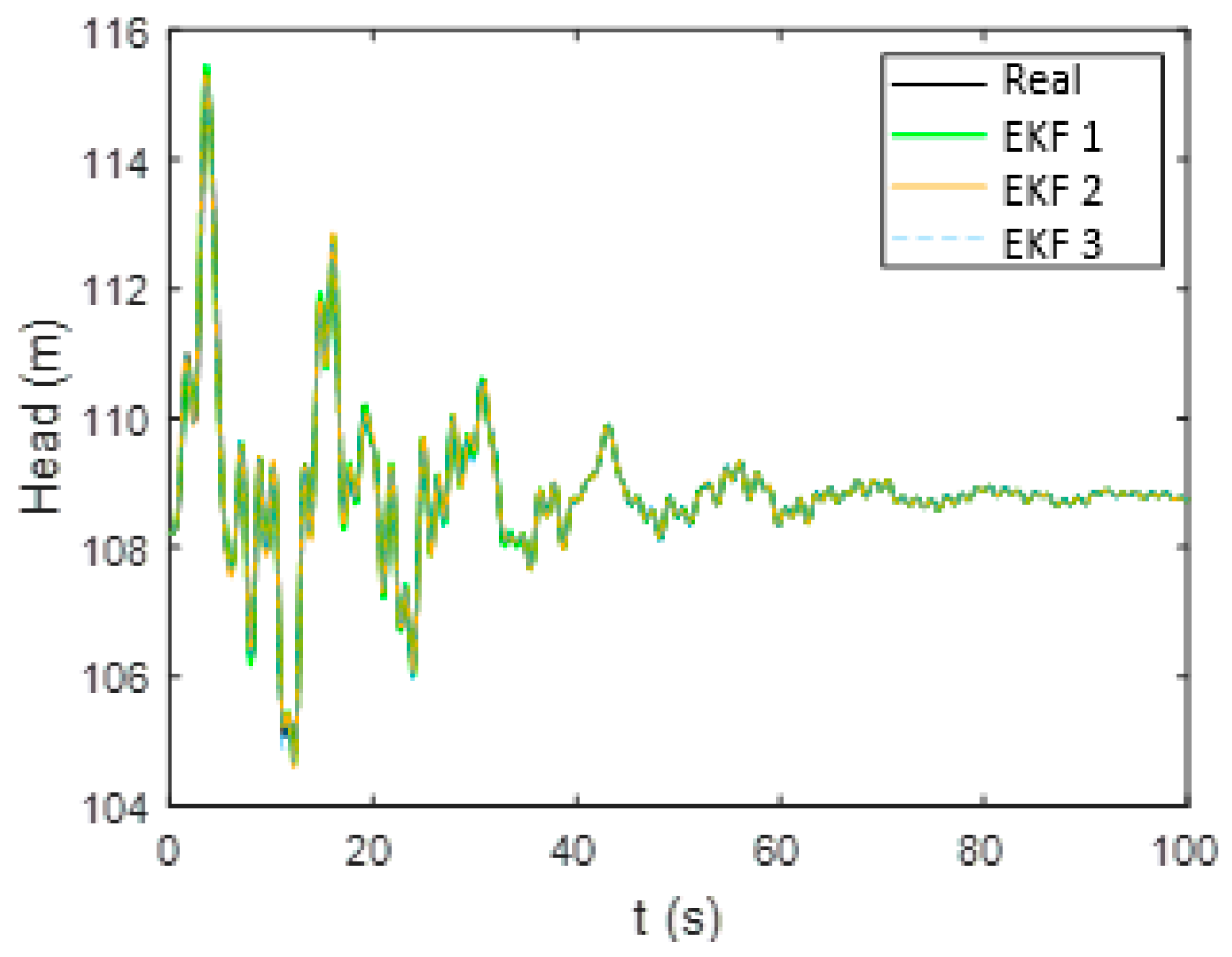
3. Transient Data Assimilation: 7-Pipe Network

The accuracy and applicability of the proposed EKF-based transient data assimilation were evaluated through numerical tests on a simple seven-pipe network shown in Figure 1. This pipe network consists of two reservoirs, seven pipes, five internal nodes, and one demand node. The diameter of each pipe was assumed to be D = 0.2 m; the pipe length is 1000 m; the wave speed is a = 1000 m/s; the Darcy–Weisbach factor is f = 0.02; and the water level of the upstream reservoir and downstream reservoirs are H_up = 50 m and H_down = 48 m, respectively. Two pressure sensors are placed at Node 1 and Node 2, respectively.

A transient event was generated by increasing the demand flow from 0 to 3 L/s in 0.5 s following a cos curve. Assuming the demand flow to be (a) Case 1.1 (from 0 to 3 L/s suddenly) or (b) Case 1.2 (zero), two EWC models were integrated into EKFs separately. Both Kalman filters with different assumptions of demand flow accurately predicted the pressure head at Node 5 (see Figure 2), indicating its ability to provide accurate real-time transient state estimation, even when subjected to sudden changes in demand.

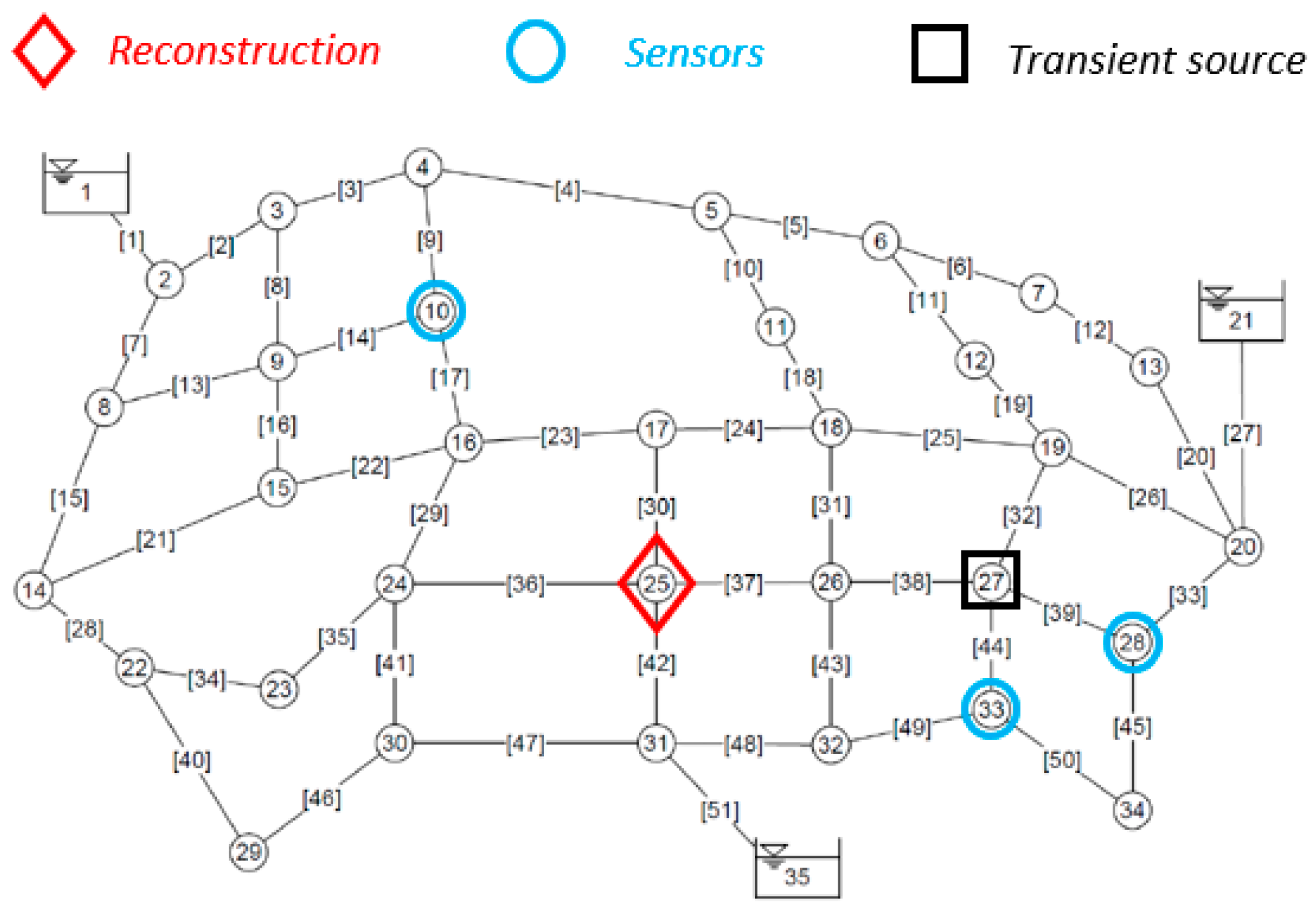
4. Transient Data Assimilation: 51-Pipe Network

A larger-scale pipe network that contains 51 pipes is analysed. The pipe configuration shown in Figure 3 was employed for hydraulic transient modelling. The wave speed of all the pipes is assumed as 1000 m/s. The range of network parameters are [450, 994] m for the pipe lengths, [304.8, 1524] mm for the pipe diameters, and [0, 280] L/s for the nodal demands. Details of the network can be found in [6].

The transient is excited by halving the demand at Node 27 smoothly within a short time of Tv = 0.2 s. Three EKFs were performed with different random seeds. In Figure 4, the predicted heads at Node 25 for all three EKFs followed the ‘real’ hydraulic head values quite closely. The small discrepancies between the EKF estimations and the “real” measurements indicate the effectiveness and robustness of the proposed EKF-based approach.

5. Conclusions

The proposed approach integrated the EWC model into the EKF to estimate the transient state (pressure and flow) in pipe networks. The study’s outcomes demonstrated that the proposed method is capable of providing accurate, real-time transient state estimations, within both simple and complex pipe networks. A direction for further work is to validate the model’s applicability for real-world water distribution systems.