The Dual Model under Pressure: How Robust Is Leak Detection under Uncertainties and Model Mismatches? †
Abstract
1. Introduction
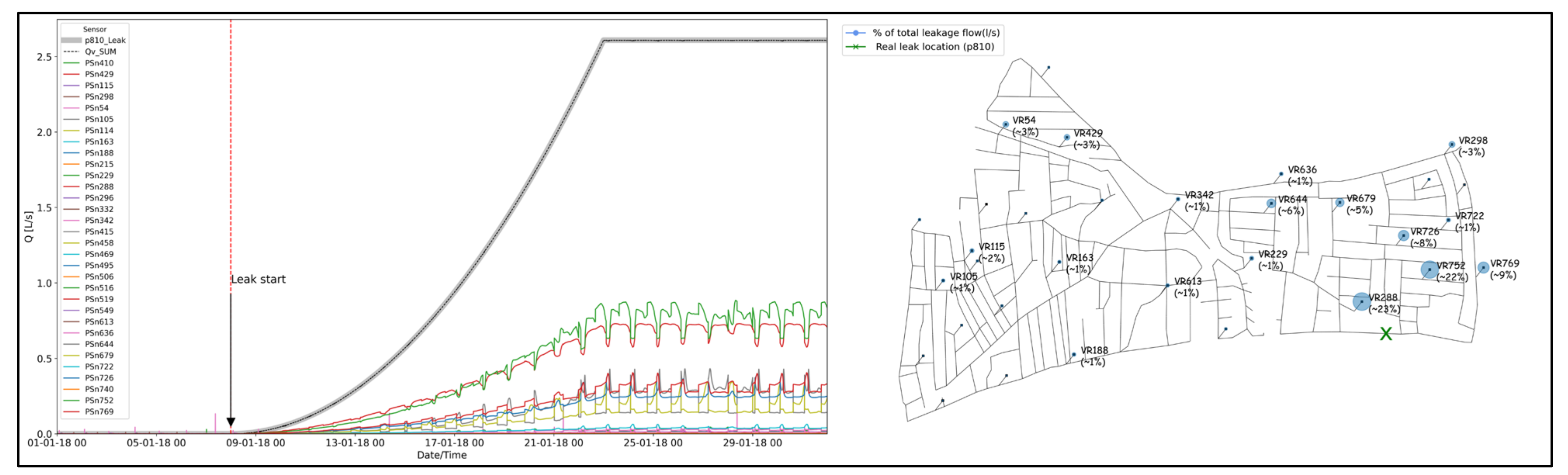
2. Methodology
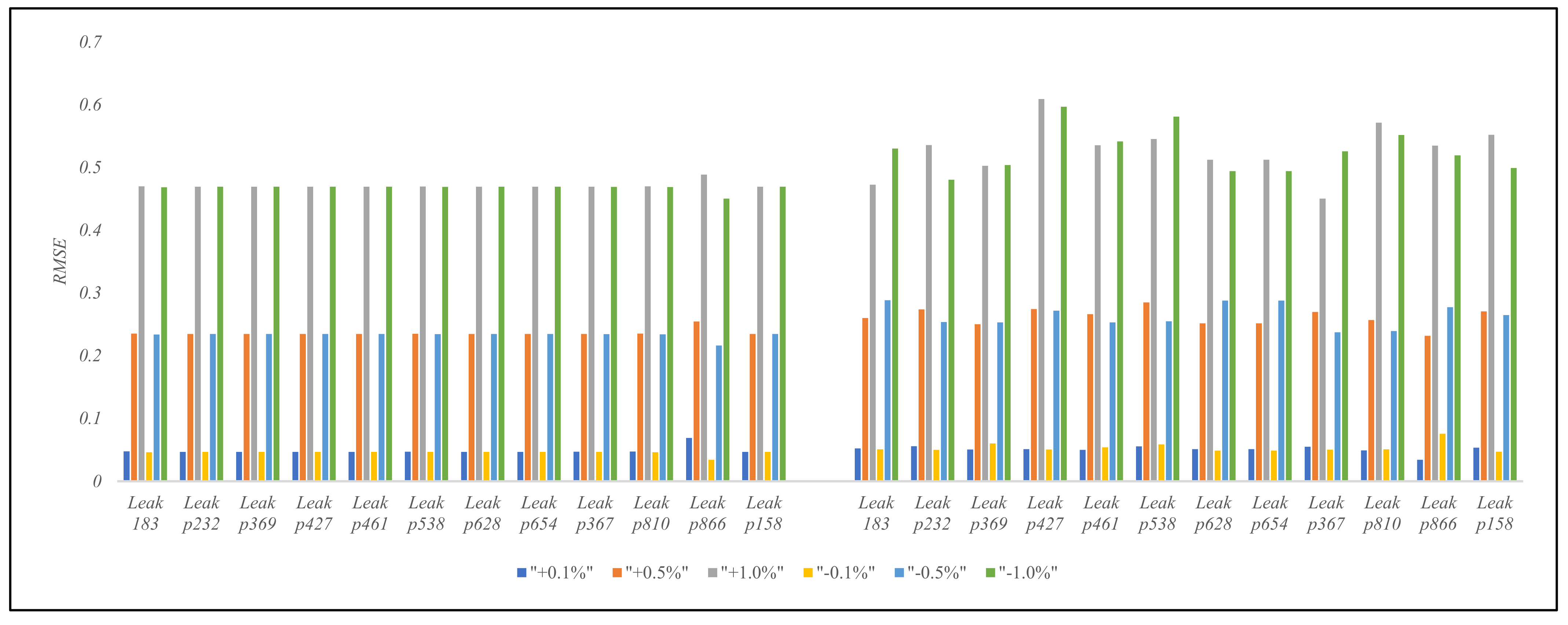
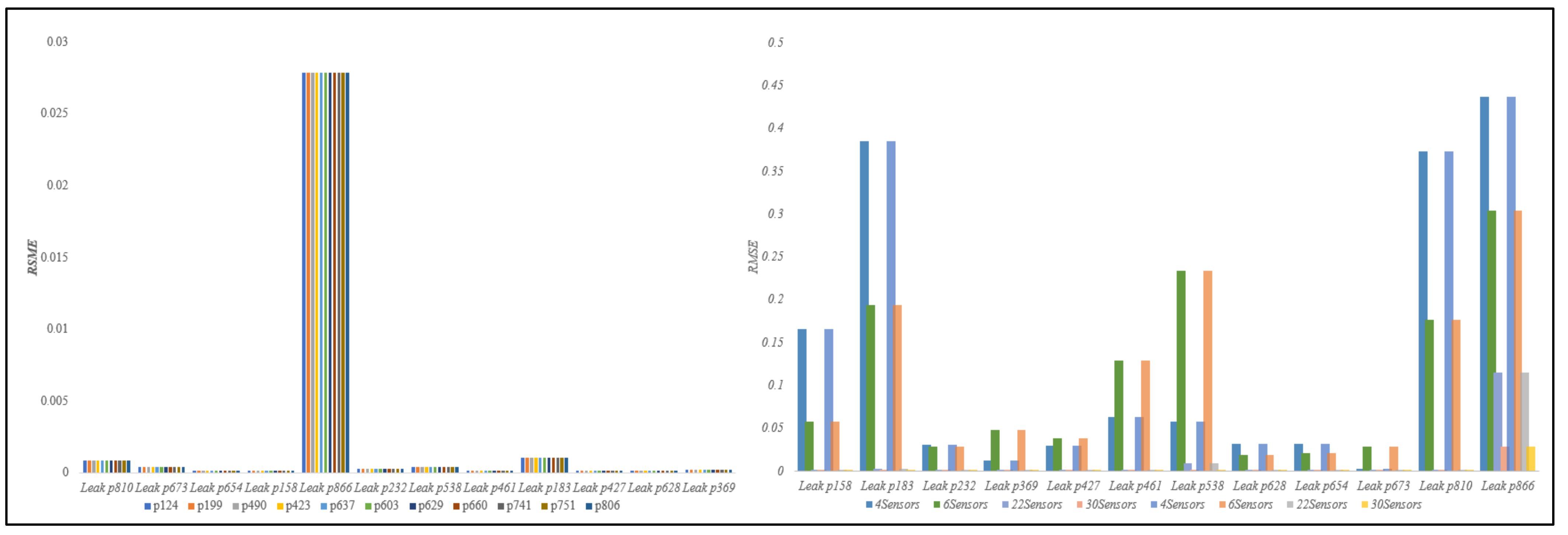
Perturbations in the Dual Model
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Steffelbauer, D.B.; Deuerlein, J.; Gilbert, D.; Abraham, E.; Piller, O. Pressure-Leak Duality for Leak Detection and Localization in Water Distribution Systems. J. Water Resour. Plan. Manag. 2022, 148, 04021106. [Google Scholar] [CrossRef]
- Vrachimis, S.G.; Eliades, D.G.; Taormina, R.; Kapelan, Z.; Ostfeld, A.; Liu, S.; Kyriakou, M.; Pavlou, P.; Qiu, M.; Polycarpou, M.M. Battle of the Leakage Detection and Isolation Methods. J. Water Resour. Plan. Manag 2022, 148, 04022068. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campbell, E.; Abraham, E.; Koslowski, J.; Piller, O.; Steffelbauer, D.B. The Dual Model under Pressure: How Robust Is Leak Detection under Uncertainties and Model Mismatches? Eng. Proc. 2024, 69, 89. https://doi.org/10.3390/engproc2024069089
Campbell E, Abraham E, Koslowski J, Piller O, Steffelbauer DB. The Dual Model under Pressure: How Robust Is Leak Detection under Uncertainties and Model Mismatches? Engineering Proceedings. 2024; 69(1):89. https://doi.org/10.3390/engproc2024069089
Chicago/Turabian StyleCampbell, Enrique, Edo Abraham, Johannes Koslowski, Olivier Piller, and David B. Steffelbauer. 2024. "The Dual Model under Pressure: How Robust Is Leak Detection under Uncertainties and Model Mismatches?" Engineering Proceedings 69, no. 1: 89. https://doi.org/10.3390/engproc2024069089
APA StyleCampbell, E., Abraham, E., Koslowski, J., Piller, O., & Steffelbauer, D. B. (2024). The Dual Model under Pressure: How Robust Is Leak Detection under Uncertainties and Model Mismatches? Engineering Proceedings, 69(1), 89. https://doi.org/10.3390/engproc2024069089







