Abstract
This article presents a practical implementation of an approach for the automated attestation of the indicators of manipulation for systems of stationary industrial robots with one arm and one clamping device. A developed mathematical model of systems for the manipulation of the metric attestation process for industrial robots is presented. Attestation is performed by properly performing the relevant calculation procedures using the CoppeliaSim and MATLAB software products. A certification example of a real robotic handling system model ABB IRB 140 and clamping device model RG2 is shown, illustrating the effectiveness of the proposed approach to improvement.
1. Introduction
The increase in the annual production and implementation of industrial robots (IR) in various industries has stabilized in the post-COVID-19 period and, according to the International Federation of Robotics, it is about 5–7% [1]. In some cases, where universality of flexible automation of machine and instrumentation engineering is important, it is necessary to have the specific technological and design characteristics and parameters of the IR, which IR manufacturers need to provide in the technical documentation [2]. Based on, and considering, such data, modern IRs can be effectively operated in flexible mechanical assembly production [3,4], ranging from flexible manufacturing cells (FMCs) to flexible production workshops and, ideally, flexible factories [5,6]. Thus, it is relevant to increase the efficiency of IR operation in FMCs and other technological structures of robot automated production systems (RAPSs) [7], where robotic technologies are implemented. In general, the above has prompted additional research on the capabilities of IRs in their various manifestations, including the attestation of IR metrics. The realization of this is the well-known automated metric attestation [8,9], which is taken here as an analog.
The essence of the IR metric attestation process is to determine the specific quantitative and qualitative parameters of the geometric characteristics of the work area (WA) of the IR [10], which ensure the required orientation of the analyzed parameter. The certification of the IR metric involves repeatedly solving the inverse kinematics problem [11] on a set of IR links and their parameters while maintaining the specified orientation of the so-called technological robotic kit (TRK) [12] with/without a manipulation object (MO) in it in the IR coordinate system [13], using certain software products. The TRK includes a clamping device (CD) with/without an MO. The final result of the IR metric certification is the parameters of the geometric characteristics of the WA, in which the TRK retains its specified (studied) orientation at the endpoint of its positioning. Visually, the certification results are presented in the form of a part WA of the analyzed IR with the defined geometric parameters of the WA, in which the required TRK orientation is maintained; this is taken into account even before the direct operation of the IR in robotic technological structures. This interpretation of the content of the IR metric certification process and its results indicates that the certification process and its results are a component of the technological preparation for the RAPS. Therefore, any actions aimed at improving any aspect of the IR metric attestation process are interpreted as leading to an increase in the effectiveness of the technological preparation [14,15] for RAPSs.
2. Literature Review
This article presents a relatively complete analysis of information sources and the feasibility of performing metric attestation [8,9]. Below are the features of information sources that are essential for the tasks solved in this paper. The main criteria for the functionality of software products that can be used to certify the IR metric are the ability to solve kinematics problems repeatedly, plan trajectories, and determine the coordinates of reference points for the further synthesis of TRK trajectories. Companies that manufacture well-known IRs, such as Kuka [16], ABB [17], Mitsubishi [18], Fanuc [19], UR [20], and others, develop software products that are used only with their products. This is due to the specifics of the manufacturing and operational technologies of the respective IRs. Therefore, the use of software products from IR manufacturers is significantly limited in implementing the IR metric certification process. Some software environments developed by companies for programming their IRs partially generate classified but incomplete information about the IR metric for specific technological tasks, such as those performed by Kuka industrial robots.
In addition to the above, there are many object-oriented software products, such as RoboDK [21], SolidWorks [22], RobotMaster [23], ROS [24], RobotWorks [25], RobotExpert [26], SolidEdge [27], CoppeliaSim (version V4.7.0 rev4) [28], and others that do not directly solve the problem of IR attestation. At the same time, as the analysis of their capabilities shows, some can be used for such research.
It is known [9] that the sequence of the IR metric attestation process using SolidWorks and RoboDK software products (analogous to this study) consists of several stages: stage E1 is the development and preparation of a 3D IR model using the SolidWorks software product, followed by its decomposition (3D IR model) into separate components (links) that are stored in a particular style format. Next, the IR coordinate system and the number of degrees of motion of its MS (manufacturing system) are selected (.dof format); stage E2 is the implementation and configuration of the generated 3D IR model in the RoboDK software product, where 3D IR components (links, etc.) are loaded, followed by their conjugation and fixation to ensure qualitative and quantitative parameters of the relative mobility of MS links and to prevent various kinds of collisions; the end-effector is selected, and the attestation and fixation of the obtained results are performed; stage E3 is the visualization, generalization, and development of recommendations for their practical use.
The practice of research using SolidWorks and RoboDK software products has shown that the implementation of E1, E2, and E3 has many shortcomings, which are caused by the features of the functionality of the RoboDK software product. Thus, the main disadvantage of stage E1 is the requirement to support 3D IR models in .stl and .obj formats. In the analog [9], this results in geometric simplification and the loss of some data. It is also impossible to convert the technological assembly of MS of IR links into these formats. The consequence of this is the problems of implementing and configuring the 3D IR model during the implementation of stage E2 (the inability to directly load the 3D IR model as one single file as a result of the technological assembly and incorrect scaling when loading each component of the 3D IR model into RoboDK). This requires step-by-step loading of the IR 3D model components, their conjugation with each other, and the further adjustment of, for example, the axis and angle of rotation of all the MS of IR links, etc. Collision detection is also performed manually. At stage E3, the user is responsible for recording, processing, and visualizing the information. A large number of routine operations indicates a low level of automation of the metric attestation process.
The analysis of the above problems of RoboDK functioning indicated the practicality of using another software product, namely, CoppeliaSim [28]. An in-depth analysis of the capabilities of CoppeliaSim has determined that using CoppeliaSim, it is possible to automate the certification process to a greater extent compared to its analog, as well as to visualize the results obtained and partially automate the process of recording and outputting the information obtained. Thanks to the Lua programming language implemented in CoppeliaSim and the automatic collision avoidance system, it is possible. These functional features provide more opportunities for further studies of IR metric attestation, primarily in the automated determination of the WA of the IR, while maintaining a specific TRK orientation, and in terms of the visualization of the results obtained. As a component of CoppeliaSim, the Lua language allows the generation of 3D IR models as separate files in the .stl extension. However, performing analysis and geometric transformations of the 3D IR model is complex. The data obtained after creating an IR model in CoppeliaSim with preservation of the orientation of the finite element, for example, a TRK, are formed in the form of matrices. These matrices contain the coordinates of the points of the right IR coordinate system, i.e., XIRYIRZIR, in which the TRK retains the specified orientation and has no collisions with other objects, including IR structural elements.
It is appropriate to emphasize that the task of automated attestation of the MS of IR metrics using the CoppeliaSim and MATLAB software products has not been previously set and, therefore, has yet to be solved. The above has determined the goal of this investigation: to highlight the content and essence of the automated implementation of the attestation process of the IR metric as an integral part of the technological preparation for a RAPS, which aims to increase the level of automation of the attestation process using CoppeliaSim and MATLAB software products.
3. Research Methodology
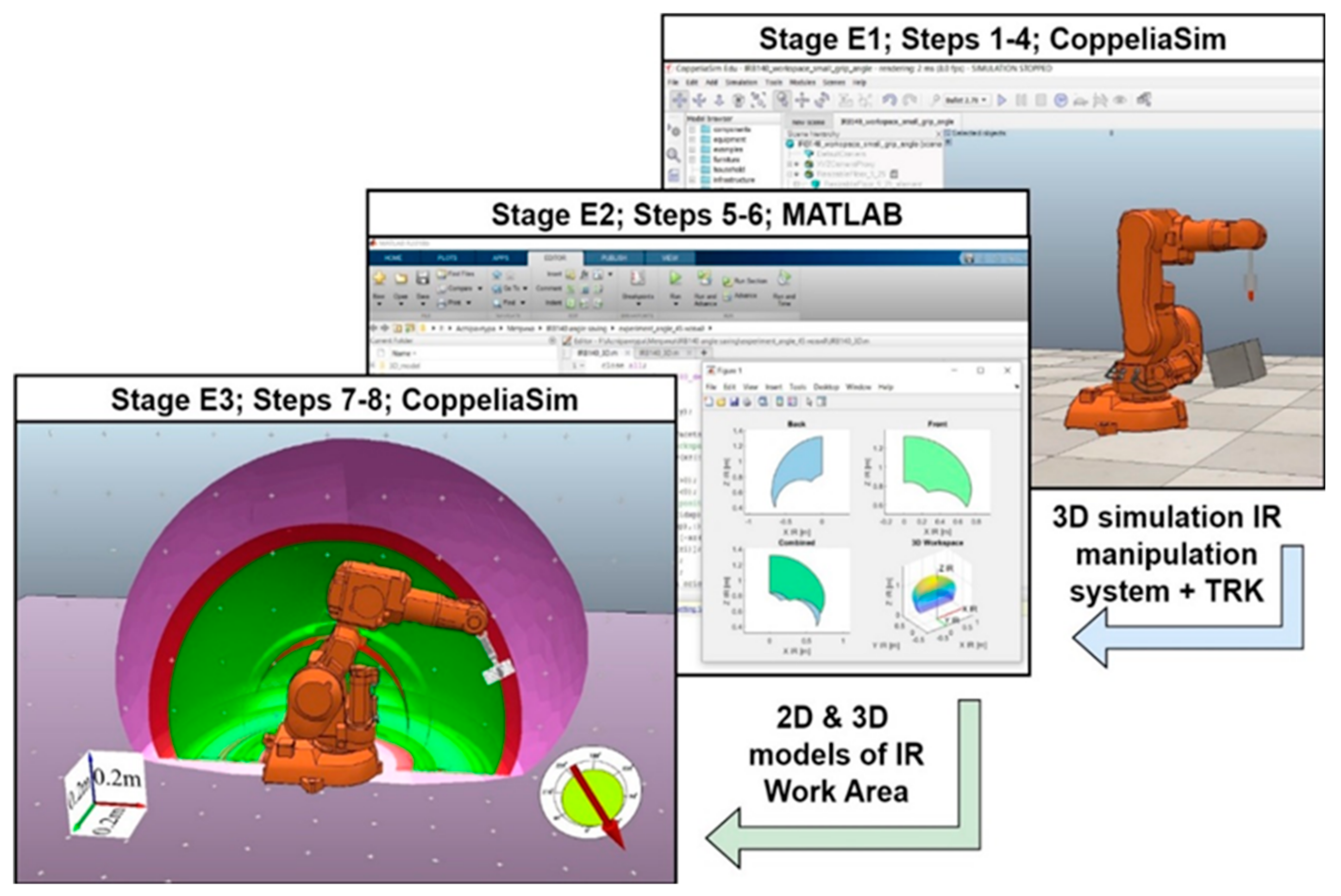
Taking into account equations as in the analog [9], this work suggests a three-stage methodology for the automated attestation of MS of an IR. Each stage involves the orderly implementation of the corresponding methodologically determined steps. Compared to the analog, CoppeliaSim and MATLAB (version R218b) [29], the use of other software products is distinctive (see Figure 1).
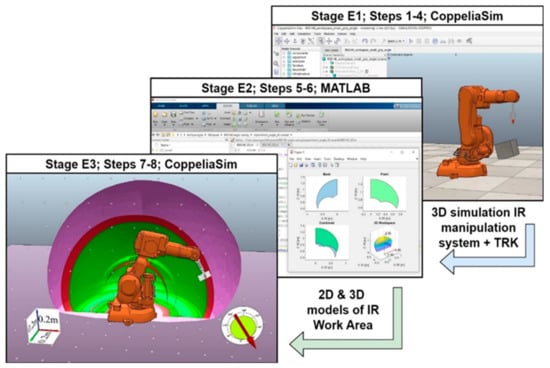
Figure 1.
A generalized scheme of the proposed methodology for automated attestation of the MS of IR metrics, performed with the help of CoppeliaSim and MATLAB software products.
Specific methodical and practical improvements have been made to the algorithms for using these software products to ensure their performance in increasing the automation of the metric attestation process and its user-friendliness. The content of the above is aimed at improving the functionality of each of them to implement an improved automated certification of the IR metric (see Figure 1). Thus, for CoppeliaSim, an orientation setter for the TRK was developed by specifying the corresponding angles of its orientation in the coordinate system of the IR under study. These are angles A, B, and C, which show the rotation (orientation) of the TRK around the XIR, YIR, and ZIR axes, respectively, or are collinear to them, and are set in the corresponding interface. This is illustrated in Figure 1, stage E3, and Figure 2a. When determining the coordinates of points that are the geometric parameters of the WA, the latter are recorded in a matrix array as numerical values for each of the XIR, YIR, and ZIR axes.
Next, MATLAB was used to analyze and transform the obtained geometric parameters of the WA, as it has built-in functions for solving such problems. Also, MATLAB can generate 2D and 3D graphical representations of the WA with the ability to reproduce them in a separate window. In our case, MATLAB generates graphical representations of the WA from the data obtained from CoppeliaSim. Such WAs being arrays of points of the coordinates that are mentioned above, which are as far as possible from the IR base and determine the geometric parameters of the WAs. However, the most crucial thing in this case is that MATLAB can generate a three-dimensional model of the WA area and the corresponding 3D file in the .stl extension. This file, or rather the 3D IR model with this extension, is used in CoppeliaSim to display the WA of the IR with the preservation of the specified TRK orientation.
The mathematical model for implementing the proposed methodology can be presented as ordered set of computational procedures , the number of which, , is equal to the number of steps in Figure 1:
The interpretation of the developed mathematical model (formalized description) according to expression (1) and Figure 1 corresponds to the above substantive essence of the process of automating the manufacturing system metric for each analyzed r-th (upper right index in (1) and further) IR and is as follows: a tuple of computational procedures is a methodologically determined ordered sequence of their (procedures, steps) execution, performed on sets of links (lir) and generalized coordinates (qjr) with a total number of nir and nqr, respectively, as well as on a set of methodologically necessary program actions for each of the software products CoppeliaSim and MATLAB involved in the attestation with a total number of nsr. It is a surjective reflection (symbol → [30]) of the Cartesian product (symbol × [31]) of the sets , , and (parameters of the metric [9]), which ensures the existence (symbol of the existence quantifier Ǝ [31]) of such a set of vectors of orientation , which is constant (const) in a specific subset of the working area , which is part (inclusion symbol ⊂ [31]) of the general working area of the analyzed r-th robot.
The role of stage E1 is to perform the following steps. St1: selecting an IR 3D model from the CoppeliaSim library or uploading another IR 3D model; St2: selecting an IR 3D finite element model (CD, tool, etc.) from the CoppeliaSim library or uploading any of the 3D models; St3: setting up the IR simulation models with the TRK and visually checking the system operation; St4: conducting the IR metric validation process of the IR 3D model with the TRK and creating an output file of coordinates of the points where the TRK maintains its orientation. MATLAB is the software product in which stage E2 is performed by implementation of St5 steps: downloading and processing the data file obtained from CoppeliaSim using MATLAB; St6: generating a graphical representation of the results of the MATLAB program and the 3D model of the WA, taking into account the specified orientation of the set of such elements (MS of IR+TRK); the steps are implemented in stage E3, executed in CoppeliaSim; St7: implementation of the 3D IR model obtained from MATLAB in CoppeliaSim; St8: visualization of the obtained results.
4. Results
The effectiveness of the approach proposed in this paper is demonstrated by the example of the automated attestation of the IR MS metric of the ABB IRB 140 model [17] and the CD model of RG2 [30] with a manipulated object (MO) in it. Fragments of the results obtained are shown in Figure 2c–e.
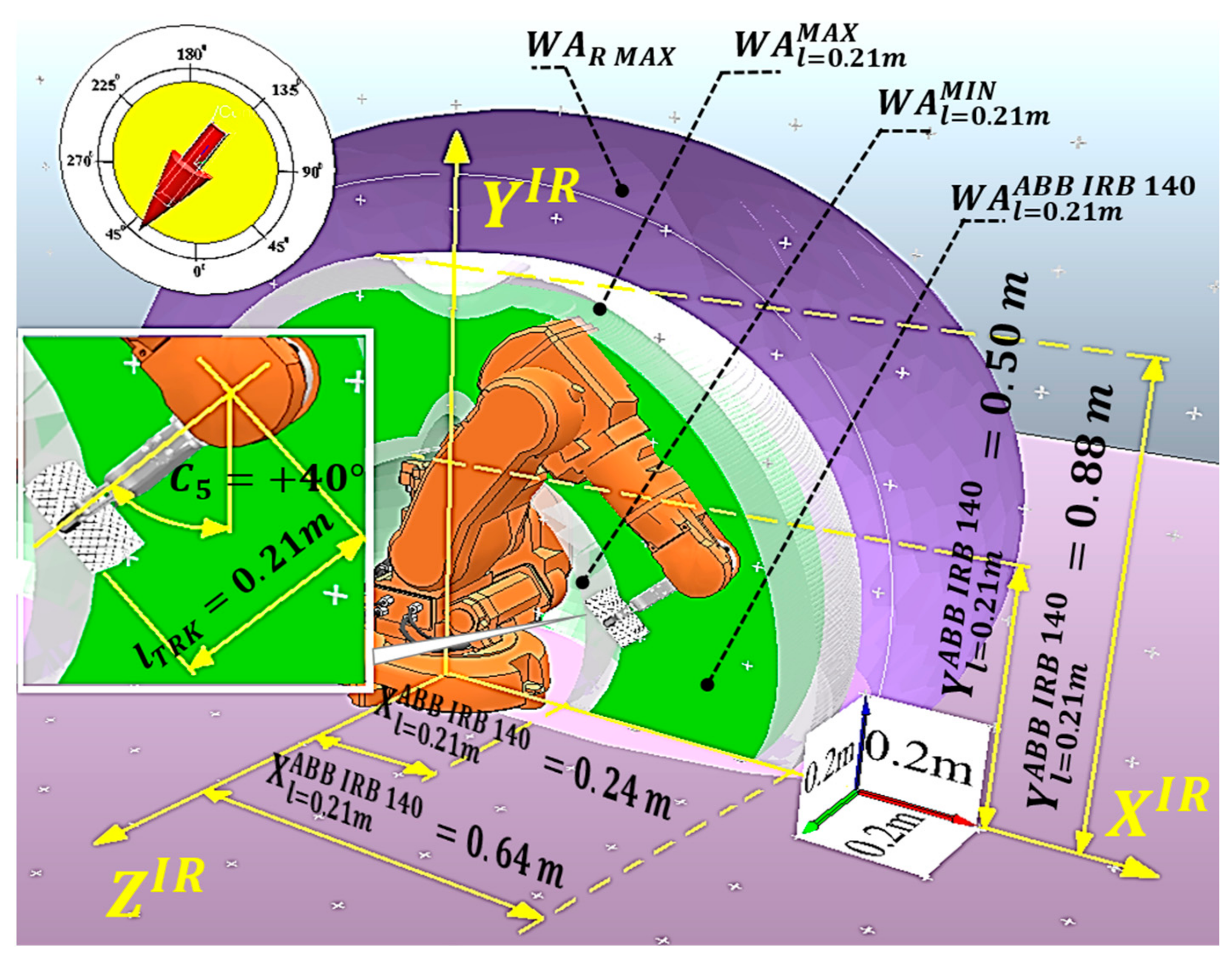
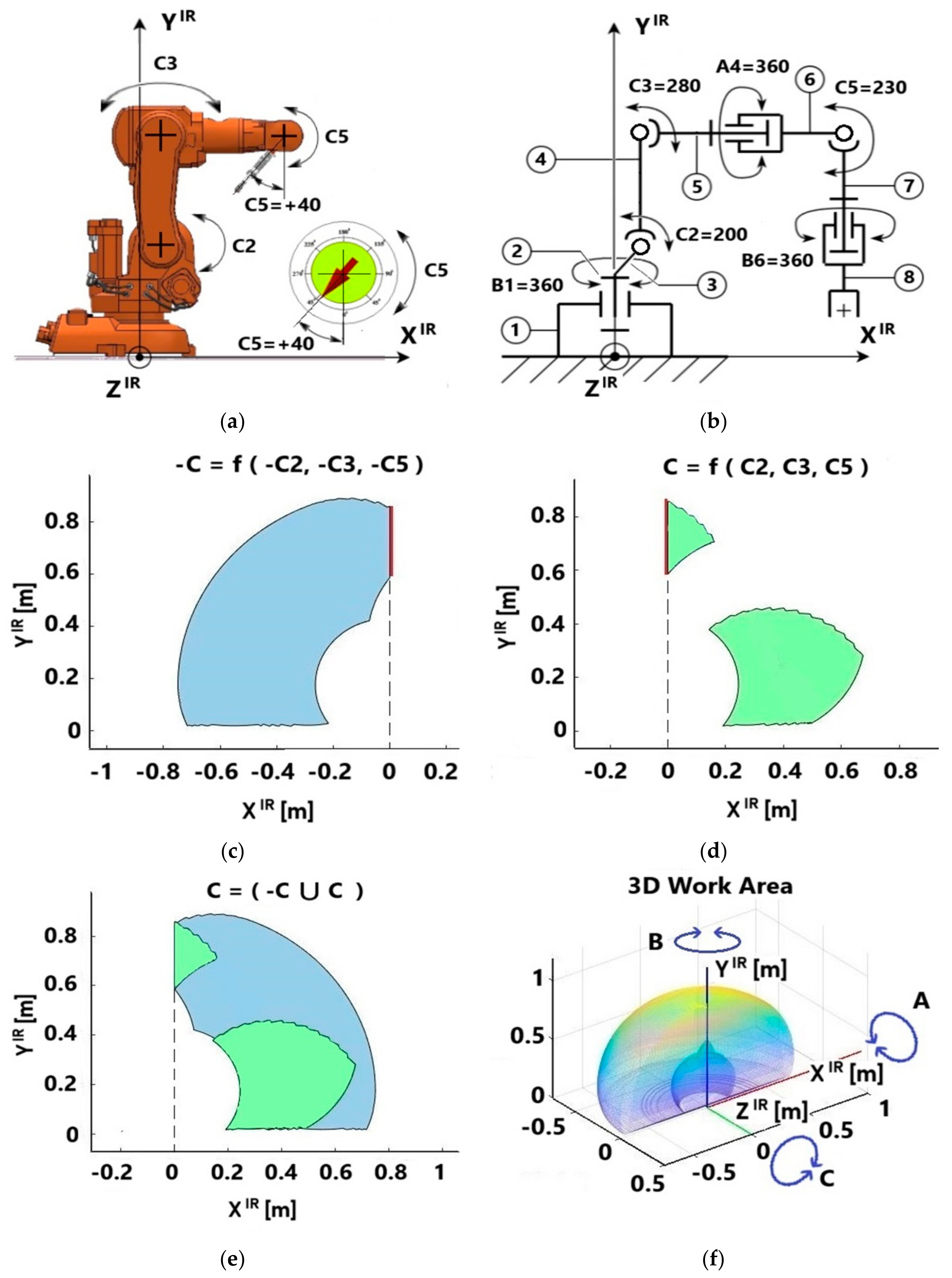
In Figure 2a shows the following elements: a general view of the analyzed IR MS of the ABB IRB 140 model (XIR YIR coordinate system) with the TRK orientation vector around the axis collinear to ZIR (in the spherical coordinate system), which is the connection of links ⑤ and ⑥, i.e., at the angular displacement C5 = + 40° (clockwise rotation of the TRK, with a + sign, otherwise, it would be C5 = + 40°). The IR is taken from the database of the software product CoppeliaSim. Otherwise, CoppeliaSim allows the user to create any IR model with/without a TRK in IR MS and with/without an MO. The above is the content of step St1. There, in the form of an arrow on a conditional dial with a gradation in degrees, the developed so-called setter of the required (studied) angular orientation of the TRK is indicated, which in this case should maintain the orientation of the TRK at C5 = + 40° and have a linear size of lTRK = 0.21 m, taking into account the actual dimensions of the CD model RG2 [30] with an MO (in length units in CoppeliaSim).
To facilitate the use of the results of step St1 and based on Figure 2, the authors developed a frame (thread) model of the kinematic structure of the ABB IRB 140 robot (see Figure 2b. It indicates the number of links in total 7, denoted as ①, …, ⑦), the types of displacements (rotational A, B, and C), and their number (6 degrees of freedom), denoted by the lower right indices when indicating the rotation of the indicated rotational movements A, B, and C of the corresponding IR links around the corresponding coordinate system of IR axes in the XIR YIR plane.
Figure 2c,d illustrate an example of the determined components of while maintaining the given orientation of the vector according to expression (1) and Figure 2a, which are part of the general working area . In Figure 2c, blue indicates the working area located in the negative direction of this robot’s XIR axis (-XIRYIR plane). Its location is determined by the possibility of simultaneous movements of all rotational movements of the MS links (the IR has a CNC contour system) along the C coordinates and this robot’s structural and kinematic features. Figure 2c is simplified by the following functional dependence (symbol f): -C = f(-C2, -C3, -C5). In Figure 2d, the green color indicates the WA displacements in the positive direction of the + XIR as the following function: C = f(C2, C3, C5).
The red line for these areas indicates the line of their mutual combination, taking into account the direction of the XIR axis. The result of their combination is the 2D model , shown in Figure 2e. In this case, the contours of these working areas in all their sections are the result of approximating the corresponding points of the contours of the working areas formed as a result of repeatedly solving the inverse kinematics problem, taking into account the adopted angular sampling . The functionality of the software product CoppeliaSim provides this. As a result, Figure 2f simplifies the working area in which the orientation vector .
The 3D model , taking into account the rotation of the link ② by an angle B1 = 180°, as the final result of the process of automated attestation of the IR MS metric of the ABB IRB 140 model IR and the coordinate system model of the RG2 model with an MO at A = 0°, B = 0°, and C = + 40° in isometry, is shown in Figure 3. Here, the area , defined by its outer contour with the maximum radius of IR MS links (Figure 2c) and the smallest kinematically and geometrically permissible radius of its IR MS, is marked in purple.
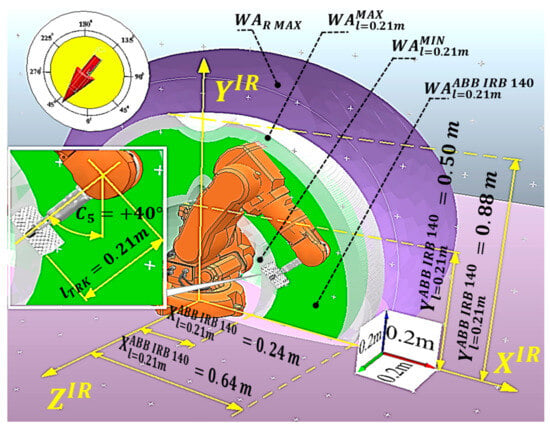
Figure 3.
Visualization (isometry) of the final result of the automated attestation process of the IR MS metric of the ABB IRB 140 model and the CD model RG2 with a prismatic MO, the dimensions of which are 0.04 × 0.04 × 0.11 m at A = 0°, B = 0°, and C5 = + 40°.
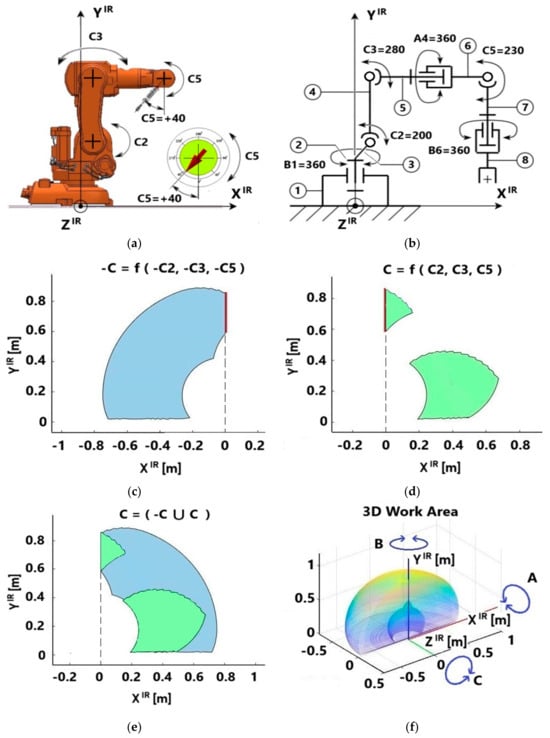
Figure 2.
Fragments of the illustration of the automated attestation of the IR MS: model ABB IRB 140 and the CD model RG2 with the MO (a); a frame (thread) model of the kinematic structure of the ABB IRB 140 robot (b); back (c), front (d) and combined (e) working area of the given orientation ; 3D form of the combined (f) working area.
Figure 2.
Fragments of the illustration of the automated attestation of the IR MS: model ABB IRB 140 and the CD model RG2 with the MO (a); a frame (thread) model of the kinematic structure of the ABB IRB 140 robot (b); back (c), front (d) and combined (e) working area of the given orientation ; 3D form of the combined (f) working area.
The working area of the given orientation is marked in green (Figure 2d). The coordinates are easily determined, taking into account the CS of IR scale of the ABB IRB 140 model. For illustrative purposes, the scale is determined by the side of a cube of 0.2 m (see Figure 3). This is the step of a conditional grid, with the nodes marked with the + white symbol. This element was also developed by the authors in CoppeliaSim. and are the boundaries within which occurs for the given conditions.
Thus, as follows from the model presented in Figure 3, for a 3D model , the latter lies within these coordinates: MIN = MIN = 0.24 m; MAX = MAX = 0.64 m; MIN = 0.50 m; MAX = 0.88 m.
5. Conclusions
Based on the results of this work, it can be concluded that the attestation of industrial robot metrics provides the possibility to consider it an a priori essential component of the technological preparation of robot automated production systems, which requires the following steps:
- The determination of the required and/or possible orientation of the technological robotic kit at a certain point of its positioning in the industrial robot working area; this is due to the requirements for the implementation of specific technologies that require ensuring the geometric and kinematic accessibility of hard-to-reach points of technological service work positions of FMCs (for example, when performing technological operations of welding, gluing, assembly, etc.);
- The analysis of the possibility of deploying and planning technological equipment, taking into account the necessary provision for a certain orientation on the technological robotic kit at the point of technological service for the industrial robot at the relevant work position on the flexible manufacturing cells;
- The synthesis of trajectories of movement in technological robotic kits in robot automated production systems, taking into account the coordinates of the point for technological service of the work position at FMCs;
- The use of the results of metric attestation both when designing new FMCs and when replanning work positions in existing flexible manufacturing cells;
- The reduction of time, intellectual, financial and other resources when placing and planning work positions in industrial robot working areas, while at the same time increasing the level of automation of this process and the visualization of its results;
- The possibility, in the case of the absence of a real industrial robot for the production system, to carry out the metric certification using digital double industrial robots. This significantly reduces the cost of the metric certification process and increases the efficiency of the technological robotic kit in robotic automated manufacturing systems. This creates prerequisites for modeling trajectories of various geometric figures with a given technological robotic kit orientation, which is interpreted as one of the obvious areas for further research.
Author Contributions
Conceptualization, methodology, and supervision, V.K. and L.D. Formal analysis, investigation, and validation, A.K. and O.D. Original draft preparation, review, editing, and visualization, I.K. and O.D. Project administration, L.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The results presented in this study may be freely shared.
Acknowledgments
The authors acknowledge the permission to publish the materials granted by the Research Department of the Technical University of Sofia, Bulgaria, and express their gratitude to this institution for their support in conducting the research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- International Federation of Robotics. Available online: https://ifr.org/ (accessed on 15 January 2024).
- Sanneman, L.; Fourie, C.; Shah, J.A. The State of Industrial Robotics: Emerging Technologies, Challenges, and Key Research Directions. Found. Trends Robot. 2021, 8, 225–306. [Google Scholar] [CrossRef]
- Keshvarparast, A.; Battini, D.; Battaia, O.; Pirayesh, A. Collaborative robots in manufacturing and assembly systems: Literature review and future research agenda. J. Intell. Manuf. 2023, 35, 2065–2118. [Google Scholar] [CrossRef]
- Jin, Z.; Marian, R.M.; Chahl, J.S. Achieving batch-size-of-one production model in robot flexible assembly cells. Int. J. Adv. Manuf. Technol. 2023, 126, 2097–2116. [Google Scholar] [CrossRef]
- Stecke, K.E. Production Planning and Scheduling in Flexible Manufacturing Systems. In Computer-Aided Production Management. IFIP State-of-the-Art Reports; Rolstadås, A., Ed.; Springer: Berlin/Heidelberg, Germany, 1988; pp. 281–287. [Google Scholar] [CrossRef]
- Monka, P.P.; Monkova, K.; Jahnátek, A.; Vanca, J. Flexible Manufacturing System Simulation and Optimization. In Experimental and Computational Investigations in Engineering. Lecture Notes in Networks and Systems; Mitrovic, N., Mladenovic, G., Mitrovic, A., Eds.; Springer: Cham, Switzerland, 2020; pp. 53–64. [Google Scholar] [CrossRef]
- Zhao, H.; Zhu, L.; Jia, Y.; Kubota, N. Focused section on advanced robotic systems for industrial automation. Int. J. Intell. Robot. Appl. 2020, 4, 133–135. [Google Scholar] [CrossRef]
- Malakov, I.; Zaharinov, V.; Nikolov, S.; Dimitrova, R. Computer-Aided Choosing of an Optimal Structural Variant of a Robot for Extracting Castings from Die Casting Machines. Actuators 2023, 12, 363. [Google Scholar] [CrossRef]
- Kyrylovych, V.; Kravchuk, A.; Melnychuk, P.; Mohelnytska, L. Automated Attestation of Metrics for Industrial Robots’ Manipulation Systems. In Advanced Manufacturing Processes II; Tonkonogyi, V., Ed.; Springer: Cham, Switzerland, 2020; pp. 813–822. [Google Scholar] [CrossRef]
- Wei, W.; Hu, G.; Chen, F.; Zhu, H. Parameterizing the Dexterous Workspace of 6R Industrial Robots. In Intelligent Robotics and Applications; Yang, H., Ed.; Springer: Singapore, 2023; pp. 431–442. [Google Scholar] [CrossRef]
- Dash, K.K.; Chaudhury, B.B.; Senapati, S.K. Inverse Kinematics Analysis of an Industrial Robot Using Soft Computing. Appl. Robot. Ind. Using Adv.Mech. 2019, 5, 183–192. [Google Scholar] [CrossRef]
- Kyrylovych, V.A. Automated Synthesis of Robotized Mechanical Assembly Technologies. Ph.D. Thesis, Kyiv Polytechnical University, Kyiv, Ukraine, 2015. [Google Scholar]
- Duysinx, P.; Geradin, M. An Introduction to Robotics: Mechanical Aspects; Pearson: Liège, Belgium, 2004. [Google Scholar]
- Javaid, M.; Haleem, A.; Singh, R.P.; Suman, R. Substantial capabilities of robotics in enhancing industry 4.0 implementation. Cogn. Robot. 2021, 1, 58–75. [Google Scholar] [CrossRef]
- Tomov, P. Stages and Structure of the Innovative Process in Automated Manufacturing. In Proceedings of the International Conference on Creative Business for Smart and Sustainable Growth (CREBUS), Sandanski, Bulgaria, 18–21 March 2019. [Google Scholar] [CrossRef]
- Kuka. Available online: https://www.kuka.com (accessed on 15 January 2024).
- ABB. Available online: https://new.abb.com (accessed on 10 January 2024).
- Mitsubishi Electic. Available online: https://www.mitsubishielectric.com (accessed on 25 January 2024).
- Fanuc. Available online: https://www.fanuc.com (accessed on 15 January 2024).
- UR. Available online: https://www.universal-robots.com (accessed on 15 January 2024).
- RoboDK. Available online: https://robodk.com (accessed on 21 January 2024).
- SolidWorks. Available online: https://www.3ds.com/products/solidworks (accessed on 22 January 2024).
- RobotMaster. Available online: https://www.robotmaster.com/en (accessed on 19 January 2024).
- ROS. Available online: https://www.ros.org (accessed on 12 January 2024).
- RobotWorks. Available online: http://www.robotworks-eu.com/products/RBWabout.htm (accessed on 11 January 2024).
- RobotExpert. Available online: https://www.plm.automation.siemens.com/global/ru/products/tecnomatix (accessed on 21 January 2024).
- Solid Edge. Available online: https://solidedge.siemens.com/en/industries/robotics-design-software (accessed on 13 January 2024).
- CoppeliaSim. Available online: http://www.coppeliarobotics.com (accessed on 21 January 2024).
- MATLAB. Available online: https://www.mathworks.com/products/matlab.html (accessed on 21 January 2024).
- OnRobot—RG2 Gripper. Available online: https://onrobot.com/en/products/rg2-gripper (accessed on 21 January 2024).
- Epp, S. Discrete Mathematics, 5th ed.; Cengage Learning: Boston, MA, USA, 2020; pp. 1–1056. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).