Infrared Thermography (IRT) Applications for Non-Destructive Inspection of Composite Parts Obtained by Continuous Fiber Additive Manufacturing: Influence of Heating Parameters on Defect Detection †
Abstract
1. Introduction
2. Methods
2.1. Experimental Plan
2.2. Application of Finite Element Method to Study the Experimental Plan
2.3. Experimental Critical Points to Be Compare with the Numerical Model
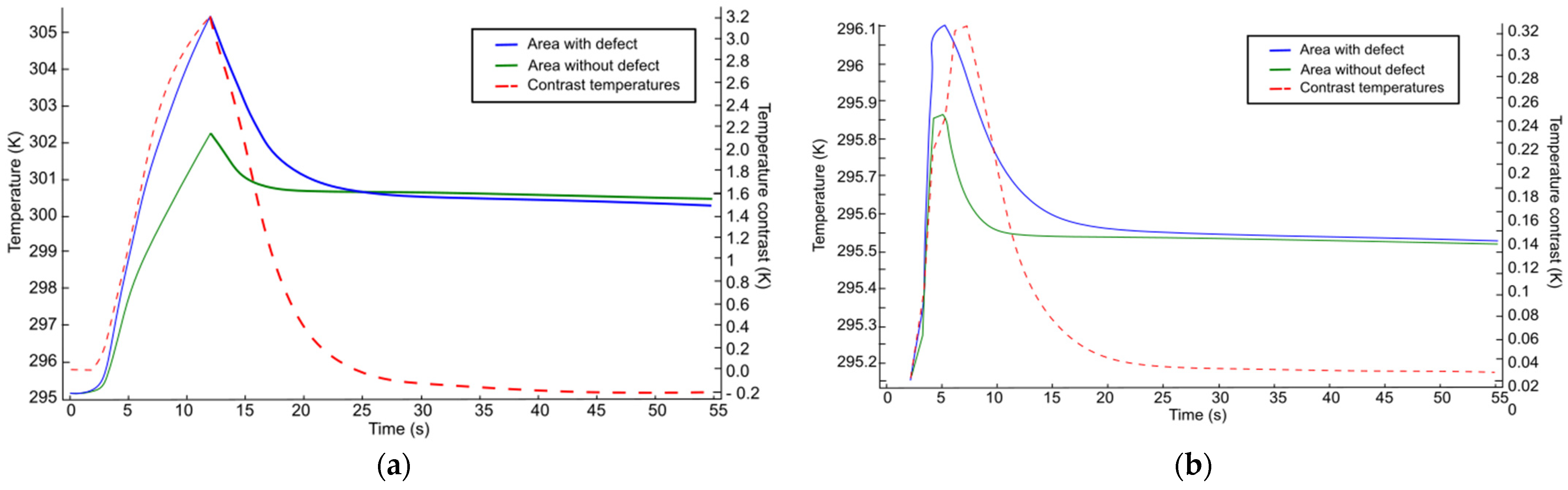
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ahmed, O.; Wang, X.; Tran, M.V.; Ismadi, M.Z. Advancements in fibre-reinforced polymer composite materials damage detection methods: Towards achieving energy-efficient SHM systems. Compos. Part B Eng. 2021, 223, 109136. [Google Scholar] [CrossRef]
- Wang, Z.; Wan, L.; Zhu, J.; Ciampa, F. Evaluation of defect depth in CFRP composites by long pulse thermography. NDT E Int. 2022, 129, 102658. [Google Scholar] [CrossRef]
- Bossi, R.H.; Georgeson, G.E. Nondestructive testing of aerospace composites polymer composites in the aerospace industry. In Polymer Composites in the Aerospace Industry; Woodhead Publishing: Sawston, UK, 2020. [Google Scholar]
- Zhuo, P.; Li, S.; Ashcroft, I.A.; Jones, A.I. Material extrusion additive manufacturing of continuous fiber reinforced polymer matrix composites: A review and outlook Material extrusion additive manufacturing of continuous fiber reinforced polymer matrix composites. Compos. Part B Eng. 2021, 224, 109143. [Google Scholar] [CrossRef]
- Karayel, E.; Bozkurt, Y. Additive manufacturing method and different welding applications. J. Mater. Res. Technol. 2020, 9, 11424–11438. [Google Scholar] [CrossRef]
- Demarbaix, A.; Ochana, I.; Levrie, J.; Coutinho, I.; Cunha, S.S., Jr.; Moonens, M. Additively Manufactured Multifunctional Composite Parts with the Help of Coextrusion Continuous Carbon Fiber: Study of Feasibility to Print Self-Sensing without Doped Raw Material. J. Compos. Sci. 2023, 7, 355. [Google Scholar] [CrossRef]
- Dizon, J.R.C.; Espera, A.H., Jr.; Chen, Q.; Advincula, R.C. Mechanical characterization of 3D-printed polymers. Addit. Manuf. 2018, 20, 44–67. [Google Scholar] [CrossRef]
- Mayr, G.; Plank, B.; Sekelja, J.; Hendorfer, G. Active thermography as a quantitative method for non-destructive evaluation of porous carbon fiber reinforced polymer. NDT&E Int. 2011, 44, 537–543. [Google Scholar]
- Deane, S.; Avdelidis, N.P.; Ibarra-Castanedo, C.; Zhang, H.; Nezhad, H.Y.; Williamson, A.A.; Mackley, T.; Davis, M.J.; Maldague, X.; Tsourdos, A. Application of NDT thermographic imaging of aerospace structures. Infrared Phys. Technol. 2019, 97, 456–466. [Google Scholar] [CrossRef]
- Hedayatrasa, S.; Poelman, G.; Segers, J.; Van Paepegem, W.; Kersemans, M. Performance of frequency and/or phase modulated excitation waveforms for optical infrared thermography of CFRPs through thermal wave radar: A simulation study. Compos. Struct. 2019, 225, 111177. [Google Scholar] [CrossRef]
- Saeed, N.; Abdulrahman, Y.; Amer, S.; Omar, M.A. Experimentally validated defect depth estimation using artificial neural network in pulsed thermography. Infrared Phys. Technol. 2019, 98, 192–200. [Google Scholar] [CrossRef]
- Notebaert, A.; Quinten, J.; Moonens, M.; Olmez, V.; Barros, C.; Cunha, S.S., Jr.; Demarbaix, A. Numerical Modelling of the Heat Source and the Thermal Response of an Additively Manufactured Composite during an Active Thermographic Inspection. Materials 2024, 17, 13. [Google Scholar] [CrossRef] [PubMed]
- Berde, N.N.; Sanap, S.B.; Thorat, S.G. Study of impact and fatigue on 3D printed. Mater. Today Proc. 2021, 47, 2376–2378. [Google Scholar] [CrossRef]



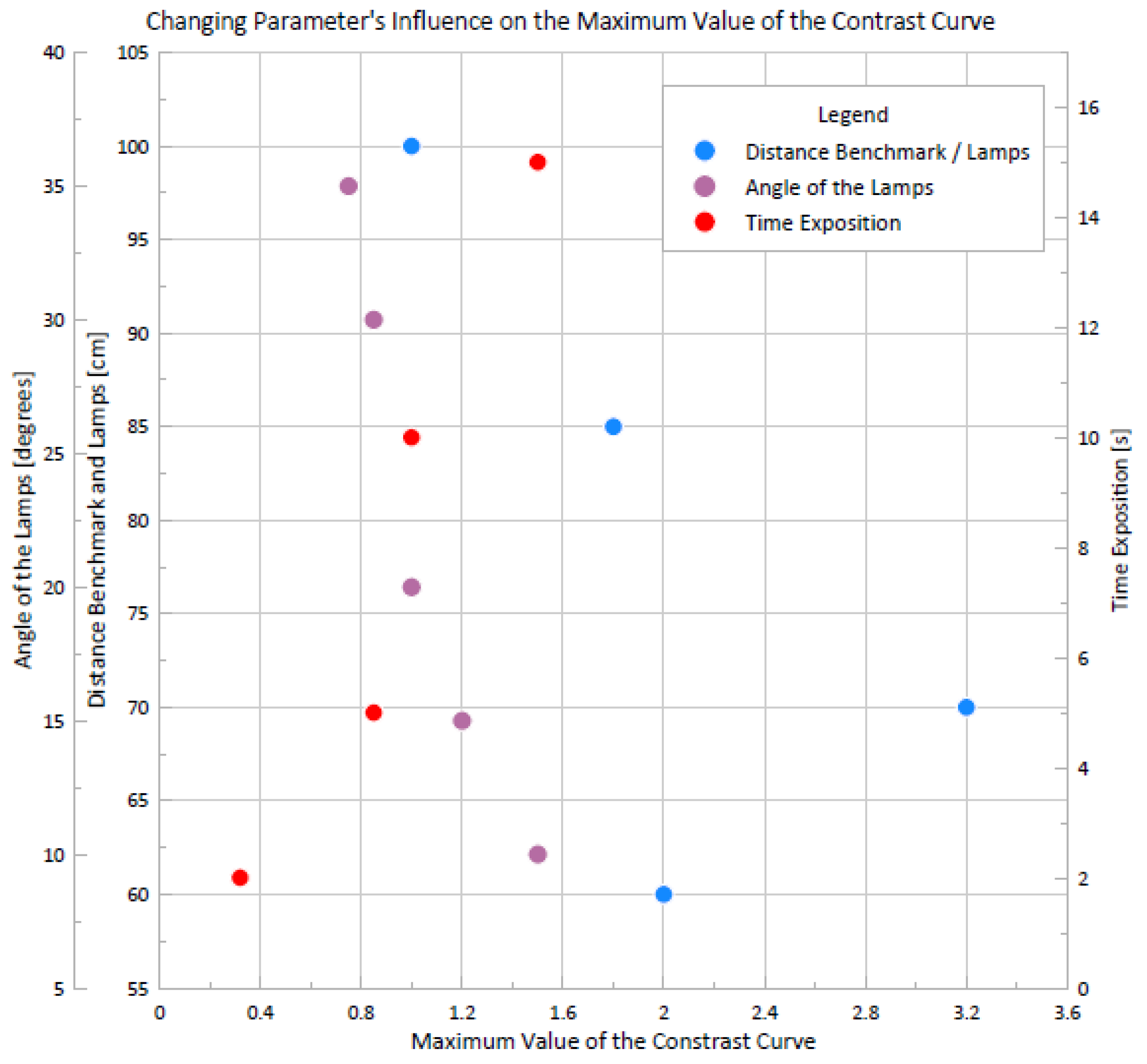
| Test Number | Distance Sample/Lamps [cm] | Lamps Angle [°] | Time Exposition [s] |
|---|---|---|---|
| 1 | 100 | 20 | 15 |
| 2 | 100 | 20 | 10 |
| 3 | 100 | 20 | 2 |
| 4 | 100 | 35 | 10 |
| 5 | 100 | 30 | 10 |
| 6 | 100 | 15 | 10 |
| 7 | 100 | 10 | 10 |
| 8 | 85 | 20 | 10 |
| 9 | 70 | 20 | 10 |
| 10 | 60 | 20 | 10 |
| Critical Point | Distance Sample/Lamps [cm] | Lamps Angle [°] | Time Exposition [s] |
|---|---|---|---|
| 1 | 100 | 20 | 2 |
| 2 | 100 | 20 | 10 |
| 3 | 100 | 20 | 15 |
| 4 | 70 | 20 | 10 |
| Critical Point | Experimental | Numerical |
|---|---|---|
| Number 1 |  |  |
| Number 2 |  |  |
| Number 3 |  | 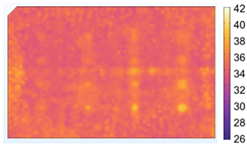 |
| Number 4 |  |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barros, C.; Notebaert, A.; Cunha, S.S., Jr.; Demarbaix, A. Infrared Thermography (IRT) Applications for Non-Destructive Inspection of Composite Parts Obtained by Continuous Fiber Additive Manufacturing: Influence of Heating Parameters on Defect Detection. Eng. Proc. 2024, 76, 96. https://doi.org/10.3390/engproc2024076096
Barros C, Notebaert A, Cunha SS Jr., Demarbaix A. Infrared Thermography (IRT) Applications for Non-Destructive Inspection of Composite Parts Obtained by Continuous Fiber Additive Manufacturing: Influence of Heating Parameters on Defect Detection. Engineering Proceedings. 2024; 76(1):96. https://doi.org/10.3390/engproc2024076096
Chicago/Turabian StyleBarros, Camila, Arnaud Notebaert, Sebastião Simões Cunha, Jr., and Anthonin Demarbaix. 2024. "Infrared Thermography (IRT) Applications for Non-Destructive Inspection of Composite Parts Obtained by Continuous Fiber Additive Manufacturing: Influence of Heating Parameters on Defect Detection" Engineering Proceedings 76, no. 1: 96. https://doi.org/10.3390/engproc2024076096
APA StyleBarros, C., Notebaert, A., Cunha, S. S., Jr., & Demarbaix, A. (2024). Infrared Thermography (IRT) Applications for Non-Destructive Inspection of Composite Parts Obtained by Continuous Fiber Additive Manufacturing: Influence of Heating Parameters on Defect Detection. Engineering Proceedings, 76(1), 96. https://doi.org/10.3390/engproc2024076096






