Abstract
This publication presents a new method by which control methods based on reinforcement learning can be combined with classical robust control methods. The combination results in a robust management system that meets high-quality criteria. The described method is presented through the control of an autonomous vehicle. By choosing the reward function chosen during reinforcement learning, various driving styles can be realized, e.g., lap time minimization, track tracking, and travel comfort. The neural network was trained using the Proximal Policy Optimization algorithm, and the robust control is based on . The two controllers are combined using a supervisor structure, in which a quadratic optimization task is implemented. The result of the method is a control structure that realizes the longitudinal and lateral control of the vehicle by specifying the reference speed and the steering angle. The effectiveness of the algorithm is demonstrated through simulations.
1. Introduction
Nowadays, with the appearance of faster and faster computer devices and hardware that appear as a result of the development of computer technology, machine learning-based methods have also begun to develop rapidly and appear in almost all scientific fields, including in control systems that solve complex tasks. A typical example of this is the control of autonomous vehicles, where various environmental perception, decision-making, and control problems must be solved in a constantly changing traffic environment. In the case of such problems, designing high-performance and reliable control solutions is a serious challenge.
A possible solution could be data-supported extensions of classic control procedures, for example, Model Predictive Control (MPC) [1,2,3], model-free control (MFC) [4,5], and robust and linear parameter variable methods [6]. In addition, robust control methods are also relevant in the context of autonomous vehicles, since these systems are usually burdened with various noises, disturbances, and uncertainties. Fortunately, however, these can be handled using classical methods such as that of Khosravani et al., where robust control was designed for a driver-in-the-loop case [7].
Another possible approach to management tasks requiring high-quality criteria is the application of machine learning-based procedures. The most common of these are usually based on some kind of deep neural network. The advantage of these algorithms is that they can significantly benefit from the large amount of data collected during real behavior, thus realizing optimal behavior [8]. Various solutions can be found in control technology, where the controller is implemented by a neural network; examples of their effectiveness can be found in [9,10,11]. However, the disadvantage of these methods is that they lack theoretical guarantees for their behavior in the general case, which would be especially important in safety-critical applications, such as vehicle control systems. Several publications attempt to validate neural network-based systems, such as that of Lelkó et al., where, by linearizing the system at different working points, a polytopic system is formed, which can be analyzed using the Lyapunov method [12]. Other possible approaches are described by Ruan et al., Huang et al., and Wu et al. [13,14,15].
The purpose of this publication is to present an integrated vehicle control strategy that combines the advantages of classical model-based control methods and modern machine learning-based methods. The combined solution is capable of high performance similar to machine learning methods while having the reliability and robustness of classical methods.
2. Combined Control Structure
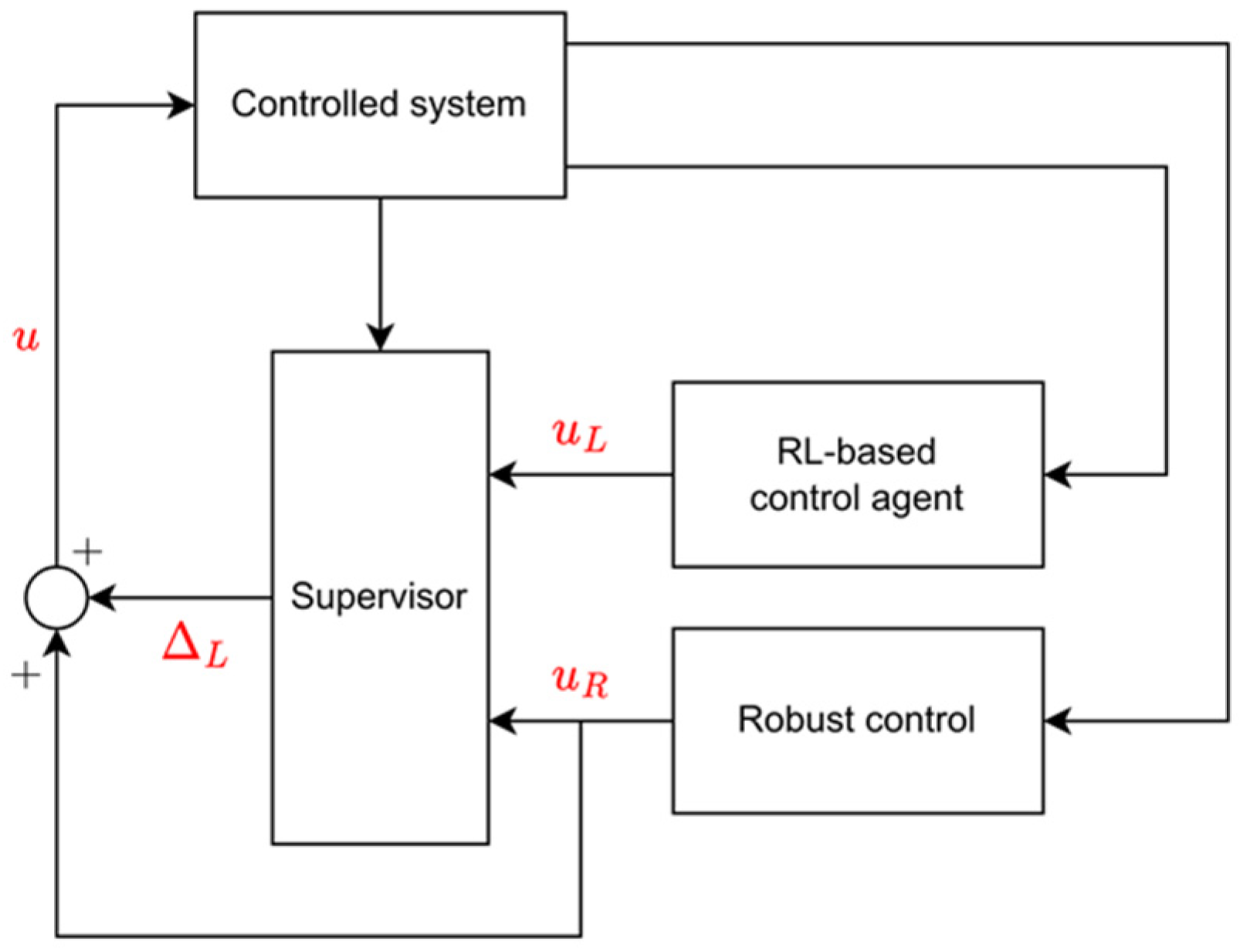
The integration of classical algorithms and methods based on machine learning was performed with the help of a supervisory controller. The resulting structure can be seen in Figure 1. In the described structure, the robust controller and the reinforcement learning-based agent (RL agent) operate independently of each other and calculate the possible control signal at every time step. However, the actual control signal is determined by the supervisory controller, taking into account the output of the two former controllers. The control signal is determined using an additive ∆L value as follows:
where denotes the output of the robust control. ΔL is a limited additive signal calculated by the monitoring controller; its values can vary between ∆Lmin and ∆Lmax.
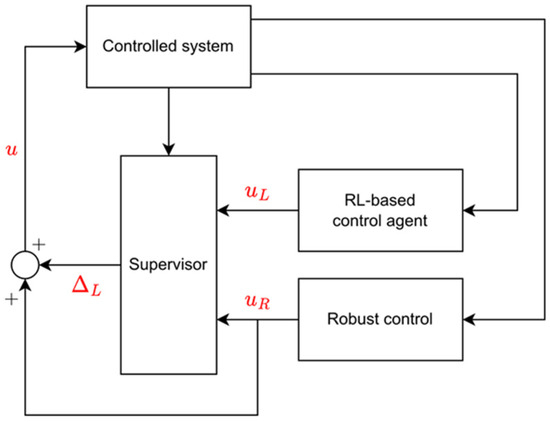
Figure 1.
Block diagram of the supervisor control structure.
The goal of the supervisory controller is to minimize the difference between the intervention proposed by the neural network and the intervention that is actually implemented, taking into account the restrictions necessary for safe movement. Robust stability is ensured by robust control. Classical methods, such as -based control design, can handle limited input disturbances and can guarantee robust stability and performance even with limited input disturbances.
The optimization task solved by the supervisor, containing the optimization
is subject to the constraints
where is the trajectory tracking error estimated based on the vehicle model. The estimation is performed by the model-based prediction layer built into the supervisor. With this optimization task, not only is the limitation of the input additive disturbance (required for robust performance) fulfilled, but other requirements can also be considered, such as, in this case, the limitation of the path tracking error, which can be used to prevent leaving the track.
3. Learning Process of the Reinforcement Learning Agent
In this section, the design process of the reinforcement controller is presented. The design method of the further control elements can be found in [15]. The reinforcement learning-based agent simultaneously controls the longitudinal and lateral dynamics of the vehicle as a high-quality control system. Being nonlinear, it can handle the nonlinearities of the vehicle model and perform optimal control according to the given reward function.
The agent is trained in a simulated environment, which is based on a complex nonlinear model of the vehicle, considering nonlinear tire characteristics, steering dynamics, real-world noises, disturbances, actuator saturation, and time delay. At the input of the agent’s implementing neural network, there are points on the center line with uniform intervals. To reduce the dimension of the task, the relative values of the points in relation to the vehicle were considered in the vehicle’s coordinate system. With this solution, the vehicle is always at the origin and faces the positive direction of the x axis. The input vector of the neural network is therefore
where N indicates the number of track points used in the calculation. This is a design parameter; with a higher value, more information is available to the network about the track in front of the vehicle, but the number of network parameters also increases, and the learning process will be longer. In the case of too-small values, there may not be enough information to have a network available to perform maneuvers. Because of this, the value of N is chosen mainly empirically, considering the geometry of the typical trajectory curves.
The reinforcement learning-based agent is trained based on a reward function. In each time step, depending on the state of the environment, the agent collects rewards based on this function, and the sum of the collected rewards characterizes the quality of the agent during learning. The aim of the learning process is therefore to maximize the collected reward.
To complete the task, a simple parameter reward function was defined:
where xLat,err is the lateral error of the track tracking, Δp is the progress of the vehicle along the center line in the given time step, δref is the reference steering angle chosen by the controller, senv denotes the state of the environment, and a is the action chosen by the agent in the given step. During teaching, in the event that the vehicle has left the edges of the track, a reward with a large negative value is applied in addition to (4), thereby punishing the system for behavior similar to this.
4. Illustration of the Presented Structure
In this chapter, the effectiveness of the presented control structure is illustrated through a simulation example. The simulation is based on the model of a small test vehicle, which is a 1:10 reduced vehicle (F1TENTH). The racing car must drive through a scaled-down 1:30-scale segment of the Formula 1 Bahrain International Circuit.
The neural network used had three hidden layers, which contained 16, 32 and 64 neurons and a ReLU-type activation layer. A hyperbolic tangent activation function was applied to the output, which takes into account the steering actuator limitations and the vehicle’s maximum speed in a continuously derivable manner. At the input of the network, N = 7 track points were used, which were located at a uniform distance of 0.5 m on the center line of the track; i.e., the agent was able to detect 3.5 m of the track in advance. The maximum speed of the vehicle is vmax = 4 m/s. During the optimization task performed in the supervisor, intervals ∆Lδ ∈ [–0.15; 0.15] and ∆Lv ∈ [−0.1; 0.1] were determined. The predictive layer performed a two-step estimation based on the simplified model of the vehicle to limit the path tracking error; the maximum allowed deviation was emax = 0.4 m for safety reasons. During the simulation, two controllers were compared: the control agent using pure reinforcement learning, which only performs the optimal control based on the reward function described in Equation (4), and the full supervisor-based system, which includes the robust controller in addition to the former.
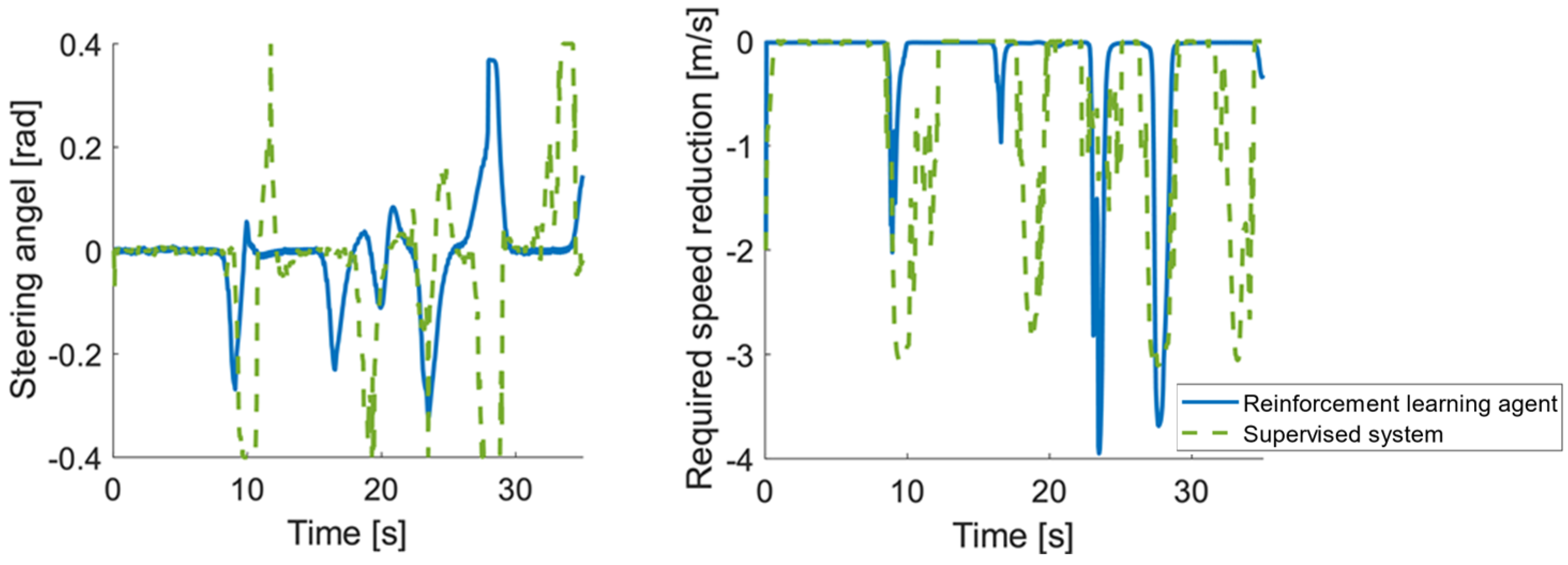
Figure 2 shows the used steering angle and suggested speed reduction. The supervisor chooses the reference speed much more conservatively; however, for the sake of more accurate trajectory tracking, it also uses larger steering interventions, thus reducing the performance of the closed loop. The result in terms of time to complete the segment is 32 s for the reinforcement learning-based agent and 35 s for the supervisory controller-based structure.
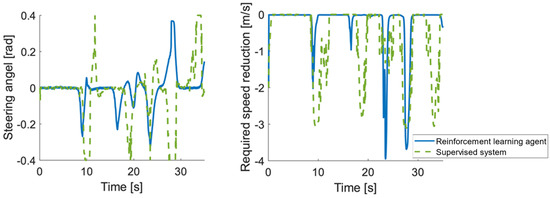
Figure 2.
Steering angle and required speed reduction suggested by the controllers.
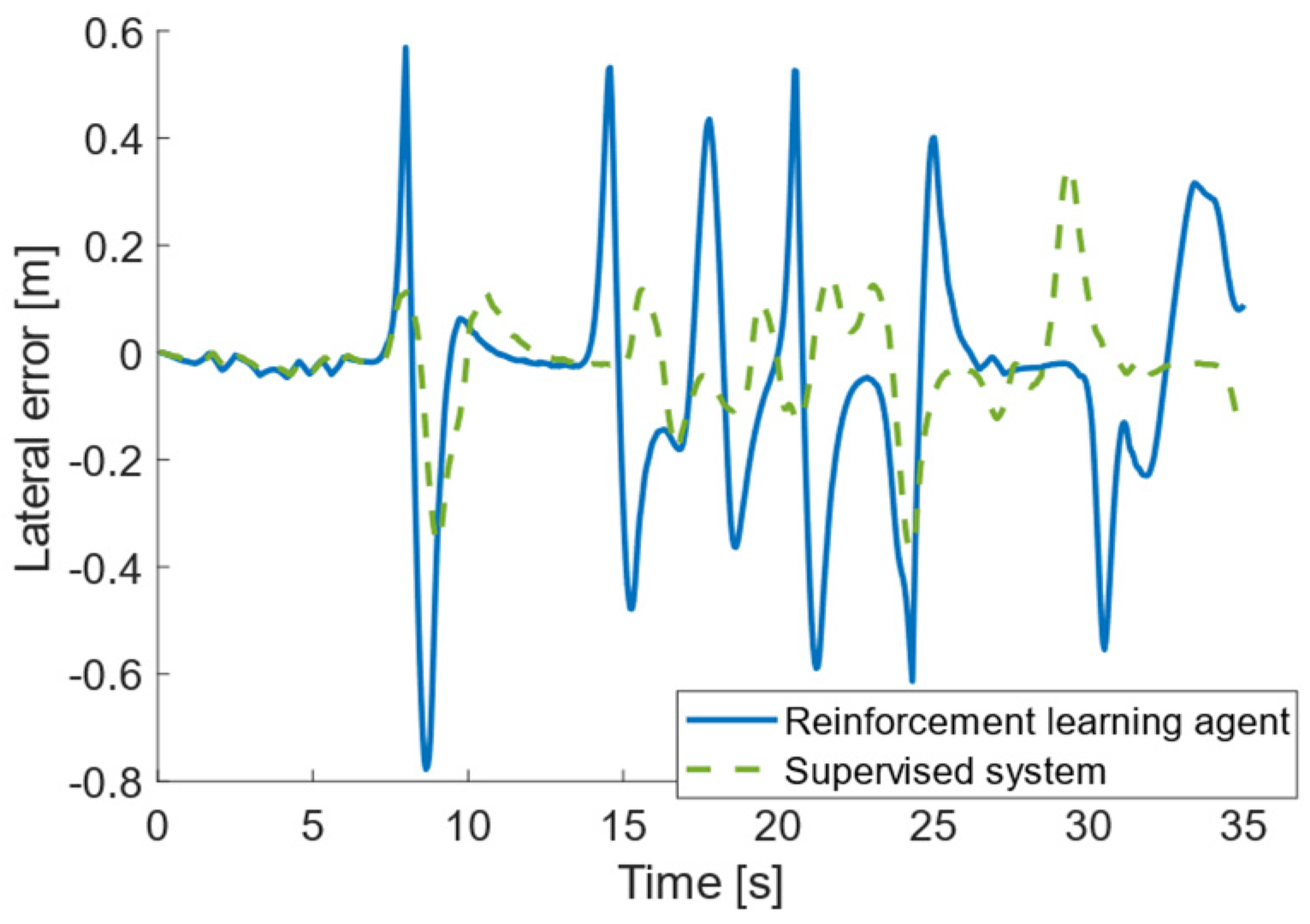
The main advantage of the supervisor-based structure in this example is the successful limitation of trajectory tracking error. An illustration of this can be seen in Figure 3, which shows the lateral error occurring during the simulation. It can be clearly seen that the system including the supervisory controller significantly reduces trajectory tracking error. The prescribed maximum value was emax = 0.4 m, which was violated several times in the case of the reinforcement learning-based agent, in the worst case, it reached almost 0.8 m, while this criterion was also successfully met in the case of the supervisory controller.
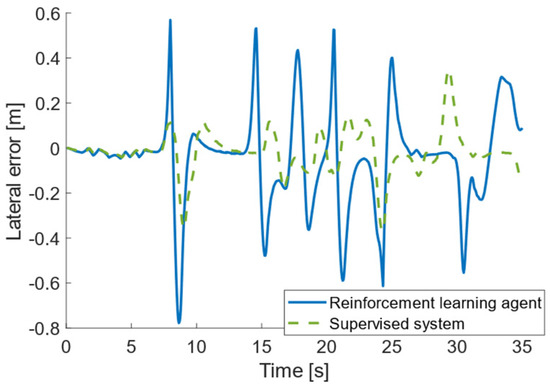
Figure 3.
Graph of track tracking errors occurring during the simulation.
In both cases, it can be said that the controllers could navigate along the track. The goal of the reinforcement learning-based agent was to minimize the lap time, and to this end, it often resulted in cutting corners to move faster and brake less. During the learning process, the path tracking error was not strictly limited; it was only considered as a penalty term in the reward function. On the other hand, with the help of quadratic optimization and model-based prediction in the supervisor, it was possible to keep the trajectory tracking error below the prescribed level. This behavior was also supported by the presented simulation. The disadvantage of the method is that, due to limitations, it is not capable of the same performance as the reinforcement learning-based agent, which is manifested in the difference in lap times; however, compared to the supervisory controller, it is able to ensure robust stability through the control and limitation of trajectory tracking error with the model-based through optimization.
5. Conclusions
This paper dealt with the description of a vehicle control structure that can be used with high efficiency for trajectory tracking. The structure consists of three parts: a classic robust control procedure, a modern data-based nonlinear control, and a supervisory controller that combines their advantages for control, robust stability, and limitation of trajectory tracking error with a slight decrease in performance.
Possible future research directions include the implementation and validation of the method on a real test vehicle. During the learning process, a model of a small test vehicle was used, which is a test vehicle that is available and has the necessary sensors and actuators to perform autonomous functions. The reward function was constructed with the possible real application in mind. While different driving behaviors can be achieved through the adequate parametrization of the reward function, the steering angle minimization increases the stability of the motion by eliminating steering oscillations due to the real-life time delays and steering dynamics. On the robust control side, the control method can handle possible modeling uncertainties, noises, and disturbances. From the point of view of applicability, therefore, the validation of safety-critical systems in a real environment is extremely important, which must also be carried out in the case of the supervisory controller-based control system.
Author Contributions
Conceptualization, B.N. and P.G.; modeling and simulation, A.L.; methodology, A.L.; supervision, B.N. and P.G. All authors have read and agreed to the published version of the manuscript.
Funding
The research included in the publication was carried out by HUN-REN SZTAKI with the support of the European Union, within the framework of the National Laboratory of Autonomous Systems (RRF-2.3.1-21-2022-00002). The research was partially supported by the Foundation R&D Programme of Széchenyi István University in the framework of the Artificial Intelligence-based Technologies and Systems Research. The work of Attila Lelkó was supported by ÚNKP-23-3, the New National Excellence Program of the National Research, Development and Innovation Office.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Dataset available on request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kabzan, J.; Hewing, L.; Liniger, A.; Zeilinger, M.N. Learning-Based Model Predictive Control for Autonomous Racing. IEEE Robot. Autom. Lett. 2019, 4, 3363–3370. [Google Scholar] [CrossRef]
- Rosolia, U.; Borrelli, F. Learning How to Autonomously Race a Car: A Predictive Control Approach. IEEE Trans. Control Syst. Technol. 2020, 28, 2713–2719. [Google Scholar] [CrossRef]
- Fliess, M.; Join, C. Machine Learning and Control Engineering: The Model-Free Case. In Proceedings of the Future Technologies Conference (FTC) 2020, Vancouver, BC, Canada, 5–6 November 2020; Arai, K., Kapoor, S., Bhatia, R., Eds.; Springer International Publishing: Cham, Switzerland, 2021; Volume 1, pp. 258–278. [Google Scholar]
- Fényes, D.; Hegedűs, T.; Németh, B.; Szabó, Z.; Gáspár, P. Robust Control Design Using Ultra-Local Model-Based Approach for Vehicle-Oriented Control Problems. In Proceedings of the 2022 European Control Conference (ECC), London, UK, 11–14 July 2022; pp. 1746–1751. [Google Scholar]
- Németh, B.; Gáspár, P. Guaranteed Performances for Learning-Based Control Systems Using Robust Control Theory. In Proceedings of the Future Technologies Conference (FTC) 2020, Vancouver, BC, Canada, 5–6 November 2020; Springer International Publishing: Cham, Switzerland, 2021; pp. 109–142. [Google Scholar]
- Khosravani, S.; Khajepour, A.; Fidan, B.; Chen, S.-K.; Litkouhi, B. Development of a Robust Vehicle Control with Driver in the Loop. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 3482–3487. [Google Scholar]
- Brüggemann, S.; Possieri, C. On the use of difference of log-sum-exp neural networks to solve data-driven model predictive control tracking problems. IEEE Control Syst. Lett. 2021, 5, 1267–1272. [Google Scholar] [CrossRef]
- He, W.; Yan, Z.; Sun, Y.; Ou, Y.; Sun, C. Neural-Learning-Based Control for a Constrained Robotic Manipulator with Flexible Joints. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5993–6003. [Google Scholar] [CrossRef] [PubMed]
- Haiyang, Z.; Yu, S.; Deyuan, L.; Hao, L. Adaptive Neural Network PID Controller Design for Temperature Control in Vacuum Thermal Tests. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; pp. 458–463. [Google Scholar]
- Zhang, M.; Wang, X.; Yang, D.; Christensen, M.G. Artificial Neural Network Based Identification of Multi-Operating-Point Impedance Model. IEEE Trans. Power Electron. 2021, 36, 1231–1235. [Google Scholar] [CrossRef]
- Lelkó, A.; Németh, B.; Gáspár, P. Stability and Tracking Performance Analysis for Control Systems with Feed-Forward Neural Networks. In Proceedings of the 2021 European Control Conference (ECC), Rotterdam, The Netherlands, 29 June–2 July 2021; pp. 1485–1490. [Google Scholar]
- Ruan, W.; Huang, X.; Kwiatkowska, M. Reachability Analysis of Deep Neural Networks with Provable Guarantees. In Proceedings of the 27th International Joint Conference on Artificial Intelligence (IJCAI), Stockholm, Sweden, 13–19 July 2018; pp. 2651–2659. [Google Scholar]
- Huang, X.; Kwiatkowska, M.; Wang, S.; Wu, M. Safety Verification of Deep Neural Networks. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NeurIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 5843–5852. [Google Scholar]
- Wu, M.; Wicker, M.; Ruan, W.; Huang, X.; Kwiatkowska, M. A Game-Based Approximate Verification of Deep Neural Networks with Provable Guarantees. Theor. Comput. Sci. 2020, 807, 298–329. [Google Scholar] [CrossRef]
- Lelkó, A.; Németh, B. Optimal Motion Design for Autonomous Vehicles with Learning Aided Robust Control. IEEE Trans. Veh. Technol. 2024, 73, 12638–12651. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).