Using Carbon Dioxide for Subsea Long-Duration Energy Storage
Abstract
:1. Introduction
2. Mathematical Models
2.1. Thermodynamic Model for Ideal Isothermal Conditions (CO2HPES Model)
2.2. Transient Thermal Model (C2O2 Model)
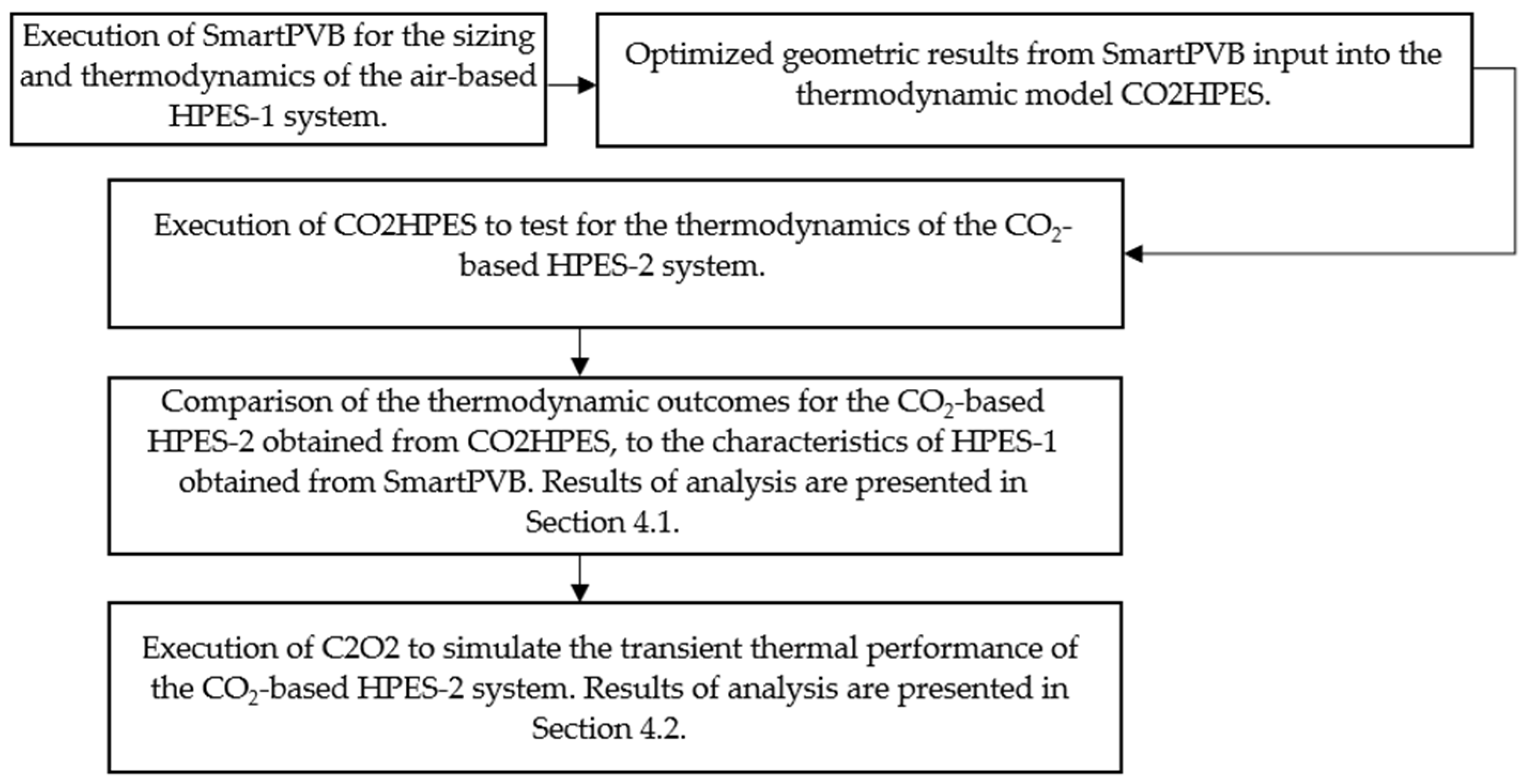
3. Methodology
4. Results and Discussion
4.1. Results from Thermodynamic Analysis Assuming Ideal Isothermal Conditions
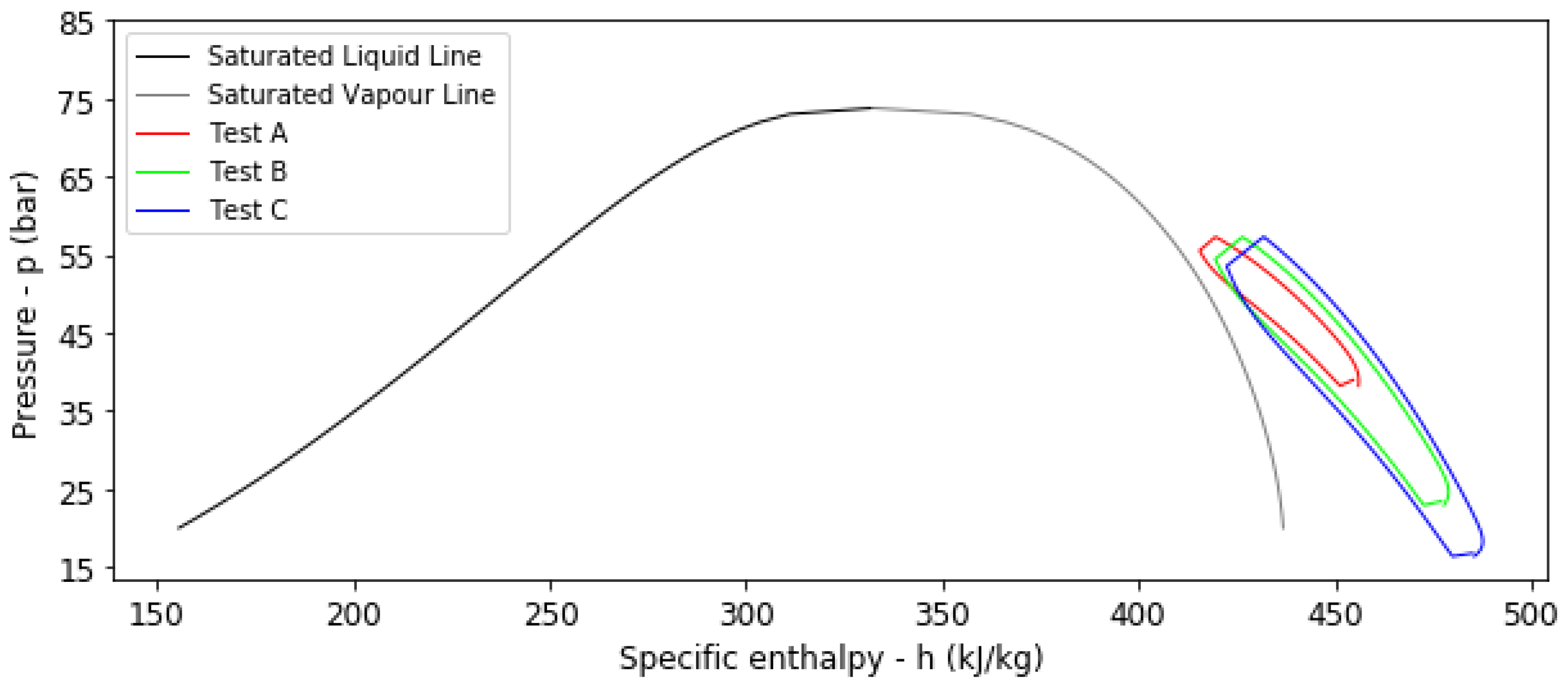
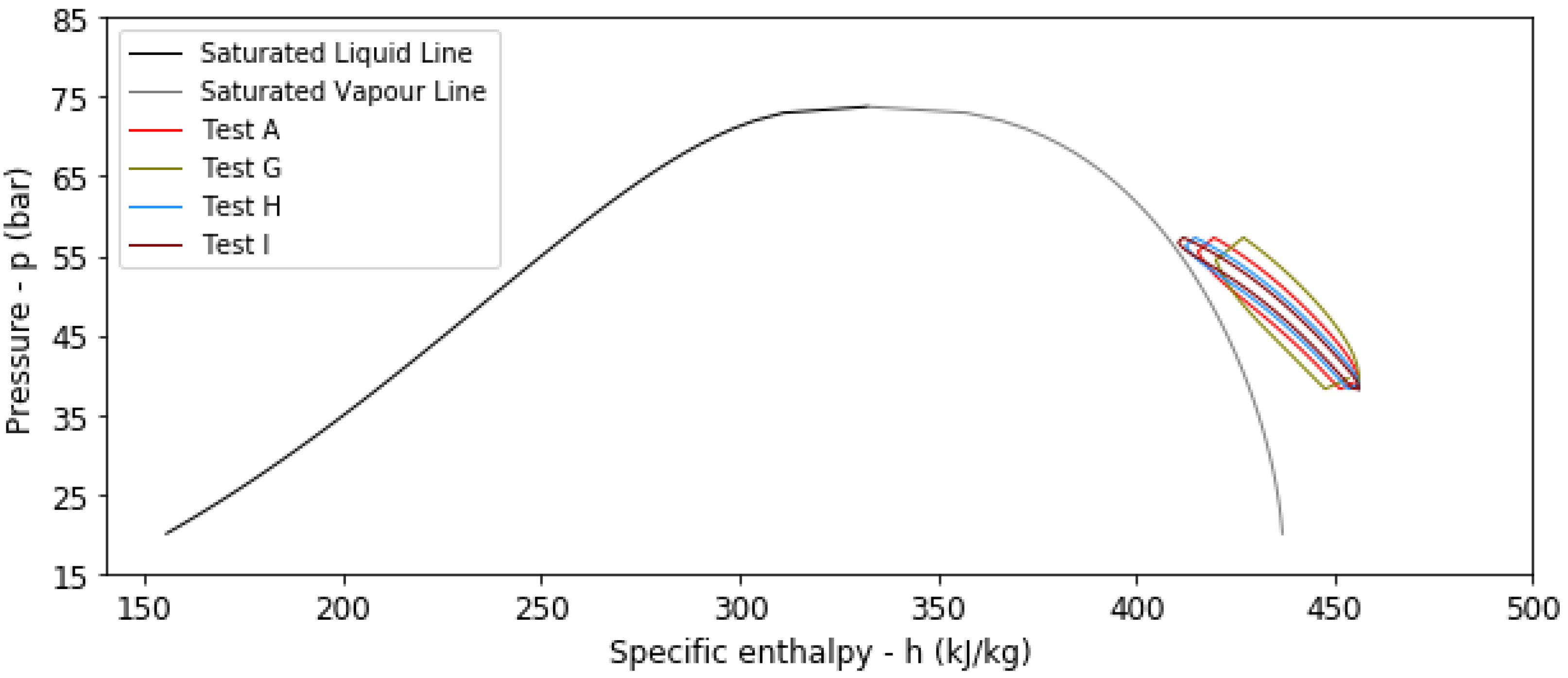
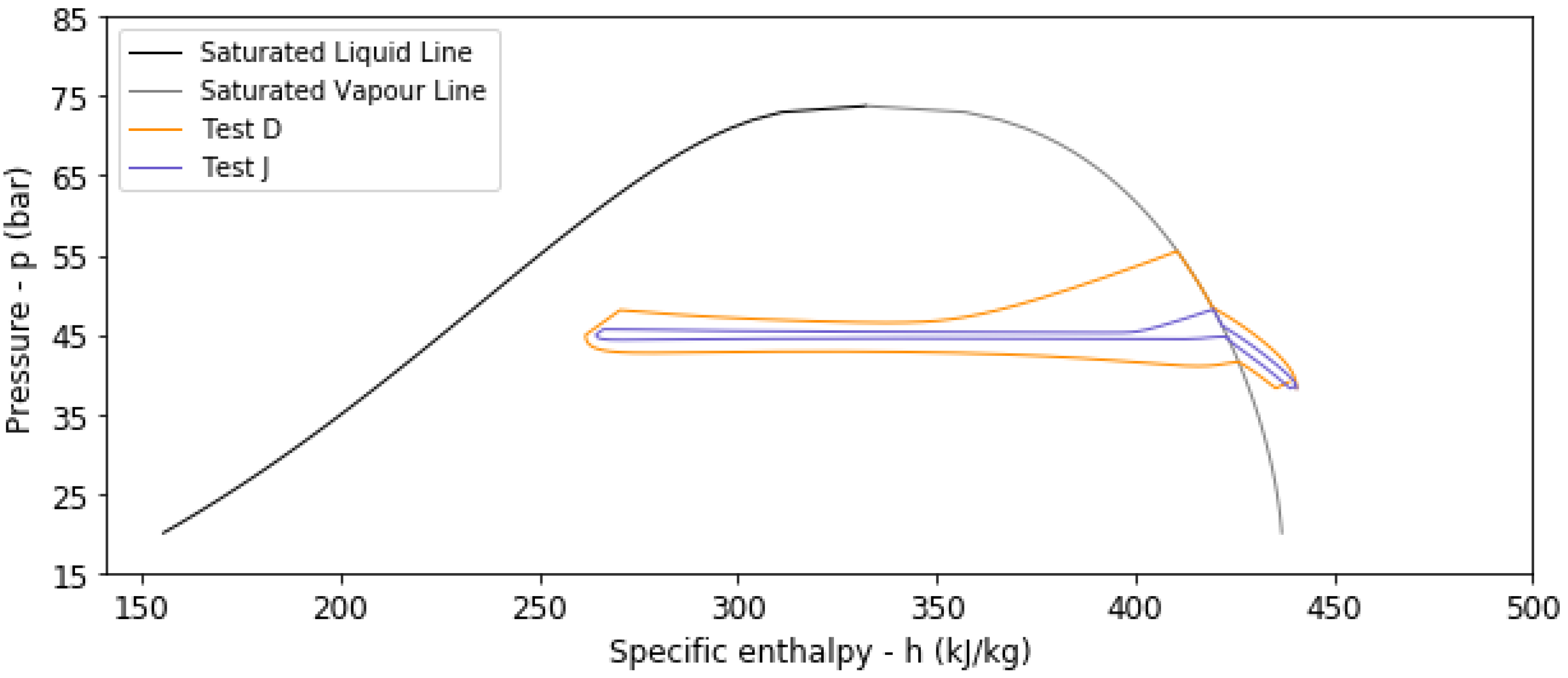
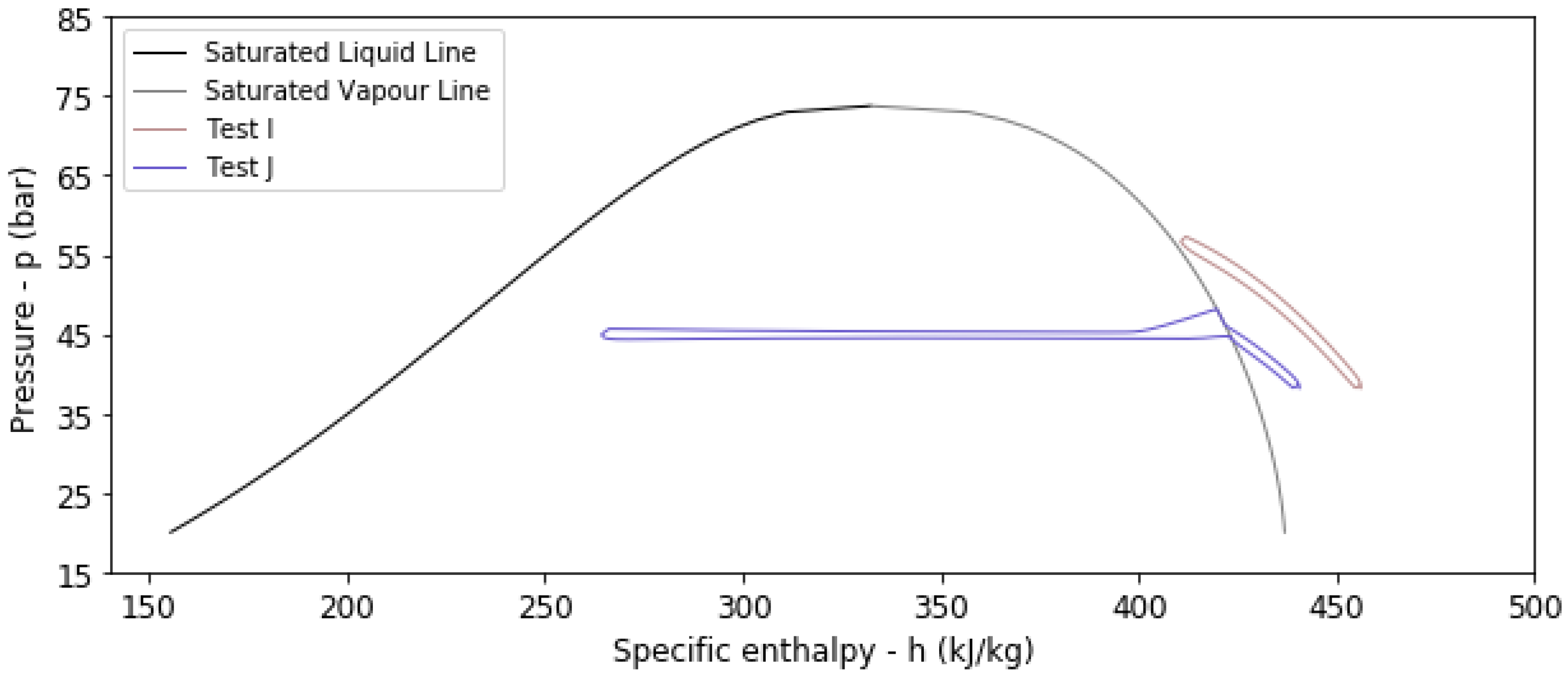
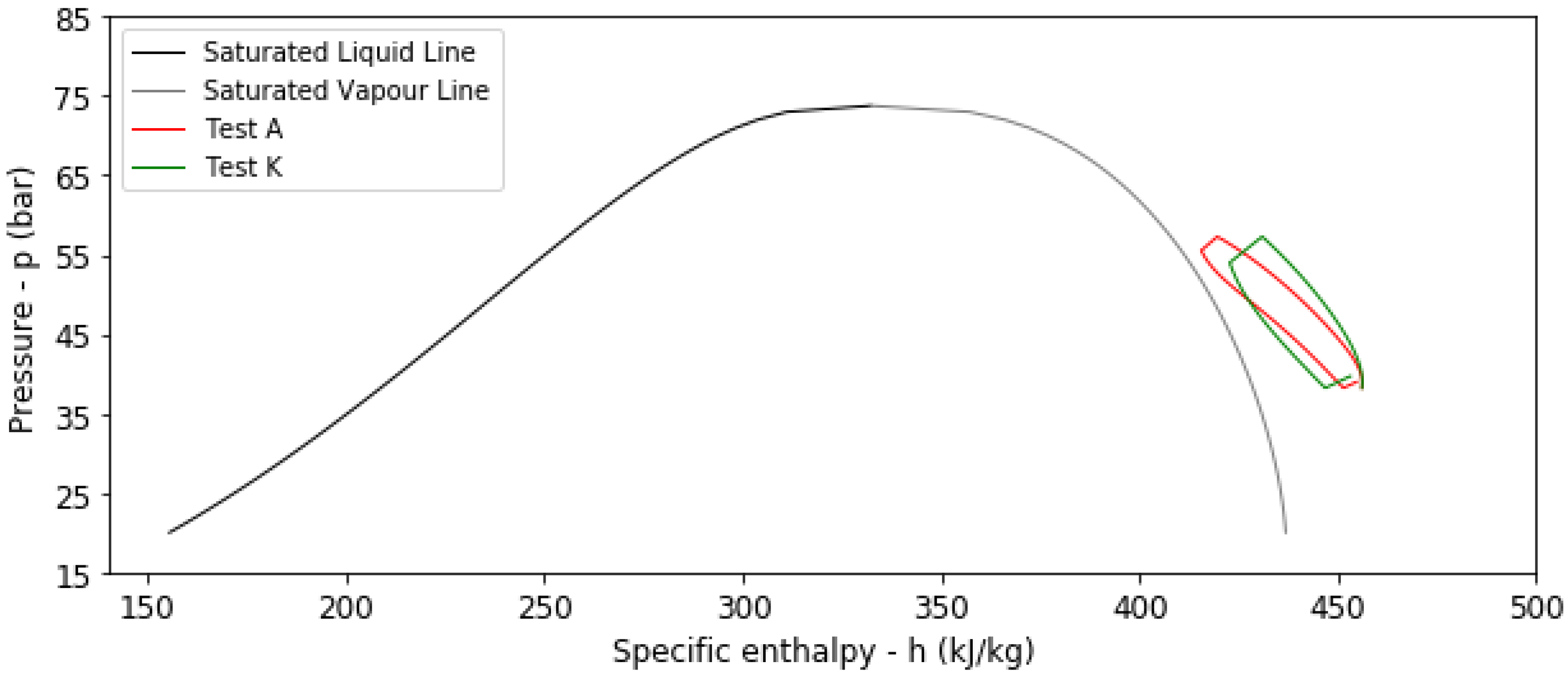
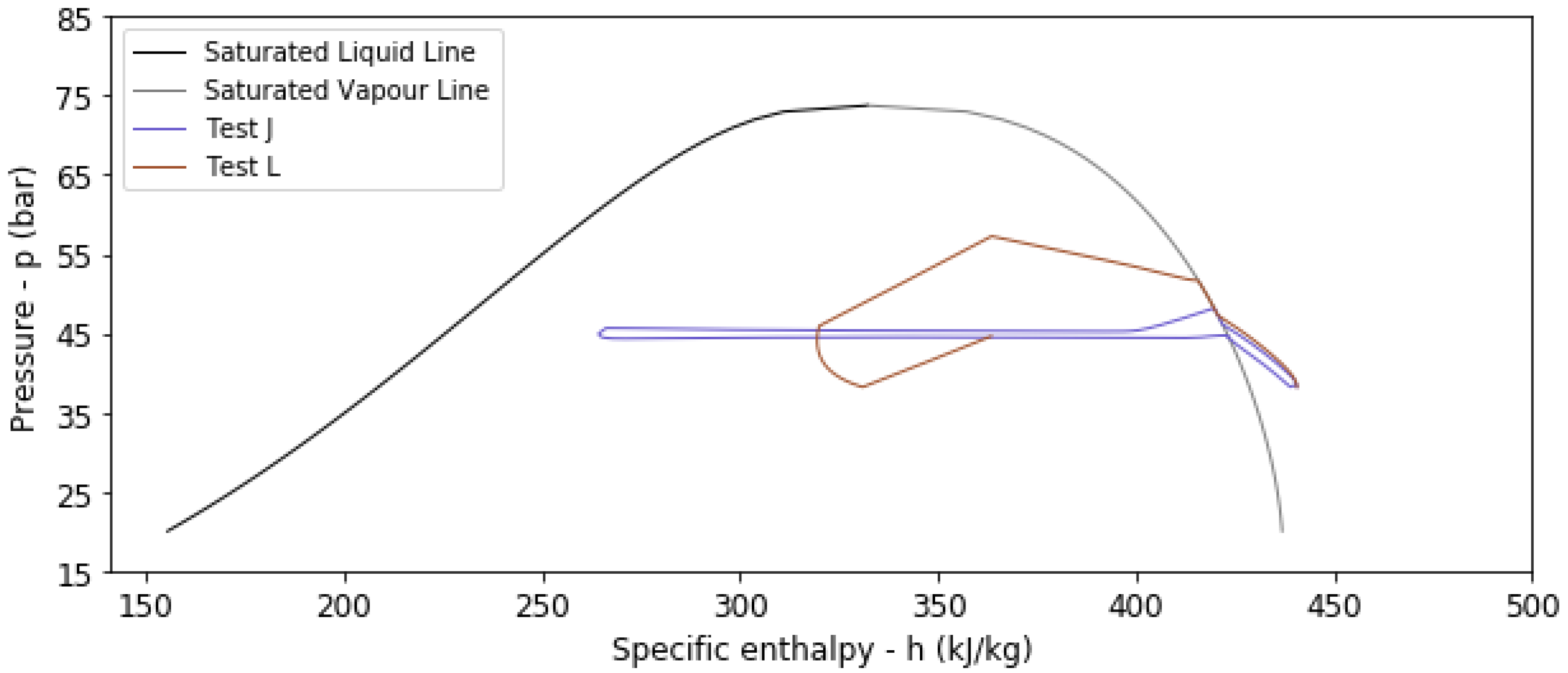
4.2. Results from Transient Thermal Analysis
5. Conclusions
- In an ideal scenario, where the CO2 gas is completely liquefied and the phase change process follows an isothermal path, the ESC (or ESD) of the HPES system operating at a peak pressure of 57.3 bar can be increased by a maximum augmentation factor α, of 2.17;
- The magnitude of α depends on multiple aspects including the dryness fraction x and the pressure ratio rp;
- The minimum α value of 1.17 has been achieved at an rp value of 3.5 and an x value of unity.
- Being limited to operate below the critical pressure of 73.8 bar limits the augmentation factor α that can be achieved;
- Transient thermal modelling that takes into account the resistance to heat transfer between the CO2 and the surrounding seawater has indicated that under certain conditions, the real operating cycle deviates appreciably from the ideal, isothermal scenario, resulting in instances when the CO2 remains in a gaseous state. Thus, despite a value of η beyond 0.90 being achievable, the ESC still remains significantly low;
- Simulations have also revealed that, for the test cases considered, operation of HPES-2 must be maintained below 288.15 K for CO2 to enter the transition region;
- Adding on to the previous point, the initial operating temperature T0 has been noted to be the main controlling parameter in determining whether the CO2 undergoes a phase change during the storage cycle (gas–liquid–gas);
- A change in dis/charging duration has been observed to contribute to a change in the η value. Yet, it does not regulate the condensation and evaporation of CO2;
- The presence of an HDPE liner reduces both the η and the β values.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Budt, M.; Wolf, D.; Span, R.; Yan, J. A Review on Compressed Air Energy Storage: Basic Principles, Past Milestones and Recent Developments. Appl. Energy 2016, 170, 250–268. [Google Scholar] [CrossRef]
- Odukomaiya, A.; Abu-Heiba, A.; Graham, S.; Momen, A.M. Experimental and Analytical Evaluation of a Hydro-pneumatic Compressed-Air Ground-Level Integrated Diverse Energy Storage (GLIDES) System. Appl. Energy 2018, 221, 75–85. [Google Scholar] [CrossRef]
- Enabling Large-Scale Offshore Energy Storage, FLASC—Renewable Energy Storage. Available online: https://offshoreenergystorage.com/ (accessed on 11 July 2024).
- Messer Group GmbH. Properties of Carbon Dioxide; Messer Group GmbH: Sulzbach, Germany.
- Vecchi, A.; Li, Y.; Ding, Y.; Mancarella, P.; Sciacovelli, A. Liquid air energy storage (LAES): A review on technology state-of-the-art, integration pathways and future perspectives. Adv. Appl. Energy 2021, 3, 10047. [Google Scholar] [CrossRef]
- Briffa, L.J.B.; Cutajar, C.; Sant, T.; Buhagiar, D. Numerical Modeling of the Thermal Behavior of Subsea Hydro-Pneumatic Energy Storage Accumulators Using Air and CO2. Energies 2022, 15, 8706. [Google Scholar] [CrossRef]
- Li, Y.; Yu, H.; Tang, D.; Li, Y.; Zhang, G.; Liu, Y. A Comparison of Compressed Carbon Dioxide Energy Storage and Compressed Air Energy Storage in Aquifers using Numerical Methods. Ren. Energy 2022, 187, 1130–1153. [Google Scholar] [CrossRef]
- Sun, W.; Liu, X.; Yang, X.; Yang, X.; Liu, Z. Design and Thermodynamic Performance Analysis of a New Liquid Carbon Dioxide Energy Storage System with Low Pressure Stores. Energy Convers. Manag. 2021, 239, 114227. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, K.; Hong, H.; Zhong, X.; Xu, J. Thermodynamic Analysis of a Novel Energy Storage System with Carbon Dioxide as Working Fluid. Ren. Energy 2016, 99, 682–697. [Google Scholar] [CrossRef]
- CO2 Battery, Energy Dome. Available online: https://energydome.com/co2-battery/ (accessed on 20 July 2024).
- Abu-Heiba, A.; Ally, M.R.; Smith, B.; Momen, A. Increasing Compressed Gas Energy Storage Density Using CO2–N2 Gas Mixture. Energies 2020, 13, 2431. [Google Scholar] [CrossRef]
- Cutajar, C.; Sant, T.; Briffa, L.J.B.; Buhagiar, D. Assessing the potential increase in the energy storage density of subsea hydro-pneumatic accumulators using CO2 in lieu of air. J. Therm. Sci. Eng. App. 2022, 15, 031001. [Google Scholar] [CrossRef]
- Churchill, S.W.; Chu, H.H.S. Correlation Equations for Laminar and Turbulent Free Convection from a Horizontal Cylinder. Int. J. Heat Mass Transf. 1975, 18, 1049–1053. [Google Scholar] [CrossRef]
- Churchill, S.W.; Bernstein, M.A. Correlating Equation for Forced Convection from Gases and Liquids to a Circular Cylinder in Crossflow. J. Heat Transf. 1977, 99, 300–306. [Google Scholar] [CrossRef]
- Ludovisi, D.; Garza, I.A. Natural Convection Heat Transfer in Horizontal Cylindrical Cavities: A Computational Fluid Dynamics (CFD) Investigation. In Proceedings of the ASME 2013 Power Conference, Boston, MA, USA, 29 July–1 August 2013. [Google Scholar]
- Gnielinski, V. New Equations for Heat and Mass Transfer in Turbulent Pipe and Channel Flow. Int. Chem. Eng. 1976, 16, 359–368. [Google Scholar]
- Thome, J.; El Hajal, J.; Cavallini, A. Condensation in horizontal tubes, part 2: New heat transfer model based on flow regimes. Int. J. Heat Mass Transf. 2003, 46, 3365–3387. [Google Scholar] [CrossRef]
- Fang, X. A new correlation of flow boiling heat transfer coefficients for carbon dioxide. Int. J. Heat Mass Transf. 2013, 64, 802–807. [Google Scholar] [CrossRef]
- Welcome to Python.org, Python. Available online: https://www.python.org/ (accessed on 25 July 2024).
- Cutajar, C.; Sant, T.; Farrugia, R.N.; Buhagiar, D. A Software Tool for the Design and Operational Analysis of Pressure Vessels Used in Offshore Hydro-Pneumatic Energy Storage. J. Energy Storage 2021, 40, 102750. [Google Scholar] [CrossRef]
- Download Mollier Charts, ChemicaLogic. Available online: https://www.chemicalogic.com/Pages/DownloadMollierCharts.html (accessed on 25 July 2024).
- Committed to the Environment (CE). CO2 Emissions of Private Aviation in Europe; Committed to the Environment (CE): Delft, The Netherlands, 2023. [Google Scholar]
- Williamson, T.D. Pipeline Services Pigging Products, Bulletin No: 3000.05.02; TDW: Tulsa, OK, USA, 2017. [Google Scholar]
- Zhu, X.; Zhang, S.; Li, X.; Wang, D.; Yu, D. Numerical simulation of contact force on bi-directional pig in gas pipeline: At the early stage of pigging. J. Nat. Gas Sci. Eng. 2015, 23, 127–138. [Google Scholar] [CrossRef]
- Canada’s Oil and Natural Gas Producers (CAPP). Use of High Density Polyethylene (HDPE) Lined Pipelines; Canada’s Oil and Natural Gas Producers (CAPP): Calgary, AB, Canada, 2022. [Google Scholar]
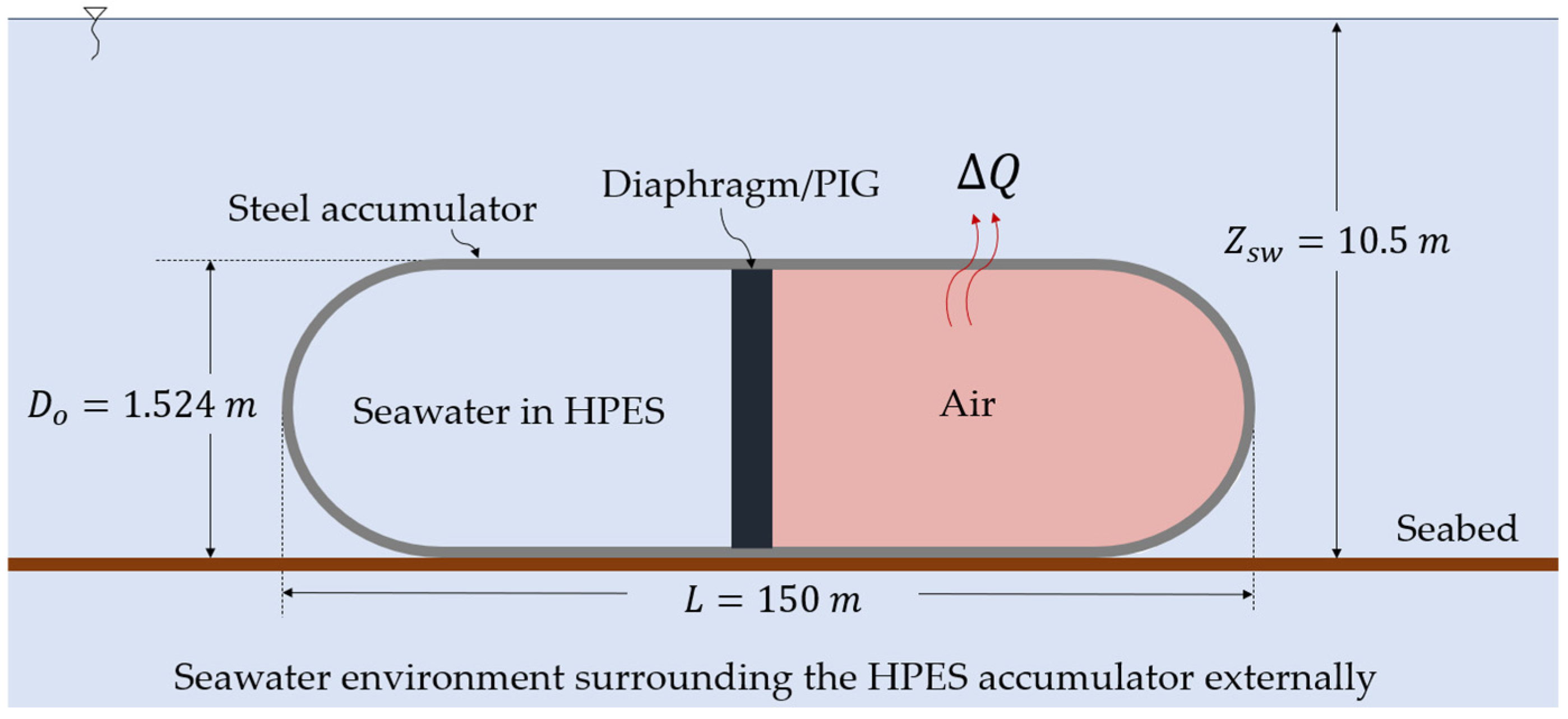
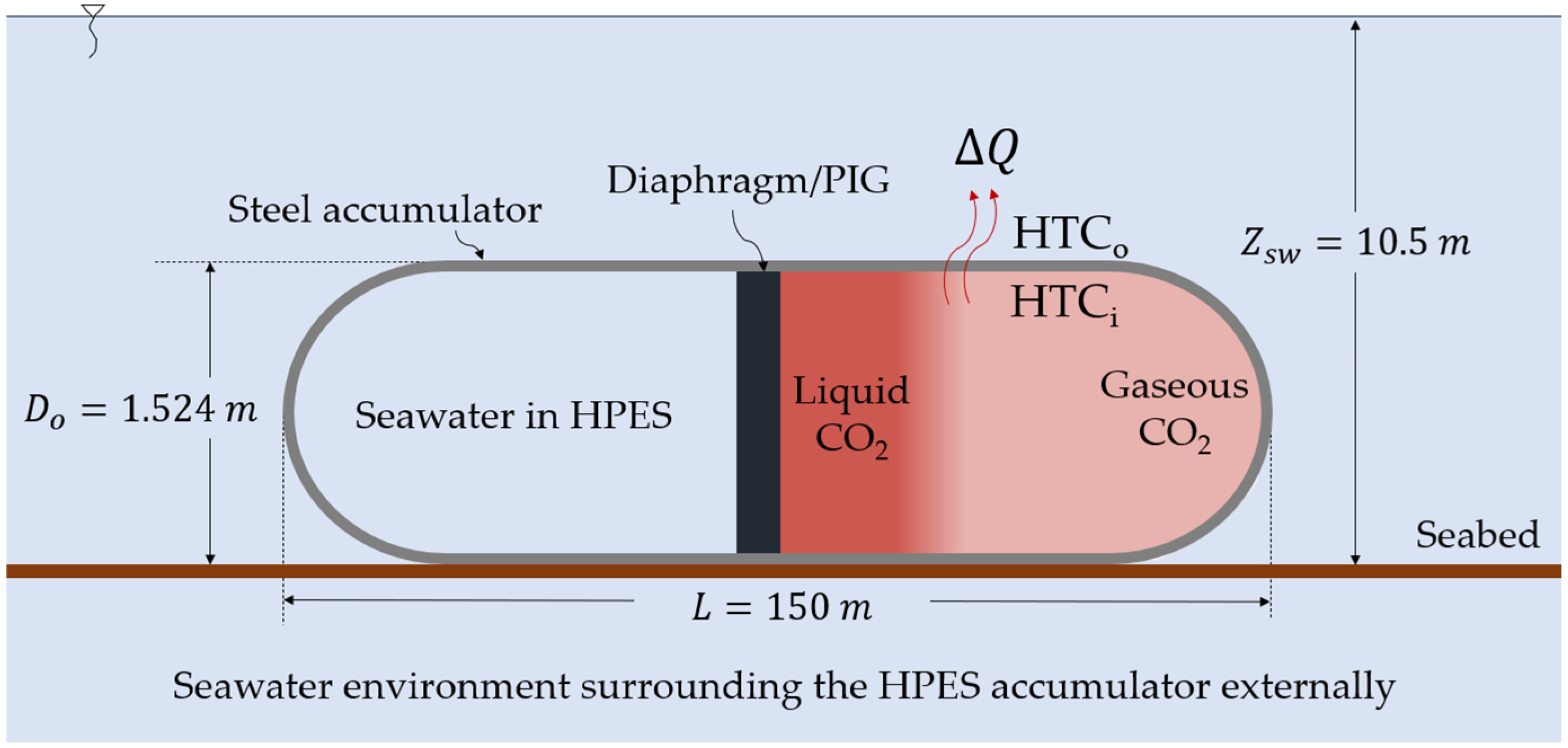


| Location | HTC | Type of Convection | Fluid | HTC |
|---|---|---|---|---|
| External | HTCo | Free | Seawater | Churchill-Chu [13] |
| External | HTCo | Forced | Seawater | Churchill-Bernstein [14] |
| Internal | HTCi | Free | Gaseous CO2 | Ludovisi-Garza [15] |
| Internal | HTCi | Forced | Gaseous CO2 | Gnielinski [16] |
| Location | HTC | Fluid | Phase Change Mode | HTC |
|---|---|---|---|---|
| Internal | HTCi | Two-phase CO2 | Condensing | Thome et al. [17] |
| Internal | HTCi | Two-phase CO2 | Evaporating | Fang et al. [18] |
| Parameter (Unit) | HPES-1 | HPES-2 |
|---|---|---|
| Compressible fluid | Air | CO2 |
| Peak pressure—pf (bar) | 57.30 | 57.30 |
| Initial pressure—p0 (bar) | 38.20 | 38.20 |
| Accumulator length—L (m) | 150 | 150 |
| Accumulator outer diameter—Do (m) | 1.524 | 1.524 |
| Accumulator inner diameter—Din (m) | 1.49 | 1.49 |
| Accumulator wall thickness—ew (mm) | 17.06 | 17.06 |
| Volumetric capacity—Vc (m3) | 261 | 261 |
| Mass of steel—ms (t) | 95 | 95 |
| Mass of working fluid—mair or mCO2 (t) | 7 | 24 |
| Ideal ESC—ESCi (kWh) | 148 | 320 |
| Test | HDPE Liner (-) | Initial Temp T0 (K) | Pressure Ratio rp (-) | Dis/Charging Time t (h) | Ideal ES C 1 ESCi (kWh) | Real ES C 2 ESCr (kWh) | Efficiency η (-) | ESC Factor β (-) |
|---|---|---|---|---|---|---|---|---|
| A | No | 293.15 | 1.5 | 6 | 320 | 160 | 0.9081 | 0.5056 |
| B | No | 293.15 | 2.5 | 6 | 262 | 177 | 0.9151 | 0.6778 |
| C | No | 293.15 | 3.5 | 6 | 220 | 161 | 0.9074 | 0.7337 |
| D | No | 283.15 | 1.5 | 6 | 260 | 248 | 0.8591 | 0.9519 |
| E | No | 288.15 | 1.5 | 6 | 288 | 166 | 0.8752 | 0.5774 |
| F | No | 298.15 | 1.5 | 6 | 340 | 149 | 0.9109 | 0.4369 |
| G | No | 293.15 | 1.5 | 3 | 320 | 150 | 0.8437 | 0.4765 |
| H | No | 293.15 | 1.5 | 12 | 320 | 165 | 0.9467 | 0.5240 |
| I | No | 293.15 | 1.5 | 24 | 320 | 169 | 0.9690 | 0.5351 |
| J | No | 283.15 | 1.5 | 24 | 260 | 234 | 0.9648 | 0.8973 |
| K | Yes | 293.15 | 1.5 | 6 | 285 | 131 | 0.8293 | 0.4584 |
| L | Yes | 283.15 | 1.5 | 24 | 235 | 178 | 0.2255 | 0.7580 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cutajar, C.; Sant, T.; Briffa, L.J. Using Carbon Dioxide for Subsea Long-Duration Energy Storage. Gases 2024, 4, 295-309. https://doi.org/10.3390/gases4030017
Cutajar C, Sant T, Briffa LJ. Using Carbon Dioxide for Subsea Long-Duration Energy Storage. Gases. 2024; 4(3):295-309. https://doi.org/10.3390/gases4030017
Chicago/Turabian StyleCutajar, Charise, Tonio Sant, and Luke Jurgen Briffa. 2024. "Using Carbon Dioxide for Subsea Long-Duration Energy Storage" Gases 4, no. 3: 295-309. https://doi.org/10.3390/gases4030017
APA StyleCutajar, C., Sant, T., & Briffa, L. J. (2024). Using Carbon Dioxide for Subsea Long-Duration Energy Storage. Gases, 4(3), 295-309. https://doi.org/10.3390/gases4030017