A Parametric Study of the Dynamic Soil–Structure Interaction for Shear Vulnerable Structures with Nonlinear Finite Element Modelling
Abstract
:1. Introduction
2. Dynamic Soil–Structure Interaction Formulation and Implicit Integration Algorithm
3. Nonlinear Computational Dynamics and the Energy Dissipation Dashpot through the Lysmer Proposal
4. Numerical Simulations of Shear Cantilevers of Free Field and Soil–Structure Interaction Systems in Dynamic Loading-Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mylonakis, G.; Gazetas, G. Seismic soils tructure interaction: Beneficial or Detrimental? J. Earthq. Eng. 2000, 4, 277–301. [Google Scholar] [CrossRef]
- Wegner, J.; Yao, M.; Zhang, X. Dynamic wave–soil–structure interaction analysis in the time domain. Comput. Struct. 2005, 83, 2206–2214. [Google Scholar] [CrossRef]
- Saouma, V.; Miura, F.; Lebon, G.; Yagome, Y. A simplified 3D model for soil-structure interaction with radiation damping and free field input. Bull. Earthq. Eng. 2011, 9, 1387–1402. [Google Scholar] [CrossRef]
- Wang, G.; Wang, Y.; Pan, P.; Wang, J. Experimental and numerical investigation on seismic response of the soil-structure cluster interaction system. Eng. Struct. 2023, 285, 116001. [Google Scholar] [CrossRef]
- Zucca, M.; Crespi, P.G.; Longarini, N. Seismic vulnerability assessment of an Italian historical masonry dry dock. Case Stud. Struct. Eng. 2017, 7, 1–23. [Google Scholar] [CrossRef]
- Dong, J.; Niu, Z.; Li, J.; Hong, G.; Pan, J.; Li, H. System identification of excited beam immersed in granular materials: A multifrequency data-based method in a variational framework. Eng. Struct. 2023, 293, 116611. [Google Scholar] [CrossRef]
- Chen, S.S.; Hou, J.G. Response of circular flexible foundations subjected to horizontal and rocking motions. Soil Dyn. Earthq. Eng. 2015, 69, 182–195. [Google Scholar] [CrossRef]
- Sheng, T.; Liu, G.B.; Bian, X.C.; Shi, W.X.; Chen, Y. Development of a three-directional vibration isolator for buildings subject to metro- and earthquake-induced vibrations. Eng. Struct. 2022, 252, 113576. [Google Scholar] [CrossRef]
- Zucca, M.; Valente, M. On the limitations of decoupled approach for the seismic behaviour evaluation of shallow multi-propped underground structures embedded in granular soils. Eng. Struct. 2020, 211, 110497. [Google Scholar] [CrossRef]
- Connolly, D.P.; Marecki, G.P.; Kouroussis, G.; Thalassinakis, I.; Woodward, P.K. The growth of railway ground vibration problems — A review. Sci. Total Environ. 2016, 568, 1276–1282. [Google Scholar] [CrossRef]
- Kavvadas, M.; Amorosi, A. A constitutive model for structured soils. Geotechnique 2000, 50, 263–273. [Google Scholar] [CrossRef]
- Savvides, A.; Papadrakakis, M. A computational study on the uncertainty quantification of failure of clays with a modified Cam-Clay yield criterion. Springer Nat. Appl. Sci. 2021, 3, 659. [Google Scholar] [CrossRef]
- Savvides, A.; Papadopoulos, L. A Neural Network Model for Estimation of Failure Stresses and Strains in Cohesive Soils. Geotechnics 2022, 2, 1084–1108. [Google Scholar] [CrossRef]
- İmamoğlu, Ç.; Dicleli, M. Effect of dynamic soil-structure interaction modeling assumptions on the calculated seismic response of railway bridges with single-column piers resting on shallow foundations. Soil Dyn. Earthq. Eng. 2024, 181, 108624. [Google Scholar] [CrossRef]
- Korre, E.; Zeghal, M.; Abdoun, T. Liquefaction in the presence of soil-structure interaction: Centrifuge tests of a sheet-pile quay wall in LEAP-2020. Soil Dyn. Earthq. Eng. 2024, 181, 108650. [Google Scholar] [CrossRef]
- Wu, Y.; Zhao, M.; Gao, Z.; Du, X. Seismic performance analysis of structure equipped with tuned mass dampers considering nonlinear soil-structure interaction effects. Structures 2024, 63, 106425. [Google Scholar] [CrossRef]
- Liu, B.; Xue, J.; Lehane, B.M.; Yin, Z.Y. Time-dependent soil–structure interaction analysis using a macro-element foundation model. Eng. Struct. 2024, 308, 118046. [Google Scholar] [CrossRef]
- Abdulaziz, M.A.; Hamood, M.J.; Fattah, M.Y. Investigating seismic behavior in adjacent structures: A study on the impact of structures embedment level and existence of dead loads considering soil-structure interaction. Results Eng. 2024, 22, 102023. [Google Scholar] [CrossRef]
- Ocak, A.; Melih Nigdeli, S.; Bekdaş, G. Optimization of the base isolator systems by considering the soil-structure interaction via metaheuristic algorithms. Structures 2023, 56, 104886. [Google Scholar] [CrossRef]
- Forcellini, D. The role of Soil Structure Interaction (SSI) on the risk of pounding between low-rise buildings. Structures 2023, 56, 105014. [Google Scholar] [CrossRef]
- Abdulaziz, M.A.; Hamood, M.J.; Fattah, M.Y. A review study on seismic behavior of individual and adjacent structures considering the soil – Structure interaction. Structures 2023, 52, 348–369. [Google Scholar] [CrossRef]
- Genç, A.F.; Atmaca, E.E.; Günaydin, M.; Altunişik, A.C.; Sevim, B. Evaluation of soil structure interaction effects on structural performance of historical masonry buildings considering earthquake input models. Structures 2023, 54, 869–889. [Google Scholar] [CrossRef]
- Shang, H.; Bao, C.; Wang, H.; Ma, X.; Cao, J.; Du, J. Seismic response analysis of frame structures with uneven settlement of foundation considering soil-structure interaction. Results Eng. 2023, 20, 101574. [Google Scholar] [CrossRef]
- Cheng, F.; Li, J.; Zhou, L.; Lin, G. Fragility analysis of nuclear power plant structure under real and spectrum-compatible seismic waves considering soil-structure interaction effect. Eng. Struct. 2023, 280, 115684. [Google Scholar] [CrossRef]
- Han, Q.; Wu, C.; Liu, M.; Wu, H. Corotational isogeometric shear deformable geometrically exact spatial form beam element for general large deformation analysis of flexible thin-walled beam structures. Thin-Walled Struct. 2024, 198, 111684. [Google Scholar] [CrossRef]
- Bielak, J.; Christiano, P. On the effective seismic input for non-linear soil-structure interaction systems. Earthq. Eng. Struct. Dyn. 1984, 12, 107–119. [Google Scholar] [CrossRef]
- Ceremonini, M.; Christiano, P.; Bielak, J. Implementation of effective seismic input for soil-structure interaction systems. Earthq. Eng. Struct. Dyn. 1988, 16, 615–625. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Z.; Bielak, J.; Conte, P.; Elgamal, A.W. Treatment of seismic input and boundary conditions in nonlinear seismic analysis of a bridge ground system. In Proceedings of the Conference: 16-th ASCE Engineering Mechanics Conference, Seattle, WA, USA, 16–18 July 2003; University of Washington: Seattle, WA, USA, 2003. [Google Scholar]
- Fattah, M.Y. A New Mapped Infinite Element for Dynamic Analysis of Soil-Structure Interaction Problems. Diyala J. Eng. Sci. 2010, 327–355. [Google Scholar]
- Fattah, M.Y.; Hamood, M.J.; Dawood, S.H. Dynamic Analysis of Soil-Structure Interaction Problems Considering Infinite Boundaries. Eng. Technol. J. Univ. Technol. 2008, 26, 725–746. [Google Scholar] [CrossRef]
- Fattah, M.Y.; Hamood, M.J.; Dawood, S.H. Dynamic Response of a Lined Tunnel with Transmitting Boundaries. Earthq. Struct. 2015, 8, 275–304. [Google Scholar] [CrossRef]
- Abdulrasool, A.S.; Fattah, M.Y.; Salim, N.M. Application of Energy Absorbing Layer to Soil-structure Interaction Analysis. IOP Conf. Ser. Mater. Sci. Eng. 2020, 737, 012094. [Google Scholar] [CrossRef]
- Tullini, N.; Tralli, A. Static analysis of Timoshenko beam resting on elastic half-plane based on the coupling of locking-free finite elements and boundary integral. Comput. Mech. 2010, 45, 211–225. [Google Scholar] [CrossRef]
- Baraldi, D.; Tullini, N. In-plane bending of Timoshenko beams in bilateral frictionless contact with an elastic half-space using a coupled FE-BIE method. Eng. Anal. Bound. Elem. 2018, 97, 114–130. [Google Scholar] [CrossRef]
- Baraldi, D.; Tullini, N. Static stiffness of rigid foundation resting on elastic half-space using a Galerkin boundary element method. Eng. Struct. 2020, 225, 111061. [Google Scholar] [CrossRef]
- Hu, Z.P.; Pan, W.H.; Tong, J.Z. Exact Solutions for Buckling and Second-Order Effect of Shear Deformable Timoshenko Beam–Columns Based on Matrix Structural Analysis. Appl. Sci. 2019, 9, 3814. [Google Scholar] [CrossRef]
- Choi, M.J.; Cho, S. Isogeometric configuration design sensitivity analysis of geometrically exact shear-deformable beam structures. Comput. Methods Appl. Mech. Eng. 2019, 351, 153–183. [Google Scholar] [CrossRef]
- Banić, D.; Turkalj, G.; Lanc, D. Stability analysis of shear deformable cross-ply laminated composite beam-type structures. Compos. Struct. 2023, 303, 116270. [Google Scholar] [CrossRef]
- Reddy, J. On locking-free shear deformable beam finite elements. Comput. Methods Appl. Mech. Eng. 1997, 149, 113–132. [Google Scholar] [CrossRef]
- Challamel, N.; Elishakoff, I. A brief history of first-order shear-deformable beam and plate models. Mech. Res. Commun. 2019, 102, 103389. [Google Scholar] [CrossRef]
- Thatikonda, N.P.; Baraldi, D.; Boscato, G.; Cecchi, A. Experimental evaluation of elastic shear components for masonry in a Cosserat Continuum. Int. J. Solids Struct. 2024, 292, 112715. [Google Scholar] [CrossRef]
- Elmeligy, O.; AbdelRahman, B.; Galal, K. Experimental investigation of the compressive and shear behaviours of grouted and hollow masonry constructed with PVA fibre-reinforced mortar and grout. Constr. Build. Mater. 2024, 415, 134954. [Google Scholar] [CrossRef]
- Wang, B.; Yin, S.; Qu, F.; Wang, F. Cyclic shear test and finite element analysis of TRC-reinforced damaged confined masonry walls. Constr. Build. Mater. 2024, 421, 135766. [Google Scholar] [CrossRef]
- Namlı, M.; Aras, F. Performance evaluation of a seismic strengthening applied on a masonry school building by dynamic analyses. Structures 2024, 62, 106200. [Google Scholar] [CrossRef]
- Silvestri, F.; de Silva, F.; Piro, A.; Parisi, F. Soil-structure interaction effects on out-of-plane seismic response and damage of masonry buildings with shallow foundations. Soil Dyn. Earthq. Eng. 2024, 177, 108403. [Google Scholar] [CrossRef]
- de Araújo, F.C.; Ribeiro, I.S.; Machado, R.M. Nonlinear analysis of semirigid steel frames having nonprismatic shear-deformable members. Eng. Struct. 2022, 257, 114047. [Google Scholar] [CrossRef]
- Qiu, Z.; Deng, M.; Tian, X.; Li, T.; Sun, H.; Cao, J. Experimental study and theoretical analysis on steel frames infilled high-ductility concrete shear walls. Constr. Build. Mater. 2024, 434, 136739. [Google Scholar] [CrossRef]
- Moeinifard, P.; Ghiami Azad, A.R.; Mirghaderi, S.R. Numerical comparison of truss-shaped lateral load-resisting systems with conventional steel shear walls. Structures 2024, 62, 106261. [Google Scholar] [CrossRef]
- He, M.; Zhang, Q.; Sun, X.; Alhaddad, W. An experimental and numerical study on the shear performance of friction-type high-strength bolted connections used for CLT-steel hybrid shear walls. Eng. Struct. 2024, 306, 117868. [Google Scholar] [CrossRef]
- Jiang, Z.Q.; Wang, J.J.; Shen, C.J.; Yan, T.; Su, L. Cyclic loading behavior of novel internally stiffened double steel plate shear wall. J. Build. Eng. 2024, 90, 109462. [Google Scholar] [CrossRef]
- Zimos, D.K.; Mergos, P.E.; Papanikolaou, V.K.; Kappos, A.J. Analysis of shear-critical reinforced concrete columns under variable axial load. Mag. Concr. Res. 2022, 74, 715–726. [Google Scholar] [CrossRef]
- Liang, D.; Xue, F. Integrating automated machine learning and interpretability analysis in architecture, engineering and construction industry: A case of identifying failure modes of reinforced concrete shear walls. Comput. Ind. 2023, 147, 103883. [Google Scholar] [CrossRef]
- Ivanov, M.L.; Chow, W.K. Structural damage observed in reinforced concrete buildings in Adiyaman during the 2023 Turkiye Kahramanmaras Earthquakes. Structures 2023, 58, 105578. [Google Scholar] [CrossRef]
- El-Azizy, O.A.; Ezzeldin, M.; El-Dakhakhni, W. Comparative analyses of reinforced masonry and reinforced concrete shear walls with different end configurations: Seismic performance and economic assessment. Eng. Struct. 2023, 296, 116852. [Google Scholar] [CrossRef]
- Yamada, H.; Yamada, R.; Tani, M.; Nishiyama, M. Damage evaluation for reinforced concrete shear walls via motion capture and optical fiber sensors. Structures 2024, 60, 105955. [Google Scholar] [CrossRef]
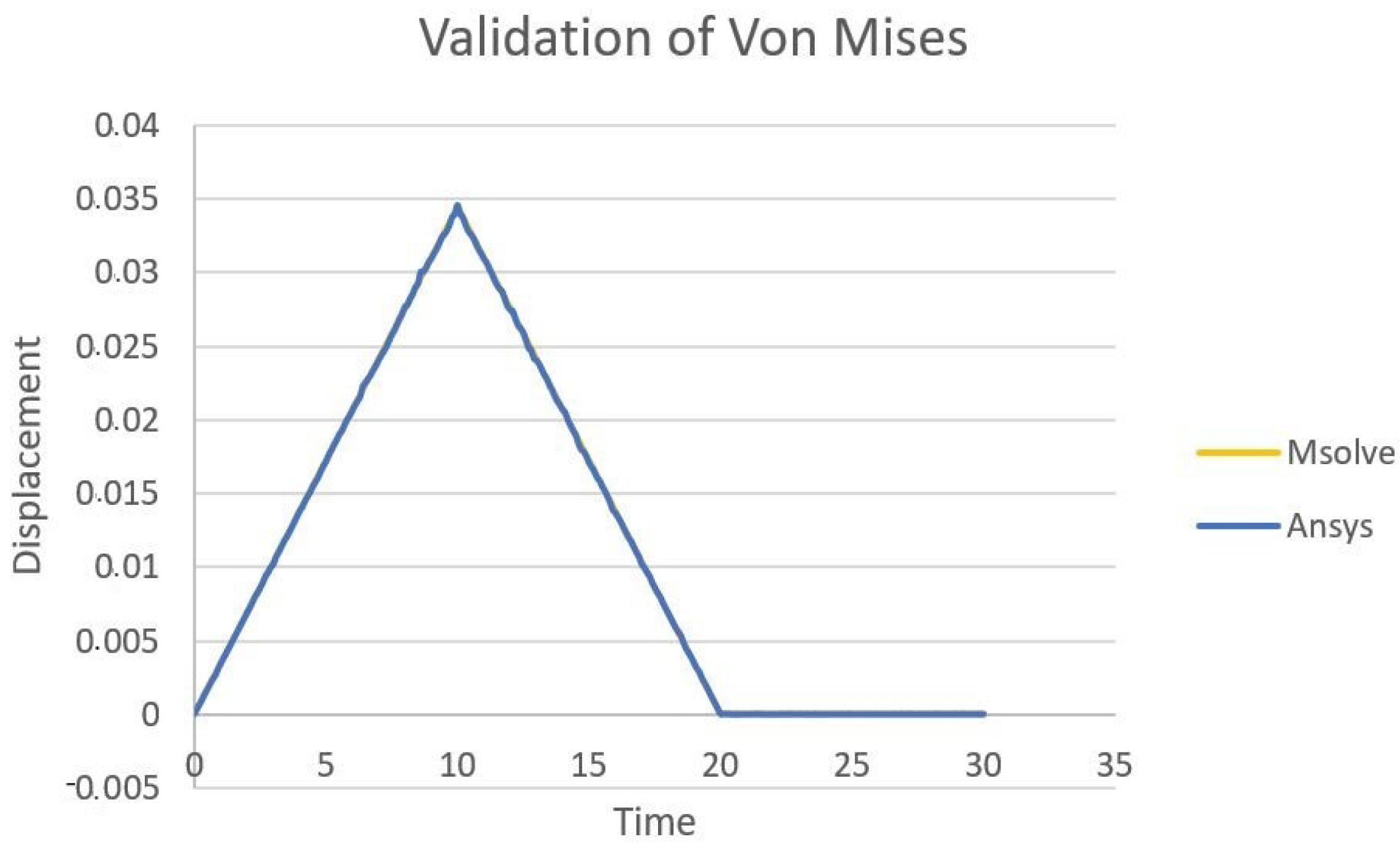
- MIDAS Users Manual. Available online: https://manual.midasuser.com/en_common/GTS%20NX/150/GTS_NX/Mesh/Property,Coordinate,Function/Material/General_Material(Behavioral_properties)/von_Mises.htm (accessed on 29 June 2024).
- Roscoe, K.; Schofield, A.; Thurairajah, A. Laboratory shear testing of soils: An Evaluation of Test Data for Selecting a Yield Criterion for Soils. In The Symposium on Laboratory Shear Testing of Soils, ASTM Committee D18 on Soils for Engineering Purposes and the National Research Council of Canada; ASTM International: West Conshohocken, PA, USA, 1963; Volume 1. [Google Scholar]
- Chakraborty, D.; Kumar, J. Use of von Mises yield criterion for solving axisymmetric stability problems. Geomech. Geoeng. 2015, 10, 234–241. [Google Scholar] [CrossRef]
- Newmark, N.M. A method of computation for structural dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. Available online: https://engineering.purdue.edu/~ce573/Documents/Newmark_A%20Method%20of%20Computation%20for%20Structural%20Dynamics.pdf (accessed on 29 June 2024).
- Simo, J.; Tarnow, N.; Wong, K. Exact energy-momentum conserving algorithms and symplectic schemes for nonlinear dynamics. Comput. Methods Appl. Mech. Eng. 1992, 100, 63–116. [Google Scholar] [CrossRef]
- Chang, S.Y. A technique for overcoming load discontinuity in using Newmark method. J. Sound Vib. 2007, 304, 556–569. [Google Scholar] [CrossRef]
- Lysmer, J.; Kuhlemeyer, R.L. Finite dynamic model for infinite media. ASCE J. Eng. Mech. Div. 1969, 95, 859–877. [Google Scholar] [CrossRef]
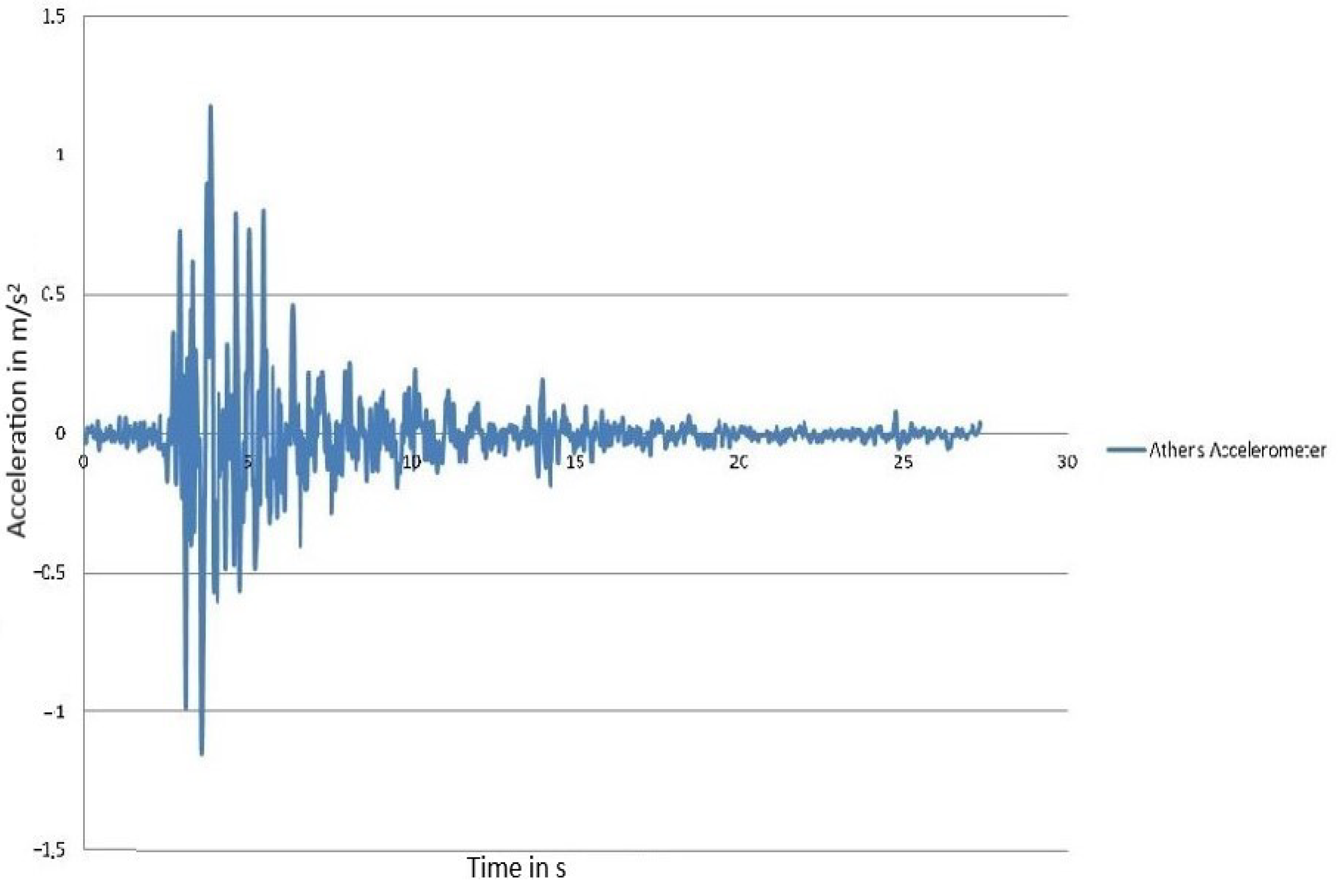
- Lekkas, E. The Athens earthquake (7 September 1999): Intensity distribution and controlling factors. Eng. Geol. 2001, 59, 297–311. [Google Scholar] [CrossRef]
- Mylonakis, G.; Voyagaki, E.; Price, T. Damage Potential of the 1999 Athens, Greece, Accelerograms. Bull. Earthq. Eng. 2003, 1, 205–240. [Google Scholar] [CrossRef]
- Renzi, S.; Madiai, C.; Vanucchi, G. A simplified empirical method for assessing seismic soil-structure interaction effects on ordinary shear-type buildings. Soil Dyn. Earthq. Eng. 2013, 55, 100–107. [Google Scholar] [CrossRef]
- Taucer, F.; Spacone, E.; Filippou, F. A Fiber Beam-Column Element for Seismic Response Analysis of Reinforced Concrete Structures; Earthquake Engineering Research Center, College of Engineering, University of California: Berkeley, CA, USA, 1991. [Google Scholar]
- Papachristidis, A.; Fragiadakis, M.; Papadrakakis, M. A 3D fibre beam-column element with shear modelling for the inelastic analysis of steel structures. Comput. Mech. 2010, 45, 553–572. [Google Scholar] [CrossRef]
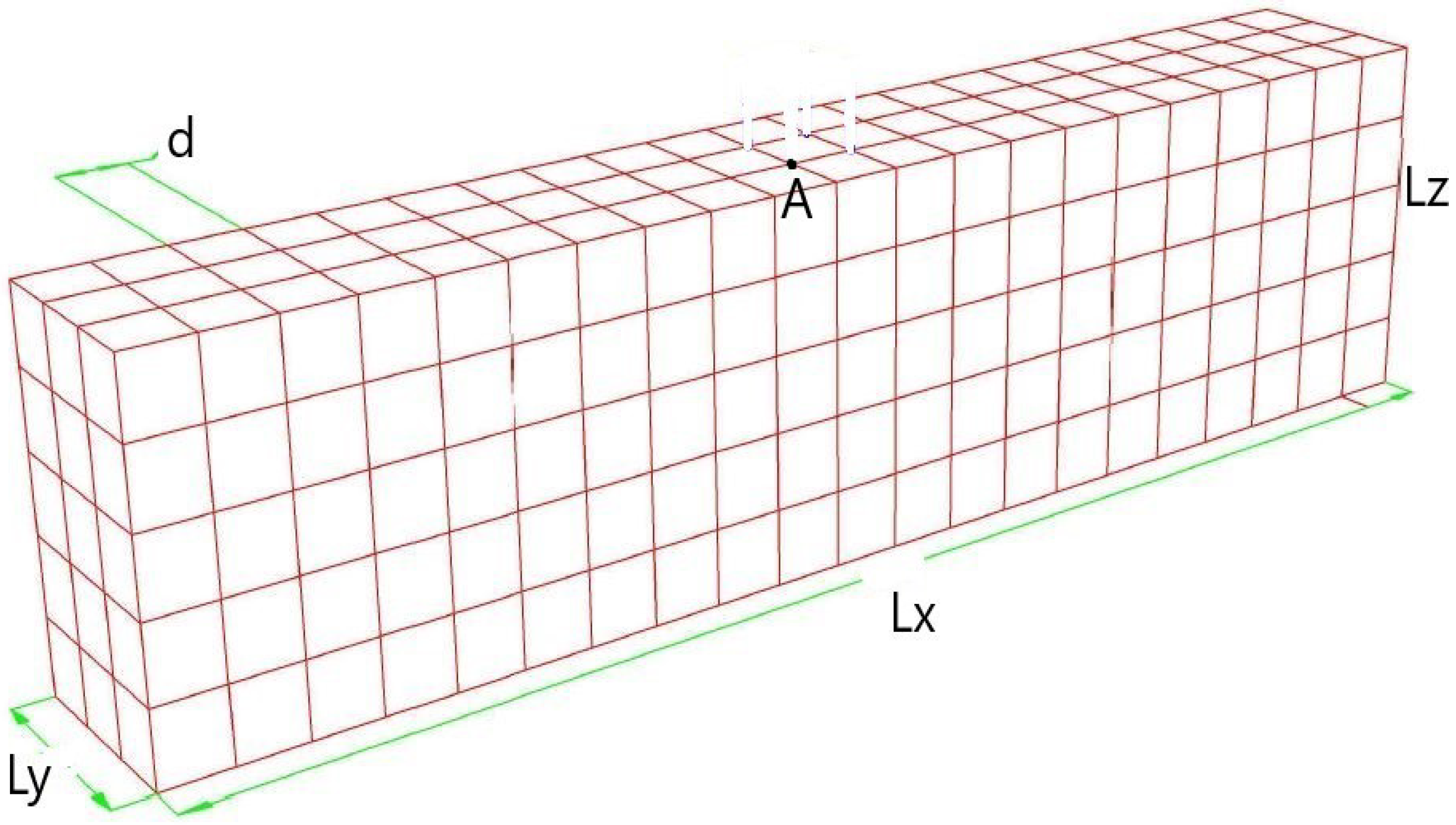
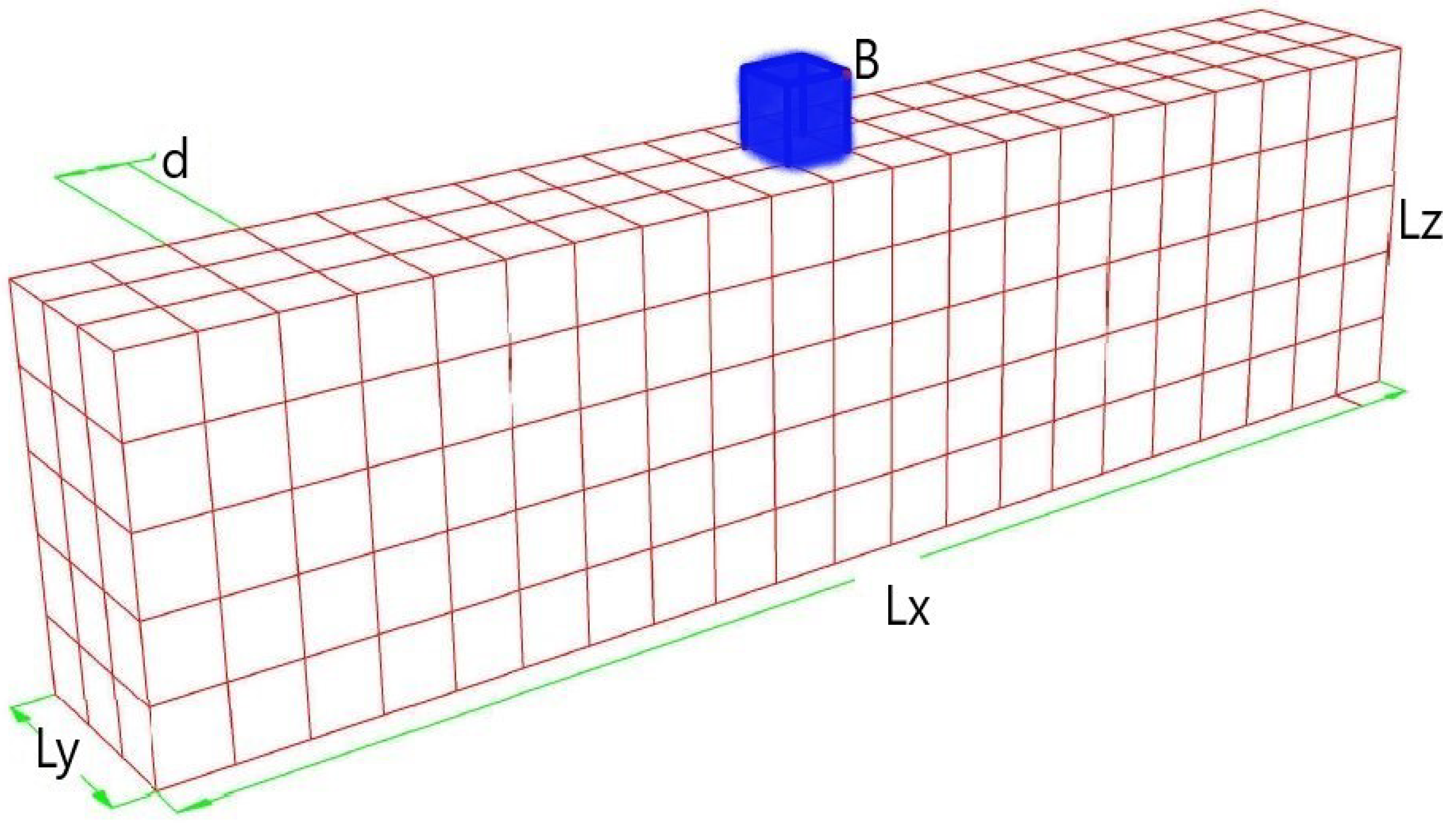

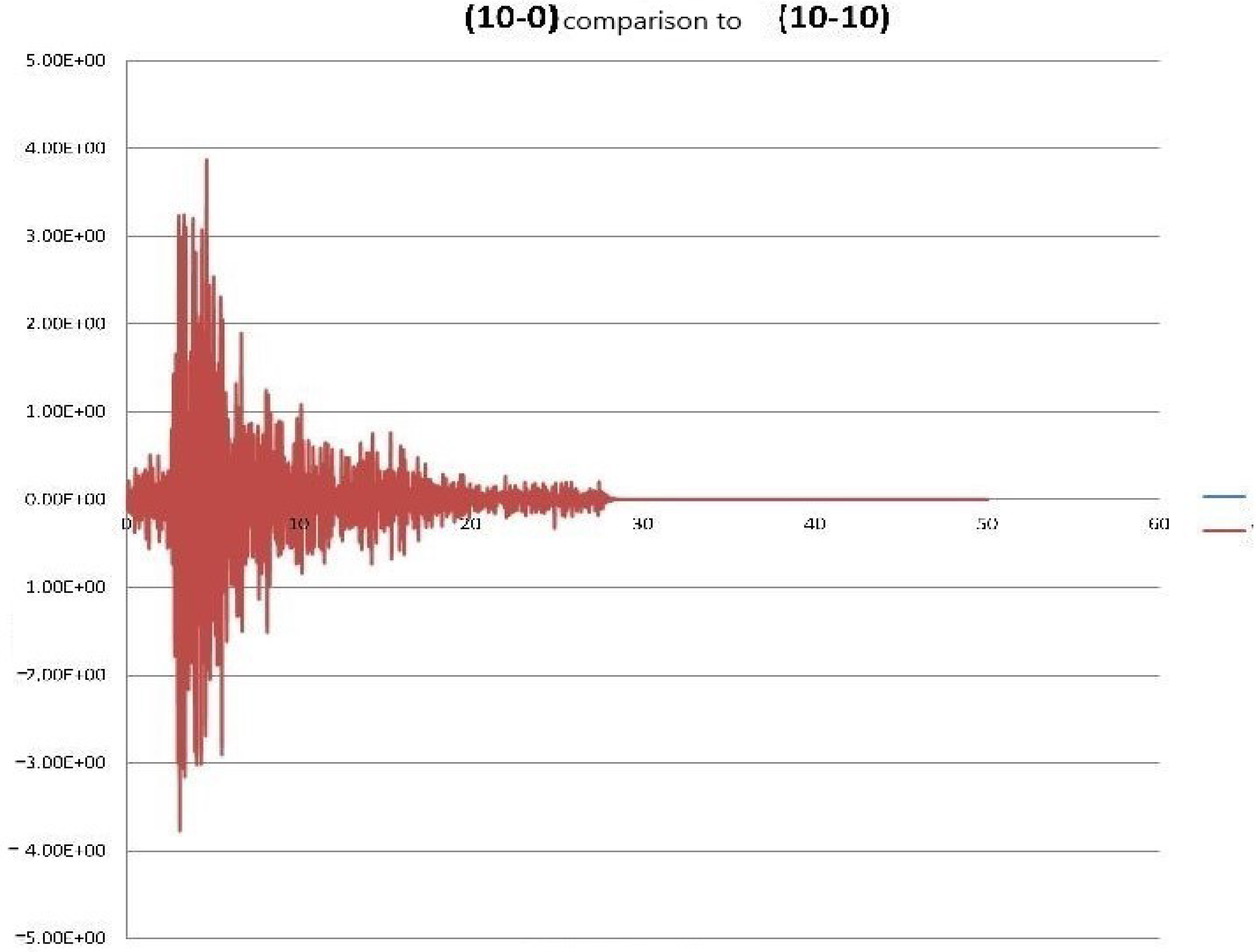
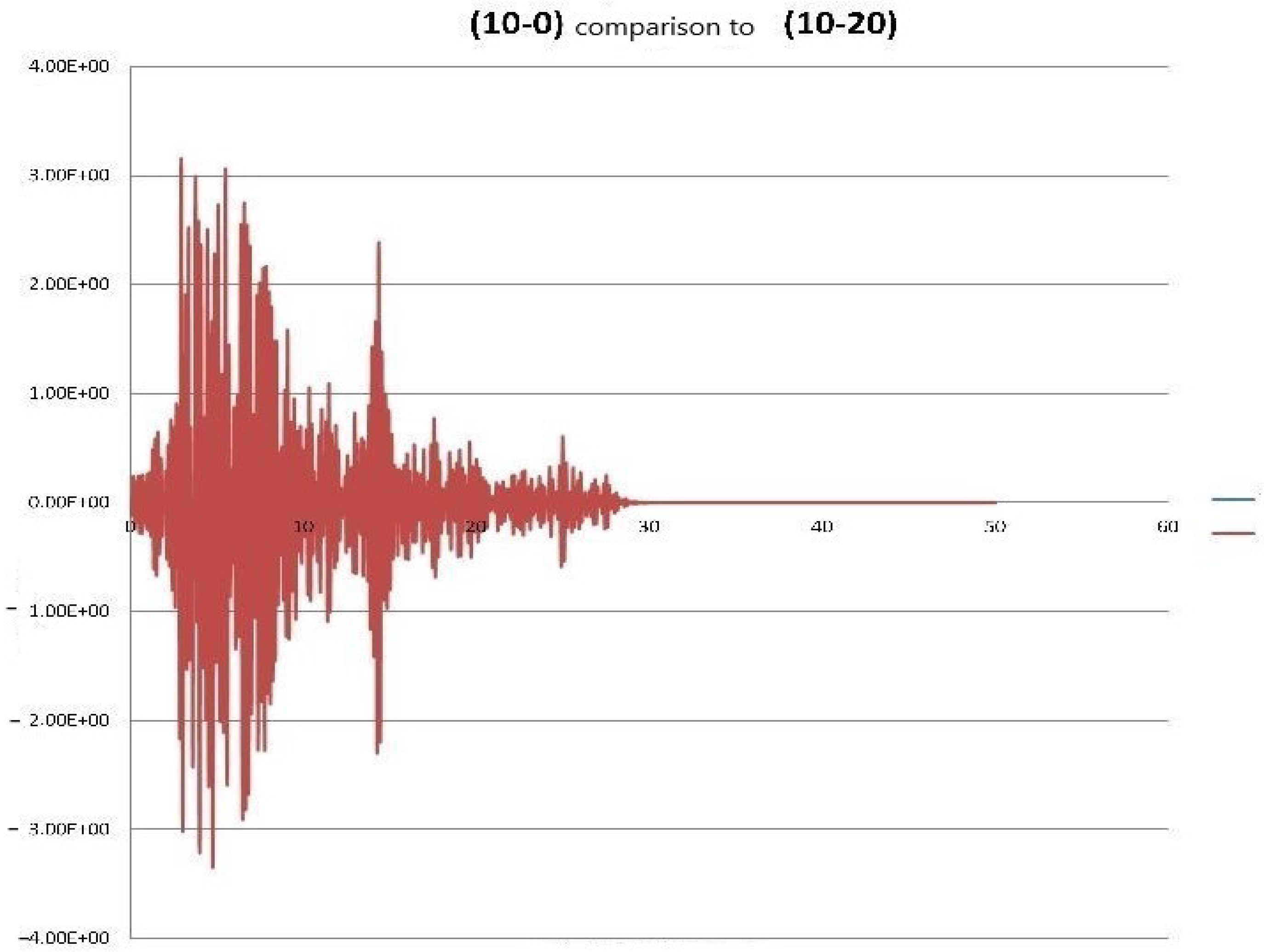

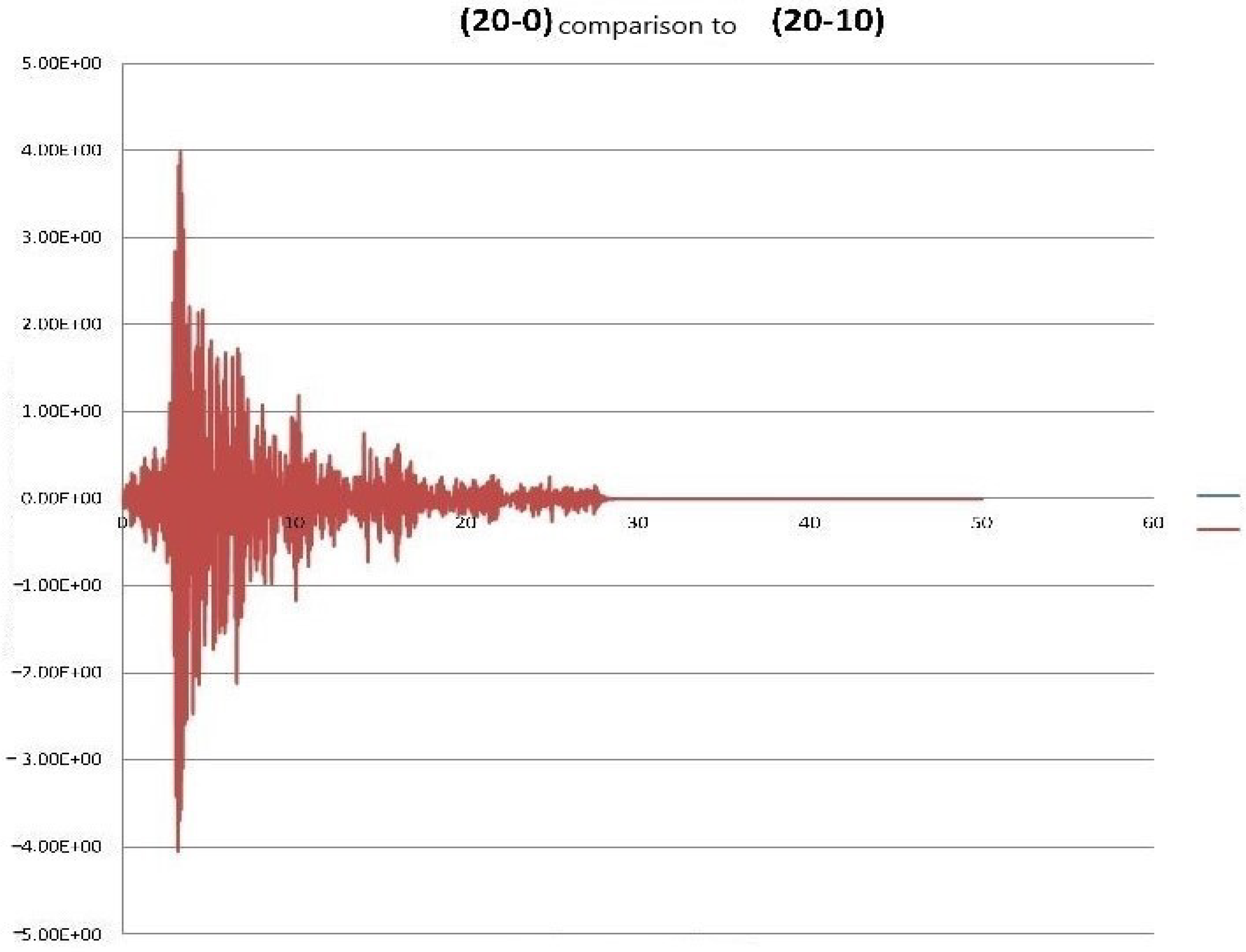

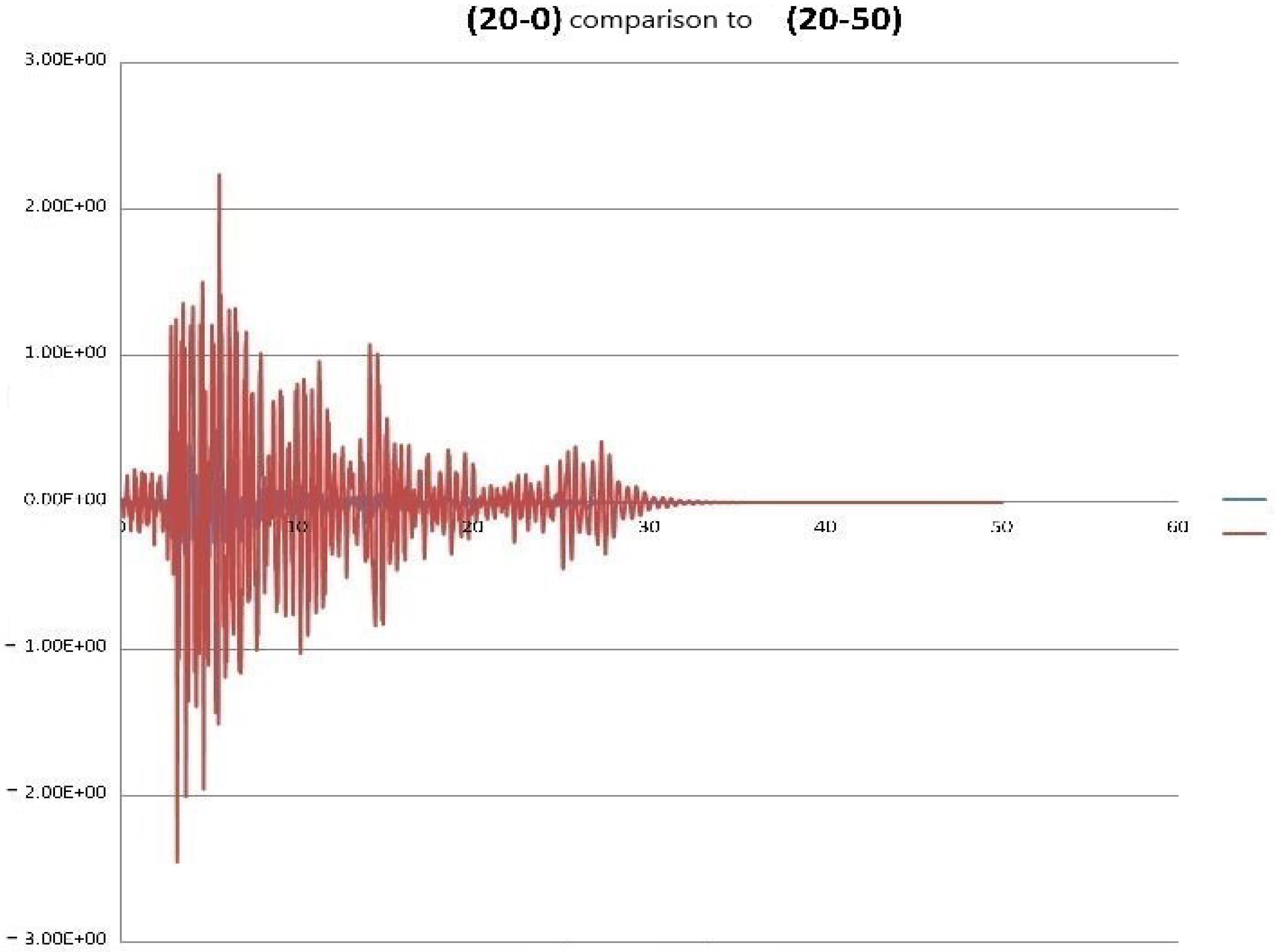
| Meshes Free Field |
| 210-30-10 |
| 210-30-20 |
| 210-30-50 |
| Meshes SSI System |
| 210-30-10-10 |
| 210-30-10-20 |
| 210-30-10-50 |
| 210-30-20-10 |
| 210-30-20-20 |
| 210-30-20-50 |
| 210-30-50-10 |
| 210-30-50-20 |
| 210-30-50-50 |
| Type | Material Constitutive Law | E (Gpa) | (MPa) | H (GPa) | |
|---|---|---|---|---|---|
| Superstructure | Von Mises | 1 | 50 | 0 | |
| Soil domain | Von Mises | 1 | 50 | 0 |
| System | E (GPa) | Ratio | Maximum Total Displacement | Maximum Total Acceleration |
|---|---|---|---|---|
| Free Field | 1 | 1 | 0.00390 | 2.052 |
| Free Field | 1 | 0.5 | 0.00383 | 2.045 |
| Free Field | 1 | 0.15 | 0.00378 | 2.038 |
| SSI System | 1 | 1 | 0.00790 | 3.045 |
| SSI System | 1 | 0.5 | 0.00775 | 3.038 |
| SSI System | 1 | 0.15 | 0.00765 | 3.036 |
| Free Field | 2 | 1 | 0.00209 | 1.030 |
| Free Field | 2 | 0.5 | 0.00205 | 1.023 |
| Free Field | 2 | 0.15 | 0.00199 | 1.020 |
| SSI System | 2 | 1 | 0.00410 | 1.520 |
| SSI System | 2 | 0.5 | 0.00398 | 1.519 |
| SSI System | 2 | 0.15 | 0.00394 | 1.518 |
| Free Field | 5 | 1 | 0.00083 | 0.750 |
| Free Field | 5 | 0.5 | 0.00088 | 0.758 |
| Free Field | 5 | 0.15 | 0.00087 | 0.749 |
| SSI System | 5 | 1 | 0.00102 | 0.860 |
| SSI System | 5 | 0.5 | 0.00104 | 0.864 |
| SSI System | 5 | 0.15 | 0.00103 | 0.859 |
| System | Size of Cube | Maximum Total Displacement | Maximum Total Acceleration |
|---|---|---|---|
| Free Field | 10 | 0.00378 | 2.038 |
| Free Field | 5 | 0.00382 | 2.032 |
| Free Field | 1 | 0.00388 | 2.030 |
| SSI System | 10 | 0.00765 | 3.036 |
| SSI System | 5 | 0.00777 | 3.030 |
| SSI System | 1 | 0.00781 | 3.028 |
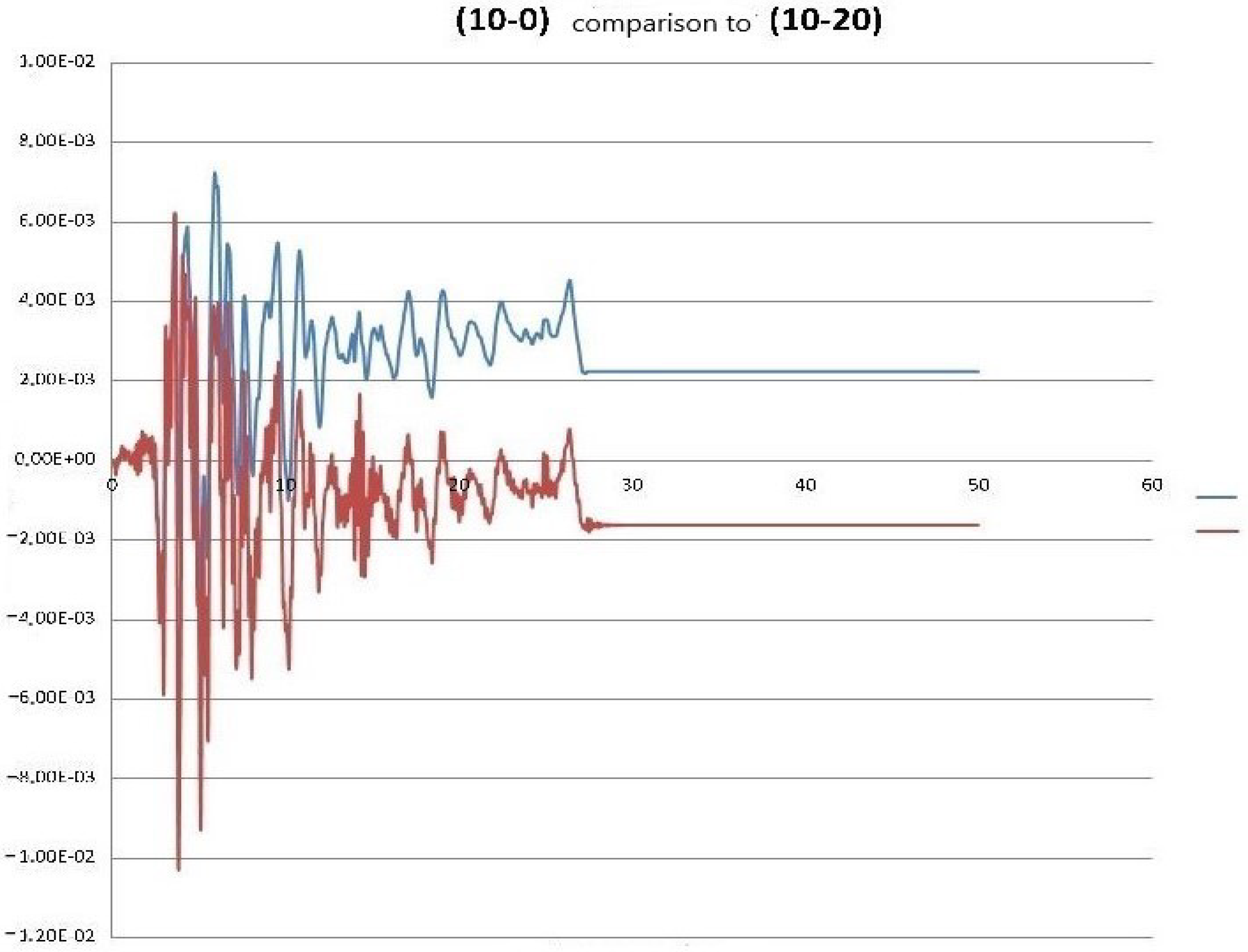
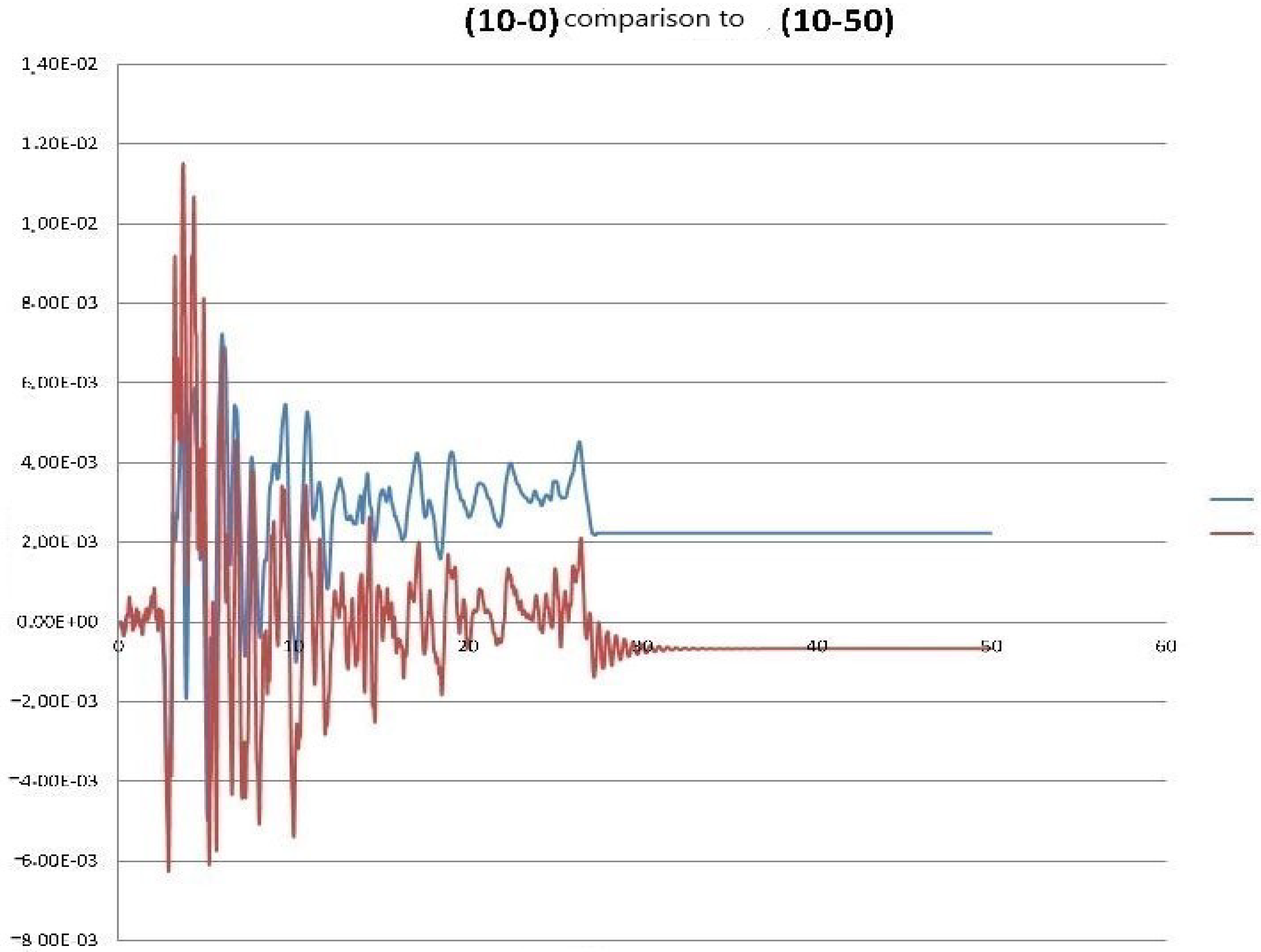
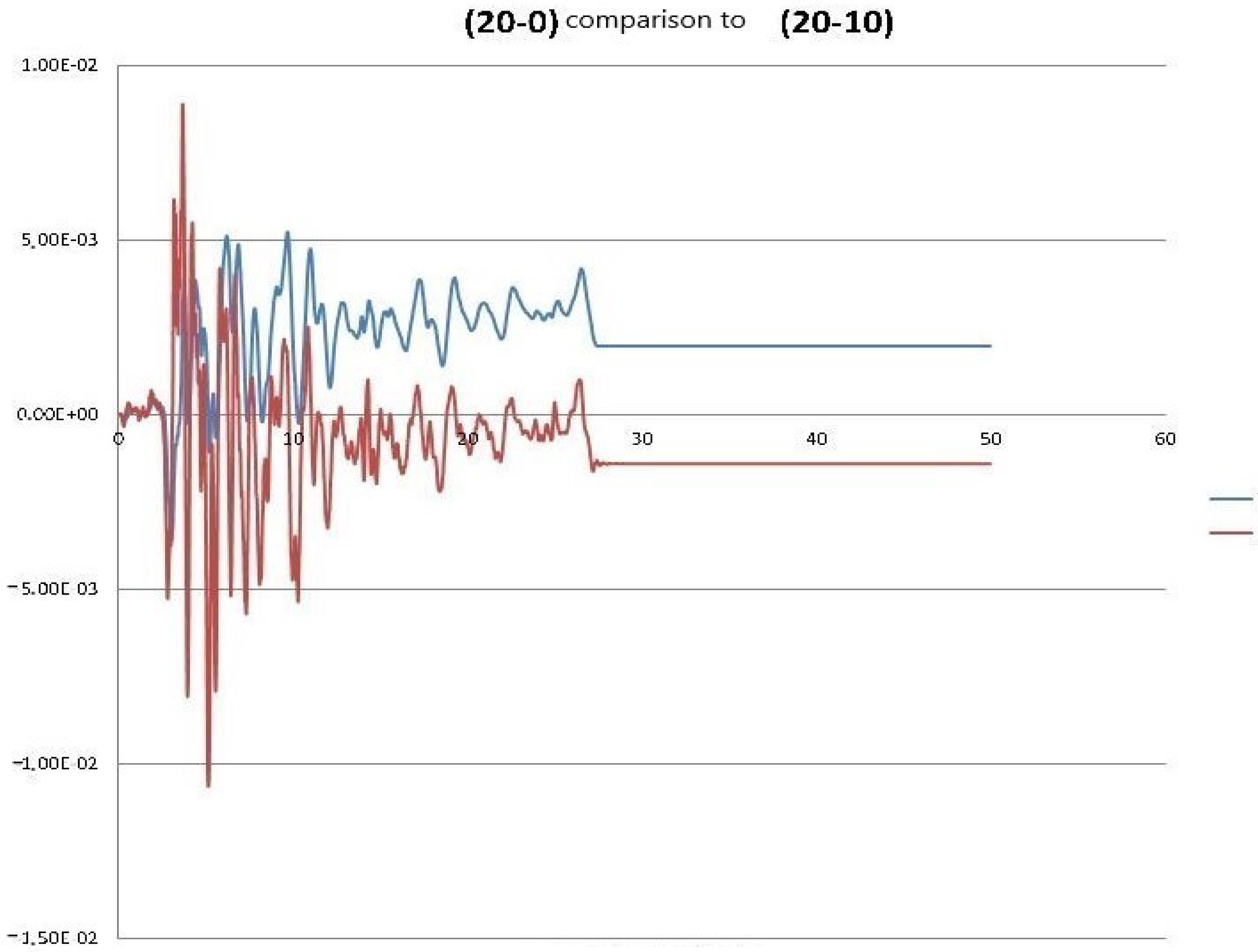
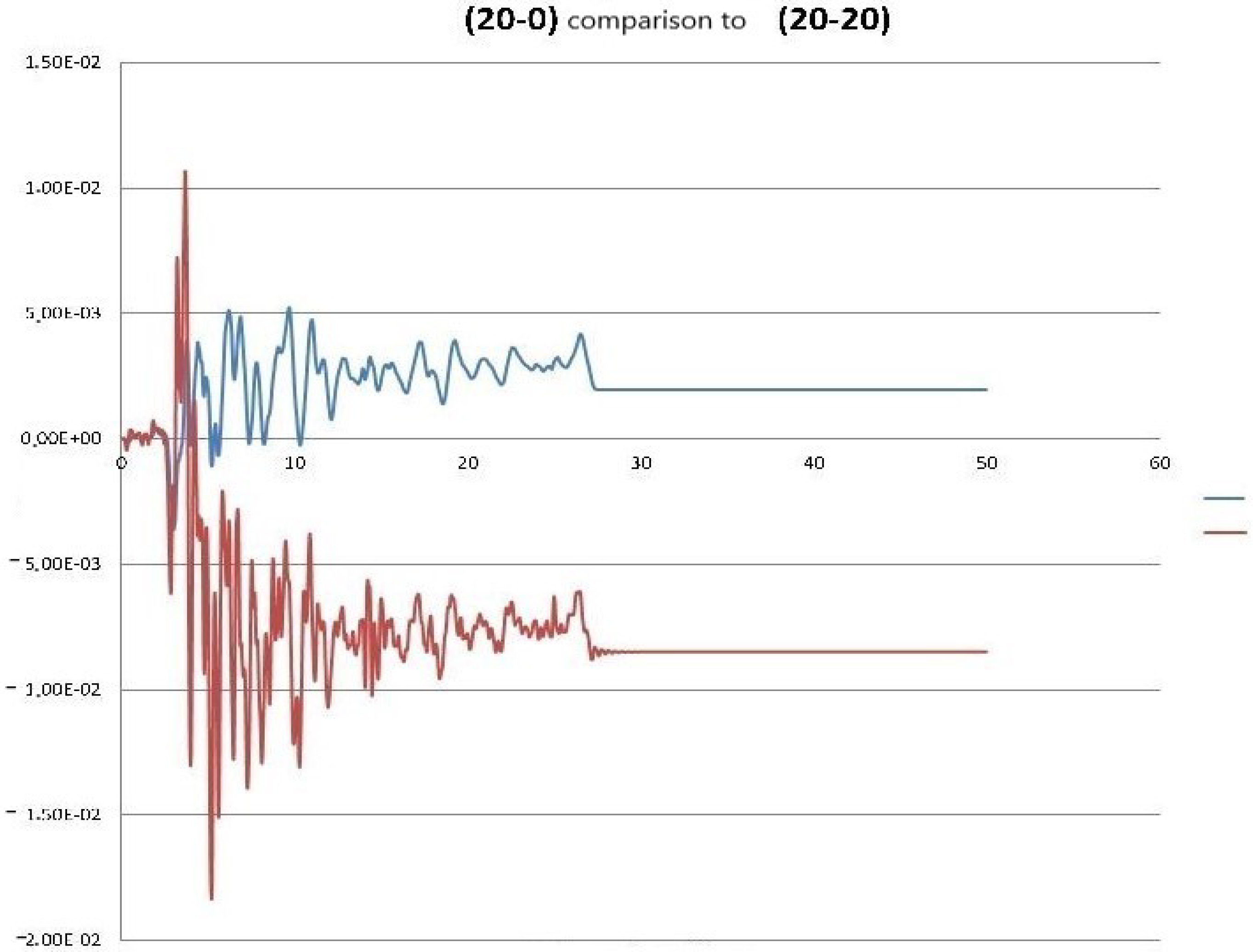
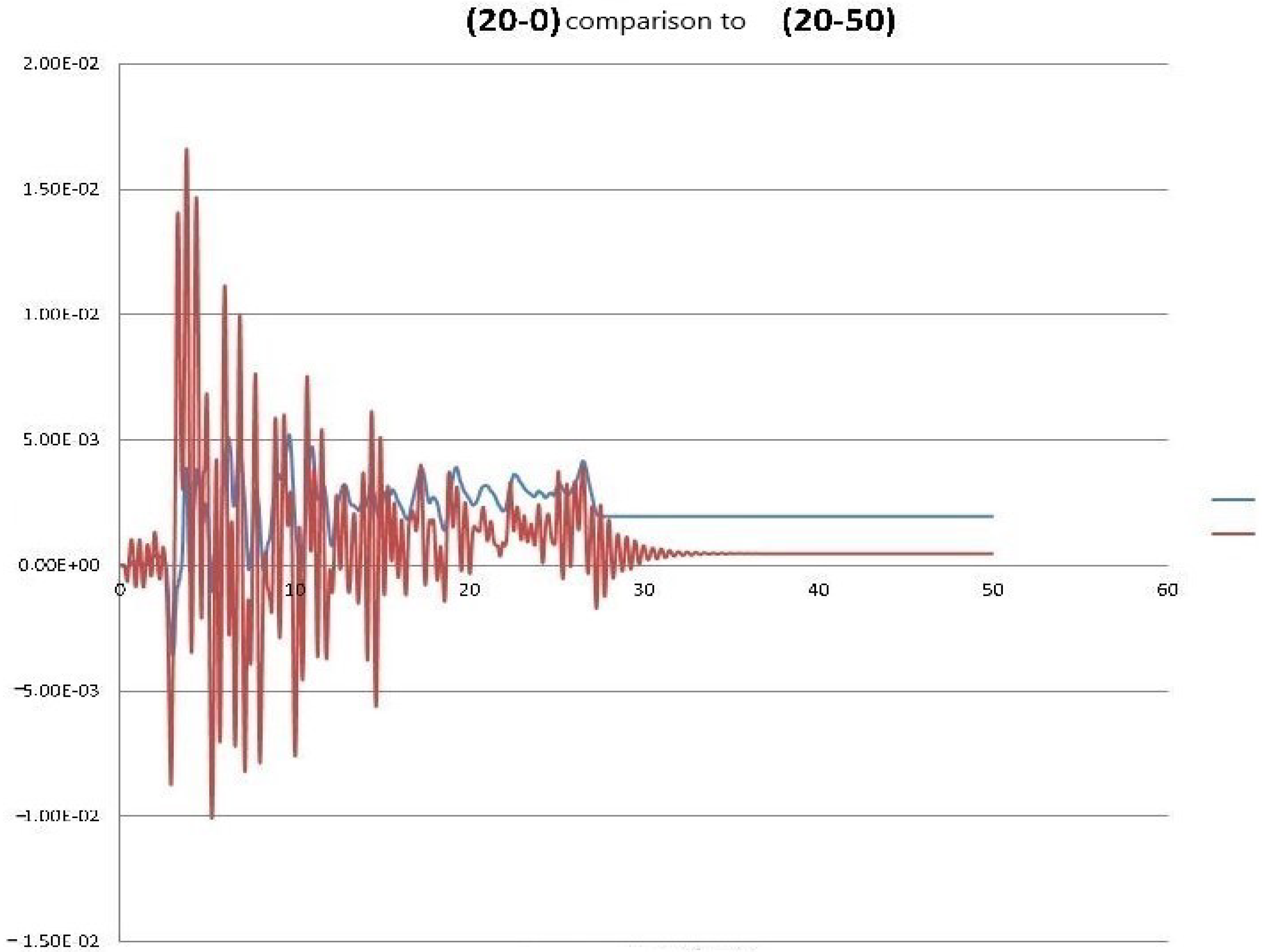
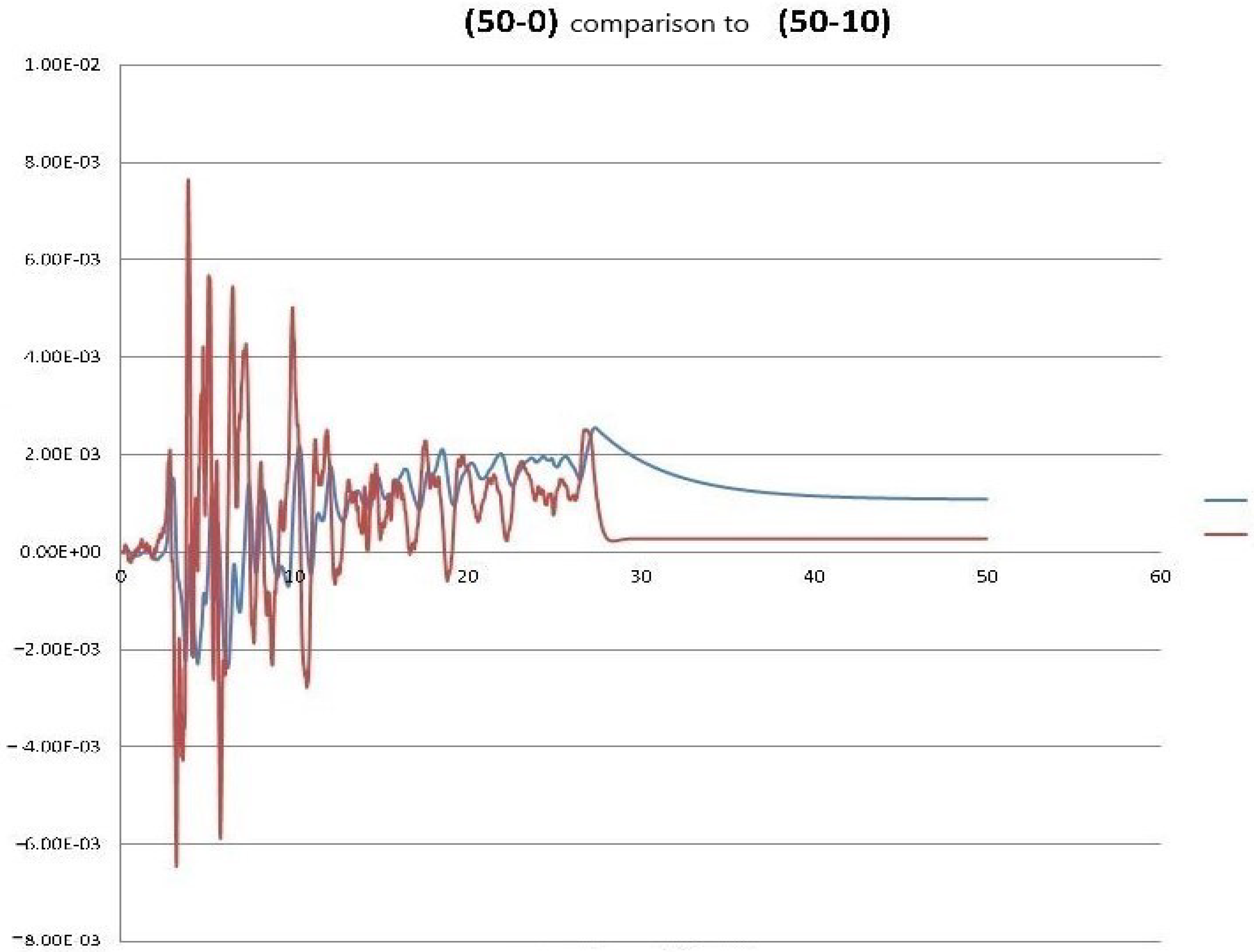
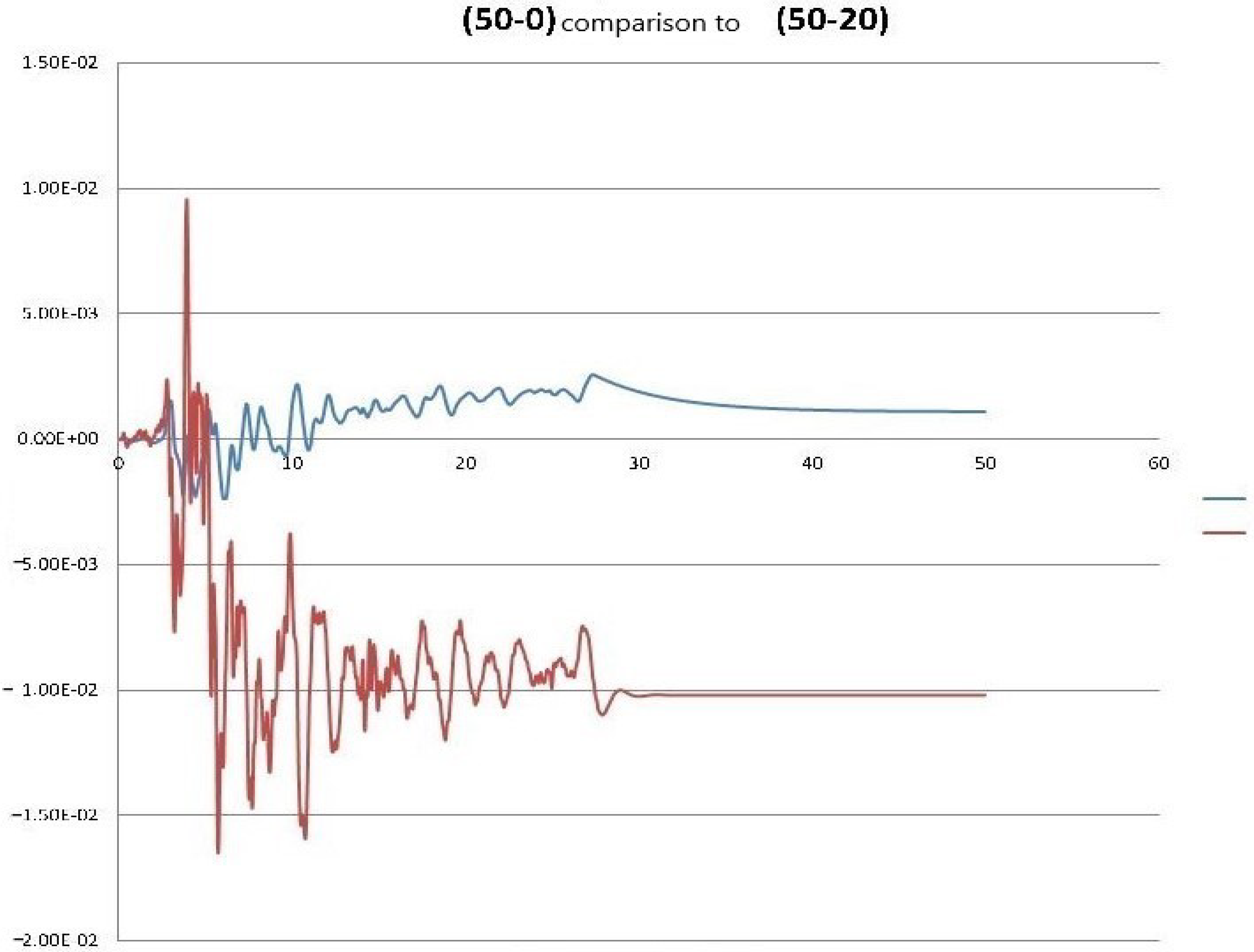
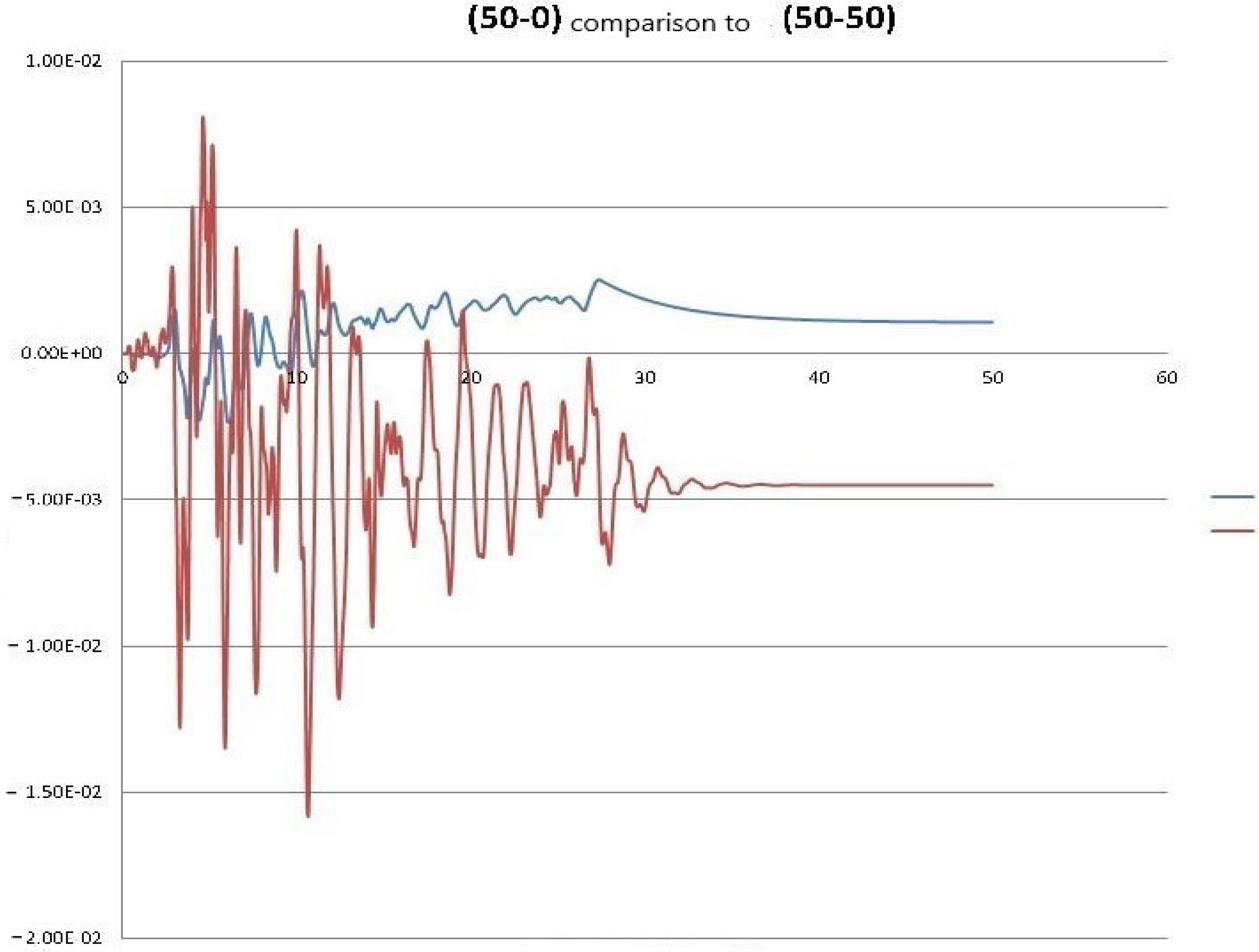
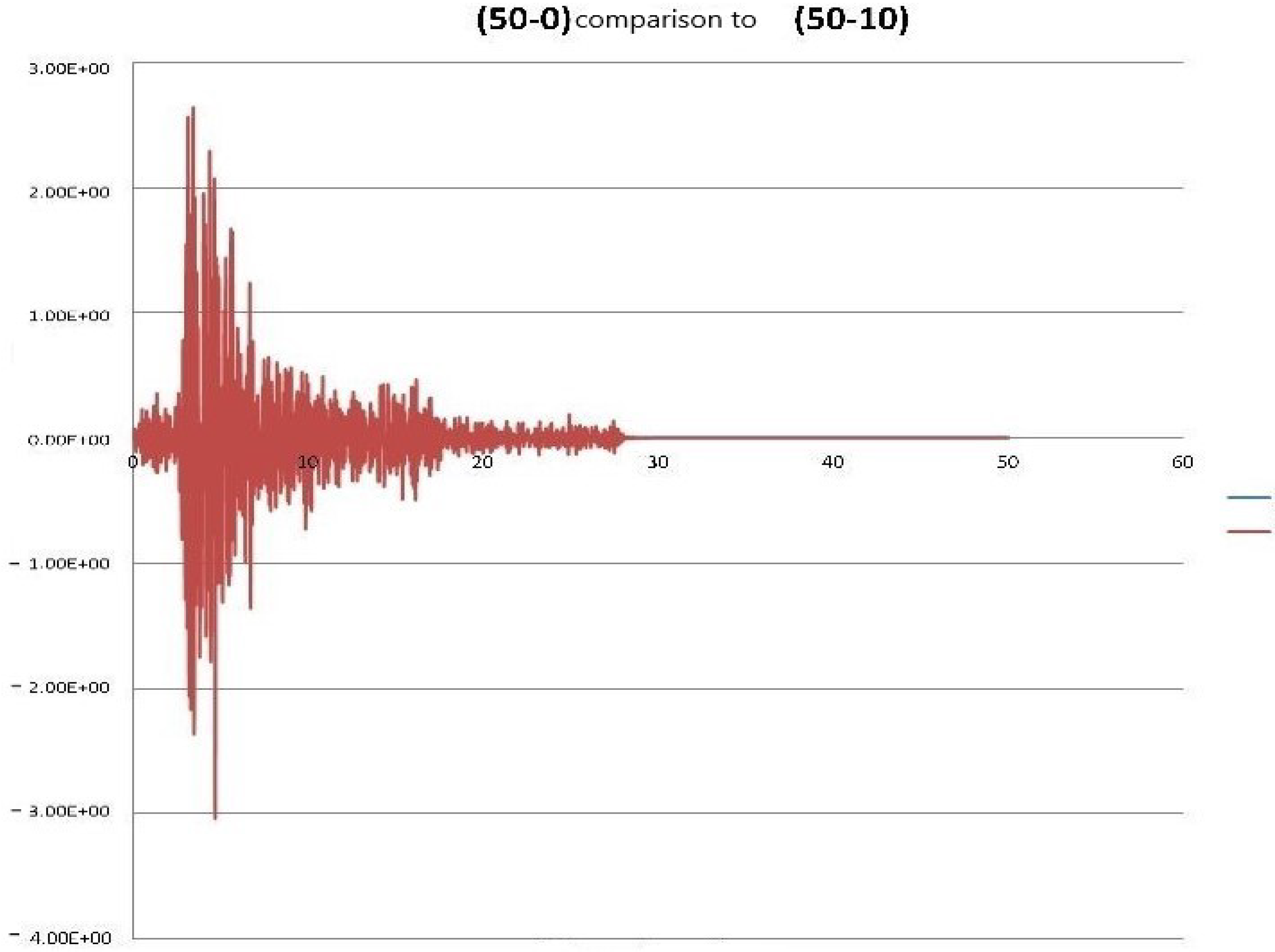
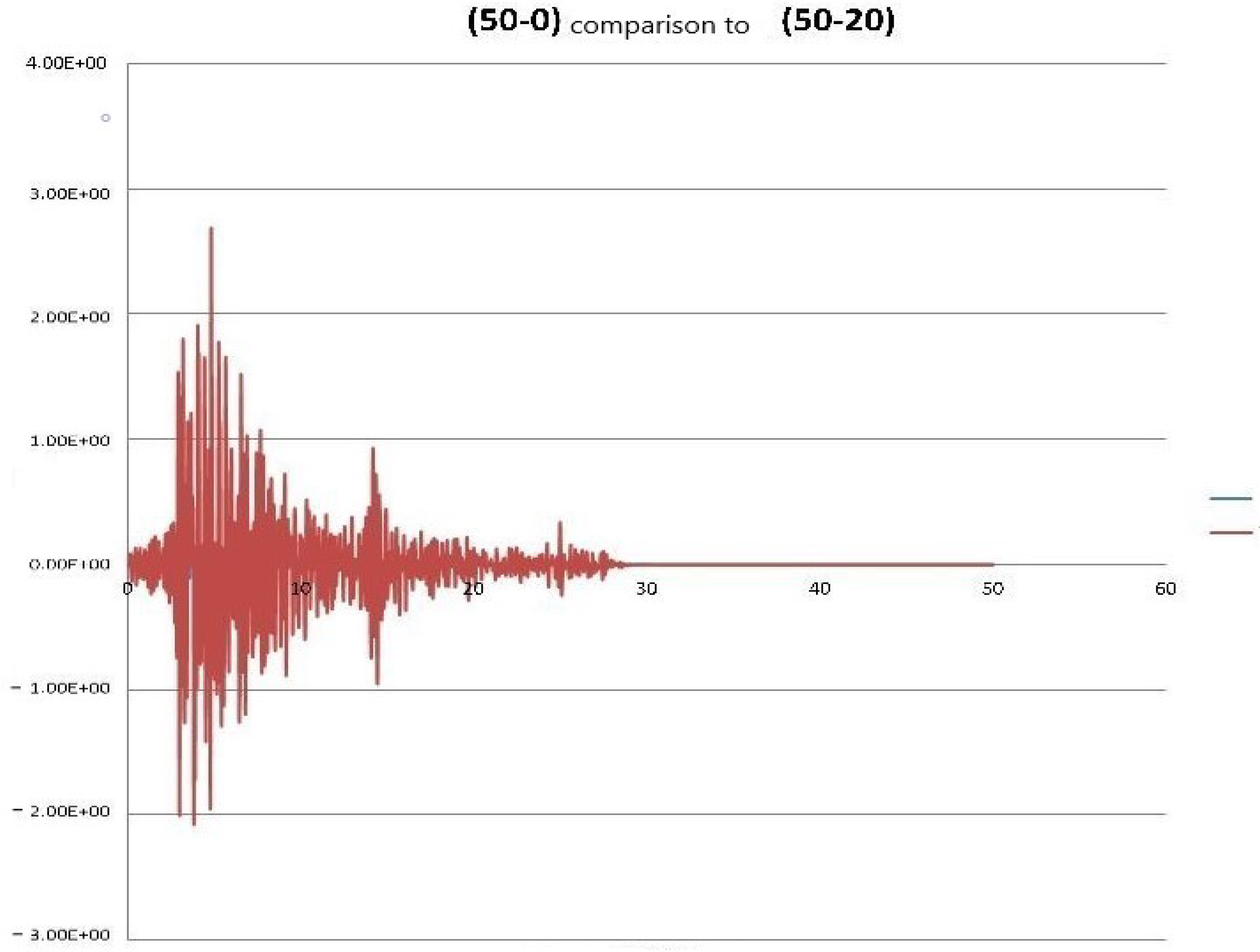
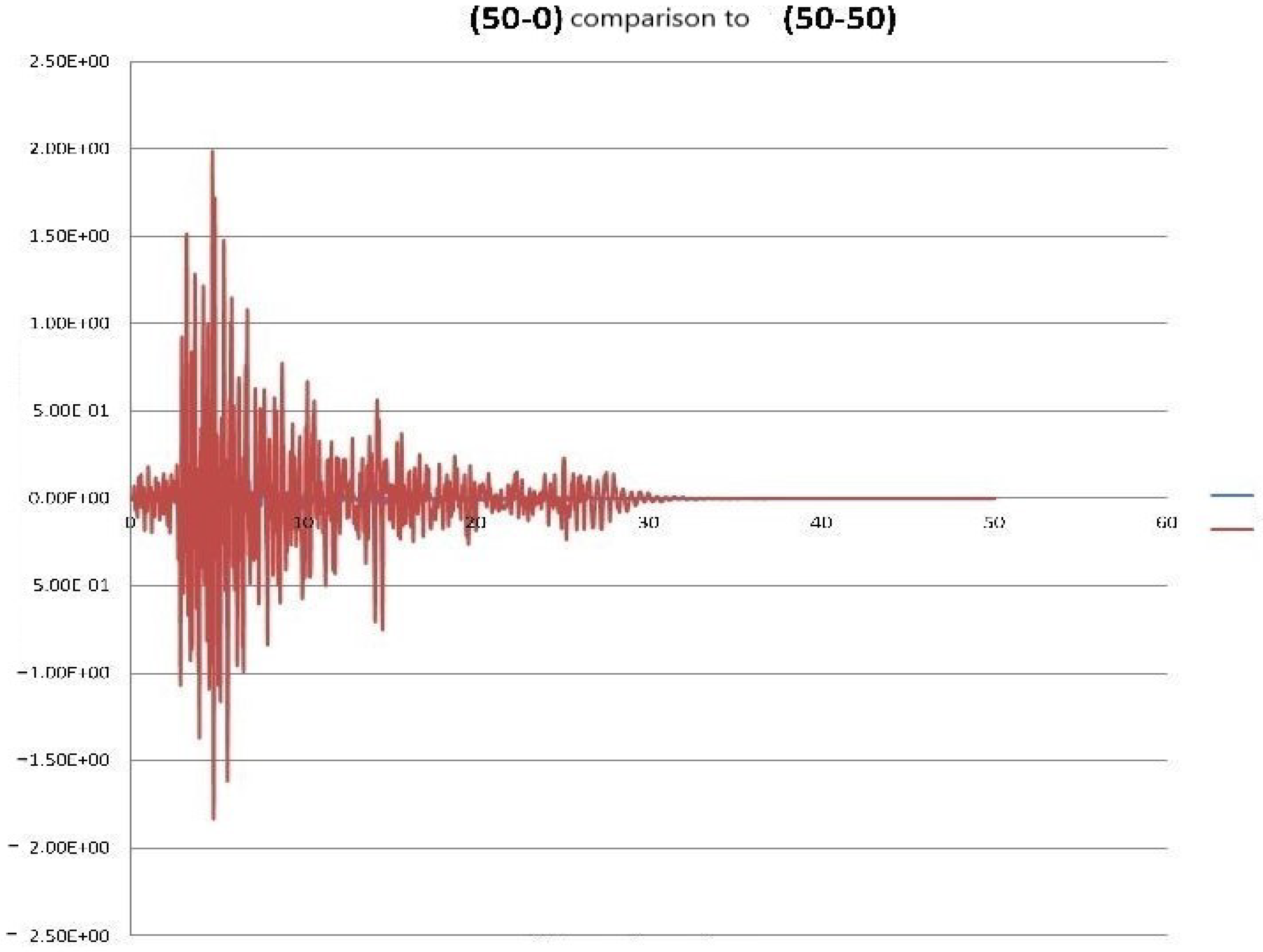
| Problem Solved (Building Height-Soil Depth) | Residual Displacement | Total Displacement | Total Acceleration | Ratio Total to Relative Displacements |
|---|---|---|---|---|
| (10-0) | 0.00224 | 0.00726 | −1.265 | 3.237 |
| (20-0) | 0.00196 | 0.00523 | -0.552 | 2.663 |
| (50-0) | 0.00109 | 0.00256 | 0.345 | 2.346 |
| (10-10) | −0.00100 | −0.00933 | 3.850 | 9.316 |
| (10-20) | −0.00162 | −0.01030 | −3.356 | 6.343 |
| (10-50) | −0.00067 | 0.01152 | 3.392 | 17.202 |
| (20-10) | −0.00140 | −0.01064 | −4.037 | 7.613 |
| (20-20) | −0.00848 | −0.01834 | −2.615 | 2.163 |
| (20-50) | 0.00048 | 0.01660 | −2.453 | 34.369 |
| (50-10) | 0.00027 | 0.00765 | −3.036 | 28.090 |
| (50-20) | −0.01022 | 0.00957 | 2.683 | 0.937 |
| (50-50) | −0.00450 | −0.01580 | 1.992 | 3.522 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savvides, A.-A. A Parametric Study of the Dynamic Soil–Structure Interaction for Shear Vulnerable Structures with Nonlinear Finite Element Modelling. Geotechnics 2024, 4, 693-717. https://doi.org/10.3390/geotechnics4030037
Savvides A-A. A Parametric Study of the Dynamic Soil–Structure Interaction for Shear Vulnerable Structures with Nonlinear Finite Element Modelling. Geotechnics. 2024; 4(3):693-717. https://doi.org/10.3390/geotechnics4030037
Chicago/Turabian StyleSavvides, Ambrosios-Antonios. 2024. "A Parametric Study of the Dynamic Soil–Structure Interaction for Shear Vulnerable Structures with Nonlinear Finite Element Modelling" Geotechnics 4, no. 3: 693-717. https://doi.org/10.3390/geotechnics4030037
APA StyleSavvides, A.-A. (2024). A Parametric Study of the Dynamic Soil–Structure Interaction for Shear Vulnerable Structures with Nonlinear Finite Element Modelling. Geotechnics, 4(3), 693-717. https://doi.org/10.3390/geotechnics4030037







