Monotonic Drained and Undrained Shear Behaviors of Compacted Slightly Weathered Tephras from New Zealand †
Abstract
:1. Introduction
2. Areas of Soil Sampling
3. Materials and Methodology
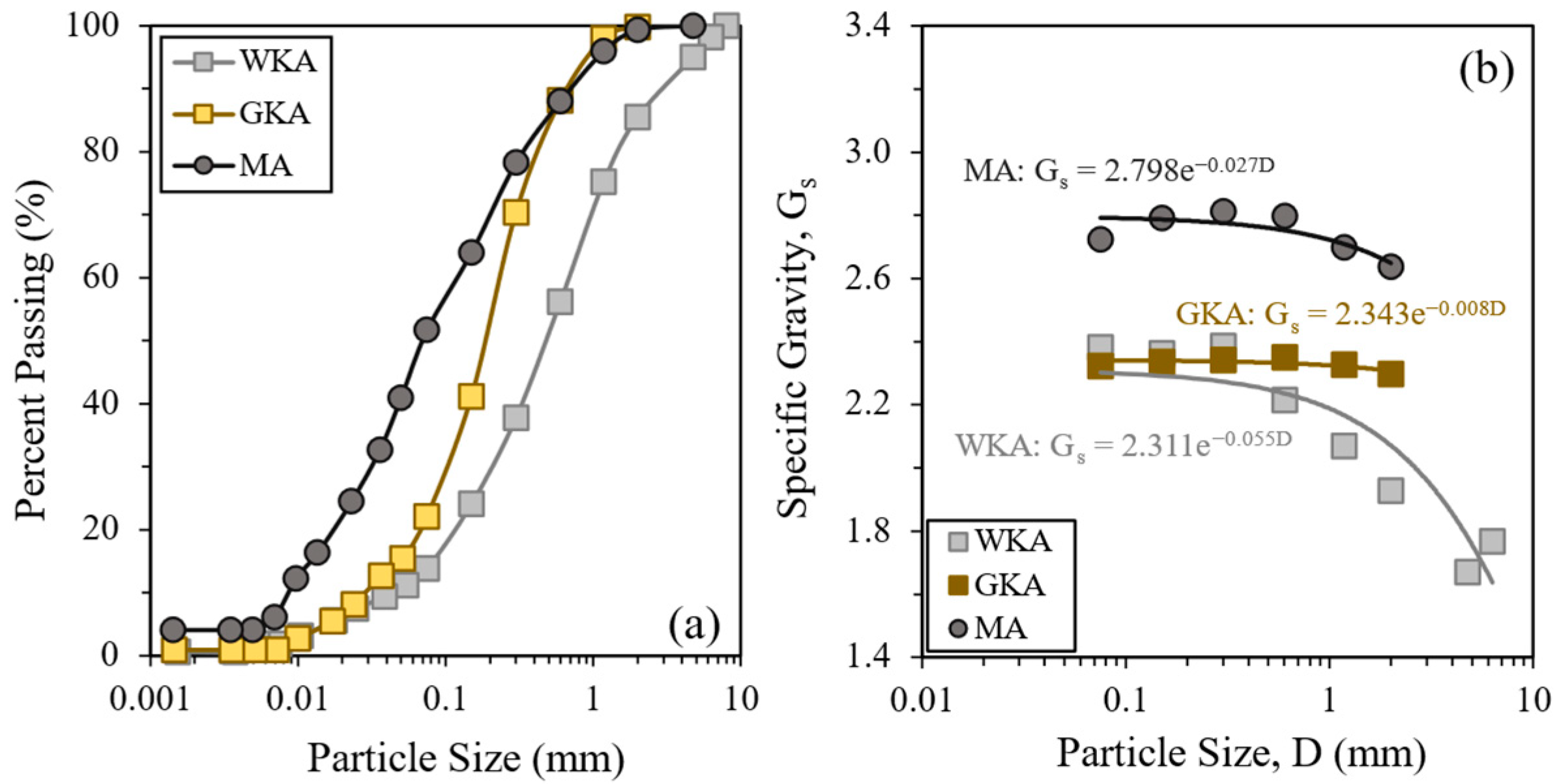
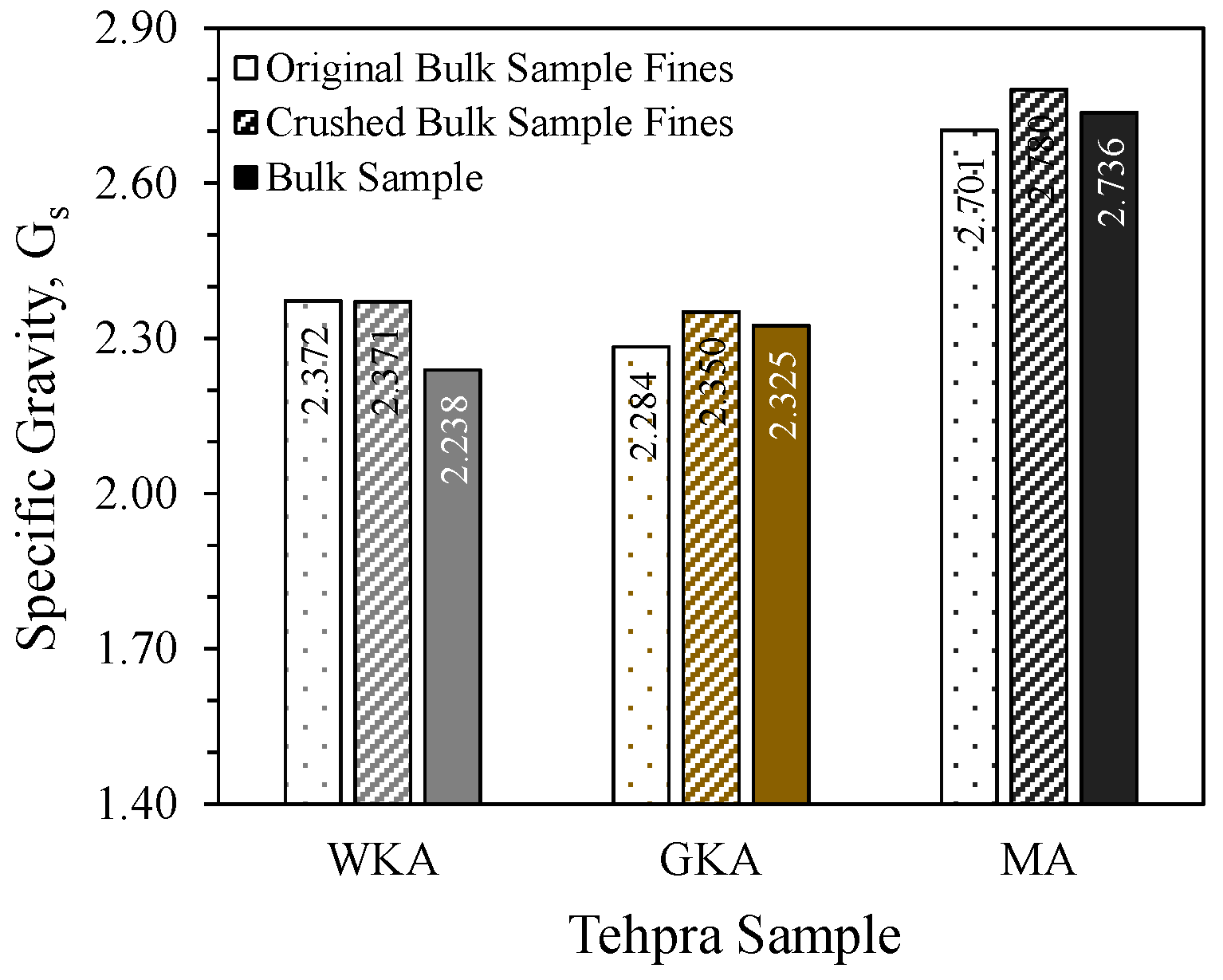
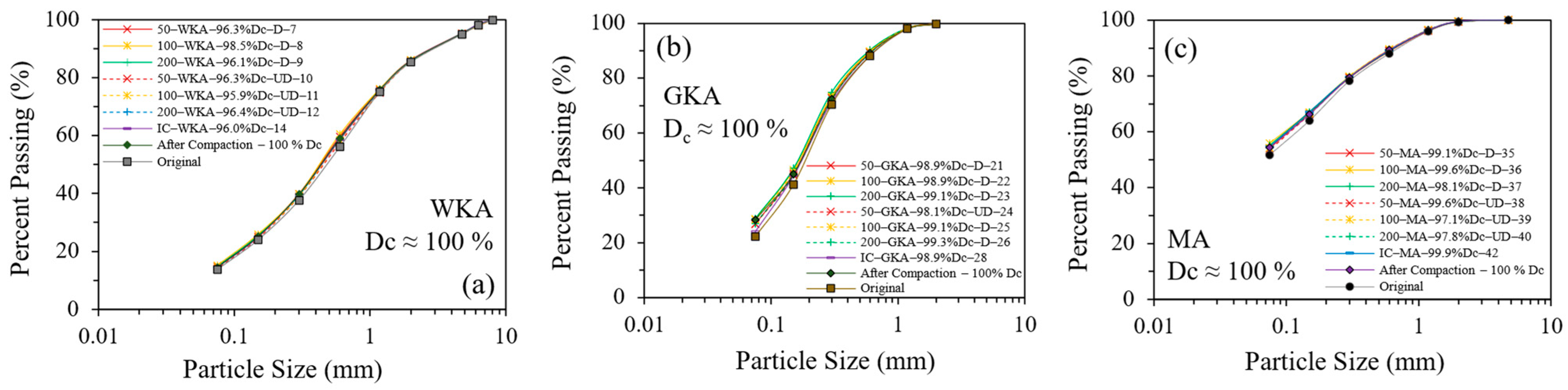
3.1. Particle Size Distribution and Specific Gravity
| Tephra Sample | Gravel (%) | Sand (%) | Fines (%) | PI (%) | D50 (mm) | Cu | Cc | Soil Classification (ASTM D2487 [27]) | Gs Bulk Sample (ASTM D854 [28]) |
|---|---|---|---|---|---|---|---|---|---|
| WKA | 5.0 | 81.2 | 13.8 | NP | 0.50 | 16.3 | 1.5 | Silty Sand (SM) | 2.238 |
| GKA | 0.3 | 77.6 | 22.1 | NP | 0.20 | 7.7 | 1.4 | Silty Sand (SM) | 2.325 |
| MA | 0.0 | 48.3 | 51.7 | 3.7 | 0.07 | 14.4 | 0.9 | Sandy Silt (ML) | 2.736 |
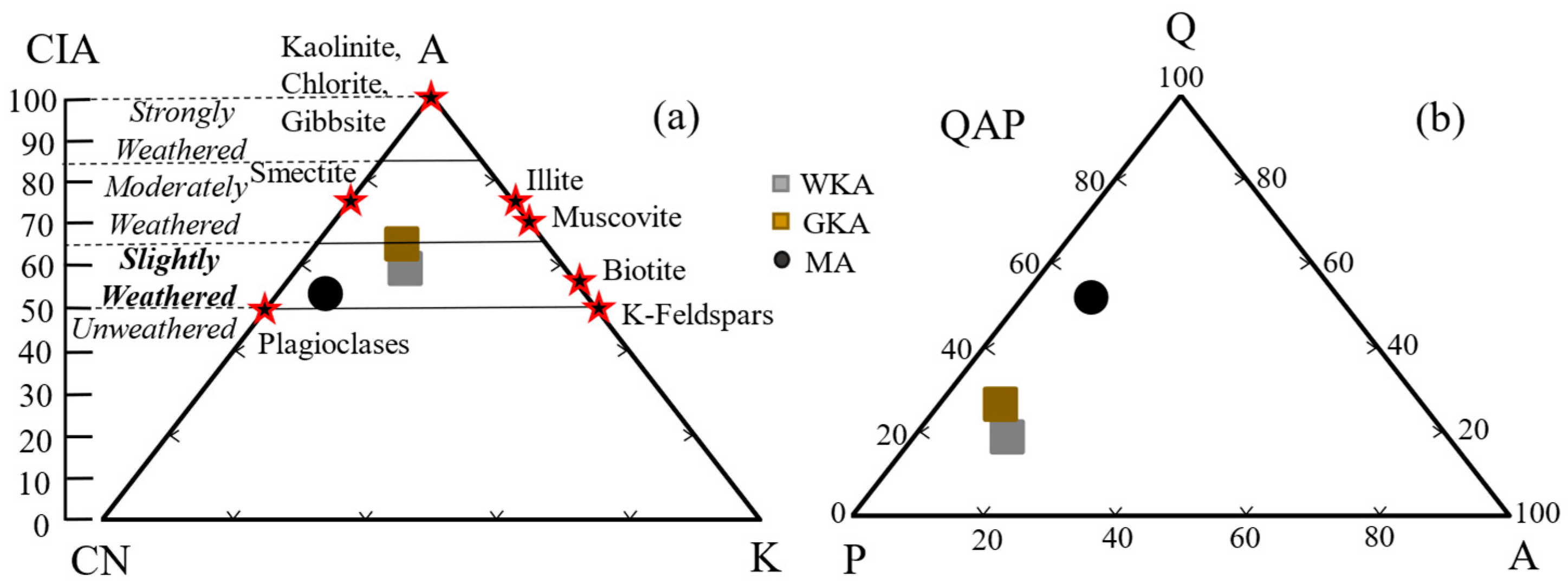
3.2. Degree of Weathering and Mineralogy
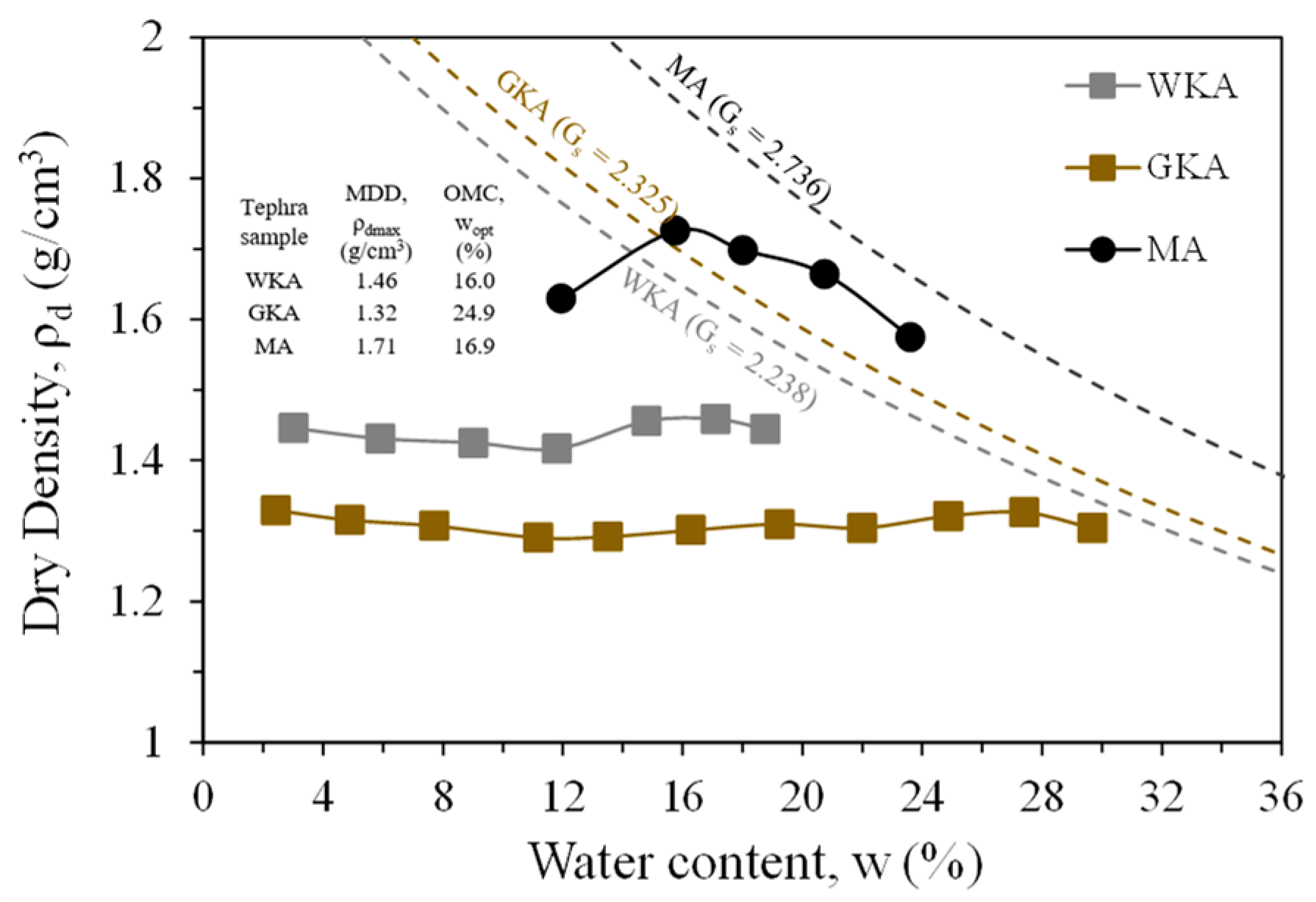
3.3. Compaction Properties
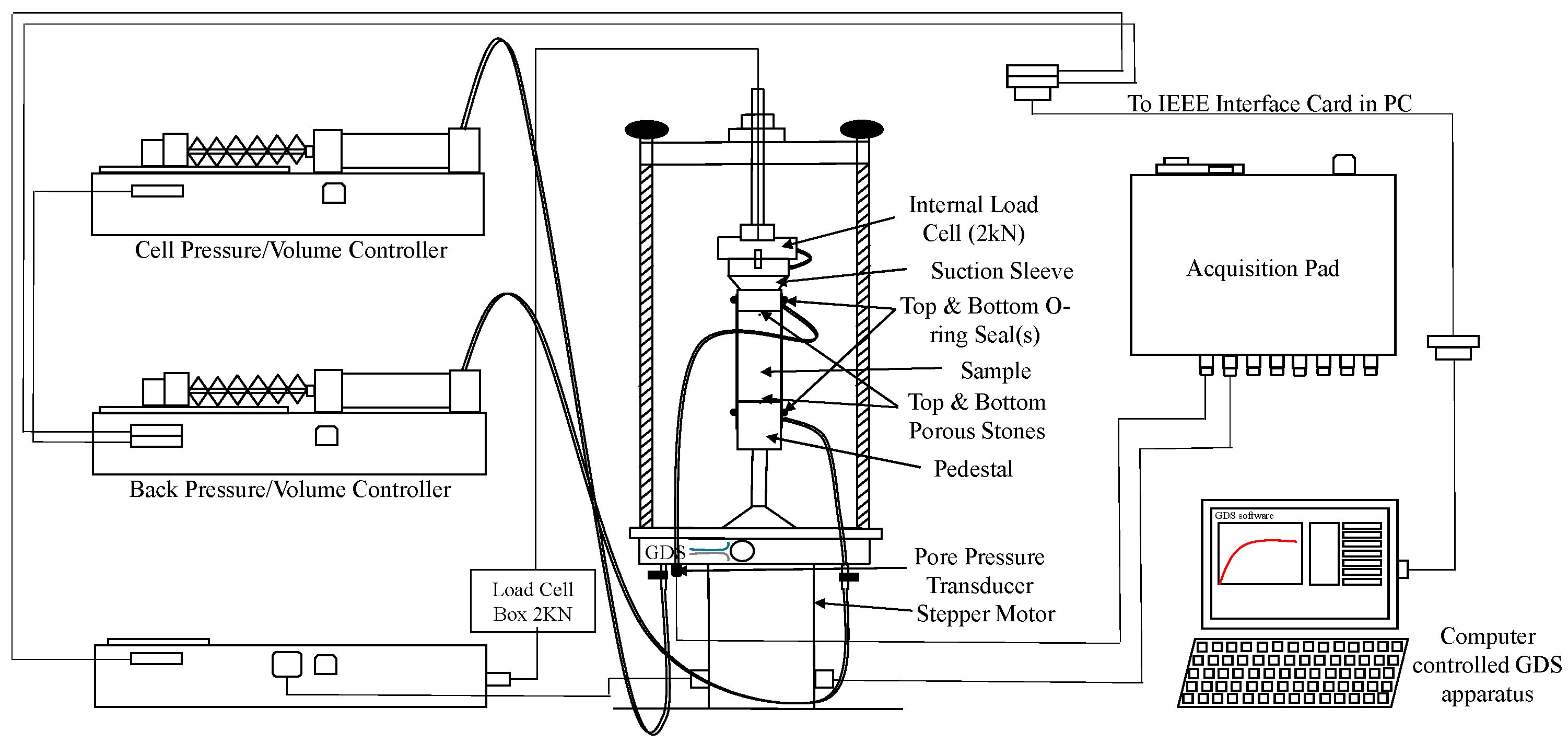
3.4. Equipment, Specimen Preparation, and Testing Procedure
4. Test Results and Discussion
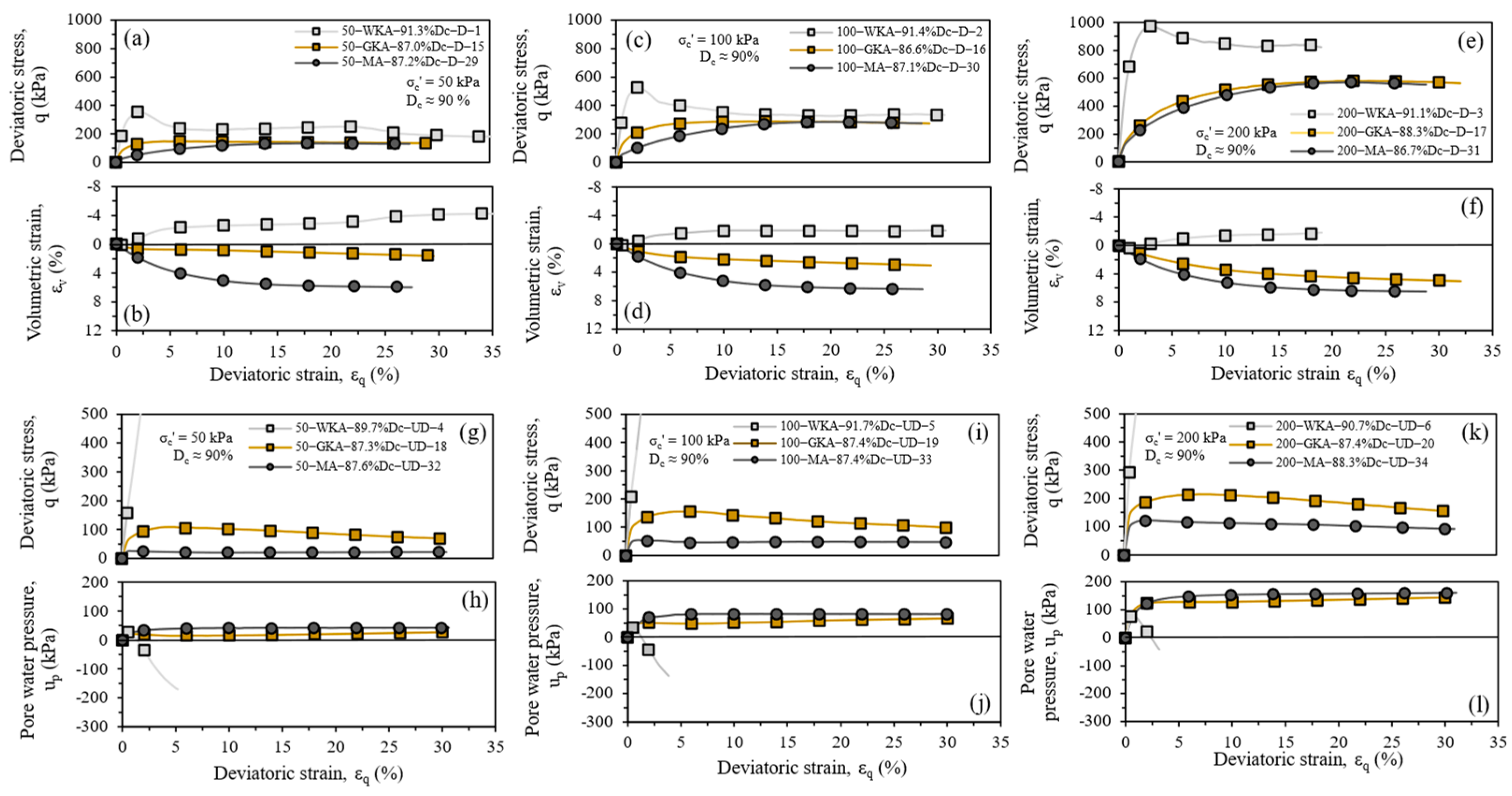
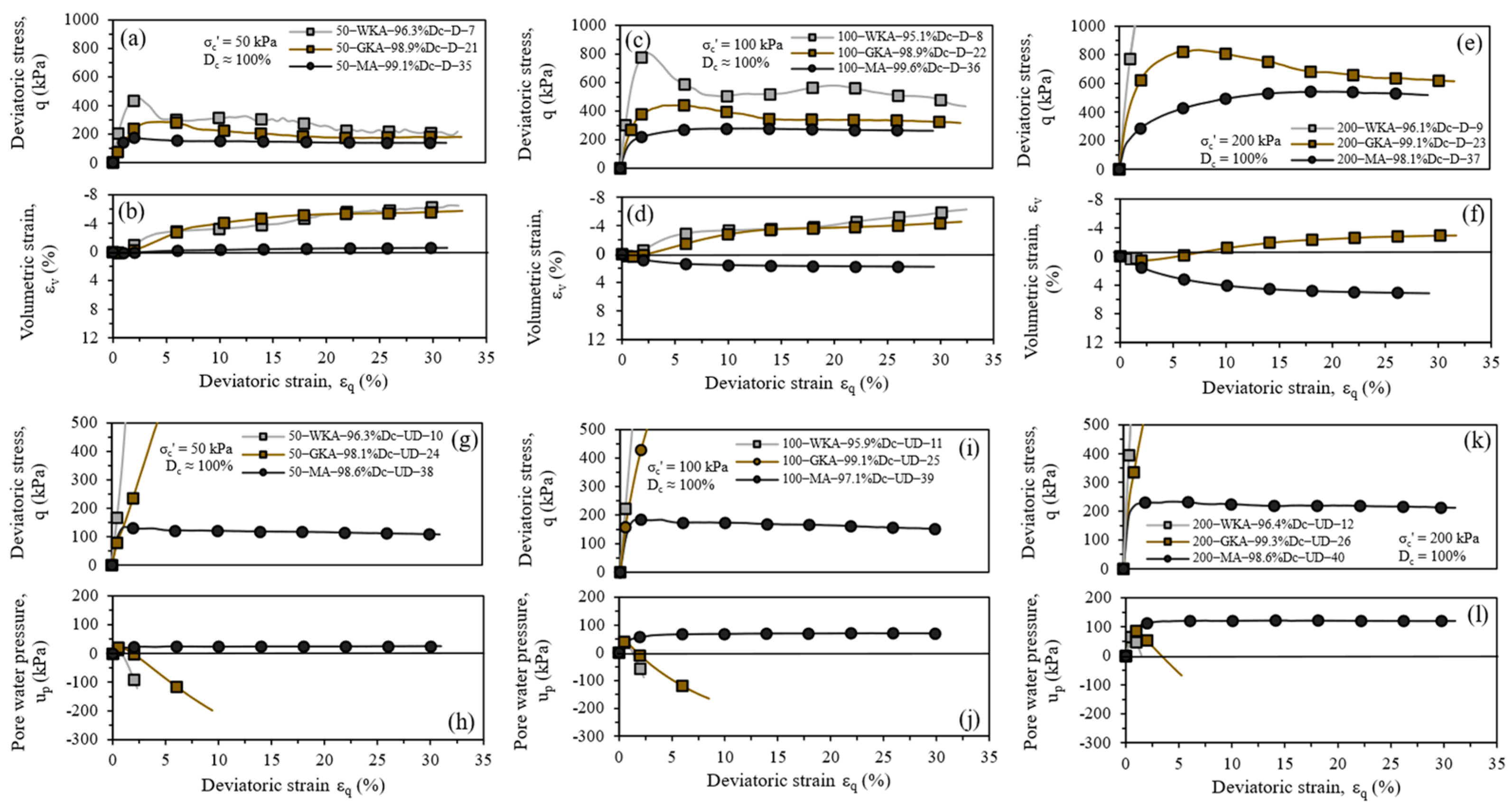
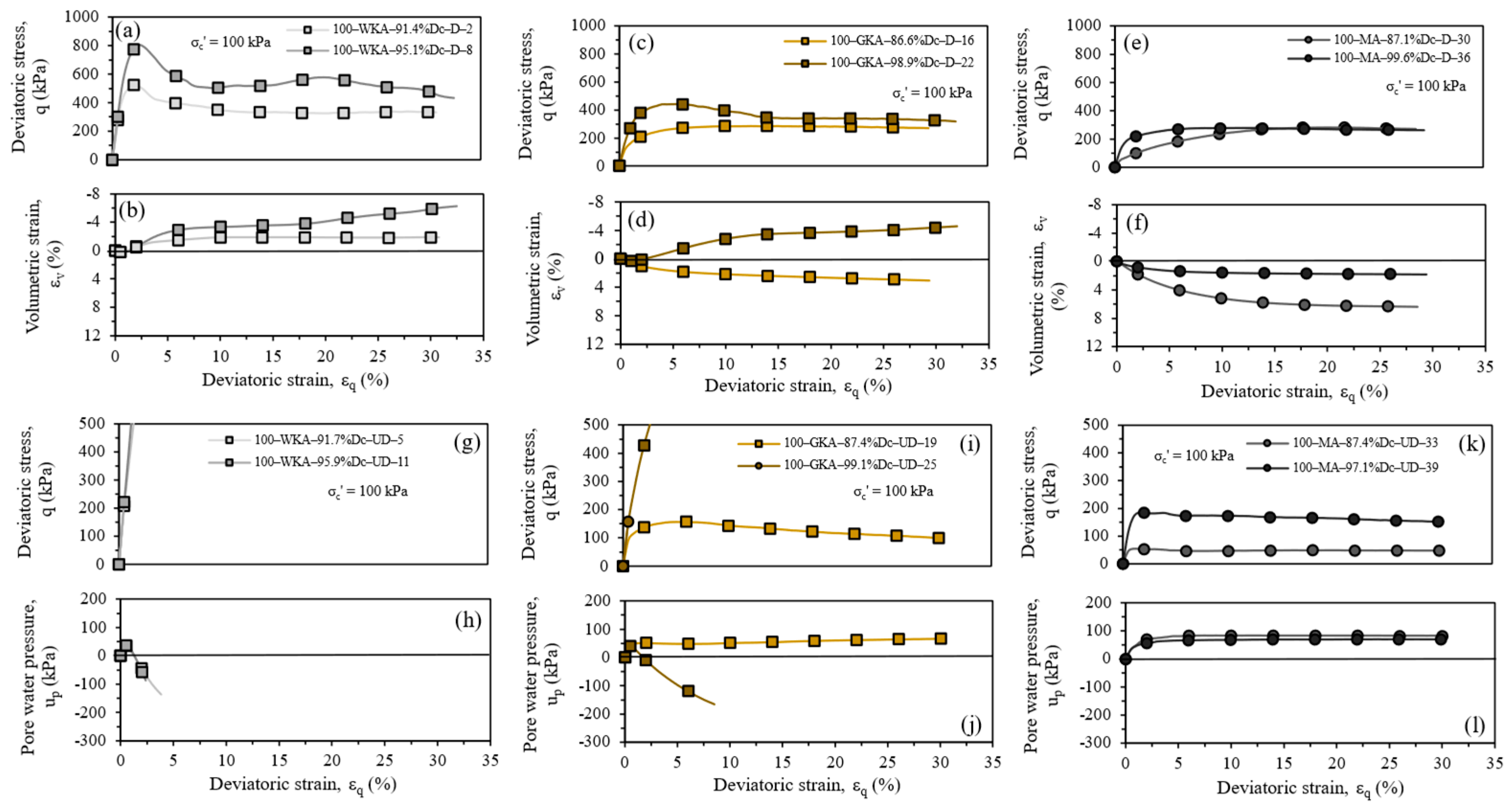
4.1. Effects of Gradation and Chemical Composition on Shear Response
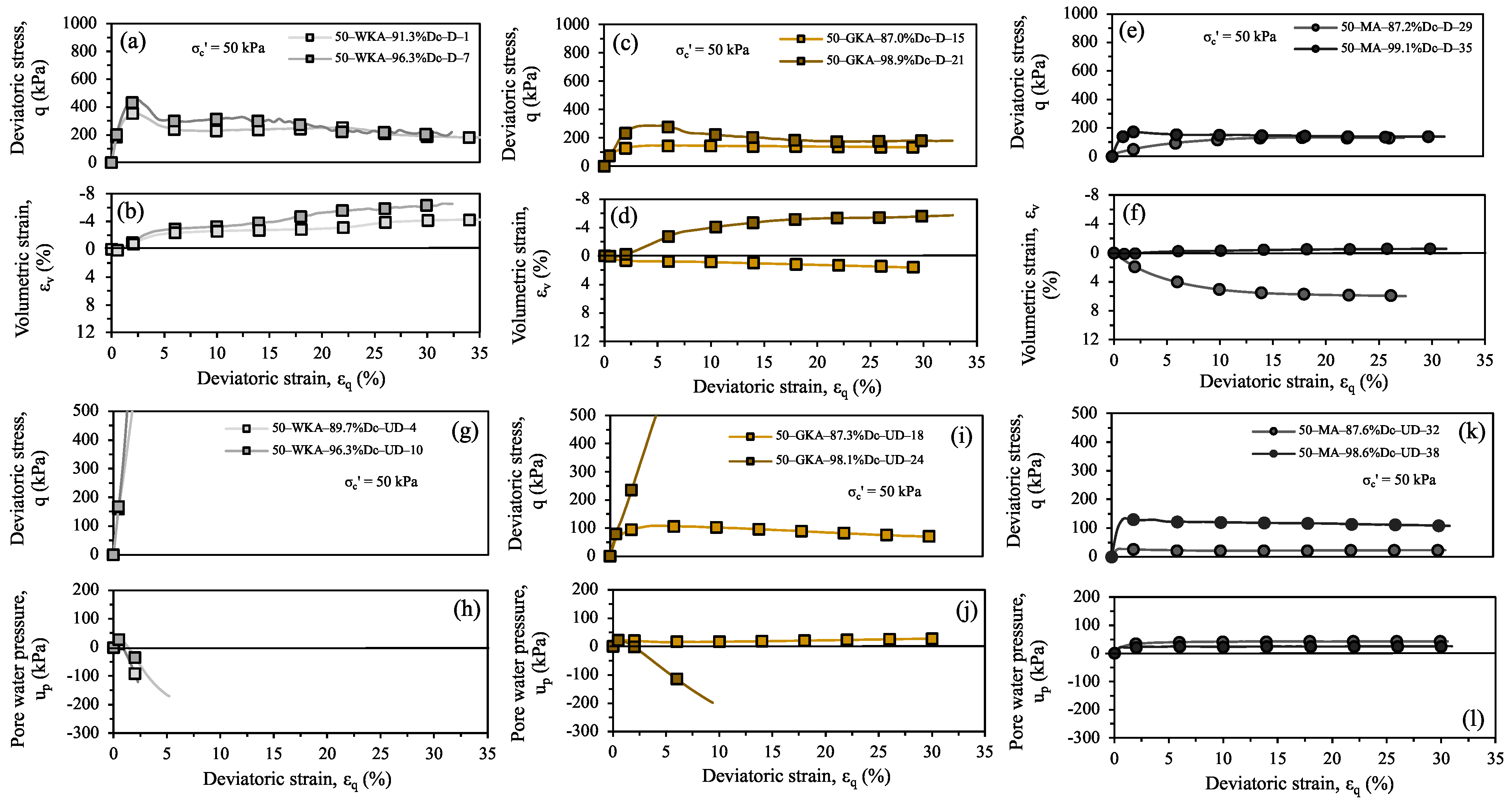
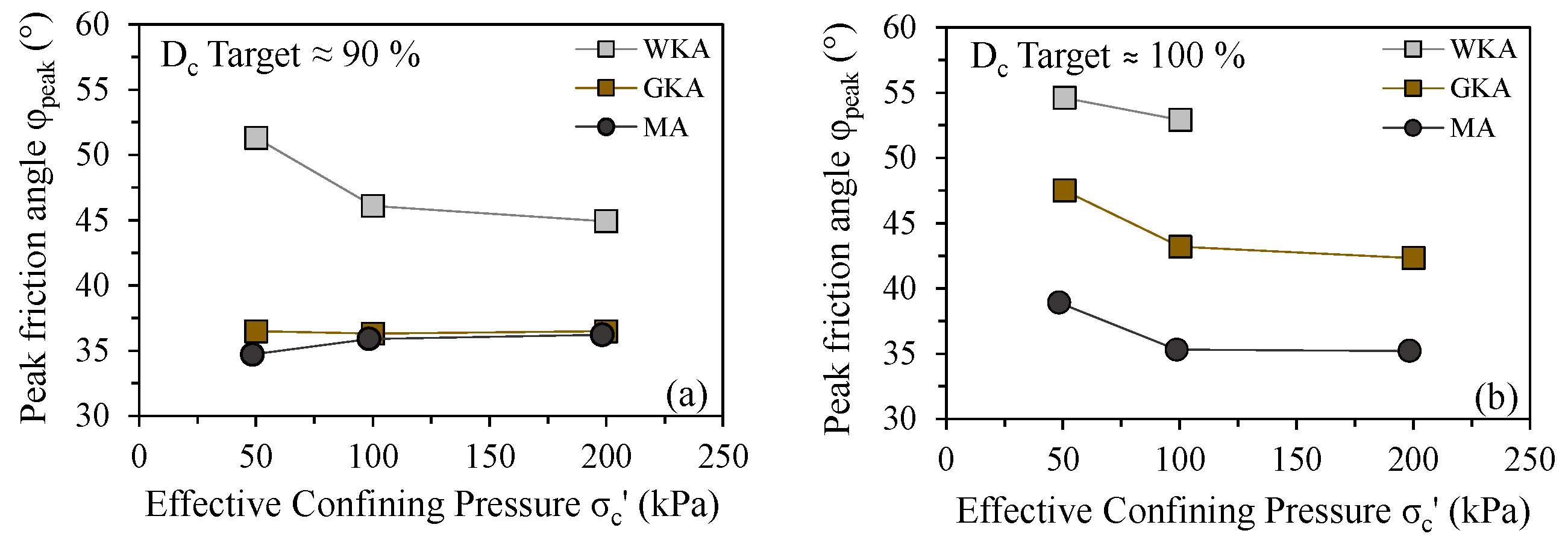
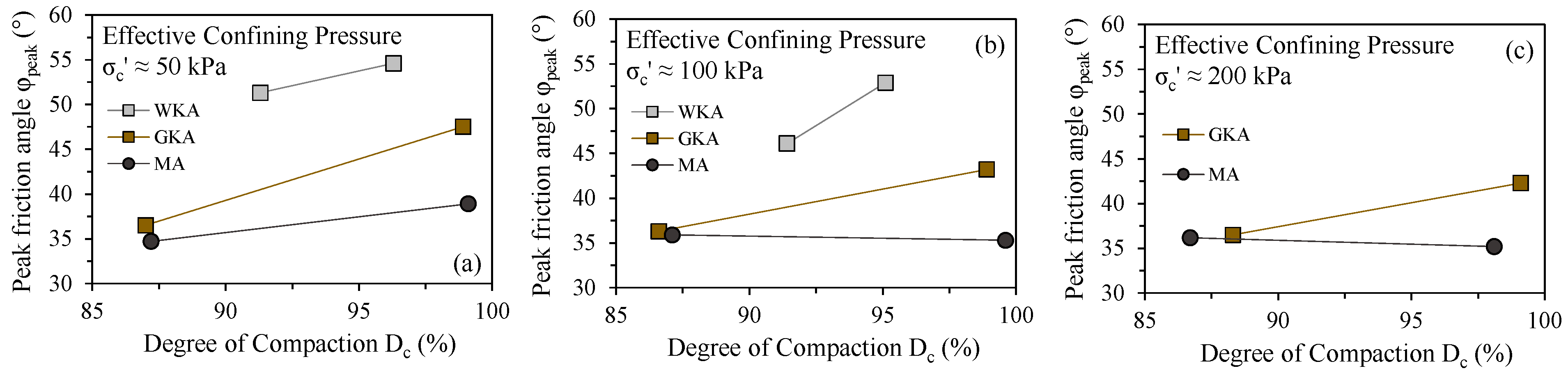
4.2. Effects of Degree of Compaction and Effective Confining Pressure on Shear Response
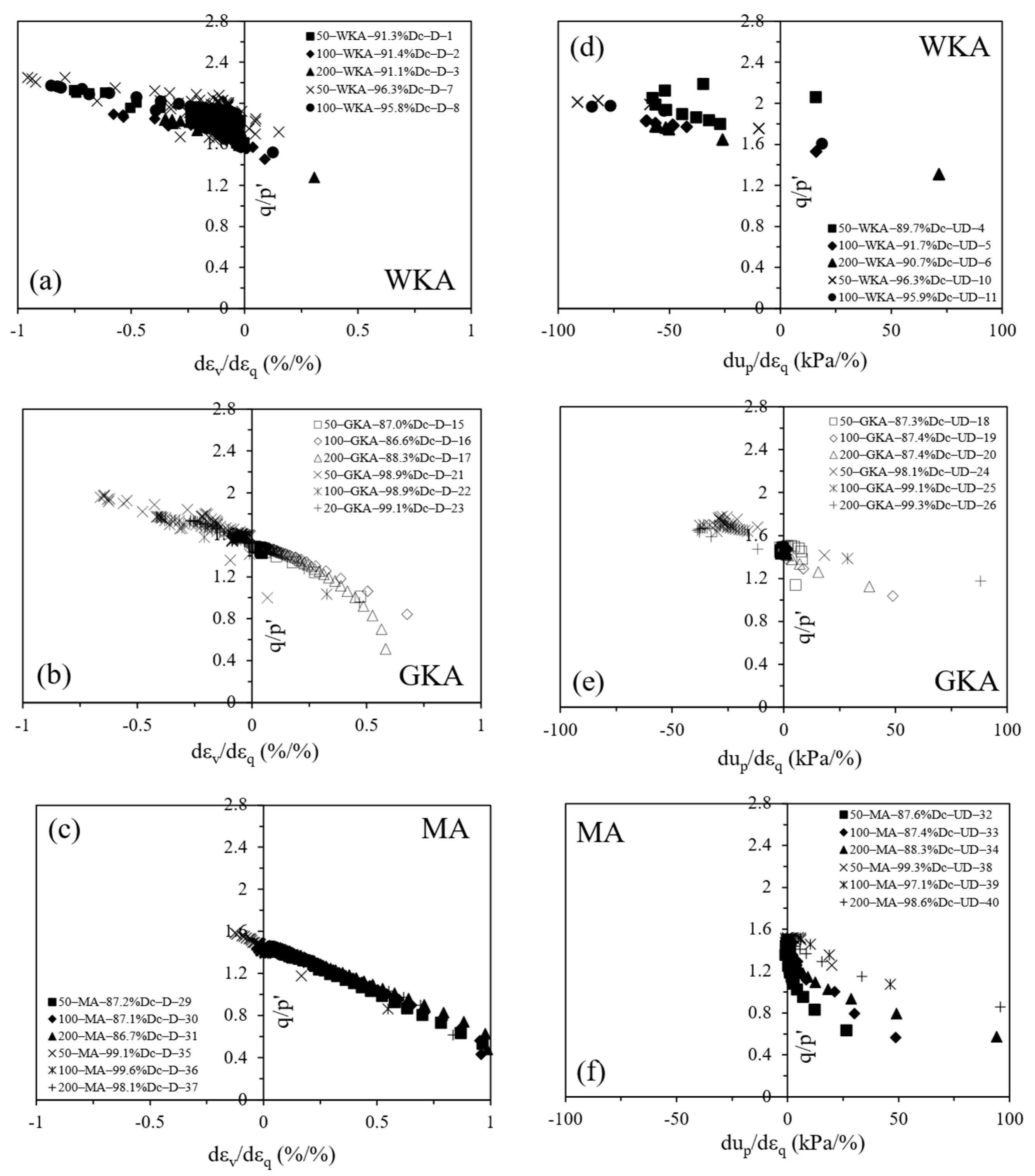
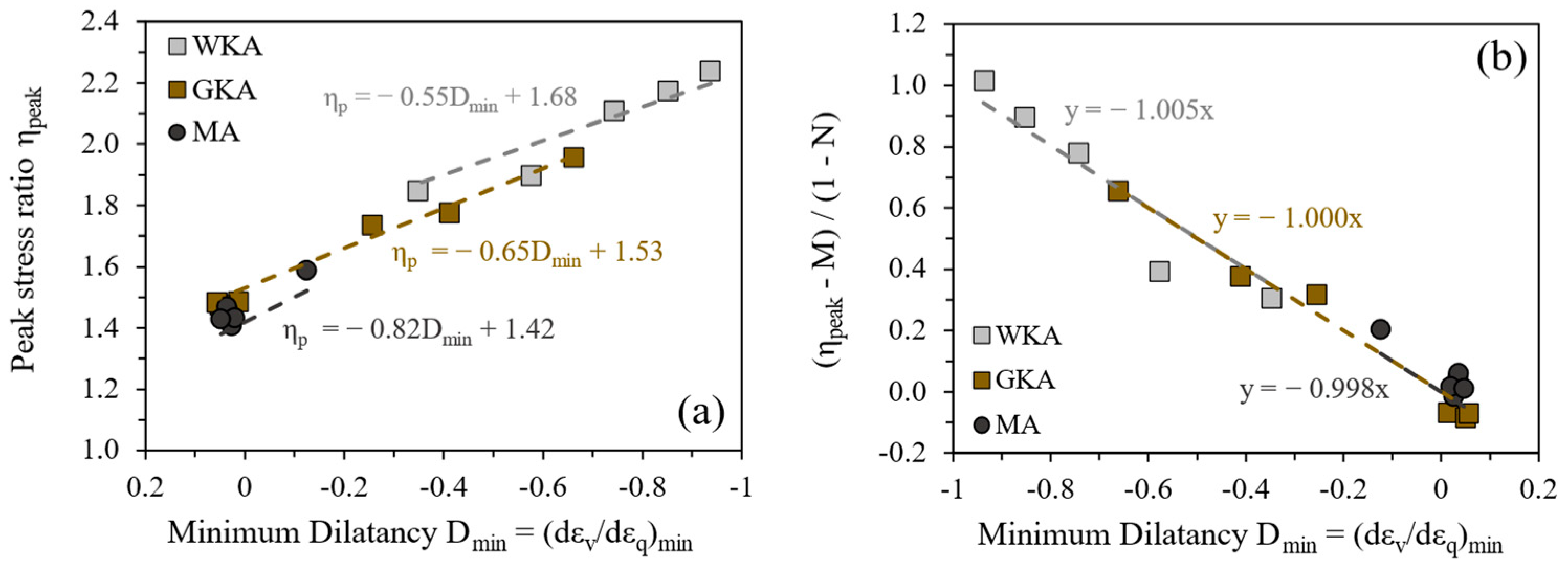
4.3. Stress Ratio, Dilatancy, and Pore Pressure Evaluations
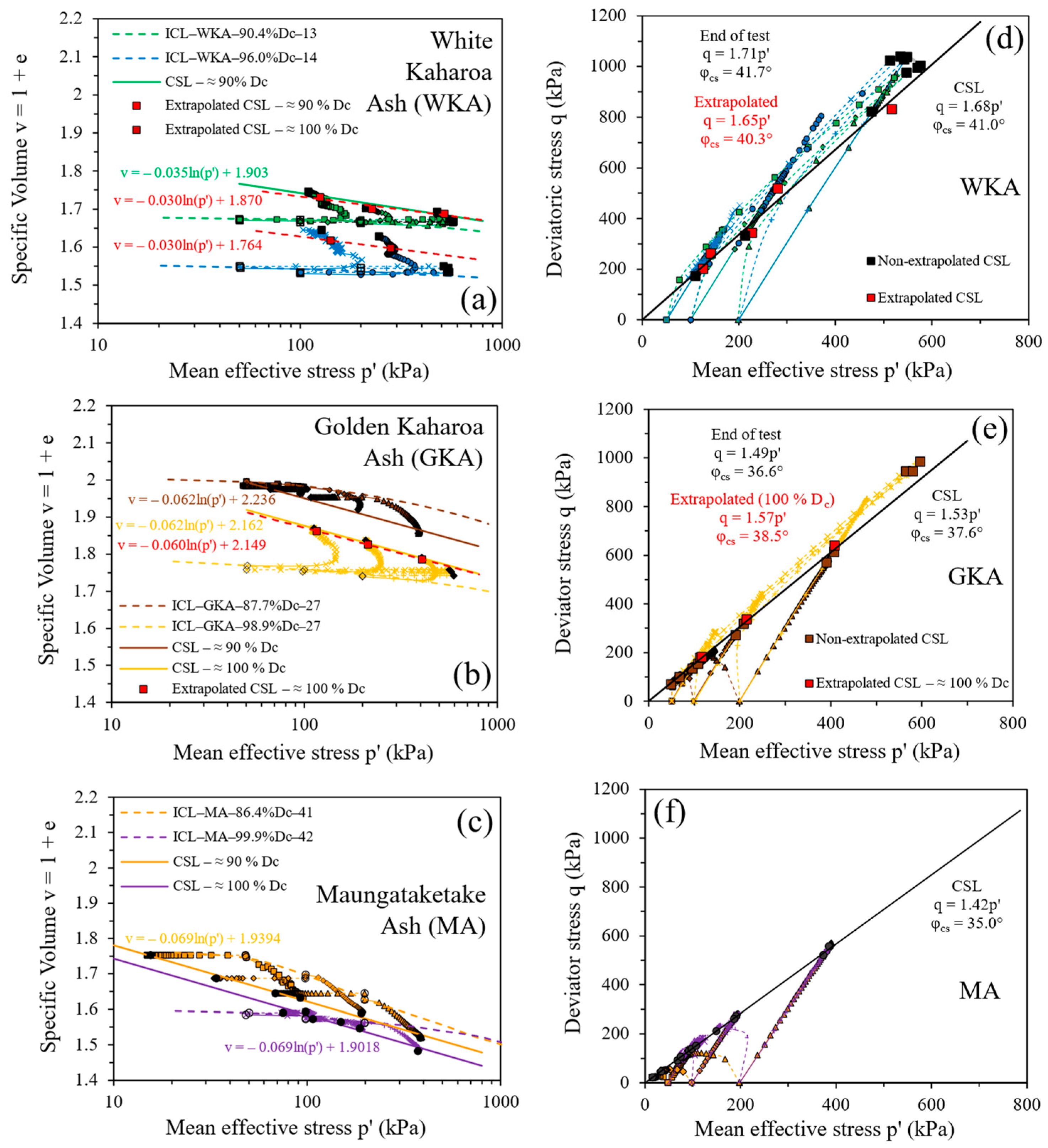
4.4. Critical State and State Parameter
4.5. Critical State Line (CSL) Projection in v–p′ and q–p′ Planes
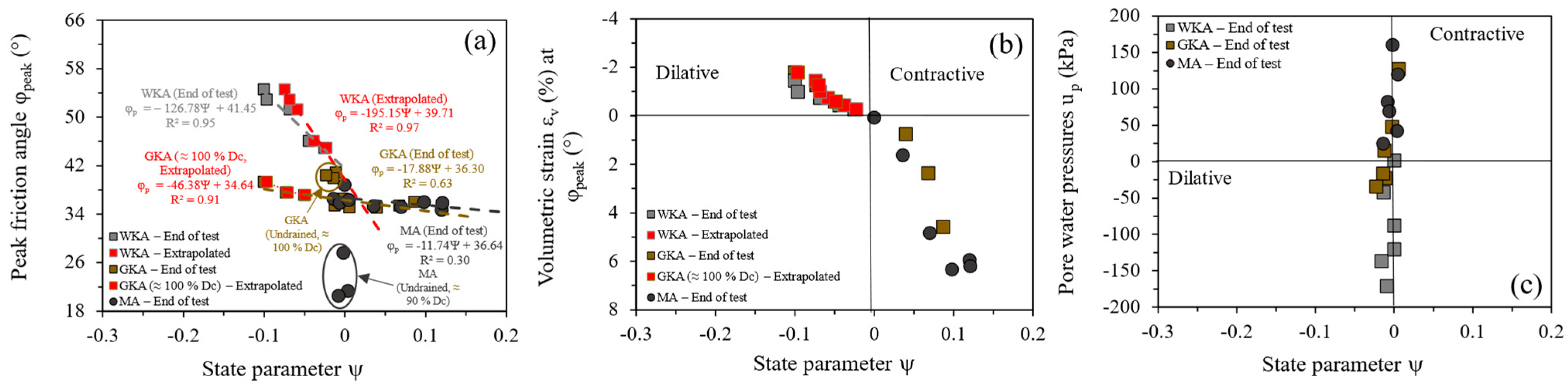
4.6. State Parameter
4.7. Particle Breakage Evaluation
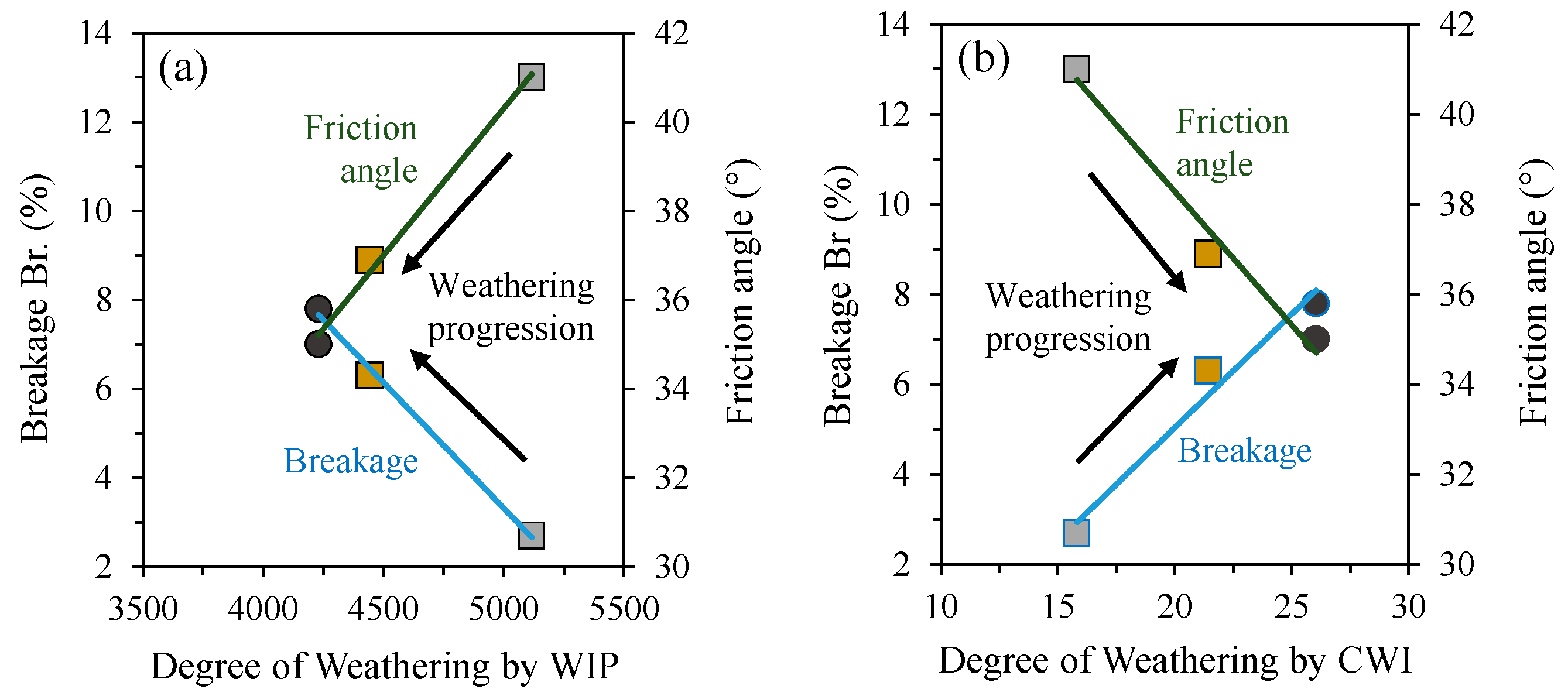
4.8. Effect of Weathering Degree and Mineralogy on Post-Shear Breakage and Friction Angle
5. Conclusions and Recommendations for Further Work
- While the least weathered WKA (closer to vent) and most weathered MA (base surge) tephras were predominantly dilative and contractive in drained conditions, the drained response exhibited by intermediately weathered GKA (away from the vent) was contractive and dilative at lower and higher degrees of compaction, respectively. In terms of undrained responses, the WKA tephra remained primarily dilative, but flow behavior initiated by dilative and then contractive responses was observed at lower and higher degrees of compaction for GKA and MA tephras, respectively.
- At large strain levels, the compacted volcanic tephras attained the critical state along with visual and non-visual appearances of localizations. Extrapolations, along with original data, indicated friction angles greater than those observed for loose sand (φ = 30°), along with measured breakage values falling below 10% post-shearing, encouraging the use of these tephras as geomaterials.
- The critical states formed unique straight lines in the q–p′ and v–ln p′ planes, along with downward movement towards smaller void ratios or specific volumes, and a rise in degree of compaction Dc in the latter plane. Thus, the framework of critical state soil mechanics was applicable to silty sands and sandy silts of volcanic origin.
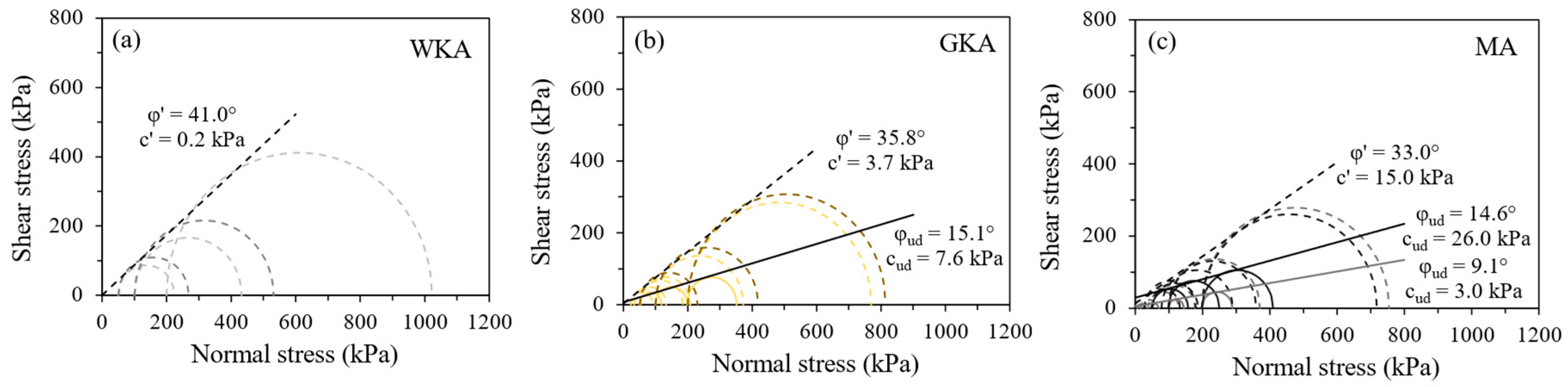
- The friction angles at peak states ranged from 35° to 55°, whereas the critical states gave a friction angle of between 35° and 43°, which were dependent on the density and stress conditions. A higher friction angle for White Kaharoa tephra resulted from the tephra’s well-graded particle size distribution, angular particle shape, and mineralogical composition (least weathered nature). Out of the crystalline silica feldspar minerals, the White Kaharoa tephra contained a large quantity of feldspars (≈76%), for which the friction angle attained a maximum of 43° at constant volume state. Thus, the frictional properties of the tephras seemed to be governed by the friction between the feldspar particles.
- The combined effects of weathering state and mineralogy indicated their influence on geotechnical characteristics such as post-shear breakage and friction angle, with higher weathering of MA resulting in higher shear breakage and lower friction angle. The corresponding highest weathering in MA ultimately reflected its compressive behavior in drained and undrained conditions, respectively. Therefore, the combination of elemental and mineralogical compositions helped in understanding the weathering nature, which further influenced strength/shear and breakage behaviors of compacted tephra deposits.
- The strength results of this study, combined with results of chemical and mineralogical investigations, indicated that silty sand tephras, if properly compacted, are suitable fills for use in typical geotechnical applications. The effects of chemical compositions on other geotechnical properties such as compressibility and cyclic behavior (i.e., seismic response under undrained cyclic shear loading) will also be presented in the upcoming papers.
- The tephra samples studied belonged to the slightly weathered category of different chemical compositions, with no clayey minerals. To illustrate the applicability of the proposed method using the degree of weathering as the influential parameter, tests on tephra samples of a more weathered nature and different chemical compositions can be performed.
- The proposed approach can also be applied to a single tephra weathered to significantly different degrees. Also, by controlling the extent of weathering under laboratory conditions, the impact of weathering on the mechanical properties of an individual volcanic soil can be checked.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Symbols and Abbreviations Used in This Study
| AVF | Auckland Volcanic Field |
| Br | Breakage |
| CIA | Chemical Index of Alteration |
| CSL | Critical state line |
| CWI | Chemical Weathering Index |
| D | Dilation rate |
| Dc | Degree of compaction |
| εq | Deviatoric strain |
| εv | Volumetric strain |
| GKA | Golden Kaharoa Ash |
| Gs | Specific gravity |
| IC | Isotropic consolidation |
| MA | Maungataketake Ash |
| Mcs | Stress ratio at critical state |
| N | Nova’s parameter |
| OVC | Okataina Volcanic Centre |
| p′ | Mean effective stress |
| p′c | Post-consolidation mean effective stress |
| p′cs | Mean effective stress at the critical state |
| p′e | Mean effective stress at the end of test |
| p′p | Mean effective stress at the peak |
| q | Deviator stress |
| qcs | Deviator stress at the critical state |
| qe | Deviator stress at the end of test |
| qp | Deviator stress at the end of peak |
| TVZ | Taupo Volcanic Zone |
| up | Pore water pressure |
| v | Specific volume |
| vc | Specific volume after consolidation |
| vcs | Specific volume at the critical state |
| ve | Specific volume at the end of test |
| WIP | Weathering Index of Parker |
| WKA | White Kaharoa Ash |
| wopt | Optimum moisture content |
| XRD | X-ray diffraction |
| XRF | X-ray fluorescence |
| Γ | Intercept of the critical state line |
| η | Stress ratio |
| ηe | Stress ratio at the end of the test |
| ηp | Stress ratio at the peak |
| λ | Slope of the critical state line |
| ρdmax | Maximum dry density |
| σc′ | Effective confining pressure |
| φ | Friction angle |
| φcs | Friction angle at the critical state |
| φe | Friction angle at the end of test |
| φp | Friction angle at the peak |
| Ψ | State parameter |
Appendix A. Examples to Estimate the Critical State
Appendix A.1. Curve Fitting Using Sigmoidal Function
- The dεv–dεq was determined using the central difference method and is plotted in Figure A1a. In a dilative material such as WKA tephra, there existed a point of inflection in the εv–εq (minimum dilatancy point) relationship, where the rate of volumetric change began to slow and the material afterwards tended to proceed towards a constant volume condition (critical state). This point was referred to as local minimum in the dεv–dεq relationship.
- A sigmoidal function was then used to fit the dεv–dεq relationship starting at the local minimum, corresponding to the point of inflection in the εv–εq relationship (Figure A1).
- The sigmoidal function was, thereafter, integrated and applied to the εv–εq (Figure A1b). The residual sum of squares between the fitting curves and test data from the points of inflection to the end of the test were calculated for each of the relationships dεv–dεq and εv–εq.
- Once the optimum fitting parameters minimizing the error between the fitting curve and test data for each relation were determined, the curves were extrapolated to the constant volume condition (Figure A1b).

Appendix A.2. Stress Ratio–Dilatancy Plots

References
- Lowe, D.J.; Balks, M.R. Introduction to tephra-derived soils and farming, Waikato-Bay of Plenty, North Island, New Zealand. In Proceedings of the University of Wisconsin-Platteville Education Abroad Program: Winterim Field Trip, Hamilton, New Zealand, 15–17 January 2019; School of Science (Earth Sciences), University of Waikato: Hamilton, New Zealand; p. 82. [Google Scholar]
- Cole, J.; Deering, C.D.; Burt, R.M.; Sewell, S.; Shane, P.; Matthews, N. Okataina Volcanic Centre, Taupo Volcanic Zone, New Zealand: A review of volcanism and synchronous pluton development in an active, dominantly silicic caldera system. Earth Sci. Rev. 2014, 128, 1–17. [Google Scholar] [CrossRef]
- Kereszturi, G.; Németh, K.; Cronin, S.J.; Agustín-Flores, J.; Smith, I.E.; Lindsay, J. A model for calculating eruptive volumes for monogenetic volcanoes—Implication for the Quaternary Auckland Volcanic Field, New Zealand. J. Volcanol. Geotherm. Res. 2013, 266, 16–33. [Google Scholar] [CrossRef]
- Hayes, J.; Wilson, T.M.; Deligne, N.I.; Cole, J.; Hughes, M. A model to assess tephra clean-up requirements in urban environments. J. Appl. Volcanol. 2017, 6, 1. [Google Scholar] [CrossRef]
- Green, R.M.; Bebbington, M.S.; Cronin, S.J.; Jones, G. Automated statistical matching of multiple tephra records exemplified using five long maar sequences younger than 75 ka, Auckland, New Zealand. Quat. Res. 2014, 82, 405–419. [Google Scholar] [CrossRef]
- Sood, S.; Chiaro, G.; Wilson, T.; Stringer, M. Physical and chemical characteristics of slightly-weathered tephras in New Zealand. Geotech. Geol. Eng. 2024, 42, 4023–4047. [Google Scholar] [CrossRef]
- Cecconi, M.; Scarapazzi, M.; Viggiani, G.M. On the geology and the geotechnical properties of pyroclastic flow deposits of the Colli Albani. Bull. Eng. Geol. Environ. 2010, 69, 185–206. [Google Scholar] [CrossRef]
- Chaneva, J.; Kluger, M.O.; Moon, V.G.; Lowe, D.J.; Orense, R.P. Monotonic and cyclic undrained behaviour and liquefaction resistance of pumiceous, non-plastic sandy silt. Soil Dyn. Earth. Eng. 2023, 168, 107825. [Google Scholar] [CrossRef]
- Miura, S.; Yagi, K.; Asonuma, T. Deformation-strength evaluation of crushable volcanic soils by laboratory and in-situ testing. Soils Found. 2003, 43, 47–57. [Google Scholar] [CrossRef]
- Vezzoli, L.; Apuani, T.; Corazzato, C.; Uttini, A. Geological and geotechnical characterization of the debris avalanche and pyroclastic deposits of Cotopaxi Volcano (Ecuador). A contribute to instability-related hazard studies. J. Volcanol. Geotherm. Res. 2017, 332, 51–70. [Google Scholar] [CrossRef]
- Haruyama, M. Effect of density on the drained deformation behavior of Shirasu (volcanic sandy soil) under three-dimensional stresses. Soils Found. 1987, 27, 1–13. [Google Scholar] [CrossRef]
- Hyodo, T.; Wu, Y.; Hyodo, M. Influence of fines on the monotonic and cyclic shear behaviour of volcanic soil “Shirasu”. Eng. Geol. 2022, 301, 106591. [Google Scholar] [CrossRef]
- Picarelli, L.; Olivares, L.; Lampitiello, S.; Darban, R.; Damiano, E. The undrained behaviour of an airfall volcanic ash. Geosciences 2020, 10, 60. [Google Scholar] [CrossRef]
- Agustian, Y.; Goto, S. Strength and deformation characteristics of scoria in triaxial compression at low confining stress. Soils Found. 2008, 48, 27–39. [Google Scholar] [CrossRef]
- Orense, R.P.; Pender, M.J.; O’Sullivan, A.S. Liquefaction Characteristics of Pumice Sands; Earthquake Commission: Wellington, New Zealand, 2012; p. 131. Available online: https://www.naturalhazards.govt.nz/resilience-and-research/research/search-all-research-reports/liquefaction-characteristics-of-pumice-sands/#:~:text=Pumice%20sands%20have%20higher%20liquefaction,in%20higher%20cyclic%20shear%20resistance (accessed on 5 August 2024).
- Iolli, S.; Modoni, G.; Chiaro, G.; Salvatore, E. Predictive correlations for the compaction of clean sands. Transp. Geotech. 2015, 4, 38–49. [Google Scholar] [CrossRef]
- De Magistris, F.S.; Tatsuoka, F. Effects of moulding water content on the stress-strain behaviour of a compacted silty sand. Soils Found. 2004, 44, 85–101. [Google Scholar] [CrossRef] [PubMed]
- Matsumura, S.; Miura, S.; Yokohama, S. Effects of compaction conditions on cyclic undrained shear properties of sandy-silt soils and its evaluation. J. Jpn. Soc. Civ. Eng. Ser. C (Geosph. Eng.) 2012, 68, 597–609. [Google Scholar] [CrossRef]
- Lindsay, J.M.; Leonard, G.S.; Smid, E.R.; Hayward, B.W. Age of the Auckland Volcanic Field: A review of existing data. N. Z. J. Geol. Geophys. 2011, 54, 379–401. [Google Scholar] [CrossRef]
- Nicol, A.; Seebeck, H.; Wallace, L. Quaternary tectonics of New Zealand. In Landscape and Quaternary Environmental Change in New Zealand; Shulmeister, J., Ed.; Atlantis Advances in Quaternary Science; Atlantis Press: Paris, France, 2017; Volume 3. [Google Scholar] [CrossRef]
- Agustín-Flores, J.; Németh, K.; Cronin, S.J.; Lindsay, J.M.; Kereszturi, G.; Brand, B.D.; Smith, I.E. Phreatomagmatic eruptions through unconsolidated coastal plain sequences, Maungataketake, Auckland Volcanic Field (New Zealand). J. Volcanol. Geotherm. Res. 2014, 276, 46–63. [Google Scholar] [CrossRef]
- Wesley, L.D. Determination of specific gravity and void ratio of pumice materials. Geotech. Test. J. 2001, 24, 418–422. [Google Scholar] [CrossRef]
- Stringer, M.E. Separation of pumice from soil mixtures. Soils Found. 2019, 59, 1073–1084. [Google Scholar] [CrossRef]
- Sood, S.; Chiaro, G.; Wilson, T.; Stringer, M. Comparison of Small-Strain Shear Modulus of Beach and Volcanic Sands; Sitharam, T.G., Kolathayar, S., Jakka, R., Eds.; Earthquake Geotechnics. Lecture Notes in Civil Engineering; Springer: Singapore, 2022; Volume 187, pp. 271–281. [Google Scholar] [CrossRef]
- Pokhrel, A.; Chiaro, G.; Kiyota, T.; Cubrinovski, M. Liquefaction characteristics of sand-gravel mixtures: Experimental observations and its assessment based on intergranular state concept. Soils Found. 2024, 62, 101444. [Google Scholar] [CrossRef]
- Umar, M.; Chiaro, G.; Kiyota, T.; Ullah, N. Deformation and cyclic resistance of sand in large-strain undrained torsional shear tests with initial static shear stress. Soils Found. 2021, 61, 765–781. [Google Scholar] [CrossRef]
- D2487; Standard Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System). ASTM International: West Conshohocken, PA, USA, 2017.
- D854; Standard Test Methods for Specific Gravity of Soil Solids by Water Pycnometer. ASTM International: West Conshohocken, PA, USA, 2014.
- Bas, M.L.; Maitre, R.L.; Streckeisen, A.; Zanettin, B.; IUGS Subcommission on the Systematics of Igneous Rocks. A chemical classification of volcanic rocks based on the total alkali-silica diagram. J. Petrol. 1986, 27, 745–750. [Google Scholar] [CrossRef]
- Nesbitt, H.W.; Fedo, C.M.; Young, G.M. Quartz and feldspar stability, steady and non-steady-state weathering, and petrogenesis of siliciclastic sands and muds. J. Geol. 1997, 105, 173–192. [Google Scholar] [CrossRef]
- Parker, A. An index of weathering for silicate rocks. Geol. Mag. 1970, 107, 501–504. [Google Scholar] [CrossRef]
- Sueoka, T. Identification and classification of granite residual soils using chemical weathering index. In Proceedings of the 2nd International Conference on Geomechanics in Tropical Soils, Singapore, 12–14 December 1988; pp. 55–61. [Google Scholar]
- D698; Standard Test Methods for Laboratory Compaction Characteristics of Soil Using Standard Effort (12,400 ft-lbf/ft3 (600 kN-m/m3)). ASTM International: West Conshohocken, PA, USA, 2012.
- Bolton, M.D. The strength and dilatancy of sands. Géotechnique 1986, 36, 65–78. [Google Scholar] [CrossRef]
- Sood, S.; Chiaro, G.; Wilson, T.; Stringer, M. Monotonic drained and undrained shear strength behaviour of compacted weathered airfall tephras. In Proceedings of the Indian Geotechnical Conference 2022 Volume 1 (IGC 2022); Lecture Notes in Civil Engineering; Jose, B.T., Sahoo, D.K., Shin, E.C., Choudhury, D., Joseph, A., Pai, R.R., Eds.; Springer: Singapore, 2024; Volume 476. [Google Scholar] [CrossRef]
- Lade, P.V.; Bopp, P.A. Relative density effects on drained sand behavior at high pressures. Soils Found. 2005, 45, 1–13. [Google Scholar] [CrossRef]
- Yoshimoto, N.; Hyodo, M.; Nakata, Y.; Orense, R.P.; Hongo, T.; Ohnaka, A. Evaluation of shear strength and mechanical properties of granulated coal ash based on single particle strength. Soils Found. 2012, 52, 321–334. [Google Scholar] [CrossRef]
- Roscoe, K.H.; Schofield, A.N.; Worth, C.P. On the yielding of soils. Géotechnique 1958, 8, 22–53. [Google Scholar] [CrossRef]
- Hyodo, M.; Hyde, A.F.; Aramaki, N.; Nakata, Y. Undrained monotonic and cyclic shear behaviour of sand under low and high confining stresses. Soils Found. 2002, 42, 63–76. [Google Scholar] [CrossRef]
- Hyodo, M.; Wu, Y.; Aramaki, N.; Nakata, Y. Undrained monotonic and cyclic shear response and particle crushing of silica sand at low and high pressures. Can. Geotech. J. 2017, 54, 207–218. [Google Scholar] [CrossRef]
- Cho, G.-C.; Dodds, J.; Santamarina, J.C. Particle shape effects on packing density, stiffness, and strength: Natural and crushed sands. J. Geotech. Geoenviron. Eng. 2006, 132, 591–602. [Google Scholar] [CrossRef]
- Haruyama, M. Geological, Physical, and Mechanical Properties of “Shirasu” and its Engineering Classification. Soils Found. 1973, 13, 45–60. [Google Scholar] [CrossRef]
- Been, K.; Jefferies, M.G. Stress-dilatancy in very loose sand. Can. Geotech. J. 2004, 41, 972–989. [Google Scholar] [CrossRef]
- Li, X.S.; Dafalias, Y.F. Dilatancy for cohesionless soils. Géotechnique 2000, 50, 449–460. [Google Scholar] [CrossRef]
- Nova, R. A constitutive model for soil under monotonic and cyclic loading. In Soil Mechanics-Transient and Cyclic Loading; Pande, G.N., Zienkiewicz, O.C., Eds.; Wiley: Chichester, UK, 1982; pp. 343–373. [Google Scholar]
- Roscoe, K.H.; Schofield, A.N.; Thurairajah, A. Yielding of clays in states wetter than critical. Géotechnique 1963, 13, 211–240. [Google Scholar] [CrossRef]
- Rowe, P.W. The stress-dilatancy relation for static equilibrium of an assembly of particles in contact. Proc. R. Soc. Lond. 1962, 269, 500–527. [Google Scholar] [CrossRef]
- Schofield, A.N.; Wroth, P. Critical State Soil Mechanics; McGraw-Hill: London, UK, 1968; Volume 310. [Google Scholar]
- Been, K.; Jefferies, M.G. A state parameter for sands. Géotechnique 1985, 35, 99–112. [Google Scholar] [CrossRef]
- Carrera, A.; Coop, M.R.; Lancellotta, R. Influence of grading on the mechanical behaviour of Stava tailings. Géotechnique 2011, 61, 935–946. [Google Scholar] [CrossRef]
- Ghafghazi, M.; Shuttle, D.A. Accurate determination of the critical state friction angle from triaxial tests. In Proceedings of the 59th Canadian Geotechnical Conference, Vancouver, BC, Canada, 1–4 October 2006. [Google Scholar]
- Murthy, T.G.; Loukidis, D.; Carraro, J.A.H.; Prezzi, M.; Salgado, R. Undrained monotonic response of clean and silty sands. Géotechnique 2007, 57, 273–288. [Google Scholar] [CrossRef]
- Xiao, Y.; Xiang, J.; Liu, H.; Ma, Q. Strength–dilatancy relation of sand containing non-plastic fines. Géotech. Lett. 2017, 7, 204–210. [Google Scholar] [CrossRef]
- Yilmaz, Y.; Deng, Y.; Chang, C.S.; Gokce, A. Strength–dilatancy and critical state behaviours of binary mixtures of graded sands influenced by particle size ratio and fines content. Géotechnique 2023, 73, 202–217. [Google Scholar] [CrossRef]
- Jefferies, M.G. Nor-Sand: A simple critical state model for sand. Géotechnique 1993, 43, 91–103. [Google Scholar] [CrossRef]
- Heitor, A.; Indraratna, B.; Kaliboullah, C.I.; Rujikiatkamjorn, C.; McIntosh, G.W. Drained and undrained shear behavior of compacted coal wash. J. Geotech. Geoenviron. Eng. 2016, 142, 04016006. [Google Scholar] [CrossRef]
- Winter, M.J.; Hyodo, M.; Wu, Y.; Yoshimoto, N.; Hasan, M.B.; Matsui, K. Influences of particle characteristic and compaction degree on the shear response of clinker ash. Eng. Geol. 2017, 230, 32–45. [Google Scholar] [CrossRef]
- Daouadji, A.; Hicher, P.Y.; Rahma, A. An elastoplastic model for granular materials taking into account grain breakage. Eur. J. Mech. A/Solids 2001, 20, 113–137. [Google Scholar] [CrossRef]
- Ghafghazi, M.; Shuttle, D.A.; DeJong, J.T. Particle breakage and the critical state of sand. Soils Found. 2014, 54, 451–461. [Google Scholar] [CrossRef]
- Kikumoto, M.; Wood, D.M.; Russell, A. Particle crushing and deformation behaviour. Soils Found. 2010, 50, 547–563. [Google Scholar] [CrossRef]
- Wood, D.M.; Maeda, K. Changing grading of soil: Effect on critical states. Acta Geotech. 2008, 3, 3–14. [Google Scholar] [CrossRef]
- Bandini, V.; Coop, M.R. The influence of particle breakage on the location of the critical state line of sands. Soils Found. 2011, 51, 591–600. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, H.; Ding, X.; Chen, Y.; Jiang, J.; Zhang, W. Influence of particle breakage on critical state line of rockfill material. Int. J. Geomech. 2016, 16, 04015031. [Google Scholar] [CrossRef]
- Chiaro, G.; Kiyota, T.; Umar, M.; Cappellaro, C. Earthquake-induced flow-type slope failure in weathered volcanic deposits—A case study: The 16 April 2016 Takanodai Landslide, Japan. Geosciences 2022, 12, 394. [Google Scholar] [CrossRef]
- Mills, P.; Moon, V. Static failure mechanisms in sensitive volcanic soils in the Tauranga Region, New Zealand. In Proceedings of the 11th Australia and New Zealand Young Geotechnical Professionals Conference, Queenstown, New Zealand, 25–28 October 2016. [Google Scholar]
- Wang, H.; Koseki, J.; Cai, F.; Nishimura, T. Undrained monotonic triaxial loading behaviors of a type of iron ore fines. Can. Geotech. J. 2018, 55, 1349–1357. [Google Scholar] [CrossRef]
- Hardin, B.O. Crushing of soil particles. J. Geotech. Eng. 1985, 111, 1177–1192. [Google Scholar] [CrossRef]
- Miura, S.; Yagi, K. Particle breakage of volcanic coarse-grained soils and its evaluation. J. Jpn. Soc. Civ. Eng. JSCE 1997, 561, 257–269. [Google Scholar] [CrossRef]
- Tasalloti, S.M.A.; Indraratna, B.; Rujikiatkamjorn, C.; Heitor, A.; Chiaro, G. A laboratory study on the shear behavior of mixtures of coal wash and steel furnace slag as potential structural fill. ASTM Int. Geotech. Test. J. 2015, 38, 361–372. [Google Scholar] [CrossRef]
- Liu, X.-Y.; Wang, C.-M.; Liu, H.-L.; Wu, D. An Experimental Investigation of the Mechanical Behavior and Particle Crushing Characteristic of Volcanic Soil. Materials 2022, 15, 5423. [Google Scholar] [CrossRef]


| Tephra Sample | Major Oxide (Wt. %) | WIP | CWI | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SiO2 | TiO2 | Al2O3 | Fe2O3 | MnO | MgO | CaO | Na2O | K2O | P2O5 | LOI | |||
| WKA | 75.1 | 0.2 | 12.3 | 1.3 | 0.1 | 0.2 | 1.1 | 3.9 | 3.4 | 0.0 | 2.0 | 5116.7 | 15.8 |
| GKA | 70.7 | 0.2 | 13.9 | 1.8 | 0.1 | 0.2 | 1.1 | 3.6 | 2.8 | 0.1 | 5.5 | 4443.0 | 21.4 |
| MA | 57.3 | 1.4 | 12.3 | 8.3 | 0.1 | 5.2 | 6.6 | 2.4 | 1.6 | 0.4 | 4.0 | 4230.3 | 26.0 |
| Mineral (Wt. %) | Tephra Sample | ||
|---|---|---|---|
| WKA | GKA | MA | |
| Glass | 78.3/0.0 | 86.2/0.0 | 38.5/0.0 |
| Silica | 4.3/19.9 | 4.1/29.5 | 27.7/44.9 |
| Feldspars | 16.4/75.6 | 9.2/66.9 | 24.7/40.2 |
| Accessories | 1.0/4.4 | 0.5/3.5 | 9.2/14.9 |
| Total Crystal Content | 21.7/100.0 | 13.8/100.0 | 61.6/100.0 |
| Test Abbreviation (“σc′−Tephra−Dc-Drainage−Test No.”) | Actual Degree of Compaction Dc (%) | Post-Consolidation | Peak State | End of Test | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p′c (kPa) | vc | qp (kPa) | p′p (kPa) | ϕp (°) | (dεv/dεq)p or (dup/dεq)p | qe (kPa) | p′e (kPa) | ϕe (°) | (dεv/dεq) or (dup/dεq)e | ve | ||
| 50−WKA−90−D-1 *^ | 91.3 | 50 | 1.670 | 356.0 | 168.9 | 51.3 | −0.754 | 173.6 | 109.8 | 38.7 | −0.015 | 1.745 |
| 100−WKA−90−D-2 *^ | 91.4 | 100 | 1.671 | 525.7 | 277.3 | 46.1 | −0.591 | 332.5 | 212.0 | 38.4 | 0.037 | 1.702 |
| 200−WKA−90−D−3 *^ | 91.1 | 200 | 1.662 | 970.5 | 525.3 | 44.9 | −0.351 | 822.7 | 475.3 | 42.2 | −0.094 | 1.692 |
| 50−WKA−90−UD−4 | 89.7 | 50 | 1.673 | 976.0 | 648.2 | 43.4 | −26.9 | 1.673 | ||||
| 100−WKA−90−UD−5 | 91.7 | 100 | 1.665 | 994.2 | 650.4 | 42.5 | −42.1 | 1.665 | ||||
| 200−WKA−90−UD−6 | 90.7 | 198 | 1.667 | 1002.3 | 576.0 | 42.4 | −51.6 | 1.667 | ||||
| 50−WKA−100−D−7 * | 96.3 | 51 | 1.544 | 450.9 | 201.5 | 54.6 | −0.956 | 217.7 | 127.8 | 41.6 | 0.020 | 1.645 |
| 100−WKA−100−D−8 * | 95.8 | 100 | 1.531 | 804.6 | 370.3 | 52.9 | −0.851 | 431.8 | 245.9 | 42.8 | −0.137 | 1.627 |
| 200−WKA−100−D−9 | 96.1 | 200 | 1.536 | 1037.9 | 548.0 | 46.0 | −0.294 | 1.534 | ||||
| 50−WKA−100−UD−10 | 96.3 | 50 | 1.549 | 1023.0 | 512.4 | 48.5 | −91.4 | 1.549 | ||||
| 100−WKA−100−UD−11 | 95.9 | 100 | 1.534 | 1038.7 | 534.3 | 47.2 | −84.6 | 1.534 | ||||
| 200−WKA−100−UD−12 | 96.4 | 200 | 1.545 | 1027.5 | 541.8 | 46.1 | −63.7 | 1.545 | ||||
| IC−WKA−90−13 | 90.4 | 20→1200 | 1.677 | |||||||||
| IC−WKA−100−14 | 96.0 | 20→1200 | 1.551 | |||||||||
| 50−GKA−90−D−15 ^ | 87.0 | 50 | 1.996 | 147.0 | 99.0 | 36.5 | 0.013 | 134.8 | 94.9 | 35.0 | 0.044 | 1.964 |
| 100−GKA−90−D−16 ^ | 86.6 | 100 | 1.981 | 287.2 | 194.7 | 36.3 | 0.050 | 272.5 | 189.8 | 35.4 | 0.046 | 1.921 |
| 200−GKA−90−D−17 ^ | 88.3 | 200 | 1.955 | 586.7 | 395.5 | 36.5 | 0.056 | 570.0 | 390.1 | 36.0 | 0.043 | 1.856 |
| 50−GKA−90−UD−18 ^ | 87.3 | 50 | 1.986 | 108.9 | 72.8 | 36.8 | 0.889 | 69.1 | 48.1 | 35.4 | −1.030 | 1.986 |
| 100−GKA−90−UD−19 ^ | 87.4 | 100 | 1.975 | 156.3 | 104.0 | 36.9 | 0.100 | 99.2 | 66.8 | 36.5 | 0.690 | 1.975 |
| 200−GKA−90−UD−20 ^ | 87.4 | 198 | 1.954 | 214.0 | 144.5 | 36.4 | −0.100 | 153.9 | 108.1 | 35.1 | 0.984 | 1.954 |
| 50−GKA−100−D−21 *^ | 98.9 | 51 | 1.769 | 286.2 | 146.3 | 47.5 | −0.662 | 179.7 | 111.9 | 32.7 | −0.062 | 1.871 |
| 100−GKA−100−D−22 *^ | 98.9 | 100 | 1.758 | 441.3 | 248.7 | 43.2 | −0.412 | 317.6 | 207.8 | 37.5 | −0.087 | 1.838 |
| 200−GKA−100−D−23 *^ | 99.1 | 200 | 1.740 | 833.0 | 479.8 | 42.3 | −0.256 | 614.3 | 406.5 | 37.1 | −0.014 | 1.791 |
| 50−GKA−100−UD−24 | 98.1 | 50 | 1.758 | 944.6 | 564.4 | 40.9 | −22.4 | 1.758 | ||||
| 100−GKA−100−UD−25 | 99.1 | 98 | 1.754 | 945.5 | 579.4 | 39.9 | −16.2 | 1.754 | ||||
| 200−GKA−100−UD−26 | 99.3 | 200 | 1.743 | 984.7 | 595.9 | 40.4 | −34.3 | 1.743 | ||||
| IC−GKA−90−27 | 87.7 | 20→1200 | 1.998 | |||||||||
| IC−GKA−100−28 | 98.9 | 20→1200 | 1.780 | |||||||||
| 50−MA−90−D−29 ^ | 87.2 | 49 | 1.747 | 138.8 | 95.5 | 34.7 | 0.026 | 129.3 | 92.2 | 34.6 | 0.013 | 1.632 |
| 100−MA−90−D−30 ^ | 87.1 | 98 | 1.698 | 283.3 | 194.4 | 35.9 | 0.035 | 272.7 | 190.8 | 35.3 | 0.019 | 1.589 |
| 200−MA−90−D−31 ^ | 87.6 | 198 | 1.626 | 571.3 | 391.0 | 36.0 | 0.036 | 557.0 | 385.6 | 35.6 | 0.000 | 1.521 |
| 50−MA−90−UD−32 ^ | 87.2 | 48 | 1.754 | 26.5 | 32.0 | 21.3 | 12.2 | 22.9 | 15.5 | 36.3 | 0.200 | 1.754 |
| 100−MA−90−UD−33 ^ | 87.4 | 98 | 1.688 | 53.7 | 67.8 | 20.5 | 30.1 | 47.3 | 34.1 | 34.2 | 0.300 | 1.688 |
| 200−MA−90−UD−34 ^ | 87.4 | 198 | 1.645 | 121.3 | 110.7 | 27.6 | 12.5 | 91.2 | 68.7 | 32.9 | 0.335 | 1.645 |
| 50−MA−100−D−35 ^ | 99.1 | 48 | 1.585 | 172.7 | 108.9 | 38.9 | −0.125 | 139.1 | 98.3 | 36.0 | −0.005 | 1.594 |
| 100−MA−100−D−36 ^ | 99.6 | 99 | 1.575 | 277.1 | 193.5 | 35.3 | 0.019 | 260.4 | 186.9 | 34.4 | 0.010 | 1.547 |
| 200−MA−100−D−37 ^ | 98.1 | 198 | 1.563 | 544.6 | 381.4 | 35.2 | 0.047 | 520.3 | 373.2 | 34.4 | 0.020 | 1.483 |
| 50−MA−100−UD−38 ^ | 99.6 | 50 | 1.590 | 106.3 | 89.4 | 36.5 | 1.7 | 107.5 | 75.1 | 35.3 | 0.000 | 1.590 |
| 100−MA−100−UD−39 ^ | 97.1 | 98 | 1.573 | 184.4 | 126.5 | 35.9 | −0.085 | 151.7 | 107.2 | 34.9 | −0.085 | 1.573 |
| 200−MA−100−UD−40 ^ | 97.8 | 198 | 1.561 | 232.5 | 157.4 | 36.3 | 1.3 | 212.0 | 149.5 | 35.0 | 0.103 | 1.565 |
| IC−MA−90−41 | 86.4 | 20→1200 | 1.760 | |||||||||
| IC−MA−100−42 | 99.9 | 20→1200 | 1.596 | |||||||||
| Test Abbreviation | Post-Consolidation | End of Test (e) | Extrapolated CS Parameters | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| p′c (kPa) | vc | qe (kPa) | p′e (kPa) | ϕe (°) | ve | qcs (kPa) | pcs’ (kPa) | vcs | Mcs | |
| 50-WKA-90-D-1 * | 50.1 | 1.670 | 173.6 | 109.8 | 38.7 | 1.745 | 201.7 | 125.2 | 1.731 | 1.61 |
| 100-WKA-90-D-2 * | 100.0 | 1.671 | 332.5 | 212.0 | 38.4 | 1.702 | 343.0 | 226.1 | 1.701 | 1.61 |
| 200-WKA-90-D-3 * | 199.8 | 1.662 | 822.7 | 475.3 | 42.2 | 1.692 | 831.9 | 516.7 | 1.687 | 1.61 |
| 50-WKA-100-D-7 ^ | 50.6 | 1.544 | 217.7 | 127.8 | 41.6 | 1.645 | 261.7 | 140.7 | 1.618 | 1.86 |
| 100-WKA-100-D-8 ^ | 100.1 | 1.531 | 431.8 | 245.9 | 42.8 | 1.627 | 518.4 | 280.2 | 1.597 | 1.85 |
| 50-GKA-100-D-21 * | 50.6 | 1.769 | 286.2 | 146.3 | 39.3 | 1.871 | 181.8 | 115.8 | 1.862 | 1.57 |
| 100-GKA-100-D-22 * | 100.1 | 1.758 | 441.3 | 248.7 | 37.5 | 1.838 | 336.0 | 214.0 | 1.826 | 1.57 |
| 200-GKA-100-D-23 * | 200.0 | 1.740 | 833.0 | 479.8 | 37.1 | 1.791 | 639.6 | 407.4 | 1.786 | 1.57 |
| Test | Breakage Br (%) | Test | Breakage Br (%) | Test | Breakage Br (%) | |||
|---|---|---|---|---|---|---|---|---|
| H [67] | M&Y [68] | H [67] | M&Y [68] | H [67] | M&Y [68] | |||
| 50-WKA-90-D-1 | 2.1 | 0.7 | 50-GKA-90-D-15 | 2.5 | 3.0 | 50-MA-90-D-29 | 7.5 | 2.7 |
| 100-WKA-90-D-2 | 2.4 | 1.4 | 100-GKA-90-D-16 | 4.9 | 3.9 | 100-MA-90-D-30 | 9.2 | 3.5 |
| 200-WKA-90-D-3 | 2.9 | 0.9 | 200-GKA-90-D-17 | 7.3 | 4.5 | 200-MA-90-D-31 | 8.8 | 3.8 |
| 50-WKA-90-UD-4 | 1.3 | 0.2 | 50-GKA-90-UD-18 | 2.5 | 3.1 | 50-MA-90-UD-32 | 8.5 | 3.0 |
| 100-WKA-90-UD-5 | 2.0 | 0.7 | 100-GKA-90-UD-19 | 3.0 | 2.8 | 100-MA-90-UD-33 | 7.6 | 3.5 |
| 200-WKA-90-UD-6 | 1.8 | 0.6 | 200-GKA-90-UD-20 | 5.2 | 2.9 | 200-MA-90-UD-34 | 7.0 | 2.8 |
| 50-WKA-100-D-7 | 4.1 | 0.9 | 50-GKA-100-D-21 | 7.7 | 4.6 | 50-MA-100-D-35 | 6.3 | 2.4 |
| 100-WKA-100-D-8 | 4.8 | 1.3 | 100-GKA-100-D-22 | 9.8 | 6.5 | 100-MA-100-D-36 | 8.6 | 4.1 |
| 200-WKA-100-D-9 | 3.2 | 0.9 | 200-GKA-100-D-23 | 11.6 | 6.7 | 200-MA-100-D-37 | 7.6 | 3.5 |
| 50-WKA-100-UD-10 | 3.2 | 1.3 | 50-GKA-100-UD-24 | 6.5 | 4.7 | 50-MA-100-UD-38 | 6.5 | 1.8 |
| 100-WKA-100-UD-11 | 1.4 | 1.3 | 100-GKA-100-UD-25 | 8.4 | 6.2 | 100-MA-100-UD-39 | 8.5 | 2.5 |
| 200-WKA-100-UD-12 | 3.6 | 1.2 | 200-GKA-100-UD-26 | 6.1 | 4.7 | 200-MA-100-UD-40 | 7.5 | 2.8 |
| IC-WKA-90-13 | 1.9 | 1.0 | IC-GKA-90-27 | 2.7 | 2.4 | IC-MA-90-41 | 6.0 | 2.4 |
| IC-WKA-100-14 | 3.6 | 0.7 | IC-GKA-100-28 | 2.8 | 2.0 | IC-MA-100-42 | 7.4 | 2.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sood, S.; Chiaro, G.; Wilson, T.; Stringer, M. Monotonic Drained and Undrained Shear Behaviors of Compacted Slightly Weathered Tephras from New Zealand. Geotechnics 2024, 4, 843-871. https://doi.org/10.3390/geotechnics4030044
Sood S, Chiaro G, Wilson T, Stringer M. Monotonic Drained and Undrained Shear Behaviors of Compacted Slightly Weathered Tephras from New Zealand. Geotechnics. 2024; 4(3):843-871. https://doi.org/10.3390/geotechnics4030044
Chicago/Turabian StyleSood, Shaurya, Gabriele Chiaro, Thomas Wilson, and Mark Stringer. 2024. "Monotonic Drained and Undrained Shear Behaviors of Compacted Slightly Weathered Tephras from New Zealand" Geotechnics 4, no. 3: 843-871. https://doi.org/10.3390/geotechnics4030044
APA StyleSood, S., Chiaro, G., Wilson, T., & Stringer, M. (2024). Monotonic Drained and Undrained Shear Behaviors of Compacted Slightly Weathered Tephras from New Zealand. Geotechnics, 4(3), 843-871. https://doi.org/10.3390/geotechnics4030044







