Quantifying the Effects of Material Input Levels on Jointed Plain Concrete Pavement (JPCP) Performance and Slab Thickness
Abstract
:1. Introduction
Significance of the Work
2. Methodology
3. Level One, Two, and Three Analyses and Results
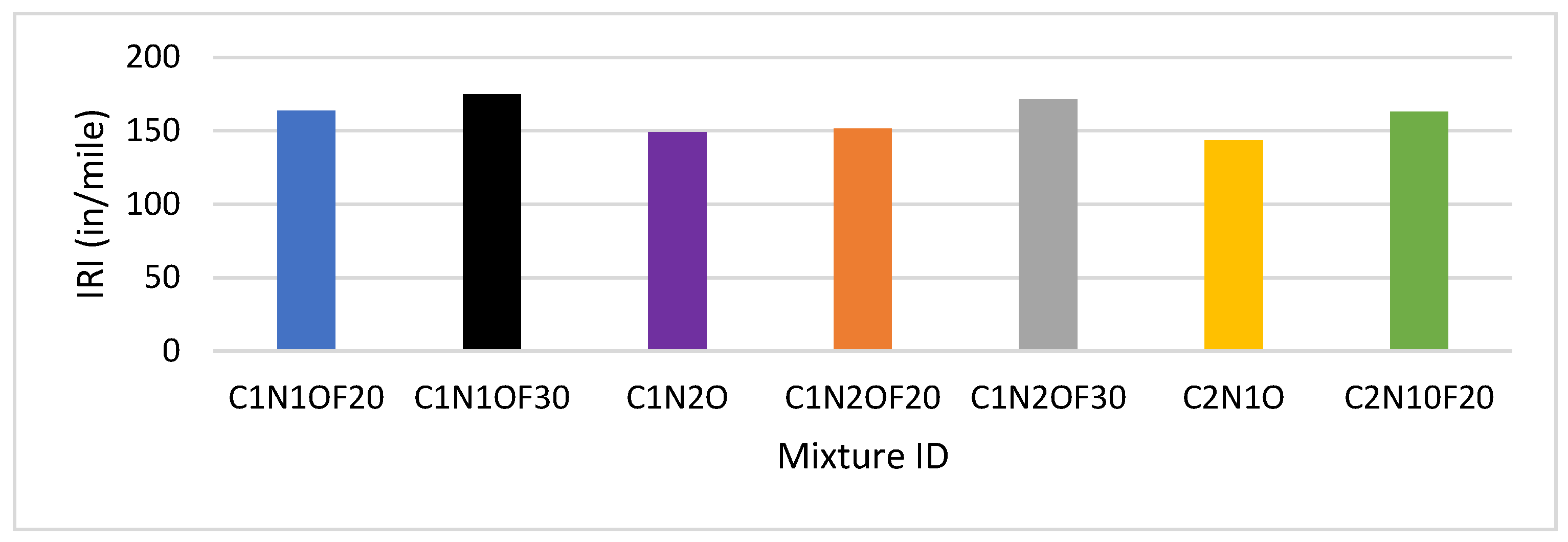
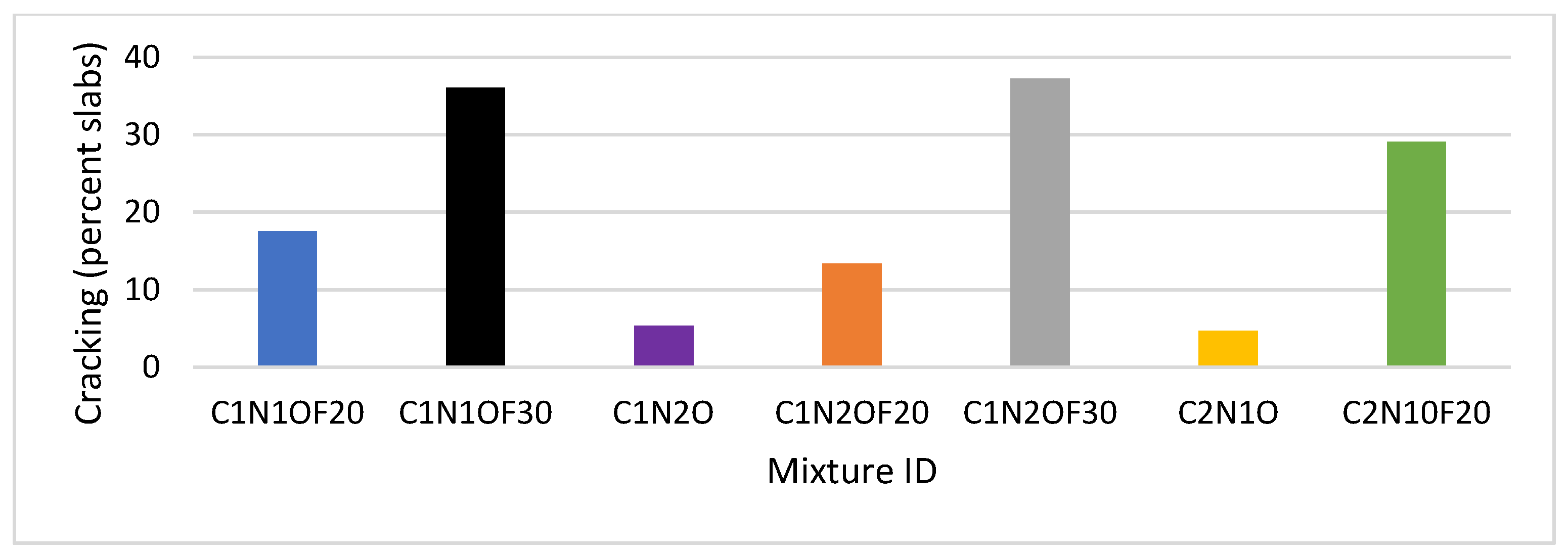
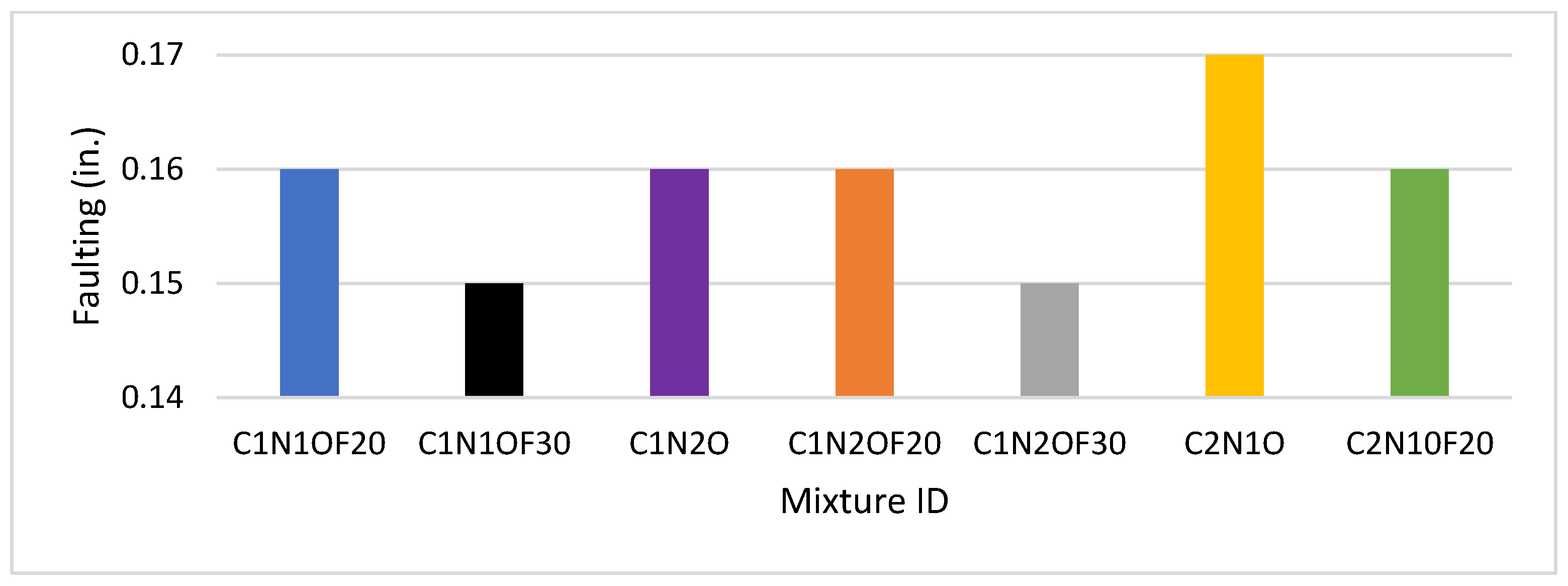
3.1. Level One Results
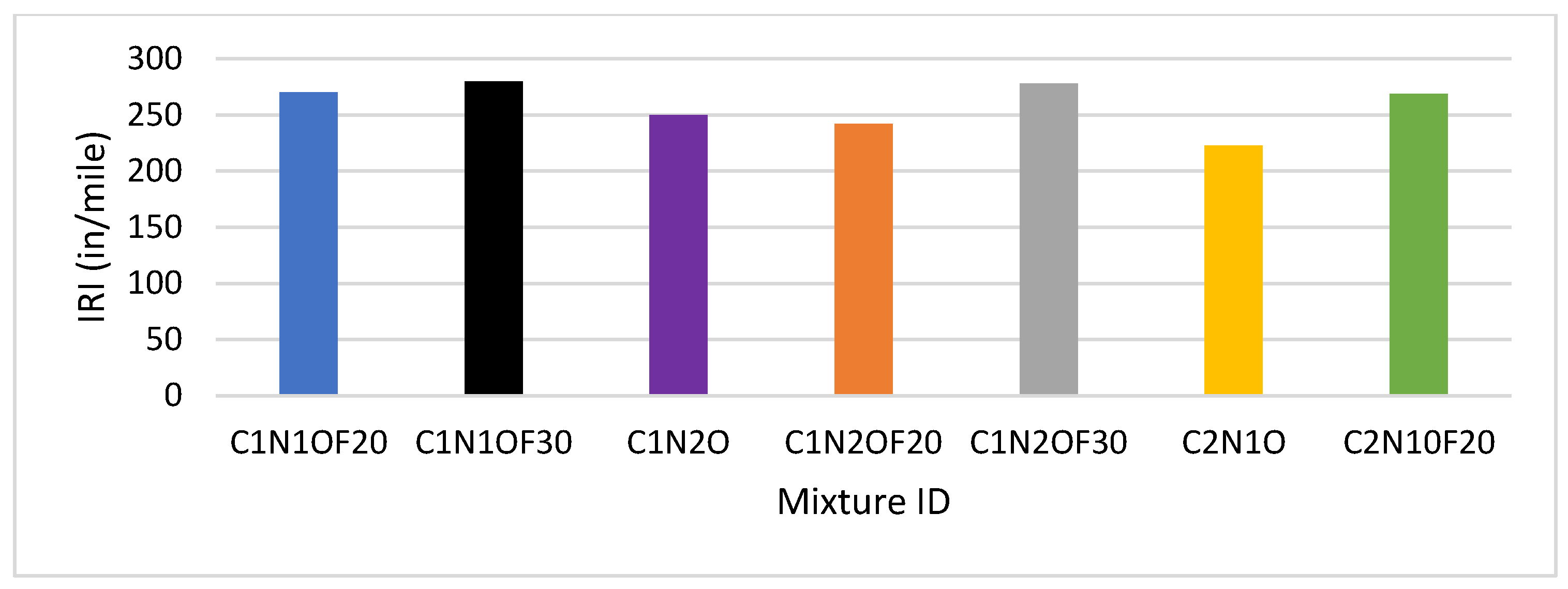
3.2. Level Two Results
3.3. Level Three Results
4. Level One, Two, and Three Indicator Comparisons
4.1. IRI Indicator Analysis
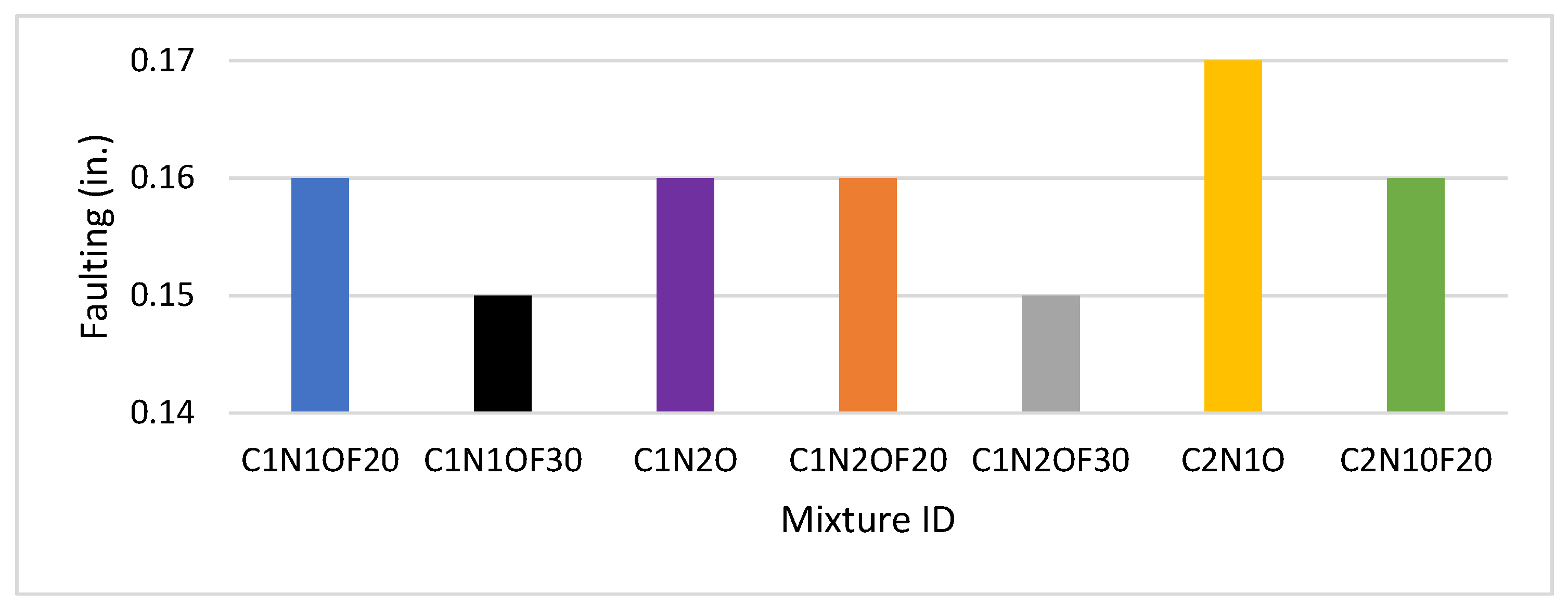
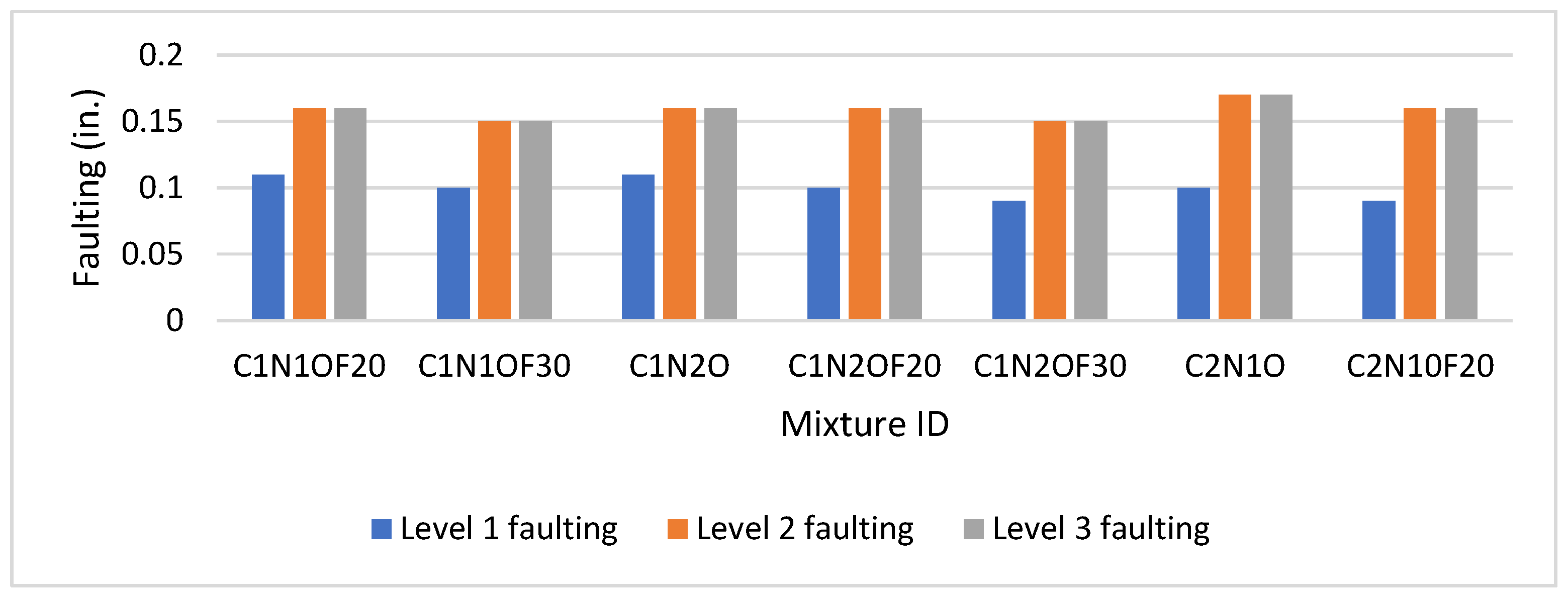
4.2. Faulting Indicator Analysis
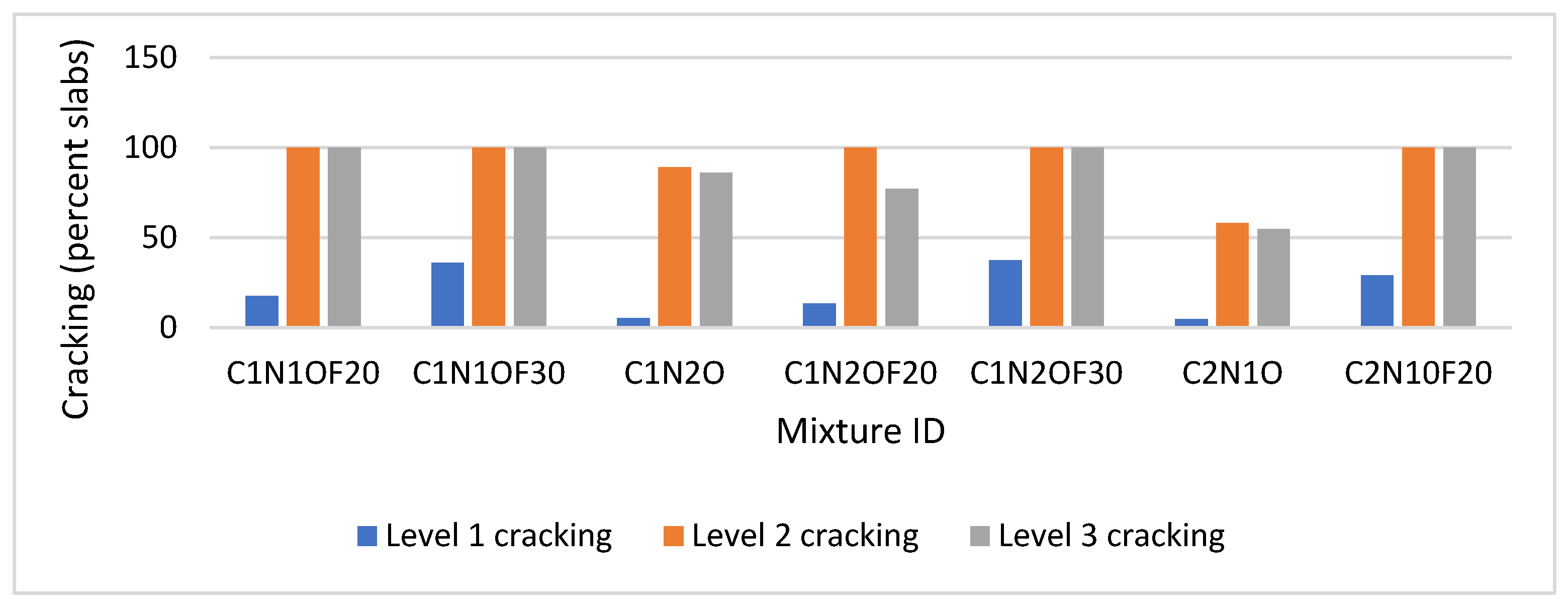
4.3. Cracking Indicator Analysis
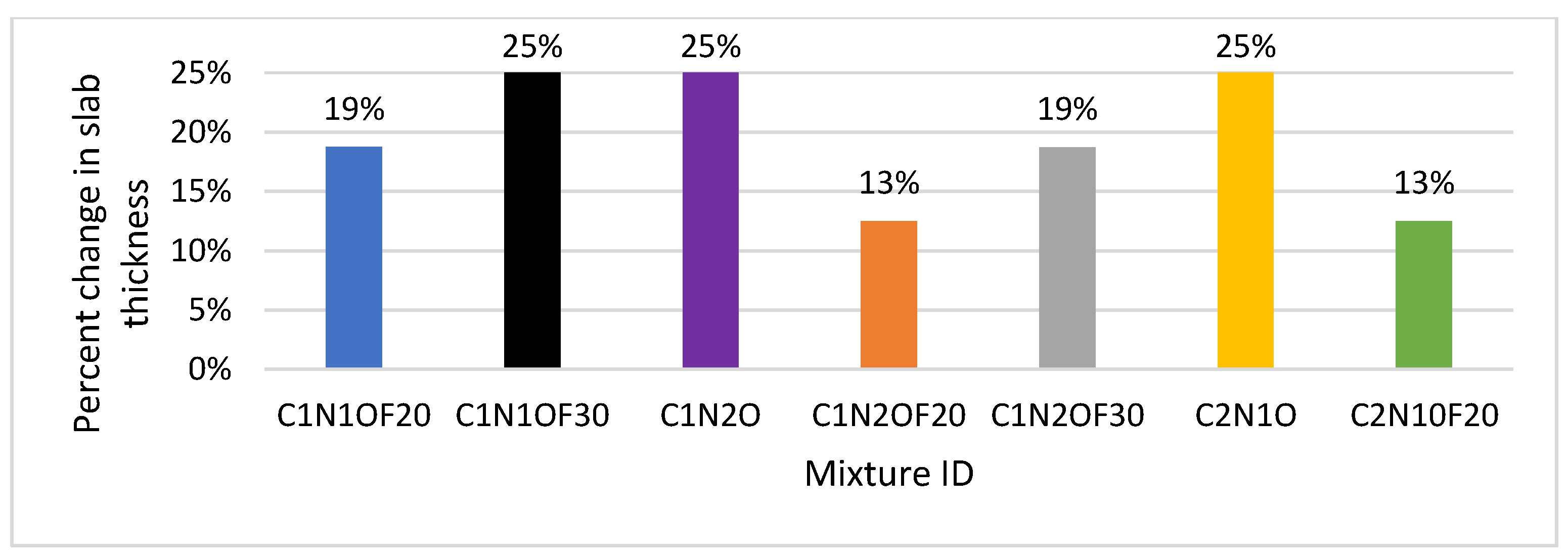
5. Effects of the Input Levels on Design Slab Thickness of JPCPs
Slab Thickness Results
6. Performance Indicator Results
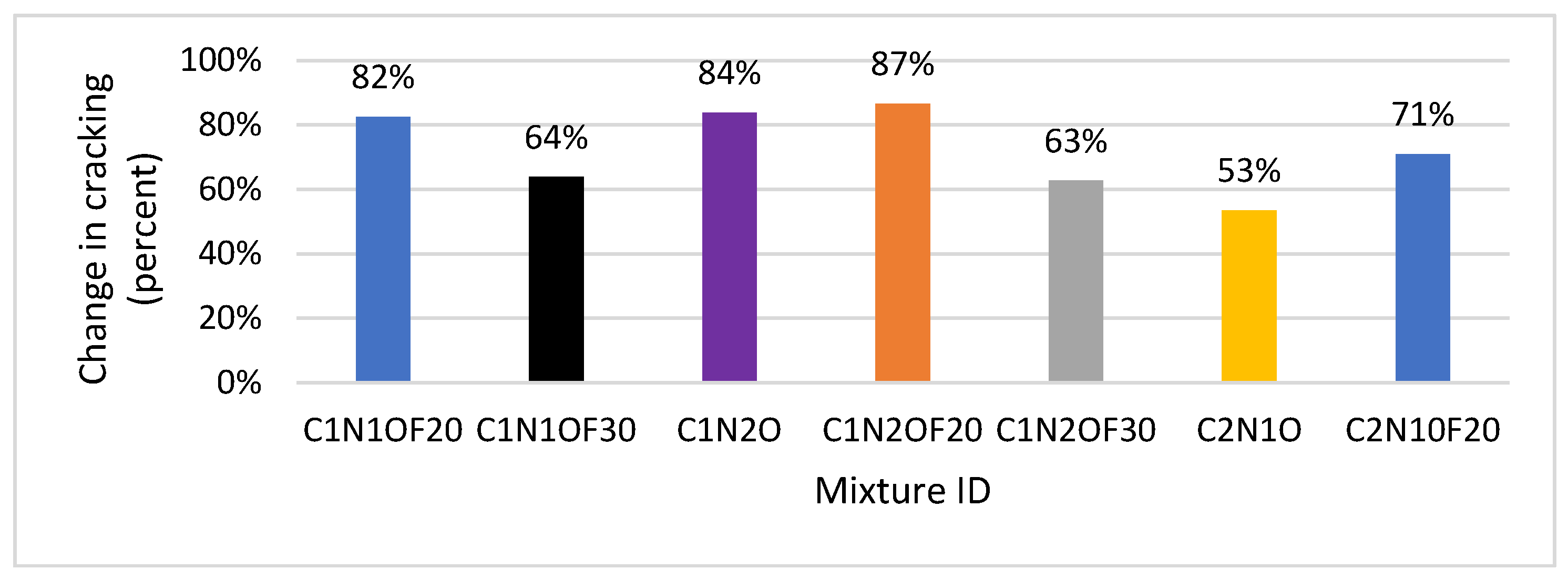
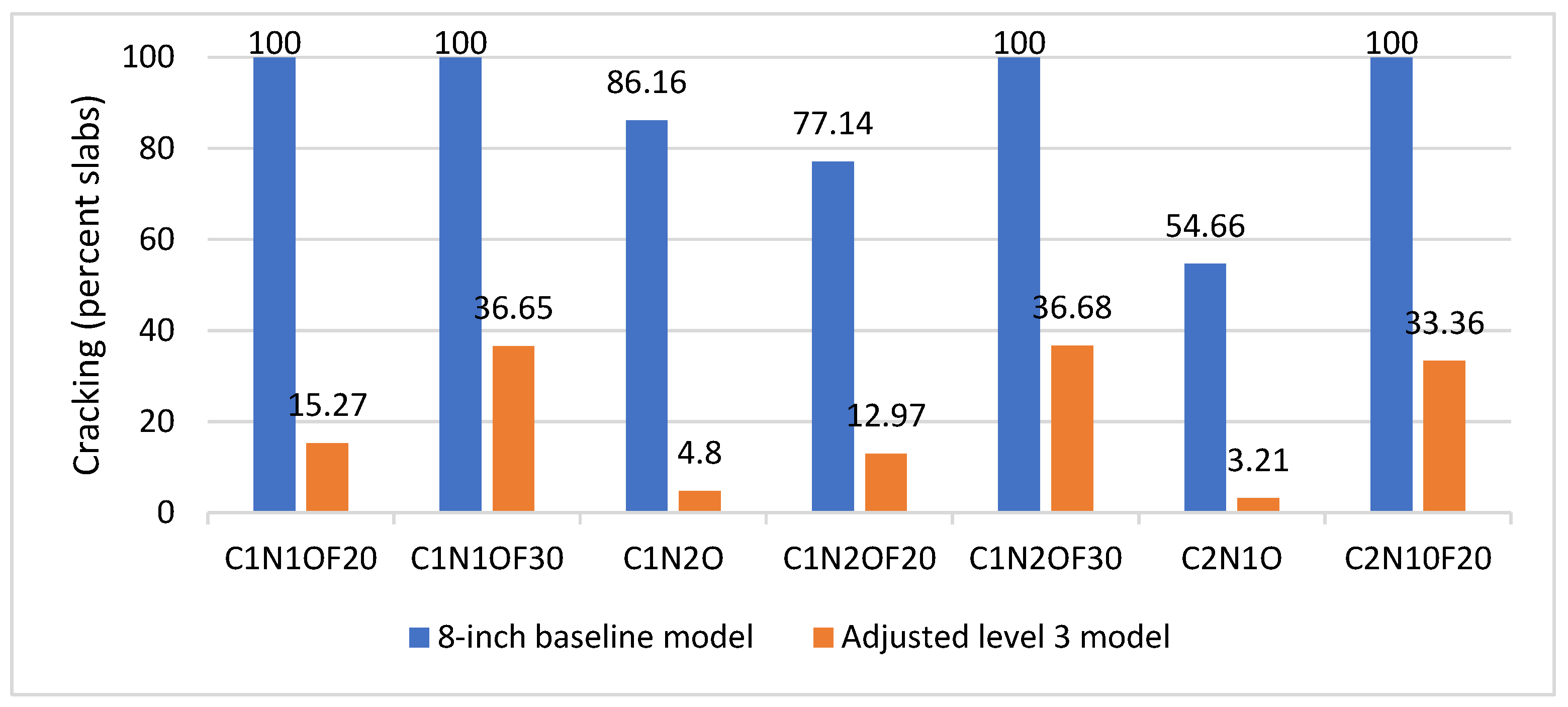
6.1. Comparison of JPCP Cracking with the Level Three Baseline Models and Readjusted Level Three Models
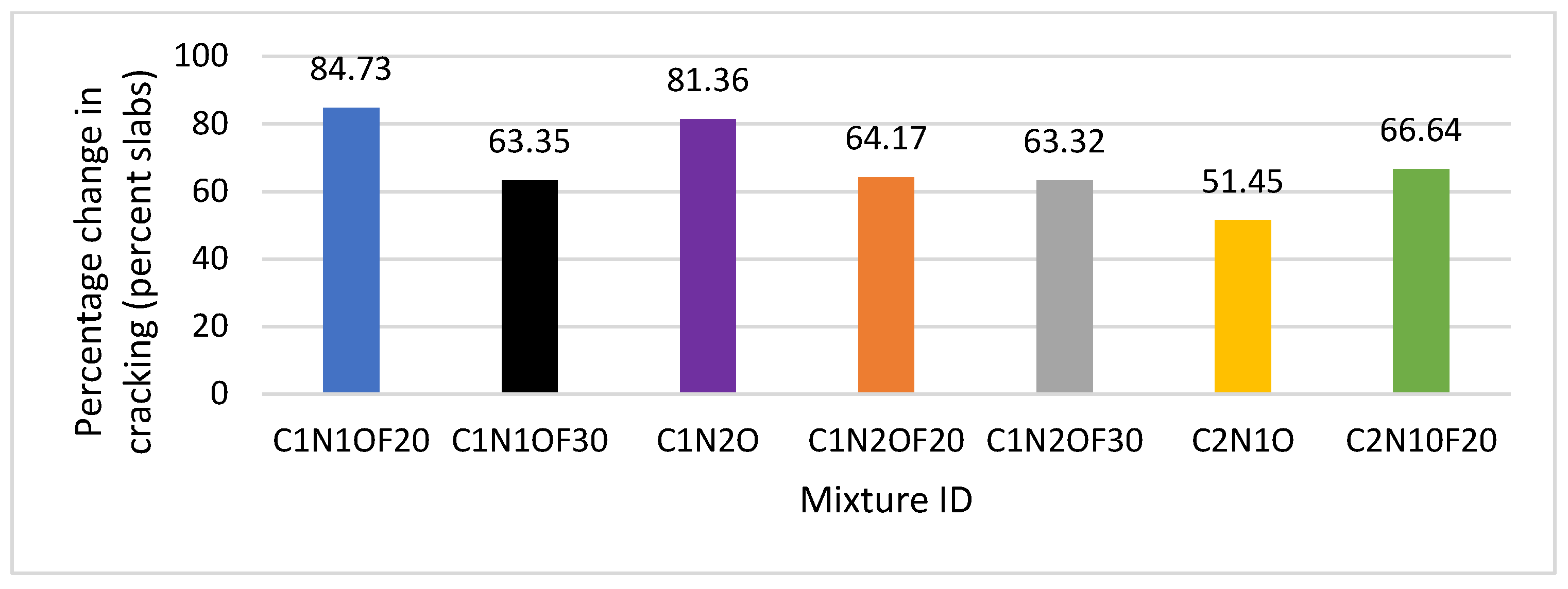
6.2. Comparison of JPCP Cracking with the Level One Baseline Models and Readjusted Level Three Models
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Symbol/Abbreviation | Description |
| AADT | Annual Average Daily Traffic |
| AASHTO | American Association of Highway and Transportation Officials |
| AASHTOWare | Software that follows AASHTO standards |
| CTE | Coefficient of Thermal Expansion |
| EM | Elastic Modulus |
| FDOT | Florida Department of Transportation |
| in. | Inch |
| IRI | International Roughness Index |
| JPCP | Jointed Plain Concrete Pavement |
| JTG D40-2002 | Specifications of Highway Cement and Concrete Pavement Design in China |
| Kpa | Kilopascal |
| LTPP | Long-Term Pavement Performance |
| M-E | Mechanistic-Empirical |
| MEPDG | Mechanistic-Empirical Pavement Design Guide |
| mi. | Mile |
| Mix ID | Mixture Identification |
| MOR | Modulus of Rupture |
| MRI | Mean Roughness Index |
| NCDOT | North Carolina Department of Transportation |
| NCHRP | National Cooperative Highway Research Program |
| NCHRP Project 1-37A | The project that produced a guide for M-E design and analysis |
| Pa | Pascal |
| Pavement-ME | Simulation Software used in this study that has AASHTOWare |
| PCC | Portland Cement Concrete |
| pcy | Pounds per Cubic Yard |
| psi | Pounds per Square Inch |
| SCDOT | South Carolina Department of Transportation |
References
- AASHTO. Guide for the Design of Pavement Structures; AASHTO: Washington, WA, USA, 1993. [Google Scholar]
- AASHTO. Mechanistic-Empirical Pavement Design Guide: A Manual of Practice; AASHTO: Washington, WA, USA, 2008. [Google Scholar]
- AASHTO. Guide for the Local Calibration of the Mechanistic-Empirical Pavement Design Guide; AASHTO: Washington, WA, USA, 2010. [Google Scholar]
- AASHTO. Mechanistic-Empirical Pavement Design Guide: A Manual of Practice, 2nd ed.; AASHTO: Washington, WA, USA, 2015. [Google Scholar]
- AASHTO. Mechanistic-Empirical Pavement Design Guide: A Manual of Practice, 3rd ed.; AASHTO: Washington, WA, USA, 2021. [Google Scholar]
- Li, Q.; Wang KC, P.; Qiu, Y. Comparative Study of Jointed Plain Concrete Pavement (JPCP) Design Methodologies in China and United States. In Proceedings of the International Conference on Transportation Engineering, Chengdu, China, 22–24 July 2007. [Google Scholar]
- Darter, M.I.; Titus-Glover, L.; Wolf, D.J. Development of a Traffic Data Input System in Arizona for the MEPDG; FHWA-AZ-13-672; Federal Highway Administration: Washington, WA, USA, 2013.
- Stone, J.R.; Kim, Y.R.; List, G.F.; Rasdorf, W.; Sayyady, F.; Jadoun, F.; Ramachandran, A.N. Development of Traffic Data Input Resources for the Mechanistic Empirical Pavement Design Process; FHWA/NC/2008-11; Department of Transportation: Raleigh, NC, USA, 2011.
- Cavalline, T.L.; Tempest, B.Q.; Blanchard, E.H.; Medlin, C.D.; Chimmula, R.R. Improved Data for Mechanistic-Empirical Design for Concrete Pavements; Final Report, Project FHWA/NC/2015-03; North Carolina Department of Transportation: Raleigh, NC, USA, 2018.
- Cavalline, T.L.; Tempest, B.Q.; Blanchard, E.; Medlin, C.; Chimmula, R.; Morrison, C. Impact of Local Calibration Using Sustainable Materials for Rigid Pavement Analysis and Design. ASCE J. Transp. Part B Pavements 2018, 144, 04018044. [Google Scholar] [CrossRef]
- Múčka, P. International roughness index specifications around the world. Road Mater. Pavement Des. 2016, 18, 929–965. [Google Scholar] [CrossRef]
- El-Saad, A.M.N.A. International Roughness Index as a Criterion in Design of Rigid Pavement. Ph.D. Thesis, Mansoura University, El-Mansoura, Egypt, 2015. [Google Scholar]
- Agurla, M.; Lin, S. Long-term pavement performance automated faulting measurement. In Proceedings of the 9th International Conference on Managing Pavement Assets, Washington, WA, USA, 18–21 May 2015. [Google Scholar]
- Jung, J.S.; Owusu-Antwi, E.B. Design Factors That Affect Joint Faulting for Jointed Plain Concrete Pavements. Int. J. Highw. Eng. 2004, 67–73. [Google Scholar]
- Saboori, A.; Lea, J.; Harvey, J.; Lea, J.; Mateos, A.; Wu, R. Pavement ME JPCP Transverse Cracking Model Calibration and Design Catalog Framework (Version 2.5.5); University of California Pavement Research Center: Davis, CA, USA, 2021. [Google Scholar]
- Saboori, A.; Harvey, J.; Lea, J.; Wu, R.; Mateos, A. Pavement ME Sensitivity Analysis (Version 2.5.3); University of California Pavement Research Center: Davis, CA, USA, 2021. [Google Scholar] [CrossRef]
- Li, R.; Cramer, S. AASHTO Mechanistic–Empirical Pavement Design Guide Parametric Study; University of Wisconsin–Madison: Madison, WI, USA, 2012. [Google Scholar]
- Hall, K.D.; Beam, S.; Lee, M. AASHTO 2002 Pavement Design Guide Design Input Evaluation Study; Final Report, TRC-0302; State Highway and Transportation Department: Washington, WA, USA, 2006.
- Hasan, M.M.; Rahman, A.; Tarefder, R.A. Investigation of Accuracy of Pavement Mechanistic Empirical Prediction Performance by Incorporating Level 1 Inputs. J. Traffic Transp. Eng. 2020, 7, 259–268. [Google Scholar] [CrossRef]
- Mbakisya, O.; Kelvin, M.; Sampson, U.; Joseph, O. Evaluation of AASHTO Mechanistic Empirical Design Guide Inputs to the Performance of Tennessee Pavements. In Proceedings of the International Road Federation World Meeting & Exhibition, Orlando, FL, USA, 6 October 2022. [Google Scholar]
- Hossain, M.; Khanum, T.; Tanesi, J.; Schieber, G.; Montney, R. The PCC Coefficient of Thermal Expansion Input for the Mechanistic-Empirical Pavement Design Guide. In Proceedings of the 85th Annual Meeting of the Transportation Research Board, National Research Council, Washington, WA, USA, 22–26 January 2006. [Google Scholar]
- Kim, S.; Ceylan, H.; Ma, D.; Gopalakrishnan, K. Calibration of pavement ME design and mechanistic-empirical pavement design guide performance prediction models for Iowa pavement systems. J. Transp. Eng. 2014, 140, 04014052. [Google Scholar] [CrossRef]
- Ping, W.V.; Kampmann, R. Engineering Properties of Florida Concrete Mixes for Implementing the AASHTO Recommended Mechanistic-Empirical Rigid Pavement Design Guide; Florida A & M University-Florida State University College of Engineering: Tallahassee, FL, USA, 2008. [Google Scholar]
- Tanesi, J.; Meininger, R. Coefficient of Thermal Expansion—Its role in concrete pavement performance. In Proceedings of the International Workshop on Best Practices for Concrete Pavements, Sao Paulo, Brazil, 21–23 October 2007. [Google Scholar]
- Ceylan, H.; Kim, S.; Gopalakrishnan, K.; Schwartz, C.W.; Li, R. Sensitivity quantification of jointed plain concrete pavement mechanistic-empirical performance predictions. Constr. Build. Mater. 2013, 43, 545–556. [Google Scholar] [CrossRef]
- Ceylan, H.; Gopalakrishnan, K.; Kim, S.; Schwartz, C.W.; Li, R. Global sensitivity analysis of jointed plain concrete pavement mechanistic–empirical performance predictions. Transp. Res. Rec. J. Transp. Res. Board 2013, 2367, 113–122. [Google Scholar] [CrossRef]
- Gassman, S.L.; Rahman, M.M. Calibration of the AASHTO Pavement Design Guide to South Carolina Conditions—Phase I: Final Report; Federal Highway Administration: Washington, WA, USA, 2016.
- Rao, C. Guidelines for PCC Inputs to AASHTOWare Pavement ME; FHWA/MS-DOT-RD-14-260; Rao Research and Consulting: Champaign, IL, USA, 2014. [Google Scholar]
- Summers, C. Investigating Time Sensitive Thermal and Mechanical Inputs for Rigid Pavements. Master’s Thesis, University of North Carolina, Charlotte, NC, USA, 2023. [Google Scholar]
- Sabih, G.; Cavalline, T.L.; Tempest, B.Q. Investigating Thermal and Mechanical Inputs for Rigid Pavement Design in North Carolina; Final Report, Project FHWA/NC/2022-07; North Carolina Department of Transportation: Raleigh, NC, USA, 2024; under preparation.











| Mixture ID | Mixture Proportions, kg/m3 (pcy) | ||||
|---|---|---|---|---|---|
| Cement | Fly Ash | Coarse Aggregate | Fine Aggregate | Water | |
| C1N1OF20 | 271.9 (458.4) | 67.9 (114.6) | 1172.4 (1976.2) | 730.6 (1231.5) | 142.3 (240) |
| C1N1OF30 | 237.9 (401.1) | 101.9 (171.9) | 1172.4 (1976.2) | 720.1 (1213.8) | 142.3 (240) |
| C1N2O | 339.9 (573.0) | 0 (0) | 1172.4 (1976.2) | 744.3 (1254.6) | 142.3 (240) |
| C1N2OF20 | 271.9 (458.4) | 67.9 (114.6) | 1172.4 (1976.2) | 723.6 (1219.7) | 142.3 (240) |
| C1N2OF30 | 237.9 (401.1) | 101.9 (171.9) | 1172.4 (1976.2) | 713.2 (1202.3) | 142.3 (240) |
| C2N1O | 339.9 (573.0) | 0 (0) | 1059.5 (1786.0) | 751.5 (1266.7) | 142.3 (240) |
| Compressive Strength, (kPa (psi)) | |||||
|---|---|---|---|---|---|
| Mixture ID | CTE @ 28 Days (cm/cm)/°C ((in./in.)/°F) | 7 Days | 14 Days | 28 Days | 90 Days |
| C1N1OF20 | 9.77 × 10−6 (5.43 × 10−6) | 19,201 (2785) | 22,311 (3236) | 29,668 (4303) | 38,996 (5656) |
| C1N1OF30 | 9.59 × 10−6 (5.33 × 10−6) | 12,789 (1855) | 14,568 (2113) | 21,897 (3176) | 29,916 (4339) |
| C1N2O | 9.65 × 10−6 (5.36 × 10−6) | 27,496 (3988) | 29,013 (4208) | 34,825 (5051) | 41,602 (6034) |
| C1N2OF20 | 9.36 × 10−6 (5.20 × 10−6) | 19,953 (2894) | 17,023 (3469) | 30,509 (4425) | 36,397 (5279) |
| C1N2OF30 | 9.29 × 10−6 (5.16 × 10−6) | 11,541 (1674) | 17,347 (2516) | 24,890 (3610) | 30,612 (4440) |
| C2N1O | 9.41 × 10−6 (5.23 × 10−6) | 28,861 (4186) | 31,619 (4586) | 40,189 (5829) | 43,126 (6255) |
| C2N1OF20 | 9.22 × 10−6 (5.12 x 10−6) | 17,354 (2517) | 20,484 (2971) | 30,068 (4361) | 31,674 (4594) |
| Mix ID | 7 Day EM (Pa (psi)) | 7 Day MOR (kPa (psi)) | 14 Day EM (Pa (psi)) | 14 Day MOR (kPa (psi)) | 28 Day EM (Pa (psi)) | 28 Day MOR (kPa (psi)) | 90 Day EM (Pa (psi)) | 90 Day MOR (kPa (psi)) |
|---|---|---|---|---|---|---|---|---|
| C1N1OF20 | 1.44 × 1010 (2.10 × 106) | 3619 (525) | 1.63 × 1010 (2.37 × 106) | 3674 (533) | 1.87 × 1010 (2.71 × 106) | 4240 (615) | 2.13 × 1010 (3.09 × 106) | 4550 (660) |
| C1N1OF30 | 1.39 × 1010 (2.02 × 106) | 3040 (441) | 1.43 × 1010 (2.08 × 106) | 3144 (456) | 1.69 × 1010 (2.45 × 106) | 3792 (550) | 1.83 × 1010 (2.65 × 106) | 4081 (592) |
| C1N2O | 1.71 × 1010 (2.49 × 106) | 4033 (585) | 1.73 × 1010 (2.51 × 106) | 4095 (594) | 1.88 × 1010 (2.72 × 106) | 4640 (673) | 2.03 × 1010 (2.94 × 106) | 4674 (678) |
| C1N2OF20 | 1.64 × 1010 (2.39 × 106) | 3723 (540) | 1.57 × 1010 (2.27 × 106) | 3743 (543) | 1.84 × 1010 (2.67 × 106) | 4219 (612) | 1.90 × 1010 (2.75 × 106) | 4426 (642) |
| C1N2OF30 | 1.58 × 1010 (2.30 × 106) | 3261 (473) | 1.50 × 1010 (2.17 × 106) | 3502 (508) | 1.72 × 1010 (2.49 × 106) | 3819 (554) | 2.03 × 1010 (2.95 × 106) | 4123 (598) |
| C2N1O | 1.78 × 1010 (2.59 × 106) | 4178 (606) | 1.69 × 1010 (2.45 × 106) | 4247 (616) | 1.83 × 1010 (2.66 × 106) | 4640 (673) | 1.90 × 1010 (2.76 × 106) | 4750 (689) |
| C2N1OF20 | 1.35 × 1010 (1.97 × 106) | 3495 (507) | 1.45 × 1010 (2.11 × 106) | 3571 (518) | 1.72 × 1010 (2.49 × 106) | 3867 (561) | 1.75 × 1010 (2.54 × 106) | 4178 (606) |
| Input Parameter | Constant Value | |
|---|---|---|
| Design life | 30 years | |
| Performance Criteria | Initial IRI, m/km (in/mi) | 0.994 (63) |
| Terminal IRI, m/km (in/mi) | 2.91 (185) | |
| Transverse cracking, percentage of cracked slabs | 10 | |
| Mean joint faulting, mm (in) | 3.05 (0.12) | |
| Traffic Data for Analysis | Two-way AADTT | 6000 |
| Number of lanes in the design direction | 2 | |
| Average axle spacing: short, medium, long, m (ft) | 3.66, 4.57, 5.49 (12, 15, 18) | |
| Percent of trucks: short, medium, long | 17, 22, 61 | |
| JPCP Design Properties | Joint spacing, m (ft) | 4.57 (15) |
| Dowel diameter, mm (in) | 31.8 (1.25) | |
| Dowel spacing, mm (in) | 305 (12) | |
| Widened slab | Not widened | |
| Tied shoulders | Tied | |
| Surface shortwave absorptivity | 0.85 |
| Mixture ID | Level One (Percentage of Cracked Slabs) | Level Three (Percentage of Cracked Slabs) |
|---|---|---|
| C1N1OF20 | 17.51 | 100 |
| C1N1OF30 | 36.13 | 100 |
| C1N2O | 5.35 | 86.16 |
| C1N2OF20 | 13.38 | 77.14 |
| C1N2OF30 | 37.29 | 100 |
| C2N1O | 4.69 | 54.66 |
| C2N1OF20 | 29.11 | 100 |
| Level 1 Cracking (Percent) | Level 3 Cracking (Percent) | ||||
|---|---|---|---|---|---|
| Mixture ID | 8 Inches | 10 Inches | 9.5 Inches | 9 Inches | |
| Percent slabs | C1N1OF20 | 17.51 | - | 15.27 | - |
| C1N1OF30 | 36.13 | 35.65 | - | - | |
| C1N2O | 5.35 | 4.8 | - | - | |
| C1N2OF20 | 13.38 | - | - | 12.97 | |
| C1N2OF30 | 37.29 | - | 36.68 | - | |
| C2N1O | 4.69 | 3.21 | - | - | |
| C2N1OF20 | 29.11 | - | - | 33.36 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McIntosh, M.D.; Sabih, G.; Summers, C.; Cavalline, T.L.; Tempest, B.Q. Quantifying the Effects of Material Input Levels on Jointed Plain Concrete Pavement (JPCP) Performance and Slab Thickness. Constr. Mater. 2024, 4, 251-270. https://doi.org/10.3390/constrmater4010014
McIntosh MD, Sabih G, Summers C, Cavalline TL, Tempest BQ. Quantifying the Effects of Material Input Levels on Jointed Plain Concrete Pavement (JPCP) Performance and Slab Thickness. Construction Materials. 2024; 4(1):251-270. https://doi.org/10.3390/constrmater4010014
Chicago/Turabian StyleMcIntosh, Megan D., Gauhar Sabih, Clarke Summers, Tara L. Cavalline, and Brett Q. Tempest. 2024. "Quantifying the Effects of Material Input Levels on Jointed Plain Concrete Pavement (JPCP) Performance and Slab Thickness" Construction Materials 4, no. 1: 251-270. https://doi.org/10.3390/constrmater4010014
APA StyleMcIntosh, M. D., Sabih, G., Summers, C., Cavalline, T. L., & Tempest, B. Q. (2024). Quantifying the Effects of Material Input Levels on Jointed Plain Concrete Pavement (JPCP) Performance and Slab Thickness. Construction Materials, 4(1), 251-270. https://doi.org/10.3390/constrmater4010014





