Experimental Study on Shear Lag Effect of Long-Span Wide Prestressed Concrete Cable-Stayed Bridge Box Girder under Eccentric Load
Abstract
:1. Introduction
2. Research Methods and Content
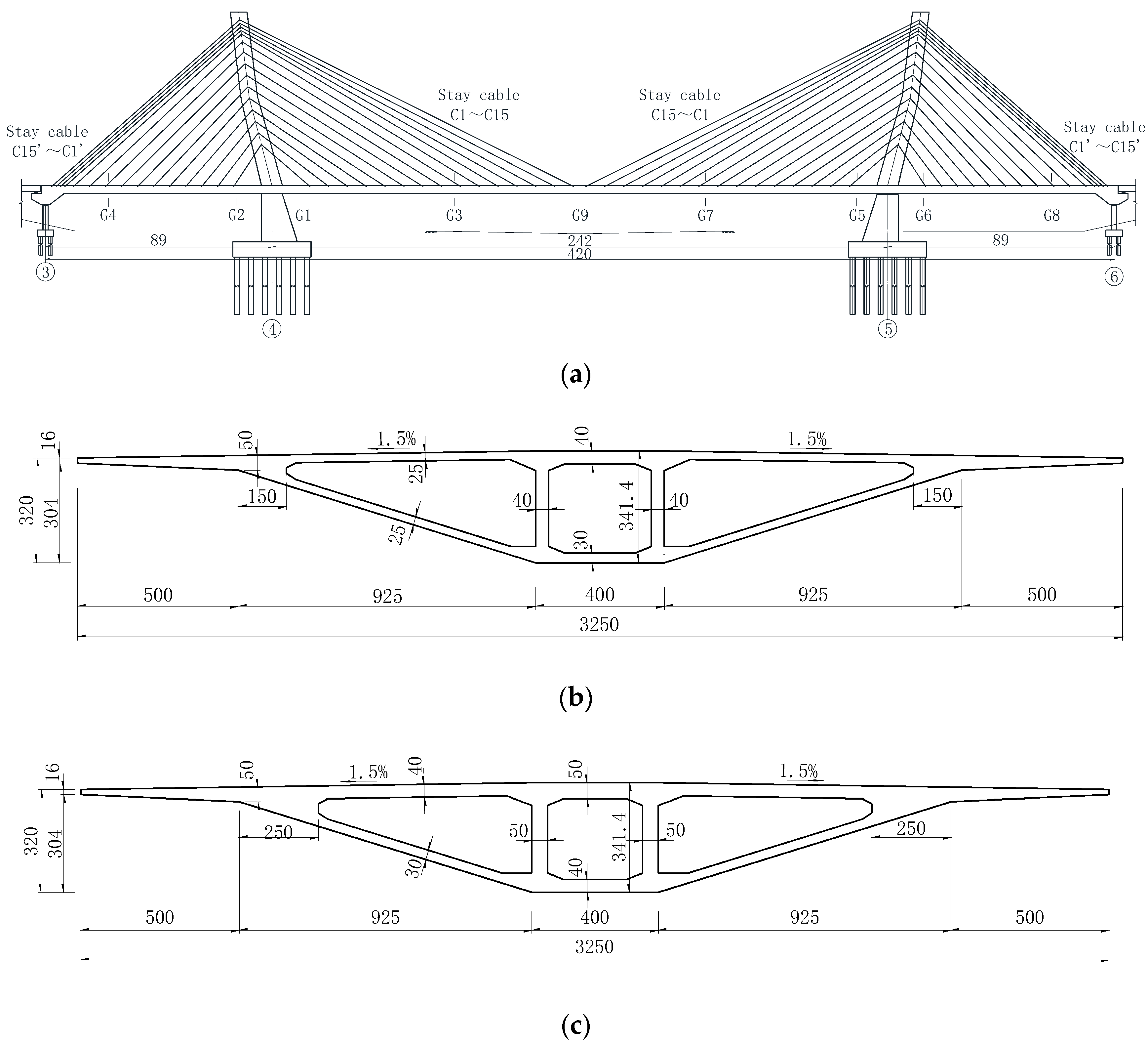
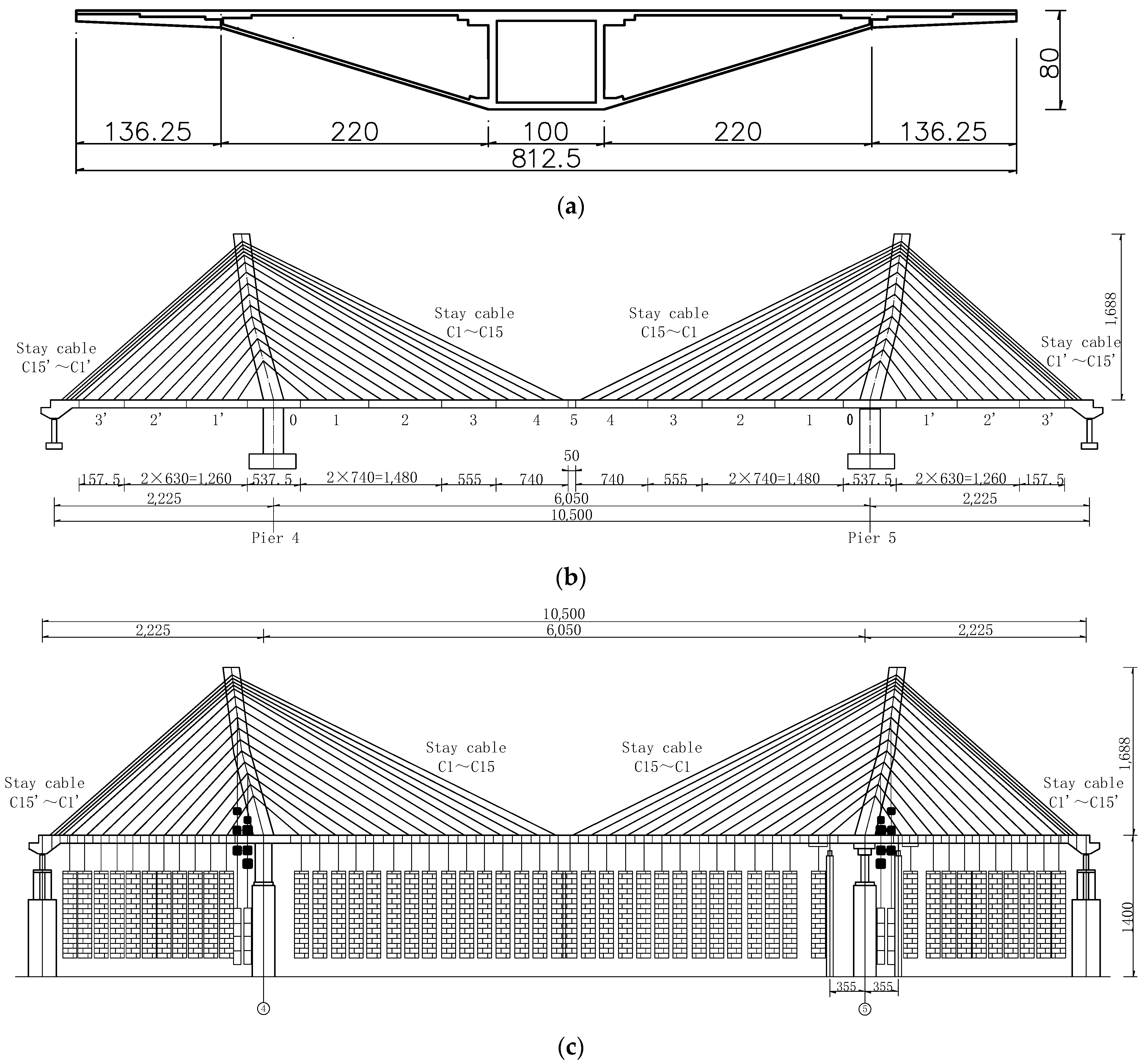
3. Background
4. Model Design and Production
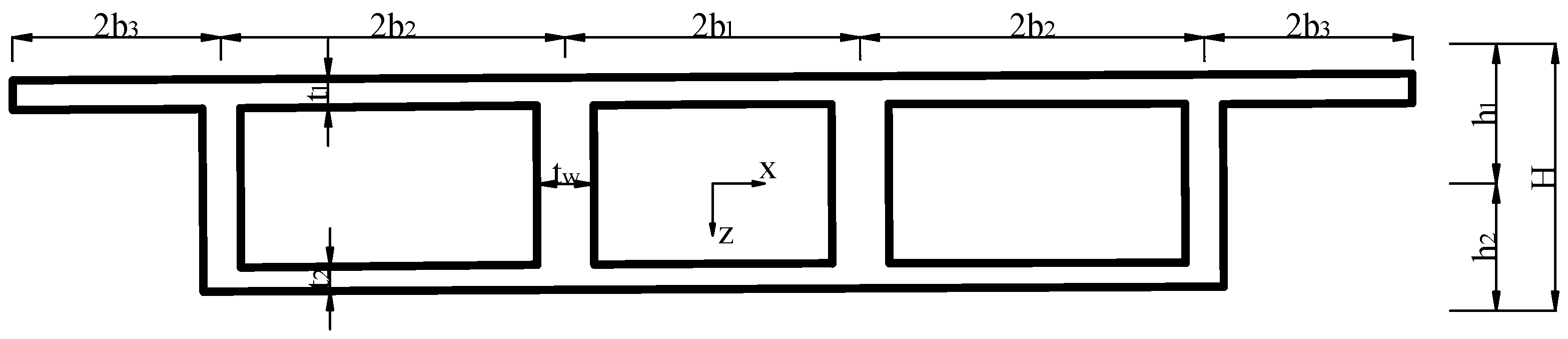
4.1. Model Design
- (1)
- Box girder design
- (2)
- Stay cable design
- (3)
- Main tower design
- (4)
- Design of bridge pier and bearing
4.2. Model Construction and Installation
4.3. Loading System and Dead Load Compensation
- (1)
- Dead load compensation of the main tower
- (2)
- Load compensation of the main girder
4.4. Loading Conditions
- (1)
- The eccentric load condition LCP1 was to load the G1 section of the mid-span main girder with a positive bending moment.
- (2)
- The eccentric load condition LCP2 was to load the G9 section of the mid-span main girder with a positive bending moment.
- (3)
- The eccentric load condition LCP3 was to load the G5 section with a negative bending moment.
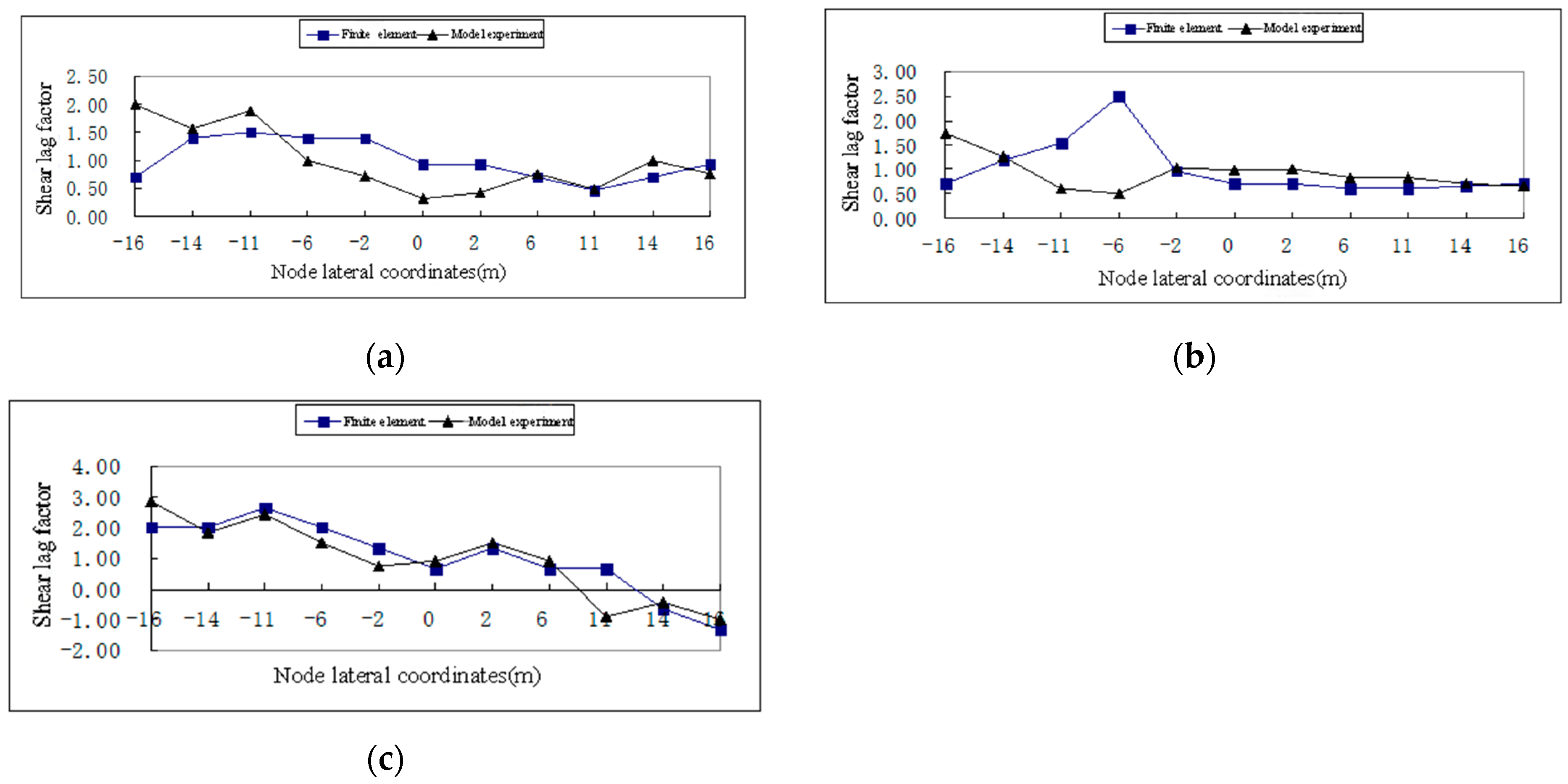
4.5. Results of Model Tests under Eccentric Loading
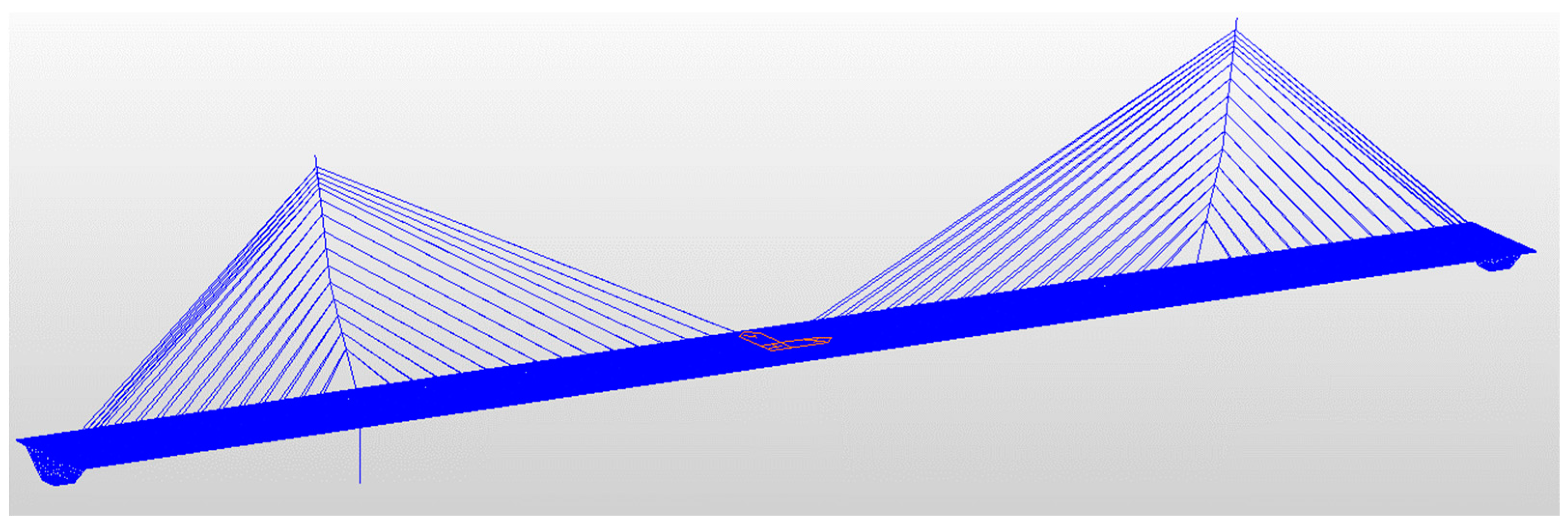
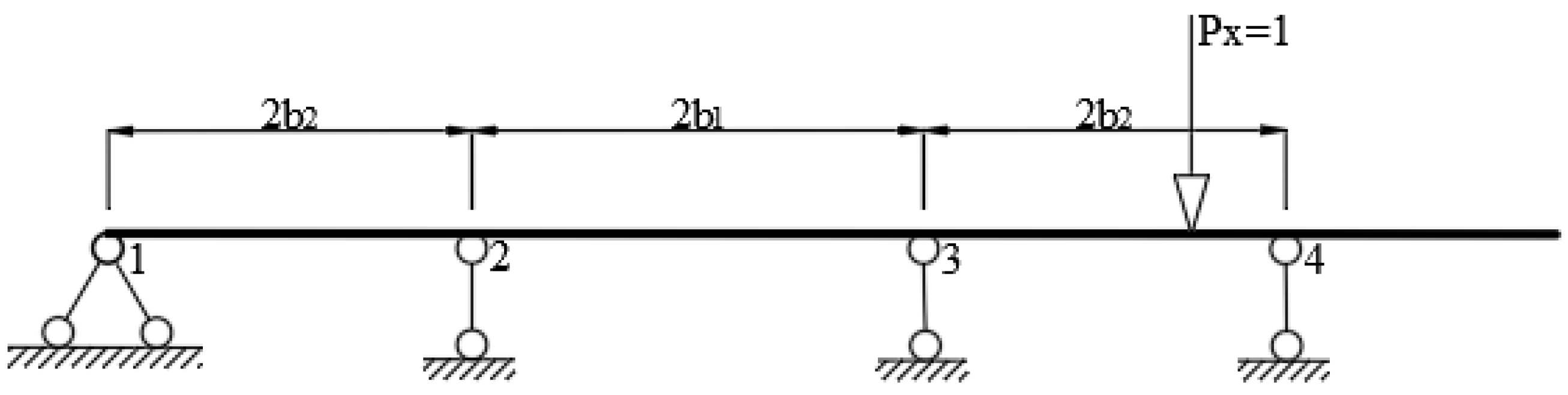
5. Spatial FE Model of Cable-Stayed Bridge with Single Cable Plane
5.1. Loading Condition of Cable-Stayed Bridge with a Single Cable Plane
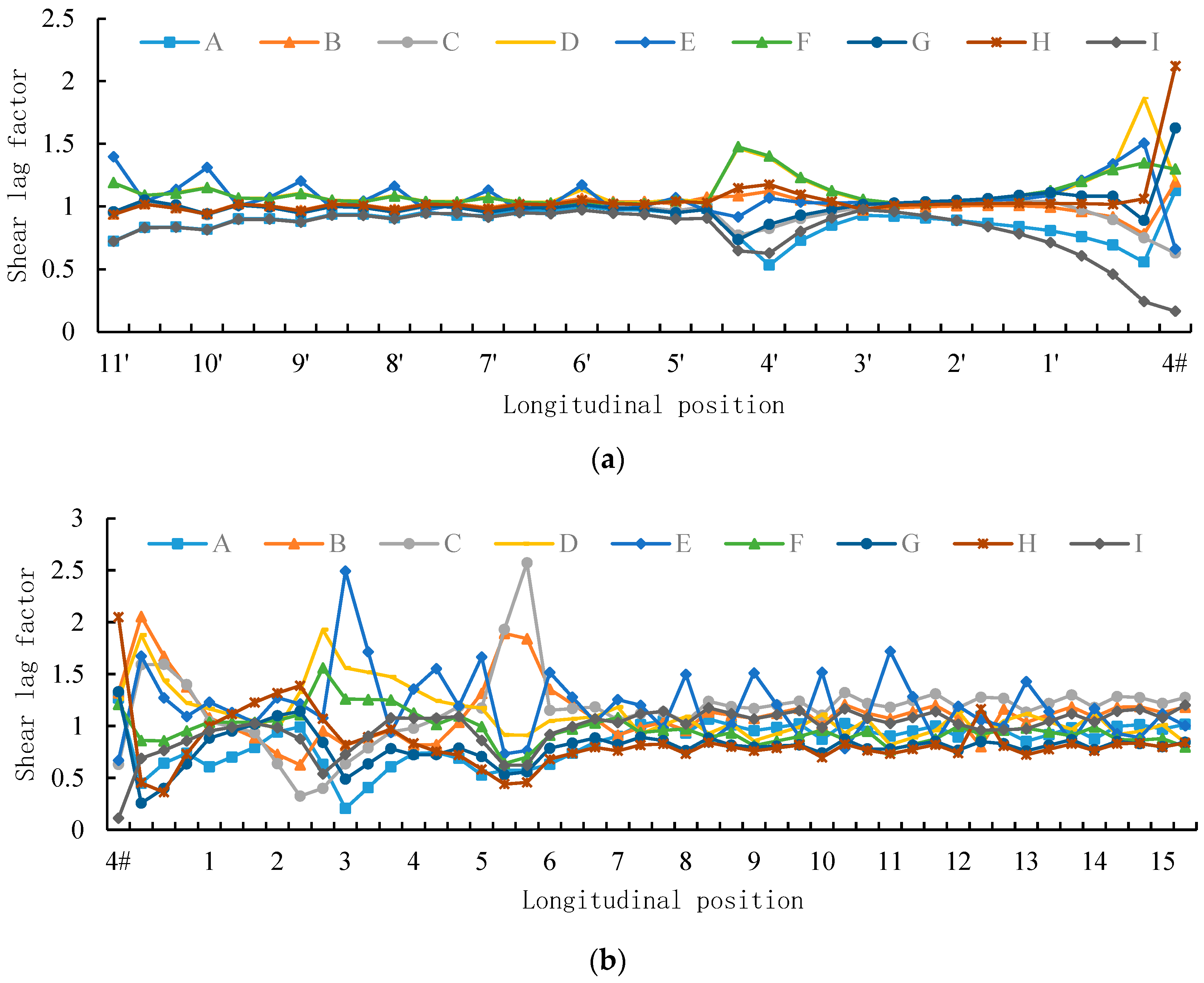
5.2. The Results of FE Calculations along the Longitudinal Direction of the Bridge under Eccentric Loading during the Bridge Completion Stage
5.3. Comparison of Shear Lag Coefficient Results of Cross-Sections under Eccentric Loading in the Bridge Formation Stage
6. Theoretical Study on Bar Simulation Method of Cross-Section Stress of Single-Box Three-Chamber Box Girder under Eccentric Load
6.1. Basic Assumption
6.2. Wing Plate Equivalent Area and Thickness Formula Derivation
6.3. Establishment of Controlling Differential Equations
6.4. Shear Flow Distribution under Eccentric Loading
6.5. Solving Differential Equations
7. Conclusions
- (1)
- The results of the model test showed that the distribution of the shear lag coefficient at the upper edge of the G1 and G5 sections of the main girder near the tower root was clearly misdistributed under the action of an eccentric load. The shear lag coefficient at the upper edge of the G9 section of the middle span main girder was relatively smooth, which indicated that the strong condition of the fix-jointed bridge tower and girder limited the torsion deformation of the section under the action of the eccentric load, such that stress near the loading position was more prominent.
- (2)
- The shear lag factor λ was related to the ratio of the bending moment to the axial force. When the bending moment axial force ratio increased, the total shear lag coefficient λ tended to the bending moment shear lag coefficient λM, while the bending moment axial force ratio decreased, and the total shear lag coefficient gradually tended to the axial force shear lag coefficient λN.
- (3)
- Using the bar simulation method, the calculation formula for the section normal stress of a single-box three-chamber box girder was derived. Under eccentric load, the shear flow was distributed in each web, and the related differential equations of the shear flow function of the top and bottom plates were obtained. By solving the matrix, the shear flow inside the stiffener and the stress on each stiffener were obtained. The theoretical analytical results were compared and verified with model test results.
- (4)
- The results of spatial FE analysis showed that, when the PC cable-stayed bridge with a single-cable plane was close to the cable force point, the normal stress of the main girder section reached its maximum at the center of the upper wing plate. As the section analyzed moved away from the cable force point, the maximum normal stress trend was as follows: the center of the upper wing plate, the junction of the upper wing plate and mid-web, and the junction of the upper wing plate and mid-web and side-web.
- (5)
- Under eccentric load, positive and negative shear lag effects coexisted at the position of the side fulcrum. Near the middle fulcrum, due to the influence of constraints at the middle fulcrum, positive and negative shear lag effects were significant and their variation range large, with the top plate in this area generating large tensile stress.
- (1)
- The force and shear lag of the main beam of a PC cable-stayed bridge are more complicated, so it is necessary to carry out in-depth analysis in order to improve them.
- (2)
- The influence of the shear lag effect on different section forms of long-span cable-stayed bridges remains to be further discussed.
- (3)
- The research on the shear lag effect of cable-stayed bridges mostly exists in the stage of theoretical research and rule summary and analysis, and the optimization scheme of each component still needs further research.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, L.F.; Leung, A.Y.T.; Li, Q.S. The stochastic finite segment in the analysis of the shear-lag effect on box-girders. Eng. Struct. 2001, 23, 1461–1468. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Dong, J.C.; Xu, T.H.; Xiao, Y.F.; Jiang, R.J.; Nie, X.M. The shear-lag effect of composite box girder bridges with corrugated steel webs and trusses. Eng. Struct. 2019, 181, 617–628. [Google Scholar] [CrossRef]
- Zanuy, C.; Martínez, E.P.; Merino, R.; Jose, M.; Carlos, B. Experimental analysis of shear-lag effect in reinforced concrete T-beams. Eng. Struct. 2022, 256, 114009. [Google Scholar] [CrossRef]
- Lin, P.Z.; Liu, F.K.; Ji, W. Analysis on shear lag effect of concrete box beam by variational principle. J. China Railw. Soc. 2013, 35, 93–98. [Google Scholar]
- Zhang, Y.Y.; Zhang, H.; Li, W.; Yang, J. Analysis on shear-lag effect of box girders based on different shear-lag generalized displacement. J. Railw. Sci. Eng. 2011, 13, 1083–1090. [Google Scholar]
- Zhu, L.; Nie, J.G.; Ji, W.Y. Positive and negative shear lag behaviors of composite twin-girder decks with varying cross-section. Sci. China Technol. Sci. 2017, 60, 116–132. [Google Scholar] [CrossRef]
- Zhou, S.J. Finite beam element considering shear-lag effect in box girder. J. Eng. Mech. 2010, 136, 1115–1122. [Google Scholar] [CrossRef]
- Li, H.; Ou, J. The state of the art in structural health monitoring of cable-stayed bridges. J. Civ. Struct. Health Monit. 2016, 6, 43–67. [Google Scholar] [CrossRef]
- Martins, A.M.; Simões, L.M.; Negrão, J.H. Optimization of cable-stayed bridges: A literature survey. Adv. Eng. Softw. 2020, 149, 102829. [Google Scholar] [CrossRef]
- Zhang, L.; Qiu, G.; Chen, Z. Structural health monitoring methods of cables in cable-stayed bridge: A review. Measurement 2021, 168, 108343. [Google Scholar] [CrossRef]
- Vazquez-Ontiveros, J.R.; Vazquez-Becerra, G.E.; Quintana, J.A.; Carrion, F.J.; Guzman-Acevedo, G.M.; Gaxiola-Camacho, J.R. Implementation of PPP-GNSS measurement technology in the probabilistic SHM of bridge structures. Measurement 2021, 173, 108677. [Google Scholar] [CrossRef]
- Javanmardi, A.; Ghaedi, K.; Huang, F.; Hanif, M.U.; Tabrizikahou, A. Application of structural control systems for the cables of cable-stayed bridges: State-of-the-art and state-of-the-practice. Arch. Comput. Methods Eng. 2022, 29, 1611–1641. [Google Scholar] [CrossRef]
- Wu, G.; Hong, X. Theoretical and experimental study on shear lag effect of partially cable-stayed bridge. J. Zhejiang Univ.-Sci. A 2005, 6, 875–877. [Google Scholar] [CrossRef]
- Sheng, X.B. Analysis of shear lag effect in the main girder of wide low-pylon cable stayed bridge. Constr. Technol. 2020, 44, 76–79. [Google Scholar]
- Burgan, B.A.; Dowling, P.J. The treatment of shear lag in design. Thin-Walled Struct. 1990, 9, 121–134. [Google Scholar] [CrossRef]
- Li, X.; Wan, S.; Zhang, Y.; Zhou, M.D.; Mo, Y.L. Beam finite element for thin-walled box girders considering shear lag and shear deformation effects. Eng. Struct. 2021, 233, 111867. [Google Scholar] [CrossRef]
- He, X.; Xiang, Y.; Chen, Z. Improved method for shear lag analysis of thin-walled box girders considering axial equilibrium and shear deformation. Thin-Walled Struct. 2020, 151, 106732. [Google Scholar] [CrossRef]
- Marin, M.; Agarwal, R.P.; Baleanu, D. On a generalized relaxed Saint–Venant principle. Bound. Value Probl. 2018, 2018, 112. [Google Scholar] [CrossRef]
- Zhu, L.; Su, R.K.L. Analytical solutions for composite beams with slip, shear-lag and time-dependent effects. Eng. Struct. 2017, 152, 559–578. [Google Scholar] [CrossRef]
- Luo, Q.Z.; Wu, Y.M.; Li, Q.S.; Tang, J.; Liu, G.D. A finite segment model for shear lag analysis. Eng. Struct. 2004, 26, 2113–2124. [Google Scholar] [CrossRef]
- Yang, Y.B.; Yang, J.P. State-of-the-art review on modal identification and damage detection of bridges by moving test vehicles. Int. J. Struct. Stab. Dyn. 2018, 18, 1850025. [Google Scholar] [CrossRef]
- Kordestani, H.; Xiang, Y.Q.; Ye, X.W.; Jia, Y.K. Application of the random decrement technique in damage detection under moving load. Appl. Sci. 2018, 8, 753. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Aoki, T. Damage detection of multi-story shear buildings due to earthquakes by model updating method. Struct. Control Health Monit. 2017, 24, e1895. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, J.H.; Li, Y.F.; Li, J.L. Analysis of Bridge Health Detection Based on Data Fusion. Adv. Civ. Eng. 2022, 2022, 6893160. [Google Scholar] [CrossRef]
- Li, Y.; Sun, X.; Bao, L. PC cable-stayed bridge main girder shear lag effects: Assessment of single cable plane in construction stage. Adv. Mater. Sci. Eng. 2020, 2020, 2646513. [Google Scholar] [CrossRef]
- Zhang, Y.G.; Li, Y.N. Analysis on Shear Lag Effect of Box Girder subject to dynamic load. Appl. Mech. Mater. 2014, 501, 811–814. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Yang, Z.J.; Liu, S.Z. Shear Lag in Thin-Walled Box Girder with Variable Section. Adv. Mater. Res. 2011, 194, 1165–1169. [Google Scholar] [CrossRef]
- Křístek, V.; Bažant, Z.P. Shear lag effect and uncertainty in concrete box girder creep. J. Struct. Eng. 1987, 113, 557–574. [Google Scholar] [CrossRef]
- Shi, J.X.; Ran, Z.H. Calculation of creep effect of extradosed cable-stayed bridge based on Midas Civil. IOP Conf. Ser. Mater. Sci. Eng. 2018, 423, 012113. [Google Scholar] [CrossRef]
- Wu, F.W.; Xue, C.F. Construction Control and Simulation Analysis of Long-Span Cable-Stayed Bridge. Adv. Mater. Res. 2011, 255, 816–820. [Google Scholar] [CrossRef]
- Wu, J.; Frangopol, D.M.; Soliman, M. Geometry control simulation for long-span steel cable-stayed bridges based on geometrically nonlinear analysis. Eng. Struct. 2015, 90, 71–82. [Google Scholar] [CrossRef]
- Sun, Y.; Xu, Y.; Lozano-Galant, J.A.; Wang, X.M.; Turmo, J. Analytical observability method for the structural system identification of wide-flange box girder bridges with the effect of shear lag. Autom. Constr. 2021, 131, 103879. [Google Scholar] [CrossRef]
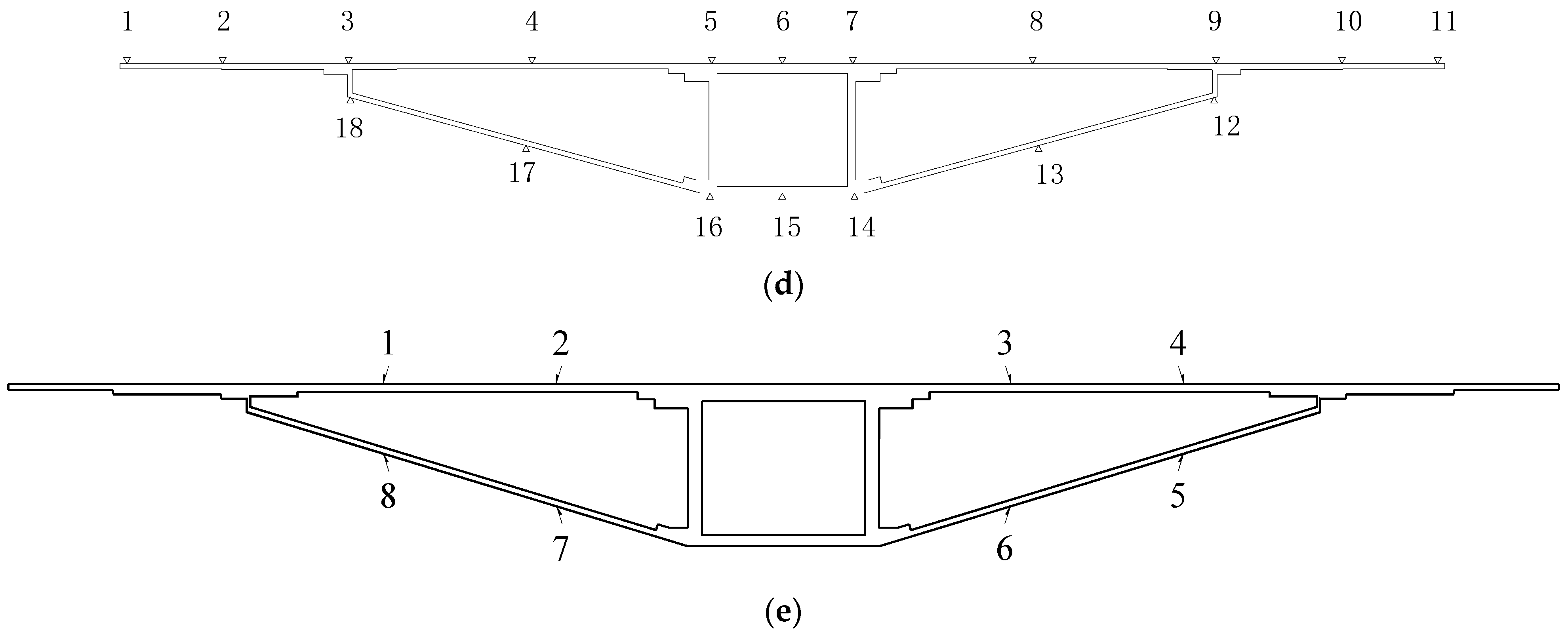


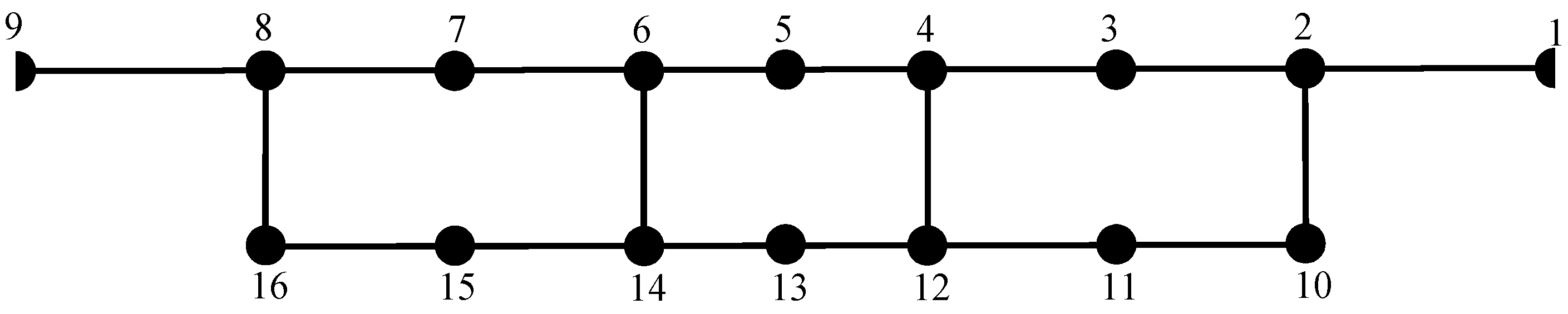

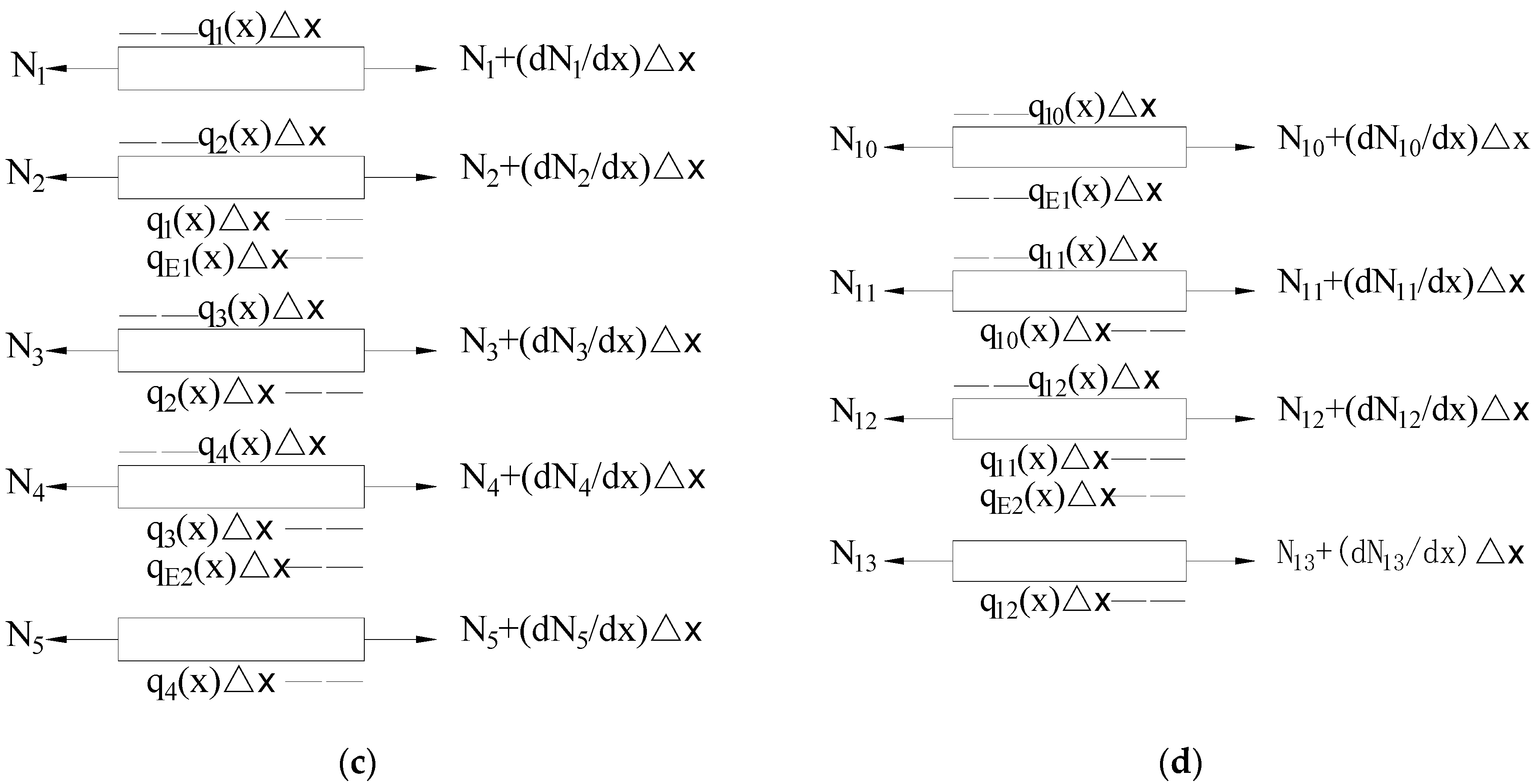
| Section | Point Number | LCP1 | LCP2 | LCP3 |
|---|---|---|---|---|
| G1 | G9 | G5 | ||
| Top plate | 1 | 1.34 | −0.95 | 1.08 |
| 2 | 1.05 | −1.02 | 0.70 | |
| 3 | 1.27 | −1.21 | 0.92 | |
| 4 | 0.67 | −1.21 | 0.57 | |
| 5 | 0.48 | −1.46 | 0.29 | |
| 6 | 0.22 | −1.40 | 0.54 | |
| 7 | 0.29 | −1.56 | 0.57 | |
| 8 | 0.51 | −0.73 | 0.35 | |
| 9 | 0.32 | −0.86 | −0.35 | |
| 10 | 0.67 | −1.81 | −0.16 | |
| 11 | 0.51 | −2.51 | −0.38 | |
| Average value | 0.67 | −1.34 | 0.38 | |
| Theoretical value | 0.85 | −1.27 | 0.52 | |
| Inclined web | 12 | −0.03 | 0.25 | −0.32 |
| 13 | −0.76 | 1.27 | −0.54 | |
| Bottom plate | 14 | −1.62 | 2.55 | — |
| 15 | −2.10 | 2.55 | −1.34 | |
| 16 | −1.72 | 2.86 | −1.27 | |
| Average value | −1.81 | 2.65 | −1.30 |
| Section | Point Number | LCP1 | LCP2 | LCP3 |
|---|---|---|---|---|
| G1 | G9 | G5 | ||
| Top Plate | 1 | 0.95 | 0.88 | 1.00 |
| 2 | 1.05 | 0.98 | 1.01 | |
| 3 | 1.11 | 0.94 | 1.05 | |
| 4 | 1.14 | 0.88 | 0.88 | |
| inclined soleplate | 5 | 1.08 | 0.84 | 0.87 |
| 6 | 1.00 | 0.90 | 0.97 | |
| 7 | 0.88 | 0.90 | 1.01 | |
| 8 | 0.97 | 0.95 | 1.00 |
| Stiffener Designation | Stiffener Area Equation |
|---|---|
| A1/A9 | |
| A2/A8 | |
| A3/A5/A7 | |
| A4/A6 | |
| A10/A16 | |
| A11/A13/A15 | |
| A12/A14 |
| Measuring Point Number | LCP1 | LCP2 | LCP3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| G1 | G9 | G5 | |||||||
| Actual Value | Theoretical Value | Error Value | Actual Value | Theoretical Value | Error Value | Actual Value | Theoretical Value | Error Value | |
| 1 | 1.34 | 1.32 | 1.49% | −0.95 | −0.97 | 2.11% | 1.08 | 1.09 | 0.93% |
| 2 | 1.05 | 1.06 | 0.95% | −1.02 | −1.01 | 0.98% | 0.70 | 0.72 | 2.86% |
| 3 | 1.27 | 1.24 | 2.36% | −1.21 | −1.19 | 1.65% | 0.92 | 0.91 | 1.09% |
| 4 | 0.67 | 0.66 | 1.49% | −1.21 | −1.20 | 0.83% | 0.57 | 0.58 | 1.75% |
| 5 | 0.48 | 0.47 | 2.08% | −1.46 | −1.45 | 0.68% | 0.29 | 0.28 | 3.45% |
| 6 | 0.22 | 0.23 | 4.55% | −1.40 | −1.39 | 0.71% | 0.54 | 0.53 | 1.85% |
| 7 | 0.29 | 0.27 | 6.90% | −1.56 | −1.54 | 1.28% | 0.57 | 0.58 | 1.75% |
| 8 | 0.51 | 0.54 | 5.88% | −0.73 | −0.72 | 1.37% | 0.35 | 0.34 | 2.86% |
| 9 | 0.32 | 0.30 | 6.25% | −0.86 | −0.88 | 2.33% | −0.35 | −0.34 | 2.86% |
| 10 | 0.67 | 0.62 | 7.46% | −1.81 | −1.82 | 0.55% | −0.16 | −0.17 | 6.25% |
| 11 | 0.51 | 0.47 | 7.84% | −2.51 | −2.49 | 0.80% | −0.38 | −0.39 | 2.63% |
| 12 | −0.03 | −0.04 | 0.00% | 0.25 | 0.24 | 4.00% | −0.32 | −0.31 | 3.13% |
| 13 | −0.76 | −0.74 | 2.63% | 1.27 | 1.26 | 0.79% | −0.54 | −0.55 | 1.85% |
| 14 | −1.62 | −1.64 | 1.23% | 2.55 | 2.57 | 0.78% | −1.24 | −1.24 | 0.00% |
| 15 | −2.10 | −1.90 | 9.52% | 2.55 | 2.57 | 0.78% | −1.34 | −1.35 | 0.75% |
| 16 | −1.72 | −1.74 | 1.16% | 2.86 | 2.88 | 0.70% | −1.27 | −1.26 | 0.79% |
| 17 | −0.89 | −0.90 | 1.12% | 0.64 | 0.66 | 3.13% | −0.73 | −0.74 | 1.37% |
| 18 | −0.29 | −0.30 | 3.45% | 0.32 | 0.31 | 3.13% | −0.03 | −0.03 | 0.00% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Xie, J.; Wang, F.; Wu, D.; Wang, J.; Liu, Y. Experimental Study on Shear Lag Effect of Long-Span Wide Prestressed Concrete Cable-Stayed Bridge Box Girder under Eccentric Load. Constr. Mater. 2024, 4, 425-443. https://doi.org/10.3390/constrmater4020023
Li Y, Xie J, Wang F, Wu D, Wang J, Liu Y. Experimental Study on Shear Lag Effect of Long-Span Wide Prestressed Concrete Cable-Stayed Bridge Box Girder under Eccentric Load. Construction Materials. 2024; 4(2):425-443. https://doi.org/10.3390/constrmater4020023
Chicago/Turabian StyleLi, Yanfeng, Jiyuan Xie, Fengchi Wang, Di Wu, Jiahui Wang, and Yanao Liu. 2024. "Experimental Study on Shear Lag Effect of Long-Span Wide Prestressed Concrete Cable-Stayed Bridge Box Girder under Eccentric Load" Construction Materials 4, no. 2: 425-443. https://doi.org/10.3390/constrmater4020023
APA StyleLi, Y., Xie, J., Wang, F., Wu, D., Wang, J., & Liu, Y. (2024). Experimental Study on Shear Lag Effect of Long-Span Wide Prestressed Concrete Cable-Stayed Bridge Box Girder under Eccentric Load. Construction Materials, 4(2), 425-443. https://doi.org/10.3390/constrmater4020023





