Local and Remote Conformational Switching in 2-Fluoro-4-Hydroxy Benzoic Acid
Abstract
:1. Introduction
2. Experimental Methods
2.1. MI-IR Experiments
2.2. Near-IR Laser Irradiation
2.3. Theoretical Computations
3. Results and Discussion
3.1. Structure and Energy of the Conformers
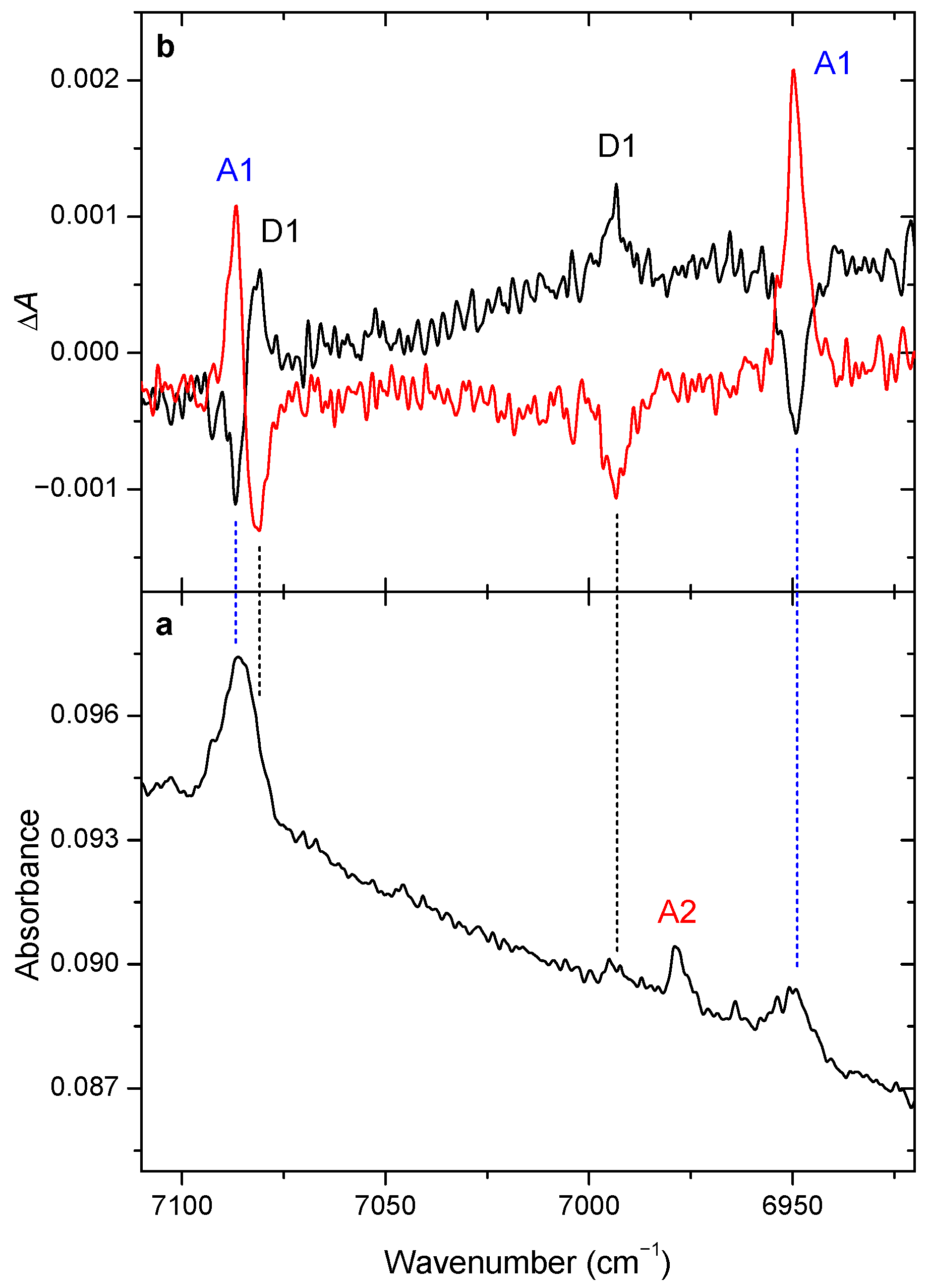
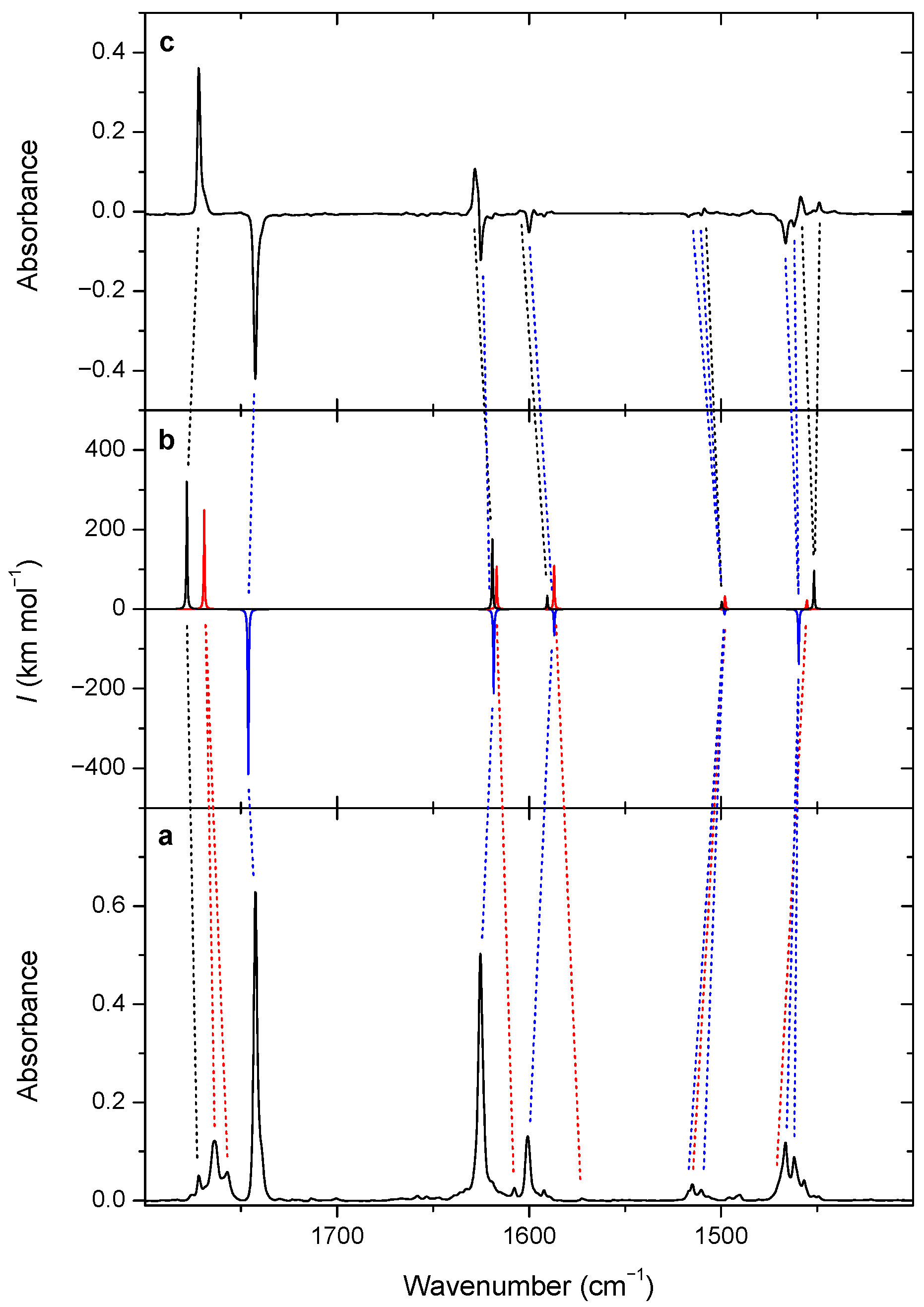
3.2. Changes upon Near-IR Irradiation, Vibrational Analysis
3.3. Kinetics of the Near-IR Induced Rotamerization, Quantum Efficiencies
3.4. Tunneling Decay Kinetics
3.5. Estimating the Tunneling Half-Life
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pettersson, M.; Lundell, J.; Khriachtchev, L.; Räsänen, M. IR Spectrum of the Other Rotamer of Formic Acid, cis-HCOOH. J. Am. Chem. Soc. 1997, 119, 11715–11716. [Google Scholar] [CrossRef]
- Pettersson, M.; Maçôas, E.M.S.; Khriachtchev, L.; Lundell, J.; Fausto, R.; Räsänen, M. Cis → trans conversion of formic acid by dissipative tunneling in solid rare gases: Influence of environment on the tunneling rate. J. Chem. Phys. 2002, 117, 9095–9098. [Google Scholar] [CrossRef] [Green Version]
- Maçôas, E.M.S.S.; Khriachtchev, L.; Pettersson, M.; Juselius, J.; Fausto, R.; Räsänen, M. Reactive vibrational excitation spectroscopy of formic acid in solid argon: Quantum yield for infrared induced trans → cis isomerization and solid state effects on the vibrational spectrum. J. Chem. Phys. 2003, 119, 11765–11772. [Google Scholar] [CrossRef]
- Maçôas, E.M.S.S.; Khriachtchev, L.; Pettersson, M.; Fausto, R.; Räsänen, M. Rotational Isomerism in Acetic Acid: The First Experimental Observation of the High-Energy Conformer. J. Am. Chem. Soc. 2003, 125, 16188–16189. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maçôas, E.M.S.S.; Khriachtchev, L.; Fausto, R.; Räsänen, M. Photochemistry and Vibrational Spectroscopy of the Trans and Cis Conformers of Acetic Acid in Solid Ar. J. Phys. Chem. A 2004, 108, 3380–3389. [Google Scholar] [CrossRef] [Green Version]
- Maçôas, E.M.S.S.; Khriachtchev, L.; Pettersson, M.; Fausto, R.; Räsänen, M. Rotational isomerism of acetic acid isolated in rare-gas matrices: Effect of medium and isotopic substitution on IR-induced isomerization quantum yield and cis → trans tunneling rate. J. Chem. Phys. 2004, 121, 1331–1338. [Google Scholar] [CrossRef] [Green Version]
- Apóstolo, R.F.G.F.G.; Bazsó, G.; Bento, R.R.F.R.F.; Tarczay, G.; Fausto, R. The first experimental observation of the higher-energy trans conformer of trifluoroacetic acid. J. Mol. Struct. 2016, 1125, 288–295. [Google Scholar] [CrossRef]
- Apóstolo, R.F.G.G.; Bazsó, G.; Ogruc-Ildiz, G.; Tarczay, G.; Fausto, R. Near-infrared in situ generation of the higher-energy trans conformer of tribromoacetic acid: Observation of a large-scale matrix-site changing mediated by conformational conversion. J. Chem. Phys. 2018, 148, 044303. [Google Scholar] [CrossRef]
- Maçôas, E.M.S.; Khriachtchev, L.; Pettersson, M.; Fausto, R.; Räsänen, M.; Maças, E.M.S.; Khriachtchev, L.; Pettersson, M.; Fausto, R.; Räsänen, M. Internal rotation in propionic acid: Near-infrared-induced isomerization in solid Argon. J. Phys. Chem. A 2005, 109, 3617–3625. [Google Scholar] [CrossRef] [Green Version]
- Bazsó, G.; Góbi, S.; Tarczay, G. Near-Infrared Radiation Induced Conformational Change and Hydrogen Atom Tunneling of 2-Chloropropionic Acid in Low-Temperature Ar Matrix. J. Phys. Chem. A 2012, 116, 4823–4832. [Google Scholar] [CrossRef]
- Halasa, A.; Lapinski, L.; Reva, I.; Rostkowska, H.; Fausto, R.; Nowak, M.J. Near-Infrared Laser-Induced Generation of Three Rare Conformers of Glycolic Acid. J. Phys. Chem. A 2014, 118, 5626–5635. [Google Scholar] [CrossRef] [PubMed]
- Reva, I.; Nunes, C.M.; Biczysko, M.; Fausto, R. Conformational switching in pyruvic acid isolated in Ar and N2 matrixes: Spectroscopic analysis, anharmonic simulation, and tunneling. J. Phys. Chem. A 2015, 119, 2614–2627. [Google Scholar] [CrossRef] [PubMed]
- Halasa, A.; Lapinski, L.; Rostkowska, H.; Reva, I.; Nowak, M.J. Tunable Diode Lasers as a Tool for Conformational Control: The Case of Matrix-Isolated Oxamic Acid. J. Phys. Chem. A 2015, 119, 2203–2210. [Google Scholar] [CrossRef] [PubMed]
- Maçôas, E.M.S.S.; Fausto, R.; Pettersson, M.; Khriachtchev, L.; Räsänen, M. Infrared-induced rotamerization of oxalic acid monomer in argon matrix. J. Phys. Chem. A 2000, 104, 6956–6961. [Google Scholar] [CrossRef] [Green Version]
- Maçôas, E.M.S.S.; Fausto, R.; Lundell, J.; Pettersson, M.; Khriachtchev, L.; Räsänen, M. Conformational Analysis and Near-Infrared-Induced Rotamerization of Malonic Acid in an Argon Matrix. J. Phys. Chem. A 2000, 104, 11725–11732. [Google Scholar] [CrossRef] [Green Version]
- Maçôas, E.M.S.S.; Fausto, R.; Lundell, J.; Pettersson, M.; Khriachtchev, L.; Räsänen, M. A matrix isolation spectroscopic and quantum chemical study of fumaric and maleic acid. J. Phys. Chem. A 2001, 105, 3922–3933. [Google Scholar] [CrossRef] [Green Version]
- Bazsó, G.; Magyarfalvi, G.; Tarczay, G. Near-infrared laser induced conformational change and UV laser photolysis of glycine in low-temperature matrices: Observation of a short-lived conformer. J. Mol. Struct. 2012, 1025, 33–42. [Google Scholar] [CrossRef]
- Bazsó, G.; Magyarfalvi, G.; Tarczay, G. Tunneling Lifetime of the ttc /VIp Conformer of Glycine in Low-Temperature Matrices. J. Phys. Chem. A 2012, 116, 10539–10547. [Google Scholar] [CrossRef]
- Bazsó, G.; Najbauer, E.E.; Magyarfalvi, G.; Tarczay, G. Near-Infrared Laser Induced Conformational Change of Alanine in Low-Temperature Matrixes and the Tunneling Lifetime of Its Conformer VI. J. Phys. Chem. A 2013, 117, 1952–1962. [Google Scholar] [CrossRef]
- Nunes, C.M.; Lapinski, L.; Fausto, R.; Reva, I. Near-IR laser generation of a high-energy conformer of L-alanine and the mechanism of its decay in a low-temperature nitrogen matrix. J. Chem. Phys. 2013, 138, 125101. [Google Scholar] [CrossRef]
- Najbauer, E.E.; Bazsó, G.; Góbi, S.; Magyarfalvi, G.; Tarczay, G. Exploring the Conformational Space of Cysteine by Matrix Isolation Spectroscopy Combined with Near-Infrared Laser Induced Conformational Change. J. Phys. Chem. B 2014, 118, 2093–2103. [Google Scholar] [CrossRef] [PubMed]
- Najbauer, E.E.; Bazsó, G.; Apóstolo, R.; Fausto, R.; Biczysko, M.; Barone, V.; Tarczay, G. Identification of Serine Conformers by Matrix-Isolation IR Spectroscopy Aided by Near-Infrared Laser-Induced Conformational Change, 2D Correlation Analysis, and Quantum Mechanical Anharmonic Computations. J. Phys. Chem. B 2015, 119, 10496–10510. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lapinski, L.; Reva, I.; Rostkowska, H.; Halasa, A.; Fausto, R.; Nowak, M.J. Conformational transformation in squaric acid induced by near-IR laser light. J. Phys. Chem. A 2013, 117, 5251–5259. [Google Scholar] [CrossRef] [PubMed]
- Halasa, A.; Lapinski, L.; Reva, I.; Rostkowska, H.; Fausto, R.; Nowak, M.J. Three Conformers of 2-Furoic Acid: Structure Changes Induced with Near-IR Laser Light. J. Phys. Chem. A 2015, 119, 1037–1047. [Google Scholar] [CrossRef]
- Kuş, N.; Fausto, R. Effects of the matrix and intramolecular interactions on the stability of the higher-energy conformers of 2-fluorobenzoic acid. J. Chem. Phys. 2017, 146, 124305. [Google Scholar] [CrossRef]
- Halasa, A.; Lapinski, L.; Rostkowska, H.; Nowak, M.J. Intramolecular Vibrational Energy Redistribution in 2-Thiocytosine: SH Rotamerization Induced by Near-IR Selective Excitation of NH 2 Stretching Overtone. J. Phys. Chem. A 2015, 119, 9262–9271. [Google Scholar] [CrossRef]
- Lopes Jesus, A.J.; Reva, I.; Araujo-Andrade, C.; Fausto, R. Conformational Switching by Vibrational Excitation of a Remote NH Bond. J. Am. Chem. Soc. 2015, 137, 14240–14243. [Google Scholar] [CrossRef]
- Halasa, A.; Reva, I.; Lapinski, L.; Rostkowska, H.; Fausto, R.; Nowak, M.J. Conformers of Kojic Acid and Their Near-IR-Induced Conversions: Long-Range Intramolecular Vibrational Energy Transfer. J. Phys. Chem. A 2016, 120, 2647–2656. [Google Scholar] [CrossRef]
- Lopes Jesus, A.J.; Nunes, C.; Fausto, R.; Reva, I.; Nunes, M.C.; Fausto, R.; Reva, I.; Nunes, C.; Fausto, R.; Reva, I. Conformational control over an aldehyde fragment by selective vibrational excitation of interchangeable remote antennas. Chem. Commun. 2018, 54, 4778–4781. [Google Scholar] [CrossRef]
- Kovács, B.; Kuş, N.; Tarczay, G.; Fausto, R. Experimental Evidence of Long-Range Intramolecular Vibrational Energy Redistribution through Eight Covalent Bonds: NIR Irradiation Induced Conformational Transformation of E-Glutaconic Acid. J. Phys. Chem. A 2017, 121, 3392–3400. [Google Scholar] [CrossRef]
- Ogruc Ildiz, G.; Fausto, R. Structural Aspects of the Ortho Chloro- and Fluoro-Substituted Benzoic Acids: Implications on Chemical Properties. Molecules 2020, 25, 4908. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef] [Green Version]
- Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Irikura, K.K. SYNSPEC; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1995. [Google Scholar]
- Peng, C.; Ayala, P.Y.; Schlegel, H.B.; Frisch, M.J. Using redundant internal coordinates to optimize equilibrium geometries and transition states. J. Comput. Chem. 1996, 17, 49–56. [Google Scholar] [CrossRef]
- Fukui, K. The Path of Chemical Reactions—The IRC Approach. Acc. Chem. Res. 1981, 14, 363–368. [Google Scholar] [CrossRef]
- Borden, W.T. Reactions that involve tunneling by carbon and the role that calculations have played in their study. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2016, 6, 20–46. [Google Scholar] [CrossRef]
- Maçôas, E.M.S.S.; Khriachtchev, L.; Pettersson, M.; Fausto, R.; Räsänen, M.M. Rotational isomerization of small carboxylic acids isolated in argon matrices: Tunnelling and quantum yields for the photoinduced processes. Phys. Chem. Chem. Phys. 2005, 7, 743–749. [Google Scholar] [CrossRef] [Green Version]
- Góbi, S.; Reva, I.; Tarczay, G.; Fausto, R. Amorphous and crystalline thioacetamide ice: Infrared spectra as a probe for temperature and structure. J. Mol. Struct. 2020, 1220, 128719. [Google Scholar] [CrossRef]
- Reva, I.; Nowak, M.J.; Lapinski, L.; Fausto, R. Spontaneous tunneling and near-infrared-induced interconversion between the amino-hydroxy conformers of cytosine. J. Chem. Phys. 2012, 136, 064511. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lapinski, L.; Reva, I.; Rostkowska, H.; Fausto, R.; Nowak, M.J. Near-IR-Induced, UV-Induced, and Spontaneous Isomerizations in 5-Methylcytosine and 5-Fluorocytosine. J. Phys. Chem. B 2014, 118, 2831–2841. [Google Scholar] [CrossRef] [PubMed]
- Lopes Jesus, A.J.; Nunes, C.M.; Reva, I.; Pinto, S.M.V.V.; Fausto, R. Effects of Entangled IR Radiation and Tunneling on the Conformational Interconversion of 2-Cyanophenol. J. Phys. Chem. A 2019, 123, 4396–4405. [Google Scholar] [CrossRef] [PubMed]
- Schreiner, P.R.; Wagner, J.P.; Reisenauer, H.P.; Gerbig, D.; Ley, D.; Sarka, J.; Császár, A.G.; Vaughn, A.; Allen, W.D. Domino Tunneling. J. Am. Chem. Soc. 2015, 137, 7828–7834. [Google Scholar] [CrossRef] [PubMed]
- Góbi, S.; Nunes, C.M.; Reva, I.; Tarczay, G.; Fausto, R. S–H rotamerization via tunneling in a thiol form of thioacetamide. Phys. Chem. Chem. Phys. 2019, 21, 17063–17071. [Google Scholar] [CrossRef]
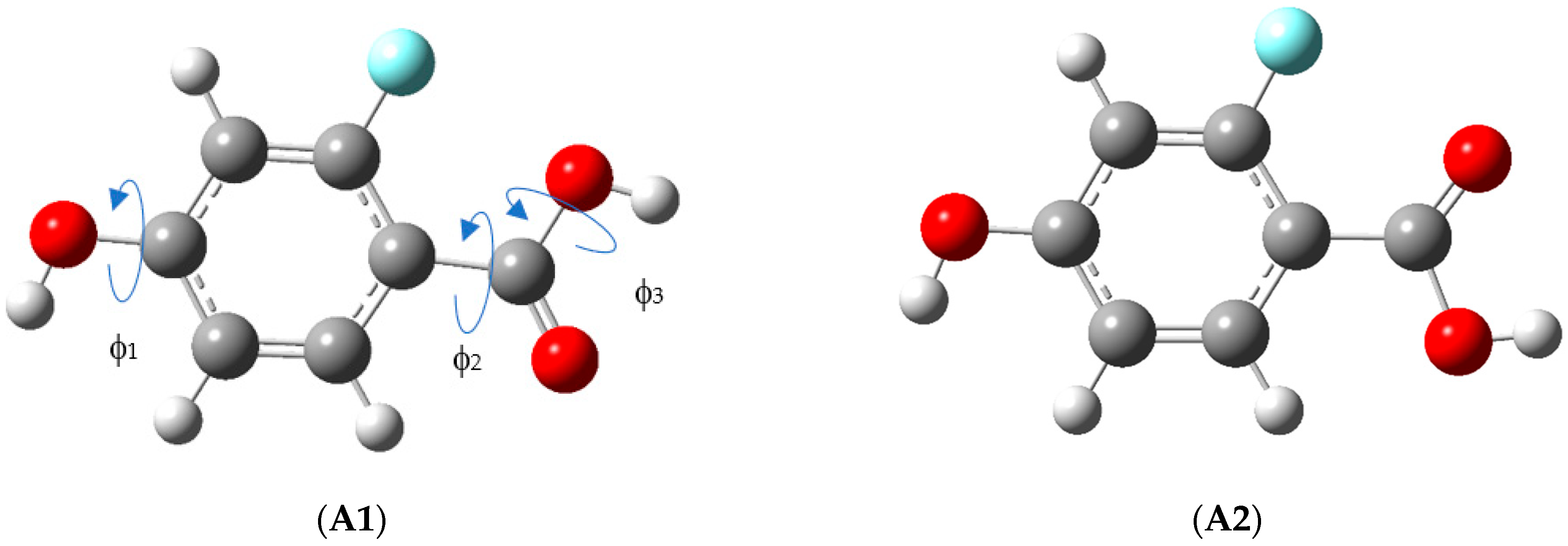
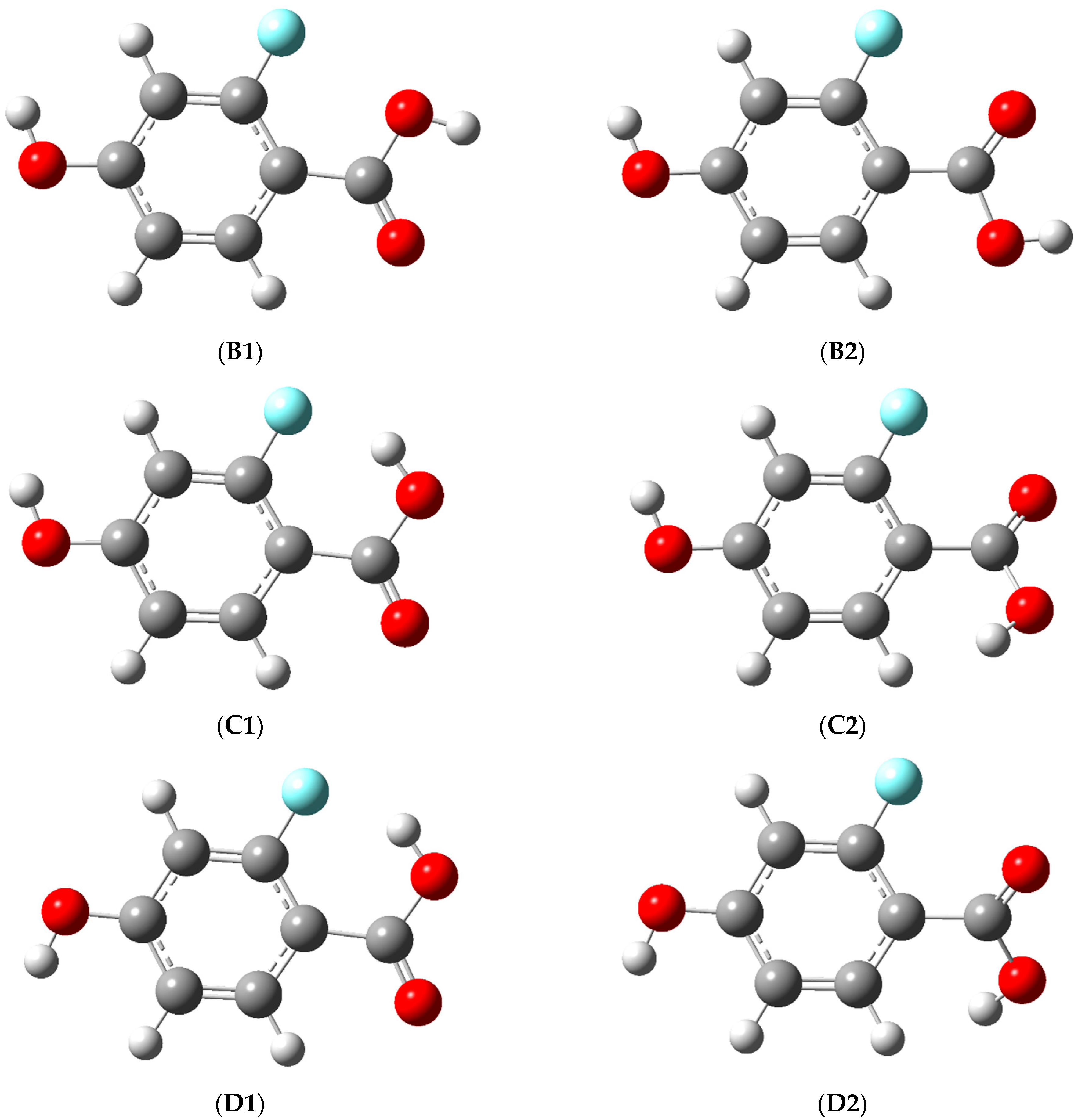

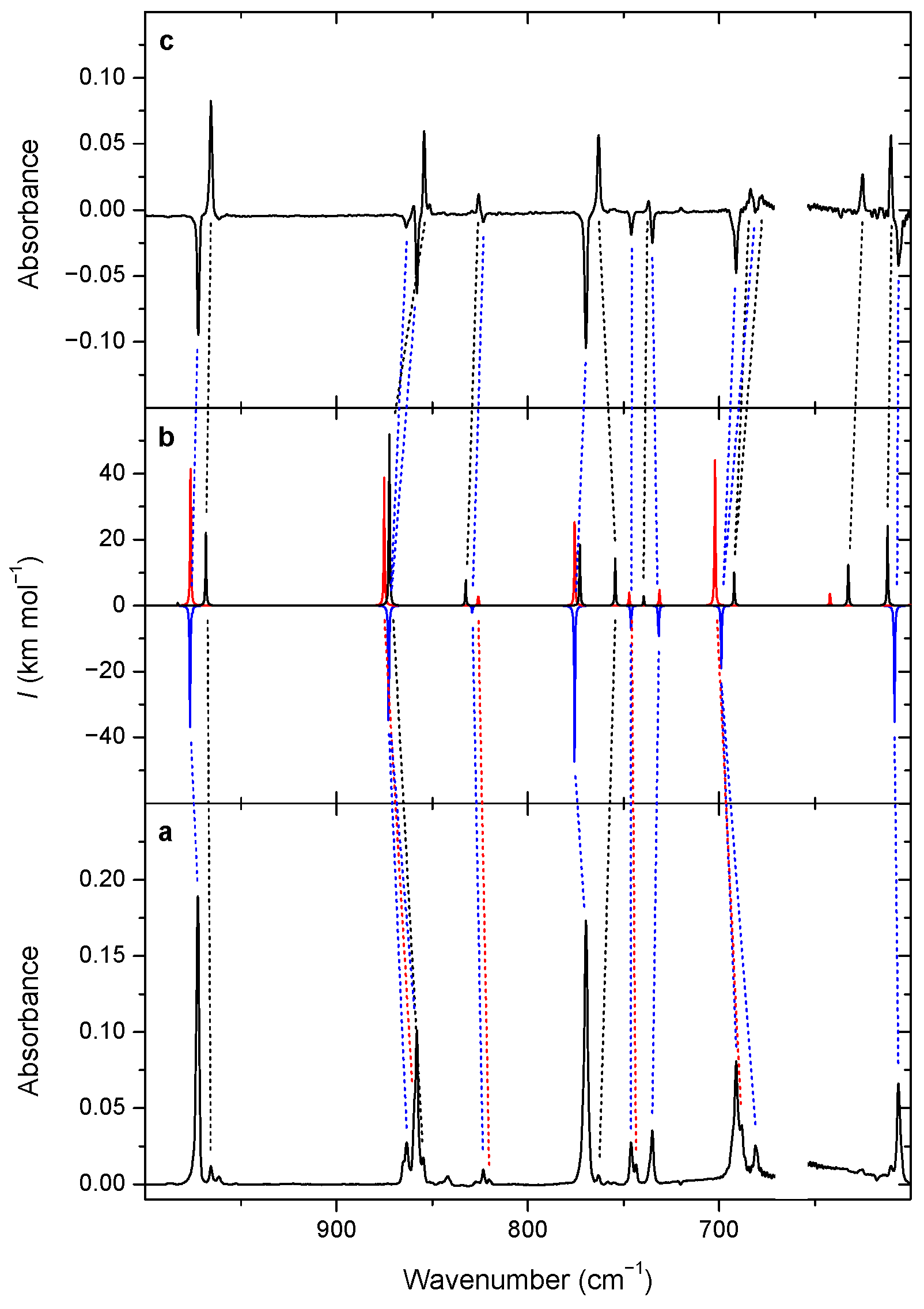
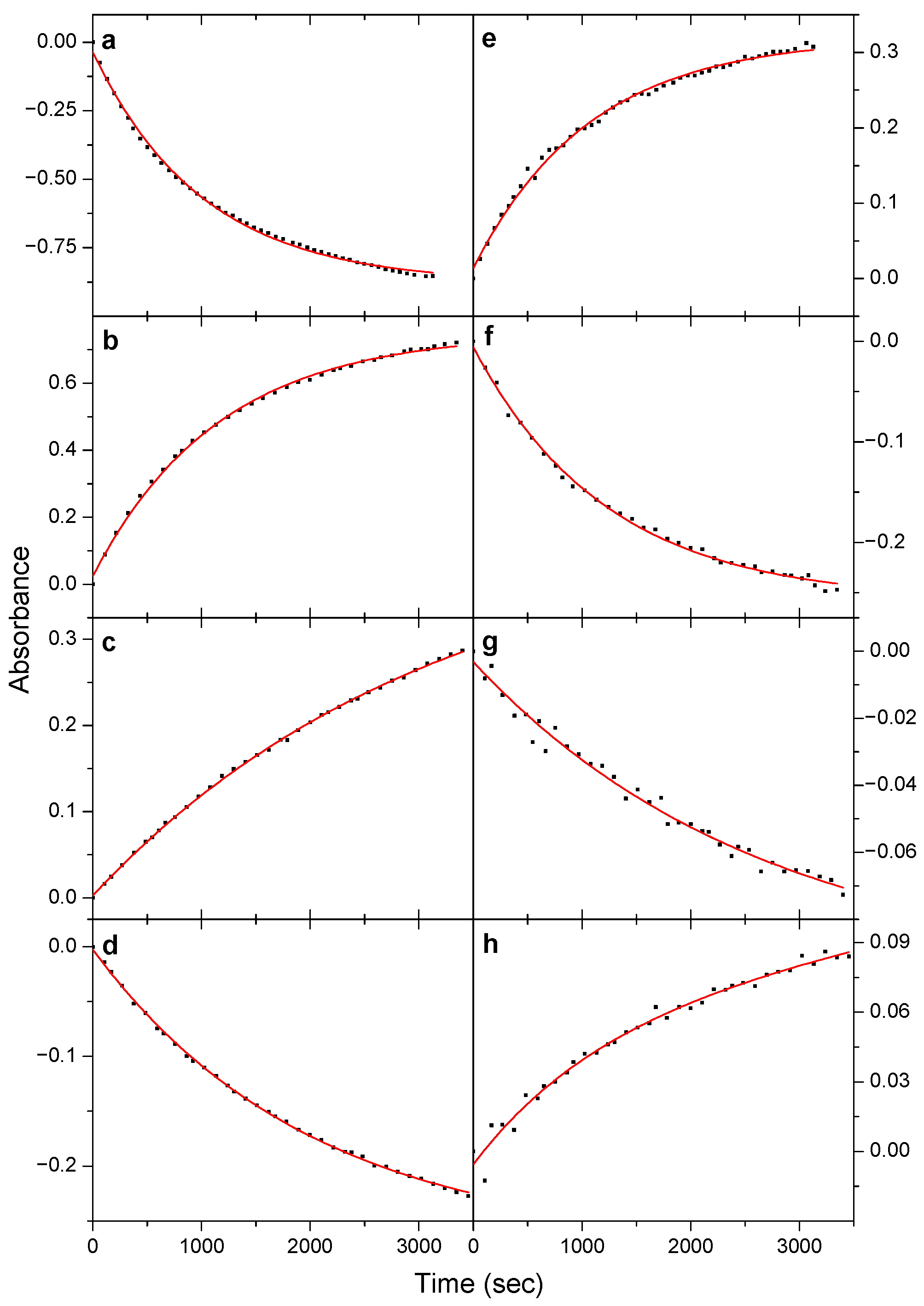
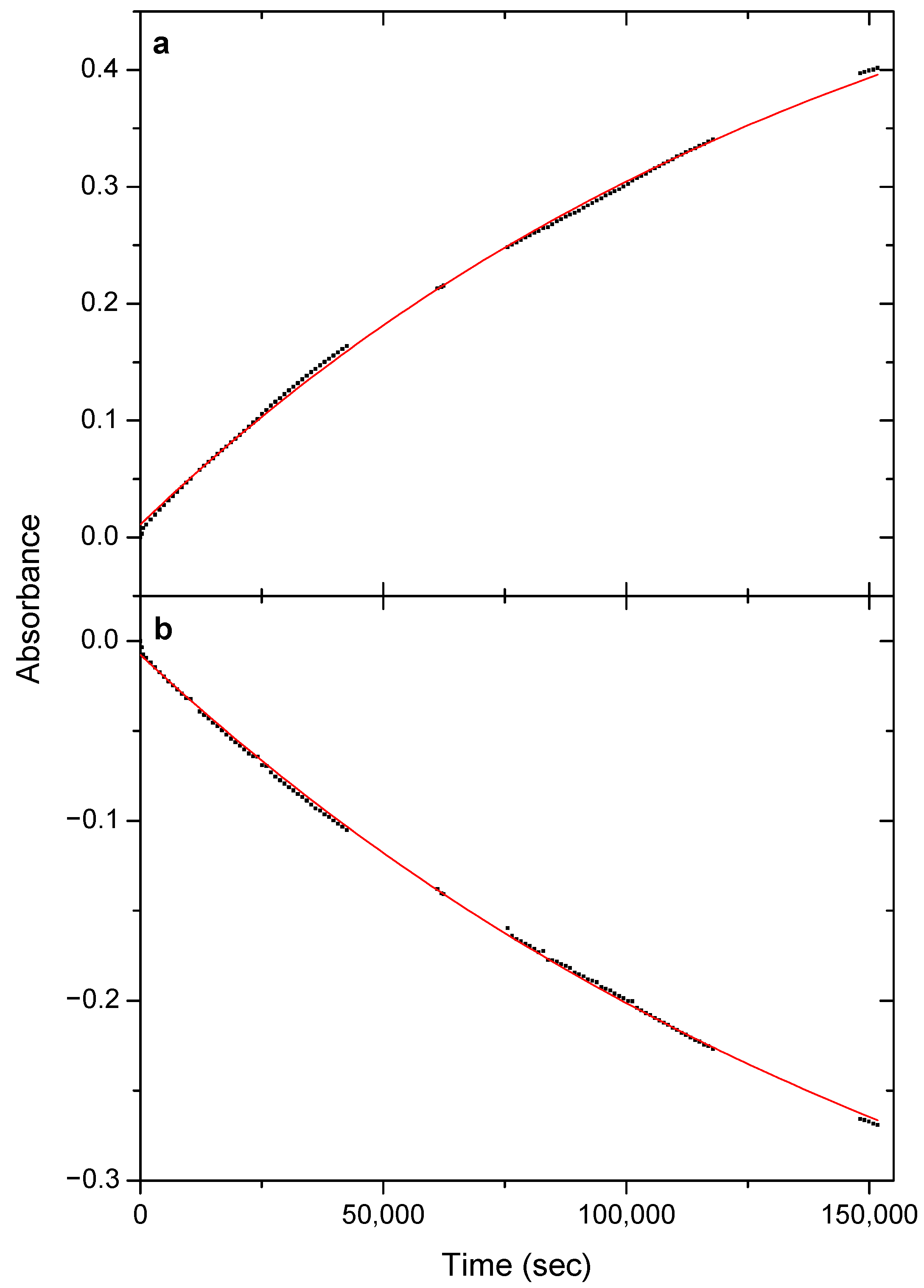
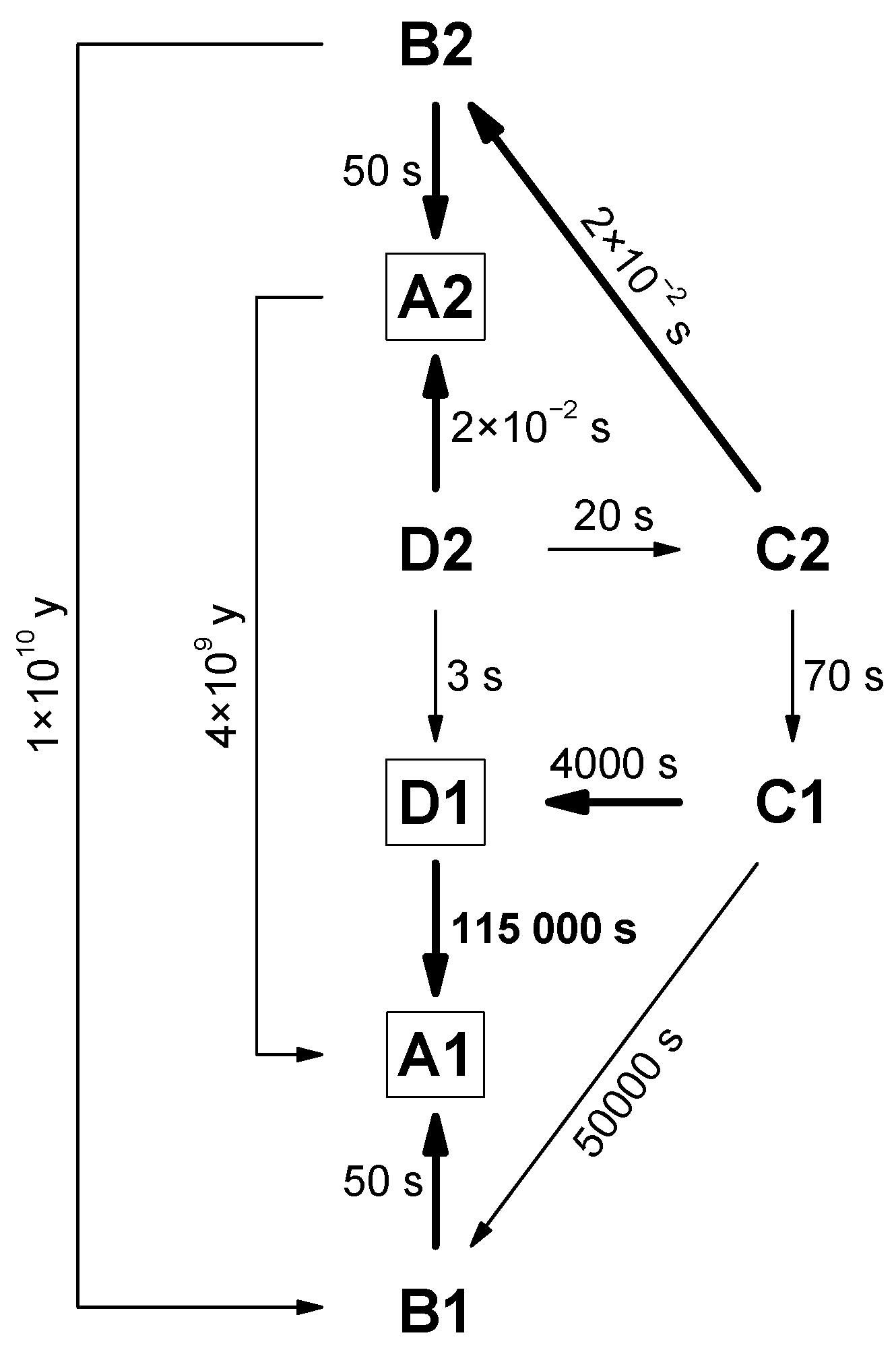
| Torsional Angles a/° | ∆EZPE,anharm b | |||
|---|---|---|---|---|
| Φ1 | Φ2 | Φ3 | ||
| A1 | 180.0 | −180.0 | 180.0 | 0.0 |
| A2 | −180.0 | 0.0 | −180.0 | 3.4 |
| B1 | 0.0 | 180.0 | 180.0 | 0.8 |
| B2 | 0.0 | 0.0 | 180.0 | 3.5 |
| C1 | 0.0 | 180.0 | 0.0 | 9.1 |
| C2 | 0.8 | −33.6 | −11.2 | 30.0 |
| C2* | −0.8 | 33.6 | 11.2 | 30.0 |
| D1 | 180.0 | 180.0 | 0.0 | 7.4 |
| D2 | 179.8 | −34.6 | −11.7 | 30.2 |
| D2* | −179.8 | 34.6 | 11.7 | 30.4 |
| Excitation Wavelength (cm−1) a | ||||
|---|---|---|---|---|
| 6952.0 (‘Local’) | 6994.9 (‘Local’) | 7093.2 (‘Remote’) | 7077.1 (‘Remote’) | |
| A1 | − | + | − | + |
| A2 | 0 | 0 | 0 | 0 |
| D1 | + | − | + | − |
| Experimental | Theoretical | Mode | Description b | ||
|---|---|---|---|---|---|
| ν (cm−1) | Irel.a | ν (cm−1) | I (km mol−1) | ||
| 1742.5 | 288 | 1746.2 | 329 | ν6 | ν(C=O) |
| 1625.1 | 80 | 1618.4 | 170 | ν7 | ν(CC)arom. |
| 1600.3 | 58 | 1586.9 | 52 | ν8 | ν(CC)arom. |
| 1517.3, 1510.5 | 6.6 | 1498.2 | 11 | ν9 | ν(CC)arom., β(CCH) |
| 1466.5, 1461.8 | 119 | 1459.6 | 113 | ν10 | ν(CC)arom., β(CCH) |
| 1376.9, 1373.3 | 11 | 1369.2 | 49 | ν11 | ν(C–C), β(COH)COOH |
| 1333.1 | 25 | 1335.4 | 46 | ν12 | ν(CC)arom. |
| 1301.0 | 148 | 1298.8 | 121 | ν13 | ν(C–O)4-OH, β(CCH) |
| 1263.0 | 29 | 1246.5 | 11 | ν14 | β(CCH) |
| 1243.9 | 1.9 | ? | ? | ||
| 1219.9 | 5.6 | 1217.7 | 21 | 2ν29 | 2δ(ring) |
| 1204.7 | 36 | 1206.4 | 22 | ν15 | β(COH)4-OH |
| 1184.9 | 128 | 1180.1 | 98 | ν16 | β(COH)COOH, β(CCH) |
| 1151.8 | 4.4 | ? | ? | ||
| 1144.2 | 44 | 1146.3 | 38 | ν17 | β(CCH) |
| 1117.4, 1114.3 | 224 | 1115.6 | 212 | ν18 | β(CCH) |
| 1094.6 | 9.7 | 1084.7 | 26 | ν19 | ν(C–O)COOH, ν(CF) |
| 972.5 | 65 | 976.6 | 29 | ν21 | β(CCC)arom. |
| 863.5, 858.0 | 44 | 872.8 | 29 | ν22 | γ(CCH) |
| 823.5 | 2.8 | 829.1 | 1.8 | ν23 | γ(CCH) |
| 769.7 | 72 | 775.6 | 37 | ν24 | τ(COOH), τ(ring) |
| 746.1 | 7.7 | 746.1 | 6.2 | ν25 | δ(ring) |
| 735.0 | 9.5 | 731.7 | 7.8 | ν26 | β(O=C–O) |
| 691.1, 680.9 | 33 | 698.9 | 17 | ν27 | τ(COOH), τ(ring) |
| 606.5 | 22 | 608.4 | 28 | ν29 | δ(ring) |
| Experimental | Theoretical | Mode | Description b | ||
|---|---|---|---|---|---|
| ν (cm−1) | Irel.a | ν (cm−1) | I (km mol−1) | ||
| 1772.0 | 409 | 1778.2 | 257 | ν6 | ν(C=O) |
| 1628.2sh | 135 | 1619.1 | 140 | ν7 | ν(CC)arom. |
| 1601.2sh,b | 15 | 1590.5 | 27 | ν8 | ν(CC)arom. |
| 1508.7, 1484.2 | 20 | 1499.6 | 16 | ν9 | β(CCH), ν(CC)arom. |
| 1458.7, 1452.1, 1449.1, 1444.1 | 95 | 1451.6 | 81 | ν10 | ν(CC)arom., β(CCH) |
| 1347.8, 1340.1 | 465 | 1307.8 | 790 | ν12 | β(COH)COOH |
| 1331.8 | 44 | 1333.1 | 34 | ν11 | ν(CC)arom., β(COH) |
| 1308.1 | 43 | ? | |||
| 1297.8 | 219 | 1298.8 | 247 | ν13 | β(CCH), ν(C–O)4-OH |
| 1251.0 | 28 | 1248.8 | 26 | ν14 | β(CCH) |
| 1226.9 | 8.3 | ? | |||
| 1215.9 | 10 | ? | |||
| 1196.1 | 31 | 1213.2 | 9.5 | ν15 | β(CCH), β(COH)COOH |
| 1179.8 | 15 | 1182.4 | 85 | ν16 | β(COH)4-OH |
| 1136.2 | 64 | 1122.1 | 97 | ν18 | β(CCH) |
| 1126.2 | 36 | 1139.6 | 10 | ν17 | β(CCH) |
| 1085.0, 1081.9 | 15 | 1060.9 | 0.012 | ν19 | ν(C–O)COOH, ν(CF) |
| 1048.3 | 14 | ? | ? | ||
| 965.6 | 70 | 968.3 | 18 | ν21 | β(CCC)arom. |
| 854.4, 851.5 | 45 | 872.4 | 41 | ν22 | γ(CCH) |
| 825.9 | 10 | 832.5 | 6.3 | ν23 | γ(CCH) |
| 763.2 | 51 | 754.4 | 11 | ν25 | β(O=C–O) |
| 736.8 | 5.5 | 739.4 | 2.3 | ν26 | δ(ring) |
| 683.5, 678.1 | 25 | 692.1 | 8.6 | ν27 | τ(COOH), τ(ring) |
| 625.1 | 24 | 632.5 | 10 | ν28 | τ(COOH), τ(ring) |
| 610.5 | 36 | 612.1 | 20 | ν29 | δ(ring) |
| Experimental | Theoretical | Mode | Description b | ||
|---|---|---|---|---|---|
| ν (cm−1) | Irel.a | ν (cm−1) | I (km mol−1) | ||
| 1763.8, 1757.3 | 378 | 1769.2 | 196 | ν6 | ν(C=O) |
| 1607.9 | 4.8 | 1616.9 | 89 | ν7 | ν(CC)arom. |
| 1572.7 | 2.2 | 1587.0 | 98 | ν8 | ν(CC)arom. |
| 1515.1 | 13 | 1498.0 | 27 | ν9 | β(CCH), ν(CC)arom. |
| 1468.4sh | 11 | 1455.3 | 18 | ν10 | ν(CC)arom., β(CCH) |
| 1357.5 | 16 | 1351.2 | 26 | ν11 | ν(CC)arom., β(COH)COOH |
| 1301.2sh | 53 | 1298.8 | 162 | ν13 | ν(C–O)4-OH, β(COH)COOH |
| 1239.0 | 8.3 | 1245.5 | 57 | ν27 + ν31 | τ(ring, COOH) + γ(CCH)COOH |
| 1177.0 | 31 | 1173.0 | 97 | ν16 | β(COH)COOH, ν(C–C) |
| 1154.5 | 1.9 | 1157.0 | 20 | ν17 | β(CCH) |
| 1128.6, 1122.0 | 123 | 1125.1 | 327 | ν18 | β(CCH) |
| 1097.2 | 2.8 | ? | ? | ||
| 1063.0, 1059.6, 1057.7 | 58 | 1048.8 | 96 | ν19 | ν(C–O)COOH |
| 859.4sh | 14 | 875.1 | 33 | ν22 | γ(CCH), τ(ring) |
| 820.3 | 1.1 | 825.9 | 2.5 | ν23 | γ(CCH), τ(COOH) |
| 770.8sh | 26 | 775.5 | 22 | ν24 | τ(COOH), γ(CCH) |
| 743.5 | 3.0 | 747.1 | 3.2 | ν25 | δ(ring) |
| 689.1 | 10 | 702.2 | 35 | ν27 | τ(ring), τ(COOH) |
| Near-IR Irradiation (cm−1) a | ||||
|---|---|---|---|---|
| 6952.0 (Local) | 6994.9 (Local) | 7093.2 (Remote) | 7077.1 (Remote) | |
| kA1 | −(9.9 ± 0.2) × 10−4 | (8.6 ± 0.2) × 10−4 | −(5.0 ± 0.1) × 10−4 | (3.2 ± 0.1) × 10−4 |
| kD1 | (9.3 ± 0.3) × 10−4 | −(8.1 ± 0.1) × 10−4 | (5.2 ± 0.5) × 10−4 | −(3.8 ± 0.5) × 10−4 |
| Aint (cm) | 1.896 | 1.039 | 1.782 | 1.126 |
| α (cm) | 5.5 × 10−17 | 4.3 × 10−17 | 5.5 × 10−17 | 4.3 × 10−17 |
| N (cm−2) | 8.0 × 1016 | 5.6 × 1016 | 7.5 × 1016 | 6.0 × 1016 |
| A | 0.0020 | 0.0008 | 0.0012 | 0.0006 |
| σi(ṽ) (cm2) | 2.5 × 10−20 | 1.4 × 10−20 | 1.6 × 10−20 | 1.0 × 10−20 |
| P (W) | 0.044 ± 0.008 | 0.045 ± 0.001 | 0.046 ± 0.001 | 0.050 ± 0.001 |
| Ephoton (J) | 1.4 × 10−19 | 1.4 × 10−19 | 1.4 × 10−19 | 1.4 × 10−19 |
| I(ṽ) (cm−2 s−1) | (3.1 ± 0.6) × 1017 | (3.2 ± 0.1) × 1017 | (3.3 ± 0.1) × 1017 | (3.6 ± 0.1) × 1017 |
| Φ(i) (E3) | 1.2 × 10−1 | 1.9 × 10−1 | 9.7 × 10−2 | 9.7 × 10−2 |
| Niso (s−1) | 7.7 × 1013 | 4.7 × 1013 | 3.8 × 1013 | 2.1 × 1013 |
| Nabs (s−1) | 1.4 × 1015 | 5.9 × 1014 | 9.1 × 1014 | 5.0 × 1014 |
| Φ(i) (E5) | 5.5 × 10−2 | 8.0 × 10−2 | 4.2 × 10−1 | 4.2 × 10−2 |
| Φ(i)average | (9 ± 3) × 10−2 | (1.4 ± 0.5) × 10−1 | (7 ± 3) × 10−2 | (7 ± 3) × 10−2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Góbi, S.; Balbisi, M.; Tarczay, G. Local and Remote Conformational Switching in 2-Fluoro-4-Hydroxy Benzoic Acid. Photochem 2022, 2, 102-121. https://doi.org/10.3390/photochem2010009
Góbi S, Balbisi M, Tarczay G. Local and Remote Conformational Switching in 2-Fluoro-4-Hydroxy Benzoic Acid. Photochem. 2022; 2(1):102-121. https://doi.org/10.3390/photochem2010009
Chicago/Turabian StyleGóbi, Sándor, Mirjam Balbisi, and György Tarczay. 2022. "Local and Remote Conformational Switching in 2-Fluoro-4-Hydroxy Benzoic Acid" Photochem 2, no. 1: 102-121. https://doi.org/10.3390/photochem2010009
APA StyleGóbi, S., Balbisi, M., & Tarczay, G. (2022). Local and Remote Conformational Switching in 2-Fluoro-4-Hydroxy Benzoic Acid. Photochem, 2(1), 102-121. https://doi.org/10.3390/photochem2010009








