Vibrational-Excitation-Induced and Spontaneous Conformational Changes in Solid Para-H₂—Diminished Matrix Effects

Abstract

Both vibrational-excitation-induced (by (N)IR laser) and spontaneous (by H atom tunneling) conformational changes are often investigated by matrix-isolation spectroscopy. It is well known that rigid hosts, such as solid noble gases, N₂, or normal-H₂, can largely affect both the quantum efficiency of the (N)IR photon-induced process and the tunneling rate. In the present study, the conformational changes of formic and acetic acids, as well as glycine, were investigated in a soft quantum host, solid para-H₂. It is shown that the tunneling rates in para-H₂ are orders of magnitude larger than those in rigid hosts. Furthermore, our results also suggest that the quantum efficiencies of some (N)IR-light-induced conformational changes are larger than in rigid matrices. These results can open a door for the applications of para-H₂ host in conformational and tunneling studies and can help understand the details of these complex processes.

1. Introduction

Matrix-isolation spectroscopy is a well-tried method to study light-induced and spontaneous conformational changes. UV irradiation is the simplest and a very frequently used method for isomerization. It can also be used to induce conformational changes, but usually, the UV absorption bands of different conformers overlap; therefore, in most cases, it is sufficient to shift the conformational ratio only to a limited extent. IR laser irradiation is a more selective method for conformational switching. In this case, a selected conformer is vibrationally excited, which can then convert into another one. When there is no spectral overlap between the excited vibrational band of the excited conformer and the bands of other conformer(s), and there is no rapid spontaneous back conversion, it allows high or complete depletion of the vibrationally excited conformer. Using this method, conformational switching was observed for many model systems, including formic [1,2,3,4,5,6], acetic [6,7,8,9], trifluoro- and tribromoacetic [10,11], propiolic [12], propionic and 2-chloropropionic [13,14], glycolic [15], α-ketocarboxylic [16], oxamic [17], dicarboxylic [18,19,20], (hetero)cyclic organic [21,22,23], and amino acids [24,25,26,27,28,29], as well as sulfur-containing compounds [30,31,32,33,34].

In the above examples, the conformational change was induced locally, i.e., in most of the cases, the first overtone of the OH stretching mode (2ν(OH)) of the carboxylic (–COOH) group was excited, which caused a trans-to-cis (or Z to E) conformational change of the –COOH group. However, vibrational excitation can also trigger a conformational change farther from the absorbing oscillator. Among the first examples, it was shown that the excitation of CH and C=O stretching overtones (2ν(CH) and 2ν(C=O)) could also induce a cis-trans conformational change in formic and acetic acid [5,9]. More recent examples include amino acids. The irradiation of the first overtone of the NH stretching mode (2ν(NH)) of glycine results in the cis-trans conversion of the –COOH group [24], while the excitation of the 2ν(OH) mode of the carboxylic hydroxyl (–OH) group can induce a conformational change in the side chain in serine [29]. Other examples of this so-called remote switching include 2-thiocytosine, in which rotamerization of the thiol (–SH) moiety was induced by the excitation of the NH₂ stretching overtone (2ν(NH₂)) [35]; in kojic acid, in which the phenolic –OH group was irradiated, and the conformational change of the hydroxymethyl (–CH₂OH) group was observed [36]; in 6-methoxyindole, in which the excitation of the 2ν(NH) stretching overtone mode induced the conformational change of the methoxy (–OCH₃) group [37]; and in glycolamide, where pumping the NH₂ stretching overtone (2ν(NH₂)) resulted in the rotation of the –CH₂OH group [38]. The selective excitation of the OH stretching overtone of one of the –COOH groups of an asymmetrical dicarboxylic acid, E-glutaconic acid, can induce the conformational change (cis-trans) of the other –COOH moiety, located at the other end of the molecule [39]. Furthermore, it was also found that the 2ν(NH) mode of each imino-thiol isomer of thioacetamide changes the orientation of a remote–SH group, while the orientation of the imino (=NH) group remains the same [40]. There are instances where the local excitation is only slightly more efficient than the remote one; a recent example is 2-fluoro-4-hydroxy benzoic acid [41]. When a high-energy conformer is prepared by the above method, it might convert to lower-energy conformers either via a low-energy classical barrier or by H atom tunneling. For several dozens of molecules the tunneling times were measured in rigid noble gas [2,7,9,10,11,13,14,16,17,22,24,25,26,31,32,34,40,41,42,43,44,45,46,47], normal-H₂ (n-H₂) [45,46,47,48], and N₂ matrices [6,10,11,12,15,25,26,27,28,29,49].

Upon studying the conformational changes in a rigid matrix, one has to keep in mind that the host may have a non-negligible effect on the quantum yields of the light-induced processes and the rate of the spontaneous ones. Not surprisingly, different quantum yields were observed for the 2ν(OH) excitation-induced cis-trans conformational change of acetic acid in different matrices [9]. For instance, photo-induced rotamerization was found to be more efficient in solid Xe than in Ar for multiple systems, whereas Kr lies between them [50]. This is likely due to the ability of the host to compensate for the energy gap between the intramolecular energy levels participating in the energy relaxation process through the conversion of the excess internal energy of the guest molecule into lattice phonons [51]. The local matrix morphology (matrix sites) is also expected to have an influence on the energy relaxation dynamics owing to its effect on the anharmonicity and intermode coupling constants [3]. It is a completely unexplored question how the host and the sites can influence the ratio of the local and remote conformational change. There might be examples when a local conformational change is sterically hindered by close packing of the host atoms while there is more space for the conformational change of a remote group.

The effect of the host is even more complicated for conformational changes by H atom tunneling. It can be expected that the tunneling rate should be principally determined by three factors. First is the dispersion interaction between the noble gas atom and the sample molecule. More precisely, the cis carboxylic acid becomes relatively more stable resulting from its higher permanent dipole moment compared to the trans form, which ensures a more intense interaction with the host environment [2]. Moreover, the stabilization is also controlled by the polarizability of the noble gas atoms; higher polarizability translates into a larger interaction [52]. Nevertheless, the extent of solvation cannot always explain everything about the tunneling behavior of carboxylic acids [53]. Secondly, the energy mismatch between the ground-state cis conformer and a vibrationally excited trans form can be overcome by the dissipation of the excess energy via a one- or multiphonon process [2,52]. Evidently, the probability of a one-phonon process is higher, resulting in a higher tunneling rate. Thirdly, reorganization of the matrix upon tunneling has been proposed to be a rate-determining step and may explain the temperature-dependence of the process as well as the dependence on the quality of the matrix, where the latter can be explained by the different reorganization energies [54,55].

It is now well documented for several model molecules, including formic and acetic [6,56], as well as propiolic acids [12], HOCO radical [49], glycine [25], alanine [26,27], cysteine [28], and serine [29], that N₂ can extremely stabilize the higher-energy conformer as compared to noble gas matrices. This stabilizing effect of the N₂ matrix as compared to the Ar matrix results in two and four orders of difference in tunneling rates for HOCO radical and formic acid, respectively [6,49,56]. This might be rationalized by the quadruple moment of N₂ [25]. The higher-energy conformer of these species has a larger dipole moment than the transition structure and the lower-energy conformer; therefore, the higher-energy form is stabilized by a dipole-quadrupole interaction. It is also important to note that in different sites, the tunneling rates can be largely different, and due to the presence of several similar but slightly different sites, often not exponential but dispersive decay kinetics is observed for the conformational change [31,57]. Finally, we can mention a very interesting phenomenon observed for tribromoacetic acid in a N₂ matrix [11]. The excitation of the 2ν(OH) mode of the trans conformer predominantly converts the molecules located in a specific matrix site into the cis form; then, upon tunneling back to the trans form populates almost exclusively another matrix site.

In the present study, we measure the quantum yields of the 2ν(OH) excitation induced cis-trans conformational change and the rates of the spontaneous conformational changes of formic and acetic acids and glycine in a quantum host, solid para-H₂ (p-H₂). Since in this host, the vibrational amplitude of the H₂ molecules is comparable with the volume of the molecule [58], it provides a soft environment in which the steric effect is a much less important, less determining factor than in rigid matrices. In addition, the intermolecular interactions between the studied and the host molecules are also considerably smaller for p-H₂ than for noble gas, normal-H₂ (n-H₂), or N₂ matrices. The comparison of the values measured in p-H₂ should allow us to understand the host effects in more detail and could result in a better match of theory and experiment.

2. Materials and Methods

The experiments were conducted on the VIZSLA setup, which consists of an ultrahigh-vacuum (UHV) compatible stainless steel chamber capable of being evacuated to a base pressure of a few 1 × 10⁻⁹ mbar when cooled [59]. For the matrix-isolation experiments, Ar (Messer, 99.9999%), n-H₂ (Messer, 99.999%), and p-H₂ were used. p-H₂ was prepared by flowing n-H₂ through porous Fe(III) oxide (Sigma-Aldrich, (St. Louis, MI, USA), hydrated, catalyst grade, 30–50 mesh) cooled down to 13.9 K wrapped around the upper cryostat of the setup. All gases were collected in the separate gas mixing line in a 1 L glass bulb for the preparation of the mixtures with the carboxylic acids or in a 0.5 L bulb for the matrix containing glycine afterwards.

On the gas mixing line, a few cm³ of formic acid (FA, Sigma-Aldrich >98%) or acetic acid (AA, Sigma-Aldrich >99%) were undergone three freeze-thaw cycles in a small glass vial in order to eliminate dissolved gases from them. The mixtures of the carboxylic acids with Ar, n-H₂, and p-H₂, respectively, were prepared by introducing a few mbar of the acid vapors into the 0.5 L glass bulb and then diluting it with the carrier gas in two steps. The mixtures were left for at least 45 min after the first dilution and for at least 30 min after the second one to obtain sufficiently homogeneous mixtures. The final sample-to-gas ratios were estimated to be 1:1000 (FA:Ar), 1:1100 (FA:n-H₂), 1:3700 (FA:p-H₂), 1:1000 (AA:Ar), 1:1100 (AA:n-H₂), and 1:1800 (AA:p-H₂), respectively. Subsequently, the mixtures were introduced into the main chamber through a copper tube with an inner diameter of 6 mm, a leak valve, and a stainless-steel capillary array ending approximately 3 cm from the substrate. The leak valves were open so that the inlet rates of the gas mixtures were 0.6–0.9 mbar L min⁻¹ when using n-H₂ or p-H₂ and 1.1–1.3 mbar L min⁻¹ when using Ar. Then, the depositions were carried out to a gold-plated silver substrate mounted on the cold finger of an RDK-415D2 cryostat (Sumitomo Heavy Industries Inc., Tokyo, Japan), which can be ultimately cooled down to 3.1 K. The temperature of the substrate, independently of the sample material, was kept at 15 K when depositing Ar-containing matrices and at 3.1 K when the carrier gases were n-H₂ or p-H₂, respectively.

The glycine sample was prepared differently. Before evacuating the chamber, a small amount of glycine (Reanal, >99%) was inserted into a quartz sample holder tube (with a 0.5 cm diameter exit hole) inside a stainless-steel oven. The whole sample inlet system is directly attached to the vacuum chamber and can be moved horizontally through vacuum-compatible bellows. The oven temperature was measured by a K-type thermocouple and controlled by a Lakeshore Model 336 controller. The volatile impurities such as water had been removed by vacuum evaporation at 100 °C before the experiments. The matrix was prepared by co-depositing glycine and the carrier gas onto the substrate. For this, the temperature of the oven with the glycine was set to 138 °C during deposition. The matrix gases were introduced by the same stainless steel capillary array used to introduce the gas mixtures in the case of the experiments carried out with carboxylic acids, which are parallel to the oven. Inlet rates of the carrier gases were 0.8 mbar L min⁻¹ when using Ar and 0.7 mbar L min⁻¹ when using n-H₂ or p-H₂, respectively.

All near-IR (NIR) irradiations were carried out by an Optical Parametric Oscillator (OPO, GWU/Spectra-Physics VersaScan MB 240, FWHM ≈ 5 cm⁻¹) pumped by a pulsed Nd:YAG laser (Spectra-Physics Quanta Ray Lab 150, P ≈ 2.1–2.2 W, λ = 355 nm, f = 10 Hz, pulse duration = 2–3 ns). All irradiations were performed at 8 K in the case of Ar and at 3.1 K for the n-H₂ and p-H₂ experiments, respectively.

The mid-IR (MIR) spectra were taken by a Bruker Invenio FT-IR spectrometer equipped with a liquid N₂-cooled mid-band Mercury Cadmium Telluride (MCT) detector working in reflection-absorption mode. Each spectrum was collected in the spectral region of 4000–600 cm⁻¹ at a resolution of 1 cm⁻¹. For every measurement, a low-pass filter with a cutoff wavelength of 1830 cm⁻¹ was inserted between the spectrometer beam source and the substrate. For the experiments with glycine, a different filter was used that lets through light only in the 1900–1200 cm⁻¹ region. This was performed to eliminate the spectral changes (e.g., cis-trans conversion of the carboxylic acids) caused by the NIR photons originating from the spectrometer beam source. During deposition, 32 scans were averaged in each minute, whereas during and after irradiation, 8 scans were averaged, requiring approximately 8 s in the case of the FA-Ar experiment, and 2 scans were averaged (roughly every 2 s) for the remaining carboxylic acid matrix-isolation experiments. In the case of the glycine experiment, 32 scans were averaged each minute during deposition and irradiation as well. In order to prevent the appearance of spectral artifacts due to the scattering of the laser beam on the substrate, another low-pass filter with a cutoff wavelength of 3860 cm⁻¹ was placed between the substrate and the infrared detector during irradiation. For the glycine experiment, this filter was in the beam path during deposition as well. The near-IR (NIR) spectra were taken by the same FT-IR spectrometer after deposition and before irradiation to find the band positions used for the excitation of the sample molecule conformers. The spectra averaged 128 scans in the case of the AA experiments, the FA-n-H₂ experiment, as well as the glycine experiment, 32 scans during the FA-p-H₂ experiment, and 256 scans in the FA-Ar experiment. The resolution was set to 1 cm⁻¹ covering the spectral range of 8000–600 cm⁻¹. The cutoff filters were taken out for the NIR measurements waiting 15 min to purge the system properly after removing/reinserting the filters. The MIR background spectra were registered right before the deposition in every experiment with carboxylic acids at 1 cm⁻¹ resolution saved in the 16,000–0 cm⁻¹ spectral region averaging 512 scans. The MIR backgrounds were saved with and without the 3860 cm⁻¹ low-pass cutoff filter in the beam path, whereas the temperature was set to 15 K while collecting the MIR backgrounds for the Ar-matrix experiments and 3.1 K for the ones performed with n-H₂ and p-H₂, respectively. Background spectra of 512 scans were taken at 8 K before deposition for the glycine experiments using the resolution of 1 cm⁻¹ in the spectral region of 16000–0 cm⁻¹ with both filters in the beam path. One NIR background with the resolution of 1 cm⁻¹ averaging 512 scans was collected at 3.1 K and was used for all the experiments performed with carboxylic acids. For the glycine experiments, NIR background spectra of 256 scans at the resolution of 0.5 cm⁻¹ were collected right before deposition at 8 K (Ar matrix) and at 3.1 K (n-H₂ and p-H₂).

The assignment of the vibrational spectra was based on the findings of previous studies on FA, AA, and glycine made in Ar matrices [3,7,24]. In order to determine the column densities, the computed anharmonic vibrational intensities were used. For this, quantum-chemical DFT computations were performed utilizing the Gaussian 09 (Rev. D01) program package [60]. The optimization of the geometric structures belonging to the minima on the potential energy surface was performed at the B3LYP/cc-pVTZ level of theory. Then, anharmonic vibrational frequencies and intensities of the minima structures were computed by vibrational perturbation theory (VPT2) at the same level of theory. The optimized geometries and the calculated vibrational properties are listed in Tables S1–S12 in the Supplementary Material.

3. Results and Discussion

3.1. Determining the Column Densities and Quantum Efficiencies

Upon NIR irradiation, the conformational changes could be followed by monitoring the MIR spectra of the matrices. The column densities of the species ($N_t$(X) for species X in cm⁻²) at timestep $t$ (in s) were determined by using their most intense bands that do not overlap with other ones; when there was more than one good candidate (such as for FA and AA), the obtained $N_t^i$(X) values obtained for the i^th vibrational mode were averaged, and an error estimation could be provided in such a case. Unfortunately, no error estimate could be given in the case of glycine since only one vibrational mode could be used to calculate the column density of the conformers. The bands that were used for the determination of the column densities and for the NIR excitations are summarized in Table S13 and Figures S1 and S2 in the Supplementary Material. The following equation could be used to calculate $N_t^i$(X) of each species for a particular vibrational mode:

$$N_t^i\left(X\right)=\ln \left(10\right)\left(A_t^i\left(X\right)/c_{\mathrm{abs}}^i\right)\cos \left(\mathsf{\alpha }\right)/2$$

(1)

where $A_t^i\left(X\right)$ is the integrated band area of the vibrational mode $i$ of species X (in cm⁻¹), $c_{\mathrm{abs}}^i$ represents the absorption coefficient of the same vibrational mode approximated by the computed MIR anharmonic intensities (in cm), whereas $\mathsf{\alpha }$ is the angle of incidence relative to the surface normal of the substrate. $\mathsf{\alpha }$ is approximately 60° in n- and in p-H₂ and 42° in Ar due to its refractive index being different from 1.0 (practically 1.3). The temporal evolution of the column densities for the FA and glycine systems are visualized in Figure 1 and Figure 2, whereas that of the AA-Ar sample can be found in the Supplementary Material (Figure S3). It is worth noting that due to the uncertainty of the theoretically obtained IR absorption coefficients, the column density profile of the decaying conformer may not perfectly match that of the forming one. In order to quantify the conversion rates, kinetic curves could be generated by fitting single-exponential functions on the column densities, where $t$ is the time since the beginning of the laser excitation, and $k$ (in s⁻¹) is the first-order rate constant of the conversion process.

$$N_t\left(X\right)=N_{t=0}\left(X\right){\mathrm{e}}^{-kt}+N_{t=\infty }\left(X\right)$$

(2)

For the growth profiles, a modified function can be used as an estimation:

$$N_t\left(X\right)=N_{t=\infty }\left(X\right)\left(1-{\mathrm{e}}^{-kt}\right)$$

(3)

Once the conversion rates are known, they can be used to estimate the quantum efficiency (${\varphi }^i$, a dimensionless value) of the processes when exciting the $i$^th NIR band of the conformer [5,9,61].

$${\varphi }^i=k_p^i/{\sigma }^{i}I$$

(4)

where $k_p^i$ is the pumping rate in s⁻¹, whereas ${\sigma }^i$ and $I$ represent the absorption cross-section of the i^th vibrational mode in cm² and the average photon flux of the laser beam at that wavelength in cm² s⁻¹, respectively. ${\sigma }^i$ can be calculated by dividing the absorbance of the excited NIR (overtone) band ($A$, dimensionless value) by the column density of the transforming conformer at the beginning of irradiation ($N_{t=0}\left(X\right)$). One also needs to take into account that the apparent thickness of the sample (therefore the $A$ value) is different for the NIR beam coming from the spectrometer for the laser beam (the latter closes at an angle of approximately 23° with the surface normal. On the other hand, $I$ is estimated by dividing the output power of the produced NIR laser light used for excitation ($P$, in W) by the photon energy ($E_{\mathrm{photon}}$, in J) times the irradiated surface area $S$ (= 1 cm²). It is important to point out that $P$ was measured at the aperture of the OPO, thus neglecting the losses due to the optical elements such as the mirrors and the window of the vacuum chamber. As such, $P$ (and therefore $I$) represents an upper estimate, meaning that the ${\varphi }_i$ values presented here are lower estimates.

Alternatively, another estimation for ${\varphi }^i$ can also be made by dividing the number of molecules converted ($n_{\mathrm{conv}}$) by the number of photons absorbed per time unit ($n_{\mathrm{abs}}$, both in s⁻¹), which can be obtained as follows:

$$n_{\mathrm{conv}}=k_p^i{N}_{t=0}\left(trans\right)S$$

(5)

$$n_{\mathrm{abs}}=\left(1-{10}^{-A}\right)IS$$

(6)

The ${\varphi }_i$ values deduced by the two approaches can then be averaged; all the values discussed above are listed in

Table 1. Calculated quantum efficiencies (${\varphi }^i$ ) of the trans-cis conversion of FA and AA upon NIR laser excitation. The applied the excitation wavenumbers are in parentheses.

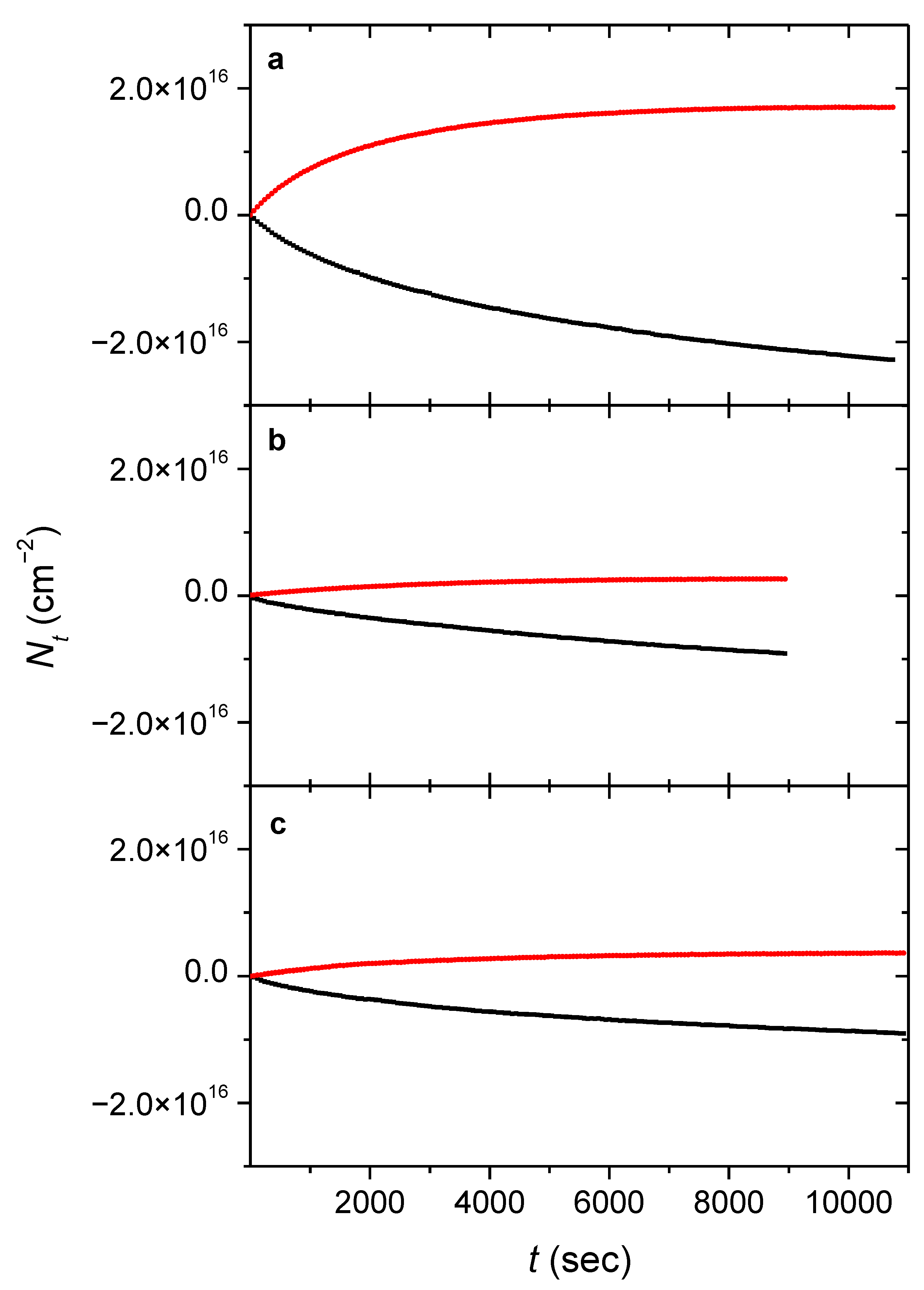
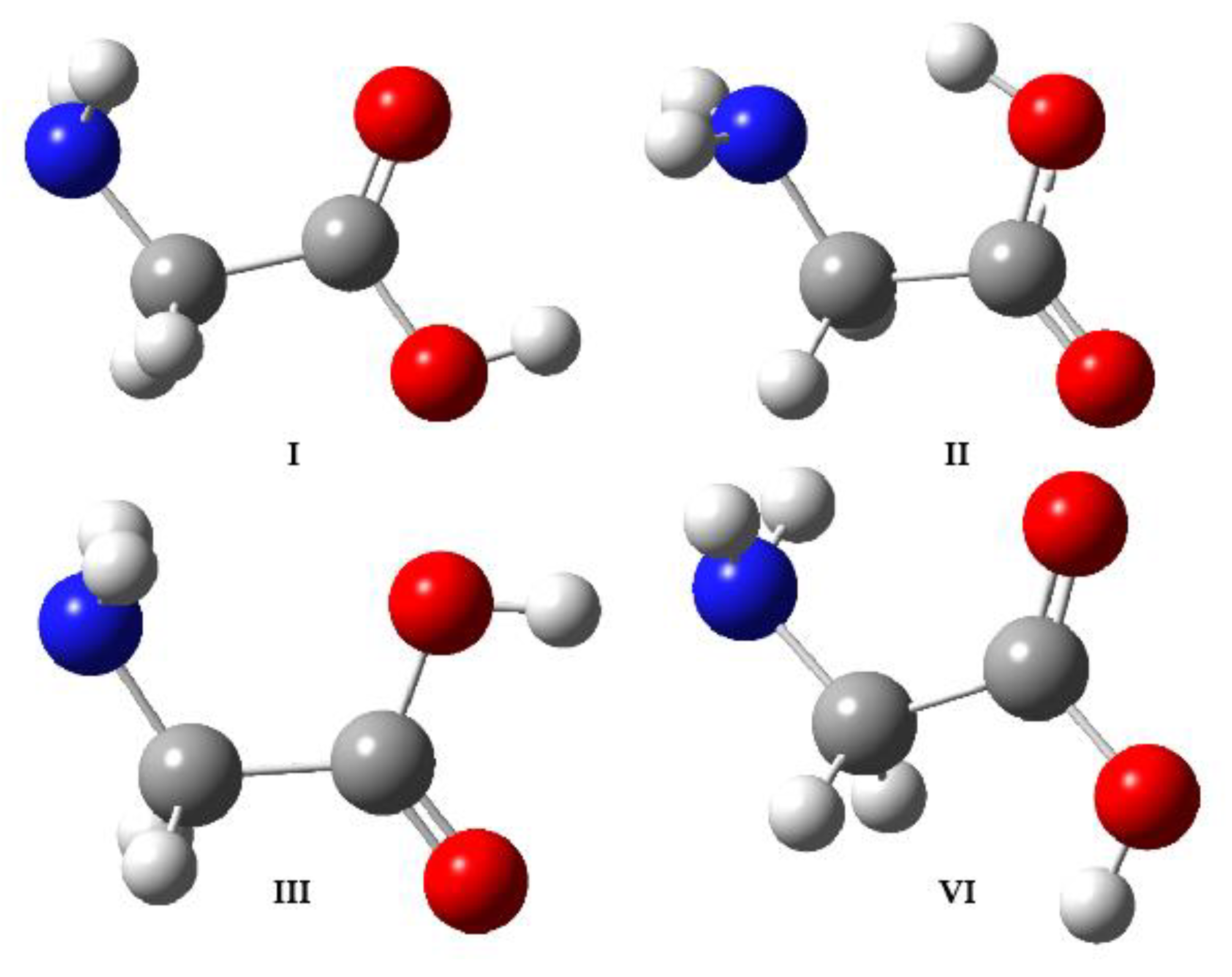
	FA				AA
	Ar (6929.9 cm−1)	Ar (6934.7 cm−1)	n-H2 (6937.6 cm−1)	p-H2 (6940.0 cm−1)	Ar (6957.9 cm−1)
$N_{t=\infty }\left(trans\right)$ (cm−2)	(2.6 ± 0.4) × 1016	(1.7 ± 0.5) × 1016	(1.8 ± 0.3) × 1016	(1.7 ± 0.1) × 1016	(5.8 ± 0.9) × 1016
$N_{t=\infty }\left(cis\right)$ (cm−2)	(5.7 ± 0.3) × 1015	(1.9 ± 0.1) × 1016	(2.5 ± 0.1) × 1015	(3 ± 1) × 1014	(5.1 ± 0.4) × 1015
$k_p^i$ (s−1)	(5.7 ± 0.4) × 10−4	(3 ± 1) × 10−3	(9.4 ± 0.2) × 10−4	(4 ± 4) × 10−3	(2.2 ± 0.1) × 10−3
$N_{t=0}\left(I\right)$ (cm−2)	(2.8 ± 0.4) × 1016	(2.8 ± 0.5) × 1016	(2.0 ± 0.3) × 1016	(1.7 ± 0.1) × 1016	(6.3 ± 0.9) × 1016
$A$	0.0108	0.0148	0.0025	0.0025	0.0183
${\sigma }^i$ (cm2)	(3.9 ± 0.6) × 10−19	(5 ± 1) × 10−19	(1.3 ± 0.2) × 10−19	(1.5 ± 0.1) × 10−19	(2.9 ± 0.5) × 10−19
$P$ (W)	7.4 × 10−3 a	7.4 × 10−3 a	2.4 × 10−2	2.4 × 10−2	2.4 × 10−2
$E_{\mathrm{photon}}$ (J)	1.4 × 10−19	1.4 × 10−19	1.4 × 10−19	1.4 × 10−19	1.4 × 10−19
$I$ (cm−2 s−1)	5.3 × 1016	5.3 × 1016	1.7 × 1017	1.7 × 1017	1.7 × 1017
${\varphi }^i$	2.8 × 10−2	1.1 × 10−1	4.3 × 10−2	1.6 × 10−1	4.5 × 10−2
$n_{\mathrm{conv}}$ (s−1)	1.6 × 1013	8.4 × 1013	1.9 × 1013	7.0 × 1013	1.4 × 1014
$n_{\mathrm{abs}}$ (s−1)	1.3 × 1015	1.8 × 1015	9.8 × 1014	9.8 × 1014	7.0 × 1015
${\varphi }_{\mathrm{alternative}}^i$	1.2 × 10−2	4.7 × 10−2	1.9 × 10−2	7.1 × 10−2	2.0 × 10−2
${\varphi }_{\mathrm{average}}^i$	(2.0 ± 0.8) × 10−2	(8 ± 3) × 10−2	(3 ± 1) × 10−2	(1.2 ± 0.5) × 10−1	(3 ± 1) × 10−2

^a With the effect of OPO bandwidth taken into account (measured value was 2.4 × 10⁻² W).

and

Table 2. Calculated quantum efficiencies (${\varphi }^i$ ) of the conversion of glycine conformer I→III upon NIR laser excitation. The applied the excitation wavenumbers are in parentheses.

	Glycine
	Ar (6968.8 cm−1)	n-H2 (6963.2 cm−1) a	p-H2 (6968.1 cm−1) a
$k_p^i$ (s−1)	(4.8 ± 0.1) × 10−4	(3.5 ± 0.1) × 10−4	(3.4 ± 0.1) × 10−4
$N_{t=0}\left(I\right)$ (cm−2)	6.0 × 1016	5.8 × 1016	5.8 × 1016
$A$	0.0043	0.0056	0.0184
${\sigma }^i$ (cm2)	7.2 × 10−20	9.7 × 10−20	3.2 × 10−19
$P$ (W)	0.021 ± 0.002	0.023 ± 0.001	0.021 ± 0.002
$E_{\mathrm{photon}}$ (J)	1.4 × 10−19	1.4 × 10−19	1.4 × 10−19
$I$ (cm−2 s−1)	(1.5 ± 0.1) × 1017	(1.6 ± 0.1) × 1017	(1.5 ± 0.1) × 1017
${\varphi }^i$	4.4 × 10−2	2.3 × 10−2	7.1 × 10−3
$n_{\mathrm{conv}}$ (s−1)	2.9 × 1013	2.0 × 1013	2.0 × 1013
$n_{\mathrm{abs}}$ (s−1)	1.5 × 1015	2.0 × 1015	6.2 × 1015
${\varphi }_{\mathrm{alternative}}^i$	1.9 × 10−2	1.0 × 10−2	3.2 × 10−3
${\varphi }_{\mathrm{average}}^i$	(3 ± 1) × 10−2	(1.7 ± 0.7) × 10−2	(5 ± 3) × 10−3

^a All conformer III had to be converted to I in H₂ matrices before the actual irradiation experiments, by exciting the 2ν(OH) mode the former at 6954.5 cm⁻¹ (n-H₂) and 6959.3 cm⁻¹ (p-H₂), respectively.

. It should also be noted that the overall uncertainty of ${\varphi }^i$ appears to be at around 50%, according to the conclusions made previously [9,40,41,61].

An important question is how $k_p^i$ is calculated, which is of fundamental importance as it partially determines how quickly an equilibrium between the higher-energy cis (E) and the lower-energy trans (Z) conformers can be reached for the carboxylic acids when exciting the latter; thus, it has a fundamental influence on the ${\varphi }^i$ values of the carboxylic acids. The same does not apply to glycine, as there was no observable tunneling of the III to I process on the experimental timescale (Scheme 1). Therefore for glycine, simply the growth rate of III was used since I follows a rather complicated (higher-order or dispersive) kinetics as a result of multiple (more and less stable) sites and also transforms into conformer II as a minor by-product, whose effects can never be perfectly eliminated. However, for the carboxylic acids, the effect of the relatively fast cis-trans back-conversion via hydrogen atom tunneling must also be considered [5,9,61]. This results in the rapid saturation of $N_t\left(cis\right)$ when pumping the trans form. Since the pumping and tunneling ($k_t^i$, also in s⁻¹) rates are identical in equilibrium, one can write that

$$k_p^i{N}_{t=\infty }\left(trans\right)=k_t^i{N}_{t=\infty }\left(cis\right)$$

(7)

which can be reformulated so that $k_p^i$ can be obtained:

$$k_p^i=k_t^i{N}_{t=\infty }\left(cis\right)/N_{t=\infty }\left(trans\right)$$

(8)

It is worth noting that $N_{t=\infty }\left(cis\text{-}\mathrm{FA}\right)$ values are smaller for the higher $k_t^i$ observed in hydrogen matrices, thus somewhat compensating the latter. Accordingly, less trans conformer can transform into cis before the rate of the reverse (tunneling) process becomes equal to the pumping rate, and thus, the equilibrium is reached earlier (Figure 1).

3.2. Cis-Trans Tunneling Rates of the Carboxylic acids

Although the NIR-induced conversion preceded the tunneling rate ($k_t^i$) measurements, as was discussed in the previous subsection, the rate of the back conversion via H atom tunneling must be determined first in order to be able to estimate the ${\varphi }^i$ values of the photon-induced processes in carboxylic acids; thus, we discuss the tunneling rates first. The spontaneous cis to trans conversion via H atom tunneling of carboxylic acids in low-temperature matrices, especially that of FA and AA, has been extensively investigated in the literature, studying the process in many different matrix environments. Thus, $k_t^i$ of FA and AA obtained here can be directly compared with previous results (

Table 3. Cis-to-trans tunneling rates ($k_t^i$, in s⁻¹) and half-lives ($t_{1/2}^i\left(cis\right)$, in s) of cis-FA and cis-AA after NIR laser excitation. Comparative data taken from the literature are in italics.

Species	Matrix	${\mathit{k}}_{\mathit{t}}^{\mathit{i}}$	${\mathit{t}}_{1/2}^{\mathit{i}}\left(\mathit{cis}\right)$	Ref.
FA	Ne	-	≈ 5 ± 1 a	[42]
	Ar	(2.6 ± 0.5) × 10−3	270 ± 50 b	-
		(2.4 ± 0.1) × 10−3	290 ± 10 c	-
		2.3 × 10−3	-	[2,5]
	Kr	≈1.5 × 10−3	-	[2]
	Xe	≈4 × 10−4	-	[2]
	N2	≈2 × 10−5	-	[6]
AA	n-H2	(6.8 ± 0.5) × 10−3	102 ± 8	-
		-	≈ 140 a	[48]
	p-H2	(2.1 ± 0.3) × 10−1	3.3 ± 0.6	-
	Ar	(2.5 ± 0.3) × 10−2	28 ± 3	-

^a determined at 4.2 K; ^b after exciting the trans-FA 2ν(OH) mode at 6929.9 cm⁻¹; ^c after exciting the trans-FA 2ν(OH) mode at 6934.7 cm⁻¹.

). We have found that $k_t^i$ of cis-FA in Ar is (2.6 ± 0.5) × 10⁻³ s⁻¹ (when the pumping wavelength was 6929.9 cm⁻¹), which agrees within error limits with the literature value of 2.3 × 10⁻³ (both values were obtained at the experimental temperature of 8 K) [2,5]. Interestingly, there seems to be no significant dependence of $k_t^i$ values of cis-FA in Ar matrix on which of the two different sites of the 2ν(OH) mode of the trans form was previously pumped ($k_t^i$ = (2.4 ± 0.1) × 10⁻³ s⁻¹ after excitation at 6929.9 cm⁻¹).

It should be noted that the tunneling rate heavily depends on the noble gas used, which was explained by the stabilization of the cis form due to solvation, phonon-assisted tunneling [2], and matrix reorganization effects [54,55]. The extent of solvation (stabilization) is related to the increased dipole moment of the cis form, having an experimental dipole moment of 3.79 D vs. 1.42 D in the case of the trans conformer [62]. The theoretical values obtained at the used B3LYP/cc-pVTZ level of theory level should also be mentioned since they agree reasonably well with the experimental ones: 3.87 D (cis-FA) and 1.51 D (trans-FA), respectively. The computed dipole moment of the transition state lies between that of the two minima (2.77 D), suggesting an intermediate degree of solvation, thus a relatively lower stabilization than in the case of the cis form.

Moreover, the level of solvation also depends on the variation in the polarizability of the noble gas atoms; the higher the permanent dipole moment and the polarizability, the larger the dipole-induced dipole interaction is. As a consequence, the cis carboxylic acid in a matrix environment becomes more stable relative to the trans conformer. Regarding the polarizability of the medium, the respective values are 0.39, 0.80, and 1.64 × 10⁻²⁴ cm³ for Ne, n-H₂, and Ar, respectively [63]. The difference between the observed tunneling rates of FA in n-H₂ and in Ar could then be explained by their different polarizabilities. Ne is an exception, though, where despite its low polarizability, the tunneling rate was found to be anomalously high, almost two orders of magnitude higher than in Ar. This finding was speculated to be caused by the small energy gap between the cis conformer and a vibrationally excited trans form. Accordingly, an efficient transformation of the former to the latter can be achieved because only one phonon is required for energy dissipation. A larger energy mismatch can undergo only through a multiphonon relaxation process, which evidently necessitates a longer period of time to proceed [42]. Similarly, in Ar, the energy gap between the ground-state cis-FA and the first excited state of the ν₈ (C–H out of plane wagging) mode of the trans-FA is small enough for a relaxation process involving only one phonon (Debye frequency at 0 K: 93 cm⁻¹, that of Ne is 75 cm⁻¹) [64]. Therefore, the tunneling rate in Ar is expected to be relatively high [2]. In other matrices, such as in Xe, the energy mismatch is larger than the Debye frequency of that particular matrix (64 cm⁻¹ at 0 K) [64], thus requiring a multiphonon process for the relaxation and resulting in the slowdown of the tunneling process by orders of magnitude [2]. The formation of complexes between FA and Xe was also proposed to account for the slower tunneling [65].

The effect of matrix reorganization on the temperature dependence of the tunneling rate has also been investigated by theoretical works [54,55]. The influence of the different matrices on the tunneling rate can be explained by the different reorganization energies; the highest value was found for Ar and lower ones for Kr, and especially for Xe, which may explain the differences in the observed tunneling rates [55].

The N₂ matrix behaves in a unique way in which a dipole-quadrupole interaction between the –OH group of the guest and the host molecule is simulated by their 1:1 complex [53]; this complexation stabilizes the cis and trans conformers more than the transition state, thus effectively raising the barrier between the energy minima [6,56]. The relatively low Debye frequency of this matrix (69 cm⁻¹) [64] may also contribute to the inefficient relaxation, thus to the slowdown of the tunneling process.

The H atom tunneling process becomes faster in n-H₂ ($k_t^i$ = (6.8 ± 0.5) × 10⁻³ s⁻¹ at 3.1 K). Interestingly, the $t_{1/2}^i\left(cis\right)$ value of the former found in the literature is ca. 140 s at 4.2 K [48], which still shows a reasonable agreement with our experimental result. This tunneling rate lies between those of cis-FA in Ne and in Ar, possibly likely due to the intermediate polarizability (thus solvation capability, see above) of n-H₂ compared to the two noble gases [48]. Moreover, n-H₂ has a nonzero quadrupole moment allowing for a small dipole-quadrupole interaction [66].

The tunneling rate is even higher in p-H₂ ($k_t^i$ = (2.1 ± 0.3) × 10⁻¹ s⁻¹ at 3.1 K), which can be due to the fact that p-H₂ is considered a soft matrix even compared to n-H_2; therefore, relaxations may proceed virtually unhindered [58]. Furthermore, unlike n-H₂, p-H₂ has zero quadrupole moment, excluding the possibility of such interactions with the isolated sample molecule [66]. Lastly, similarly to Ne, the Debye-frequencies of solid n-H₂ and p-H₂ are expected to be relatively high owing to their low masses (e.g., the derived value for p-H₂ is 88 cm⁻¹) [67], whereas the energy mismatch between cis and a vibrationally-excited trans form may be small. All the three effects listed above may contribute to the fast tunneling also by providing a possibility for a one-phonon relaxation mechanism rather than a multiphonon one.

In contrast, $k_t^i$ of AA in Ar was found to be similar to that of FA in Ar or in n-H₂ and p-H₂ ((2.5 ± 0.3) × 10⁻² s⁻¹ at 8 K) and quite similar to the literature value ((2.23 ± 0.07) × 10⁻² s⁻¹ at 8 K) [9]. The higher rate found for AA compared to FA was explained by the presence of the methyl rotor providing efficient deactivation channels by its low-frequency vibrational modes [9]. It should be noted that $k_t^i$ was determined to be similar in Kr ((1.86 ± 0.02) × 10⁻² s⁻¹ at 8 K) to that in Ar [9] and a couple of hundred times slower in N₂ (≈3 × 10⁻⁵ s⁻¹ at 8 K) [6], according to what is expected based on the findings discussed above for FA. However, unlike in the case of FA, $k_t^i$ is some five times higher in Xe ((1.04 ± 0.05) × 10⁻¹ s⁻¹ at 8 K) than in Ar or Kr [9], implying that many different effects counterbalancing each other have to be taken into careful consideration [68]. Unfortunately, the tunneling rate of cis-AA becomes so high in the hydrogen matrices, that this conformer could not be observed and therefore $k_t^i$ could not be determined. Nevertheless, a rough estimate can be given by making a few assumptions, which is detailed in the next subsection.

It is also important to point out that the glycine conformer VI could not be detected in n-H₂ and p-H₂, either, also possibly due to its rapid tunneling back to conformer I. $t_{1/2}^i\left(cis\right)$ of VI in Ar (4 ± 1 s) is comparable to that of the cis-FA in p-H₂, and it is expected to have even higher values in n-H₂ and in p-H₂, most likely making the detection of VI in these matrix environments unfeasible.

3.3. Quantum Efficiency of the Processes

Before discussing the results, it must be highlighted that the spectral bandwidth of the laser light originating from our OPO device is larger than what was used previously in Ref. [5] (FWHM ≈ 5 cm⁻¹ vs. 0.1 cm⁻¹, respectively). Accordingly, the bandwidth of the laser beam is comparable to or even broader than that of the vibrational overtone band upon its excitation in the case of our setup. As a consequence, a considerable part of the incoming photons cannot be absorbed by the examined molecular system. Furthermore, the absorption efficiency of the photons having different wavelengths varies greatly for a particular process; thus, only an averaged, general ${\varphi }_i$ value can be accessed when using a pumping source with a relatively large spectral bandwidth. These considerations also imply that our setup is less sensitive to the excitation wavelength used as long as it is chosen to be close enough to the absorption band selected for excitation. In contrast to this, having a laser beam with an appropriately small bandwidth allows for the precise determination of ${\varphi }^i$ at a certain wavelength, for instance, exactly at the peak maximum. However, the latter is inherently more sensitive to the proper selection of the laser wavelength when exciting an absorption band. A wrongly wavelength-calibrated OPO may cause much more serious issues in this case.

While keeping this in mind, we chose to excite the 2ν(OH) mode of the samples to find out the ${\varphi }_i$ values of the trans-cis (for FA and AA) and the I→III (glycine) isomerization processes. The experiments with carboxylic acids were performed in Ar so that the quantum efficiencies of the processes made in this matrix environment may serve as references and thus can be directly compared with those obtained by earlier studies made on these systems [5,9]. For instance, the ${\varphi }^i$ of FA was found to be (2.0 ± 0.8) × 10⁻² (excitation wavelength 6929.9 cm⁻¹), which is roughly an order of magnitude lower than that of the literature value of 1.7 × 10⁻¹ [5]. In contrast, the ${\sigma }^i$ value of FA in Ar is similar to the one discussed in the literature [61]. The discrepancy in ${\varphi }^i$ may at least partially originate from the above-mentioned difference between the bandwidths of the OPO devices used; the excited overtone band of FA in Ar is about four times less broad (FWHM ≈ 1 cm⁻¹) than that of the laser light exiting our OPO device, resulting in the fact that only part of the incoming photons are actually absorbed by the vibrational overtone causing an apparently lower ${\varphi }^i$ for our setup, and indeed, the ${\varphi }^i$ of FA in Ar increases to (6 ± 3) × 10⁻² if a Gaussian laser spectrum is assumed and this effect is taken into account. Interestingly, if the other matrix site of the FA 2ν(OH) band at 6934.7 cm⁻¹ is excited, the ${\varphi }^i$ becomes larger equaling (8 ± 3) × 10⁻¹ (Table 1) being closer to the aforementioned literature value. However, this site was determined to have a ${\varphi }^i$ of 7 × 10⁻² previously [5], which agrees well with our data. The scaling of ${\varphi }^i$ taking the bandwidth into account is not necessary for the results of other experiments (e.g., FA in hydrogen matrices or AA in Ar), where the bandwidths of the excited overtone bands were significantly larger and comparable to that of the NIR laser beam, therefore the latter is not expected to have a significant influence on the apparent ${\varphi }^i$ value.

As far as the effect of different matrix environments is concerned, ${\varphi }^i$ increases marginally (possibly within experimental uncertainty) when using different noble gases according to their increasing polarizability (c.f. 2.2 × 10⁻², 2.6 × 10⁻², and 3.5 × 10⁻² for AA in Ar, Kr, and Xe, respectively) [9]. The relative ratio of the ${\varphi }^i$ values in various cryogenic environments are directly related to the $k_p^i$ values that can be observed in different matrices since the other two quantities that determine ${\varphi }^i$ (${\sigma }^i$ and $I$, equation (4)) have a small variation. Moreover, it can be concluded that the efficiency of the process does not change significantly when using n-H₂ instead of Ar (${\varphi }^i$ = (3 ± 1) × 10⁻²). Interestingly, a so-called ‘light-induced mobility’ effect was observed by a previous work in the FA-n-H₂ system upon NIR laser irradiation, i.e., FA dimer formation was observed when exciting the monomeric form [48]. This phenomenon was completely absent in our case, and the lack of it in our experiments may be explained by the lower temperature achieved by our setup (4.2 vs. 3.1 K), making our matrix more rigid than in the earlier work. In contrast to what is observed in n-H₂, ${\varphi }^i$ is evidently higher in p-H₂ ((1.2 ± 0.5) × 10⁻¹, Table 1) than in the other two matrices. This finding indicates that a simple change in the relative amount of the nuclear spin isomers in solid H₂ may result in a significant increase in ${\varphi }^i$ as well.

What can be summarized in general about AA is that the determined ${\varphi }^i$ in Ar ((3 ± 1) × 10⁻²) is similar to the previously obtained value (2.2 × 10⁻²) [9,61] and is similar to that of FA when exciting the 6929.9 cm⁻¹ band ((2.0 ± 0.8) × 10⁻²). Interestingly, earlier studies found that ${\varphi }^i$ of FA was almost an order of magnitude higher compared to that of AA, which was explained by the presence of the methyl rotor enabling more energy relaxation channels thus allowing for a more efficient de-excitation [9]. Nevertheless, based on the findings with FA, the rotamerization process is expected to become even more efficient in p-H₂. However, $N_t\left(cis\text{-}\mathrm{AA}\right)$ becomes so small in hydrogen matrices due to the expectedly very quick reverse (H atom tunneling) process, that all of its vibrational bands (including its most intense ν (C=O) stretching band) are below the IR detection limit (even during the laser excitation), thus unfortunately preventing us from determining $k_p^i$ in these environments. Nevertheless, a rough estimate for the low limit after a few assumptions is given below.

First, based on the findings of the experiments with FA, ${\varphi }^i$ in Ar and in n-H₂ are similar, whereas ${\sigma }^i$ in the latter is about one-third of that in Ar; therefore, the same can be assumed for AA as well. Accordingly, if we take the ${\varphi }^i$ and ${\sigma }^i$ values of the AA-Ar system, make a correction to the latter, and take into account that $I$ was 1.5 × 10¹⁷ cm⁻² s⁻¹, $k_p^i$ for the AA-n-H₂ can be estimated using Equation (4), which equals 5.1 × 10⁻³ s⁻¹. The alternative way can also be used to estimate $k_p^i$ (3.5 × 10⁻³ s⁻¹); for this ${\varphi }_{\mathrm{alternative}}^i$ (presumed to be identical to that of the AA-Ar system), $N_{t=0}\left(trans\right)$ (1.5 × 10¹⁶ cm⁻²), $A$ (0.0068) are needed to be known utilizing Equations (5) and (6). Then, Equation (7) can be used to obtain $k_t^i$ by knowing $N_{t=\infty }\left(trans\right)$ (1.5 × 10¹⁶ cm⁻² by assuming that only a negligible portion of trans-AA transforms upon irradiation), $N_{t=\infty }\left(cis\right)$ (<1.5 × 10¹³ cm⁻² based on the assumption that the ν(C=O) mode is below the detection limit; therefore, its integrated area is less than 0.001 cm⁻¹), and using the mean value of the two $k_p^i$ values obtained by the two alternative methods (roughly 4.3 × 10⁻³ s⁻¹). This translates into a $k_t^i$ value of >4.3 × 10⁰ s⁻¹ (equaling $t_{1/2}^i\left(cis\right)\approx$ 0.16 s). The same considerations can be applied to the AA-p-H₂ system, except that ${\varphi }^i$ is expected to be approximately 3.4 times higher than in Ar (as deduced from the results with FA, equaling 2.0 × 10⁻¹); the same correction factor for ${\varphi }_{\mathrm{alternative}}^i$ (1.1 × 10⁻¹) was found to be 4.4, whereas $N_{t=0}\left(trans\right)=N_{t=\infty }\left(trans\right)$, $N_{t=\infty }\left(cis\right)$, $A$, and $I$ are equal to 1.9 × 10¹⁶ cm⁻², < 1.5 × 10¹³ cm⁻², 00061, 1.6 × 10¹⁷ cm⁻² s⁻¹ and respectively. Consequently, the mean $k_p^i$ value is 5.3 × 10⁻³ s⁻¹ yielding a $k_t^i$ value of > 6.7 × 10⁰ s⁻¹ (i.e., $t_{1/2}^i\left(cis\right)\approx$ 0.10 s).

Regarding glycine, we did not expect to see the rotamerization of I→VI involving the H atom of the –OH group of the molecule in hydrogen matrices owing to the expected extremely rapid back conversion via tunneling. Instead, the emphasis was put on the laser-induced conversion of I→III, resulting in the rotation of the whole –COOH moiety. The ${\varphi }^i$ of the I→III conversion shows a weaker dependence on the matrix than that of the FA, and it ranges between 5 × 10⁻³ (in p-H₂) and 3 × 10⁻² (in Ar). Importantly, these values are more than an order of magnitude higher than that of the I→VI process (determined to be 8 × 10⁻⁴ in Ar), according to what is expected [25]. Even though the value obtained in the p-H₂ matrix is some six times lower, it could be at least partially explained by the ${\sigma }^i$ higher than in Ar or in n-H₂ matrices, which is expected to be some 3–4 times lower in hydrogen matrix compared to Ar based on the results with FA. Consequently, ${\sigma }^i$ in the p-H₂ is probably overestimated, which causes the discrepancy between the results. The seemingly more or less independent nature of the I→III conversion on the chosen media is somewhat unexpected since the rotation of the –COOH group should be more hindered in rigid (Ar, n-H₂) matrices than in a soft matrix (p-H₂). In order to explain this finding, it could be speculated that in p-H₂, a fast forward-backward I⇌VI conversion takes place in parallel with the main I→III rotamerization, thus decreasing the apparent efficiency of the latter process. This hypothesis could be verified by a future study on model systems, where the rotation of the –OH group is hindered.

4. Conclusions

FA, AA, and glycine samples were investigated in Ar, n-H₂, and p-H₂ matrices. The tunneling rates were determined, and the one obtained for FA in Ar is in good agreement with the literature value ((2.6 ± 0.5) × 10⁻³ s⁻¹ vs. 2.3 × 10⁻³ s⁻¹) [2,5]. The half-life of cis-FA in n-H₂ is still not particularly different from the one found in the literature (102 ± 8 vs. 140 s) [48]. Most importantly, $k_t^i$ of cis-FA has been determined in p-H₂ for the first time, and it was found to be (2.1 ± 0.3) × 10⁻¹ s⁻¹, i.e., almost two orders of magnitude higher than that in Ar or even in n-H₂. With regard to AA, its $k_t^i$ in Ar was determined to be (2.5 ± 0.3) × 10⁻² s⁻¹ which, similarly to cis-FA, compares very well with the literature value ((2.23 ± 0.07) × 10⁻² s⁻¹) [9]. Unfortunately, due to the extremely rapid back conversion of cis-AA to its trans form via H atom tunneling, $k_t^i$ could not be determined in hydrogen matrix although they are expected to be even higher than in Ar matrix and a low limit be given (>4.3 × 10⁻⁰ s⁻¹ and >6.7 × 10⁻⁰ s⁻¹ in n-H₂ and in p-H₂, respectively). These values signify a cis-AA half-life in these media in the order of a few tenths of seconds. No tunneling between the conformers could be detected in the experiments carried out with glycine.

As far as the quantum efficiencies of the NIR laser-induced trans to cis conversion are concerned, the ${\varphi }^i$ value for FA in Ar was obtained to be (2.0 ± 0.8) × 10⁻² (i.e., 2%) when pumping the trans-FA overtone band 6929.9 cm⁻¹. This value is remarkably different from earlier results when the same pumping wavelength was used to generate the cis form (1.7 × 10⁻¹) [5]. However, the bandwidth of the laser beam was quite different in the two cases: our result shows more like an averaged value over the whole absorption peak, whereas the smaller bandwidth used in the earlier work allowed for the determination at a very precise wavelength (possibly nearby the maximum of the excited NIR band). Nonetheless, ${\varphi }^i$ was also calculated for another NIR overtone band of cis-AA at 6934.7 cm⁻¹ ((8 ± 3) × 10⁻²), which shows a much better agreement with the literature value of 7 × 10⁻² [5]. Regarding the behavior of this process in hydrogen matrices, ${\varphi }^i$ does not differ much in n-H₂ (3 ± 1) × 10⁻² from that taken in Ar, however, the process proceeds more efficiently in p-H₂ (1.2 ± 0.5) × 10⁻¹. For AA, owing to the rapid tunneling in the hydrogen matrices, only ${\varphi }^i$ in Ar could be determined (3 ± 1) × 10⁻², which is within error limits with the one found in the literature (2.2 × 10⁻²) [9,61]. As for glycine, the ${\varphi }^i$ values for the I→VI conversion were not determined, the ${\varphi }^i$ values for the I→III conversion in the three environment (Ar, n-H₂, and p-H₂) are (3 ± 1) × 10⁻², (1.7 ± 0.7) × 10⁻², and (5 ± 3) × 10⁻³, respectively. This result contradicts the intuition, where one would expect a more efficient process in the case of the softer p-H₂ matrix. The discrepancy could be resolved by assuming a fast forward-backward I⇌VI conversion occurring simultaneously with the main I→III conversion, which would decrease the observed efficiency of the latter process.

The present results imply that in the case of spontaneous conformational change in solid p-H_2, the matrix effects are diminished as compared to rigid hosts. This offers an excellent possibility for the comparison of the theoretical models with experimentally measured tunneling rates. The results also suggest that the quantum efficiencies of some (N)IR-light-induced conformational changes are larger in solid p-H₂ than in rigid hosts. The present study raises some new questions as well. Can conformational changes with large site rearrangements be induced by NIR laser radiation in p-H₂? How does the shift from a rigid to a soft matrix affect the ratio of the quantum efficiencies of local and remote conformational changes? We plan to address these and similar questions in subsequent studies.