Design and Modelling of an Induction Heating Coil to Investigate the Thermal Response of Magnetic Nanoparticles for Hyperthermia Applications
Abstract
1. Introduction
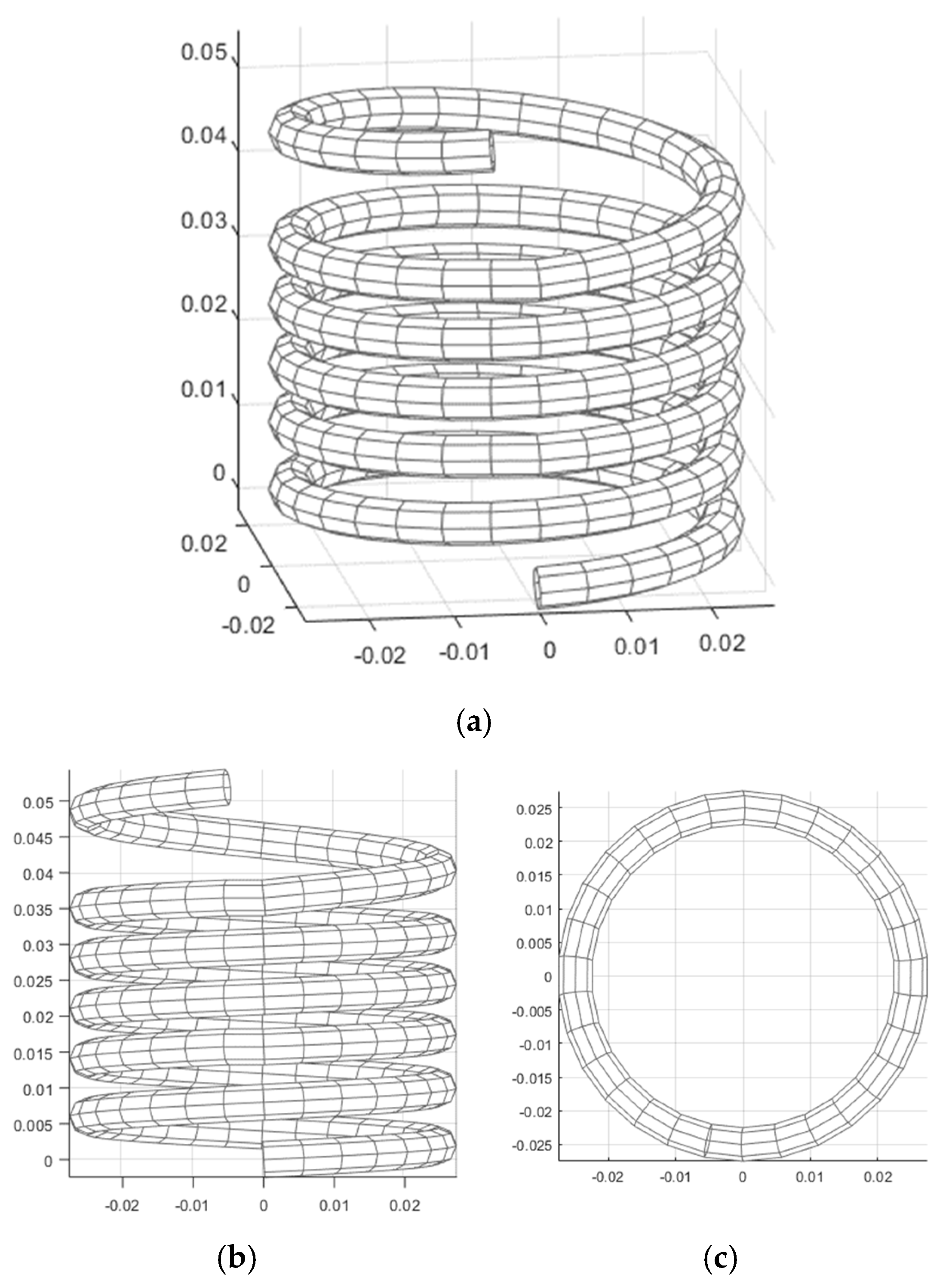
2. Induction Coil Circuit Design
3. Methods and Results
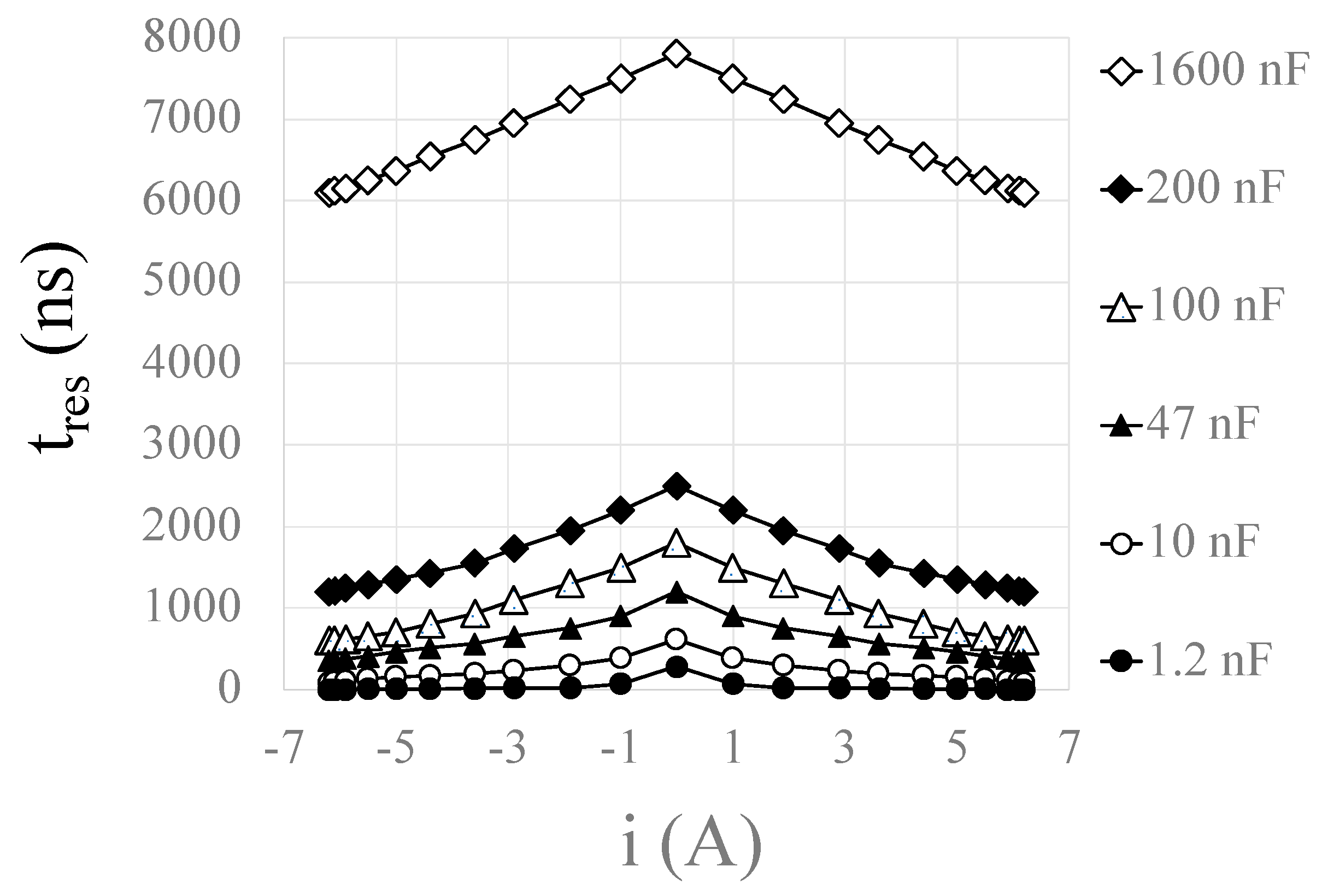
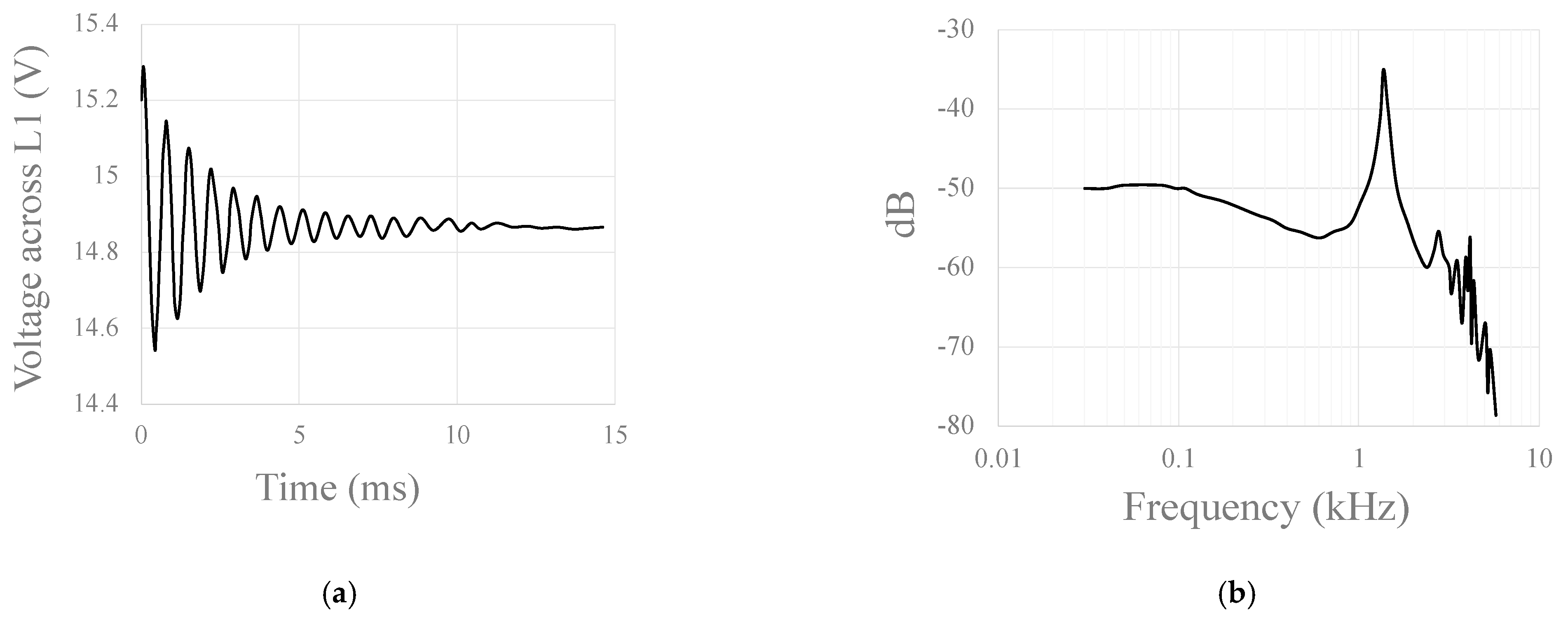
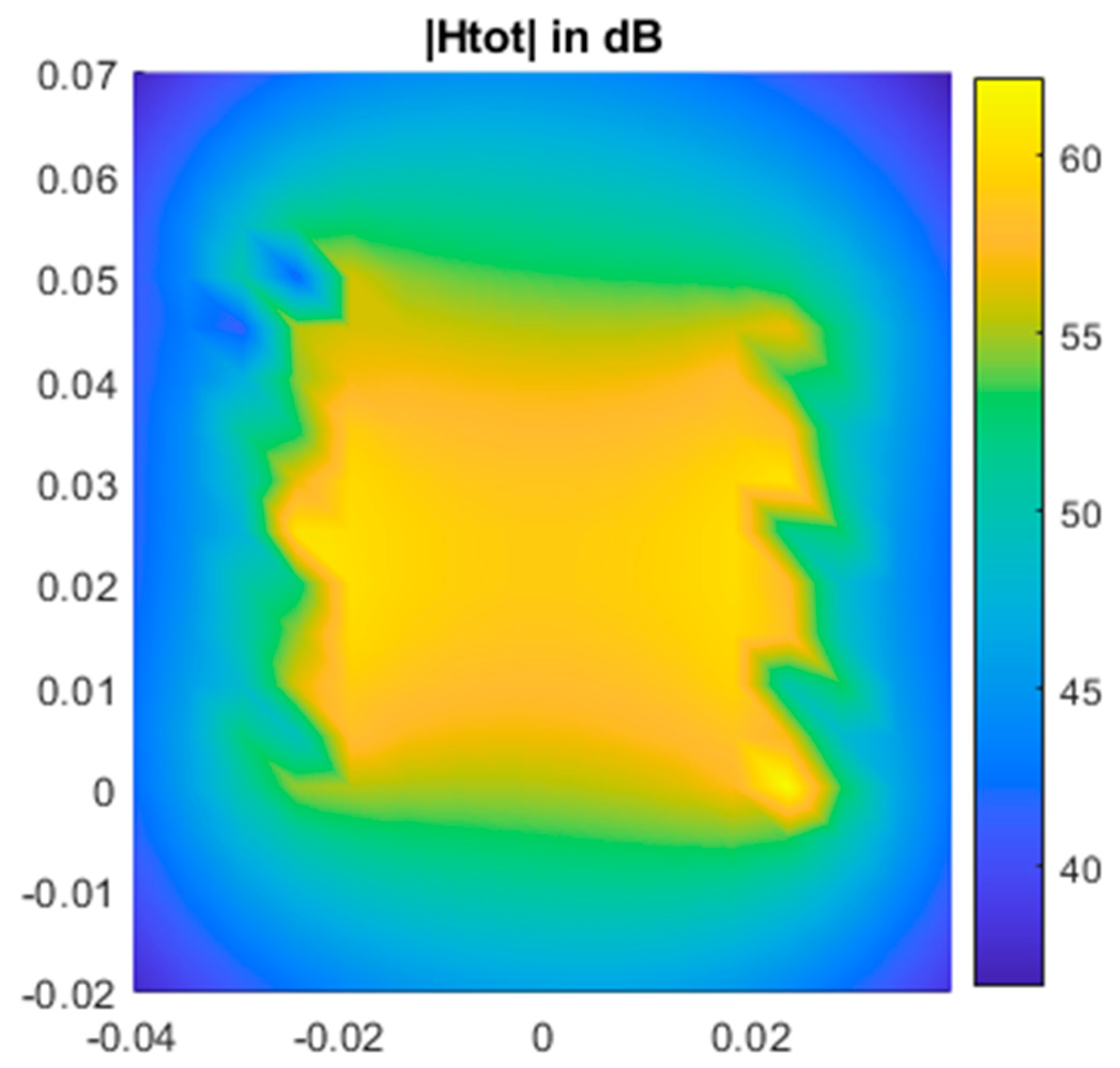
3.1. MATLAB and LTspice Modelling of Circuit
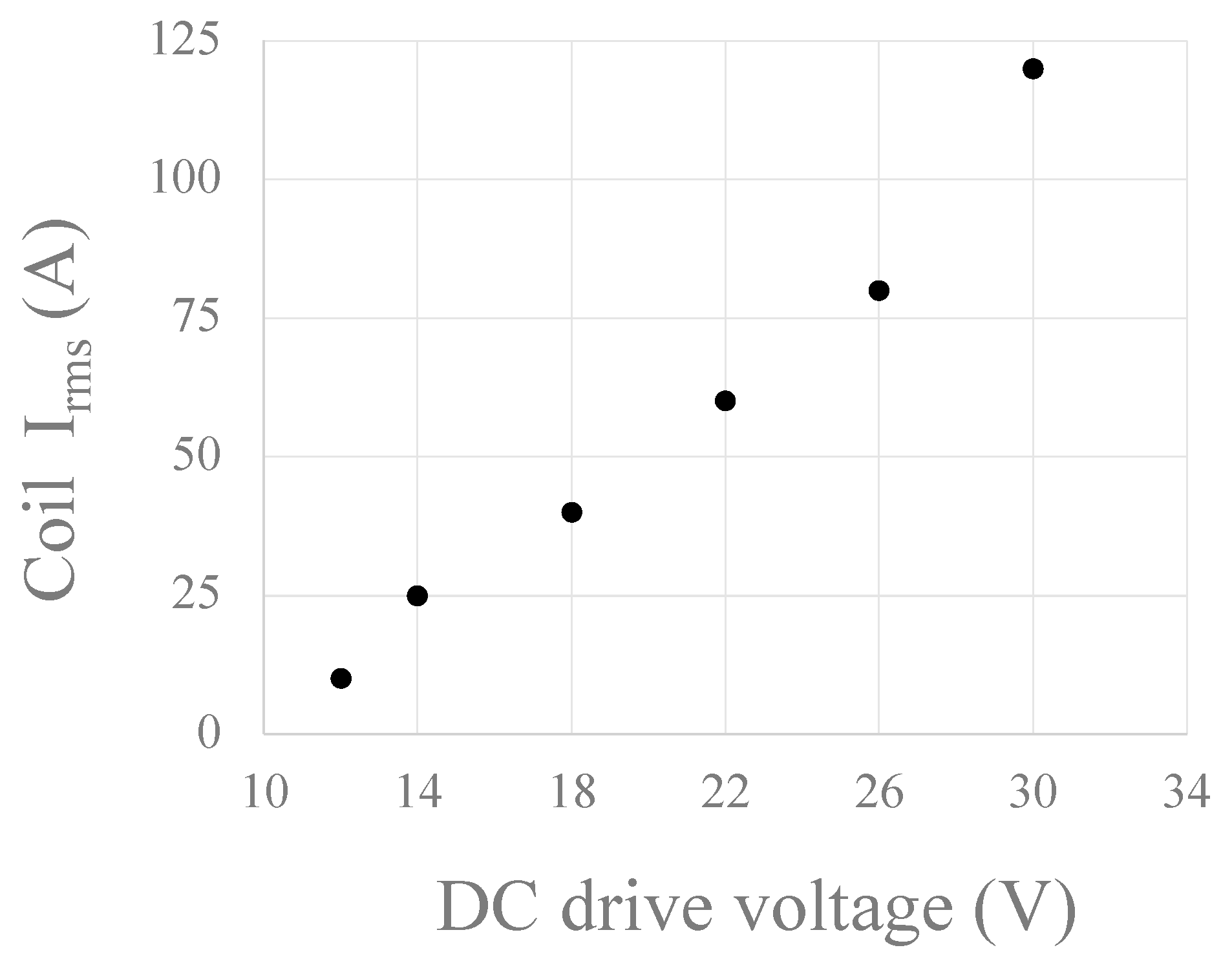
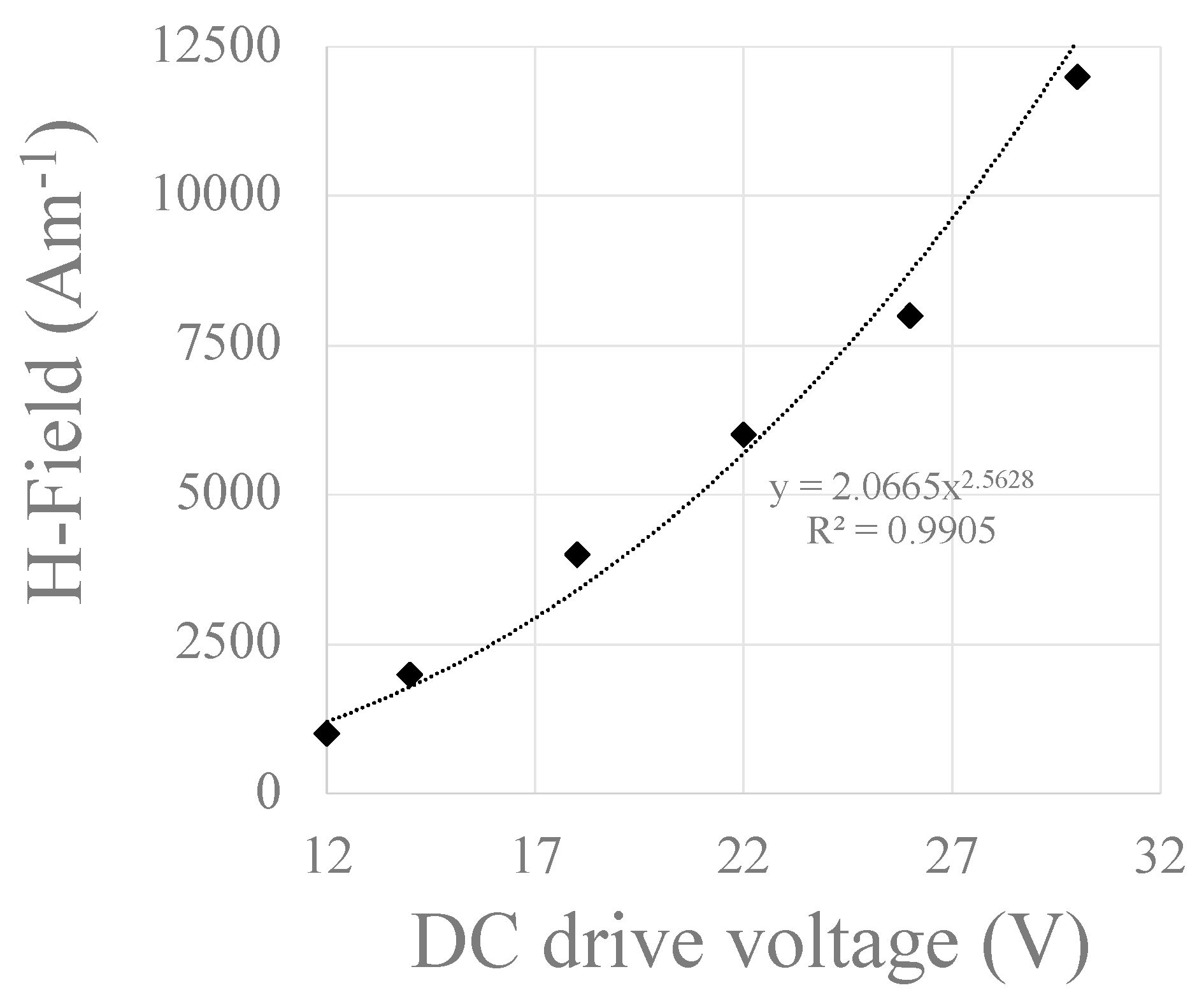
3.2. Testing the Circuit with Copper Coil Attached
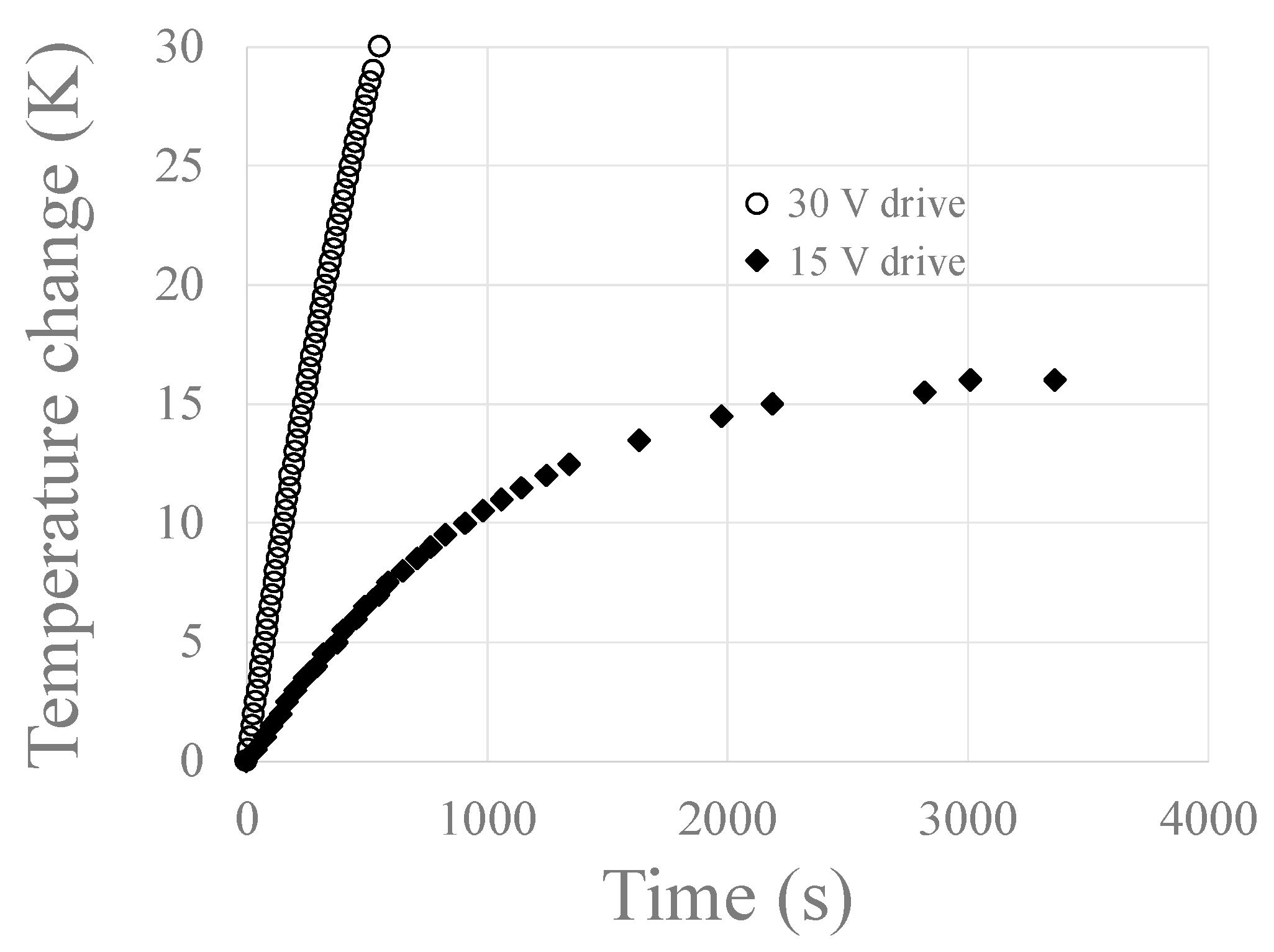
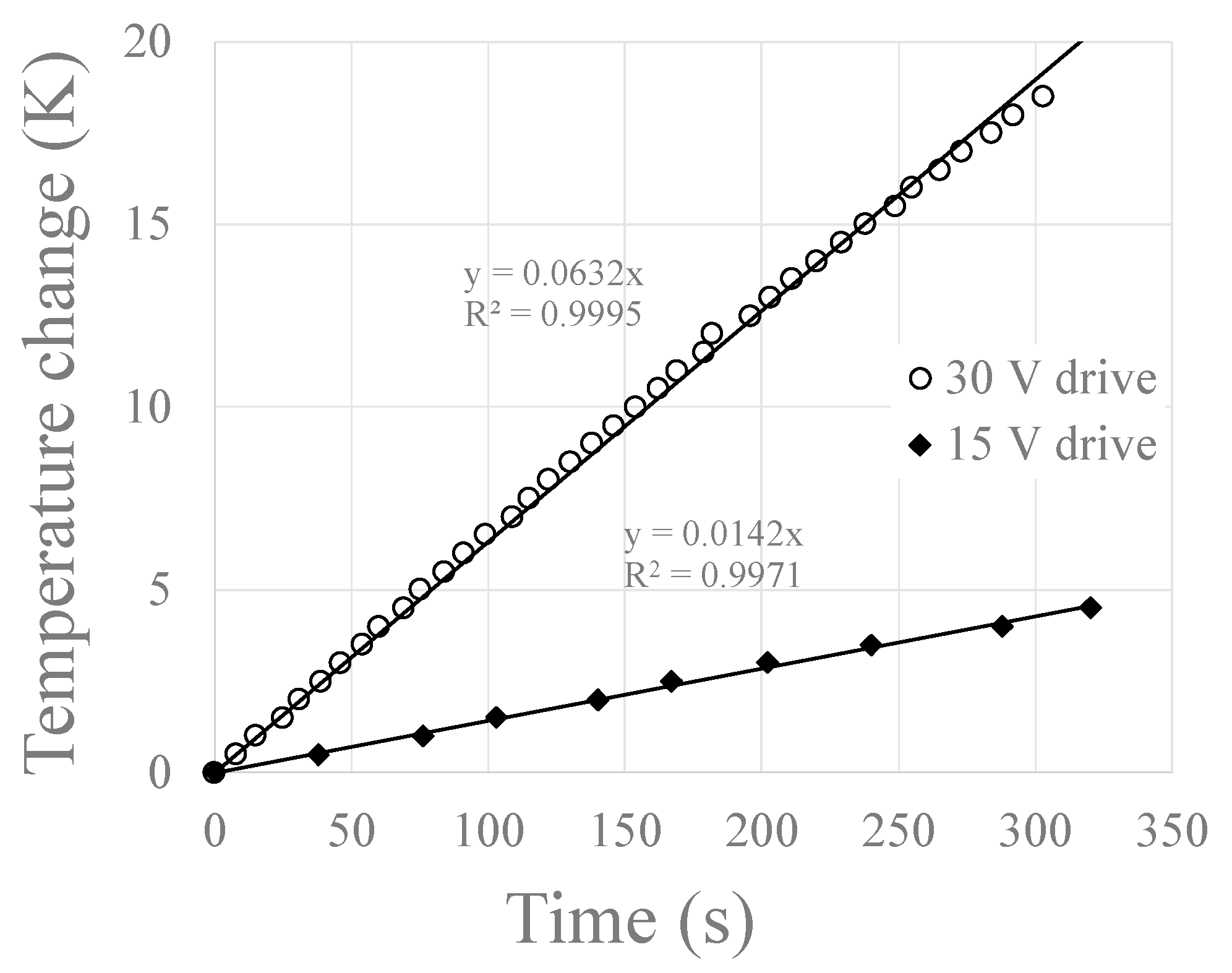
3.3. Using the IHC to Heat Magnet Nanoparticles
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ferlay, J.; Soerjomataram, I.; Dikshit, R.; Eser, S.; Mathers, C.; Rebelo, M.; Parkin, D.M.; Forman, D.; Bray, F. Cancer incidence and mortality worldwide: Sources, methods and major patterns in GLOBOCAN 2012. Int. J. Cancer 2015, 136, E359–E386. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, A.S.; Ormiston-Smith, N.; Sasieni, P.D. Trends in the lifetime risk of developing cancer in Great Britain: Comparison of risk for those born from 1930 to 1960. Br. J. Cancer 2015, 112, 943–947. [Google Scholar] [CrossRef] [PubMed]
- American Cancer Society. Cancer Facts & Figures 2023; American Cancer Society: Atlanta, GA, USA, 2023. [Google Scholar]
- Raouf, I.; Khalid, S.; Khan, A.; Lee, J.; Kim, H.S.; Kim, M.H. A review on numerical modeling for magnetic nanoparticle hyperthermia: Progress and challenges. J. Therm. Biol. 2020, 91, 102644. [Google Scholar] [CrossRef] [PubMed]
- Maier-Hauff, K.; Ulrich, F.; Nestler, D.; Niehoff, H.; Wust, P.; Thiesen, B.; Orawa, H.; Budach, V.; Jordan, A. Efficacy and safety of intratumoral thermotherapy using magnetic iron-oxide nanoparticles combined with external beam radiotherapy on patients with recurrent glioblastoma multiforme. J. Neuro-Oncol. 2011, 103, 317–324. [Google Scholar] [CrossRef]
- Study of Focal Ablation of the Prostate with NanoTherm® Therapy System for Intermediate-Risk Prostate Cancer. ClinicalTrials.gov Identifier: NCT05010759, Start Date 30 November 2021, Completion Date October 2025. Available online: https://classic.clinicaltrials.gov/ct2/show/NCT05010759 (accessed on 15 December 2023).
- Kraus, S.; Tal, C.; Shalev, B.; Eltanani, M.; Rukenstein, P.; Arbib, S.; Eck, M.; Khandadash, R.; Atar, S.; Cyjon, A.; et al. Initial safety and feasibility results from a first-in-human clinical trial evaluating a novel magnetic hyperthermia approach for the treatment of metastatic solid tumors. Cancer Res. 2023, 83 (Suppl. 8), CT170. [Google Scholar] [CrossRef]
- Rouni, M.A.; Shalev, B.; Tsanidis, G.; Markakis, I.; Kraus, S.; Rukenstein, P.; Suchi, D.; Shalev, O.; Samaras, T. A Validated Methodological Approach to Prove the Safety of Clinical Electromagnetic Induction Systems in Magnetic Hyperthermia. Cancers 2024, 16, 621. [Google Scholar] [CrossRef] [PubMed]
- Salloum, M.; Ma, R.; Zhu, L. An in-vivo experimental study of temperature elevations in animal tissue during magnetic nanoparticle hyperthermia. Int. J. Hyperth. 2008, 24, 589–601. [Google Scholar] [CrossRef] [PubMed]
- Caro, C.; Guzzi, C.; Moral-Sánchez, I.; Urbano-Gámez, J.D.; Beltrán, A.M.; García-Martín, M.L. Smart Design of ZnFe and ZnFe@Fe Nanoparticles for MRI-Tracked Magnetic Hyperthermia Therapy: Challenging Classical Theories of Nanoparticles Growth and Nanomagnetism. Adv. Healthc. Mater. 2024, e2304044. [Google Scholar] [CrossRef] [PubMed]
- Paez-Muñoz, J.M.; Gámez, F.; Fernández-Afonso, Y.; Gallardo, R.; Leal, M.P.; Gutiérrez, L.; de la Fuente, J.M.; Caro, C.; García-Martín, M.L. Optimization of iron oxide nanoparticles for MRI-guided magnetic hyperthermia tumor therapy: Reassessing the role of shape in their magnetocaloric effect. J. Mater. Chem. B 2023, 11, 11110–11120. [Google Scholar] [CrossRef]
- Islam, W.; Niidome, T.; Sawa, T. Enhanced Permeability and Retention Effect as a Ubiquitous and Epoch-Making Phenomenon for the Selective Drug Targeting of Solid Tumors. J. Pers. Med. 2022, 12, 1964. [Google Scholar] [CrossRef]
- Bromma, K.; Banister, A.; Kowalewski, A.; Cicon, L.; Chithrani, D.B. Elucidating the fate of nanoparticles among key cell components of the tumor microenvironment for promoting cancer nanotechnology. Cancer Nanotechnol. 2020, 11, 8. [Google Scholar] [CrossRef]
- Wathoni, N.; Puluhulawa, L.E.; Joni, I.M.; Muchtaridi, M.; Mohammed, A.F.A.; Elamin, K.M.; Milanda, T.; Gozali, D. Monoclonal antibody as a targeting mediator for nanoparticle targeted delivery system for lung cancer. Drug Deliv. 2022, 29, 2959–2970. [Google Scholar] [CrossRef]
- Kamaly, N.; Xiao, Z.; Valencia, P.M.; Radovic-Moreno, A.F.; Farokhzad, O.C. Targeted polymeric therapeutic nanoparticles: Design, development and clinical translation. Chem. Soc. Rev. 2012, 41, 2971–3010. [Google Scholar] [CrossRef]
- Attia, M.F.; Anton, N.; Wallyn, J.; Omran, Z.; Vandamme, T.F. An overview of active and passive targeting strategies to improve the nanocarriers efficiency to tumour sites. J. Pharm. Pharmacol. 2019, 71, 1185–1198. [Google Scholar] [CrossRef]
- Oroojalian, F.; Beygi, M.; Baradaran, B.; Mokhtarzadeh, A.; Shahbazi, M.A. Immune Cell Membrane-Coated Biomimetic Nanoparticles for Targeted Cancer Therapy. Small 2021, 17, 2006484. [Google Scholar] [CrossRef]
- Gupta, D.; Roy, P.; Sharma, R.; Kasana, R.; Rathore, P.; Gupta, T.K. Recent nanotheranostic approaches in cancer research. Clin. Exp. Med. 2024, 24, 8. [Google Scholar] [CrossRef]
- Fernandes, S.; Fernandez, T.; Metze, S.; Balakrishnan, P.B.; Mai, B.T.; Conteh, J.; De Mei, C.; Turdo, A.; Di Franco, S.; Stassi, G.; et al. Magnetic Nanoparticle-Based Hyperthermia Mediates Drug Delivery and Impairs the Tumorigenic Capacity of Quiescent Colorectal Cancer Stem Cells. ACS Appl. Mater. Interfaces 2021, 13, 15959–15972. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Zhu, W.; Li, G.; Ma, X.; Zhang, Y.; Chen, S.; Tiwari, S.; Shi, K.; Zhang, S.; et al. Comprehensive understanding of magnetic hyperthermia for improving antitumor therapeutic efficacy. Theranostics 2020, 10, 3793–3815. [Google Scholar] [CrossRef]
- Farzanegan, Z.; Tahmasbi, M. Evaluating the applications and effectiveness of magnetic nanoparticle-based hyperthermia for cancer treatment: A systematic review. Appl. Radiat. Isot. 2023, 198, 110873. [Google Scholar] [CrossRef] [PubMed]
- Andreu, I.; Natividad, E. Accuracy of available methods for quantifying the heat power generation of nanoparticles for magnetic hyperthermia. Int. J. Hyperth. 2013, 29, 739–751. [Google Scholar] [CrossRef]
- Lee, J.-H.; Kim, B.; Kim, Y.; Kim, S.-K. Ultra-high rate of temperature increment from superparamagnetic nanoparticles for highly efficient hyperthermia. Sci. Rep. 2021, 11, 4969. [Google Scholar] [CrossRef] [PubMed]
- Jiang, P.S.; Drake, P.; Cho, H.J.; Kao, C.H.; Lee, K.F.; Kuo, C.H.; Lin, X.Z.; Lin, Y.J. Tailored nanoparticles for tumour therapy. J. Nanosci. Nanotechnol. 2012, 12, 5076–5081. [Google Scholar] [CrossRef] [PubMed]
- Hergt, R.; Andra, W.; D’Ambly, C.; Hilger, I.; Kaiser, W.; Richter, U.; Schmidt, H.-G. Physical limits of hyperthermia using magnetite fine particles. IEEE Trans. Magn. 1998, 34, 3745–3754. [Google Scholar] [CrossRef]
- Etheridge, M.L. Understanding the Benefits and Limitations of Magnetic Nanoparticle Heating for Improved Applications in Cancer Hyperthermia and Biomaterial Cryopreservation. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2013. Available online: https://hdl.handle.net/11299/171091 (accessed on 27 July 2021).
- Mohan, N.; Undeland, T.M.; Robbins, W.P. Power Electronics: Converters, Applications, and Design, 3rd ed.; Wiley: Hoboken, NJ, USA, 2002; ISBN 13 978-0471226932. [Google Scholar]
- Ashique, R.H.; Salam, Z.; Maruf, H.; Shihavuddin, A.; Islam, T.; Rahman, F.; Kotsampopoulos, P.; Fayek, H.H. A Comparative Analysis of Soft Switching Techniques in Reducing the Energy Loss and Improving the Soft Switching Range in Power Converters. Electronics 2022, 11, 1062. [Google Scholar] [CrossRef]
- Cho, J.-G.; Baek, J.-W.; Jeong, C.-Y.; Rim, G.-H. Novel zero-voltage and zero-current-switching full-bridge PWM converter using a simple auxiliary circuit. IEEE Trans. Ind. Appl. 1999, 35, 15–20. [Google Scholar] [CrossRef]
- Kwon, Y.-S.; Yoo, S.-B.; Hyun, D.-S. Half-bridge series resonant inverter for induction heating applications with load-adaptive PFM control strategy. In Proceedings of the APEC ′99. Fourteenth Annual Applied Power Electronics Conference and Exposition. 1999 Conference Proceedings (Cat. No.99CH36285), Dallas, TX, USA, 14–18 March 1999; Volume 1, pp. 575–581. [Google Scholar] [CrossRef]
- Tong, S.; Quinto, C.A.; Zhang, L.; Mohindra, P.; Bao, G. Size-Dependent Heating of Magnetic Iron Oxide Nanoparticles. ACS Nano 2017, 11, 6808–6816. [Google Scholar] [CrossRef] [PubMed]
- Attar, M.M.; Amanpour, S.; Haghpanahi, M.; Haddadi, M.; Rezaei, G.; Muhammadnejad, S.; HajiAkhoundzadeh, M.; Barati, T.; Sadeghi, F.; Javadi, S. Thermal analysis of magnetic nanoparticle in alternating magnetic field on human HCT-116 colon cancer cell line. Int. J. Hyperth. 2016, 32, 858–867. [Google Scholar] [CrossRef] [PubMed]
- Blinov, A.; Korkh, O.; Chub, A.; Vinnikov, D.; Peftitsis, D.; Norrga, S.; Galkin, I. High Gain DC–AC High-Frequency Link Inverter with Improved Quasi-Resonant Modulation. IEEE Trans. Ind. Electron. 2021, 69, 1465–1476. [Google Scholar] [CrossRef]
- Algaddafi, A.E. Designing and Building a Novel Magnetic Heating System to Investigate the Dependence of the Magnetic System on the Optical Emission from Nanoparticles. Ph.D. Thesis, University of Bradford, Bradford, UK, 2022. [Google Scholar]
- Maxwell, J.C. A Treatise on Electricity and Magnetism; Oxford University Press: Oxford, UK, 1873. [Google Scholar]
- Raff, S.J. Ampere’s Law and the Vector Potential. Am. J. Phys. 1958, 26, 454–460. [Google Scholar] [CrossRef]
- Atkinson, W.J.; Brezovich, I.A.; Chakraborty, D.P. Usable frequencies in hyperthermia with thermal seeds. IEEE Trans. Biomed. Eng. 1984, BME-31, 70–75. [Google Scholar] [CrossRef]
- Hergt, R.; Dutz, S. Magnetic particle hyperthermia—Biophysical limitations of a visionary tumour therapy. J. Magn. Magn. Mater. 2007, 311, 187–192. [Google Scholar] [CrossRef]
- Drake, P.; Cho, H.-J.; Shih, P.-S.; Kao, C.-H.; Lee, K.-F.; Kuo, C.-H.; Lin, X.-Z.; Lin, Y.-J. Gd-doped iron-oxide nanoparticles for tumour therapy via magnetic field hyperthermia. J. Mater. Chem. 2007, 17, 4914–4918. [Google Scholar] [CrossRef]
- Le Fèvre, R.; Durand-Dubief, M.; Chebbi, I.; Mandawala, C.; Lagroix, F.; Valet, J.-P.; Idbaih, A.; Adam, C.; Delattre, J.-Y.; Schmitt, C.; et al. Enhanced antitumor efficacy of biocompatible magnetosomes for the magnetic hyperthermia treatment of glioblastoma. Theranostics 2017, 7, 4618–4631. [Google Scholar] [CrossRef] [PubMed]
- Pucci, C.; Degl’Innocenti, A.; Gümüş, M.B.; Ciofani, G. Superparamagnetic iron oxide nanoparticles for magnetic hyperthermia: Recent advancements, molecular effects, and future directions in the omics era. Biomater. Sci. 2022, 10, 2103–2121. [Google Scholar] [CrossRef] [PubMed]
- Nain, S.; Kumar, N.; Chudasama, B.; Avti, P.K. The SLP estimation of the nanoparticle systems using size-dependent magnetic properties for the magnetic hyperthermia therapy. J. Magn. Magn. Mater. 2023, 565, 170219. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drake, P.; Algaddafi, A.; Swift, T.; Abd-Alhameed, R.A. Design and Modelling of an Induction Heating Coil to Investigate the Thermal Response of Magnetic Nanoparticles for Hyperthermia Applications. BioMedInformatics 2024, 4, 1006-1018. https://doi.org/10.3390/biomedinformatics4020056
Drake P, Algaddafi A, Swift T, Abd-Alhameed RA. Design and Modelling of an Induction Heating Coil to Investigate the Thermal Response of Magnetic Nanoparticles for Hyperthermia Applications. BioMedInformatics. 2024; 4(2):1006-1018. https://doi.org/10.3390/biomedinformatics4020056
Chicago/Turabian StyleDrake, Philip, Ali Algaddafi, Thomas Swift, and Raed A. Abd-Alhameed. 2024. "Design and Modelling of an Induction Heating Coil to Investigate the Thermal Response of Magnetic Nanoparticles for Hyperthermia Applications" BioMedInformatics 4, no. 2: 1006-1018. https://doi.org/10.3390/biomedinformatics4020056
APA StyleDrake, P., Algaddafi, A., Swift, T., & Abd-Alhameed, R. A. (2024). Design and Modelling of an Induction Heating Coil to Investigate the Thermal Response of Magnetic Nanoparticles for Hyperthermia Applications. BioMedInformatics, 4(2), 1006-1018. https://doi.org/10.3390/biomedinformatics4020056








