Analyzing Patterns of Service Utilization Using Graph Topology to Understand the Dynamic of the Engagement of Patients with Complex Problems with Health Services
Abstract
1. Introduction
1.1. Engagement of Patients with the Healthcare Service System
1.2. Graph/Network Modeling and Analysis
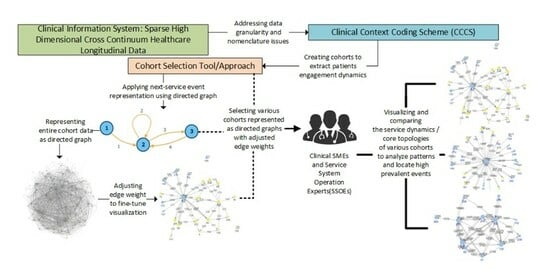
2. Objectives
- Can patient journeys be recorded as sequences of service encounters, using a directed graph that can then be used to identify high-prevalence sequences within and across persons?
- With the proposed methodology, to what extent can one cut across the complexity of a cross-continuum service structure to capture the dynamics of the journey of patients with complex issues that clearly portray their engagement with the service system, to help to locate potential operational problems?
3. Methods
3.1. Addressing Data Granularity Issues
3.2. Representing Patient Access to Healthcare Service Systems as a Graph
4. Analysis and Results
4.1. Cohort Selection, Analysis Setup, and Visualization Adjustment
4.2. Cohort Topologies’ Comparison
4.3. Representing a Cohort Topology Using Transition Probability
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Yu, W.; Ravelo, A.; Wagner, T.H.; Phibbs, C.S.; Bhandari, A.; Chen, S.; Barnett, P.G. Prevalence and costs of chronic conditions in the VA health care system. Med. Care Res. Rev. 2003, 60, 146S–167S. [Google Scholar] [CrossRef] [PubMed]
- Hoffman, C.; Rice, D.; Sung, H.-Y. Persons with chronic conditions: Their prevalence and costs. JAMA 1996, 276, 1473–1479. [Google Scholar] [CrossRef] [PubMed]
- Dalgleish, T.; Black, M.; Johnston, D.; Bevan, A. Transdiagnostic approaches to mental health problems: Current status and future directions. J. Consult. Clin. Psychol. 2020, 88, 179–195. [Google Scholar] [CrossRef] [PubMed]
- Mirolla, M. The Cost of Chronic Disease in Canada; GPI Atlantic Glen Haven: Glen Haven, NS, Canada, 2004. [Google Scholar]
- Anderson, G.F. Chronic Care: Making the Case for Ongoing Care; Robert Wood Johnson Foundation: Princeton, NJ, USA, 2010. [Google Scholar]
- Charlson, M.; Charlson, R.E.; Briggs, W.; Hollenberg, J. Can disease management target patients most likely to generate high costs? The impact of comorbidity. J. Gen. Intern. Med. 2007, 22, 464–469. [Google Scholar] [CrossRef] [PubMed]
- Thorpe, K.E.; Ogden, L.L.; Galactionova, K. Chronic conditions account for rise in Medicare spending from 1987 to 2006. Health Aff. 2010, 29, 718–724. [Google Scholar] [CrossRef] [PubMed]
- Bambi, J.; Santoso, Y.; Sadri, H.; Moselle, K.; Rudnick, A.; Robertson, S.; Chang, E.; Kuo, A.; Howie, J.; Dong, G.Y.; et al. A Methodological Approach to Extracting Patterns of Service Utilization from a Cross-Continuum High Dimensional Healthcare Dataset to Support Care Delivery Optimization for Patients with Complex Problems. BioMedInformatics 2024, 4, 946–965. [Google Scholar] [CrossRef]
- Bambi, J.; Santoso, Y.; Sadri, H.; Moselle, K.; Howie, J.; Robertson, S.; Rudnick, A.; Chang, E.; Eliott, L.; Kuo, A. Approaches to Generating Patterns of Service Utilization for Patients with Complex Conditions: Graph Community Detection vs. Natural Language Processing Clustering. 2024. [Google Scholar]
- Prasse, B.; Van Mieghem, P. Predicting network dynamics without requiring the knowledge of the interaction graph. Proc. Natl. Acad. Sci. USA 2022, 119, e2205517119. [Google Scholar] [CrossRef] [PubMed]
- Zhong, C.; Arisona, S.M.; Huang, X.; Batty, M.; Schmitt, G. Detecting the dynamics of urban structure through spatial network analysis. Int. J. Geogr. Inf. Sci. 2014, 28, 2178–2199. [Google Scholar] [CrossRef]
- Barabási, A.-L.; Loscalzo, J.; Silverman, E.K. Network Medicine: Complex Systems in Human Disease and Therapeutics; Harvard University Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Ahmedt-Aristizabal, D.; Armin, M.A.; Denman, S.; Fookes, C.; Petersson, L. Graph-based deep learning for medical diagnosis and analysis: Past, present and future. Sensors 2021, 21, 4758. [Google Scholar] [CrossRef] [PubMed]
- Wysocki, K.; Ritter, L. Diseasome. Annu. Rev. Nurs. Res. 2011, 29, 55–72. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Wang, Y.; Wang, Y.; Zhao, E.; Yuan, Y. Leveraging graph-based hierarchical medical entity embedding for healthcare applications. Sci. Rep. 2021, 11, 5858. [Google Scholar] [CrossRef] [PubMed]
- Panteli, D.; Legido-Quigley, H.; Reichebner, C.; Ollenschläger, G.; Schäfer, C.; Busse, R. Clinical practice guidelines as a quality strategy. Improv. Healthc. Qual. Eur. 2019, 233. [Google Scholar] [CrossRef]
- Ellrodt, G.; Cook, D.J.; Lee, J.; Cho, M.; Hunt, D.; Weingarten, S. Evidence-based disease management. JAMA 1997, 278, 1687–1692. [Google Scholar] [CrossRef] [PubMed]
- Aggarwal, N.; Ahmed, M.; Basu, S.; Curtin, J.J.; Evans, B.J.; Matheny, M.E.; Nundy, S.; Sendak, M.P.; Shachar, C.; Shah, R.U. Advancing artificial intelligence in health settings outside the hospital and clinic. NAM Perspect. 2020, 2020. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Yang, D.; Yin, X. Patient similarity via joint embeddings of medical knowledge graph and medical entity descriptions. IEEE Access 2020, 8, 156663–156676. [Google Scholar] [CrossRef]
- El Emam, K.; Arbuckle, L. Anonymizing Health Data: Case Studies and Methods to Get You Started; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2013. [Google Scholar]
- Bambauer, J.; Muralidhar, K.; Sarathy, R. Fool’s gold: An illustrated critique of differential privacy. Vand. J. Ent. Tech. L. 2013, 16, 701. [Google Scholar]
- Xu, C.; Ren, J.; Zhang, Y.; Qin, Z.; Ren, K. DPPro: Differentially Private High-Dimensional Data Release via Random Projection. IEEE Trans. Inf. Forensics Secur. 2017, 12, 3081–3093. [Google Scholar] [CrossRef]
- Alhanani, R.A.; Abouchabaka, J. An overview of different techniques and algorithms for network topology discovery. In 2014 Second World Conference on Complex Systems (WCCS); IEEE: Piscataway, NJ, USA, 2014; pp. 530–535. [Google Scholar]
- Koval, A.; Moselle, K. Clinical Context Coding Scheme—Describing Utilisation of Services of Island Health between 2007–2017. In Proceedings of the Conference of the International Population Data Linkage Association, Banf, AB, Canada, 12–14 September 2018. [Google Scholar]
- Pósfai, M.; Barabási, A.-L. Network Science; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Durand, A.-C.; Palazzolo, S.; Tanti-Hardouin, N.; Gerbeaux, P.; Sambuc, R.; Gentile, S. Nonurgent patients in emergency departments: Rational or irresponsible consumers? Perceptions of professionals and patients. BMC Res. Notes 2012, 5, 525. [Google Scholar] [CrossRef]
- Uscher-Pines, L.; Pines, J.; Kellermann, A.; Gillen, E.; Mehrotra, A. Emergency department visits for nonurgent conditions: Systematic literature review. Am. J. Manag. Care 2013, 19, 47–59. [Google Scholar]
- Johannes, B.; Graaf, D.; Blatt, B.; George, D.; Gonzalo, J.D. A multi-site exploration of barriers faced by vulnerable patient populations: A qualitative analysis exploring the needs of patients for targeted interventions in new models of care delivery. Prim. Health Care Res. Dev. 2019, 20, e61. [Google Scholar] [CrossRef] [PubMed]
- Christiani, A.; Hudson, A.L.; Nyamathi, A.; Mutere, M.; Sweat, J. Attitudes of Homeless and Drug-Using Youth Regarding Barriers and Facilitators in Delivery of Quality and Culturally Sensitive Health Care. J. Child Adolesc. Psychiatr. Nurs. 2008, 21, 154–163. [Google Scholar] [CrossRef] [PubMed]
- Cradock-O’Leary, J.; Young, A.S.; Yano, E.M.; Wang, M.; Lee, M.L. Use of General Medical Services by VA Patients With Psychiatric Disorders. Psychiatr. Serv. 2002, 53, 874–878. [Google Scholar] [CrossRef] [PubMed]
- Calder, R.; Dunkin, R.; Rochford, C.; Nichols, T. Australian Health Services: Too Complex to Navigate; The Australian Health Policy Collaboration, Victoria University: Melbourne, Australia, 2019. [Google Scholar]
- Clarfield, A.M.; Bergman, H.; Kane, R. Fragmentation of care for frail older people—An international problem. Experience from three countries: Israel, Canada, and the United States. J. Am. Geriatr. Soc. 2001, 49, 1714–1721. [Google Scholar] [CrossRef] [PubMed]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bambi, J.; Santoso, Y.; Moselle, K.; Robertson, S.; Rudnick, A.; Chang, E.; Kuo, A. Analyzing Patterns of Service Utilization Using Graph Topology to Understand the Dynamic of the Engagement of Patients with Complex Problems with Health Services. BioMedInformatics 2024, 4, 1071-1084. https://doi.org/10.3390/biomedinformatics4020060
Bambi J, Santoso Y, Moselle K, Robertson S, Rudnick A, Chang E, Kuo A. Analyzing Patterns of Service Utilization Using Graph Topology to Understand the Dynamic of the Engagement of Patients with Complex Problems with Health Services. BioMedInformatics. 2024; 4(2):1071-1084. https://doi.org/10.3390/biomedinformatics4020060
Chicago/Turabian StyleBambi, Jonas, Yudi Santoso, Ken Moselle, Stan Robertson, Abraham Rudnick, Ernie Chang, and Alex Kuo. 2024. "Analyzing Patterns of Service Utilization Using Graph Topology to Understand the Dynamic of the Engagement of Patients with Complex Problems with Health Services" BioMedInformatics 4, no. 2: 1071-1084. https://doi.org/10.3390/biomedinformatics4020060
APA StyleBambi, J., Santoso, Y., Moselle, K., Robertson, S., Rudnick, A., Chang, E., & Kuo, A. (2024). Analyzing Patterns of Service Utilization Using Graph Topology to Understand the Dynamic of the Engagement of Patients with Complex Problems with Health Services. BioMedInformatics, 4(2), 1071-1084. https://doi.org/10.3390/biomedinformatics4020060