Abstract
Self-supervised learning (SSL) has gained significant attention in the past decade for its capacity to utilize non-annotated datasets to learn meaningful data representations. In the medical domain, the challenge of constructing large annotated datasets presents a significant limitation, rendering SSL an ideal approach to address this constraint. In this study, we introduce a novel pretext task tailored to stimulus-driven eye movement data, along with a denoising task to improve the robustness against simulated eye tracking failures. Our proposed task aims to capture both the characteristics of the pilot (brain) and the motor (eye) by learning to reconstruct the eye movement position signal using up to 12.5% of the unmasked eye movement signal patches, along with the entire REMOBI target signal. Thus, the encoder learns a high-dimensional representation using a multivariate time series of length 8192 points, corresponding to approximately 40 s. We evaluate the learned representation on screening eight distinct groups of pathologies, including dyslexia, reading disorder, and attention deficit disorder, across four datasets of varying complexity and size. Furthermore, we explore various head architecture designs along with different transfer learning methods, demonstrating promising results with improvements of up to approximately 15%, leading to an overall macro F1 score of 61% and 61.5% on the Saccade and the Vergence datasets, respectively. Notably, our method achieves macro F1 scores of 64.7%, 66.1%, and 61.1% for screening dyslexia, reading disorder, and attention deficit disorder, respectively, on clinical data. These findings underscore the potential of self-learning algorithms in pathology screening, particularly in domains involving complex data such as stimulus-driven eye movement analysis.
1. Introduction
Eye movement data analysis holds significant promise in uncovering insights into brain disorders and pathologies. Abnormalities in eye movements often serve as valuable markers for various neurological conditions, making the examination of eye movement patterns crucial for early detection and intervention strategies. In our daily lives, we make about 150,000 movements per day, corresponding to 3 movements per second. This abundance of data underscores the potential for understanding underlying neurological conditions through eye movement analysis.
While statistical frameworks [1,2,3,4] and machine learning algorithms [5,6,7,8,9,10] have been employed for analyzing eye movement data, recent advancements in deep learning [11,12,13,14,15,16,17,18] have shown great potential in automating the analysis process. These approaches not only automate feature extraction but also enhance the resilience of learning algorithms to noise, thereby maximizing the information encoded in the data. However, training such algorithms requires annotated data, and imposing the annotation can drastically increase the difficulty of dataset construction. In response to this challenge, alternative approaches such as unsupervised learning [19] and self-supervised representation learning [20,21] are being explored.
However, two limitations arise, namely the sample size and model size. While the effect of these two limitations may not be significant when training using a research dataset, in clinical datasets, which represent the real-model use case, the screening task complexity is higher due to the increase in input and output (pathology class) variability, making training small models prone to underfitting. For instance, clinical data exacerbate challenges such as low signal-to-noise ratio and inherent variability stemming from population diversity and data recording protocols. Additionally, the high variability of the target class distribution poses a challenge. As a result, small-sized models, due to limited expressivity, tend to underfit when confronted with these challenges. Notably, there is a gap in the literature concerning the evaluation of large architectures’ performance on pathology screening tasks of eye movement time series trained using deep learning algorithms, including self-supervised learning methods. In scenarios lacking a big dataset, highly expressive models are prone to learning the training set without necessarily generalizing. This issue is particularly acute with Transformers, given their high expressivity and absence of weight sharing inherent in Convolutional Neural Network (CNN) architectures.
On the other hand, constructing a large clinical annotated dataset can be challenging, especially for rare illnesses. One approach is using self-supervised learning (SSL) algorithms. SSL involves training the model on a non-annotated dataset to learn a pretext task that compresses the input space into a low-dimensional representation. The model weights are then fine-tuned on a smaller annotated dataset for the downstream task (the main task). A possible option for the pretext task is masked modeling, which was introduced on Bidirectional Encoder Representations from Transformers (BERTs) [22] and has since been extensively explored in different fields, including natural language processing (NLP) [23,24,25] and computer vision domains [26,27,28,29].
Our approach is inspired by the work of [29], although we employ a different pretext task tailored specifically to stimulus-driven eye movement time series data. Furthermore, we refine the masking heuristic to suit time series data and the characteristics of an eye movement position signal. For instance, a fundamental distinction between image and time series data structures lies in their information density [30]. In time series data, missing masks can be readily addressed through interpolation. Additionally, temporal dependency, inherent to time series data, implies a sequential ordering of data points, unlike the spatially independent nature of images. Moreover, when dealing with eye movement time series data, local failures in the eye tracking system result in sparse regions with reduced sampling rates. Furthermore, errors in eye tracking predictions introduce noise into the input space, leading to a low signal-to-noise ratio.
To address these challenges, we adapt the masking process to simulate eye tracking failures and introduce noise signal corruption to emulate inaccuracies in eye tracking predictions. Our proposed masking heuristic represents a generalization of patch-based and random masking strategies, incorporating variable masking densities during training to account for different scenarios.
Furthermore, we introduce a corruption heuristic tailored to our domain to enhance the complexity of the pretext task. This encourages the capture of mutual information between different time series and learned representations by maximizing their mutual information lower bound [31,32]. Additionally, we refine our noise modeling to better replicate the noise present in our data.
Finally, we integrate the target signal into the decoder to mitigate the effects of hard masking and temporal dependencies in our data. This replacement of the patch filling task aims to capture both the characteristics of the pilot (brain) and the motor (eye) by analyzing present patches relative to their corresponding stimulus signals, thereby uncovering missing zones given in the stimulus signal.
As a result of these adjustments, we demonstrated that it is possible to reconstruct eye movement time series data using only up to 12.5% of initial eye movement signals combined with REMOBI target signals. Our studies make the following main contributions:
- We propose an extension of the masked autoencoder (MAE) for modeling eye movement time series, aiming to learn meaningful high-dimensional representations through semi-supervised learning on eye movement data.
- We introduce a novel pretext task tailored to stimulus-driven eye movement analysis. First, we introduce a masking heuristic. Furthermore, we condition the reconstruction task with the stimulus signal, enabling the model to learn to capture eye movement characteristics and use them to reconstruct the initial signal with masking of up to 87.5% of the initial eye movement signals. Finally, we incorporate a noise injection heuristic to increase the robustness of the trained model by emulating intrinsic noise in eye movement position signal.
- We compare our method with two different unsupervised learning methods, as well as training using supervised learning.
- We explore using the high-dimensional learned representations to screen eight groups of pathologies on four different characteristic datasets.
- Demonstrating the feasibility of reconstructing eye movement time series data using only a small portion, up to 12.5%.
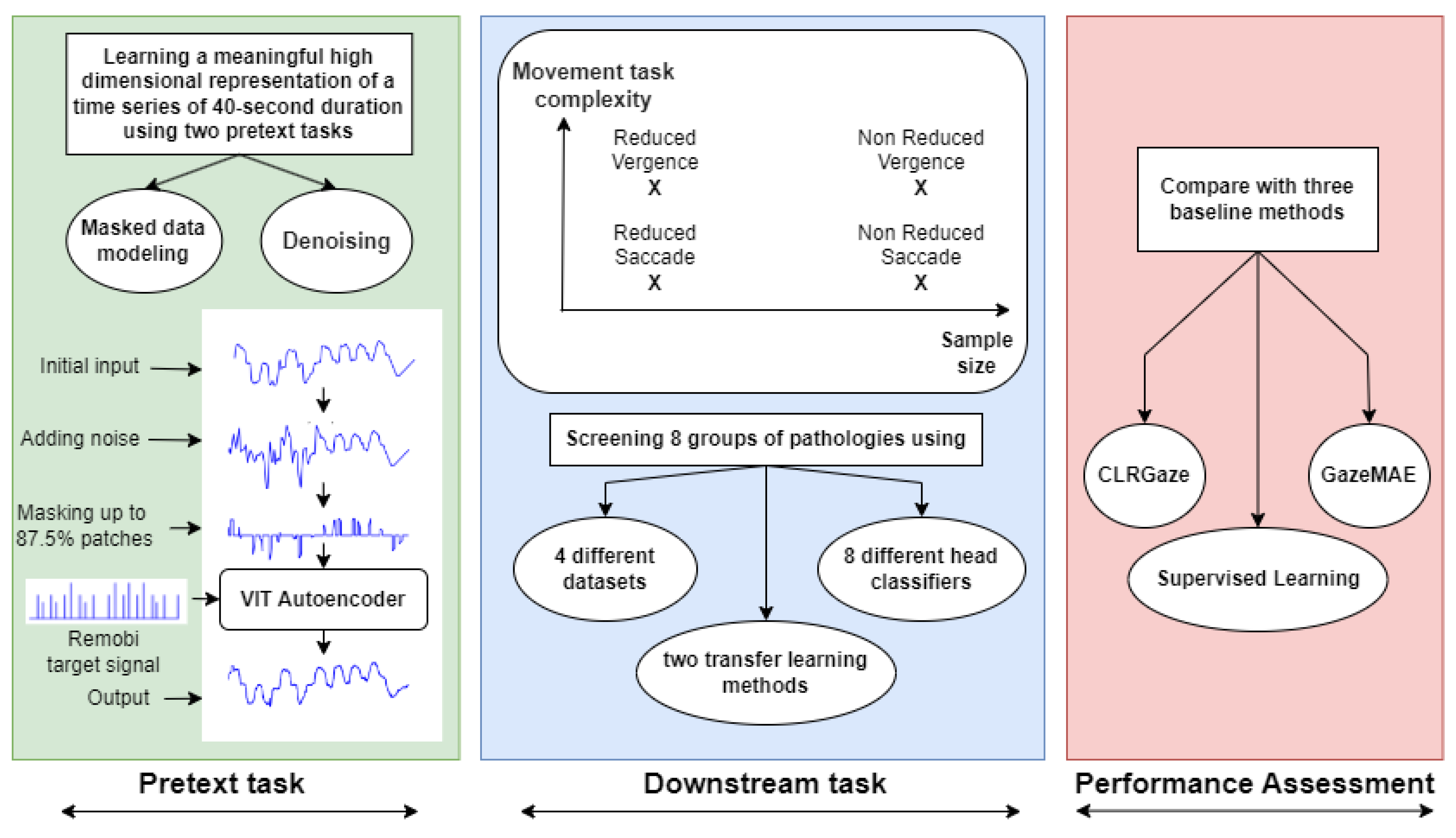
Figure 1 offers a visual summary of the exploration presented in this study.
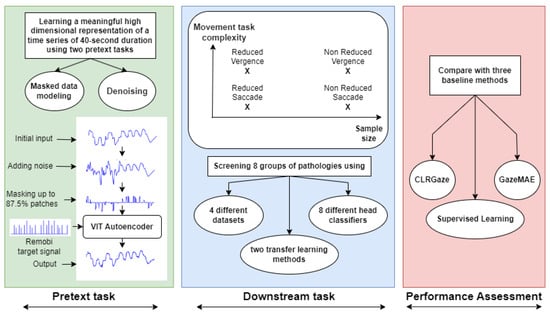
Figure 1.
A visual abstract of the exploration detailed in our preliminary study.
2. Related Work
Autoencoder: This is an unsupervised method for learning a low-dimensional representation [33,34,35] comprising two models (an encoder and a decoder). The encoder performs feature selection by compressing the input into a low-dimensional representation. Subsequently, the decoder learns to reconstruct the original input features from the output of the encoder. This algorithm is trained by minimizing mean-squared error during reconstruction. Another variant of this algorithm is a variational autoencoder [36,37], which introduces a probabilistic perspective by regularizing the latent space through an assumption of conditional multi-Gaussian distribution in that space. As a result, the encoder predicts both mean and standard deviation for each Gaussian component conditioned by input; meanwhile, the decoder samples from this learned distribution to construct the initial input.
Denoising autoencoder: This is a special form of autoencoder, which aims to increase the robustness of the learned representation by training the model to remove noise from the input [38,39]. Each input datum is corrupted before being passed to the encoder, and then the autoencoder minimizes the reconstruction error between the uncorrupted input and the reconstructed input. In our approach, we follow the same method, aiming to mimic the inherent noise produced by an eye-tracking system error by generating additional noise that is proportional to the signal amplitude, to encourage the model to learn to exploit the correlation of the different multivariate components, as well as the overall response represented by the eye signal relative to the target signal to filter the noise.
Masked data modeling: This involves removing patches in each sample during training. The model then needs to use the learned representation for the unmasked region to retrieve information from the masked region. Initially used in NLP [22], this technique showed promising results when evaluated on downstream tasks. Kaming He et al. [29] explored its application on ImageNet as a pretext task and reported an accuracy of 87.8 on ImageNet-1k without relying on data augmentation techniques, using only cropping instead of contrastive learning.
Additionally, alongside our study, two other studies [30,40] have pursued similar objectives: Ti-MAE [40], which focuses on training MAE with time series data by replacing a continuous masking strategy with a random time masking strategy introduced in MAE and evaluating it on classification tasks where it achieves consistent improvement across all evaluated forecasting datasets; and MTSMAE [30], which introduces a patch embedding method more suited for MAE application to time series characteristics.
In our approach, we investigate different directions by designing a novel masking heuristic that can be seen as a generalization of patch-based and random masked modeling. The proposed masked modeling method is inspired by the problem of eye tracking system failure.
Self-supervised learning: This involves two stages of training. In the first stage, the model is trained using annotated data to learn a low-dimensional and meaningful representation. The second stage fine-tunes the model for a specific downstream task using an additional annotated dataset. The first stage can incorporate a pretext task such as regression with pseudo-labels [41,42,43], a contrastive method [44,45,46,47], or an adversarial method [48,49,50]. Finally, a more complete taxonomy of unsupervised representation learning is presented in [51].
Our study considers the mask filling task as a pretext task while viewing the denoising task with dual purposes; it serves as a pretext task in the first stage and subsequently acts as a preliminary step for the downstream tasks in the second stage.
Application to eye movement: To address the challenge of analyzing eye movements through eye movement data [19,20,21,52,53,54,55], one can first learn to estimate eye movement position coordinates. Subsequently, these estimated eye movements can be utilized to learn to identify corresponding pathologies within the eye movement data. Self-supervised learning techniques have been employed in different studies to address these phases, demonstrating promising outcomes. Bautista et al. [19] utilized a temporal convolutional network autoencoder to derive meaningful representations from eye movement position and velocity segments separately using unsupervised algorithms. They assessed the efficacy of this embedding by training a linear Support Vector Machine (SVM) for patient identification tasks, achieving accuracies of up to 93.9% for stimulus tasks and up to 87.8% for biometric tasks. In a second approach [21], they applied the same encoder architecture for self-supervised contrastive learning, achieving an accuracy of up to 94.5% for biometric tasks. However, there was a noticeable decrease in generalization performance when assessing datasets not included in the training/testing split algorithm. In another study, Lee et al. investigated the detection of abnormal behavior during screen observation using self-supervised contrastive learning, achieving an accuracy of 91% in identifying abnormal eye movements associated with attention lapses.
On the other hand, the papers [20,53,54,55] explore the application of SSL for eye movement coordinate estimation. In our study, we prefer using the Pupil solution for the estimation due to its physiological criteria and high accuracy. This solution has been extensively used in studies. Therefore, in this study, we explored learning the screening task from eye movement position signals.
3. Materials and Methodology
3.1. Saccade and Vergence Eye Movement
Saccades and vergence eye movements are the most common eye movements we make in everyday life, enabling us to explore our 3D environment, read, and react to targets. Saccades are rapid and abrupt movements that center the target on the retina by changing the direction of our gaze. During saccades, both eyes coordinate to generate movements in the same direction and by the same amount. In contrast, vergence movements are more complex, involving the eyes moving in opposite directions. They allow the fixation point to either move away (diverge) by decreasing the angle of vergence or to be brought closer (converge) by increasing the angle of vergence.
Moreover, each movement can be decomposed into a conjugate saccade component and a disconjugate component. The conjugate component, representing the mean values of the position signal of both eyes, analyzes movements that change the direction of gaze to place the fixation point in space without altering the depth of the fixated points, thus aiding in the analysis of the saccade movement. Conversely, the disconjugate component, corresponding to the difference in the position signal of both eyes, analyzes movements that alter the depth of gaze by shifting the fixation point on the optical axis, thereby facilitating the analysis of the vergence movement. Finally, in Appendix A, Figure A1, we provide an overview of the four signals, presenting the left and right position signals along with the conjugate and disconjugate components for both saccade and vergence recordings. It is important to note that this figure provides an illustration using a high signal-to-noise recording to emphasize the differences between these two movements, thereby enhancing clarity in comparison.
3.2. Eye Movement Recording
Our data are recorded from various clinical centers across Europe. These centers utilize the REMOBI technology (patent WO2011073288) for conducting tests that stimulate various eye movements, such as saccades and vergence, alongside the AIDEAL technology (patent PCT/EP2021/062224) to analyze the resulting recording. Additionally, eye movements are recorded using a Pupil Core head-mounted video-oculography device [56] to record eye movements at a frequency of 200 Hz per eye, providing real-time gaze position estimation for both the left and right eyes along the vertical (y) and horizontal (x) axes. All data records undergo anonymization in compliance with European regulations on personal data before being stored in our database. The same experimental setting has been employed across multiple studies for analyzing eye movements, utilizing statistical methods [1,2,3,4] as well as machine learning algorithms [5,6].
3.3. REMOBI Saccade and Vergence Tests
Our database encompasses a diverse range of eye movement recordings captured through different modes using REMOBI, including saccade, vergence, combined movements, vestibular tracking, and fixation, as well as recordings from non-stimulus-driven tasks like reading and viewing images.
For this study, we exclusively utilize the saccade and vergence recordings to construct each of the four classification datasets. The remaining groups are solely employed in the initial learning stage to train the encoder. Consequently, we provide a more detailed examination of the REMOBI saccade and vergence tests in our study.
During the saccade test, patients were instructed to fix an illuminated LED stimulus along a horizontal axis to elicit right and left saccadic movements. Similarly, during the vergence test, stimuli were presented over the optical axis to stimulate both conjugate and disconjugate vergence movements. Each test comprised 40 movements (20 leftward and 20 rightward) during the saccade test (20 convergence and 20 divergence) and during the vergence test. The duration and position of the LEDs were randomized to prevent anticipation of movement in both tests. The purpose of conducting these tests is to further analyze specific eye movements related to each task, using the software AIDEAL.
3.4. Dataset Overview
Using our intern database, we synthesized two datasets. The first dataset (Ora-M) encompasses all the data collected before 2022, including the non-annotated data, and is used for the pre-training task, while the second one (Ora23) contains all the annotated data gathered before 2023. To construct the segmented Ora23 dataset, We follow the same approaches outlined in [12], which were also employed in the creation of Ora22, as utilized in our prior study.
- ORA-M: This includes a variety of eye movement visual tasks, namely vestibular, fixation, combined, image, reading, saccade, vergence, and random tracking. The distribution of visual tasks in the ORA-M dataset is illustrated in Figure A2, which contains a total of 15673 recordings. Each recording corresponds to a multivariate eye movement position time series, encompassing the angular coordinates of the left and right eyes along both horizontal and vertical axes. These recordings typically span a duration ranging from 1 to 5 min, yielding approximately 9000 and 45,000 coordinate points, respectively. The three dominant visual tasks are reading, followed by vergence and saccade with a percentage of 35.63 %, 24.87%, and 21.72%, respectively. All the eye movement recording data are merged into one comprehensive database, including both annotated and non-annotated data.
- ORA23: This contains only annotated data of the saccade and vergence tests. These data are used separately to construct two sub-datasets, namely the saccade visual task dataset, and similarly, the vergence visual task dataset. The saccade dataset consists of 92,207 time series of a duration of 5 s, corresponding to approximately 750 points, recorded from 3081 patients. Similarly, the vergence dataset consists of 95,630 segments of a duration of 5 s, recorded from 3228 patients. These sub-datasets are utilized for the downstream task in our study.
3.5. Train/Test Split
Training using the SSL paradigm involves two stages of learning. In our setting, the first stage (pretext task) corresponds to masked data modeling, while the second stage (downstream task) corresponds to screening diseases. Below, we present the train/test split for each of the pretext and the downstream tasks. Note that all the heuristics discussed below are performed at the subject identifier level. Then, the corresponding data of each identifier is gathered to form the corresponding set. This approach guarantees the absence of data from the same subject in both the train and the test sets.
For the pretext task, we use the ORA-M dataset. Sixty percent of the data are used for model training, while the remaining data are used for the evaluation of the reconstruction error and assessing overfitting. On the other hand, for the downstream task, two distinct train/test splits are explored to train and evaluate our methods. We present the two heuristics with a specific emphasis on mitigating their potential limitations, namely, information leakage and distribution shift.
- Random Split Strategy: All Ora23 data are utilized for constructing both the training and test sets in this scenario. The data are randomly partitioned, allocating 30% for training and reserving 70% for testing. The training set is crucial for fine-tuning the model. However, this approach introduces a potential risk of information leakage due to the overlap between the data used for the pretext task and the downstream task, as the model—despite lacking access to labels during the pretext task—retains knowledge of the underlying data structure.
- Temporal Split Strategy: In response to the identified information leakage risk, a temporal split strategy is proposed. Data collected between 2022 and 2023 are exclusively used for testing, ensuring no overlap between patient data in the training and test sets. However, this strategy sacrifices the guarantee of similar distributions between the training and test datasets. Moreover, the SSL algorithm is intended to be used in a scenario where we have few annotated data, and one large non-annotated set; thus, in order to align with the principles of self-supervised learning (SSL), only 20% of subjects from the data collected before 2022 are utilized for training, resulting in a reduced training set size compared to the pretext task.
Finally, in Appendix A, Table A1, we display the counts of the train and test sets for each of the two approaches applied to the saccade and vergence datasets, yielding four distinct datasets. These datasets exhibit distinct characteristics in terms of sample size and task complexity. Additionally, owing to variations in the sizes of the training sets, we denote the datasets produced using the first method (Random Split Strategy) as the non-reduced datasets, while the reduced dataset denotes the dataset generated using the second heuristic (Temporal Split Strategy).
3.6. Problem Statement
Our dataset, labeled as , comprises N instances. Each pair represents a multivariate time series of length T: , corresponding to the horizontal and vertical angular positions of both eyes for each point within the T-length interval, along with the latency target signal encoding stimulus information such as different LED states and the type of eye movement test, and the target class , corresponding to eight annotations. Our objective is to predict class given the input . Our recordings of eye movements consist of approximately 30,000 time points, which are typically too long for one-shot processing; therefore, we suggest a segment-based approach by working on segments of size 8096, representing a 40-second recording split into 16 segments of size 512. As a result, each sample has 16 multivariate time series (segments) of length 512 and 5 channels.
Our objective is first to train a Vision Transformer (ViT) autoencoder on the non-annotated ORA-M dataset to learn high-dimensional representations for each sample through our proposed pretext task. Subsequently, we aim to use the learned representation to tackle the downstream task of disease classification.
3.7. Preprocessing
We follow the same procedure as outlined in our previous studies. We conduct two levels of data cleaning: a low-pass filtering step with a cutoff frequency of 33 Hz, and a z-score filtering step, where we eliminate data points with z-scores exceeding 2.5. Instead of implementing the standardization technique suggested in prior research, we normalize each eye movement sample channel separately using statistics per channel and sample individually. This is equivalent to applying the instance normalization technique with no momentum. Each latency signal is shifted with a different constant to encode the test type within range, then scaled using a min–max scaler.
4. Method
To train our architecture, we use the self-supervised learning algorithm proposed in [29]. This approach addresses the challenge of a small annotated sample size by employing a two-stage learning algorithm. In the initial stage, the model is trained on a large non-annotated dataset to learn a pretext task and create low-dimensional meaningful representations for each sample. Subsequently, the model is fine-tuned on a smaller annotated dataset for the downstream task. All the proposed methods are implemented, trained and evaluated using the PyTorch Framework.
4.1. Architecture
Our architecture uses a Transformer-based design, which has been shown to address the information bottleneck in long-term time series data when using recurrent neural networks (RNNs) in sequence to sequence (seq2seq). Figure A3 in Appendix A presents an overview of the proposed architecture. It consists of an embedding module for processing each sample, masking up to 87.5% of the patch and applying corruption to the remaining patches, an encoder for constructing high-dimensional embeddings for each remaining patch, a decoder for reconstructing the latent representations of patches and restoring masked patch embeddings, and finally, a reconstruction module that linearly projects different patches and flattens the output to form the initial sample. This architecture is similar to the VIT autoencoder used in [29], but with some minor modifications in feature space as well as incorporated masking and corruption modules. The different modules are detailed below:
- Embedding: This takes a tensor of shape (Batch, 8192, 5) and converts it to a set of k stems within the second axis, with k as the number of unmasked stem. First, each batch tensor is processed with a 2D convolutional layer with strides equal to 16 and 192 filters, outputting a 512 patch with a representation dimension of 192. Then, k patches are filtered using our patch masking heuristic and processed with the patch corruption module. Finally, a learned position embedding weight vector is added to enable the encoder to capture the temporal-order structure.
- Encoder: The encoder is designed to learn a low-dimensional representation for each unmasked patch. It consists of 16 attention blocks stacked vertically, utilizing the attention block module from the timm library [57]. Similar to MAE, we process only the unmasked patches and replace masked representations with a learnable vector.
- Decoder: The decoder reconstructs the masked patch using information from the retained patches. A smaller decoder is used to enhance the relevance of learned representation by the encoder. Each missing mask is replaced with a learned vector, aiming to retrieve the initial sample space cardinality of shape (Batch, 512, 192). The latency layer is then combined with each learned embedding and passed to the decoder in order to recover missing information using the encoded representation.
- Reconstruction head: The module aims to reconstruct the original time series from the reconstructed patches. This is achieved by linearly projecting different representations to recover the original patch dimensions. At this stage, the output has a shape of (Batch, n_patches, dim). Finally, the last two dimensions are flattened to retrieve the initial input space dimension.
4.2. Pretext Task
Pretext task selection is crucial for SSL. The connection between the pretext task and downstream task affects the efficacy of learned representation on the main task. We introduce a novel pretext task which learns to capture the characteristics of eye and brain responses relative to the stimulus signal in order to fill the masked region. Furthermore, our pretext task is inspired by the masked autoencoder (MAE) and, more generally, by the masked modeling method, but tailored to our problem to accommodate the characteristics of eye movement multivariate position time series, including a low signal-to-noise ratio stemming from errors in eye tracking prediction and sparse regions due to eye tracking failure. To address these issues, we propose a masking heuristic that simulates eye tracking failure and introduces signal corruption noise to replicate inaccurate eye tracking predictions.
4.2.1. Masking Strategy
Our Proposed Algorithm
Our algorithm is parameterized by a number of splits N and a maximum masking ratio . To control the patching density of our data, we first construct a list of sorted indexes of the different patches. Then, we split the list into N sublists. For each sublist, we sample a masking ratio () from the interval , and then mask the corresponding consecutive indexes. The different operations are presented in detail below:
- Construct a list (P) of the sorted indexes of each patch.
- Split the list into N sublists defined by
- For each sublist , randomly sample a mask ratio from the interval , as well as a starting offset from the interval , with m defined by
- Contiguously select indexes starting from the offset in each sublist , and discard the remaining indexes. The set of retained indexes for each sublist , given the sampled random mask ratio as well as the offset , is defined by
Our proposed masking model has parameters:
- Granularity N: These parameters control the granularity of the segmentation. It is initialized to 1 and incremented after each batch in the cyclic interval .
- Length : This parameter accounts for the number of consecutive retained indexes in each sublist , and defined by (1), with the masked ratio sampled for the sublist .
- Offset : This parameter represents the position of the first retained index in each sublist .
These parameters, chained together, allow for controlling the masking density. For instance, controls the length of the different patches, while N controls how finely each list index is divided. Note that the length varies for each sublist i.
Analyzing Algorithmic Extremes
We notice two extreme cases for this algorithm. The first case is when N is minimal (), and is maximal, thus sampled to . And the second case is when N is maximal and is minimal for each sublist, thus equal to 1.
When N is minimal, the algorithm will select one contiguous segment of length ranging from to of the initial length, depending on P, which is hard for the model because the learning task becomes similar to the forecasting task. On the other hand, the second extreme is when N is maximal, hence equal to 64. Then, the algorithm will approximate the uniform sampling of the unmasked region by splitting the time series into 64 lists of 8 consecutive indexes, and then randomly retain 1 index per sublist.
Our strategy is motivated by the fact that for time series signals, if the density of the masked points is placed randomly on the time series, the task becomes very easy to infer the correct unmasked value, up to a certain precision, by just connecting the dots. As a result, we would sample some segments where we have a relatively large zone of masked area to encourage the model to learn to predict the time series eye movement signal by sampling using the previous trials and the target signal.
Moreover, to mitigate the hard sampling effect, we considered passing to the decoder the target signal, which encodes the position of the stimuli during each time step. As a result, the decoder output is conditioned with the target signal as well as the learned representation of the unmasked patch.
4.2.2. Learning to Capture Eye and Brain Response Characteristics Relative to the Target
We introduce a sophisticated self-learning method for analyzing eye movement time series data. Traditional approaches typically focus solely on response data, by masking several patches in the time series, and asking the model to fill the missing information. However, our method breaks from convention by incorporating both the target signal and the eye movement response signal. This holistic approach mirrors the physiological integration observed in the brain, where stimulus and response preparation are intertwined. By conditioning the algorithm with both stimulus and response signals, we aim to stimulate a more realistic and physiologically relevant learning process. This method acknowledges the dynamic properties of stimuli over time and the need for movement responses to adapt accordingly. By integrating both stimulus and response in the learning process, our approach seeks to achieve a more intelligent and realistic model. This innovative methodology holds promise for developing physiologically accurate self-learning algorithms applicable to various contexts, including complex scenarios.
4.2.3. Corruption Strategy
Sampling the Corruption Noise
To create the corruption process, our goal is to produce a vector noise similar to the observed data noise but significantly higher in order to challenge the reconstruction process and encourage the model to utilize other segments with target signals for denoising. The implementation involves generating random noise from a normal distribution with standard deviation , upsampling the noise using bilinear interpolation to mimic correlated noise over time for added realism, and then multiplying each noise point by the local signal amplitude to control the signal-to-noise ratio.
Varying the Corruption Policy within Each Group
The motivation for processing each group differently is to enhance the homogeneity of denoising difficulty within each batch. We investigate eight corruption modes for every batch, which is evenly divided into eight subgroups. For each subgroup, we apply the following processing steps:
- Group 1: Right eye signal corruption.
- Group 2: Left eye signal corruption.
- Group 3: Left and right eye signal corruption.
- Group 4: Right eye signal corruption with a probability of 0.5 for each point.
- Group 5: Left eye signal corruption with a probability of 0.5 for each point.
- Group 6: Left and right eye signal corruption with a probability of 0.5 for each point.
- Groups 7 and 8: No corruption is applied.
The motivation behind processing each group differently is to increase the homogeneity of the denoising difficulty within each batch.
4.3. Downstream Task
Head Classifier Design
We evaluate the pertinence of the learned representation on the annotated Ora dataset. To learn the multi-annotation classification task, we stacked on top of the learned embeddings a head classifier. However, screening each group of the eight different pathologies may require more than one linear layer. As a result, we explored other classifiers to improve the model performance on the downstream task.
In Figure A4 of Appendix A, we present an overview of the different explored module designs. H0, H1, H2, H3, H4, H5, H6, and H7 are depicted in subfigures (a), (b), (c), (d), (e), (f), (g) and (h), respectively. The main idea explored in our experimentation is increasing the input space by incorporating segment normalization statistics within the encoder output, increasing the expressivity of the head classifier by using a new Transformer block on top of the 16 pre-trained Transformer blocks, and finally exploiting, in addition to the CLS slice, the remaining encoder output tensor by processing each temporal slice separately, then aggregating the different classification slices by means to increase model resilience.
- Linear probing: Traditionally, linear probing is used to evaluate the pertinence of the learned representation, using a linear classifier, trained on the CLS slice or using the mean aggregation of the encoder output within the temporal dimension. The head classifier (H0) is a layer perceptron with sigmoid activation. We follow the same approach outlined in [29] by adding between the head classifier and the encoder a batch normalization layer without affine transformation.
- Incorporating the normalization statistics: For instance, while applying a per sample normalization within the temporal dimension, the input variability is reduced, thus making the pretext task easier. We hypothesize that two encoder embeddings become incomparable by altering information such as the amplitudes, thus affecting the classification performance on the second learning stage. Thus, in H1, we incorporate the normalization statistics within the encoder CLS slice. Additionally, batch-normalization is applied, followed by a two-layer perceptron, as presented in subfigure (b).
- Adding additional attention blocks: In H2, H3, and H4, we added an additional Transformer block-LN on top of the encoder output. In H2, the normalization statistics are concatenated with the block output; meanwhile, in H3 and H4, they are concatenated with the block input. This allows the added attention module to take advantage of information statistics. Furthermore, the CLS is processed using a perceptron head in H2 and H3, while in H4, it is processed with a two-layer perceptron with an additional dropout of 0.5 before reaching the last linear layers. An overview of the three head classifiers is presented in Appendix A, Figure A4, in subfigures (c), (d) and (e).
- Exploiting the entire encoder output: In H5, H6, and H7, rather than collecting the CLS slice, we leverage the entire tensor. Similarly, we present in subfigures (f), (g) and (h) the corresponding three architectures, respectively. In H5, the initial step involves processing each encoder output with the block module. Subsequently, the resulting tensor is averaged along the temporal dimension, concatenated with the normalization statistics, processed through batch normalization, and finally fed into a two-layer perceptron. Conversely, in H6 and H7, the normalization statistics are first stacked with the encoder output and then passed through an additional block-LN, enabling the block-LN to capitalize on these features. The processing of the block-LN output differs between H6 and H7. In H6, the block-LN output is flattened and directed to the perceptron classifier. In contrast, in H7, a two-layer perceptron is employed as a head with a dropout of 0.2 before the last layer. Moreover, instead of collecting the CLS slice or averaging by mean, all slices are concurrently processed with a two-layer perceptron, and the resulting output is averaged along the temporal dimension. Finally, a dropout of 0.2 is applied before the last layer.
4.4. Model Training
The training loop and evaluation presented above are implemented using custom code with PyTorch. Additionally, for the encoder and the decoder, we used the timm library [57] VIT model, adapting it to integrate different model designs as presented in Appendix A, Figure A3 and Figure A4. Finally, the data generator is implemented in PyTorch. For each batch, the generator randomly selects a set of recordings, then samples 16 consecutive segments from each observation to construct each training batch along with its corresponding annotation that are used for the second learning stage.
The pre-training is performed using two NVIDIA V100 GPUs, while the second-stage learning is performed using a different GPU for evaluation (NVIDIA A100 80 GB). The different hyperparameters are manually optimized.
4.4.1. First-Stage Model Training
We set the minimal masking ratio to 75%. The embedding dimension is set to 192. We set the patch size to 16 to reduce the temporal dimension to 512. Finally, for the masking module, the number of splits is set using an incrementation counter modulo 64.
We train the model using AdamW with a learning rate initialized at . By minimizing the mean-squared error of the initial and the reconstructed masked regions, the two beta optimizer parameters ( and ) are set to 0.9 and 0.95, respectively. Finally, we set the weight decay to 0.05.
In addition, we use the learning rate scheduler defined below, which corresponds to a cosine annealing schedule, with a linear warm-up phase starting from the first epoch until epoch 200.
We use a batch size of 96, which corresponds to an effective batch size of 1536 segments. Additionally, we train the model for 300 epochs, taking approximately 48 h, using one GPU V100.
4.4.2. Second-Stage Model Training
To learn the classification task, we stack each of the different proposed head classifiers on top of the learned encoder; then, we use transfer learning to adapt the resulting models to downstream tasks. We experiment with two transfer learning techniques. In the first approach, we freeze the encoder weights and train only the head classifier. In the second approach, we fine-tune the encoder weights along with training the head classifier. Finally, to evaluate our method, we perform a final training for each head classifier by training the “en” model (encoder + head) using classical supervised learning, without pre-training.
Optimizer
We used the AdamW with default beta hyperparameters of (0.9,0.999) and the learning rate scheduler defined below:
All the different training settings in the three regimes are similar, except for the optimization hyperparameters, namely the learning rate, the weight decay, and the model’s weight state and initialization. The different parameters are summarized in Table A2 of Appendix A.
Additionally, for the two transfer learning regimes, we experimented with a smaller learning rate, lower than the final learning rate of the first stage. However, we found that the resulting model performance was less optimal relative to when retraining with an initial learning rate of 0.001.
Loss Function
Recall that our classification problem is a multi-annotation problem, where each sample can have one or multiple positive classes. Thus, we consider learning a binary classifier for each class by learning a per-class distribution. To mitigate dataset imbalance, we use focal loss optimization and per-sample loss weighting based on class weight, with binary focal losses independently optimized for each class using a gamma value of 3. We experiment with both binary cross-entropy and focal loss. We observe that substituting focal loss with binary cross-entropy results in a decrease in generalization ability within the positive classes, consistently for all the methods and for all the head classifiers. Therefore, we consider using focal loss for all downstream experiments. Additionally, to achieve class balancing, we perform class balancing by setting the focal loss alpha hyperparameters for each class. The different alpha parameters are summarized in Table A3. Note that the different parameters are set by monitoring the loss stability within each class on the first four epochs and can be further optimized.
Additional Training Setting
Note that when training the head H0 using a frozen encoder weight, which is known as linear probing in the literature, we follow the training setup as outlined in [29,41], by disabling weight decay, and normalizing the model output using batch normalization without learning parameters, followed by a linear layer.
We use a batch size of 64. Note that each sample contains 16 segments of length 512 each, corresponding to an effective batch size of 1024 segments. We train the model for 100 epochs with a warm-up of 10 epochs.
Early Stopping
Additionally, we employ the early stopping callback set for 10 epochs. Each class demonstrates different convergence speeds, prompting us to strike a balance by focusing on the most representative class in terms of samples across the four datasets. For instance, our primary aim is to enhance the screening of scholarly disorders.
Through experimentation, we discovered that setting the early stopping based on the global F1 score leads to situations where the overall unweighted performance appears good, yet certain classes exhibit low performance. Consequently, we established the criterion solely on the macro F1 of three classes to ensure high performance within those three, which are also the most representative in our dataset: classes 0, 1, and 4, corresponding to scholarly disorders (dyslexia, reading disorder, attention deficit).
Another consideration is using the weighted global F1 to account for the number of instances in each class. However, such an approach would result in different criteria per method, rendering the final results incomparable across the various datasets.
4.4.3. Model Evaluation
To evaluate the generalization ability of our proposed architectures, we consider the macro F1 score for each class. Additionally, we consider aggregating the different per-class F1 scores into global metrics. The different metric definitions are presented in ascending order, with each high-level metric using the metric scores of the lower level to aggregate different scores:
- Per-class Micro F1: The positive micro F1 is defined by the harmonic mean of precision and recall, . When computing the positive micro F1 score, the precision and recall of the positive class are used. Similarly, for the negative F1 score, the precision and recall of the negative class are used.
- Adding additional attention blocks: Per-class Macro F1 score: This corresponds to the unweighted mean of the positive and negative micro F1 scores for a corresponding class.
- Global F1 score: This corresponds to the mean of the macro F1 scores within each class. Similarly, we define the global positive F1 score and the global negative F1 score, which are computed using the per-class positive F1 score and the negative F1 score, respectively.
4.4.4. Additional Baseline
In addition to the supervised learning paradigm, we compare our proposed method with two additional unsupervised learning techniques that have been previously explored for eye movement analysis: CLRGaze [21] and Gazemae [19]. Both baselines are first pre-trained on our pretext dataset and then fine-tuned on our different datasets.
- Gazemae: We employ the method presented in [19], which involves training a temporal convolutional autoencoder using the variational autoencoder (VAE) approach.
- CLRGaze: We utilize the encoder training method proposed in [21], which extends the SIMCLR approach to eye movement time series.
Finally, the two baselines applied their methods to a temporal convolutional network (TCN). For a fair comparison, we substitute the TCN used in the two baselines with our VIT autoencoder for Gazemae, and the VIT encoder only for CLRGaze.
5. Results
We assess the relevance of the learned encoder representation on the multi-annotation classification task, using the annotated Ora dataset. We first, provide a qualitative estimation of the model performance on the pretext task; then, we present the quantitative result on the downstream task.
5.1. A Qualitative Overview of the Model Performance on the Pretext Task
In Appendix A, Figure A5, we present an overview of the performance of the autoencoder in terms of the ability to reconstruct the signal, evaluated on the test set. The first column corresponds to the initial signal, the second column corresponds to the noise-injected signal, the third column corresponds to the target signal masked, the fourth column corresponds to the masked eye movement signal, and the final column corresponds to the reconstructed signal. Additionally, the even rows (in red) correspond to the position conjugate signal within the X-axis, corresponding to the mean values of the eye within the same axis, while the odd rows (in red) correspond to the disconjugate signal (the difference between the two eyes). Furthermore, the first four rows correspond to samples where easy masking with hard noise injection is applied, while on the other hand, the last four rows correspond to cases where the masking is hard but the injected noise is relatively low.
5.2. A Comparison with the Existing Literature
Table 1 presents the different methods’ performances in terms of global macro F1 score, as well as positive and negative global F1 scores, when training on the four datasets. Overall, the model performances are higher in the non-reduced datasets relative to the reduced variants for each of the two visual tasks (saccade and vergence).

Table 1.
Presentation of the global macro, positive (Pos.), and negative (Neg.) F1 scores on the different downstream experiments, applied to the reduced saccade dataset.
Additionally, the fine-tuning transfer learning method consistently shows better performance relative to the encoder freezing method across different datasets, with improvements of 1.2, 1.6, 0.5, and 0.4 points on each of the four datasets, respectively. Notably, the difference in performance is amplified for the GazeMAE, with improvements of 8.7, 6.2, 13.9, and 10.3 points for the four datasets, respectively.
For instance, ORA-MAE exhibits the best performance on all datasets except for the reduced saccade dataset, achieving global F1 scores of 60.5% and 60.9% on the two unreduced datasets (saccade and vergence), and 53.5% and 51.9% on the two reduced datasets. Additionally, relative to the supervised learning baseline, SSL improves the global F1 score by 2.3 and 1.1 points on the two unreduced datasets (saccade and vergence), and by 0.4 points on the reduced vergence dataset. However, on the reduced saccade dataset, the performance difference is not consistent; while it improves the global F1 score on the vergence visual task, the performance on the reduced saccade dataset decreases by 0.4 points.
When considering the overall model performance in screening the positive class, the best performance is achieved by GazeCLR on the reduced variant of both the saccade (28.2%) and vergence (28.7%) datasets. On the other hand, when considering the non-reduced variant, ORA-MAE achieves the best performance (37.7% and 36.5%). Finally, when considering the performance in screening the negative class, the best performance is consistently achieved with our method across all datasets except the reduced dataset, where the classic supervised learning-based method achieves the best performance (80.3%).
5.3. Improving Classification Performance Using Different Head Architecture
To improve the generalization performance on the downstream task, we substitute our initial head classifier (H1) with the remaining other presented heads, and performed the training of the two transfer learning methods, as well as their corresponding baseline trained using supervised learning framework. First, we present the overall performance across each of the three explored learning methods. Further, we present the overall performance of each head separately, with a focus on the different global F1 scores for each head and for each of the four datasets separately. Finally, we provide in the appendix the per-class macro F1 score upon which the global F1 scores are computed for each presented experiments.
5.3.1. An Overview of the Global Performance of Different Heads
Before analyzing each head classifier separately, we provide, in Table 2, a summary of the overall head performance for each of the three training regimes and each of the four datasets. This summary includes the mean, standard deviation, minimum and maximum values, and the coefficient of variability and the gain, which will be further analyzed in the discussion section.

Table 2.
Summary of the mean, standard deviation, coefficient of variability, minimum and maximum values, and the gain relative to the initial head classifier’s F1 score across the 7 experimented head classifiers for each of the three methods and each of the four experimental datasets.
Overall, within the four datasets, the fine-tuning regime achieves the highest score in terms of average performance, with a global F1 score of 60.8%, and the lowest variability. Moreover, the level of variability is consistent across the four datasets, with the fine-tuning approach exhibiting the lowest variability while experimenting with the different datasets, whereas the second transfer learning method (freezing) exhibits the highest variability, suggesting the importance and relevance of exploring different head designs for this method.
Finally, considering the maximum achieved global F1 score on the vergence dataset, the freezing strategy achieves the best score of 61.5%, with a 1-point improvement relative to the fine-tuning approach. On the remaining datasets, the difference in terms of maximum score between the two transfer learning methods is less than 0.2, with maximal F1 scores of up to 61.3%, 53.9%, and 55.7% on the saccade dataset, and the reduced saccade and vergence datasets, respectively.
5.3.2. Reduced Datasets
Table 3 and Table 4 present the global macro F1 score, as well as the positive and negative global micro F1 when trained and evaluated using the reduced variant of the saccade and the vergence datasets, respectively.

Table 3.
Presentation of the global macro, positive and negative F1 scores on the different downstream experiments applied to the reduced saccade dataset.

Table 4.
Presentation of the global macro, positive and negative F1 scores on the different downstream experiments applied to the reduced vergence dataset.
Overall the, the best performances, in terms of global F1 score, are achieved when fine-tuning the trained encoder using H5 and H6 on the reduced vergence and saccade datasets, respectively (55.7 % and 53.9%). Moreover, in the two datasets, when increasing the head classifier complexity, SSL shows the best performance, relative to the baseline with an improvement up to 2.8 and 1.5 points in the reduced variant of the vergence and the saccade datasets, respectively.
Additionally, H5 shows the best performance trade-off when performing fine-tuning in the two datasets. On the other hand, the performance of the encoder freezing strategy on the two datasets are optimal when using H7 (55.5% and 53.8%). Finally, increasing the complexity of the different head does not improve the performance. Only H2 performs better than 23.4% in the saccade visual task, corresponding to the H1 variant when incorporating the normalization statistics.
When considering the global ability to screen the positive class, H3 shows the best performance on the two transfer learning methods on the saccade dataset ( 28% and 26%), while on the vergence dataset, flattening the entire encoder feature map further improves the performance (29% and 30.8 %). Finally, in Appendix A, Table A6 and Table A7, we present the per-class performance in terms of the F1 macro score when evaluated on the vergence dataset.
5.3.3. Non-Reduced Datasets
Table 5 and Table 6 present the macro F1 metrics for each of the seven head classifiers and each of the three training regimes when trained on the saccade and vergence datasets. Additionally, for each dataset and each of the seven experimented heads, two proposed transfer learning methods outperform the supervised learning methods in terms of the global macro F1 score, corresponding to the mean of the macro F1 score within the different classes.

Table 5.
Presentation of the global macro, positive, and negative F1 scores on the different downstream experiments applied to the saccade dataset.

Table 6.
Presentation of the global macro, positive, and negative F1 scores on the different downstream experiments when trained on the vergence dataset. For each regime, the best metrics score is highlighted in bold.
When considering the vergence dataset, H7 achieves the highest scores in terms of global F1 (61.5%), positive F1 (37.1%), and negative F1 (85.9%) when trained using the freezing encoder strategy. On the other hand, when considering the saccade dataset, the same method also achieves the highest macro F1 score (61%), while H5, when trained using fine-tuning, achieves a slightly higher performance by 0.3 points. It also achieves the best score in terms of the global positive F1 score (37.8%).
Additionally, when considering the head performance on each learning method, H7 achieves the best overall performance on the two datasets (61.5% and 61.0%). However, when trained using the fine-tuning regime, both H7 and H5 achieve the best trade-off within the two datasets. When training H5, we achieve macro F1 scores of 61.3% and 59.7% on the saccade and vergence datasets, respectively, while using H7, we achieve 60.5% on both datasets.
Finally, in Appendix A, Table A6 and Table A7, we present the per-class macro F1 score for the two corresponding datasets.
5.3.4. Analyzing the Optimized Overall Method Performance
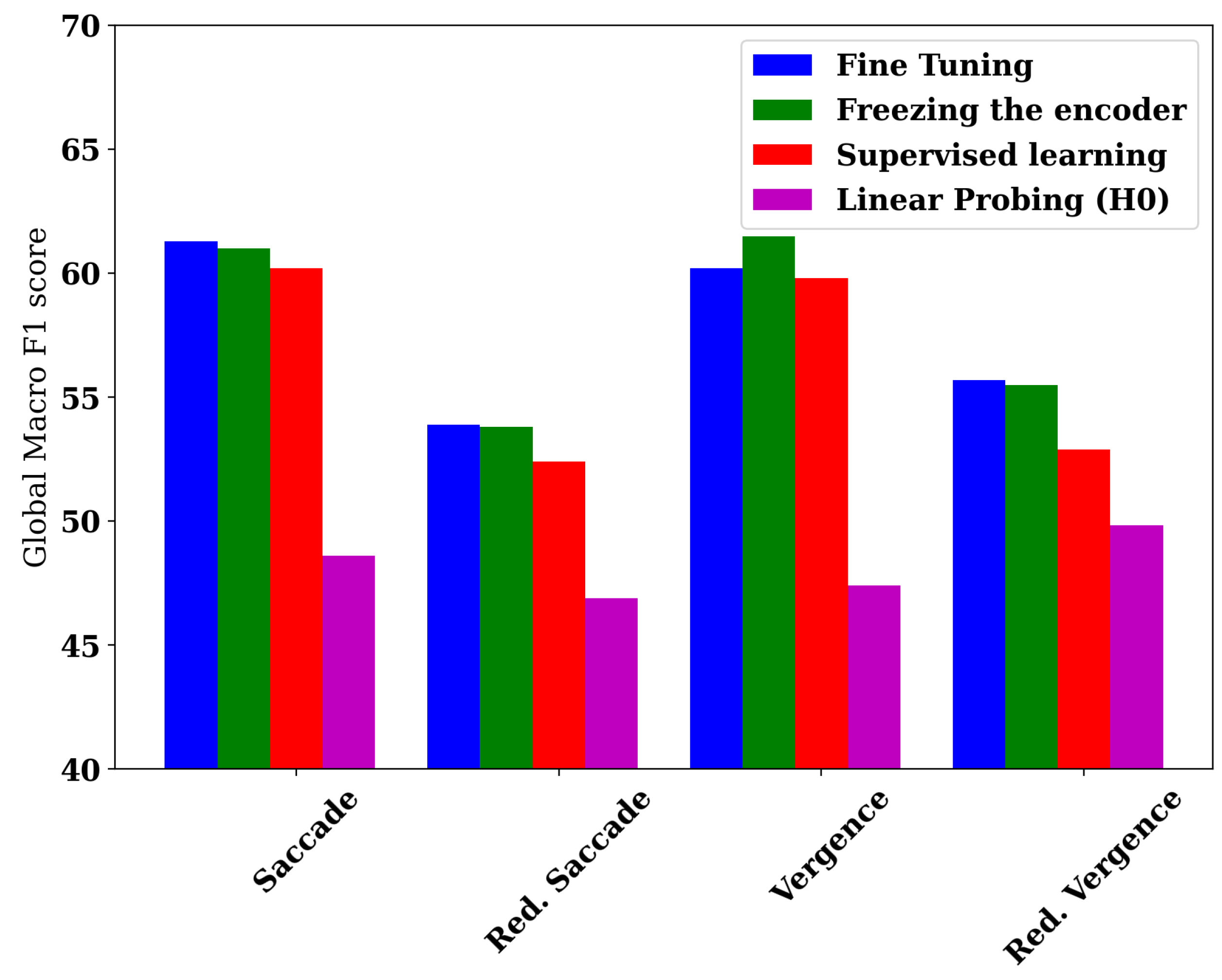
To assess the importance of head optimization, we present in Figure 2 a barplot illustrating the best head performance of each of the four learning methods: the fine-tuning approach, supervised learning, and the freezing of the encoder strategy, including the linear probing variant.
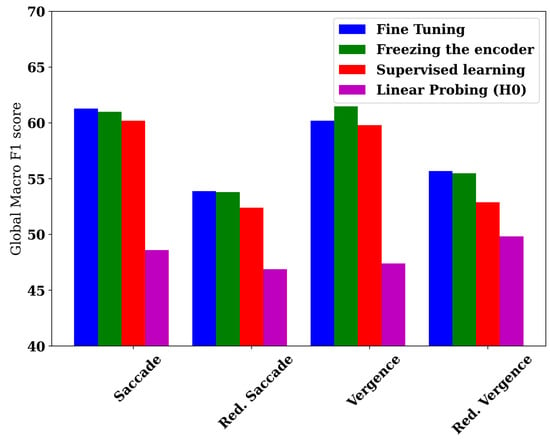
Figure 2.
A barplot depicting the performance of the best model variant for each of the four datasets.
While H0 exhibits poor results relative to the supervised learning baseline, showing a decrease of 11.6 and 5.5 points in the two saccade dataset variants, and 2.4 and 3.1 in the two vergence variants, performing head-based optimization enables the freezing-based method to outperform the same baseline, with improvements of 0.8 and 1.4 points in the saccade variants, and 1.7 and 2.6 points in the two vergence variants.
For instance, H7, when trained using the freezing of the encoder strategies, consistently achieves the best performance across all datasets, except for the reduced vergence dataset, where it attains the second-best performance. This allows the encoder–freezing-based transfer learning method to achieve the highest performance, with a global macro F1 score of 61.5%. This corresponds to macro F1 scores of 64.7%, 66.1%, and 61.1% on our main target classes (0, 1, and 4), namely dyslexia, reading disorder, and attention deficit, thereby enabling the use of AI for screening scholar disorders to prevent academic failure.
6. Discussion
6.1. Analyzing Performance Gains through Head Classifier Design Optimization
The different heads are trained and evaluated on four different datasets. Therefore, directly comparing them is not appropriate due to the presence of several biases, including the task complexity as well as the sample size. As a result, we are interested in comparing their gains, defined as the difference in terms of global F1 score between each best head score and the corresponding baseline head (H1). Then, we explore the impact of optimizing the head classifier in terms of the obtained gain.
Initially, using Table 2, we compare the gain obtained across the three regimes. Then, we investigate the high variability under the freezing transfer learning regime. Finally, we analyze the effect of sample size by comparing, for each of the two visual tasks and each of the two transfer learning methods, their corresponding gains on both the large (non-reduced) and the small (reduced) datasets.
6.1.1. A Comparison of the Performance Gains within Different Training Methods
When analyzing the gains of each of the two transfer learning regimes on the reduced and non-reduced datasets, the gain in the reduced dataset is higher (2.4, 2.7, 2.2, and 3.6 points), relative to the non-reduced dataset (0.4, 0.6, 0, and 1.2 points).
For each of the four datasets, when comparing the difference in gain between the two transfer learning regimes, we observe a mean difference of 0.3 on the two non-saccade datasets (0.2 and 0.4) and a mean difference of 1.3 points on the two vergence datasets (1.2 and 1.4), where the learning task is more complex due to the nature of the vergence eye movement.
This can be attributed to the nature of the two transfer learning algorithms and the complexity of the downstream task. While the fine-tuning regime allows for optimizing the model weights on the second task, thus making the head design optional, the freezing regime relies heavily on the complexity of the head classifier to learn the downstream task using the learned representation.
On the other hand, in supervised learning scenarios, the observed gains are relatively modest (less than 0.6 in loss). In this regime, where the entire network undergoes training, the addition of a complex head classifier atop corresponds to simply stacking additional layers, thus resulting in only marginal increases in model expressivity. We hypothesize that the marginal increase is mainly attributed to the incorporated normalization statistics.
6.1.2. On the Importance of Exploring Various Head Classifier Designs When Freezing the Encoder
When examining the variability of global F1 scores across the different head classifiers on each of the four datasets, our analysis reveals a notable increase in the coefficient of variability within the freezing regime compared to the fine-tuning regime, by a factor of 1.89. This heightened sensitivity to classifier design variations can be attributed to disparities in model expressivity among different heads.
In the fine-tuning regime, model expressivity is predominantly influenced by the trainable encoder’s capacity. However, in the freezing regime, where the entire encoder weights are fixed, the model’s expressivity in learning classification from a pre-learned representation is solely dependent on the corresponding trainable head’s expressivity.
As result, in the second transfer learning method, which involves freezing the encoder, the best performance is obtained with the biggest head in terms of model expressivity (H7).
This phenomenon becomes more pronounced when increasing the complexity of the downstream task. For instance, when freezing the encoder, the performance gain is more significant in the vergence visual task compared to the saccade visual task, evident in both the non-reduced (0.6 vs. 1.2 points) and reduced datasets (2.7 vs. 3.6 points).
6.1.3. Effect of Sample Size on Representation Relevance
For each dataset and transfer learning scenario, when comparing the difference in gains between the reduced and non-reduced variants, we consistently observe a difference greater than 2 points. Specifically, we note differences of 2.0 and 2.1 points for the saccade visual task, and 2.2 and 2.4 points for the vergence dataset. This suggests that the significance of enhancing the head classifier complexity, in terms of global F1 score, is inversely proportional to the sample size.
Thus, increasing the dataset size enriches the learned representation, rendering additional layers (i.e., head classifiers) relatively unnecessary during retraining. Conversely, for small datasets, augmenting the head classifier complexity during downstream task learning enhances generalization ability. For instance, when considering the method showing the best overall performance, namely the fine-tuning regime, we observe relatively low gains of 0.4 and 0 in the two non-reduced datasets. However, when training on the two reduced datasets using the same setting, gains of 2.4 and 2.2 are achieved.
6.2. Comparing SSL and SL Algorithms under Different Settings
Comparing the difference in the model performance, when training using self-supervised learning (SSL) with fine-tuning and supervised learning (SL), the difference in global F1 score increases in the reduced dataset: from 1.1 points to 1.5 points in the saccade dataset, and from 0.4 to 3.8 points in the vergence dataset. This confirms the potential of the SSL algorithm when facing a small-sized dataset. Additionally, when comparing the same difference in the saccade dataset vs. vergence dataset, which is more complex, we observe that the same difference increases by increasing the task complexity. For instance, the difference of the performance, in terms of global macro F1 score, increases from 1.5 (saccade) to 3.8 (vergence) points in the reduced datasets. Finally, when considering the reduced vergence dataset, the difference in the performance of the two frameworks, and in the saccade dataset vs. reduced vergence dataset, we observe that the difference becomes higher due to the presence of the two factors discussed above (increasing the task complexity and reducing the training set size).
6.3. Additional Design Choice
6.3.1. Architecture Building Block Choice
Traditionally, CNNs have shown great performance compared to Transformer-based architectures on small datasets, attributed to implicit regularization such as weight sharing. However, applying the MAE algorithm directly to CNNs has several limitations that are not evident when incorporating it to build a CNN autoencoder for the MAE task [29]. For instance, ref. [58] investigated solving the distribution shift problem by using sparse convolution. On the other hand, RNNs have been used for seq2seq modeling before Transformers [59].
Ref. [30], on the other hand, explored building the autoencoder using an RNN architecture. While the model achieves promising results on the different evaluated datasets, when varying the input size of the encoder from 336 to 1440 on the ETTh2 dataset, the model’s mean-squared error (MSE) is correlated with the encoder input information (input size).
For example, with our input size of 8192, which is due to our sample length, RNNs may not be suited as they suffer from the information bottleneck issue [60]. Instead, we use Transformer architecture, which shows better performance on long-length input in seq2seq models [61] by allowing the model to focus on different parts of the input instead of having fixed-size context vectors. As a result, we build our encoder and decoder using Vanilla Transformer.
6.3.2. Combining the Masking and Denoising Pretext Task
While the masking-based algorithm can be regarded as an extreme case of the denoising algorithm, with generated noise that makes the signal constant within time (hence, masked), the two tasks aim to learn different objectives.
For instance, as opposed to the masking algorithm, where the masked zones are ignored by the encoder, the objective is to reconstruct them using the unmasked zone. In the denoising algorithm, the objective is to extract the information from the noisy or corrupted signal.
However, the noise in our signal is very high due to the noise inherent from the eye-tracking system. As a result, we consider training the model to denoise the signal. On the other hand, masking autoencoders are more suited for attention-based architecture and have been used in the literature recently, showing better performance when used as a pretext task for SSL.
In our approach, we considered the masking heuristic for performance and the denoising heuristic because it is a realistic task and required for the model to correctly perform the downstream classification. As a result, it is not only a pretext task but can also be regarded as a preliminary task for classification.
6.3.3. Passing the Target Signal to the Decoder
Adding the target signal to the decoder: Our choice to perform this is motivated by the fact that this information is never deteriorated, as opposed to eye movement time series, whose accuracy is mainly influenced by the accuracy of the eye-tracking system. As a result, our approach aims to encourage the model to reconstruct the inaccurate eye movement region by observing the accurate region and the target signal, which encodes the stimulus state.
6.3.4. Using High Sample Signal Frequency
Our time series recordings are registered with a frequency of 200 Hz. As a result, a 2-minute eye movement recording corresponds to a multivariate time series of 24,000 points. In order to mitigate the long sample length problem, a different approach would be to downsample each recording to 60 Hz, for example, before processing. However, in our approach, we aim to study eye movement at a low level, providing the model with the ability to analyze each saccadic movement.
The average duration of a saccadic movement is between 20 ms and 40 ms, which corresponds to lengths between 4 and 8 points. As a result, decreasing the frequency further could compromise the model’s ability to capture such patterns.
7. Limitations and Future Directions
7.1. Cross-Validation Evaluation
This study represents a preliminary exploration into various settings for each of the two learning stages. Due to computational constraints, we were only able to perform each training once. However, a promising avenue for future research involves employing multi-fold cross-validation with the best settings identified in this study. This approach would help mitigate the variability in performance estimation, thereby enhancing the reliability of the reported results.
7.2. Comparing the Reduced and Non-Reduced Datasets
The performance on the two variants (reduced and non-reduced) is different and consistent across the saccade and the vergence datasets. For the saccade dataset, this difference can be attributed to the reduction in sample size, as presented in Appendix A, Table A1. Another possible risk, which may contribute to amplifying this difference, is the presence of a subset of shared unlabeled data to be used in the pretext task and for evaluating the downstream task.
We hypothesize that the difference in performance is attributed to the differences in sample size rather than the risk of information leak, because, while the supervised learning-based training is not concerned with this limitation (risk of leak), the difference in performance (non-reduced vs. reduced) is also present in supervised learning models (red), as depicted in Figure 2. Moreover, the difference is bigger relative to the SSL-based model (7.8 and 7.1 points in the saccade and the vergence datasets, respectively). Meanwhile, a future direction would be to eliminate this bias risk and perform the two-stage training to perform all the experiments to confirm our hypothesis.
7.3. Conducting More In-Depth Evaluation
In this exploratory study, our objective is to explore different settings in preliminary studies to optimize our algorithm’s components. Due to the high number of experiments conducted and the computational costs associated with each experiment, we conduct each one only once. However, a future direction is to determine the optimal settings from this exploration and conduct more in-depth experiments, including cross-validation, and adapt our evaluation method to evaluate statistically the different findings and comparison.
At this stage, we propose a self-learning method tailored for stimulus-driven datasets. This method focuses solely on eye movement data obtained during stimulus-driven tests, where the information relative to the stimulus is encoded in a time series. Such a constraint aims to simplify our task’s complexity [12], thereby reducing the intricacy of the learning process. Consequently, the generalizability of our findings to non-stimulus-driven datasets remains unexplored.
7.4. Pretext Task Reconstruction
The results are very promising for the signal reconstruction task; the model was able to remove noise corruption. Figure A5 in Appendix A presents an illustration of the reconstructed signal. The model was evaluated only visually by inspecting its predictions and comparing them to the baseline. The model achieved an MSE of 0.017; however, it is difficult to interpret this score. A future direction would be to integrate this architecture into the ideal preprocessing for the denoising task and as a backbone for the classification task. Another important direction is to introduce the confidence level time series to the model and update it according to the quantity of noise added.
7.5. Exploiting the First-Layer Decoders
Another important direction is exploring the incorporation of the first-layer decoders within the final encoder architecture. For instance, the encoder embedding and the stimulus target signal are combined at the decoder level, allowing the decoder to capture the relationship between these two sources of information. By incorporating the first decoder layers, we aim to integrate the knowledge learned from the pretext task into the analysis of eye movement data relative to the target signal. Such a mechanism improves the generalization performance on the downstream task. For example, our findings in the ablation study published in [62] reveal that incorporating the REMOBI target signal improves the global macro F1 score by an average of 2 points across the three folds.
7.6. Toward a Unified Meta Model
In contrast to the conventional practice of employing a distinct model for each study and screening task, our objective is to establish a singular meta model trained on the entirety of available annotated data. This approach not only facilitates an increase in model complexity but also maximizes the data size accessible for training purposes. The unified meta model serves as a comprehensive representation of the underlying patterns present in the diverse datasets. In the proposed methodology, for each specific study, we leverage the pre-trained meta model to derive a meaningful representation from the input space. This process allows us to extract essential features and patterns encapsulated within the vast and heterogeneous data. Subsequently, a secondary classifier is trained atop the meta model’s output, specifically tailored to the target class distribution and eye movement types relevant to the corresponding study.
By utilizing a pre-trained meta model, instead of the model learning a mapping from the original input space of 8192, it focuses on the more condensed and informative representation of size 512 generated by the meta model. we thus substantially reduce the amount of data required for training the subsequent classifiers.
8. Conclusions
In this preliminary study, we introduce a novel self-supervised learning pretext task, tailored to stimulus-driven eye movement data, coupled with a denoising task to enhance resilience against simulated eye tracking errors.
The proposed pretext task aims to capture both the cognitive (brain) and the motor (eye) aspects by reconstructing the eye movement position signal using up to 12.5% of unmasked eye movement signal patches, along with the entire REMOBI target signal. Consequently, the encoder learns a high-dimensional representation of a multivariate time series of length 8192 points, corresponding to approximately 40 s, while the decoder learns the reconstruction task, using the learned representation along with the REMOBI target signal.
In the subsequent learning phase (downstream task), we evaluate the learned encoder representation on screening eight groups of pathological tasks, including dyslexia, reading disorders, and attention deficit disorders, using various datasets, and compare our method with two different SSL approaches as well as a supervised learning regime. Moreover, we conduct an exploratory analysis employing various head architectures and different transfer learning techniques to optimize performance on the downstream task. Our approach achieved macro F1 scores of 61.5% on the vergence dataset and 64.7%, 66.1%, and 61.1% on dyslexia, reading disorders, and attention deficit disorders, respectively. These results highlight the potential of self-learning algorithms in facilitating the screening process for a spectrum of pathologies, paving the way for further advancements in this field.
9. Patents
Zoï Kapoula has applied for patents for the technology used to conduct this experiment: REMOBI table (patent US8851669, WO2011073288); AIDEAL analysis software (EP20306166.8, 7 October 2020; EP20306164.3, 7 October 2020—Europe). Patent application pending EP22305903.1.
Author Contributions
Supervision, Z.K. and T.P.; methodology, A.E.E.H.; software, A.E.E.H.; validation, T.P. and Z.K.; formal analysis, A.E.E.H.; investigation, A.E.E.H.; resources, Z.K. and T.P.; data curation, A.E.E.H.; Conceptualization, A.E.E.H.; writing—original draft, A.E.E.H.; writing—review and editing, Z.K. and T.P.; visualization, A.E.E.H.; project administration, Z.K. and T.P.; funding acquisition, Z.K. All authors have read and agreed to the published version of the manuscript.
Funding
Alae Eddine El Hmimdi is funded by Orasis-Ear and ANRT, CIFRE.
Informed Consent Statement
This meta-analysis drew upon data sourced from Orasis Ear, in collaboration with clinical centers employing Remobi and Aideal technology. Participating centers agreed to store their data anonymously for further analysis.
Data Availability Statement
The datasets generated and/or analyzed during the current study are not publicly available. This meta-analysis drew upon data sourced from Orasis Ear, in collaboration with clinical centers employing REMOBI and Aideal technology. Participating centers agreed to store their data anonymously for further analysis. However, upon reasonable request, they are available from the corresponding author.
Acknowledgments
This work was granted access to the HPC resources of IDRIS under the allocation 2024-AD011014231 made by GENCI.
Conflicts of Interest
Zoï Kapoula is the founder of Orasis-EAR.
Appendix A
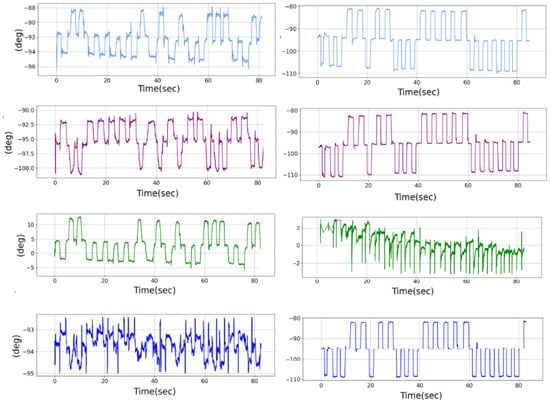
Figure A1.
An overview of the left and right position signals during the saccade (right columns) and vergence (left columns) tests. The first and second rows correspond to the left eye and right eye position signals, respectively. Additionally, the last two rows correspond to the disconjugate and conjugate signals. Note that the conjugate signal allows for better analysis of the saccade recording, while the disconjugate signal facilitates better analysis of the vergence recording.
Figure A1.
An overview of the left and right position signals during the saccade (right columns) and vergence (left columns) tests. The first and second rows correspond to the left eye and right eye position signals, respectively. Additionally, the last two rows correspond to the disconjugate and conjugate signals. Note that the conjugate signal allows for better analysis of the saccade recording, while the disconjugate signal facilitates better analysis of the vergence recording.
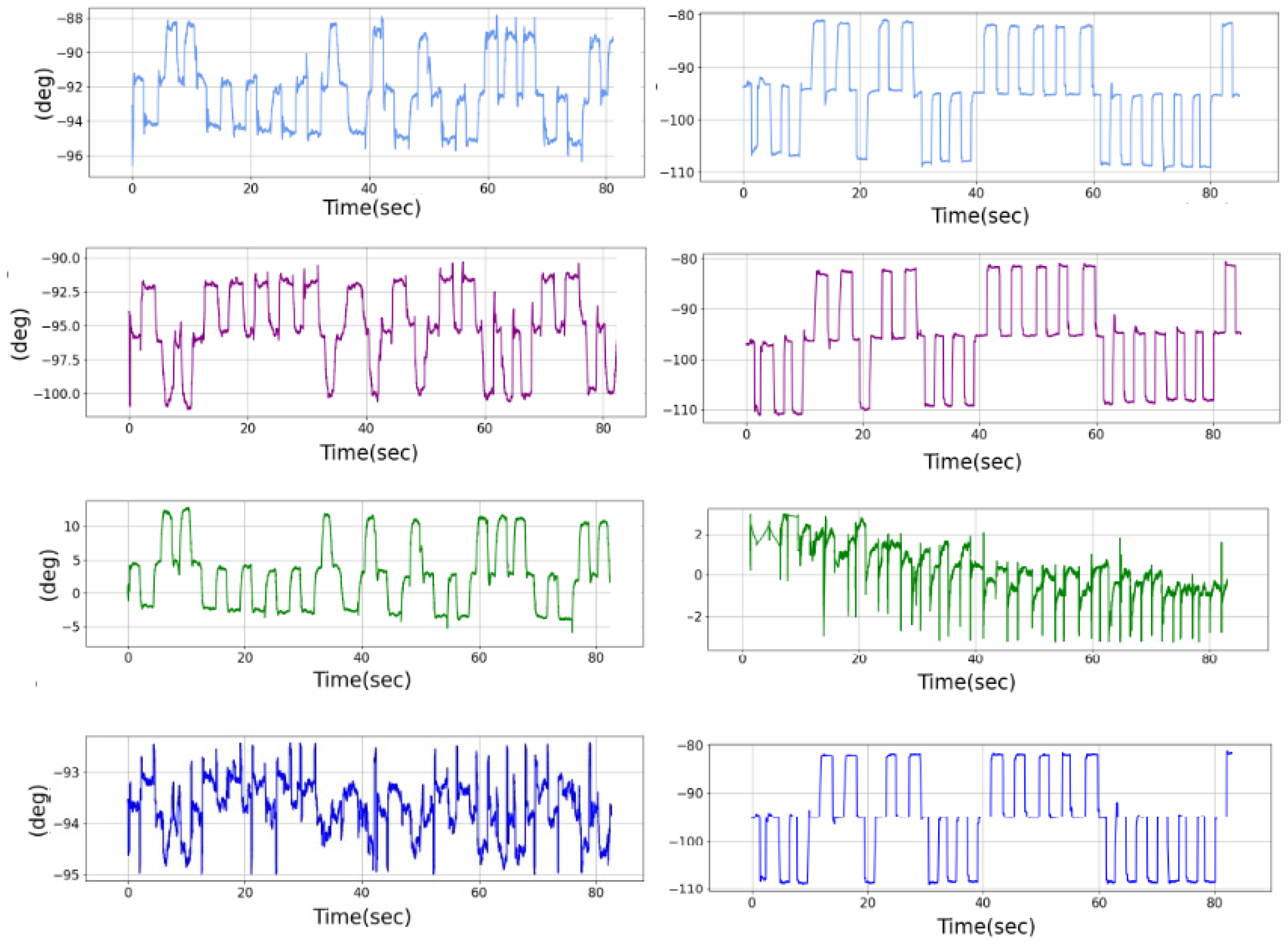
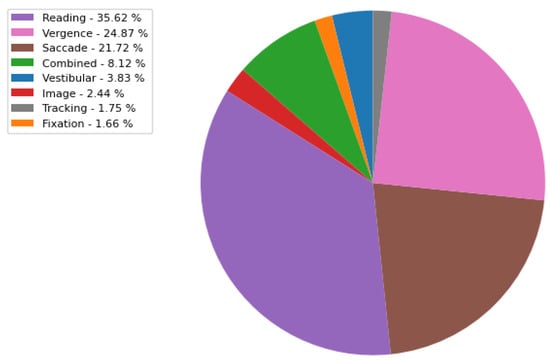
Figure A2.
Visual task distribution pie chart for the different eye movement recording types on Ora-M.
Figure A2.
Visual task distribution pie chart for the different eye movement recording types on Ora-M.
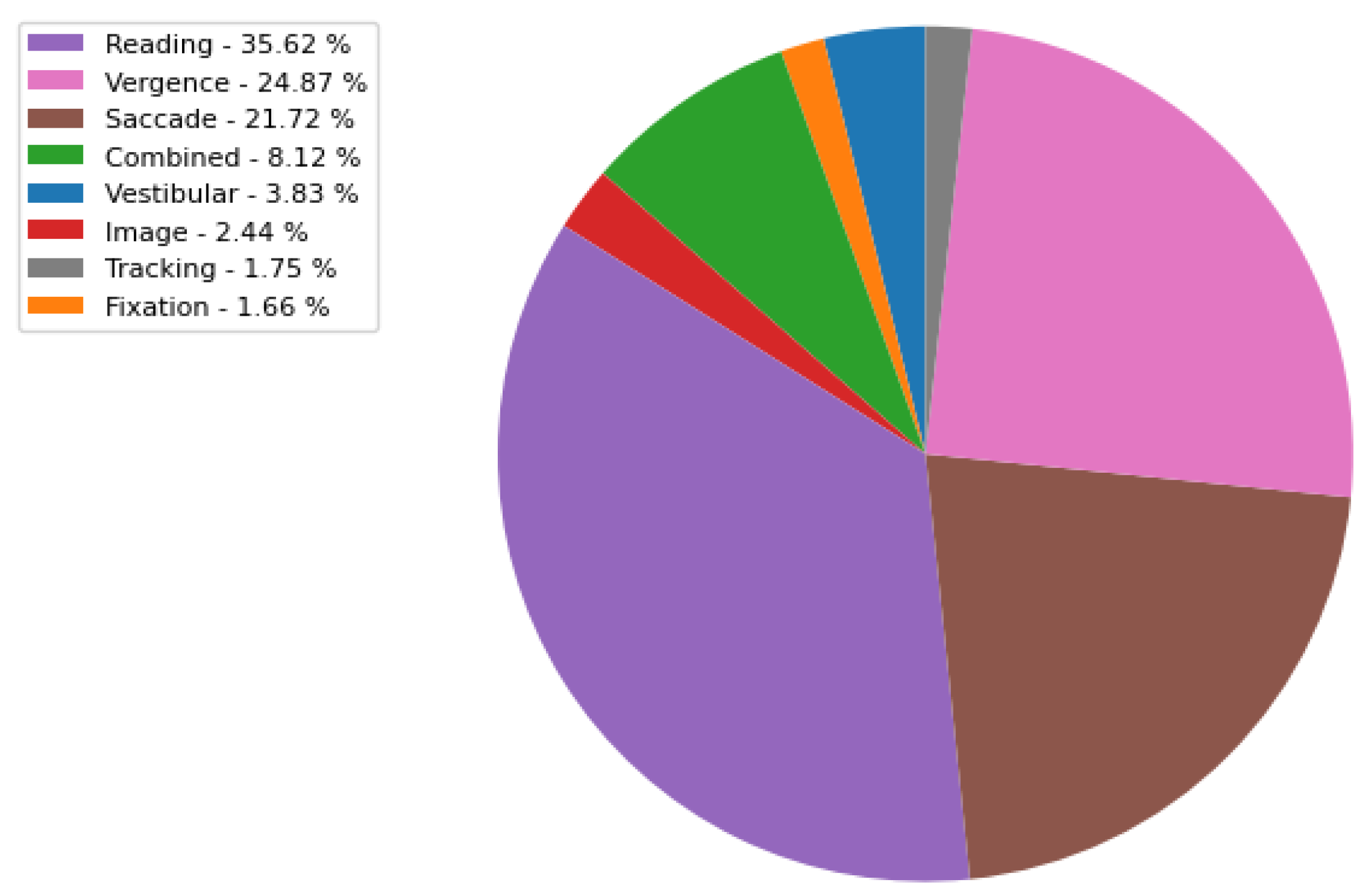

Table A1.
Train and test sets’ per-class counts for each dataset of the four datasets, used for the downstream task.
Table A1.
Train and test sets’ per-class counts for each dataset of the four datasets, used for the downstream task.
| Saccade | Vergence | |||||||
|---|---|---|---|---|---|---|---|---|
| Reduced | Non-Reduced | Reduced | Non-Reduced | |||||
| Class | Train | Test | Train | Test | Train | Test | Train | Test |
| 0 | 5302 | 9170 | 17,458 | 33,090 | 4830 | 9076 | 16,714 | 33,676 |
| 1 | 3970 | 12,898 | 24,180 | 46,864 | 6696 | 13,136 | 24,714 | 47,998 |
| 2 | 7552 | 2832 | 5612 | 12,056 | 3622 | 2750 | 5616 | 12,088 |
| 3 | 4162 | 3212 | 6572 | 14,022 | 2960 | 3358 | 6134 | 13,734 |
| 4 | 5200 | 12,132 | 22,606 | 43,520 | 4496 | 11,840 | 21,066 | 42,862 |
| 5 | 2904 | 4752 | 7956 | 17,974 | 2212 | 5712 | 12,200 | 18,730 |
| 6 | 5156 | 7570 | 14,280 | 28,826 | 2552 | 6708 | 12,258 | 25,158 |
| 7 | 1802 | 1784 | 3490 | 7,178 | 1616 | 2812 | 4958 | 10,728 |
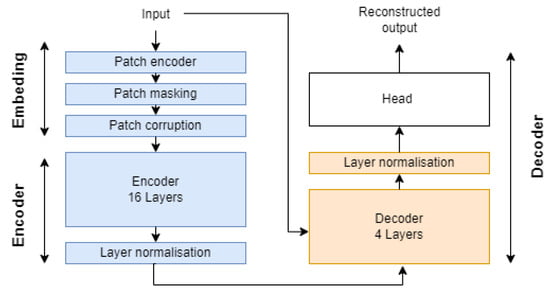
Figure A3.
An overview of the proposed architecture; note that the decoder takes as input the encoder embedding as well as the REMOBI target signal.
Figure A3.
An overview of the proposed architecture; note that the decoder takes as input the encoder embedding as well as the REMOBI target signal.
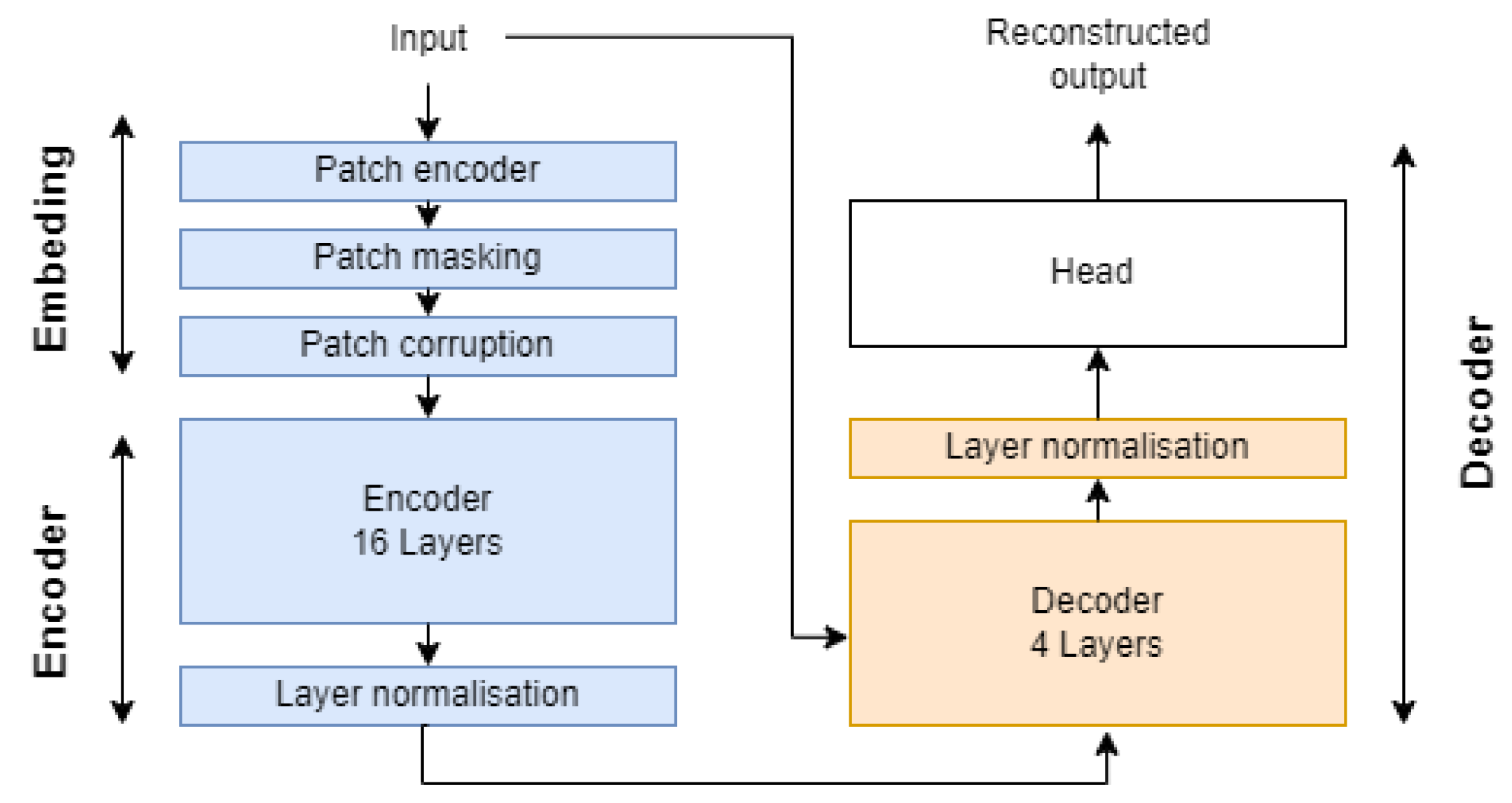
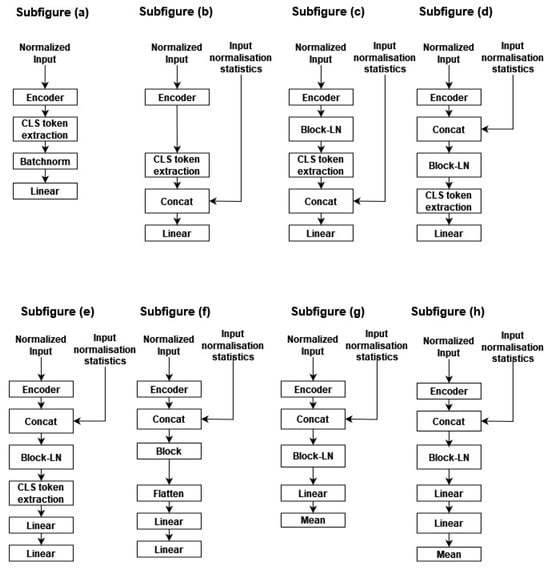
Figure A4.
An overview of the 8 explored head classifiers for the downstream task. For simplicity, we omit the activation layers, dropout layer, as well as the layers expanding the normalization features’ dimensional tensors to have a compatible shape with the output feature map. The flattening layer reduces the temporal dimension. For the Transformer block (Block), we use the timm library implementation. Furthermore, block-LN corresponds to the block implementation followed by a LayerNorm layer.
Figure A4.
An overview of the 8 explored head classifiers for the downstream task. For simplicity, we omit the activation layers, dropout layer, as well as the layers expanding the normalization features’ dimensional tensors to have a compatible shape with the output feature map. The flattening layer reduces the temporal dimension. For the Transformer block (Block), we use the timm library implementation. Furthermore, block-LN corresponds to the block implementation followed by a LayerNorm layer.
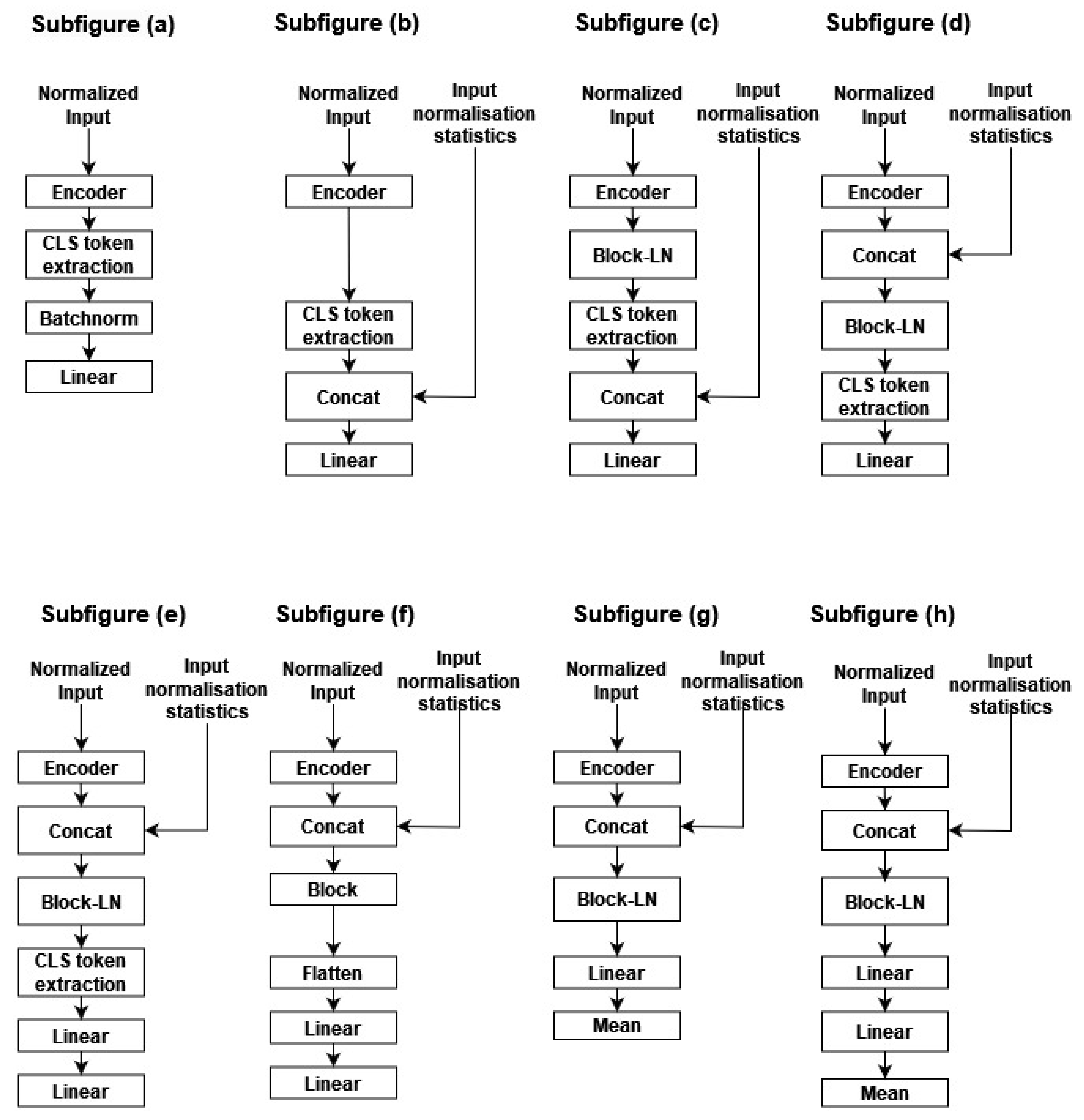
Figure A5.
Overview of autoencoder performance in signal reconstruction. Columns represent (1) initial signal, (2) noise-injected signal, (3) target signal masked, (4) masked eye movement signal, and (5) reconstructed signal. Even rows (in red) show the position of conjugate signals within the X-axis, corresponding to mean eye values, while odd rows (in red) display disconjugate signals (the difference between the eyes). The first four rows depict samples with easy masking and hard noise injection, while the last four rows illustrate cases with hard masking and relatively low noise injection.
Figure A5.
Overview of autoencoder performance in signal reconstruction. Columns represent (1) initial signal, (2) noise-injected signal, (3) target signal masked, (4) masked eye movement signal, and (5) reconstructed signal. Even rows (in red) show the position of conjugate signals within the X-axis, corresponding to mean eye values, while odd rows (in red) display disconjugate signals (the difference between the eyes). The first four rows depict samples with easy masking and hard noise injection, while the last four rows illustrate cases with hard masking and relatively low noise injection.
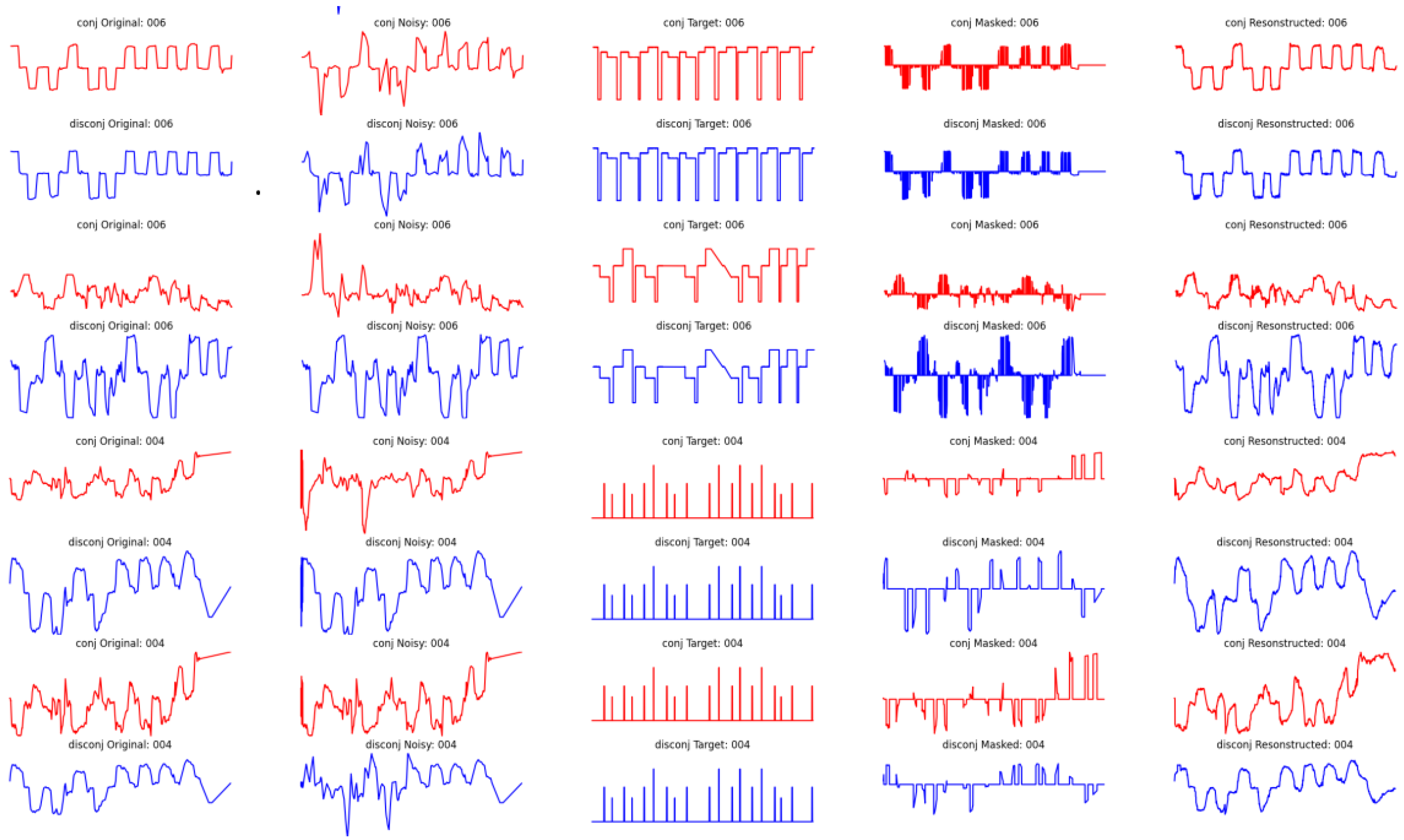

Table A2.
Second-stage optimization settings.
Table A2.
Second-stage optimization settings.
| Training Type | Initial Learning Rate | Weight Decay | Initialization | Encoder Weights |
|---|---|---|---|---|
| Freezing | 0 | Pretext Weight | Frozen | |
| Fine-tuning | Pretext Weight | Trainable | ||
| Sup. Learning | Random | Trainable |

Table A3.
Alpha (class balancing) parameters on the focal loss for non-reduced and reduced values. Note that the different hyperparameters are shared across the two visual tasks.
Table A3.
Alpha (class balancing) parameters on the focal loss for non-reduced and reduced values. Note that the different hyperparameters are shared across the two visual tasks.
| Non-Reduced | Reduced | |
|---|---|---|
| Class 0 | 0.73 | 0.8 |
| Class 1 | 0.61 | 0.8 |
| Class 2 | 0.9 | 0.8 |
| Class 3 | 0.88 | 0.8 |
| Class 4 | 0.67 | 0.8 |
| Class 5 | 0.83 | 0.8 |
| Class 6 | 0.81 | 0.8 |
| Class 7 | 0.31 | 0.2 |

Table A4.
Per-class sample macro F1 scores for each downstream method when training the vergence dataset. The best metrics for each head classifier are highlighted in bold. Note that Head0 corresponds to the linear probing method.
Table A4.
Per-class sample macro F1 scores for each downstream method when training the vergence dataset. The best metrics for each head classifier are highlighted in bold. Note that Head0 corresponds to the linear probing method.
| Technique | Head | Class 0 | Class 1 | Class 2 | Class 3 | Class 4 | Class 5 | Class 6 | Class 7 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 60.5 | 64.9 | 54.1 | 53.1 | 61.0 | 63.0 | 59.8 | 67.4 | |
| 2 | 61.4 | 63.6 | 56.2 | 53.1 | 59.0 | 61.9 | 59.8 | 67.0 | |
| Fine-tuning | 3 | 62.2 | 66.6 | 56.0 | 49.0 | 60.1 | 60.7 | 58.0 | 64.2 |
| 4 | 61.6 | 64.9 | 54.9 | 50.6 | 59.6 | 61.1 | 59.9 | 65.0 | |
| 5 | 64.0 | 66.0 | 55.4 | 50.6 | 58.3 | 60.3 | 55.4 | 67.3 | |
| 6 | 63.9 | 65.2 | 54.2 | 51.3 | 58.7 | 59.8 | 59.6 | 69.1 | |
| 7 | 61.9 | 65.6 | 56.2 | 50.6 | 59.2 | 62.3 | 62.0 | 66.0 | |
| 0 | 52.6 | 53.6 | 47.1 | 40.5 | 47.0 | 50.5 | 41.9 | 45.8 | |
| 1 | 61.0 | 63.7 | 57.0 | 51.2 | 57.4 | 63.3 | 58.9 | 61.7 | |
| 2 | 62.3 | 64.8 | 56.5 | 52.3 | 58.2 | 60.6 | 58.9 | 68.0 | |
| Freezing | 3 | 62.1 | 63.6 | 55.3 | 52.4 | 59.3 | 62.4 | 57.5 | 68.5 |
| 4 | 61.4 | 64.1 | 54.4 | 51.0 | 59.7 | 63.0 | 58.5 | 67.0 | |
| 5 | 61.7 | 63.0 | 56.3 | 51.7 | 58.2 | 62.4 | 58.0 | 68.7 | |
| 6 | 58.9 | 61.5 | 53.5 | 50.9 | 57.0 | 59.5 | 57.7 | 68.7 | |
| 7 | 64.7 | 66.1 | 56.6 | 53.5 | 61.1 | 63.4 | 58.2 | 68.4 | |
| 1 | 59.8 | 61.9 | 53.1 | 50.0 | 57.5 | 60.7 | 57.7 | 65.1 | |
| 2 | 59.7 | 63.1 | 53.5 | 51.1 | 56.0 | 60.0 | 57.9 | 66.9 | |
| Sup. Learning | 3 | 60.4 | 61.7 | 54.3 | 50.7 | 55.8 | 60.9 | 56.8 | 67.2 |
| 4 | 62.2 | 63.4 | 55.4 | 52.7 | 57.7 | 61.5 | 58.5 | 66.9 | |
| 5 | 60.0 | 62.9 | 55.2 | 51.0 | 57.3 | 62.7 | 58.2 | 67.8 | |
| 6 | 59.3 | 62.4 | 53.1 | 49.7 | 57.3 | 60.7 | 57.9 | 67.5 | |
| 7 | 59.6 | 63.8 | 55.8 | 51.8 | 58.1 | 61.0 | 58.3 | 65.3 |

Table A5.
Per-class sample macro F1 scores for each downstream method when training the saccade dataset. The best metrics for each head classifier are highlighted in bold. Note that Head0 corresponds to the linear probing method.
Table A5.
Per-class sample macro F1 scores for each downstream method when training the saccade dataset. The best metrics for each head classifier are highlighted in bold. Note that Head0 corresponds to the linear probing method.
| Technique | Head | Class 0 | Class 1 | Class 2 | Class 3 | Class 4 | Class 5 | Class 6 | Class 7 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 64.6 | 64.8 | 57.3 | 54.4 | 60.2 | 63.3 | 61.2 | 61.3 | |
| 2 | 63.9 | 65.6 | 57.5 | 56.3 | 60.2 | 63.2 | 61.7 | 60.9 | |
| Fine-tuning | 3 | 64.3 | 64.4 | 56.6 | 53.9 | 59.2 | 63.0 | 58.5 | 59.6 |
| 4 | 64.5 | 65.9 | 57.5 | 55.0 | 60.5 | 64.2 | 59.9 | 60.2 | |
| 5 | 64.6 | 65.2 | 56.3 | 56.0 | 61.5 | 64.3 | 61.1 | 61.3 | |
| 6 | 64.1 | 66.0 | 56.6 | 55.0 | 59.3 | 65.3 | 61.2 | 60.7 | |
| 7 | 64.9 | 63.6 | 56.2 | 54.4 | 59.9 | 64.0 | 61.0 | 59.9 | |
| 0 | 48.9 | 53.5 | 50.5 | 43.8 | 46.0 | 53.1 | 44.8 | 48.5 | |
| 1 | 64.3 | 63.5 | 58.4 | 54.8 | 58.4 | 62.4 | 60.8 | 60.5 | |
| 2 | 62.4 | 63.4 | 58.9 | 55.6 | 58.8 | 64.9 | 60.8 | 59.0 | |
| Freezing | 3 | 63.2 | 65.0 | 56.9 | 56.3 | 60.1 | 63.4 | 61.2 | 59.4 |
| 4 | 61.4 | 61.8 | 57.2 | 56.2 | 60.0 | 67.1 | 59.1 | 61.2 | |
| 5 | 63.5 | 63.7 | 56.2 | 53.6 | 57.9 | 65.5 | 61.9 | 60.3 | |
| 6 | 59.5 | 59.9 | 55.9 | 53.2 | 57.0 | 62.0 | 59.1 | 61.0 | |
| 7 | 62.8 | 64.4 | 57.7 | 54.3 | 60.7 | 67.6 | 60.7 | 59.7 | |
| 1 | 62.9 | 62.2 | 57.8 | 55.5 | 56.8 | 62.7 | 59.4 | 61.5 | |
| 2 | 61.8 | 61.8 | 56.0 | 53.9 | 57.0 | 61.1 | 60.0 | 59.5 | |
| Sup. Learning | 3 | 63.5 | 63.0 | 57.2 | 53.8 | 58.1 | 61.6 | 60.9 | 59.4 |
| 4 | 61.9 | 62.5 | 56.8 | 54.2 | 55.5 | 62.7 | 59.3 | 58.2 | |
| 5 | 63.6 | 61.8 | 56.8 | 53.1 | 59.8 | 64.0 | 60.5 | 62.1 | |
| 6 | 61.1 | 59.2 | 56.1 | 53.1 | 56.4 | 59.7 | 57.9 | 60.6 | |
| 7 | 63.6 | 65.0 | 57.1 | 54.9 | 57.6 | 61.7 | 59.5 | 62.1 |

Table A6.
Per-class sample macro F1 scores for each downstream method when training the reduced vergence dataset. The best metrics for each head classifier are highlighted in bold. Note that Head0 corresponds to the linear probing method.
Table A6.
Per-class sample macro F1 scores for each downstream method when training the reduced vergence dataset. The best metrics for each head classifier are highlighted in bold. Note that Head0 corresponds to the linear probing method.
| Technique | Head | Class 0 | Class 1 | Class 2 | Class 3 | Class 4 | Class 5 | Class 6 | Class 7 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 59.6 | 61.4 | 45.7 | 52.6 | 51.5 | 51.1 | 54.3 | 52.3 | |
| 2 | 57.3 | 62.6 | 47.0 | 55.3 | 58.3 | 56.5 | 52.3 | 46.8 | |
| Fine-tuning | 3 | 61.9 | 67.0 | 52.3 | 50.6 | 54.6 | 54.3 | 52.4 | 48.9 |
| 4 | 55.7 | 62.8 | 48.8 | 52.2 | 56.2 | 52.2 | 53.5 | 52.2 | |
| 5 | 58.6 | 62.8 | 57.1 | 54.1 | 59.7 | 53.2 | 52.6 | 47.1 | |
| 6 | 57.8 | 62.1 | 45.0 | 52.9 | 54.3 | 57.1 | 49.0 | 47.9 | |
| 7 | 55.5 | 61.7 | 46.8 | 52.3 | 53.5 | 54.2 | 48.8 | 48.1 | |
| 0 | 55.7 | 56.7 | 49.1 | 46.7 | 46.3 | 50.7 | 42.4 | 51.2 | |
| 1 | 60.5 | 61.0 | 49.0 | 48.7 | 49.8 | 52.1 | 46.6 | 47.5 | |
| 2 | 59.7 | 61.2 | 48.2 | 47.8 | 47.0 | 52.7 | 54.0 | 47.5 | |
| Freezing | 3 | 58.6 | 59.4 | 57.7 | 49.5 | 49.1 | 49.1 | 48.3 | 47.5 |
| 4 | 57.3 | 59.0 | 52.6 | 48.8 | 54.2 | 51.4 | 51.4 | 47.0 | |
| 5 | 60.5 | 63.9 | 58.6 | 49.6 | 53.1 | 51.5 | 53.6 | 53.5 | |
| 6 | 57.0 | 54.5 | 49.8 | 47.2 | 49.5 | 46.8 | 50.5 | 47.5 | |
| 7 | 60.8 | 64.1 | 51.0 | 51.2 | 56.1 | 50.0 | 53.8 | 49.3 | |
| 1 | 57.1 | 56.4 | 49.5 | 48.9 | 51.2 | 52.7 | 54.0 | 53.7 | |
| 2 | 55.2 | 58.7 | 48.9 | 51.1 | 47.1 | 49.6 | 45.6 | 52.4 | |
| Sup. Learning | 3 | 56.9 | 58.9 | 52.5 | 49.6 | 47.8 | 51.0 | 47.9 | 47.4 |
| 4 | 57.3 | 58.7 | 53.1 | 51.2 | 48.7 | 54.6 | 47.1 | 47.6 | |
| 5 | 59.2 | 58.9 | 53.2 | 50.1 | 47.1 | 54.3 | 47.3 | 47.7 | |
| 6 | 53.7 | 56.0 | 47.0 | 51.3 | 50.2 | 56.0 | 55.6 | 46.6 | |
| 7 | 53.2 | 56.6 | 51.7 | 53.6 | 50.6 | 49.5 | 52.6 | 47.9 |

Table A7.
Per-class sample macro F1 scores for each downstream method when training the reduced saccade dataset. The best metrics for each head classifier are highlighted in bold. Note that Head0 corresponds to the linear probing method.
Table A7.
Per-class sample macro F1 scores for each downstream method when training the reduced saccade dataset. The best metrics for each head classifier are highlighted in bold. Note that Head0 corresponds to the linear probing method.
| Technique | Head | Class 0 | Class 1 | Class 2 | Class 3 | Class 4 | Class 5 | Class 6 | Class 7 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 56.4 | 55.7 | 49.8 | 48.5 | 49.3 | 52.7 | 47.7 | 51.7 | |
| 2 | 56.8 | 60.6 | 50 | 50.2 | 55.1 | 52.6 | 51.8 | 48 | |
| Fine-tuning | 3 | 55.4 | 57.6 | 59.1 | 47.6 | 50.9 | 54.5 | 46 | 52.4 |
| 4 | 58.2 | 60.7 | 53.3 | 50.2 | 52.3 | 54.1 | 49.4 | 47 | |
| 5 | 52.5 | 56.4 | 51.4 | 50.6 | 60.1 | 55.1 | 50.6 | 47.7 | |
| 6 | 55.7 | 60.1 | 54.3 | 48.1 | 54.6 | 56.7 | 53.6 | 47.9 | |
| 7 | 58.4 | 56.7 | 52.7 | 50.7 | 52.8 | 53.8 | 47.4 | 48.6 | |
| 0 | 49.3 | 51.6 | 52 | 46.3 | 41.7 | 48.3 | 40.3 | 46.1 | |
| 1 | 54.2 | 54.1 | 52.2 | 50.8 | 49 | 51 | 49.6 | 48 | |
| 2 | 59.8 | 56.7 | 53.1 | 49.7 | 50.9 | 55 | 48.9 | 47.5 | |
| Freezing | 3 | 60.9 | 57.9 | 54.4 | 49.9 | 49.1 | 54.5 | 52.5 | 49.7 |
| 4 | 59 | 58.3 | 54.4 | 54.8 | 50.1 | 51.6 | 54.1 | 47.4 | |
| 5 | 57 | 55.8 | 55.8 | 46.1 | 51.3 | 55.1 | 49.3 | 48 | |
| 6 | 50.7 | 51.1 | 50.4 | 53.3 | 50.8 | 53.2 | 51 | 47.8 | |
| 7 | 58.8 | 59.1 | 54.9 | 50.8 | 51.6 | 53.6 | 53.3 | 48 | |
| 1 | 51.5 | 55.8 | 53.2 | 48.1 | 52.2 | 56 | 50.9 | 47.2 | |
| 2 | 57.7 | 57.9 | 56.1 | 46.8 | 47.6 | 52.5 | 51 | 49.7 | |
| Sup. Learning | 3 | 53.1 | 56.7 | 50.2 | 45.6 | 51.5 | 52.7 | 49 | 47.9 |
| 4 | 54.9 | 53.8 | 51 | 49.5 | 51.9 | 51.4 | 49.1 | 47.5 | |
| 5 | 53.5 | 59.3 | 49.7 | 53.5 | 49.6 | 51.4 | 48.8 | 49 | |
| 6 | 55.4 | 54.7 | 48.7 | 50.6 | 48.8 | 50.2 | 51.9 | 49.6 | |
| 7 | 58.1 | 55.5 | 50.9 | 46.4 | 49.2 | 51.1 | 46.5 | 48 |
References
- Ward, L.M.; Kapoula, Z. Dyslexics’ Fragile Oculomotor Control Is Further Destabilized by Increased Text Difficulty. Brain Sci. 2021, 11, 990. [Google Scholar] [CrossRef] [PubMed]
- Ward, L.M.; Kapoula, Z. Differential diagnosis of vergence and saccade disorders in dyslexia. Sci. Rep. 2020, 10, 22116. [Google Scholar] [CrossRef]
- Ward, L.M.; Kapoula, Z. Creativity, Eye-Movement Abnormalities, and Aesthetic Appreciation of Magritte’s Paintings. Brain Sci. 2022, 12, 1028. [Google Scholar] [CrossRef] [PubMed]
- Kapoula, Z.; Morize, A.; Daniel, F.; Jonqua, F.; Orssaud, C.; Bremond-Gignac, D. Objective evaluation of vergence disorders and a research-based novel method for vergence rehabilitation. Transl. Vis. Sci. Technol. 2016, 5, 8. [Google Scholar] [CrossRef]
- El Hmimdi, A.E.; Ward, L.M.; Palpanas, T.; Kapoula, Z. Predicting dyslexia and reading speed in adolescents from eye movements in reading and non-reading tasks: A machine learning approach. Brain Sci. 2021, 11, 1337. [Google Scholar] [CrossRef]
- El Hmimdi, A.E.; Ward, L.M.; Palpanas, T.; Sainte Fare Garnot, V.; Kapoula, Z. Predicting Dyslexia in Adolescents from Eye Movements during Free Painting Viewing. Brain Sci. 2022, 12, 1031. [Google Scholar] [CrossRef]
- Rizzo, A.; Ermini, S.; Zanca, D.; Bernabini, D.; Rossi, A. A machine learning approach for detecting cognitive interference based on eye-tracking data. Front. Hum. Neurosci. 2022, 16, 806330. [Google Scholar] [CrossRef] [PubMed]
- Bixler, R.; D’Mello, S. Automatic gaze-based user-independent detection of mind wandering during computerized reading. User Model. User-Adapt. Interact. 2016, 26, 33–68. [Google Scholar] [CrossRef]
- Asvestopoulou, T.; Manousaki, V.; Psistakis, A.; Smyrnakis, I.; Andreadakis, V.; Aslanides, I.M.; Papadopouli, M. Dyslexml: Screening tool for dyslexia using machine learning. arXiv 2019, arXiv:1903.06274. [Google Scholar]
- Nilsson Benfatto, M.; Öqvist Seimyr, G.; Ygge, J.; Pansell, T.; Rydberg, A.; Jacobson, C. Screening for dyslexia using eye tracking during reading. PLoS ONE 2016, 11, e0165508. [Google Scholar] [CrossRef]
- Vajs, I.A.; Kvaščev, G.S.; Papić, T.M.; Janković, M.M. Eye-tracking Image Encoding: Autoencoders for the Crossing of Language Boundaries in Developmental Dyslexia Detection. IEEE Access 2023, 11, 3024–3033. [Google Scholar] [CrossRef]
- El Hmimdi, A.E.; Kapoula, Z.; Sainte Fare Garnot, V. Deep Learning-Based Detection of Learning Disorders on a Large Scale Dataset of Eye Movement Records. BioMedInformatics 2024, 4, 519–541. [Google Scholar] [CrossRef]
- Chen, S.; Zhao, Q. Attention-based autism spectrum disorder screening with privileged modality. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1181–1190. [Google Scholar]
- Jiang, M.; Zhao, Q. Learning visual attention to identify people with autism spectrum disorder. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 3267–3276. [Google Scholar]
- Tao, Y.; Shyu, M.L. SP-ASDNet: CNN-LSTM based ASD classification model using observer scanpaths. In Proceedings of the 2019 IEEE International Conference on Multimedia & Expo Workshops (ICMEW), Shanghai, China, 8–12 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 641–646. [Google Scholar]
- Vajs, I.; Ković, V.; Papić, T.; Savić, A.M.; Janković, M.M. Dyslexia detection in children using eye tracking data based on VGG16 network. In Proceedings of the 2022 30th European Signal Processing Conference (EUSIPCO), Belgrade, Serbia, 29 August–2 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1601–1605. [Google Scholar]
- Harisinghani, A.; Sriram, H.; Conati, C.; Carenini, G.; Field, T.; Jang, H.; Murray, G. Classification of Alzheimer’s using Deep-learning Methods on Webcam-based Gaze Data. Proc. ACM Hum.-Comput. Interact. 2023, 7, 1–17. [Google Scholar] [CrossRef]
- Sun, J.; Liu, Y.; Wu, H.; Jing, P.; Ji, Y. A novel deep learning approach for diagnosing Alzheimer’s disease based on eye-tracking data. Front. Hum. Neurosci. 2022, 16, 972773. [Google Scholar] [CrossRef] [PubMed]
- Bautista, L.G.C.; Naval, P.C. Gazemae: General representations of eye movements using a micro-macro autoencoder. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 7004–7011. [Google Scholar]
- Jindal, S.; Manduchi, R. Contrastive representation learning for gaze estimation. In Proceedings of the Annual Conference on Neural Information Processing Systems, New Orleans, LA, USA, 10–16 December 2023; pp. 37–49. [Google Scholar]
- Bautista, L.G.C.; Naval, P.C. CLRGaze: Contrastive Learning of Representations for Eye Movement Signals. In Proceedings of the 2021 29th European Signal Processing Conference (EUSIPCO), Dublin, Ireland, 23–27 August 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1241–1245. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Radford, A.; Narasimhan, K.; Salimans, T.; Sutskever, I. Improving language understanding by generative pre-training. OpenAI Blog, 2018; preprint. [Google Scholar]
- Radford, A.; Wu, J.; Child, R.; Luan, D.; Amodei, D.; Sutskever, I. Language models are unsupervised multitask learners. OpenAI Blog 2019, 1, 9. [Google Scholar]
- Song, K.; Tan, X.; Qin, T.; Lu, J.; Liu, T.Y. Mass: Masked sequence to sequence pre-training for language generation. arXiv 2019, arXiv:1905.02450. [Google Scholar]
- Chen, M.; Radford, A.; Child, R.; Wu, J.; Jun, H.; Luan, D.; Sutskever, I. Generative pretraining from pixels. In Proceedings of the International Conference on Machine Learning, Virtual Event, 13–18 July 2020; pp. 1691–1703. [Google Scholar]
- Bao, H.; Dong, L.; Piao, S.; Wei, F. Beit: Bert pre-training of image transformers. arXiv 2021, arXiv:2106.08254. [Google Scholar]
- Xie, Z.; Zhang, Z.; Cao, Y.; Lin, Y.; Bao, J.; Yao, Z.; Dai, Q.; Hu, H. Simmim: A simple framework for masked image modeling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA., 18–24 June 2022; pp. 9653–9663. [Google Scholar]
- He, K.; Chen, X.; Xie, S.; Li, Y.; Dollár, P.; Girshick, R. Masked autoencoders are scalable vision learners. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 16000–16009. [Google Scholar]
- Tang, P.; Zhang, X. MTSMAE: Masked Autoencoders for Multivariate Time-Series Forecasting. In Proceedings of the 2022 IEEE 34th International Conference on Tools with Artificial Intelligence (ICTAI), Macao, China, 31 October–2 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 982–989. [Google Scholar]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.A.; Bottou, L. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Lee, W.H.; Ozger, M.; Challita, U.; Sung, K.W. Noise learning-based denoising autoencoder. IEEE Commun. Lett. 2021, 25, 2983–2987. [Google Scholar] [CrossRef]
- Hinton, G.E.; Zemel, R. Autoencoders, minimum description length and Helmholtz free energy. Adv. Neural Inf. Process. Syst. 1993, 6, 3–10. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Baldi, P. Autoencoders, unsupervised learning, and deep architectures. In Proceedings of the ICML Workshop on Unsupervised and Transfer Learning, JMLR Workshop and Conference Proceedings, Bellevue, WA, USA, 2 July 2011; pp. 37–49. [Google Scholar]
- Kingma, D.P.; Welling, M. An introduction to variational autoencoders. Found. Trends® Mach. Learn. 2019, 12, 307–392. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Bajaj, K.; Singh, D.K.; Ansari, M.A. Autoencoders based deep learner for image denoising. Procedia Comput. Sci. 2020, 171, 1535–1541. [Google Scholar] [CrossRef]
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.A. Extracting and composing robust features with denoising autoencoders. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 1096–1103. [Google Scholar]
- Li, Z.; Rao, Z.; Pan, L.; Wang, P.; Xu, Z. Ti-MAE: Self-Supervised Masked Time Series Autoencoders. arXiv 2023, arXiv:2301.08871. [Google Scholar]
- Doersch, C.; Gupta, A.; Efros, A.A. Unsupervised visual representation learning by context prediction. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1422–1430. [Google Scholar]
- Noroozi, M.; Favaro, P. Unsupervised learning of visual representations by solving jigsaw puzzles. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 69–84. [Google Scholar]
- Gidaris, S.; Singh, P.; Komodakis, N. Unsupervised representation learning by predicting image rotations. arXiv 2018, arXiv:1803.07728. [Google Scholar]
- Yang, X.; Zhang, Z.; Cui, R. Timeclr: A self-supervised contrastive learning framework for univariate time series representation. Knowl.-Based Syst. 2022, 245, 108606. [Google Scholar] [CrossRef]
- Yue, Z.; Wang, Y.; Duan, J.; Yang, T.; Huang, C.; Tong, Y.; Xu, B. Ts2vec: Towards universal representation of time series. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 22 February–1 March 2022; Volume 36, pp. 8980–8987. [Google Scholar]
- Tonekaboni, S.; Eytan, D.; Goldenberg, A. Unsupervised representation learning for time series with temporal neighborhood coding. arXiv 2021, arXiv:2106.00750. [Google Scholar]
- Zhang, X.; Zhao, Z.; Tsiligkaridis, T.; Zitnik, M. Self-supervised contrastive pre-training for time series via time-frequency consistency. Adv. Neural Inf. Process. Syst. 2022, 35, 3988–4003. [Google Scholar]
- Yoon, J.; Jarrett, D.; Van der Schaar, M. Time-series generative adversarial networks. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Desai, A.; Freeman, C.; Wang, Z.; Beaver, I. Timevae: A variational auto-encoder for multivariate time series generation. arXiv 2021, arXiv:2111.08095. [Google Scholar]
- Esteban, C.; Hyland, S.L.; Rätsch, G. Real-valued (medical) time series generation with recurrent conditional gans. arXiv 2017, arXiv:1706.02633. [Google Scholar]
- Meng, Q.; Qian, H.; Liu, Y.; Xu, Y.; Shen, Z.; Cui, L. Unsupervised Representation Learning for Time Series: A Review. arXiv 2023, arXiv:2308.01578. [Google Scholar]
- Lee, S.W.; Kim, S. Detection of Abnormal Behavior with Self-Supervised Gaze Estimation. arXiv 2021, arXiv:2107.06530. [Google Scholar]
- Du, L.; Zhang, X.; Lan, G. Unsupervised Gaze-aware Contrastive Learning with Subject-specific Condition. arXiv 2023, arXiv:2309.04506. [Google Scholar]
- Yu, Y.; Odobez, J.M. Unsupervised representation learning for gaze estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 7314–7324. [Google Scholar]
- Park, S.; Mello, S.D.; Molchanov, P.; Iqbal, U.; Hilliges, O.; Kautz, J. Few-shot adaptive gaze estimation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9368–9377. [Google Scholar]
- Pupila Capture Eye Tracker. Available online: https://pupil-labs.com/ (accessed on 29 March 2024).
- Pytorch Image Models (timm). Available online: https://timm.fast.ai/ (accessed on 29 March 2024).
- Tian, K.; Jiang, Y.; Diao, Q.; Lin, C.; Wang, L.; Yuan, Z. Designing bert for convolutional networks: Sparse and hierarchical masked modeling. arXiv 2023, arXiv:2301.03580. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017; 30, arXiv:1706.03762. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Pouyanfar, S.; Sadiq, S.; Yan, Y.; Tian, H.; Tao, Y.; Reyes, M.P.; Shyu, M.L.; Chen, S.C.; Iyengar, S.S. A survey on deep learning: Algorithms, techniques, and applications. ACM Comput. Surv. (CSUR) 2018, 51, 1–36. [Google Scholar] [CrossRef]
- El Hmimdi, A.E.; Palpanas, T.; Kapoula, Z. Efficient Diagnostic Classification of Diverse Pathologies through Contextual Eye Movement Data Analysis with a Novel Hybrid Architecture. BioMedInformatics 2024, 4, 1457–1479. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).