The “Growth Curve”: An Autocorrelation Effect
Abstract
:1. Introduction
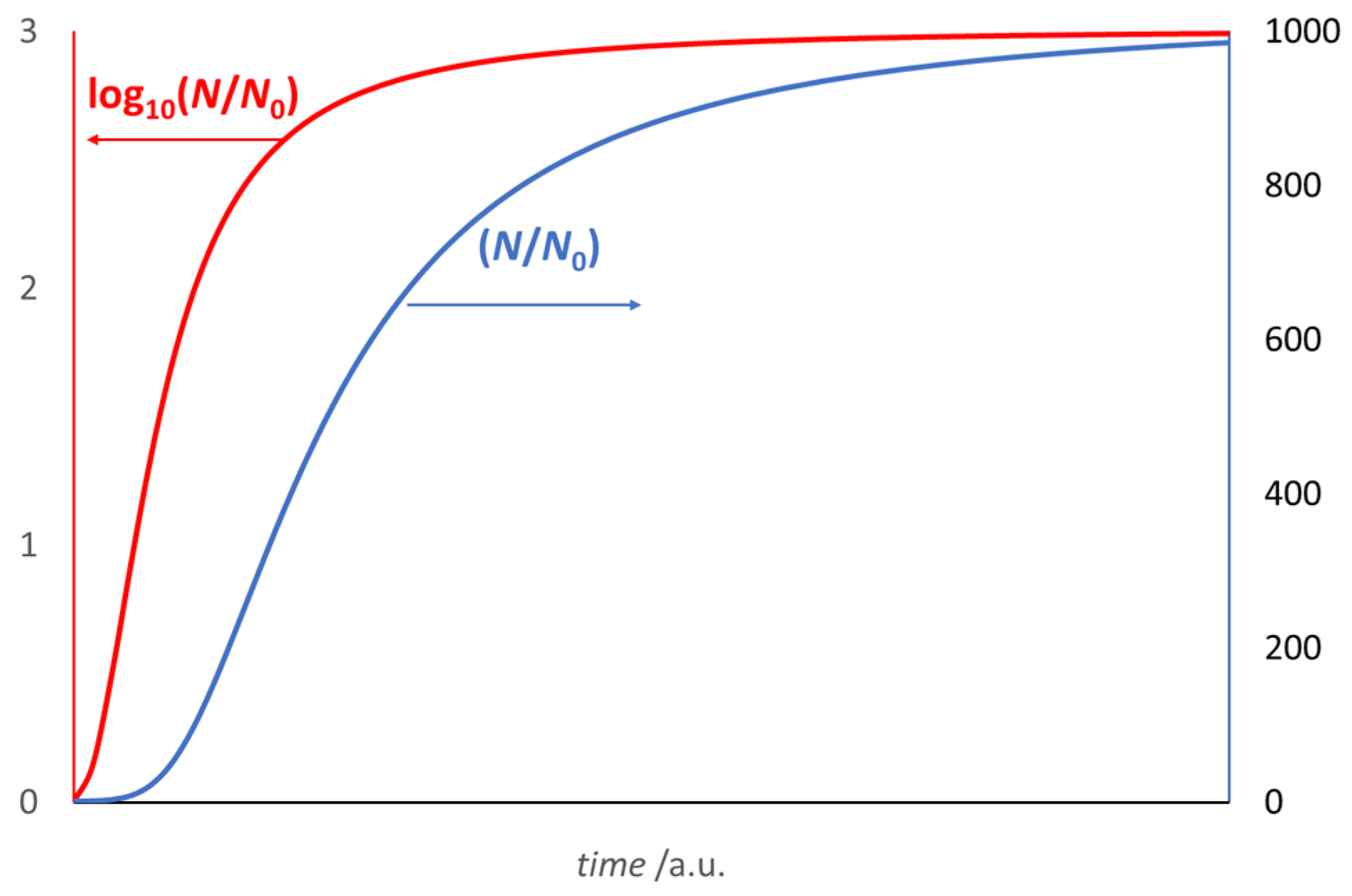
2. An Ideal Behavior as a Reference for Any Microbial Culture
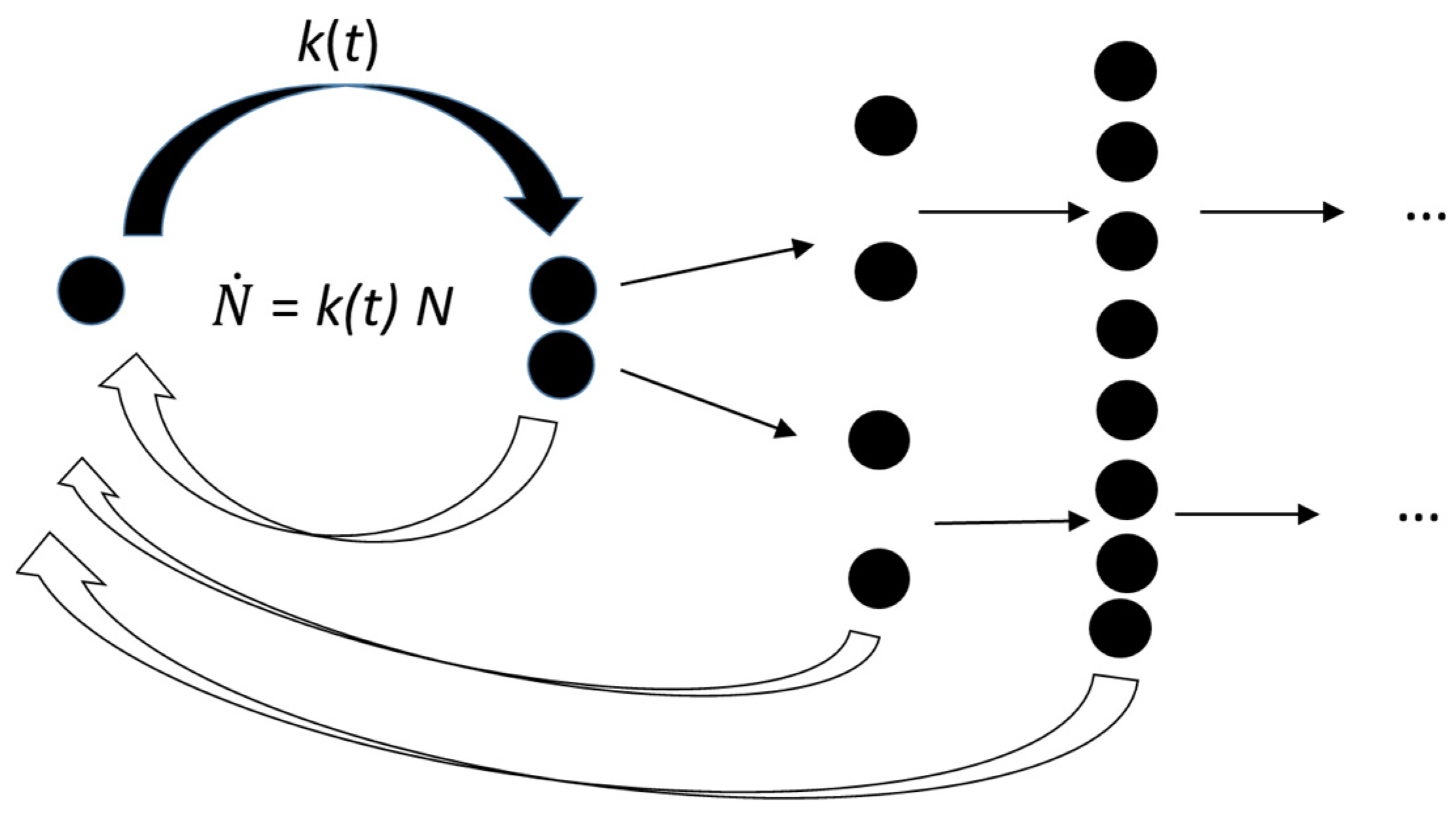
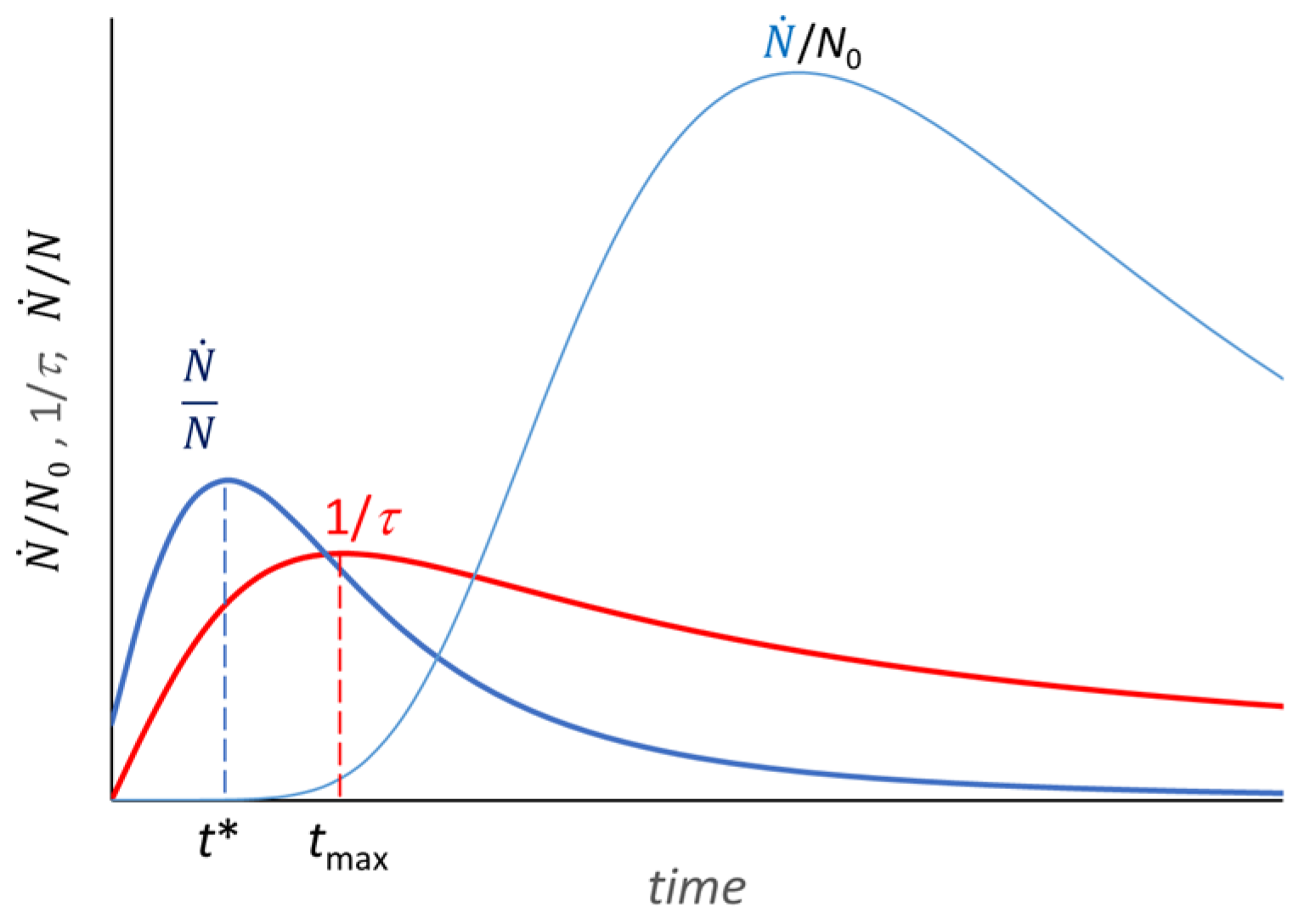
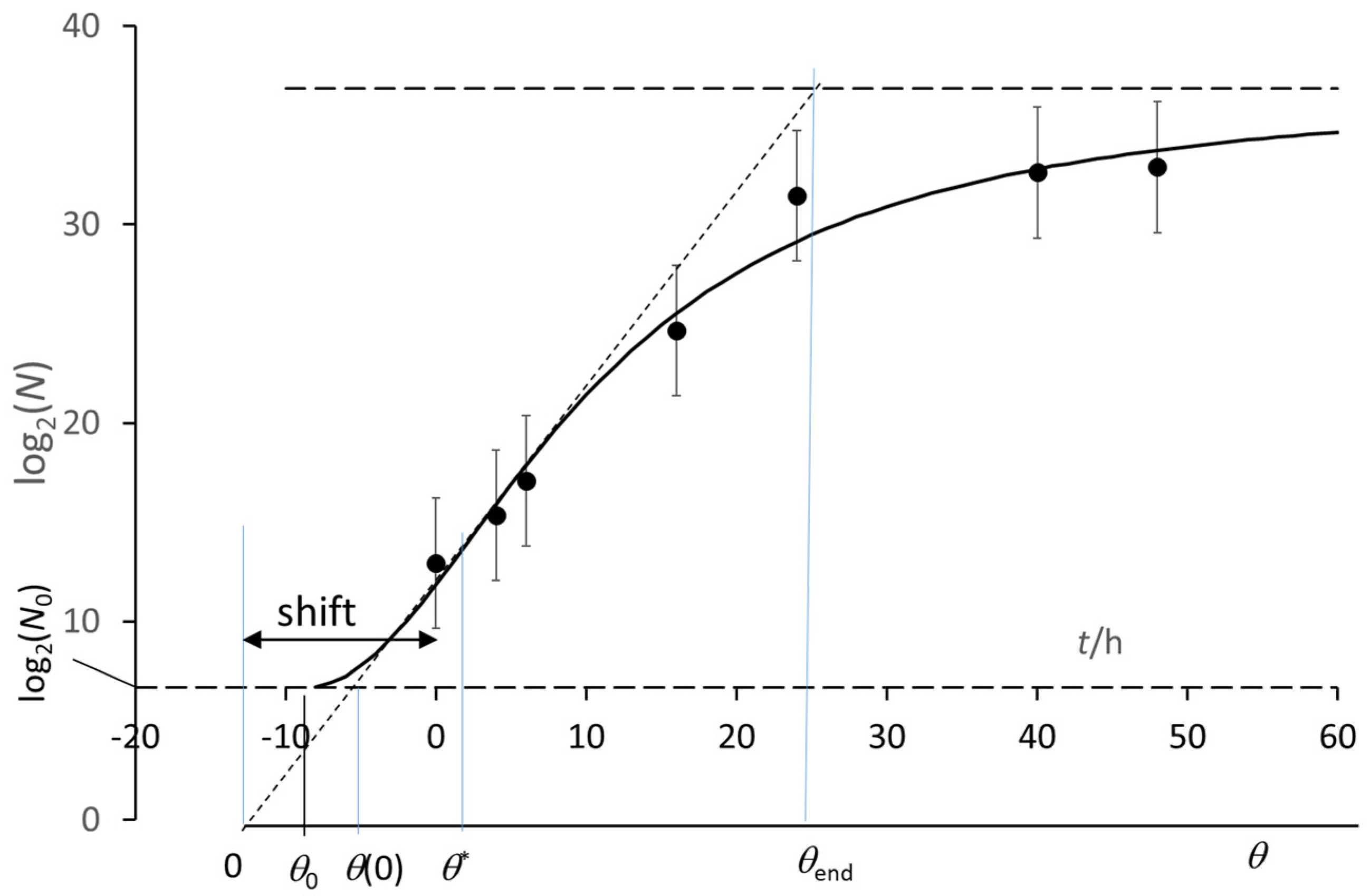
3. The Growth Curve: The Result of an Auto Correlation Effect
- and
- and
- (θ* − θend) = 2(θ* − θ0),
- [θ* − θ(0)] = 2 [θ(0) − θ0],
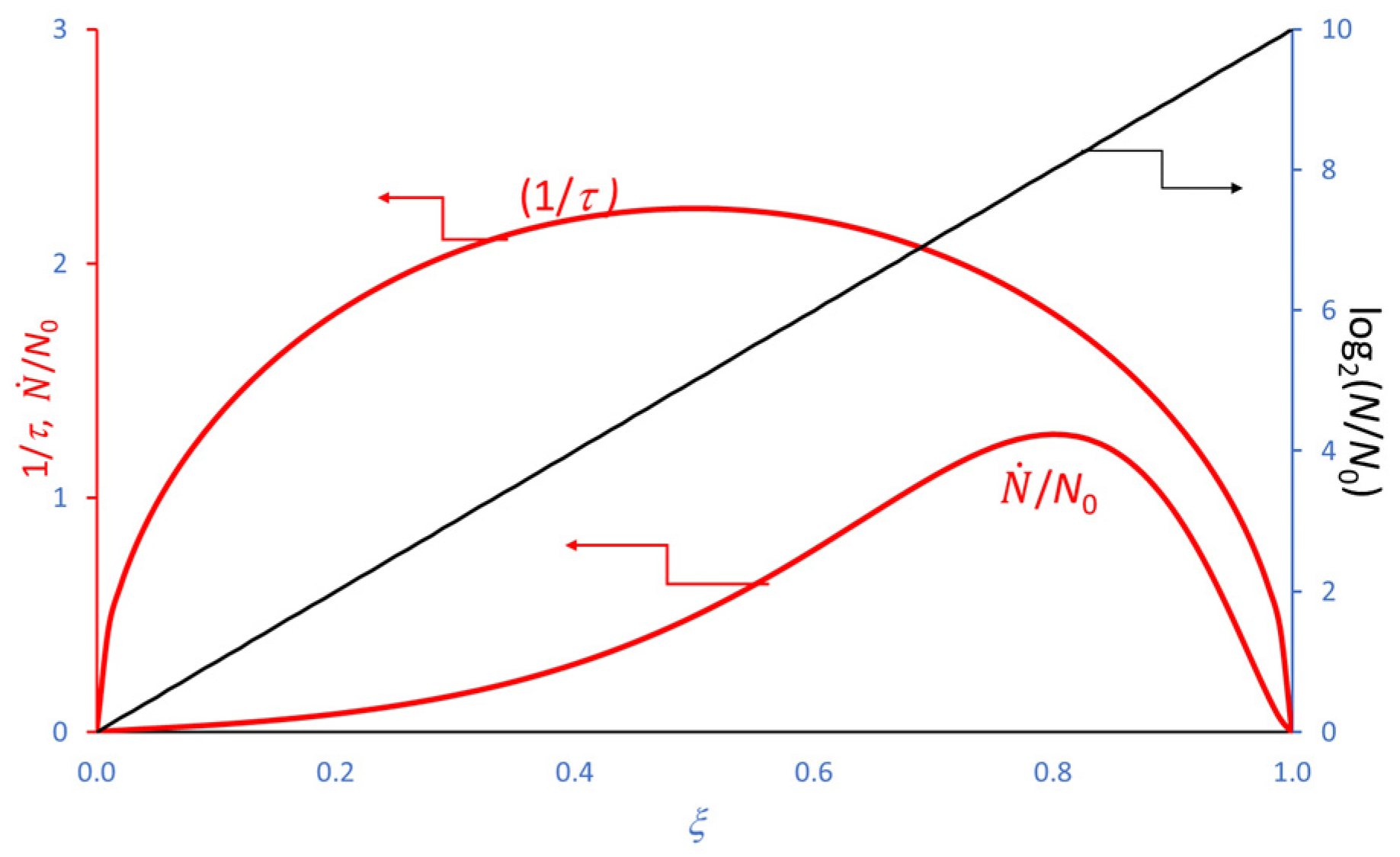
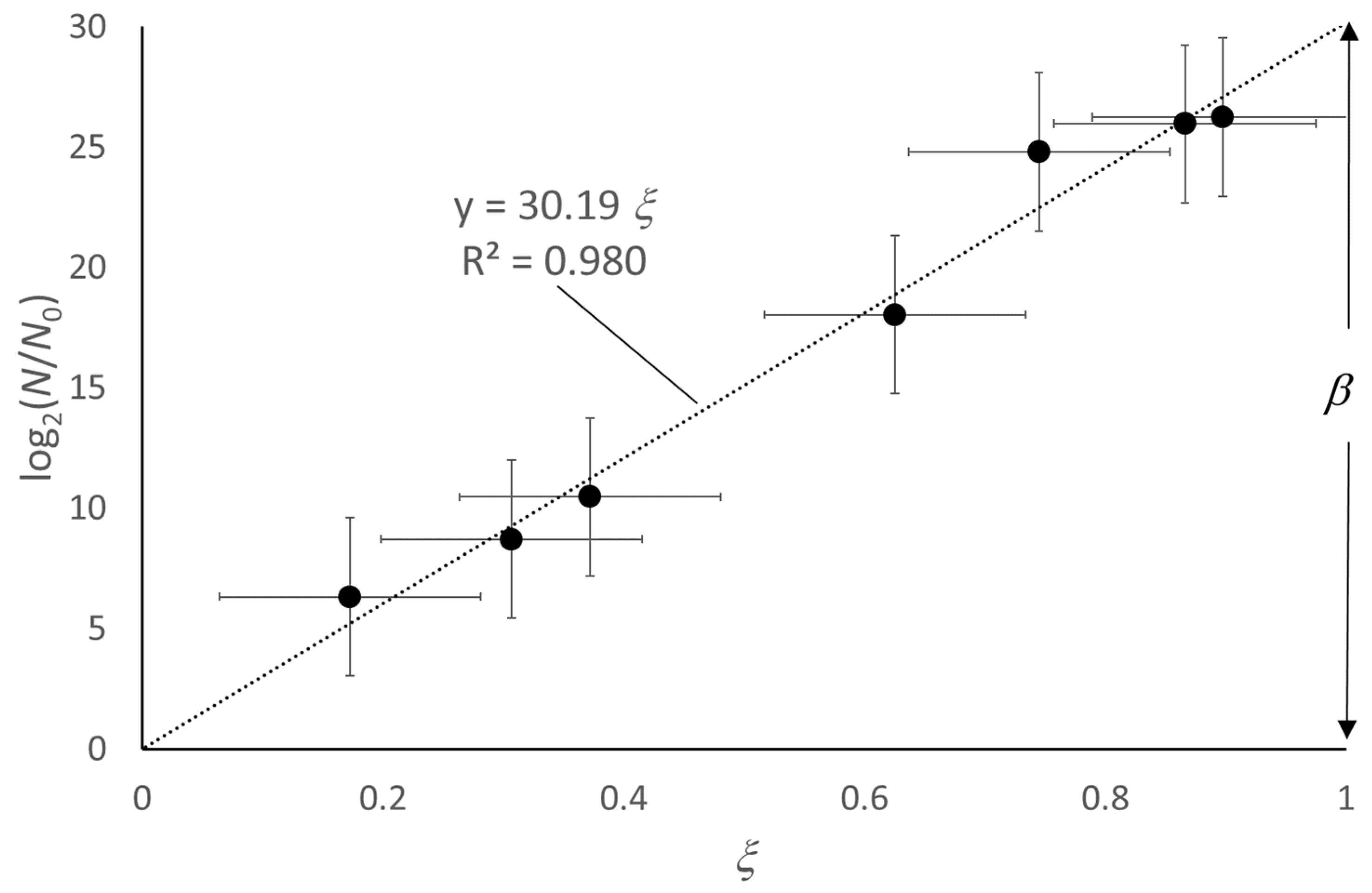
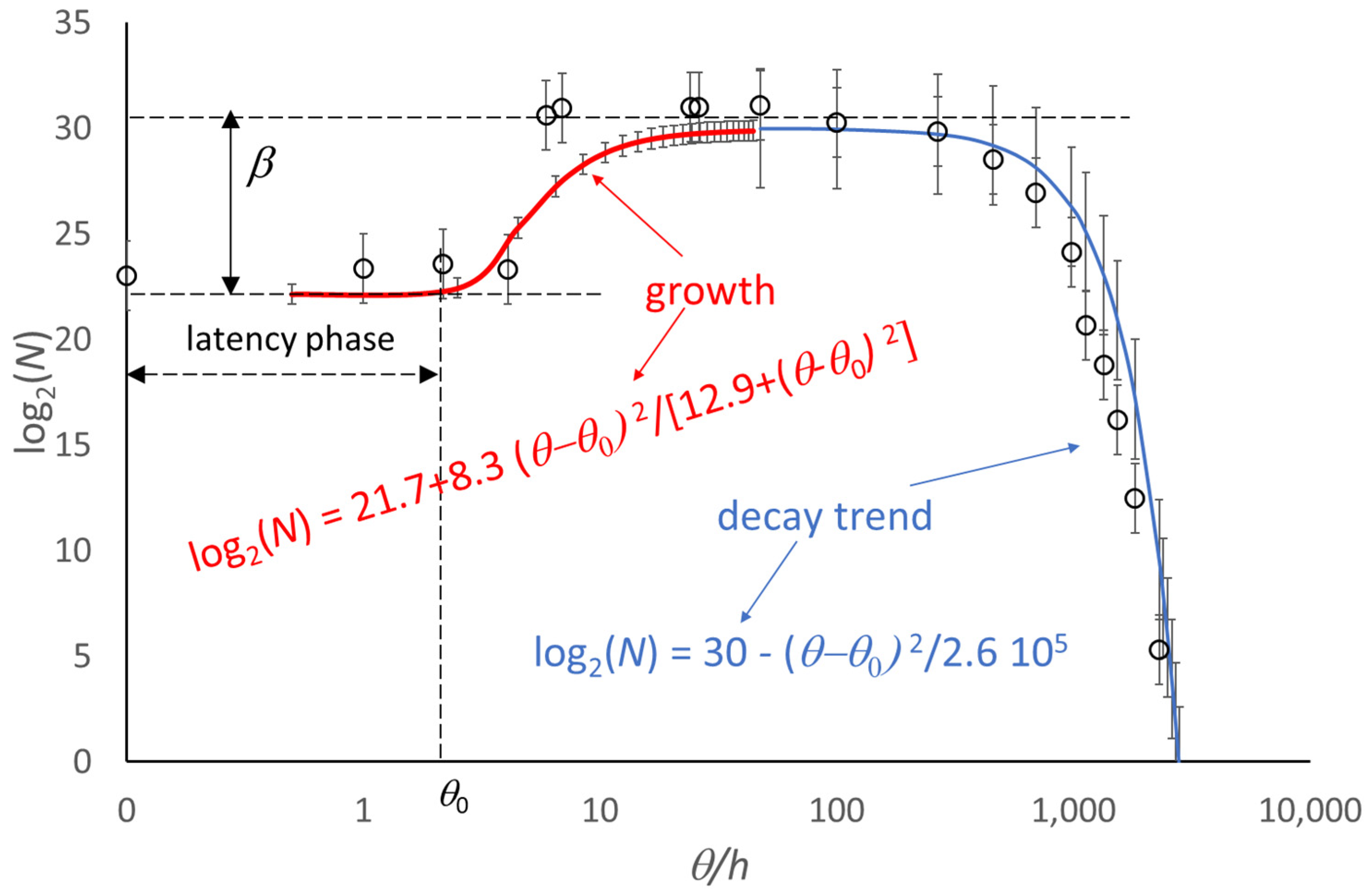
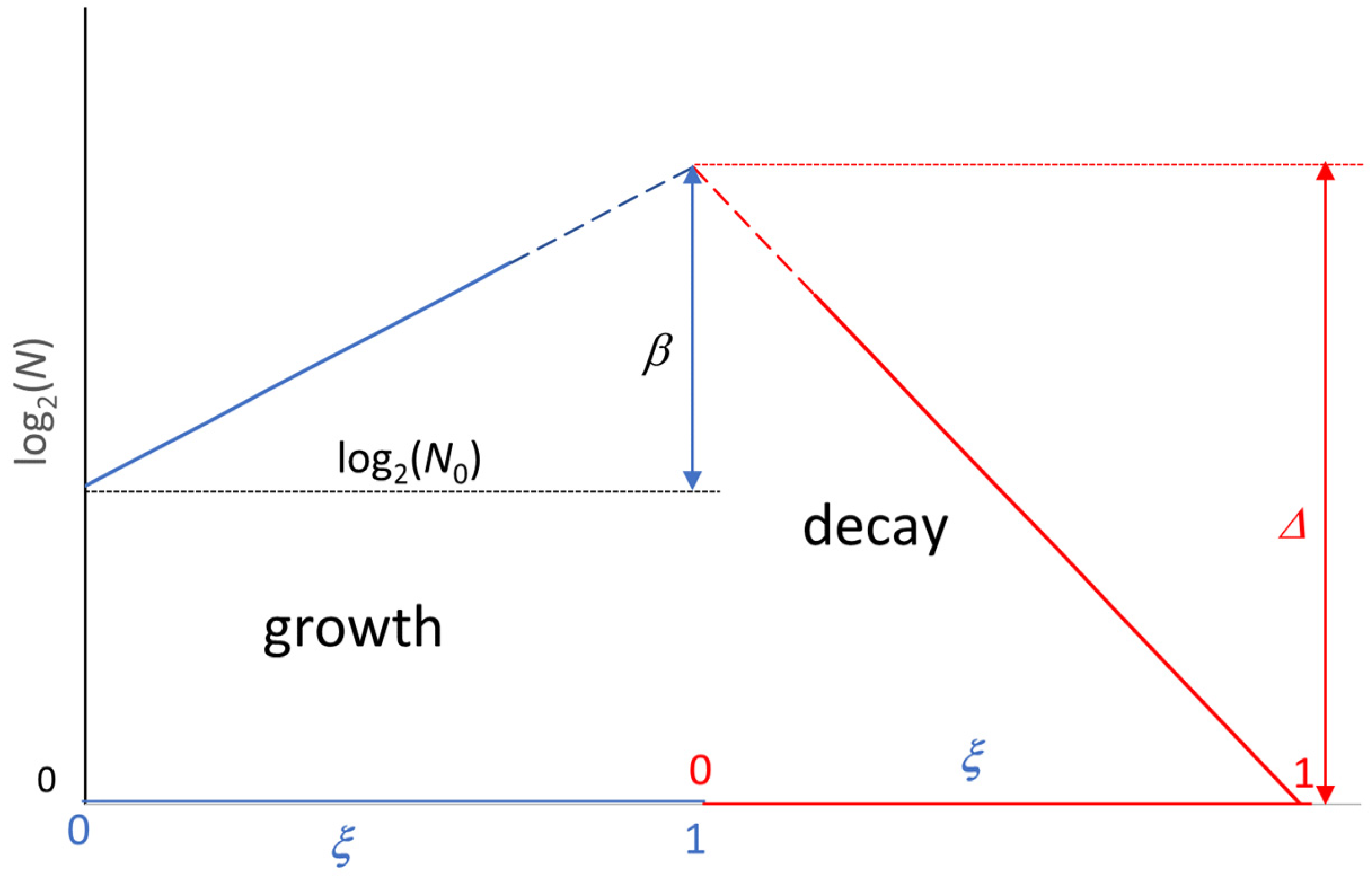
4. Extension of the Model to the Decay Phase
5. Use of the Model
- identify the time origin θ = 0 by extrapolating the straight-line tangent to the experimental growth at its steepest point down to log(N) = 0 (no matter the log base);
- adjust the time scale;
- discard all data that correspond to negative θ;
- use only the remaining data that are significantly above the value of N0;
- use the equation (or equivalent for other log bases) for the best fit.
- It provides an ideal and common reference behavior for every microbial culture; the comparison between different growth curves of real microbial cultures simply requires a check of the values of α, β, and θ0. The effects observed by varying the conditions of a given microbial culture (starting population density, temperature, pH, kind of substrate, water activity, etc.) produce a quantitative response in different values of α, β and θ0. This can be of help in predictive microbiology investigations.
- Although based on the best fit of the growth curve in the log(N)-vs-t format, the model applies to the natural N-vs-t scale, as it defines an ideal trend related to a time origin, θ = 0, where N = 1.
- A naked-eye analysis of the experimental growth curve allows for a tentative identification of its steepest point, a tentative drawing of the tangent to the growth curve, and a tentative location of the time origin for the ideal culture, which allow some quick qualitative predictions. One can perfect this approach through iterative best fits with the normal time scale in order to identify t* and quantify the slope of the straight-line tangent to the experimental growth curve and adjust the assessment of the origin of the time scale for the virtual microbial culture.
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Neidhardt, F.C. Bacterial growth: Constant obsession with dN/dt. J. Bacteriol. 1999, 181, 7405–7408. [Google Scholar] [CrossRef]
- Lopez, S.; Prieto, M.; Dijkstra, J.; Dhanoad, M.S.; France, J. Statistical evaluation of mathematical models for microbial growth. Int. J. Food Microbiol. 2004, 96, 289–300. [Google Scholar] [CrossRef] [PubMed]
- Antolinos, V.; Muñoz-Cuevas, M.; Ros-Chumillas, M.; Periago PMFernández, P.S.; Le Marc, Y. Modelling the effects of temperature and osmotic shifts on the growth kinetics of Bacillus weihenstephanensis in broth and food products. Int. J. Food Microbiol. 2012, 158, 36–41. [Google Scholar] [CrossRef] [PubMed]
- Mellefont, L.A.; McMeekin, T.A.; Ross, T. Effect of relative inoculum concentration on Listeria monocytogenes growth in co-culture. Int. J. Food Microbiol. 2008, 121, 157–168. [Google Scholar] [CrossRef] [PubMed]
- Baranyi, J.; George, S.M.; Kutalik, Z. Parameter Estimation for the Distribution of Single Cell Lag Times. J. Theor. Biol. 2009, 259, 24–30. [Google Scholar] [CrossRef] [PubMed]
- Gime’nez, B.; Dalgaard, P. Modelling and predicting the simultaneous growth of Listeria monocytogenes and spoilage micro-organisms in cold-smoked salmon. J. Appl. Microbiol. 2004, 96, 96–109. [Google Scholar] [CrossRef]
- Vadasz, P.; Vadasz, A.S. Biological implications from an autonomous version of Baranyi and Roberts growth model. Int. J. Food Microbiol. 2007, 114, 357–365. [Google Scholar] [CrossRef]
- Baranyi, J.; Pin, C. Estimating Bacterial Growth Parameters by Means of Detection Times. Appl. Environ. Microbiol. 1999, 65, 732–736. [Google Scholar] [CrossRef]
- Baranyi, J.; Pin, C.; Ross, T. Validating and comparing predictive models. Int. J. Food Microbiol. 1999, 48, 159–166. [Google Scholar] [CrossRef]
- Buchanan, R.L.; Whiting, R.C.; Damert, W.C. When is simple good enough: A comparison of the Gompertz, Baranyi, and three-phase linear models for fitting bacterial growth curves. Food Microbiol. 1997, 14, 313–326. [Google Scholar] [CrossRef]
- Swinnen, I.A.M.; Bernaerts, K.; Dens, E.J.J.; Geeraerd, A.H.; Van Impe, J.F. Predictive modelling of the microbial lag phase: A review. Int. J. Food Microbiol. 2004, 94, 137–159. [Google Scholar] [CrossRef]
- Schaechter, M. From growth physiology to systems biology. Int. Microbiol. 2006, 9, 157–161. [Google Scholar] [PubMed]
- Gonze, D.; Coyte, K.Z.; Lahti, L.; Faust, K. Microbial communities as dynamical systems. Curr. Opin. Microbiol. 2018, 44, 41–49. [Google Scholar] [CrossRef]
- Good, B.H.; Hallatschek, O. Effective models and the search for quantitative principles in microbial evolution. Curr. Opin. Microbiol. 2018, 45, 203–212. [Google Scholar] [CrossRef]
- Bertrand, R.L. Lag phase is a dynamic, organized, adaptive, and evolvable period that prepares bacteria for cell division. J. Bacteriol. 2019, 201, e00697-18. [Google Scholar] [CrossRef]
- Scott, M.; Hwa, T. Bacterial growth laws and their applications. Curr. Opin. Biotechnol. 2011, 22, 559–565. [Google Scholar] [CrossRef] [PubMed]
- Basan, M.; Honda, T.; Christodoulou, D.; Hörl, M.; Chang, Y.u.-F.; Leoncini, E.; Mukherjee, A.; Okano, H.; Taylor, B.R.; Silverman, J.M.; et al. A universal trade-off between growth and lag in fluctuating environments. Nature 2020, 584, 470–474. [Google Scholar] [CrossRef] [PubMed]
- Dens, E.J.; Bernaerts, K.; Standaert, A.R.; Van Impe, J.F. Cell division theory and individual-based modeling of microbial lag Part I. Int. J. Food Microbiol. 2005, 101, 303–318. [Google Scholar] [CrossRef]
- Dens, E.J.; Bernaerts, K.; Standaert, A.R.; Kreft, J.-U.; Van Impe, J.F. Cell division theory and individual-based modeling of microbial lag Part II. Int. J. Food Microbiol. 2005, 101, 319–332. [Google Scholar] [CrossRef]
- Atolia, E.; Cesar, S.; Arjes, H.A.; Rajendram, M.; Shi, H.; Knapp, B.D.; Khare, S.; Aranda-Díaz, A.; Lenski, R.E.; Huang, K.C. Environmental and physiological factors affecting high-throughput measurements of bacterial growth. mBio 2020, 11, e01378-20. [Google Scholar] [CrossRef]
- Baranyi, J. Comparison of Stochastic and Deterministic Concepts of Bacterial Lag. J. Theor. Biol. 1998, 192, 403–408. [Google Scholar] [CrossRef]
- Sutton, S. Measurement of Microbial Cells by Optical Density. J. Valid. Technol. 2011, 17, 42–46. [Google Scholar]
- Schiraldi, A. Microbial growth in planktonic conditions. Cell Develop. Biol. 2017, 6, 1–6. [Google Scholar] [CrossRef]
- Schiraldi, A. A self-consistent approach to the lag phase of planktonic microbial cultures. Single Cell Biol. 2017, 6, 3. [Google Scholar] [CrossRef]
- Schiraldi, A. Growth and decay of a planktonic microbial culture. Int. J. Microbiol. 2020, 2020, 4186468. [Google Scholar] [CrossRef]
- Schiraldi, A.; Foschino, R. An alternative model to infer the growth of psychrotrophic pathogenic bacteria. J. Appl. Microbiol. 2022, 132, 642–653, (and related “Supporting Information”). [Google Scholar] [CrossRef]
- Schiraldi, A.; Foschino, R. Time scale of the growth progress in bacterial cultures: A self-consistent choice. RAS Microbiol. Infect. Dis. 2021, 1, 1–8. [Google Scholar] [CrossRef]
- Schiraldi, A. Batch Microbial Cultures: A Model that can account for Environment Changes. Adv. Microbiol. 2021, 11, 630–645. [Google Scholar] [CrossRef]
- Schiraldi, A. The Origin of the Time Scale: A Crucial Issue for Predictive Microbiology. J. Appl. Environ. Microbiol. 2022, 10, 35–42. [Google Scholar] [CrossRef]
- Schiraldi, A. The growth curve of microbial cultures: A model for a visionary reappraisal. Appl. Microbiol. 2023, 3, 288–296. [Google Scholar] [CrossRef]
- Schiraldi, A. The growth of microbial cultures complies with the laws of thermodynamics. Biophys. Chem. 2024, 307, 107177. [Google Scholar] [CrossRef] [PubMed]
- Egli, T. Microbial growth and physiology: A call for better craftsmanship. Front. Microbiol. 2015, 6, 287–298. [Google Scholar] [CrossRef] [PubMed]
- Fessas, D.; Schiraldi, A. Isothermal calorimetry and microbial growth: Beyond modeling. J. Therm. Anal. Calorim. 2017, 130, 567–572. [Google Scholar] [CrossRef]
- Doona, C.J.; Feeherry, F.E.; Ross, E.W. A quasi-chemical model for the growth and death of microorganisms in foods by non-thermal and high-pressure processing. Int. J. Food Microbiol. 2005, 100, 21–32. [Google Scholar] [CrossRef] [PubMed]
- Peleg, M. A Model of Microbial Growth and Decay in a Closed Habitat Based on Combined Fermi’s and the Logistic Equations. J. Sci. Food Agric. 1996, 71, 225–230. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schiraldi, A. The “Growth Curve”: An Autocorrelation Effect. Appl. Microbiol. 2024, 4, 1257-1267. https://doi.org/10.3390/applmicrobiol4030086
Schiraldi A. The “Growth Curve”: An Autocorrelation Effect. Applied Microbiology. 2024; 4(3):1257-1267. https://doi.org/10.3390/applmicrobiol4030086
Chicago/Turabian StyleSchiraldi, Alberto. 2024. "The “Growth Curve”: An Autocorrelation Effect" Applied Microbiology 4, no. 3: 1257-1267. https://doi.org/10.3390/applmicrobiol4030086
APA StyleSchiraldi, A. (2024). The “Growth Curve”: An Autocorrelation Effect. Applied Microbiology, 4(3), 1257-1267. https://doi.org/10.3390/applmicrobiol4030086





