Creation of a Spatiotemporal Algorithm and Application to COVID-19 Data
Abstract
1. Introduction
2. Spatiotemporal Data Analysis and Clustering
2.1. Training the Algorithm for Spatiotemporal Data
2.2. Key Parameters of the Developed Algorithm
2.3. Best Matching Unit and Prototype Vectors
| Algorithm 1: Spatiotemporal Clustering Algorithm (proposed in this study and inspired by the works of Aaron et al. [29,30]). |
 |
2.4. Summary of the Algorithm and Detailed Steps
3. Application to COVID-19 Dataset and Results
3.1. COVID-19 Dataset
3.2. Clustering Results and Discussion
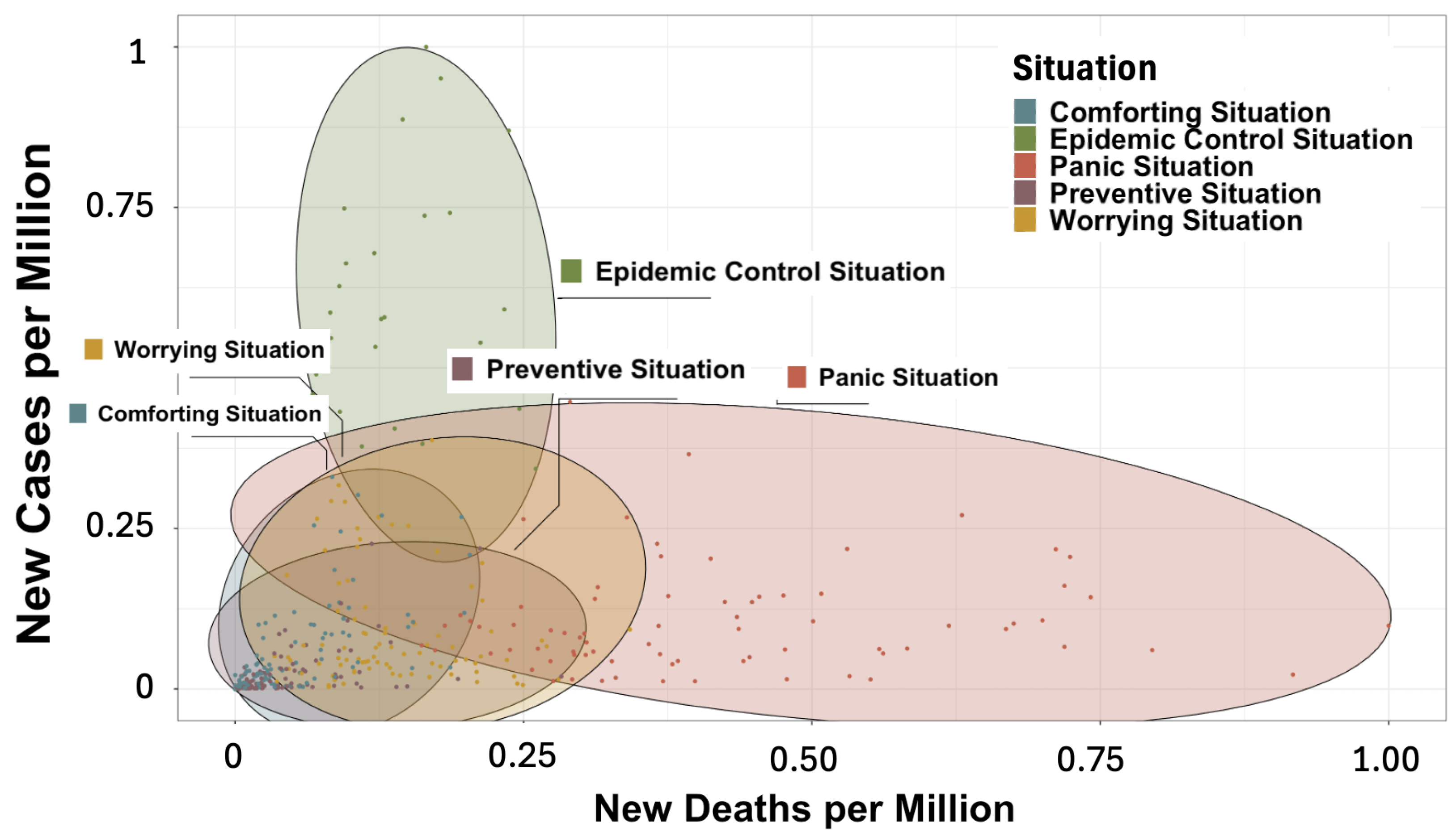
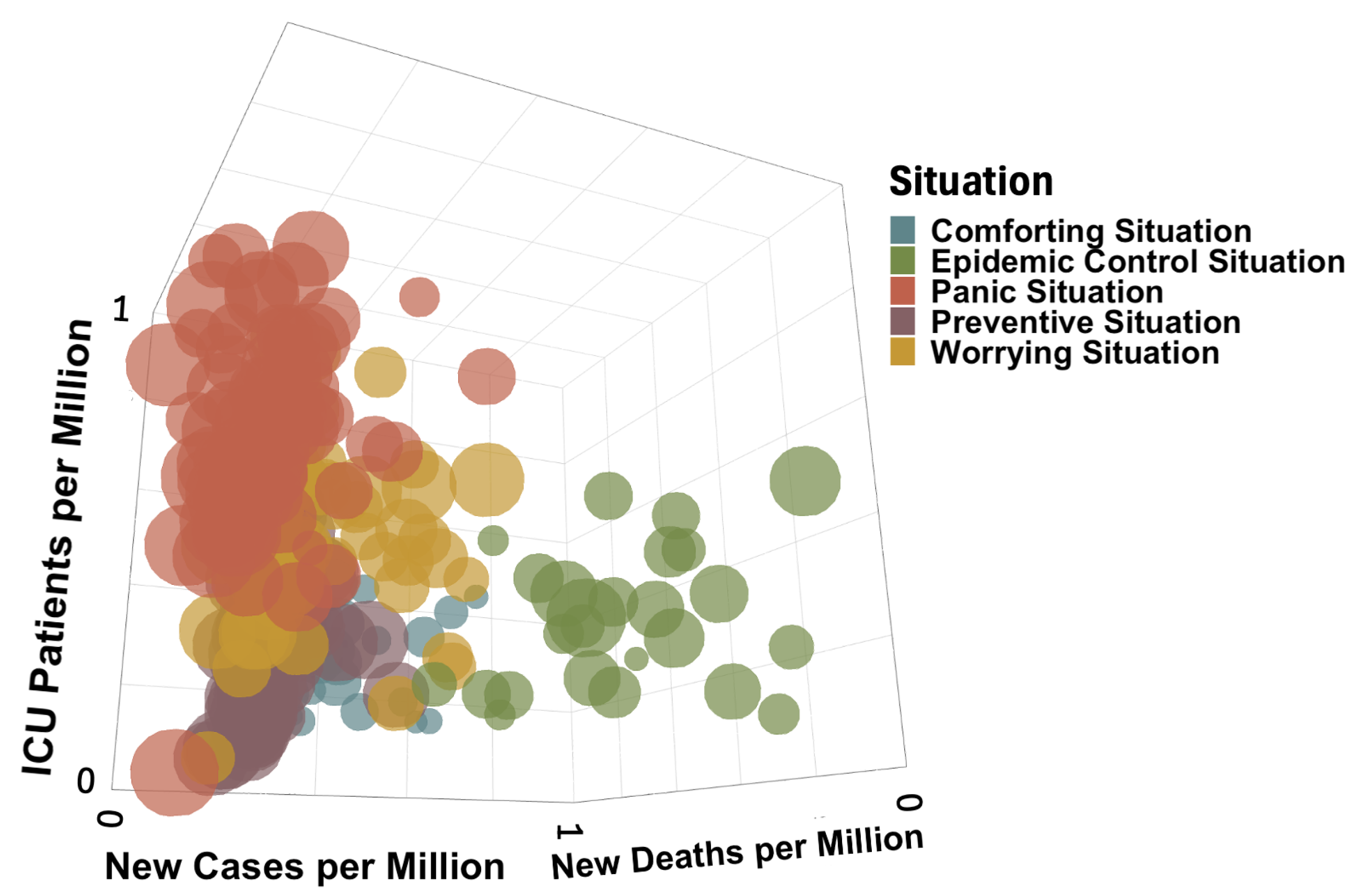
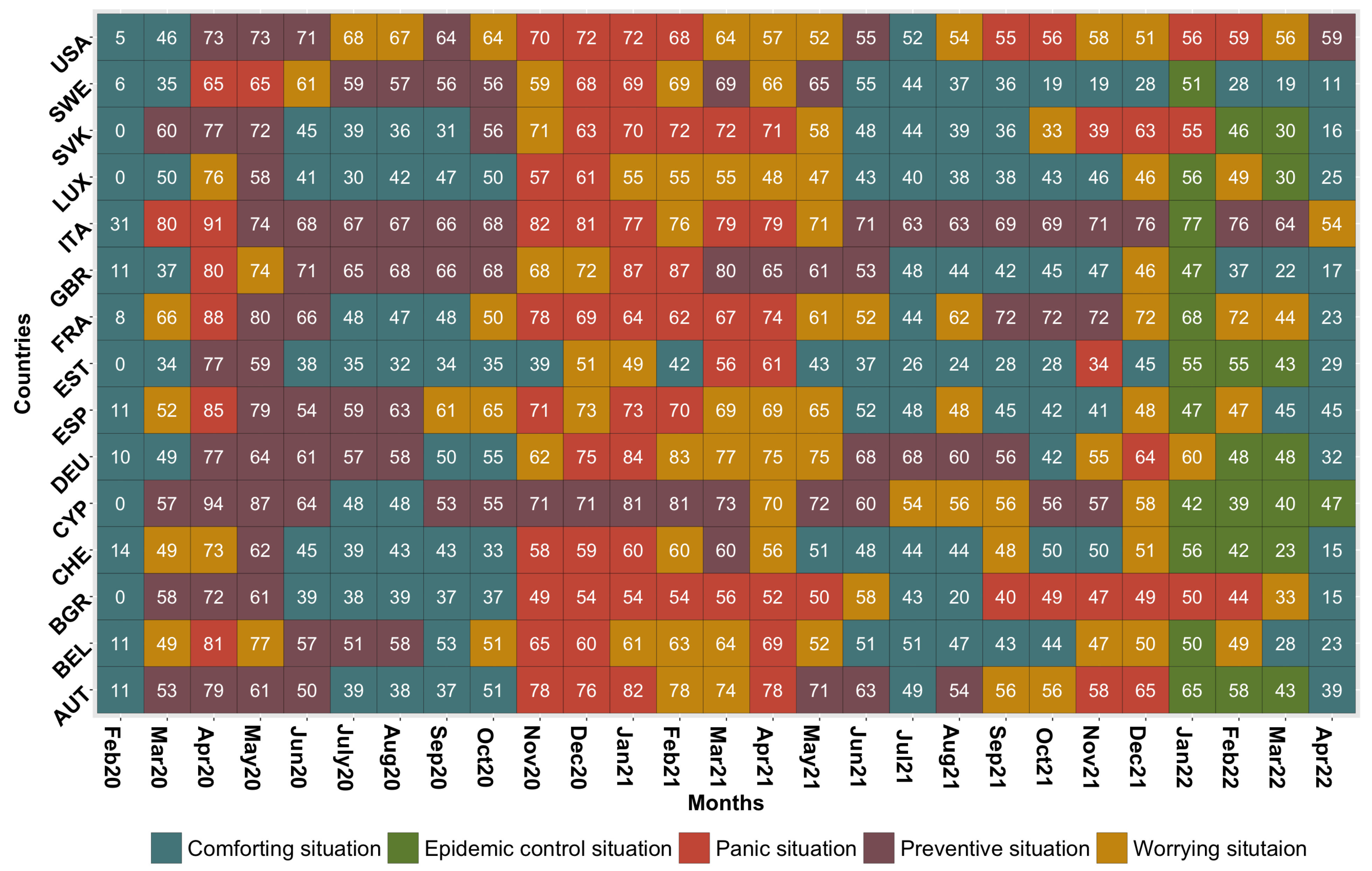
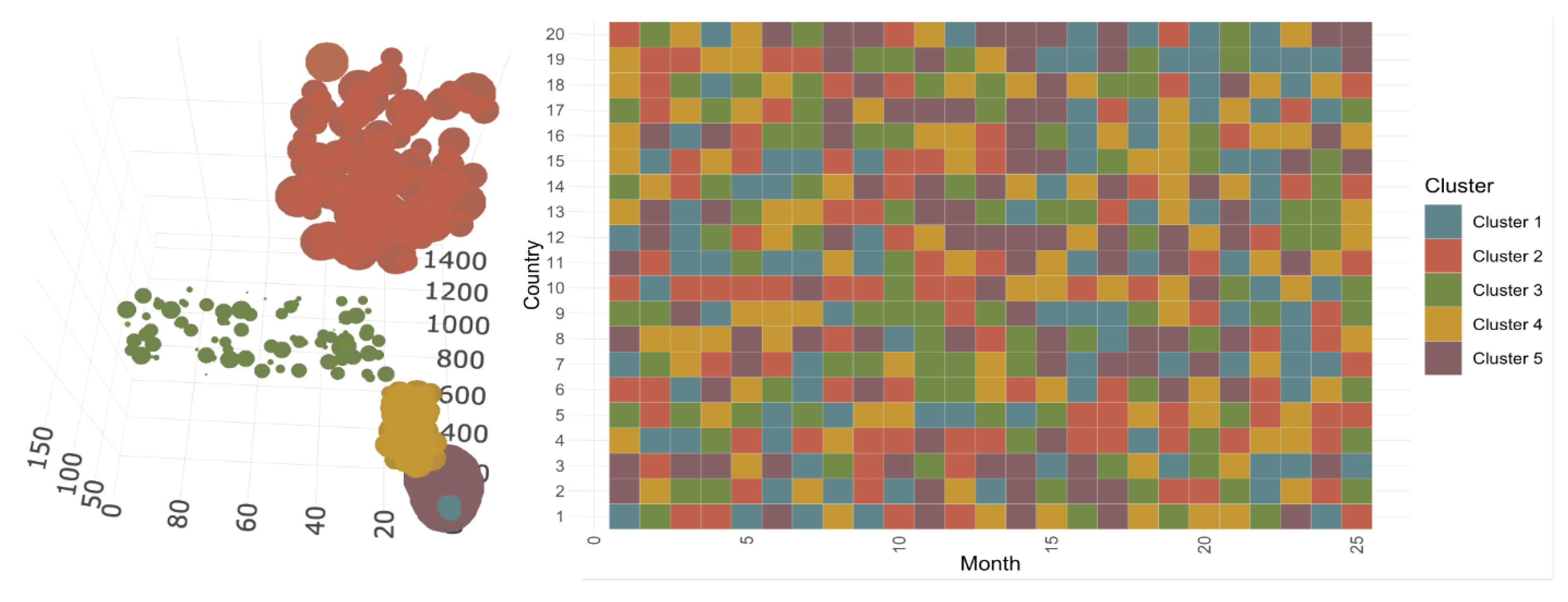
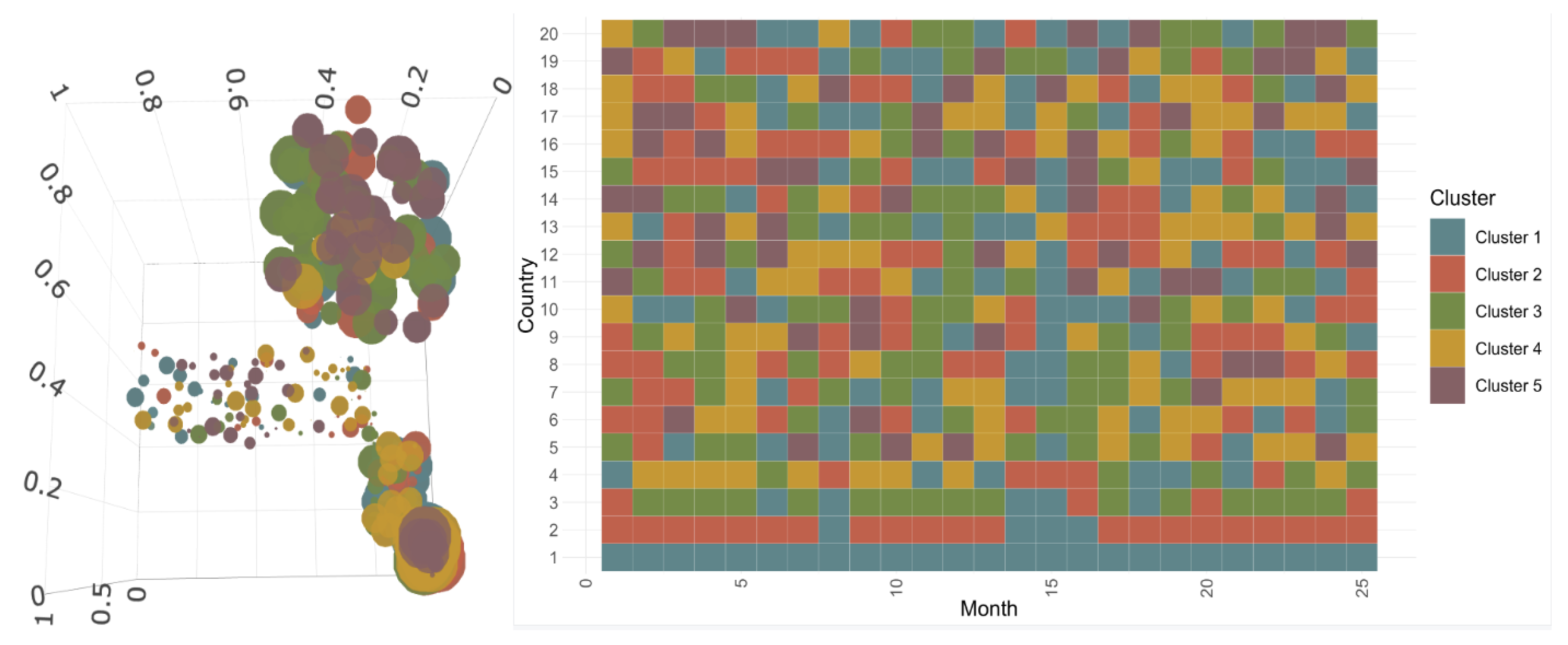
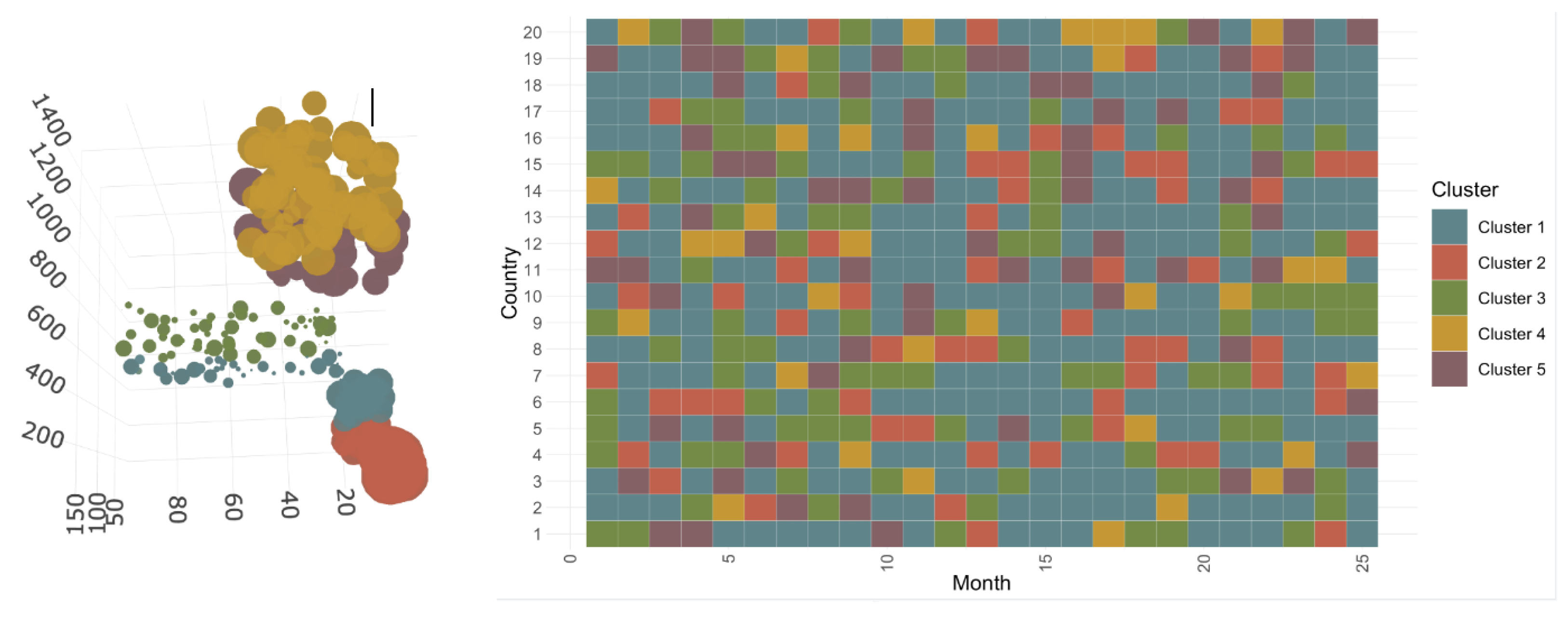
3.2.1. Construction and Composition of the Different Classes
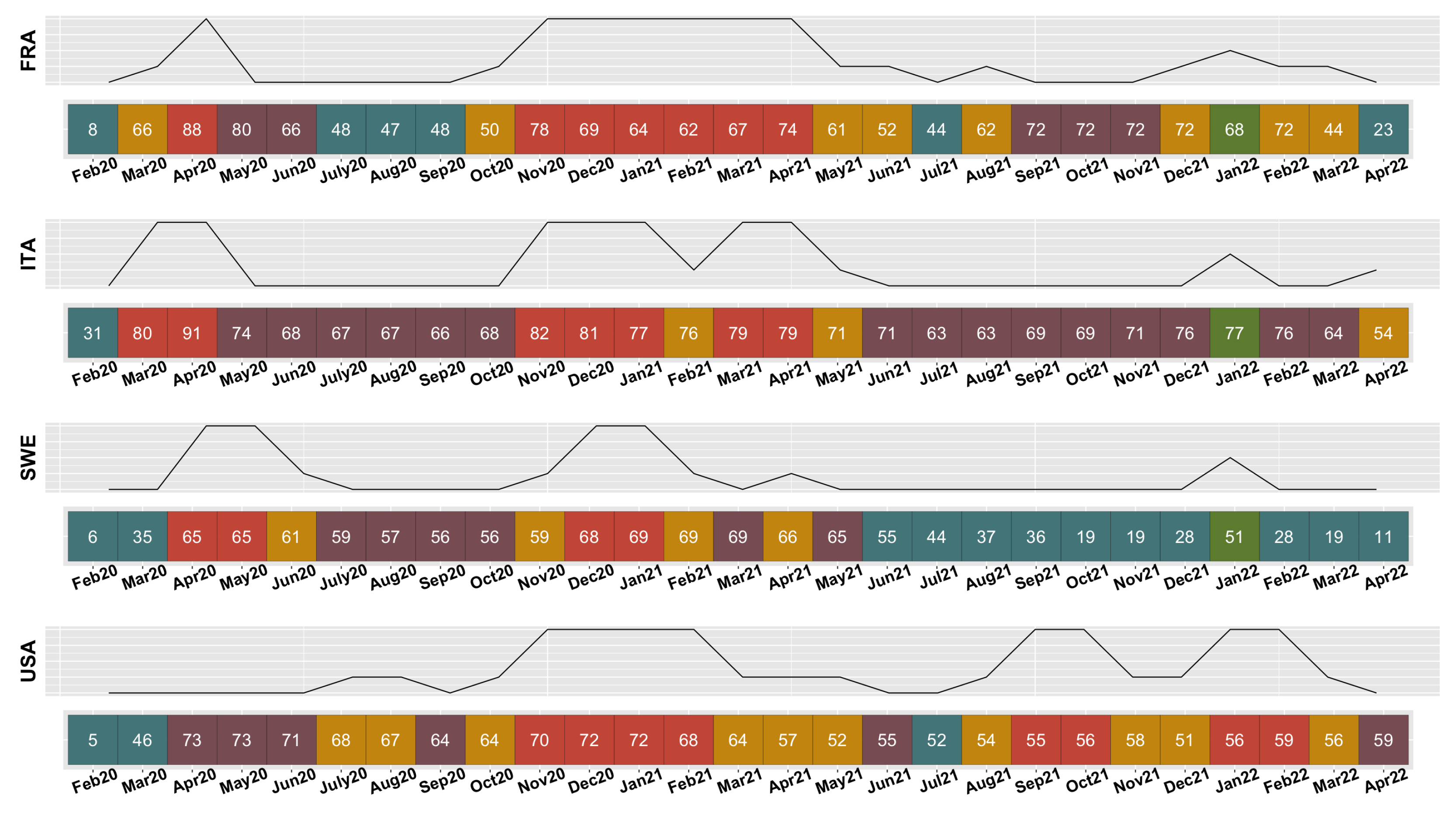
3.2.2. Evolution of COVID-19 in France, Italy, Sweden, and the United States
4. Advantages and Utility of the Constructed Algorithm
Theoretical Comparison of Clustering Methods
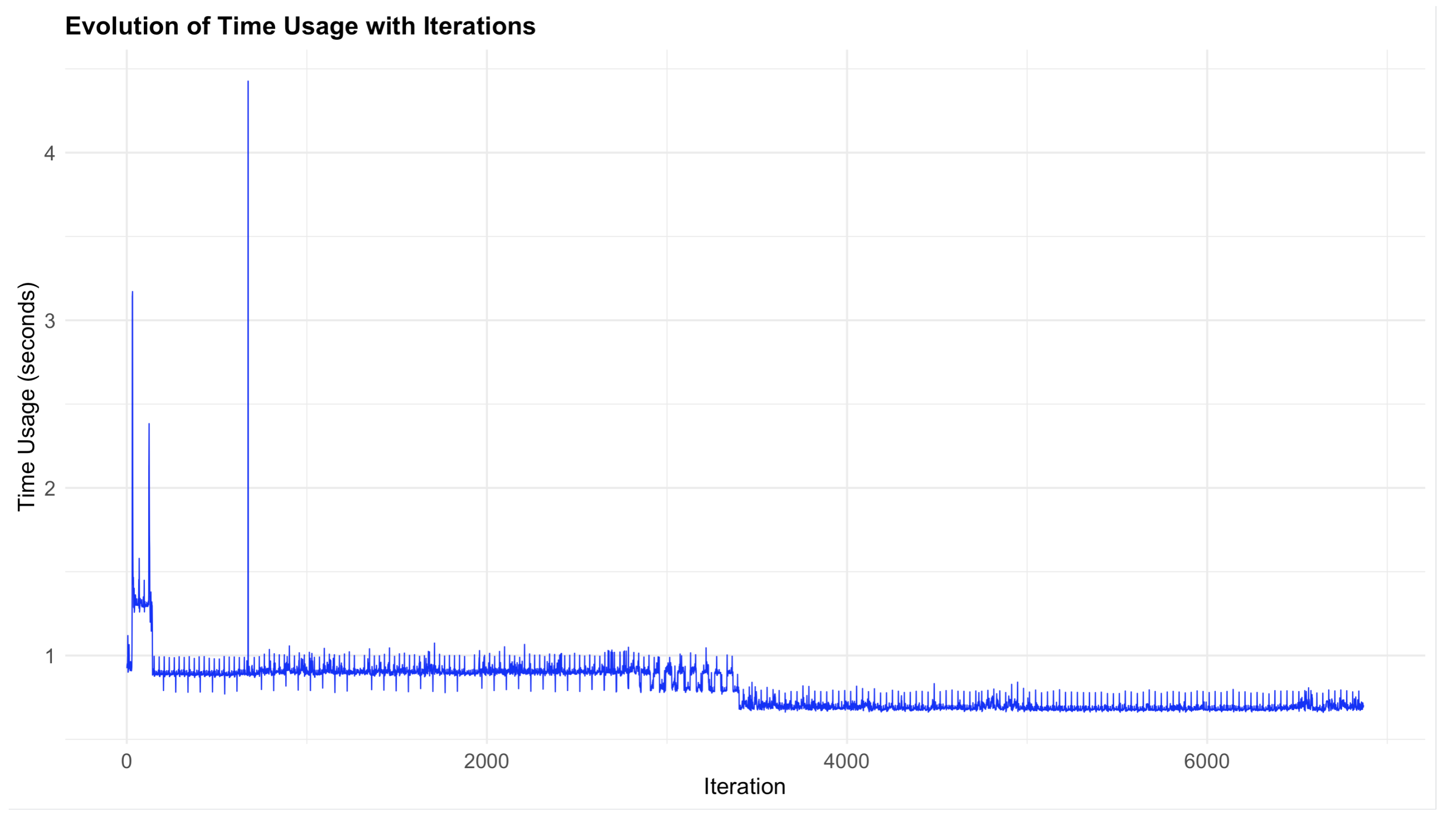
5. Time and Space Complexity Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rios, R.A.; Nogueira, T.; Coimbra, D.B.; Lopes, T.J.S.; Abraham, A.; de Mello, R.F. Country Transition Index Based on Hierarchical Clustering to Predict Next COVID-19 Waves. Sci. Rep. 2021, 11, 15271. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z. Spatiotemporal Evolution Patterns of the COVID-19 Pandemic Using Space-Time Aggregation and Spatial Statistics: A Global Perspective. ISPRS Int. J. Geo-Inf. 2021, 10, 519. [Google Scholar] [CrossRef]
- Spassiani, I.; Sebastiani, G.; Palù, G. Spatiotemporal Analysis of COVID-19 Incidence Data. Viruses 2021, 13, 463. [Google Scholar] [CrossRef]
- Yu, H.; Li, J.; Bardin, S.; Gu, H.; Fan, C. Spatiotemporal Dynamic of COVID-19 Diffusion in China: A Dynamic Spatial Autoregressive Model Analysis. ISPRS Int. J. Geo-Inf. 2021, 10, 510. [Google Scholar] [CrossRef]
- Signorelli, C.; Odone, A.; Gianfredi, V.; Bossi, E.; Bucci, D.; Oradini-Alacreu, A.; Frascella, B.; Capraro, M.; Chiappa, F.; Blandi, L.; et al. The Spread of COVID-19 in Six Western Metropolitan Regions: A False Myth on the Excess of Mortality in Lombardy and the Defense of the City of Milan. Acta Bio Med. Atenei Parm. 2020, 91, 23. [Google Scholar]
- Wieler, L.H.; Rexroth, U.; Gottschalk, R. Emerging COVID-19 Success Story: Germany’s Push to Maintain Progress. 2021. Available online: https://ourworldindata.org/covid-exemplar-germany (accessed on 3 July 2024).
- Usuelli, M. The Lombardy Region of Italy Launches the First Investigative COVID-19 Commission. Lancet 2020, 396, e86–e87. [Google Scholar] [CrossRef] [PubMed]
- Korhonen, J.; Granberg, B. Sweden Backcasting, Now?—Strategic Planning for COVID-19 Mitigation in a Liberal Democracy. Sustainability 2020, 12, 4138. [Google Scholar] [CrossRef]
- Rozanova, L.; Temerev, A.; Flahault, A. Comparing the Scope and Efficacy of COVID-19 Response Strategies in 16 Countries: An Overview. Int. J. Environ. Res. Public Health 2020, 17, 9421. [Google Scholar] [CrossRef] [PubMed]
- Centers for Disease Control and Prevention. COVID-19 Incidence, by Urban-Rural Classification—United States, January 22–October 31, 2020. Morb. Mortal. Wkly. Rep. 2020, 69, 1753–1757. [Google Scholar]
- Velicu, M.A.; Furlanetti, L.; Jung, J.; Ashkan, K. Epidemiological Trends in COVID-19 Pandemic: Prospective Critical Appraisal of Observations from Six Countries in Europe and the USA. BMJ Open 2021, 11, e045782. [Google Scholar] [CrossRef]
- Cascini, F.; Failla, G.; Gobbi, C.; Pallini, E.; Luxi, J.H.; Villani, L.; Quentin, W.; Boccia, S.; Ricciardi, W. A Cross-Country Comparison of COVID-19 Containment Measures and Their Effects on the Epidemic Curves. BMC Public Health 2022, 22, 1765. [Google Scholar] [CrossRef] [PubMed]
- Ndayishimiye, C.; Sowada, C.; Dyjach, P.; Stasiak, A.; Middleton, J.; Lopes, H.; Dubas-Jakóbczyk, K. Associations between the COVID-19 Pandemic and Hospital Infrastructure Adaptation and Planning—A Scoping Review. Int. J. Environ. Res. Public Health 2022, 19, 8195. [Google Scholar] [CrossRef] [PubMed]
- Ciulla, M.; Marinelli, L.; Di Biase, G.; Cacciatore, I.; Santoleri, F.; Costantini, A.; Dimmito, M.P.; Di Stefano, A. Healthcare Systems across Europe and the US: The Managed Entry Agreements Experience. Healthcare 2023, 11, 447. [Google Scholar] [CrossRef] [PubMed]
- Lau, Y.-Y.; Dulebenets, M.A.; Yip, H.-T.; Tang, Y.-M. Healthcare Supply Chain Management under COVID-19 Settings: The Existing Practices in Hong Kong and the United States. Healthcare 2022, 10, 1549. [Google Scholar] [CrossRef]
- Primc, K.; Slabe-Erker, R. The Success of Public Health Measures in Europe during the COVID-19 Pandemic. Sustainability 2020, 12, 4321. [Google Scholar] [CrossRef]
- Liu, S.; Ermolieva, T.; Cao, G.; Chen, G.; Zheng, X. Analyzing the Effectiveness of COVID-19 Lockdown Policies Using the Time-Dependent Reproduction Number and the Regression Discontinuity Framework: Comparison between Countries. Eng. Proc. 2021, 5, 8. [Google Scholar] [CrossRef]
- Wang, W.; Gurgone, A.; Martínez, H.; Góes, M.C.B.; Gallo, E.; Kerényi, Á.; Turco, E.M.; Coburger, C.; Andrade, P.D.S. COVID-19 Mortality and Economic Losses: The Role of Policies and Structural Conditions. J. Risk Financ. Manag. 2022, 15, 354. [Google Scholar] [CrossRef]
- Cheam, A.S.M.; Marbac, M.; McNicholas, P.D. Model-Based Clustering for Spatiotemporal Data on Air Quality Monitoring. Environmetrics 2017, 28, e2437. [Google Scholar] [CrossRef]
- Wu, X.; Zurita-Milla, R.; Kraak, M.-J.; Izquierdo-Verdiguier, E. Clustering-Based Approaches to the Exploration of Spatio-Temporal Data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 1387–1391. [Google Scholar] [CrossRef]
- Deng, M.; Liu, Q.; Wang, J.; Shi, Y. A General Method of Spatio-Temporal Clustering Analysis. Sci. China Inf. Sci. 2013, 56, 1–14. [Google Scholar] [CrossRef]
- Izakian, H.; Pedrycz, W.; Jamal, I. Clustering Spatiotemporal Data: An Augmented Fuzzy C-Means. IEEE Trans. Fuzzy Syst. 2012, 21, 855–868. [Google Scholar] [CrossRef]
- Hoffman, F.M.; Hargrove, W.W.; Mills, R.T.; Mahajan, S.; Erickson, D.J.; Oglesby, R.J. Multivariate Spatio-Temporal Clustering (MSTC) as a Data Mining Tool for Environmental Applications. In Proceedings of the 4th International Congress on Environmental Modelling and Software, Barcelona, Spain, 7–10 July 2008. [Google Scholar]
- Hagenauer, J.; Helbich, M. Hierarchical Self-Organizing Maps for Clustering Spatiotemporal Data. Int. J. Geogr. Inf. Sci. 2013, 27, 2026–2042. [Google Scholar] [CrossRef]
- Win, K.N.; Chen, J.; Chen, Y.; Fournier-Viger, P. PCPD: A Parallel Crime Pattern Discovery System for Large-Scale Spatiotemporal Data Based on Fuzzy Clustering. Int. J. Fuzzy Syst. 2019, 21, 1961–1974. [Google Scholar] [CrossRef]
- Tuite, A.R.; Guthrie, J.L.; Alexander, D.C.; Whelan, M.S.; Lee, B.; Lam, K.; Ma, J.; Fisman, D.N.; Jamieson, F.B. Epidemiological Evaluation of Spatiotemporal and Genotypic Clustering of Mycobacterium Tuberculosis in Ontario, Canada. Int. J. Tuberc. Lung Dis. 2013, 17, 1322–1327. [Google Scholar] [CrossRef] [PubMed]
- Léger, A.-E.; Mazzuco, S. What Can We Learn from the Functional Clustering of Mortality Data? An Application to the Human Mortality Database. Eur. J. Popul. 2021, 37, 769–798. [Google Scholar] [CrossRef] [PubMed]
- Levantesi, S.; Nigri, A.; Piscopo, G. Clustering-Based Simultaneous Forecasting of Life Expectancy Time Series through Long-Short Term Memory Neural Networks. Int. J. Approx. Reason. 2022, 140, 282–297. [Google Scholar] [CrossRef]
- Aaron, C.; Perraudin, C.; Rynkiewicz, J. Curves Based Kohonen Map and Adaptative Classification: An Application to the Convergence of the European Union Countries. In Proceedings of the Conference WSOM, WSOM’03, Kyushu Institute of Technology, Kitakyushu, Japan, 11–14 September 2003; pp. 324–330. [Google Scholar]
- Aaron, C.; Perraudin, C.; Rynkiewicz, J. Adaptation de l’algorithme SOM à l’analyse de données temporelles et spatiales: Application à l’étude de l’évolution des performances en matière d’emploi. In Proceedings of the ASMDA 2005, Applied Stochastic Models and Data Analysis; A Conference of the Quantitative Methods in Business and Industry Society, Brest, France, 17–20 May 2005; pp. 480–488. [Google Scholar]
- Na, S.; Xumin, L.; Yong, G. Research on K-means Clustering Algorithm: An Improved K-means Clustering Algorithm. In Proceedings of the 2010 Third International Symposium on Intelligent Information Technology and Security Informatics, Ji’an, China, 2–4 April 2010; pp. 63–67. [Google Scholar]
- Miljković, D. Brief Review of Self-Organizing Maps. In Proceedings of the 2017 40th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 22–26 May 2017; pp. 1061–1066. [Google Scholar]
- Bullinaria, J.A. Self Organizing Maps: Fundamentals, Introduction to Neural Networks: Lecture 16. University of Birmingham, UK. Available online: https://www.cs.bham.ac.uk/~jxb/NN/l16.pdf (accessed on 3 July 2024).
- Natita, W.; Wiboonsak, W.; Dusadee, S. Appropriate Learning Rate and Neighborhood Function of Self-Organizing Map (SOM) for Specific Humidity Pattern Classification over Southern Thailand. Int. J. Model. Optim. 2016, 6, 61. [Google Scholar] [CrossRef]
- Caliński, T.; Harabasz, J. A Dendrite Method for Cluster Analysis. Commun. Stat. Theory Methods 1974, 3, 1–27. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A Graphical Aid to the Interpretation and Validation of Cluster Analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Gaber, M.M.; Vatsavai, R.R.; Omitaomu, O.A.; Gama, J.; Chawla, N.V.; Ganguly, A.R. Knowledge Discovery from Sensor Data: Second International Workshop, Sensor-KDD 2008, Las Vegas, NV, USA, 24–27 August 2008, Revised Selected Papers; Springer: Berlin/Heidelberg, Germany, 2010; Volume 5840. [Google Scholar]
- Pitafi, S.; Anwar, T.; Sharif, Z. A Taxonomy of Machine Learning Clustering Algorithms, Challenges, and Future Realms. Appl. Sci. 2023, 13, 3529. [Google Scholar] [CrossRef]



| Parameter | Explanation |
|---|---|
| M | Number of study periods. Represents the number of distinct temporal periods considered in the analysis. |
| S | Number of populations. Represents the number of distinct populations (e.g., countries) considered in the analysis. |
| D | Data Set. Collection of N data objects characterized by , where s denotes a population and m denotes a period. |
| X | Data Representation. Vector of variables associated with each data point in D, enabling comparisons and similarity calculations. |
| K | Desired number of groups. Represents the desired final number of clusters or prototypes aimed to be formed within the data. |
| Ultimate Superclasses. Subset of P obtained using ascending hierarchical method, representing the final groups. | |
| Learning Rate. Percentage by which the algorithm learns during each iteration, influencing modification of prototype vectors. | |
| Temporal Neighborhood Function. Governs intensity with which neurons having different times than BMU approach a data point. | |
| Spatial Neighborhood Function. Determines intensity with which neurons with same period as BMU approach a data point. | |
| Temporal Radius. Defines extent of temporal influence, allowing adjustments in temporal neighborhood function. | |
| Spatial Radius. Controls spatial influence on clustering, impacting spatial neighborhood function. | |
| Total Spatial Iterations. Represents total number of spatial iterations, influencing cluster evolution over space. | |
| Total Temporal Iterations. Represents total temporal iterations within each spatial iteration, allowing exploration of temporal patterns. | |
| Clustering Target. Desired final number of clusters or prototypes aimed to be formed within the data. | |
| Initial Spatial Radius. Initial spatial radius for neighborhood functions. | |
| Final Spatial Radius. Final spatial radius for neighborhood functions. | |
| Initial Temporal Radius. Initial temporal radius for neighborhood functions. | |
| Final Temporal Radius. Final temporal radius for neighborhood functions. | |
| E | Number of Randomly Selected Populations. Represents number of randomly selected populations from the dataset. |
| Prototype Vector. Serves as the prototype vector associated with neuron k, evolving during clustering to capture cluster characteristics. | |
| BMU | Best Matching Unit. Identifies the neuron with the prototype vector closest to the data point, pivotal in clustering. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bou Sakr, N.; Mansour, G.; Salhi, Y. Creation of a Spatiotemporal Algorithm and Application to COVID-19 Data. COVID 2024, 4, 1291-1314. https://doi.org/10.3390/covid4080092
Bou Sakr N, Mansour G, Salhi Y. Creation of a Spatiotemporal Algorithm and Application to COVID-19 Data. COVID. 2024; 4(8):1291-1314. https://doi.org/10.3390/covid4080092
Chicago/Turabian StyleBou Sakr, Natalia, Gihane Mansour, and Yahia Salhi. 2024. "Creation of a Spatiotemporal Algorithm and Application to COVID-19 Data" COVID 4, no. 8: 1291-1314. https://doi.org/10.3390/covid4080092
APA StyleBou Sakr, N., Mansour, G., & Salhi, Y. (2024). Creation of a Spatiotemporal Algorithm and Application to COVID-19 Data. COVID, 4(8), 1291-1314. https://doi.org/10.3390/covid4080092






