Impact of Angular Speed Calculation Methods from Encoder Measurements on the Test Uncertainty of Electric Motor Efficiency
Abstract
1. Introduction
2. Angular Speed Calculation Methods
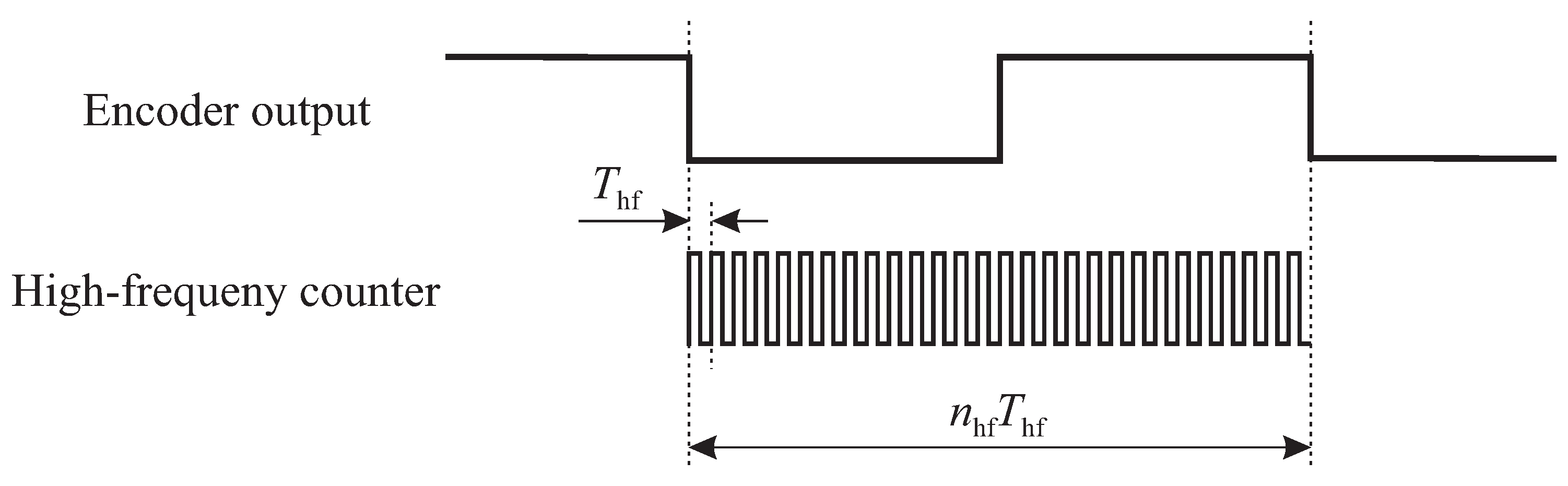
2.1. Frequency Measurement
2.2. Period Measurement
3. Uncertainty Analysis of the Angular Speed Calculation Methods
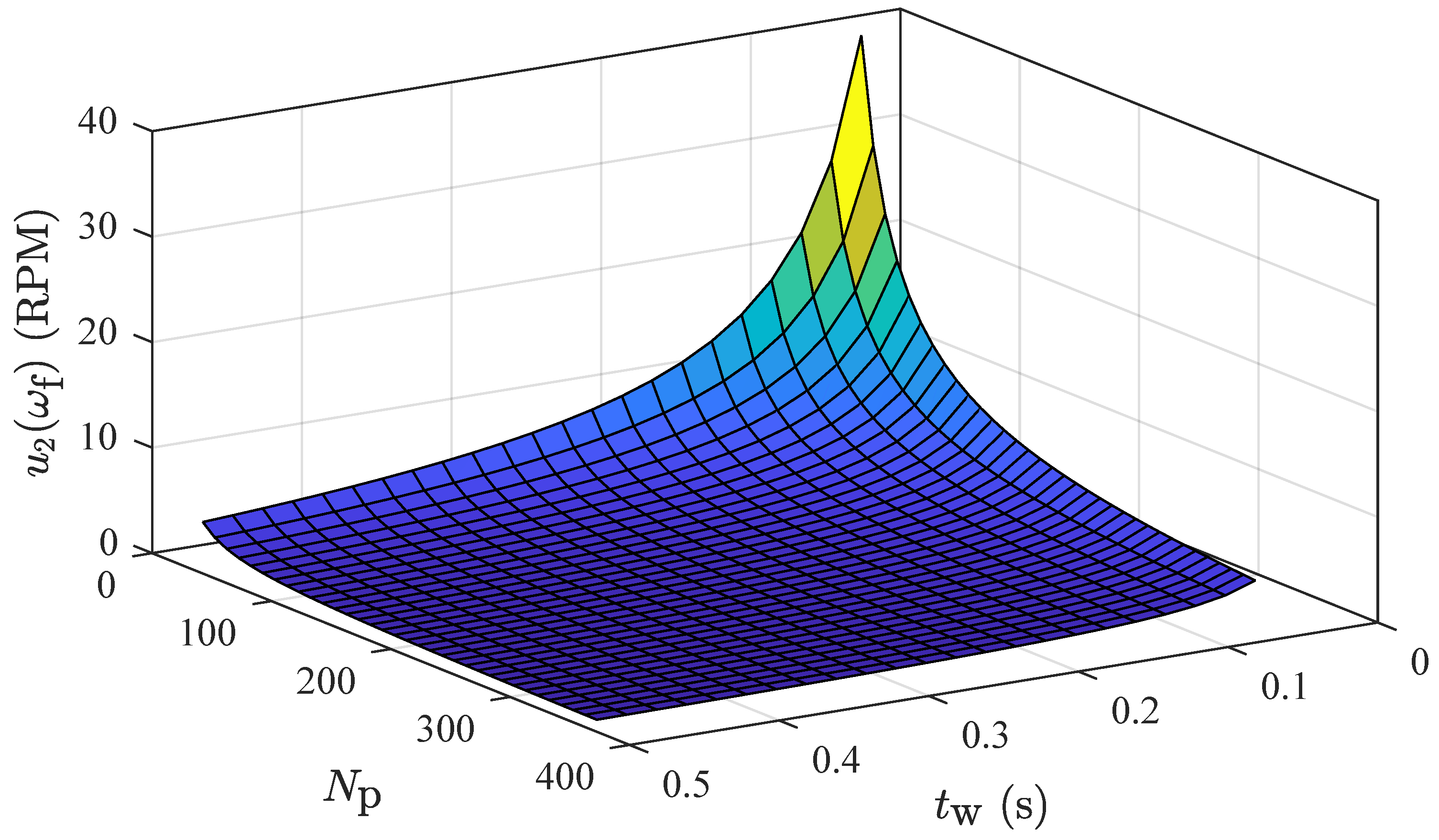
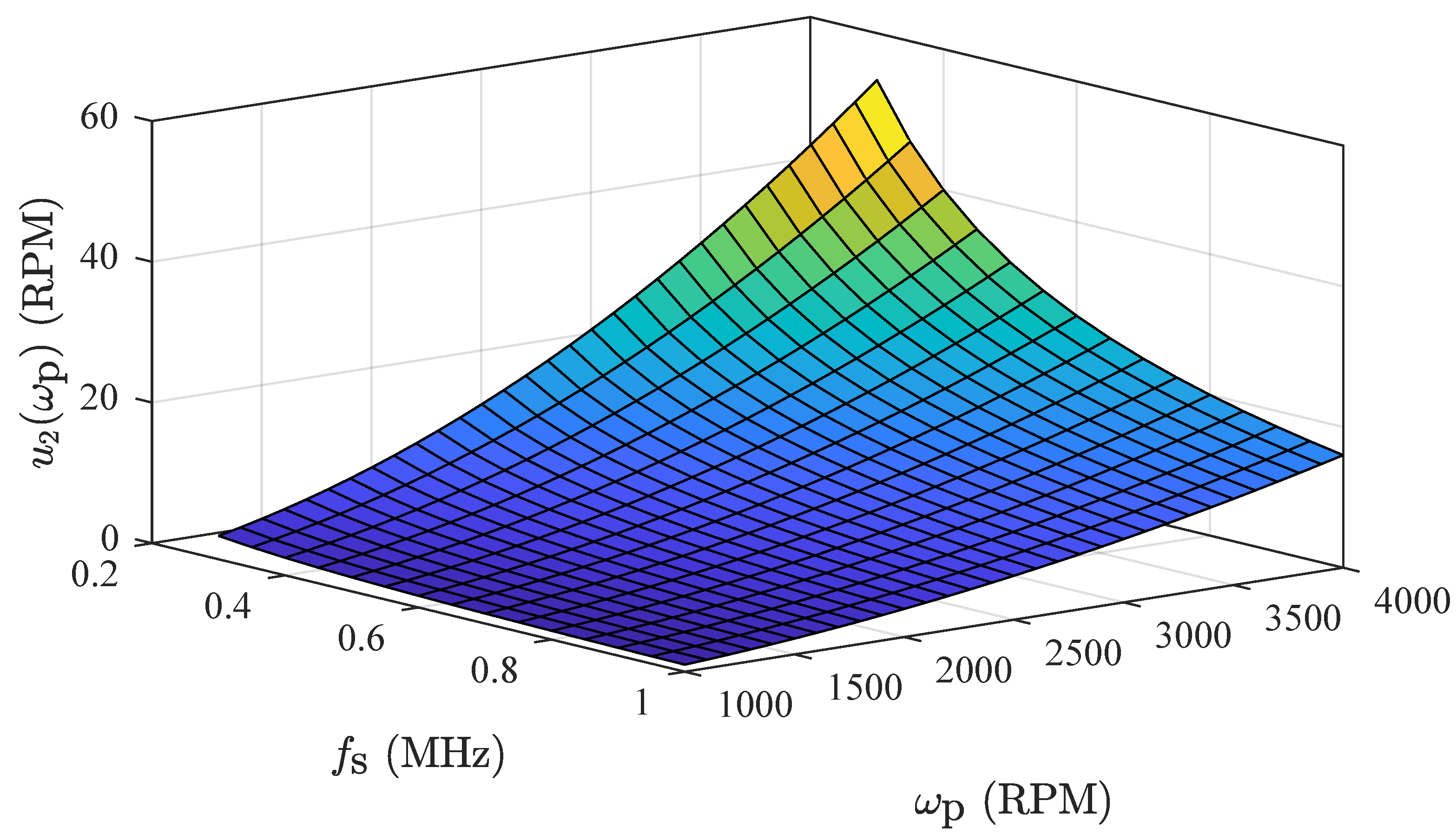
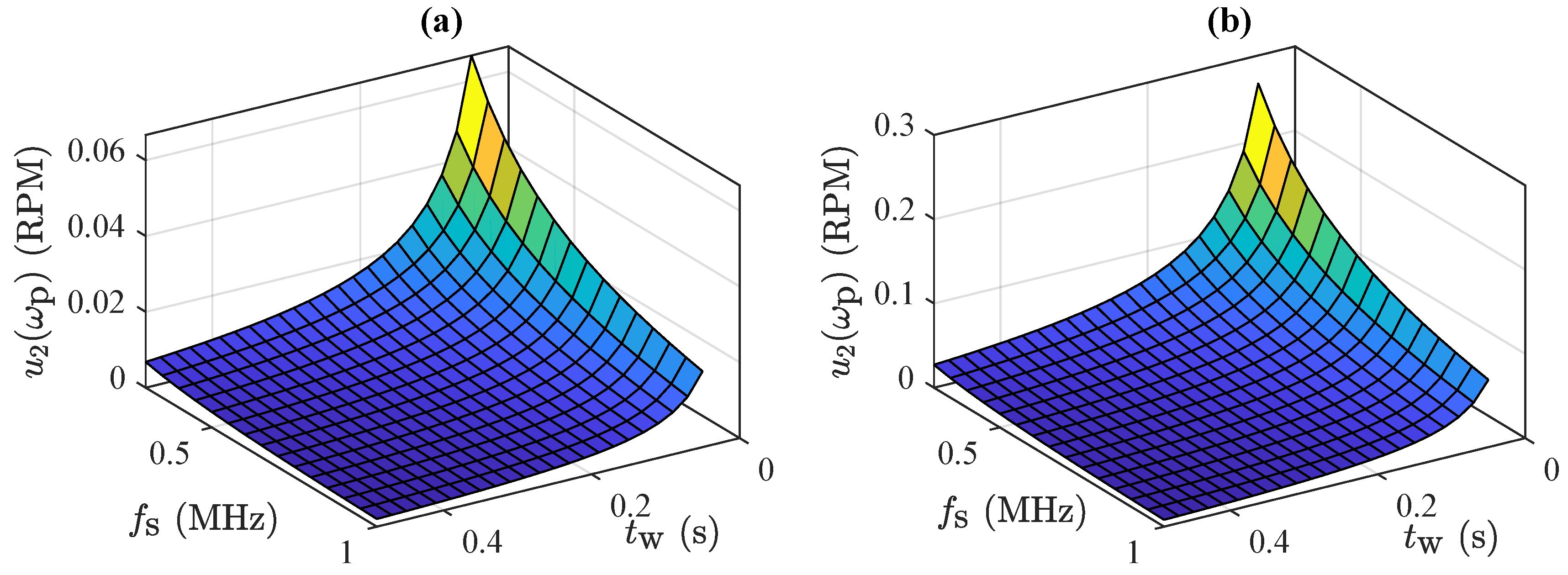
3.1. Frequency Measurement
- : repeatability
- : method resolution
- : time base variability
- : non-uniformity of encoder markings
3.2. Period Measurement
- : repeatability
- : method resolution
- : timing resolution of the DAQ
- : non-uniformity of encoder markings
4. Test Rig
5. Experimental Study of Angular Speed Uncertainty
5.1. Steady-State Comparison
5.2. Dynamic Comparison
6. Impacts on Efficiency Test Uncertainty
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dinolova, P.; Ruseva, V.; Dinolov, O. Energy Efficiency of Induction Motor Drives: State of the Art, Analysis and Recommendations. Energies 2023, 16, 7136. [Google Scholar] [CrossRef]
- Ferreira, F.J.; de Almeida, A.T. Reducing Energy Costs in Electric-Motor-Driven Systems: Savings Through Output Power Reduction and Energy Regeneration. IEEE Ind. Appl. Mag. 2018, 24, 84–97. [Google Scholar] [CrossRef]
- Caruso, M.; Tommaso, A.D.; Miceli, R.; Nevoloso, C.; Spataro, C. Uncertainty evaluation in the differential measurements of power losses in a power drive system. Measurement 2021, 183, 109795. [Google Scholar] [CrossRef]
- IEC 60034-30-1:2014; Rotating Electrical Machines—Part 30-1: Efficiency Classes of Line Operated AC Motors (IE Code). International Eletrotechnical Comission: Geneva, Switzerland, 2006.
- Aarniovuori, L.; Kolehmainen, J.; Kosonen, A.; Niemela, M.; Pyrhonen, J. Uncertainty in motor efficiency measurements. In Proceedings of the 17th International Conference on Electrical Machines and Systems, Hangzhou, China, 22–25 October 2014; IEEE: New York, NY, USA, 2014; pp. 323–329. [Google Scholar] [CrossRef]
- Lu, S.M. A review of high-efficiency motors: Specification, policy, and technology. Renew. Sustain. Energy Rev. 2016, 59, 1–12. [Google Scholar] [CrossRef]
- Kumar, R.; Sah, B.; Kumar, P. Stray Loss Formulation for Inverter-Driven Induction Motors for a Wide Range of Switching Frequency and Motor’s Loading. IEEE Trans. Ind. Electron. 2024, 71, 2385–2394. [Google Scholar] [CrossRef]
- Song, Z.; Weidinger, P.; Kumme, R. Accurate Rotational Speed Measurement for Determining the Mechanical Power and Efficiency of Electrical Machines. In Proceedings of the 2021 24th International Conference on Electrical Machines and Systems (ICEMS), Gyeongju, Republic of Korea, 31 October–3 November 2021; pp. 1641–1645. [Google Scholar] [CrossRef]
- Lorenz, R.; Van Patten, K. High-resolution velocity estimation for all-digital, AC servo drives. IEEE Trans. Ind. Appl. 1991, 27, 701–705. [Google Scholar] [CrossRef]
- Briz, F.; Cancelas, J.; Diez, A. Speed measurement using rotary encoders for high performance AC drives. In Proceedings of the IECON’94—20th Annual Conference of IEEE Industrial Electronics, Bologna, Italy, 5–9 September 1994; Volume 1, pp. 538–542. [Google Scholar] [CrossRef]
- Stojkovic, N.; Stare, Z.; Mijat, N. Dual-mode digital revolution counter. In Proceedings of the IMTC 2001, 18th IEEE Instrumentation and Measurement Technology Conference, Rediscovering Measurement in the Age of Informatics (Cat. No.01CH 37188), Budapest, Hungary, 21–23 May 2001; Volume 2, pp. 950–954. [Google Scholar] [CrossRef]
- Petrella, R.; Tursini, M.; Peretti, L.; Zigliotto, M. Speed measurement algorithms for low-resolution incremental encoder equipped drives: A comparative analysis. In Proceedings of the 2007 International Aegean Conference on Electrical Machines and Power Electronics, Bodrum, Turkey, 10–12 September 2007; pp. 780–787. [Google Scholar] [CrossRef]
- Ilmiawan, A.F.; Wijanarko, D.; Arofat, A.H.; Hindersyah, H.; Purwadi, A. An easy speed measurement for incremental rotary encoder using multi stage moving average method. In Proceedings of the 2014 International Conference on Electrical Engineering and Computer Science (ICEECS), Denpasar, Indonesia, 24–25 November 2014; pp. 363–368. [Google Scholar] [CrossRef]
- Kazemirova, Y.; Podzorova, V.; Anuchin, A.; Lashkevich, M.; Aliamkin, D.; Vagapov, Y. Speed Estimation Applying Sinc-filter to a Period-based Method for Incremental Position Encoder. In Proceedings of the 2019 54th International Universities Power Engineering Conference (UPEC), Bucharest, Romania, 3–6 September 2019. [Google Scholar] [CrossRef]
- Anuchin, A.; Podzorova, V.; Kazemirova, Y.; Chen, H.; Lashkevich, M.; Savkin, D.; Demidova, G. Speed Measurement for Incremental Position Encoder Using Period-Based Method with Sinc3 Filtering. IEEE Sens. J. 2023, 23, 5073–5083. [Google Scholar] [CrossRef]
- JJCGM 100:2008; Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement. International Organization for Standardization: Geneva, Switzerland, 2008.
- Machado, J.P.Z.; Flesch, R.C.C.; Schaefer, M.M.; de Santana, R.H. Bearing heating open-loop control system to reduce variability in BLDC motor tests. In Proceedings of the 2023 7th International Symposium on Instrumentation Systems, Circuits and Transducers (INSCIT), Rio de Janeiro, Brazil, 28 August–1 September 2023; pp. 107–112. [Google Scholar] [CrossRef]
- Killedar, J. Dynamometer; Xlibris: Bloomington, IN, USA, 2012. [Google Scholar]
- Blondel, A. Measurements of The Energy of Polyphase Currents. In Proceedings of the International Electrical Congress, Chicago, IL, USA, 21–25 August 1893; American Institute of Electrical Engineers: New York, NY, USA, 1894. [Google Scholar]
- IEEE Std 115-2019 (Revision of IEEE Std 115-2009); IEEE Guide for Test Procedures for Synchronous Machines Including Acceptance and Performance Testing and Parameter Determination for Dynamic Analysis. IEEE: New York, NY, USA, 2020; pp. 1–246. [CrossRef]
- Webster, J.G.; Eren, H. (Eds.) Measurement, Instrumentation, and Sensors Handbook, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]

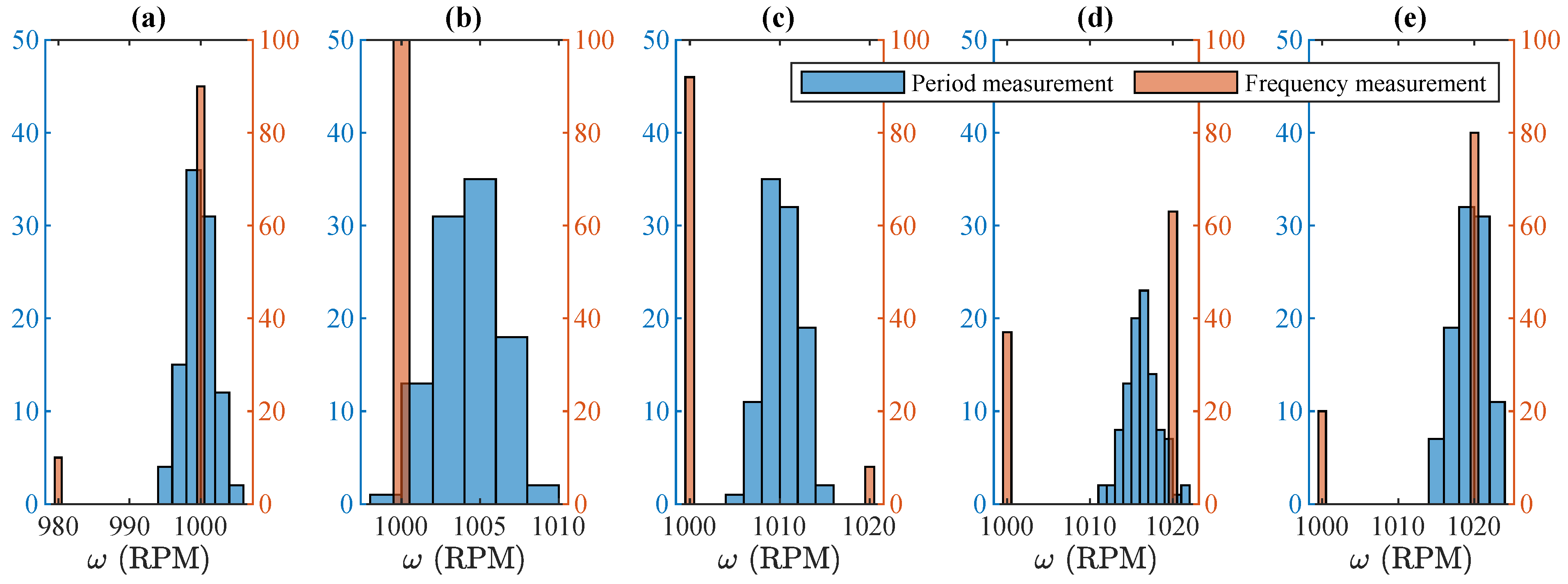
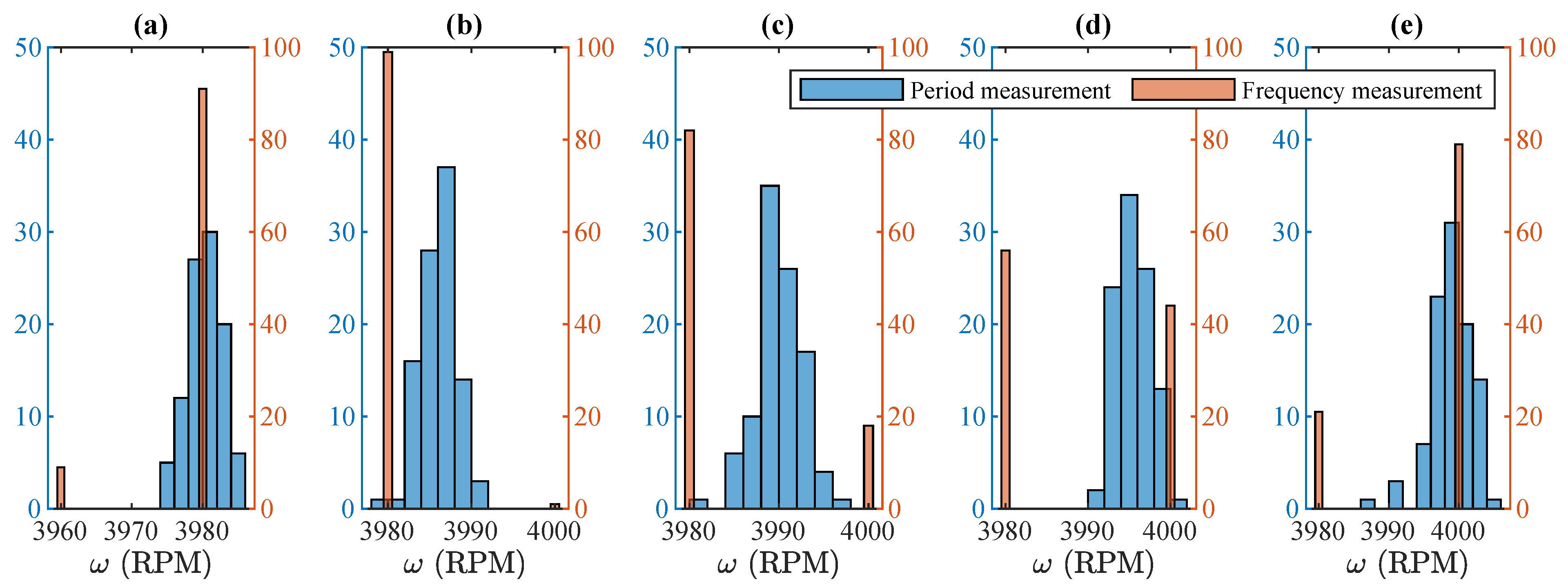
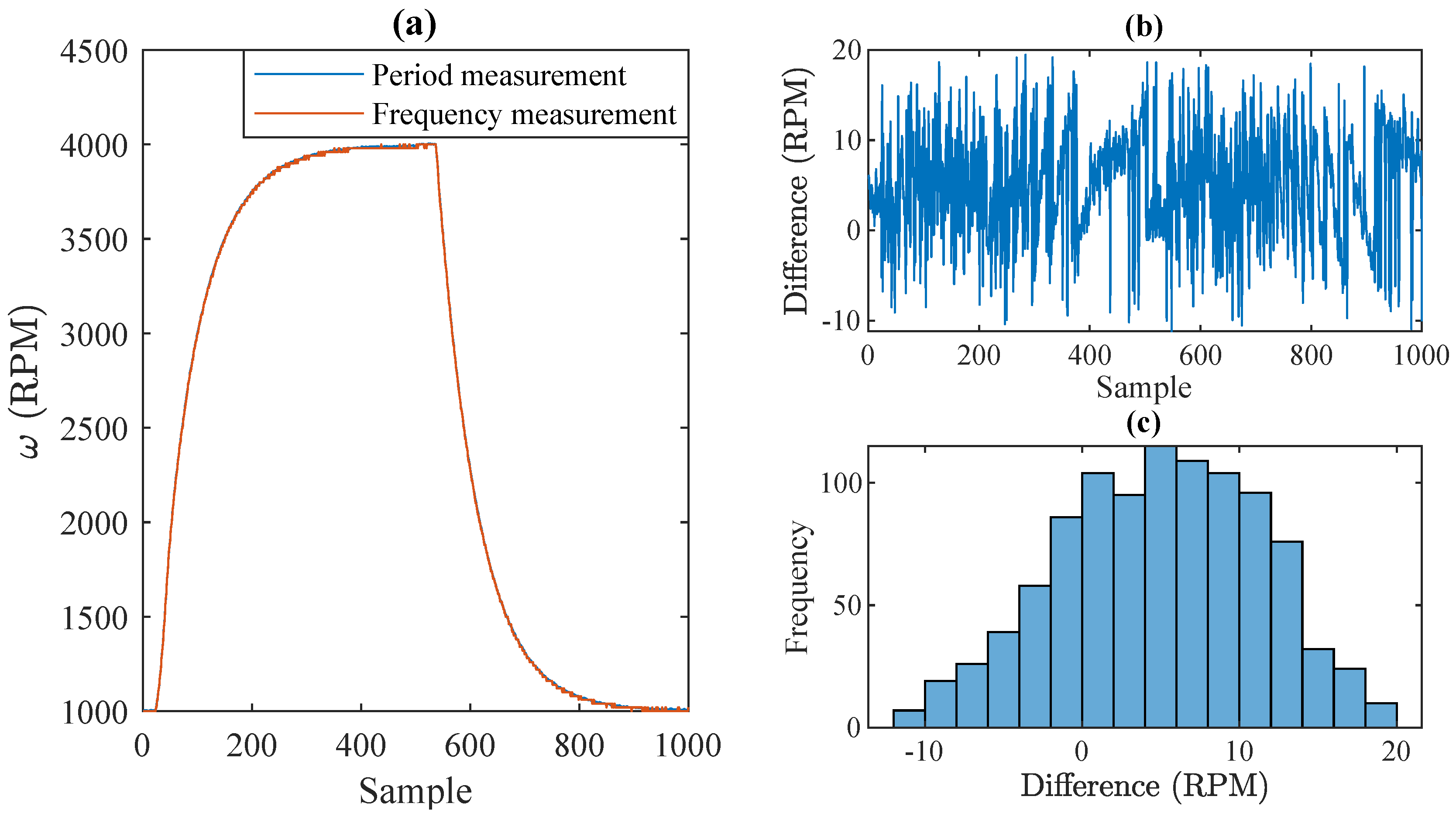
| [RPM] | [RPM] | [%] | [RPM] | [%] |
|---|---|---|---|---|
| 1000 | 999.7 | −0.03 | 998.0 | −0.20 |
| 1005 | 1004.3 | −0.07 | 1000.0 | −0.50 |
| 1010 | 1010.3 | 0.03 | 1001.6 | −0.83 |
| 1015 | 1016.2 | 0.12 | 1012.6 | −0.24 |
| 1020 | 1019.4 | −0.06 | 1016.0 | −0.39 |
| 3980 | 3980.4 | 0.01 | 3978.2 | −0.05 |
| 3985 | 3986.0 | 0.02 | 3980.2 | −0.12 |
| 3990 | 3990.0 | 0.01 | 3983.6 | −0.16 |
| 3995 | 3995.5 | 0.01 | 3988.8 | −0.16 |
| 4000 | 3998.9 | −0.03 | 3995.8 | −0.11 |
| Uncertainty Component | DOF | Type | Probability Distribution | Standard Uncertainty [RPM] |
|---|---|---|---|---|
| 99 | A | Normal | 0.211 | |
| ∞ | B | Rectangular | 0.023 | |
| ∞ | B | Rectangular | 0.006 | |
| 32 | B | Normal | 0.375 |
| [RPM] | [RPM] | [RPM] | [RPM] | [RPM] |
|---|---|---|---|---|
| 1000 | 999.71 | 0.86 | 998 | 23 |
| 1005 | 1004.29 | 0.85 | 1000 | 23 |
| 1010 | 1010.27 | 0.85 | 1001 | 23 |
| 1015 | 1016.24 | 0.85 | 1012 | 23 |
| 1020 | 1019.44 | 0.87 | 1016 | 23 |
| 3980 | 3980.43 | 0.93 | 3978 | 23 |
| 3985 | 3985.98 | 0.90 | 3980 | 23 |
| 3990 | 3990.01 | 0.94 | 3983 | 23 |
| 3995 | 3995.52 | 0.89 | 3988 | 23 |
| 4000 | 3998.89 | 0.99 | 3995 | 23 |
| Quantity | Symbol | Mean | U | Contribution (%) | |
|---|---|---|---|---|---|
| Angular speed [RPM] | 999.78 | 11.56 | 23 | 97.8 | |
| Torque [N.m] | 250.01 | 0.16 | 0.33 | 0.3 | |
| Electrical power [W] | P | 31.78 | 0.05 | 0.10 | 1.9 |
| Efficiency [%] | 82.36 | 0.96 | 1.90 | 100.0 |
| Quantity | Symbol | Mean | U | Contribution (%) | |
|---|---|---|---|---|---|
| Angular speed [RPM] | 1000.31 | 0.38 | 0.75 | 12.3 | |
| Torque [N.m] | 250.01 | 0.16 | 0.33 | 12.5 | |
| Electrical power [W] | P | 31.78 | 0.05 | 0.10 | 75.2 |
| Efficiency [%] | 82.36 | 0.15 | 0.30 | 100.0 |
| Quantity | Symbol | Mean | U | Contribution (%) | |
|---|---|---|---|---|---|
| Angular speed [RPM] | 3999.99 | 11.56 | 23 | 89.8 | |
| Torque [N.m] | 250.01 | 0.20 | 0.40 | 6.7 | |
| Electrical power [W] | P | 119.74 | 0.07 | 0.14 | 3.5 |
| Efficiency [%] | 87.46 | 0.27 | 0.53 | 100.0 |
| Quantity | Symbol | Mean | U | Contribution (%) | |
|---|---|---|---|---|---|
| Angular speed [RPM] | 3999.99 | 0.40 | 0.80 | 1.1 | |
| Torque [N.m] | 250.01 | 0.20 | 0.40 | 65.6 | |
| Electrical power [W] | P | 119.74 | 0.07 | 0.14 | 33.3 |
| Efficiency [%] | 87.46 | 0.09 | 0.17 | 100.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Machado, J.P.Z.; Thaler, G.; Pacheco, A.L.S.; Flesch, R.C.C. Impact of Angular Speed Calculation Methods from Encoder Measurements on the Test Uncertainty of Electric Motor Efficiency. Metrology 2024, 4, 164-180. https://doi.org/10.3390/metrology4020011
Machado JPZ, Thaler G, Pacheco ALS, Flesch RCC. Impact of Angular Speed Calculation Methods from Encoder Measurements on the Test Uncertainty of Electric Motor Efficiency. Metrology. 2024; 4(2):164-180. https://doi.org/10.3390/metrology4020011
Chicago/Turabian StyleMachado, João P. Z., Gabriel Thaler, Antonio L. S. Pacheco, and Rodolfo C. C. Flesch. 2024. "Impact of Angular Speed Calculation Methods from Encoder Measurements on the Test Uncertainty of Electric Motor Efficiency" Metrology 4, no. 2: 164-180. https://doi.org/10.3390/metrology4020011
APA StyleMachado, J. P. Z., Thaler, G., Pacheco, A. L. S., & Flesch, R. C. C. (2024). Impact of Angular Speed Calculation Methods from Encoder Measurements on the Test Uncertainty of Electric Motor Efficiency. Metrology, 4(2), 164-180. https://doi.org/10.3390/metrology4020011








